Reliability of assessing trunk motor control using position and force tracking and stabilization tasks

Abstract

System-based methods have been applied to assess trunk motor control in people with and without back pain, although the reliability of these methods has yet to be established. Therefore, the goal of this study was to quantify within- and between-day reliability of assessing trunk motor control using systems-based methods involving position and force tracking and stabilization tasks. Ten healthy subjects performed six tasks, involving tracking and stabilizing of trunk angular position in the sagittal plane, and trunk flexion and extension force. Tracking tasks involved following a one-dimensional, time-varying input signal displayed on a screen by changing trunk position (position tracking) or trunk force (force tracking). Stabilization tasks involved maintaining a constant trunk position (position stabilization) or constant trunk force (force stabilization) while a sagittal plane disturbance input was applied to the pelvis using a robotic platform. Time and frequency domain assessments of error (root mean square and H2 norm, respectively) were computed for each task on two separate days. Intra-class correlation coefficients (ICC) for error and coefficients of multiple correlations (CMC) for frequency response curves were used to quantify reliability of each task. Reliability for all tasks was excellent (between-day ICC ≥ 0.8 and CMC > 0.75, within-day CMC > 0.85). Therefore, position and force control tasks used for assessing trunk motor control can be deemed reliable.

Introduction

Impairments in trunk motor control have been associated with back pain. Studies have shown that individuals with back pain have poorer trunk proprioception (Brumagne et al., 2000, Brumagne et al., 2004, Newcomer et al., 2000), delayed trunk muscle reflex response (Radebold et al., 2000, Radebold et al., 2001, Reeves et al., 2005, Cholewicki et al., 2005), more trunk kinematic variability (Vogt et al., 2001), and poorer postural control (Radebold et al., 2001, Luoto et al., 1998) than healthy individuals. Despite growing evidence demonstrating motor control deficits with back pain, our understanding of how these impairments lead to or result from back pain is still underdeveloped. This lack of understanding is in part due to the complexity of the motor control system, and how parts of the system contribute to its overall behavior.

To resolve the complexity in motor control, some researchers have applied system-based methods to study human movement, including trunk motor control (Franklin, 2006, Moorhouse and Granata, 2007, Franklin et al., 2008, Reeves et al., 2009, Hodges et al., 2009, Zeinali-Davarani et al., 2008, Peterka, 2002, Maurer et al., 2005, Goodworth and Peterka, 2009(Bazrgari et al., 2011)). Typically in these studies, input disturbances are applied to the trunk/pelvis and the ability of the motor control system to reject these disturbances is assessed. For more details on system-based methods readers are referred to Jagacinski and Flach (2003). However, for system-based methods to be useful, they must be demonstrated to be reliable. To our knowledge, there is only one study assessing the reliability of system-based methods using position disturbances applied directly to the trunk during a force control task (Hendershot et al., 2012). The within-day reliability (ICCs 0.48–0.95) was consistently better than between-day reliability (0.19–0.72) for predicting system properties (i.e., trunk mass and stiffness, reflex gains and delays).

The goal of this study was to assess the within- and between-day reliability of a set of motor control tasks involving trunk angular position and force tracking, and trunk angular position and force stabilization. Throughout the paper, angular position will be referred to as position for concise presentation.

Methods

Subjects

Ten healthy subjects were recruited for the study (Table 1). Subjects were in good general health with no history of back pain lasting longer than 3 days or any neurological condition that could affect motor control. Subjects were instructed to wear their corrective lens if their eyesight was impaired. Michigan State University’s Institutional Review Board approved the research protocol and all subjects signed an informed consent form prior to testing. Subjects were tested on two days, separated by a minimum of 24 hours.

Table 1.

Characteristics of the subjects (standard deviations in parenthesis).

	Females	Males
Height [m]	1.66 (0.08)	1.78 (0.09)
Weight [kg]	60.7 (10.7)	80.5 (4.4)
Age [yrs]	29.7 (12.7)	35.5 (16.3)
N	6	4

Data collection

Fig 1 depicts the components for a generic trunk motor control system. The plant, denoted by P, is a function of the plant parameters, which characterizes physical aspects of the subject (e.g., anthropometrics, trunk stiffness, trunk damping, etc…), whereas, the collection of control processes, denoted by K, is a function of controller parameters which represents the control logic for ensuring stable trunk behavior. The reference input and the disturbance input signals are denoted by r(t) and d(t), respectively; while the output signal of the system is y(t). The error signal e(t) represents the difference between the reference input and the output signals of the system (i.e., e(t)=r(t)−y(t)). For tracking tasks, the control objective is an output y(t) that follows a time-varying reference input r(t) such that y(t) → r(t) so that e(t) → 0. For stabilization tasks, the control objective is an output y(t) that rejects disturbances d(t) and follows a constant reference input r(t)=c such that y(t) → r(t) so that e(t) → 0. In both cases, the objective of the control system in Fig 1 is to minimize error e(t) for either a time-varying reference r(t) or disturbance d(t) input.

Figure 1.

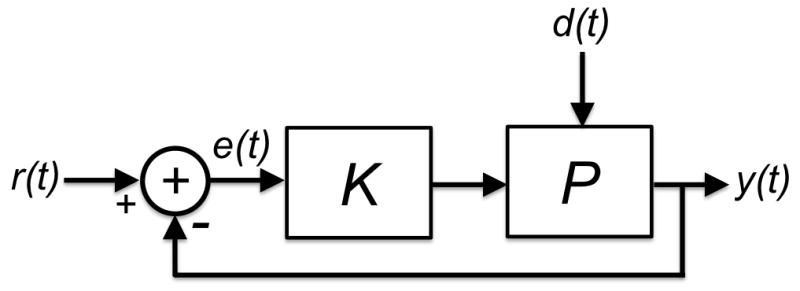
Components of the trunk motor control system.

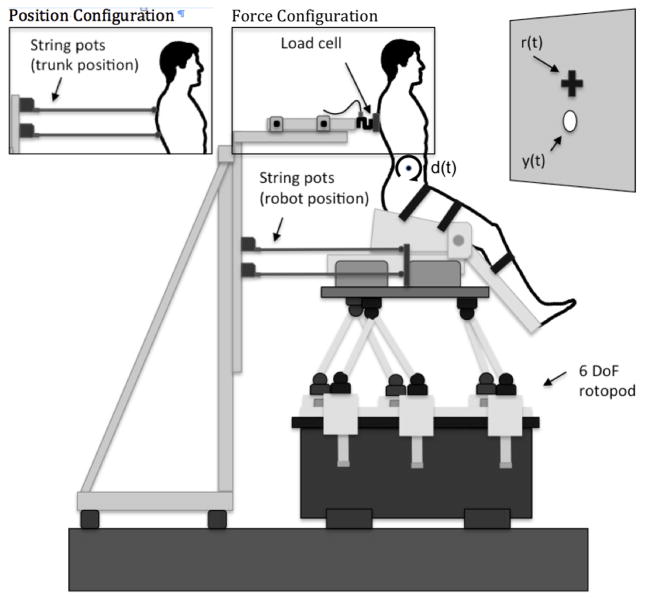
The trunk motor control system was assessed using one-dimensional position tracking and stabilization, and force tracking and stabilization tasks in the sagittal plane. Trunk position tracking and stabilization were performed using an experimental set-up that included a robotic platform (Mikrolar Rotopod R-3000, Hampton, NH), for applying disturbances to the pelvis, string potentiometers (Celesco SP2-50, Chatsworth, CA) to record the angular displacement of the robot and the trunk, and a monitor (Samsung SyncMaster SA650; height 27cm, width 47.5 cm) to display both reference input r(t) and the output y(t) signals. For trunk position stabilization, the monitor was turned off so that no feedback regarding the reference input r(t) and output y(t) was provided. Preliminary work indicated that reliability was improved when performing the position stabilization task without visual feedback (unpublished data). Trunk force tracking and stabilization were performed using an experimental set-up that included a robotic platform for applying disturbances to the pelvis, string potentiometers to record the position of the robot, a single axis load cell (Artech 20210, Riverside, CA) to record the force applied by the trunk, and a monitor to display both reference input r(t) and the output y(t) signals (Fig. 2). Trunk force tracking and stabilization were performed in both flexion and extension directions.

Figure 2.

Experimental set-up for trunk force tracking and stabilization task. Subjects were strapped to the robot seat such that the hip and knee angle were approximately 120 degrees. This posture was chosen to allow subjects to maintain natural lordosis in the lumbar spine. Subjects were encouraged to maintain an upright posture and to avoid “slouching” during the trials. Subjects performed all tasks with their arms crossed in front of their body. Visual feedback was provided from a monitor placed 1 meter in front of the subject with the center of the monitor at eye height. For tracking tasks, the reference input signal r(t) varied within a range equal to 60% of the full screen height, centered around the middle screen. This visual resolution was consistent for stabilization tasks and between days.

For the tracking task, subjects were instructed to keep either their trunk position (position tracking) or force (force tracking), denoted by y(t) on Fig. 2, on the time-varying reference signal r(t). While tracking, no pelvic disturbances were applied (d=0). Reference signals r(t) during the tracking task represented a pseudorandom square wave trajectory that varied in amplitude as well as hold period (see Table 2 for signal characteristics).

Table 2.

Characteristics of input signals for tracking tasks. The reference input signal r(t) for tracking tasks and disturbance input signal d(t) for stabilization tasks had a frequency range of 0.5–3.5 Hz and a duration of 30 seconds.

Task	d(t) Amplitude	r(t) Amplitude
Position tracking	0°	a ± 2° centered around 0°
Force tracking	0°	b ± 6 % centered around 10 %
Position stabilization	a ± 2° centered around 0°	0°
Force stabilization	a ± 2° centered around 0°	b 10 %

^a0° represents an upright trunk position. Position disturbances of the trunk were about L5 spinal level.

^bFor force tasks, the level of force exerted on the load cell, was set as a % of the maximum strength estimated from the literature (Descarreaux et al., 2007, McNeill et al., 1980, Cholewicki et al., 2011, Reeves et al., 2008) and expressed in Nm about L5 spinal level. For males, the maximum strength was 120 Nm in flexion and 220 Nm in extension. For females, the maximum strength was 80 Nm in flexion and 150 Nm in extension. The distance from L5 to the load cell was used to convert moment effort to force effort.

For the stabilization task, displacement disturbances d(t) were applied to the pelvis using a robotic platform. Subjects were instructed to keep either their trunk position upright (position stabilization) or trunk force constant (force stabilization) while disturbances d(t) were applied. Disturbance signals d(t) during stabilization tasks represented a pseudorandom sum-of-sine waves trajectory generated from a flat velocity power spectrum (see Table 2 for signal characteristics).

For each task, subjects performed 5 trials (two 15-sec. practice trials and three 30-sec. full length trials) with approximately 30-sec. of rest given between trials. The order in which the tasks were completed was consistent between days and between subjects (see Table 3 through 6 for order).

Table 3.

Mean (standard deviations in parenthesis) for RMS for the various trunk motor control tasks. P-values indicate the level of significance between performance measures on day 1 and day 2.

Task	RMS		P-value
	Day 1	Day 2
1. Position tracking	1.47 (0.09)	1.42 (0.08)	0.055
2. Position stabilization	0.70 (0.23)	0.68 (0.18)	0.630
3. Flexion force tracking	12.15 (2.53)	12.02 (2.55)	0.330
4. Flexion force stabilization	4.56 (0.94)	4.33 (0.96)	0.060
5. Extension force tracking	29.26 (6.91)	29.28 (6.91)	0.942
6. Extension force stabilization	7.33 (1.81)	6.62 (1.72)	0.066

Table 6.

Intra-class correlation coefficients (ICC (3, k)) quantifying the between-day reproducibility of performance measures in various trunk motor control tasks. The 95% confidence intervals and standard error of measurement (SEM (3,k) are presented in parenthesis.

Task	RMS	H2 norm
1. Position tracking	0.80 (CI 0.18–0.95, SEM 0.04)	0.80 (CI 0.18–0.95, SEM <0.01)
2. Position stabilization	0.87 (CI 0.49–0.97, SEM 0.07)	0.86 (CI 0.44–0.97, SEM <0.01)
3. Flexion force tracking	0.99 (CI 0.98–1.00, SEM 0.20)	0.99 (CI 0.97–1.00, SEM 0.10)
4. Flexion force stabilization	0.97 (CI 0.86–0.99, SEM 0.18)	0.98 (CI 0.91–0.99, SEM <0.01)
5. Extension force tracking	1.00 (CI 0.99–1.00, SEM 0.44)	1.00 (CI 0.98–1.00, SEM 0.50)
6. Extension force stabilization	0.90 (CI 0.59–0.98, SEM 0.56)	0.95 (CI 0.81–0.99, SEM 0.02)

Data analysis

The error signal e(t) represented the accuracy of trunk motor control. The root mean square (RMS) measure was used to quantify the size of the error signal in the time domain. Accuracy was also assessed in the frequency domain. Given the input r(t) for tracking and d(t) for stabilization, and the output y(t), the associated frequency response of the trunk motor control system was identified in a nonparametric way (Fig 3E–F, Fig 4E–F). The transfer function from the input to the output was estimated without any prior knowledge of the model (i.e., in Fig 1, P and K are unknown). The system identification technique was based on empirical transfer function estimation and periodograms (Ljung, 1999, Brillinger, 2001).

Figure 3.

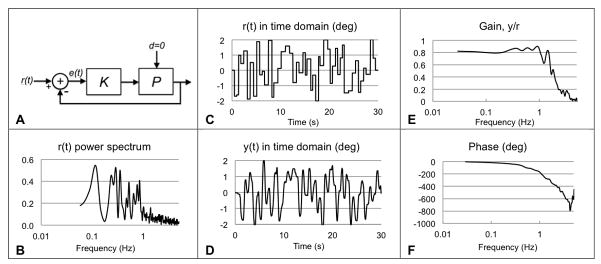
Frequency response analysis for position tracking. A: input-output model for the trunk motor control system with a time-varying position reference signal r(t). B: power spectrum of the reference input signal r(t) used during tracking. C: trajectory of the reference signal r(t) displayed on the screen. D: trunk output y(t). Time domain signals (C–D) are converted to the frequency domain (panels E–F). Gain (panel E) represents the control system’s ability to track the reference input signal r(t). If the control system tracks the input signal perfectly, the gain will be 1 across all frequencies. Phase angle θ (panel F) represents the lag in the system. Lag indicates that the control system responds to the reference input signal r(t) after some delay T where θ=360fT and f is frequency.

Figure 4.

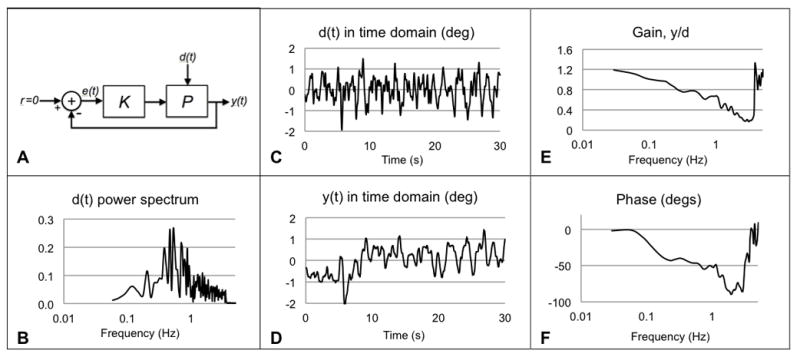
Frequency response analysis for position stabilization. A: the input-output model for the trunk motor control system with a time-varying disturbance signal d(t). B: power spectrum of the disturbance input signal d(t) used during the stabilization task. C: trajectory of the disturbance input signal d(t) applied by the robotic platform to the pelvis. D: trunk output y(t). Time domain signals (C–D) are converted to the frequency domain (panels E–F). Gain (panel E) represents the control system’s ability to reject the disturbance input signal d(t). If the control system rejects the disturbance perfectly, the gain will be 0 across all frequencies. Phase angle θ (panel F) represents the lag in the system. Lag indicates that the control system responds to the disturbance input signal d(t) after some delay T where θ = 360fT and f is frequency.

The estimated frequency characteristics of the transfer function from the input to the output were then used to assess error in the frequency domain. In the past, the performance measure H2 norm has been used to assess error of the trunk motor control system in the frequency domain (Xu et al., 2010). The H2 norm of a system is the asymptotic standard deviation of the output signal when the input is considered as a unit variance white noise. For the tracking task, the output frequency response power spectrum y(f) was divided by the input signal’s power spectrum r(f) (Fig 3B). The H2 norm of this frequency response was computed over the passband region, defined as the largest contiguous frequency band containing >3% of the maximum power. In this configuration, the H2 norm represents a measure of the output signal energy over the defined passband region. For the stabilization task, the H2 norm was computed based on the frequency response of output/input ratio y(f)/d(f) (Fig 4E), which gives a normalized measure of the output signal energy over the passband region. For both tracking and stabilization tasks, H2 norm was normalized by the length of the passband region.

Within- and between-day reliability of the frequency response curves were quantified with coefficient of multiple correlations (CMC) modified from Kadaba et al. (1989). In this modified measure, the frequency response curves in a three dimensional space (complex domain and frequency domain) replaced the role of time-series curves originally used in CMC by Kadaba et al. (1989). From these frequency response curves, several performance measures of the trunk control system can be obtained including H2 norm. Also, the between-day reliability for RMS and H2 norm was quantified with intra-class correlation coefficients (ICC(3,k)) (Portney and Watkins, 1993), which was then used to calculate the standard error of measurement

$$\mathit{SEM}(3,k)={SD}_{\mathit{pool}}\ast (\sqrt{1-\mathit{ICC}(3,k)})$$

where SD_pool represents the pooled standard deviation.

In addition, task improvements due to learning were assessed using a repeated-measures ANOVA that compared the mean values for RMS and H2 norm between days. For tests of significance, an alpha critical level was set at 0.05.

Results

The within- and between-day reliability of the frequency response curves for the various tasks were high (CMC > 0.75, see Table 5). Based on the criteria of Cicchetti (1994), the between-day reliability of performance measures, RMS and H2 norm, were also excellent (ICC(3,k) > 0.80, see Table 6). SEM was typically better for H2 norm than RMS, with the exception of extension force tracking (Table 6), which probably reflects the smaller standard deviation for the H2 norm (Table 4).

Table 5.

Coefficients of multiple correlations (CMC) quantifying the reproducibility of the frequency response curves for various trunk motor control tasks. The task number represents the order in which the tasks were completed. The coefficients are averaged across 10 subjects with 95% confidence intervals presented in parentheses.

Task	Within-day reliability	Between-days reliability
1. Position tracking	0.96 (0.94–0.98)	0.95 (0.93–0.97)
2. Position stabilization	0.86 (0.83–0.89)	0.76 (0.70–0.81)
3. Flexion force tracking	0.98 (0.97–0.99)	0.97 (0.95–0.98)
4. Flexion force stabilization	0.95 (0.93–0.96)	0.89 (0.85–0.93)
5. Extension force tracking	0.96 (0.93–0.99)	0.96 (0.93–0.99)
6. Extension force stabilization	0.91 (0.88–0.94)	0.83 (0.75–0.92)

Table 4.

Mean (standard deviations in parenthesis) for H2 norm for the various trunk motor control tasks. P-values indicate the level of significance between performance measures on day 1 and day 2.

Task	H2 norm		P-values
	Day 1	Day 2
1. Position tracking	35.95 (4.88)a	33.53 (4.52) a	0.081
2. Position stabilization	0.83 (0.92) a	0.58 (0.44) a	0.154
3. Flexion force tracking	2.48 (1.08)	2.45 (1.07)	0.645
4. Flexion force stabilization	0.092 (0.040)	0.081 (0.035)	*0.014
5. Extension force tracking	14.87 (7.12)	14.93 (6.97)	0.885
6. Extension force stabilization	0.21 (0.10)	0.18 (0.11)	0.092

^avalues were multiplied by 10³ so that they would fit in table.

^*indicates significant for an alpha critical level of p<0.05.

In terms of differences between days (Tables 3 and 4), only the performance in the flexion force stabilization task for the H2 norm measure was significantly different between days (p=0.014), indicating that subjects’ performance on day 2 was better than on day 1. Several other measures approached significance: position tracking (RMS p=0.055, H2 norm p=0.081), flexion force stabilization (RMS p=0.060), and extension force stabilization (RMS p=0.066, H2 norm p=0.092). These data suggest that learning over the two days may have occurred for some tasks.

Discussion

Results support the notion that trunk motor control can be reliably assessed with system-based methods involving position and force tracking and stabilization tasks. The excellent reliability found in the present study matches the results of previous studies investigating time domain error (RMS) in postural control during unstable seated balancing (Lariviere et al., 2013, Cholewicki et al., 2000), although others studies using similar methods reported reliability that ranged from poor to moderate (ICCs 0.22 – 0.65) (Lee and Granata, 2008, van Dieën et al., 2010). Differences in reliability between studies may be a result of differences in task difficulty, which appears to affect reliability (Lee and Granata, 2008), or possibly differences in the analysis used to assess reliability. The two studies that had higher reliability used Pearson’s correlation coefficients (Cholewicki et al., 2000, Lariviere et al., 2013), while the two studies with lower reliability used intra-class correlation coefficients (Lee and Granata, 2008, van Dieen et al., 2010). Given that our statistical analysis used the more conservative, intra-class correlation coefficients, it appears that our system-based methods for assessing trunk motor control may have higher reliability than unstable seated balancing. In terms of system-based methods, the set of tasks used to assess force stabilization in the present study also appear to be more reliable (between-day ICCs 0.83–0.98) than the force stabilization task used in the past (between-day ICCs 0.19–0.72) (Hendershot et al., 2012); however, it should be noted that different properties of the system were assessed in the two studies making a direct comparison not feasible.

At this stage, it is unclear how generalizable the results are to other populations; however, there is some evidence to suggest that reliability of trunk motor control may not be as high in individuals with LBP (Lariviere et al., 2013). This may be explained by the variability in pain, which fluctuates in individuals suffering LBP (Suri et al., 2011). Trunk motor control appears to be affected by pain (Hodges et al., 2003, Hodges et al., 2006, Radebold et al., 2000, Reeves et al., 2005), including postural control (Radebold et al., 2001). Therefore, one of the goals of this line of research is to develop tests that are sensitive to changes in trunk motor control that may result from pain reduction and disability following LBP treatment.

The order in which the tasks were completed was not randomized. The consistent order was chosen to minimize the time required for data collection and to minimize the effects of testing order on reliability. As shown in Table 3 and 4, some learning may have occurred in position tracking, flexion force stabilization, and extension force stabilization. However, it should be noted that the reliability for these tasks still remained excellent. The time of day for testing was not controlled for each subject and it is possible that reliability might have been additionally improved with more consistency in this variable. Finally, the relatively small sample size (n=10) may have resulted in a large confidence interval for ICCs for position tracking and stabilization (Table 6).

One concern with testing, which could influence reliability, is the amount of time required to complete the full set of tasks. Data collection took approximately 1–1.5 hours for the full set of position and force control tasks. Physical fatigue and mental weariness become an issue with a long duration testing session. On the other hand, learning becomes an issue if not enough practice is given. Subjects performed only two 15-sec. practice trials to reduce the risk of physical fatigue and a reduction in attentiveness, which seems sufficient to produce reliable assessment of trunk motor control. However, future studies should specifically address the learning effects in these motor control tasks.