Submillisecond mixing in a continuous-flow, microfluidic mixer utilizing mid-infrared hyperspectral imaging detection

Abstract

We report a continuous-flow, microfluidic mixer utilizing mid-infrared hyperspectral imaging detection, with an experimentally determined, submillisecond mixing time. The simple and robust mixer design has the microfluidic channels cut through a polymer spacer that is sandwiched between two IR transparent windows. The mixer hydrodynamically focuses the sample stream with two side flow channels, squeezing it into a thin jet and initiating mixing through diffusion and advection. The detection system generates a mid-infrared hyperspectral absorbance image of the microfluidic sample stream. Calibration of the hyperspectral image yields the mid-IR absorbance spectrum of the sample versus time. A mixing time of 269 μs was measured for a pD jump from 3.2 to above 4.5 in a D₂O sample solution of adenosine monophosphate (AMP), which acts as an infrared pD indicator. The mixer was further characterized by comparing experimental results with a simulation of the mixing of an H₂O sample stream with a D₂O sheath flow, showing good agreement between the two. The IR microfluidic mixer eliminates the need for fluorescence labeling of proteins with bulky, interfering dyes, because it uses the intrinsic IR absorbance of the molecules of interest, and the structural specificity of IR spectroscopy to follow specific chemical changes such as the protonation state of AMP.

Introduction

Microfluidic mixing has developed into a useful tool for studying fast kinetics of biomolecular reactions on the microsecond to millisecond timescale.^1–7 As the field has evolved, the need for simple, fast, and cheap mixers with more robust and sensitive detection techniques has grown. Fluorescence spectroscopy is the most common detection method in microfluidic mixing systems because of its simplicity and its single molecule detection sensitivity.^{2, 6–15} Molecules that do not contain an intrinsic fluorophore (such as tryptophan in proteins), however, require labeling with extrinsic dyes for fluorescence detection. The introduction of these probes into various regions of the molecule risks perturbing both the structure and dynamics being studied, and in some instances it is not possible to probe the specific structural dynamics of interest.^{16, 17, 30, 31} In contrast, infrared spectroscopy has the ability to follow intrinsic functional groups that serve as “labels” in the infrared region, such as backbone or side chain carbonyl and amide groups, thus providing a direct and broadly applicable detection method for microfluidic mixers. Most molecules exhibit absorbance in the mid-IR region and the inherent chemical specificity of infrared spectroscopy is useful for probing molecular structure, such as secondary structure of proteins.^18,19 Infrared spectroscopy has been implemented as a detection method in microfluidic mixers in a variety of forms, including FTIR,^{3, 4, 7, 20–23} attenuated total reflectance,^24–26 and IR absorbance using a broadband synchrotron source.¹ Nevertheless, the modest time-resolution and sensitivity of these approaches has limited the application of infrared spectroscopy as a probe of reaction kinetics in microfluidic mixers.

One of the most important characteristics of any microfluidic system is the mixing time, because it sets the lower limit on the timescale of events that can be observed. Mixing times on the microsecond timescale are crucial for following the kinetics of biomolecular reactions.²⁷ Continuous, laminar-flow fluorescence mixers have demonstrated experimental mixing times on the order of 50 μs,^{2, 10, 15} with an estimated theoretical limit as low as 1 μs.²⁸ These fast mixing times are achieved by hydrodynamically focusing the sample stream to a very small width (about 1 μm) using the surrounding sheath stream. Because the flow is laminar, the streams do not physically mix; instead, mixing occurs by diffusion of a reactive species from the sheath stream into the sample stream, and depending on the design of the mixer, by chaotic advection.¹⁵ In many mixer designs, the mixing time is limited by the diffusion time, which depends on the width of the sample stream. Focusing the sample stream as tightly as possible (to minimize the diffusion length) minimizes the mixing time. A practical limit to the size of the sample stream, however, is set by the spatial resolution and sensitivity of the detection method. The spatial resolution of IR detection methods represents an inherent disadvantage of this approach, because it is determined by the diffraction limit of the 3–10 μm mid-IR probe light, typically several microns. For this reason, an IR mixer must use a wider sample stream than a comparable fluorescence mixer would use, resulting in a longer mixing time. The theoretical limit of such an IR mixer was previously estimated to be 400 μs based on simulations.⁴ But the shortest experimentally demonstrated mixing time of an IR mixer is greater than a millisecond, and most fast IR mixers do not record spectra in timescales under the millisecond threshold.^{1, 3, 4, 7, 20–22, 24–26, 29–31} Clearly there is a need to develop a fast IR mixer than can access the microsecond time regime.

Here, we report a continuous, laminar flow, microfluidic mixing system that achieves a mixing time of a few hundred microseconds, using mid-IR hyperspectral imaging as the detection method. The mixer is constructed using a “sandwich” technique, wherein the microfluidic channels are laser machined through a polymer spacer that is sandwiched between two IR transparent windows. The flowing sample stream is imaged using a mid-IR quantum cascade laser (QCL) source and a mercury cadmium telluride (MCT) 128×128 focal plane array imaging IR detector.^24,32,33 The kHz frame rate of the array detector enables rapid signal averaging of spectral images acquired at each probe wavelength as the laser is scanned across the spectral region of interest. This approach produces a hyperspectral image that contains the infrared absorbance spectrum at each pixel along the flowing sample stream. Using a distance to time calibration, the spatial image is converted to time, producing the time dependence of the infrared absorbance following rapid diffusional mixing. We demonstrate the characteristics and capabilities of this system with mixing experiments and computer simulations, including a fast pH jump (since the experiment is conducted in D₂O with deuterated buffer, it is actually a “pD jump”) detected using an infrared “pD indicator,” adenosine monophosphate (AMP), and an H₂O/D₂O mixing experiment that follows the diffusion of water. The latter experiment allowed for direct comparison of the mixer performance to predictions from a simulation. The pD jump experiments demonstrate a mixing time of 269 μs by recording the time dependence of the IR spectrum of the AMP pD indicator.

Experimental

Mixer Design and Fabrication

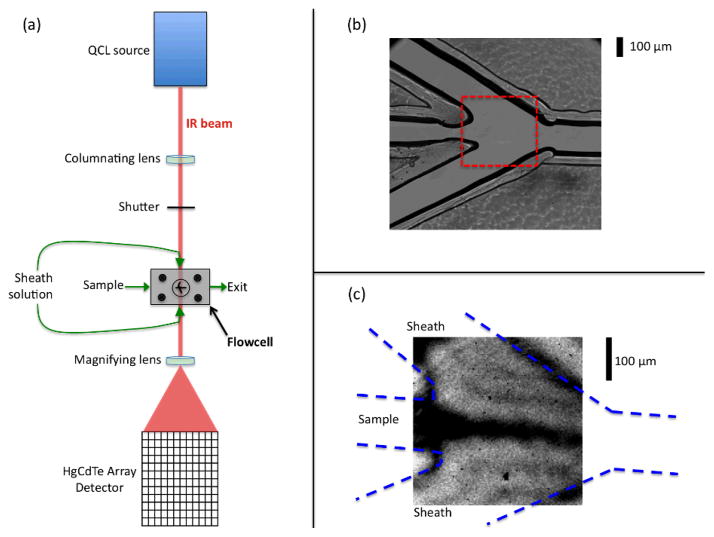
The key component of the mixer is a 75 μm thick polychloro-trifluoroethylene spacer (PCTFE spacer; CS Hyde, Lake Villa, IL) through which the microfluidic channels have been cut. The channels are cut with a CO₂ laser cutter (Speedy300 Laser Engraver, Trotec, Canton, MI) at the Invention Studio of the Georgia Institute of Technology (Atlanta, GA), according to the design shown in Fig. 1b. The mixing region is defined by the point where the central sample channel meets the two side channels at a 30° angle. The side (sheath) flow hydrodynamically focuses the sample into a thin jet (Fig. 1c). The flowing streams exit through a single channel, on the right side of Fig 1b. Each channel is 110–150 μm wide and 75 μm deep (set by the spacer thickness), with the side channels being slightly wider than the sample channel. The spacer is sandwiched between two IR transparent windows, each made of a different material (one CaF₂ and the other ZnSe) to minimize etalon effects in the cell. The windows are held in place by a custom-made stainless steel housing that also provides the plumbing connections. The stainless steel housing has three inlets and one outlet that fit PEEK tubing connections (Idex, Oak Harbor, WA) used for fluid delivery. Sample and sheath solutions are flowed using syringe pumps (KD Scientific, Holliston, MA). Typical flow rates range from 0.5–2.0 μL min⁻¹ for the sample, and 15–20 μL min⁻¹ for the sheath solution. It is important to note that this setup is easily altered to incorporate other mixer designs, such as changes to the channel configuration and spacer thicknesses, by simply switching out polymer spacers.

Figure 1.

Experimental design: (a) Schematic of the optical setup of the infrared flow system. (b) A magnified visible image of the mixer showing the three inlet channels coming together at the mixing region, and the exit channel. (c) A mid-IR transmission image of the portion of the cell indicated by the dashed box in part (b), which is the region that is routinely analyzed during flow experiments. This image was acquired with H₂O flowing as the sample and D₂O flowing as the sheath solution. The QCL is tuned to 1636 cm⁻¹, a frequency that is strongly absorbed by H₂O (the dark regions correspond to low transmittance).

Optical Setup

An IR imaging system was specifically designed and optimized to probe the change in absorbance in the microfluidics sample stream. The optical setup (Figure 1a) uses a quantum cascade laser (QCL; Daylight Solutions, San Diego, CA) as the IR source, operating in continuous wave mode with a bandwidth of 0.1 cm⁻¹. A 500 mm focal length CaF₂ lens collimates the laser beam, which then passes through a shutter for acquiring light and dark (background) images. A dark image is subtracted from those with the laser unblocked to remove the dark noise of the detector. The laser illuminates the mixer uniformly throughout the imaging region. The transmitted laser beam is magnified by a short focal length CaF₂ lens (25.4 mm) and imaged onto an Hg:Cd:Te focal plane array (FPA) detector. All components of the optical setup are housed in an airtight box that is continuously purged with dry air to minimize interference from water vapor absorbance.²²

The FPA detector contains a grid of 128 × 128 pixels that is used to acquire an image of the transmitted IR intensity in the range from 2–12 μm. Typical detector integration times are short (~40 μs) to minimize dark noise and noise from low frequency mechanical vibrations. The detector gain, bias and DC offset are adjusted to use the full dynamic range of the detector. The laser is scanned in 1 cm⁻¹ steps and 1000 images are acquired at each probe frequency at the full 1 kHz FPA frame rate, then signal averaged to decrease the noise level.

A hyperspectral absorbance image is produced by acquiring both a sample and a background image at each probe wavelength and then computing absorbance as the negative log of the ratio of sample to background. Sample and background images are acquired with and without the sample jet present, simply by turning the sample flow on and off, respectively. Since it takes some time to stabilize the sample jet, sample images are acquired at each probe wavelength first, and then the sample flow is turned off, the cell is equilibrated and the background images are acquired by repeating the probe wavelength scan. This procedure produces a hyperspectral absorbance image in which each pixel contains the absorbance spectrum over the full range scanned.

Mixer Calibration

The linear flow velocity of the sample was calibrated using a procedure previously developed by our group.⁹ Briefly, the method employs a confocal fluorescence microscope (Olympus IX81; Center Valley, PA) to image a flowing stream of 40 nm Europium (Eu) carboxylate-modified fluorescent nanospheres (Life Technologies, Grand Island, NY). A 375 nm laser focused to a sharp line orthogonal to the flow direction was positioned to excite the nanospheres at a single point along the flow. The beads are transiently excited as they pass through the focused laser line, and emit at 610 nm. As the beads flow away from the excitation beam, the emission decays with a known lifetime of 548 μs.⁹ The linear flow velocity is determined by measuring the flow distance over which the emission decays. This flow velocity is a characteristic of the flow cell and is transferrable to the IR experiments.

The linear flow velocity of the sample is not constant throughout the mixer, because it is initially significantly slower than that of the sheath flow, but it is accelerated through the mixing region. Therefore, the flow calibration was obtained at multiple points along the flow, by varying the position of the 375 nm excitation laser line. Initially, the mixer was calibrated with the laser positioned at the start of the exit channel (Fig. 1b), a position where the sample channel is already focused to its final width. The mixer was calibrated at side flow rates of 15 – 25 μL min⁻¹ in 1 μL min⁻¹ intervals, while the sample flow was kept constant. The calibration procedure was repeated for various positions of the line-focused excitation laser, from the point where the three channels of the mixer initially merge (distance = 0 μm) to approximately the exit channel (distance = 320 μm) in 10 μm intervals. The side flow rates were kept constant at 20 μL min⁻¹ as the laser position was varied. This procedure established the positional dependence of the flow velocity through the usable region of the mixer.

AMP pD jump

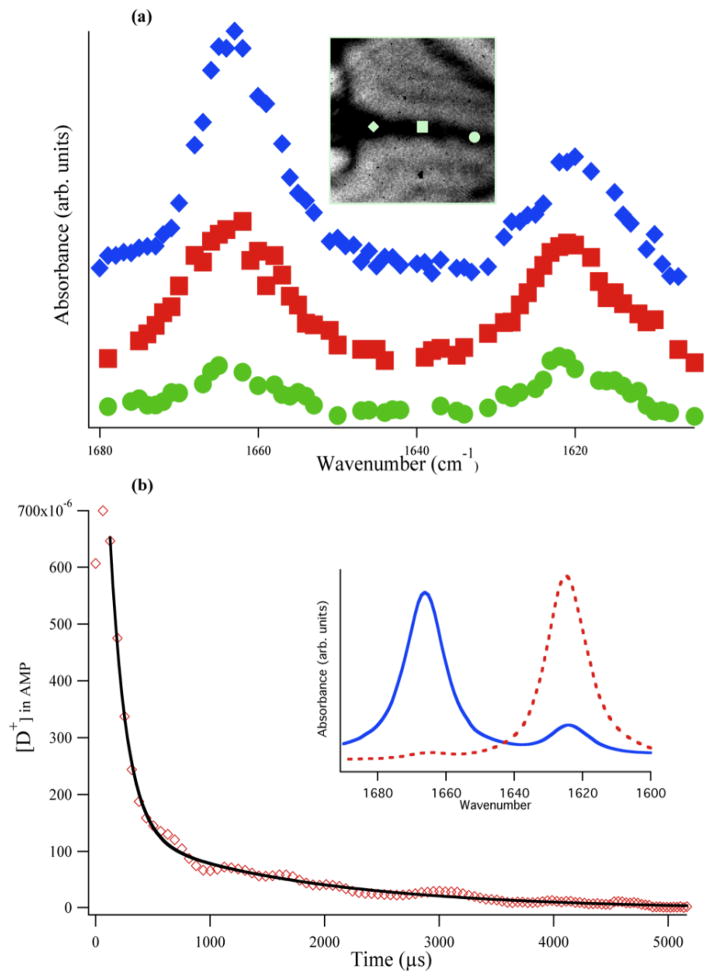
Adenosine monophosphate (AMP) was purchased from Sigma-Aldrich (St. Louis, MO) and dissolved in D₂O (Cambridge Isotopes, Tewksbury, MA) at a concentration of 25 mg/mL for both equilibrium FTIR and IR mixing experiments. The pD of the AMP solution was adjusted with DCl solution (Sigma-Aldrich). Equilibrium FTIR data were acquired on a Varian 660-IR spectrometer. For mixing experiments, the pD of the AMP solution was adjusted to a starting point of 3.2. A sheath solution of 250 mM phosphate buffer at pD 6.9 was used to induce a pD jump. Data were collected with the AMP sample flowing at 0.60 μL min⁻¹ and each side flowing at 17 μL min⁻¹. Spectra were collected from 1600–1680 cm⁻¹, with detailed pD analysis occurring at 1624 and 1666 cm⁻¹, corresponding to intense IR absorbance peaks of AMP (Figure 3 inset).

Figure 3.

AMP pD jump experiment (pD 3.2 AMP sample solution and pD 6.9 250 mM phosphate sheath flow): (a) IR spectra of AMP at three different locations along the sample jet for a sample flow rate of 13 μL/min (offset vertically for clarity). The IR image of the jet is shown in the inset with the approximate location of the three spectral traces indicated by the respective symbols. In the pre-focusing region (diamond), little mixing has occurred because the 1666 cm⁻¹ peak remains dominant. At the downstream positions, the relative peak amplitudes change, indicating the rise in pD. The overall absorbance also decreases, due to diffusion of AMP out of the sample stream. (b) AMP pD jump plotted as [D⁺] versus time (diamonds; average of 20 separate jumps). The pre-focused region (first three points) represents the dead time (127 ± 6 μs) of the mixer, with very little mixing occurring in this region. Efficient mixing occurs in the focused region, evident by the sharp decrease in [D⁺], which is fit to a biexponential decay (see text). Inset: equilibrium FTIR spectra of AMP at pD 3.2 (solid trace) and at pD 5.8 (dashed trace).

Theoretical Modeling

To assess the flow dynamics and mixing behavior, COMSOL Multiphysics Version 4.3a (Comsol Inc., Stockholm, Sweden) was used to simulate the mixer. A laminar flow, stationary study using transport of dilute species was carried out in order to simulate how a sample would mix with the sheath solution. Within the mixer, the flow velocity, u, is dictated by the incompressible Navier-Stokes equation:

$$\rho \left(u·\nabla \right)u=\nabla ·\left[-pI+\mu \left(\nabla u+{(\nabla u)}^T\right)\right]+F$$ (1)

where ρ is the fluid density, u is the velocity field, p is the pressure, μ is the dynamic viscosity, and F is a volume force, such as gravity. The local concentration of the reactant was the main result followed in the simulations and is governed by Fick’s law, which is described by the diffusion and convection equation:

$$\nabla ·\left(-D\nabla c\right)+u·\nabla c=R$$ (2)

where D is the diffusion coefficient of the reactant, c is the concentration of the reactant, and R is the consumption rate of the reactant. Simulations were carried out using the diffusion coefficient of water molecules, D = 2.2 × 10⁻⁹ m²/s,³⁴ for direct comparison with the H₂O/D₂O mixing experiments. Other parameters used in simulation can be found in the Supplementary Information.

Results and Discussion

Mixer calibration

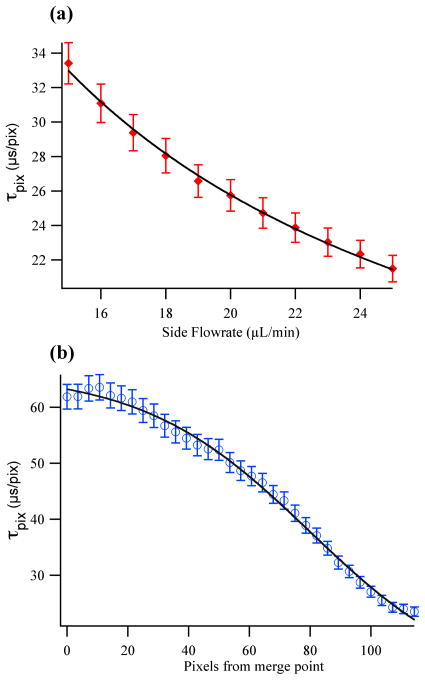
The linear flow velocity of the mixer was calibrated using a confocal fluorescence microscope to measure the fluorescence decay of Eu nanospheres, as previously described.⁹ This calibration procedure yields a value for the time per pixel (τ_pix) along the sample flow that can be transferred to the IR imaging system using the relative spatial resolutions of the two systems. A conversion factor of 5.5 was determined from the ratio of the spatial resolution of the fluorescence microscope (0.50 ± 0.01 μm/pixel) to that of the IR microscope (2.8 ± 0.1 μm/pixel).

Figure 2a plots the time per pixel, τ_pix, versus sheath flow rates, measured at a position near the exit channel, for which the sample stream is focused to its final width. The data fit well to an inverse dependence on the volumetric flow rate (v), τ_pix ∞ 1/v, as expected. The time per pixel values range from about 21 to 33 μs pixel⁻¹ for the highest and lowest side flow rates, respectively. Varying the flow rate across this range provides a means to control the time resolution of the detection system, the full time window accessible with the field of view observed by the array detector, and indirectly, the mixing time since the width of the jet is sensitive to the sheath flow rate (see below).

Figure 2.

IR microfluidic mixer calibration data: (a) Time per pixel, τ_pix versus side flow rate, v for the range typically used in mixing experiments (15–25 μL min⁻¹). The data fit well (line) to an inverse dependence on the flow rate, τ_pix μ 1/v. (b) τ_pix versus position downstream from the merge point at a fixed side flow rate of 20 μL min⁻¹. The experimental data are fit (line) to equation 3.

The calibration of the linear flow velocity must also account for the acceleration of the sample stream by the sheath solution. Assuming incompressible flow, when the side channels focus the sample into a small jet, the sample stretches and its velocity increases; therefore, the amount of time represented per pixel decreases.³⁵ The region where the jet is being focused by the side flows, denoted here as the “pre-focused region”, is characterized by slower flow. Since the flow velocity varies along the sample jet, we repeated the time per pixel calibration as a function of position through the entire pre-focused region as shown in Figure 2b. The position dependence of the flow velocity was mapped by moving the excitation laser line a total of 320 μm in intervals of 10 μm, from the initial merge point of the three channels (pre-focused region) to the exit channel (focused region) at a constant side flow rate of 20 μL min⁻¹. The observed behavior is sigmoidal as expected for the transition from the pre-focused to the focused region, hence the data were fit to a sigmoid function in the form:

$${\mathrm{\tau }}_{\mathit{pix}}={\mathrm{\tau }}_{max}+\frac{{\mathrm{\tau }}_{min}}{1+exp\left(x_{\mathit{half}}-x/\mathit{rate}\right)}$$ (3)

To apply this calibration to all side flow rates from 15 – 25 μL min⁻¹, only the τ_min value in Equation 3 is altered (τ_max is set by the sample flow rate, which was kept constant). The τ_min values for this range of flow rates was determined by the first calibration in the focused flow (Fig. 2a). Taken together, these calibrations enable the conversion of a spatial image to a temporal one in a straightforward manner, with numerical integration of the sigmoid fit adjusted for the τ_min value that corresponds to the experimental side flow rate. Finally, when converting from distance to time in the flow experiments described below, the error from the calibration fits was propagated through the calculation of the mixing times, so that the reported values account for this uncertainty.

AMP pD jump

The mixing time of the IR microfluidic system was characterized by measuring the time to achieve a pD jump of about 3 units, using AMP as an infrared pD indicator. Since protons or deuterons diffuse more rapidly than most molecules, a pD jump should represent a lower limit of the mixing time for the specific configuration of the system (flow rates and jet size). In addition, since many biomolecular reactions can be initiated by a change in pD (such as an enzyme reaction, or protein folding), these experiments demonstrate the feasibility of this approach. The mixing is observed as an exponential decay of the deuteron concentration in the focused region and therefore the total mixing time is reported as the 1/e time of the fit, plus the “dead time” represented by the pre-focused region (see below).

AMP is an ideal infrared pD indicator, because it has an infrared spectrum that is strongly dependent on pD in a biologically relevant range. It has two strong and clearly resolved IR absorbance bands at 1666 and 1624 cm⁻¹, corresponding to the protonated and deprotonated states of the adenosine ring, respectively.³⁶ The pK_a for this transition occurs at 3.8 (or 3.4 in pD units, as applicable in this study).³⁷ The equilibrium FTIR spectra (inset, Fig. 3b) show the pD dependence of these modes. The 1624 cm⁻¹ mode has previously been assigned to the ring C=N stretching vibration of neutral adenosine.³⁶ At low pD, this band shifts to higher frequency as expected for protonation of the ring structure.³⁶ Thus, the relative intensity of these two bands is an indicator of the solution pD; for the protonated (or deuterated) adenosine ring structure below pD 3.4, the absorbance at 1666 cm⁻¹ dominates, but as the pD shifts up towards neutral, the 1624 cm⁻¹ peak instead becomes dominant. A titration curve was created by measuring the FTIR spectrum of AMP in D₂O as a function of pD (Fig. S1) and determining the ratio of the integrated absorbance of the 1666 and 1624 cm⁻¹ peaks (Figure S3). Using a ratiometric method removes the dependence of the absorbance on the total concentration of AMP, which is necessary because the AMP concentration is continuously changing in a mixing experiment, due to diffusion of AMP out of the sample stream. The normalized absorbance data are related to the pD and pK_a by equation (4):

$$\frac{A_{1666c{m}^{-1}}}{A_{1624c{m}^{-1}}}=\frac{[D^{+}]+c_1{K}_a}{c_2[D^{+}]+c_3{K}_a}$$ (4)

A pD jump is generated by flowing an AMP solution initially at pD 3.2 through a sheath buffer at neutral pD. The buffering capacity of the sheath solution (250 mM phosphate) is more than sufficient to raise the small volume of the AMP sample stream to a final pD that equals the starting sheath buffer pD. The AMP is dissolved in pure D₂O (no buffer), to minimize the intrinsic buffering capacity of the sample. The rate of “deprotonation” (deuteron dissociation) of the acid form of AMP is fast compared to the rate of the pD jump (set by the diffusion-limited equilibration of the deuteron concentration in the sample stream with the surrounding sheath buffer, see below). Therefore, the lifetime of the AMP IR absorbance change is attributed solely to the mixing time of the system (the pD jump) rather than the “deprotonation” reaction itself.

Figure 3a shows the AMP IR absorbance spectra at three separate pixels located in the sample jet at various distances downstream from the merge point of the sample and side flows. A slow side flow rate of 13 μL min⁻¹ was used for this acquisition to test the mixer performance at long times, resulting in a relatively slow pD jump. The top spectrum (diamonds) is from a pixel located in the pre-focused region at roughly 1 ms in time after the merge point of the three channels,; since the peak at 1666 cm⁻¹ is still dominant, not much mixing of the sample and sheath has occurred and the pD remains close to its starting point of 3.2. The middle spectrum (squares) is located in the focused region, over 3 ms from the merge point, at a pixel where mixing has started to occur. Mixing is evident from the shift in relative intensity of the two peaks, with the nearly equal intensity of the 1666 and 1624 cm⁻¹ peaks indicating a jump past the pK_a of AMP, to an approximate pD of 4. Lastly, the bottom spectrum (circles) corresponds to a time of over 5 ms from the merge point. The concentration of AMP has been diluted by diffusion of AMP out of the sample stream, causing the overall absorbance to decrease. Nevertheless, it is clear that the 1624 cm⁻¹ peak is now the largest peak and the pD jump has progressed closer to neutral pD.

The limit of the mixing time was measured by generating a pD jump using a fast sheath flow rate of 17 μL/min, as shown in Figure 3b (faster sheath flow rates are possible, but the small jet size produced makes it difficult to detect the AMP absorbance). The pD of the sample solution as a function of time is determined using a multi-step analysis of the data. After using Beer’s law to determine the absorbance at each pixel in the IR image, an image line profile analysis is used to obtain the absorbance at each pixel along the sample jet. This analysis selects the sample path in the image plot, to follow the z-axis values (absorbance) versus either the x- or y-axis values (distance in pixels along the jet). This analysis is repeated for each probe frequency. Next, the ratio of the absorbance profiles at 1666 and 1624 cm⁻¹ is computed and then converted to pD using the FTIR calibration. The outcome is the pD profile versus pixel number along the jet. Finally, pixel number is converted to time using the calibration described above, yielding the pD or [D⁺] versus time as shown in Fig. 3b.

There are two key features evident in the time dependence of [D⁺] for the pD jump shown in Fig. 3b. First, there is the region immediately after the three inlet channels meet at the merge point (time = 0), where the sheath solutions are acting to hydrodynamically focus the sample to a thin jet (pre-focused region). The sample is squeezed from its starting width of approximately 110 μm to less than 20 μm within the first few time points. As is evident in Fig. 3b, the deuteron concentration in the AMP sample stays relatively constant for the first 127 ± 6 μs, indicating that little mixing occurs in the pre-focused region. Since these early time points are measured at the center of the pre-focused sample flow, they do not account for any mixing that occurs at the sample/sheath flow interface. Therefore, these early time points represent the “dead-time” of the mixer. After the pre-focused region, the deuteron concentration decays rapidly; this decay was fit with a biexponential function with lifetimes of 142 ± 16 μs (90%) and 1.6 ± 0.1 ms (10%). The primary (142 μs) phase is due to the dominance of the advection process at early times, as the sample and sheath flows come together, whereas the slower small amplitude phase is dominated by diffusion of deuterons out of the focused sample stream. Since 90% of the pD jump occurs in the first phase, we use its lifetime of 142 μs to characterize the mixing time. The pD is raised from its initial value of 3.2 to over 4.5 within this fast phase of the jump. The dead-time of 127 μs was added to the fast phase decay time to yield an overall mixing time of 269 ± 16 μs. The total error reported here originates from the calibrations of the time per pixel and the deuteron concentration, and is propagated through to the time domain. To our knowledge, this experimental mixing time is the shortest reported for any microfluidic mixer that utilizes IR spectroscopy to probe the reaction progress.

H₂O/D₂O mixing and simulation

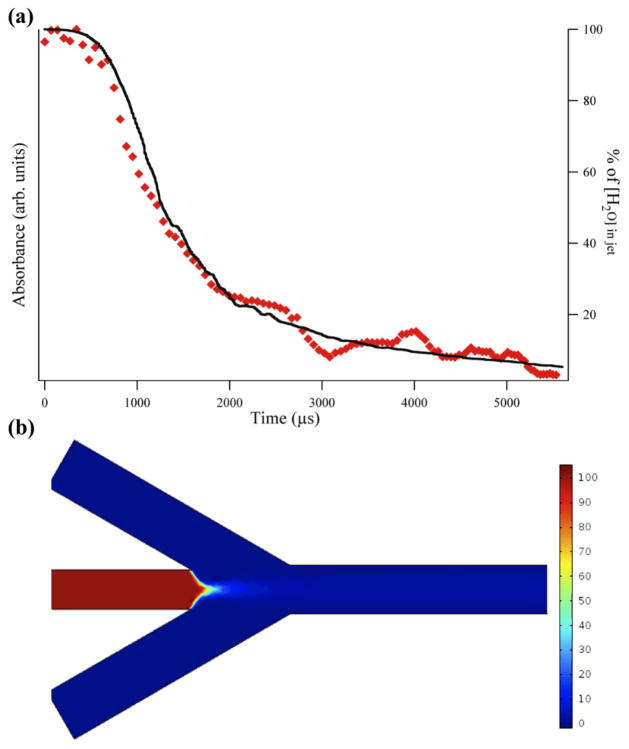
We also characterized the mixing of an H₂O sample into a D₂O sheath flow because it represents a simple mixing process in the absence of any chemical reaction. This mixing experiment serves as a model system for comparing experimental results with the predictions of a simulation using COMSOL Multiphysics software to model the mixing. The molecular diffusion of water can be modeled in a straightforward way using Fick’s law, whereas proton (or deuteron) diffusion is a more complex process that is still of research interest.³⁸ The H₂O/D₂O mixing experiment used a strongly absorbing H₂O sample flowed through a D₂O sheath solution at 0.60 and 17 μL min⁻¹, respectively. Since the water IR absorbance is strongly shifted by isotope substitution, a single probe frequency at 1636 cm⁻¹ was sufficient to fully characterize the H₂O/D₂O mixing, even though the IR spectrum is broad and featureless in this region.

The mixing of the H₂O sample stream with the D₂O sheath is observed as an exponential decay of the H₂O IR absorbance as shown in Figure 4a (diamonds, left axis). The COMSOL simulation of the mixing is overlaid on the experimental points (line, right axis). The simulation predicts the concentration of H₂O in the sample stream as a function of time, where the concentration is initially 100% before mixing with the side channels, but then decreases through the processes of diffusion and advection. The COMSOL simulation used the actual geometry and dimensions of the mixer (Figure 4b) as well as the flow velocities calculated from the volumetric flow rates. The diffusion coefficient of water in water is 2.2 × 10⁻⁹ m² s⁻¹ (all other relevant simulation parameters can be found in the Supplementary Information). The simulation closely matches the experimentally observed mixing process. The same dead-time of about 550 μs is observed for the pre-focused region in both the experiment and simulation. The exponential decay of the H₂O concentration in the focused region has a lifetime of 934 ± 46 μs for the experiment, and 908 ± 28 μs for the simulation, again in good agreement. Combining the dead-time and exponential decay time yields a total mixing time of approximately 1.5 ms. This mixing time is much slower than the AMP pD jump, in part due to the faster diffusion of deuterons compared to water, but also because the pD jump experiment used a higher sheath flow rate, resulting in stronger advective mixing and a tighter focus of the sample stream hence a shorter diffusion distance.

Figure 4.

Comparison of experimental results and simulation of H₂O/D₂O mixing: (a) IR absorbance decay of H₂O sample mixing with D₂O sheath solution monitored at 1636 cm⁻¹ (diamonds, left axis). The data are the average of four separate acquisitions. The solid line (right axis) is the COMSOL simulation of the mixing using mixer dimensions, flow rates, and diffusion coefficients that mirror the experimental conditions. (b) Surface plot from the COMSOL simulation showing the concentration of the H₂O sample. The H₂O is hydrodynamically focused into a jet and mixes by advection and diffusion with the D₂O sheath solution, evident by the drop in concentration of the H₂O in the sample stream.

A rapid decrease in the H₂O concentration in the sample jet is observed in both the experiment and simulation. The timescale for this decrease is too short to be simply a consequence of diffusional mass transport and therefore must have a large contribution from advective forces acting on the jet.³⁵ This effect can be explained further with the advection-diffusion equation that describes the evolution of the concentration of a solute, c, as:

$${\partial }_{t}c=-\mathrm{v}·\nabla c+D{\nabla }^{2}c$$ (5)

where the solute with molecular diffusion constant is moving in a solvent with velocity, v. After this equation is made dimensionless, it is evident that for a fluid flow with a characteristic length of L and a velocity, V, the molecular diffusion term of equation (5), D∇²c, is dominant for systems with a small Peclet number (Pe < 1) where Pe = VL/D. On the other hand, when Pe ≫ 1, the advection term, −v·∇c, becomes dominant. When applied to our mixer, even when the three channels initially merge and the velocity is at its lowest, the Peclet number is still much greater than one, putting it well into the advection-dominant regime.³⁵

The advection process has important consequences for microfluidic mixing experiments with proteins. Conceptually, these experiments rely on slow diffusion of a protein out of the sample stream compared to diffusion of a reacting substrate into it, such that the protein concentration in the sample stream remains high. In real mixers, however, advection complicates this process because it reduces the protein concentration in the sample stream. The concentration decreases more quickly as the sheath flow rate is increased and advection becomes stronger (Figure S3). Therefore, a balance must be achieved between a high sheath flow rate, in order to decrease the mixing time, and a flow rate that is slow enough to maintain a sufficient concentration of the sample in the jet during the entire time course of the reaction. The latter depends on the initial concentration and the detection limit of protein signal being monitored. This balance was the basis of choosing a sheath flow rate of 17 μL min⁻¹ for the H₂O/D₂O mixing experiment, rather than 25 μL min⁻¹, even though in principle a faster mixing time is obtainable. Clearly, the ultimate limit will be determined by the sensitivity of the IR absorbance detection method, which has yet to be fully optimized.

Conclusions

We have developed a continuous-flow, microfluidic mixing system utilizing mid-IR hyperspectral absorbance imaging to monitor reaction progress, with a sub-millisecond mixing time. The mixer uses a simple sandwich configuration of a laser machined polymer spacer in between two IR transparent windows to create a laminar flow, hydrodynamically focused, closed channel mixer. The mixer and infrared imaging system were experimentally calibrated in order to establish a time per pixel based on flow rates and position within the mixer. The mixing time and feasibility of the mixer for studying biomolecular reactions were then established through an AMP pD jump experiment. An acidic AMP sample was mixed with a neutral phosphate buffer to induce a pD jump through the pK_a value of AMP, while following two IR absorbance peaks in the 1600 cm⁻¹ region corresponding to the two protonation states. Lastly, an H₂O/D₂O mixing experiment was used to follow the absorption decay of the water at 1636 cm⁻¹ and to model that decay with computational simulation. The simulation matched well with the experimentally obtained data.

The reported mixing time of 269 ± 16 μs, is the fastest experimental mixing time to date of any microfluidic mixing system that uses IR spectroscopy for detection of the reaction progress. Using IR spectroscopy alleviates any need for fluorescence labeling, and so avoids the inherent problems of appending large reporter dyes to the biomolecules of interest. Infrared absorbance of a protein or its substrate or both can be followed through the time course of a reaction using this approach. The connection of IR spectra with specific structural features, such as the protein amide I vibration makes this approach widely applicable to biological reactions such as protein folding and enzymatic reactions.