Geometric Sensitivity of a Pinhole Collimator

Abstract

Geometric sensitivity for single photon emission computerized tomography (SPECT) is given by a double integral over the detection plane. It would be useful to be able to explicitly evaluate this quantity. This paper shows that the inner integral can be evaluated in the situation where there is no gamma ray penetration of the material surrounding the pinhole aperature. This is done by converting the integral to an integral in the complex plane and using Cauchy’s theorem to replace it by one which can be evaluated in terms of elliptic functions.

1 Introduction

Nuclear-medicine imaging provides images that assess how the body is functioning [1, 2], as opposed to anatomical modalities (e.g., x-ray computed tomograpy, commonly known as a CT or ‘CAT’ scans) that provide little or no information about function, but great detail of the body’s structure. Nuclear-medicine images the biodistribution of radiolabeled molecules that are typically intravenously injected into the patient in tracer (i.e., non-pharmacological) quantitites. The compounds may have different biochemical properties that affect the biodistribution and, hence, the choice of pharmaceuticals used to assess the disease state of a patient.

Two common nuclear-medicine techniques are single photon emission computed tomography (SPECT) and positron emission tomography (PET). Molecules labeled with a SPECT tracer emit a single photon. PET tracers emit a positron, which annihilates with a nearby electron to produce two nearly back-to-back photons at 511 keV, the rest energy of an electron. The line of these two photons contains the emission point of the positron. Many photon pairs are detected in coincidence and reconstructed into a three-dimensional (3D) image of the tracer’s distribution.

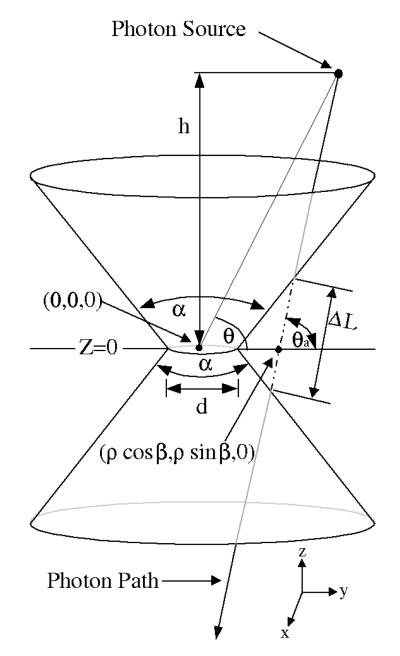
Since SPECT tracers emit only one photon, the detection of the photon itself gives little information about the location of the emission since neither the direction nor origin of the emission is known. Consequently, SPECT uses collimation that allows only photons along certain lines to be detected. The origin is still unknown, but the 3D image may be reconstructed when photons from numerous angles are detected [3, 4]. Pinhole collimation is often used when a small organ (e.g., the thyroid) is imaged by a large detector with a SPECT tracer. Figure 1 is a diagram of the apparatus. It is not hard to see that the pinhole collimation’s geometric efficiency, namely, the fraction of emitted photons that pass through the circular aperture of the collimator, is approximately given by:

$$g=\frac{d^2{\sin }^3\theta }{16h^2},$$ (1.1)

where d is the diameter of the pinhole, h is the perpendicular distance, and θ is the incidence angle of the photon on the aperture plane at the center of aperture. This formula becomes exact in the limit that d goes to zero. Also, an exact formula is easily obtained when $\theta =\frac{\pi }{2}$:

$$g(\theta =\frac{\pi }{2})=\frac{1}{2}-\frac{1}{2}{\left[1+{\left(\frac{d}{2h}\right)}^2\right]}^{-\frac{1}{2}}\approx \frac{1}{2}-\frac{1}{2}\left[1-\frac{1}{2}{\left(\frac{d}{2h}\right)}^2\right]=\frac{d^2}{16h^2}.$$ (1.2)

We derive stronger versions of these two results in the next section. But the main goal of this paper is to simplify the integral representation for the geometric sensitivity without taking d or θ − π/2 to be small. We are concerned with the case where there is no penetration in the sense that not all gamma rays are stopped by the attenuating material surrounding the pinhole aperture. We take θ ≠ π/2. The geometric sensitivity, as defined above, is given by the integral over the aperture of the flux times the sine of the incidence angle at that point on the aperture:

$$g=\frac{1}{4\pi h^2}{\int }_0^{\frac{d}{2}}\rho d\rho {\int }_0^{2\pi }d\beta {\sin }^3\theta a,$$ (1.3)

where ρ and β are polar coordinates on the aperture plane and θ_a is the incidence angle of the photon at a particular value of ρ and β, and is given by [6]:

$${\cot }^2\theta a={\cot }^2\theta -2\frac{\rho }{h}\cot \theta \cos (\beta -\varphi )+\frac{{\rho }^2}{h^2},$$

where ϕ is the third coordinate of the point source. For integrals over 2π the difference β − ϕ can be replaced with only β without loss of generality. This yields

$${\sin }^2{\theta }_a={\left[{\csc }^2\theta -2\frac{\rho }{h}\cot \theta \cos \beta +\frac{{\rho }^2}{h^2}\right]}^{-1}.$$

Figure 1.

Perspective View of the Knife-edge Pinhole Collimator. A point source at z = h and angle θ emits a photon that intersects the z = 0 plane at (ρ cos β, ρ sin β, 0) with an incident angle θ_a. The acceptance angle of the collimator is α and the diameter of the aperture is d. ΔL is the path length of the photon in the attenuating medium. Reproduced from [6] with permission (© 2001 IEEE).

Applying this to (1.3),

$$g=\frac{1}{4\pi h^2}{\int }_0^{\frac{d}{2}}\rho d\rho {\int }_0^{2\pi }d\beta {\left[{\csc }^2\theta -2\frac{\rho }{h}\cot \theta \cos \beta +\frac{{\rho }^2}{h^2}\right]}^{-\frac{3}{2}},$$ (1.4)

When there is penetration the above would be modified to

$$g=\frac{1}{4\pi h^2}{\int }_0^{\infty }\rho d\rho {\int }_0^{2\pi }d\beta {\left[{\csc }^2\theta -2\frac{\rho }{h}\cot \theta \cos \beta +\frac{{\rho }^2}{h^2}\right]}^{-\frac{3}{2}}{e}^{-\mu \Delta L},$$ (1.5)

where the path length through attenuating material, ΔL, is zero for $\rho <\frac{d}{2}$ and is otherwise given by (11) in Ref. [6].

Thus, (1.5) can be re-written as

$$\begin{array}{cc}\hfill g& =g_{\mathrm{NP}}+\frac{1}{4\pi h^2}{\int }_{\frac{d}{2}}^{\infty }\rho d\rho {\int }_0^{2\pi }d\beta {\left[{\csc }^2\theta -2\frac{\rho }{h}\cot \theta \cos \beta +\frac{{\rho }^2}{h^2}\right]}^{-\frac{3}{2}}{e}^{-\mu \Delta L},\hfill \\ \hfill & =g_{\mathrm{NP}}+g_{\mathrm{PEN}},\hfill \end{array}$$

where g_PEN is the efficiency due to penetration and g_NP, the efficiency under the assumption of no penetration, is given by (1.4).

In this paper we use complex variable methods to calculate the β integral in (1.4).

2 Two approximations for g_NP

The special form of g_NP makes it easy to derive approximations for d/h small and for θ − π/2 small which generalize equations (1.1) and (1.2). Before doing this, we observe that only even powers of d and of θ − π/2 can occur in the expansion of g_NP. We see this by writing the integral as the sum of integrals from 0 to π and from π to 2π.

2.1 The expansion for d small

Let us, in this section, denote g_NP by g. Upon substituting $r=\frac{d}{2h}$ and $\eta =\frac{\rho }{h}$ into (1.4) we obtain

$$\begin{array}{cc}\hfill g(r,\theta )& =\frac{1}{4\pi }{\int }_0^{2\pi }{\int }_0^r{[{\csc }^2\theta -2\eta \cot \theta \cos \beta +{\eta }^2]}^{-\frac{3}{2}}\eta d\eta d\beta .\hfill \\ \hfill & =\frac{1}{4\pi }{\int }_0^{2\pi }\left({\int }_0^r\eta \varphi (\beta ,\eta ,\theta )d\eta \right)d\beta .\hfill \end{array}$$

Clearly, g(0, θ) = 0. Since

$$g_r(r,\theta )=\frac{1}{4\pi }{\int }_0^{2\pi }r\varphi (\beta ,r,\theta )d\beta$$

we have g_r(0, θ) = 0. Differentiating (2.1) three more times with respect to r we obtain

$$\begin{array}{cc}\hfill g_{\mathit{rr}}(r,\theta )=& \frac{1}{4\pi }{\int }_0^{2\pi }\left(r{\varphi }_r\right(\beta ,0,\theta )+\varphi (\beta ,r,\theta \left)\right)d\beta \hfill \\ \hfill g_{\mathit{rrr}}(r,\theta )=& \frac{1}{4\pi }{\int }_0^{2\pi }\left(r{\varphi }_{\mathit{rr}}\right(\beta ,0,\theta )+2{\varphi }_r(\beta ,r,\theta \left)\right)d\beta \hfill \\ \hfill g_{\mathit{rrrr}}(r,\theta )=& \frac{1}{4\pi }{\int }_0^{2\pi }\left(r{\varphi }_{\mathit{rrr}}\right(\beta ,0,\theta )+3{\varphi }_{\mathit{rr}}(\beta ,r,\theta \left)\right)d\beta \hfill \end{array}$$

and then setting r = 0 in each of the resulting equations we obtain

$$\begin{array}{cc}\hfill g_{\mathit{rr}}(0,\theta )=& \frac{1}{4\pi }{\int }_0^{2\pi }\varphi (\beta ,0,\theta )d\beta \hfill \\ \hfill g_{\mathit{rrr}}(0,\theta )=& \frac{1}{2\pi }{\int }_0^{2\pi }{\varphi }_r(\beta ,0,\theta )d\beta \hfill \\ \hfill g_{\mathit{rrrr}}(0,\theta )=& \frac{3}{4\pi }{\int }_0^{2\pi }{\varphi }_{\mathit{rr}}(\beta ,0,\theta )d\beta .\hfill \end{array}$$

For convenience let us write

$$u={\csc }^2\theta \text{and}v=\cot \theta$$

so ϕ becomes

$$\varphi (\beta ,r,\theta )={(u-2\mathit{vr}\cos \beta +r^2)}^{-\frac{3}{2}}.$$

Then

$$\begin{array}{cc}\hfill \varphi (\beta ,0,\theta )=& u^{-\frac{3}{2}}\hfill \\ \hfill {\varphi }_r(\beta ,0,\theta )=& 3u^{-5∕2}v\cos \beta \hfill \\ \hfill {\varphi }_{\mathit{rr}}(\beta ,0,\theta )=& 15u^{-\frac{7}{2}}{v}^2{\cos }^2\beta -3u^{-\frac{5}{2}}.\hfill \end{array}$$

We substitute into the Taylor expansion

$$g(r,\theta )=g(0,\theta )+g_r(0,\theta )r+\frac{1}{2!}{g}_{\mathit{rr}}(0,\theta )r^2+\frac{1}{3!}{g}_{\mathit{rrr}}(0,\theta )r^3+\frac{1}{4!}{g}_{\mathit{rrrr}}(0,\theta )r^4+\dots$$

and obtain

$$\begin{array}{cc}\hfill g(r,\theta )& =\frac{1}{2}\left(\frac{1}{4\pi }{\int }_0^{2\pi }{u}^{-\frac{3}{2}}d\beta \right)r^2+\frac{1}{3!}\left(\frac{3}{2\pi }{\int }_0^{2\pi }6u^{-\frac{5}{2}}v\cos \beta d\beta \right)r^3\hfill \\ \hfill & +\frac{1}{4!}\left(\frac{1}{4\pi }{\int }_0^{2\pi }3(15u^{-\frac{7}{2}}{v}^2{\cos }^2\beta -3u^{-\frac{5}{2}})d\beta \right)r^4+.\dots \hfill \end{array}$$

Since

$${\int }_0^{2\pi }\cos \beta d\beta =0\text{and}{\int }_0^{2\pi }{\cos }^2\beta d\beta =\pi$$

and u⁻¹ = sin² θ we obtain

$$g(r,\theta )=\frac{r^2}{4}{\sin }^3\theta +\frac{3}{32}(5{\sin }^5\theta {\cos }^2\theta -2{\sin }^5\theta )r^4+.\dots$$

Finally we replace cos² θ by 1 − sin² θ and r by d/2h and obtain.

$$g_{\mathrm{NP}}=\frac{1}{16}{\sin }^3\theta {\left(\frac{d}{h}\right)}^2+\frac{3}{512}{\sin }^5\theta (3-5{\sin }^2\theta ){\left(\frac{d}{h}\right)}^4+\mathcal{O}\left(d^6\right),$$ (2.1)

2.2 The expansion for $\theta -\frac{\pi }{2}$ small

To start we let

$$f(\theta ,\eta ,\beta )={({\csc }^2\theta -2\eta \cot \theta \cos \beta +{\eta }^2)}^{-\frac{3}{2}}$$

and compute its Taylor expansion at $\theta =\frac{\pi }{2}$,

$$\begin{array}{cc}\hfill f(\theta ,\eta ,\beta )& ={(1+{\eta }^2)}^{-\frac{3}{2}}-3{(1+{\eta }^2)}^{-\frac{5}{2}}\eta \cos \beta (0-\frac{\pi }{2})\hfill \\ \hfill & +\frac{1}{2!}\left(15{(1+{\eta }^2)}^{-\frac{7}{2}}{\eta }^2{\cos }^2\beta -3{(1+{\eta }^2)}^{-\frac{5}{2}}\right){(\theta -\frac{\pi }{2})}^2\hfill \\ \hfill & +\mathcal{O}{(\theta -\frac{\pi }{2})}^3.\hfill \end{array}$$

Since

$$g_{\mathrm{NP}}=\frac{1}{4\pi }{\int }_0^{2\pi }{\int }_0^{d∕2h}f(\theta ,\eta ,\beta )\eta d\eta d\beta$$

and since we know that only even powers of θ − π/2 occur, we obtain

$$g_{\mathrm{NP}}=\frac{1}{2}\left(1-\frac{1}{\sqrt{1+{\left(\frac{d}{2h}\right)}^2}}\right)-\frac{3}{8}\frac{{\left(\frac{d}{2h}\right)}^2}{{(1+{\left(\frac{d}{2h}\right)}^2)}^{5∕2}}{(\theta -\frac{\pi }{2})}^2+\mathcal{O}{(\theta -\frac{\pi }{2})}^4.$$

3 The Contour Integral

We have

$$I={\int }_0^{2\pi }d\beta {\left[{\csc }^2\theta -2\frac{\rho }{h}\cot \theta \cos \beta +\frac{{\rho }^2}{h^2}\right]}^{-\frac{3}{2}}$$ (3.1)

and

$$g_{\mathrm{NP}}=\frac{1}{4\pi h^2}{\int }_0^{\frac{d}{2}}I\rho d\rho .$$

I may be re-cast as a contour integral by setting z = e^iβ:

$$\begin{array}{cc}\hfill I& ={\int }_{\Gamma }\frac{\mathit{dz}}{\mathit{iz}}{\left[\frac{-b}{2z}(z^2-2\frac{a}{b}z+1)\right]}^{-\frac{3}{2}}\hfill \\ \hfill & ={\left(\frac{2}{b}\right)}^{\frac{3}{2}}\frac{1}{i}{\int }_{\Gamma }{\left[\frac{(z-x_0)(x_1-z)}{z}\right]}^{-\frac{3}{2}}\frac{\mathit{dz}}{z}\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill \Gamma & \text{is the unit circle}\hfill \\ \hfill a& ={\csc }^2\theta +\frac{{\rho }^2}{h^2}\hfill \\ \hfill b& =2\frac{\rho }{h}\cot \theta \hfill \\ \hfill x_0& =\frac{a}{b}\left[1-\sqrt{1-\frac{b^2}{a^2}}\right]\hfill \\ \hfill x_1& =\frac{a}{b}\left[1+\sqrt{1-\frac{b^2}{a^2}}\right].\hfill \end{array}$$

We note that a > b and so 0 < x₀ < 1 < x₁.

In this section we take ρ, θ, and h to be constant. We write

$$\begin{array}{cc}\hfill F\left(z\right)& =\left[\frac{z}{(z-x_0)(x_1-z)}\right]{\left[\frac{z}{\left(\right(z-x_0\left)\right(x_1-z\left)\right)}\right]}^{1∕2}\left[\frac{1}{z}\right]\hfill \\ \hfill & =\frac{1}{(z-x_0)(x_1-z)}{\left[\frac{z}{(z-x_0)(x_1-z)}\right]}^{\frac{1}{2}}\hfill \end{array}$$

and

$$I={\left(\frac{2}{b}\right)}^{3∕2}\frac{1}{i}{\int }_{\Gamma }F\left(z\right)\mathit{dz}.$$

We need to be careful because of the square roots. We use the usual convention that

$$\underset{y\to 0^{\pm }}{\lim }\sqrt{-1+\mathit{iy}}=\pm i.$$

We wish to show that F(z) is holomorphic (and single-valued) in

$$\{z:\mid z\mid <1\}-\{x:0<x<x_0\}.$$

To isolate the square root factor in F we set

$$g\left(z\right)=\frac{z}{(z-x_0)(x_1-z)}.$$

We take ∣z∣ ≤ 1. If in addition Re z < 0 and ∣Im z∣ << ∣z − x₀∣ then Re (z − x₀)(x₁ − z) < 0. This implies that g(z) never takes on negative real values and so has a single-valued square root in Re z < 0. Similarly, if ∣z∣ ≤ 1, and Re z > x₀ (no condition on Im z now) then Re (z − x₀)(x₁ − z) > 0 and g(z) has a single-valued square root Re z > x₀.

It follows from Cauchy’s Theorem that the integral of F(z) over the unit circle Γ is equal to the integral over the “ barbell” γ around 0 and x₀. More explicitly, γ is the boundary of

$$B=B_{∊}\left(0\right)\cup B_{∊}\left(x_0\right)\cup R$$

where B_∊(x) is the ball of radius ∊ and centered at x and R is the rectangle

$$R=\{z=x+\mathit{iy}:0\le x\le x_0,-\delta \le y\le \delta \}$$

with δ << ∊. See Figure 2.

Figure 2.

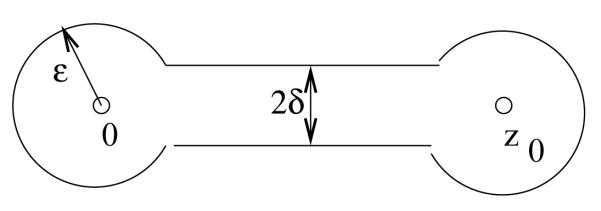
The curve γ

The curve γ decomposes into smooth pieces which we describe using the angle α = arcsin(δ/∊).

$$\begin{array}{cc}\hfill {\gamma }_r=& \{z:\mid z-x_0\mid =∊,-\pi +\alpha \le \arg z-x_0\le \pi -\alpha \}\hfill \\ \hfill {\gamma }_l=& \{z:\mid z\mid =∊,\alpha \le \arg (z)\le 2\pi -\alpha \}\hfill \\ \hfill {\gamma }_{\pm }=& \{z:z=x\pm i\delta ,∊\cos \alpha \le x\le x_0-∊\cos \alpha \}.\hfill \end{array}$$

To bound the integral over γ1 we set z = ∊e^iθ.

$$\begin{array}{cc}\hfill \mid {\int }_{{\gamma }_l}F\left(z\right)\mathit{dz}\mid & =\mid {\int }_{\alpha }^{2\pi -\alpha }F\left(∊e^{i\theta }\right)∊e^{i\theta }d\theta \mid \hfill \\ \hfill & =\mathcal{O}\left({∊}^{3∕2}\right).\hfill \end{array}$$

To evaluate ∫_γr F(z)dz we set z = x₀ + ∊e^iθ. Then

$$F(x_0+∊e^{i\theta })=C{∊}^{-\frac{3}{2}}{e}^{-\frac{3}{2}i\theta }+\mathcal{O}\left({∊}^{-1∕2}\right)$$

with

$$C=\frac{x_0^{1∕2}}{{(x_1-x_0)}^{3∕2}}$$ (3.2)

and so

$$\begin{array}{cc}\hfill {\int }_{{\gamma }_r}F\left(z\right)\mathit{dz}& ={\int }_{-\pi +\alpha }^{\pi -\alpha }\left({∊}^{-\frac{3}{2}}{\mathit{Ce}}^{-\frac{3}{2}i\theta }+\mathcal{O}\left({∊}^{-\frac{1}{2}}\right)\right)∊{\mathit{ie}}^{i\theta }(1+\mathcal{O}(∊\left)\right)d\theta \hfill \\ \hfill & ={\int }_{-\pi +\alpha }^{\pi -\alpha }\mathit{Ci}{∊}^{-\frac{1}{2}i\theta }+\mathcal{O}\left({∊}^{\frac{1}{2}}\right)d\theta .\hfill \end{array}$$

Since α = O(∊), we may set α = 0 and absorb the error in the O(∊^1/2) term. We then do the integration and obtain

$${\int }_{{\gamma }_r}F\left(z\right)\mathit{dz}=\frac{4\mathit{iC}}{\sqrt{∊}}+\mathcal{O}\left({∊}^{\frac{1}{2}}\right).$$ (3.3)

We want to compute the integral of F over γ₊. We need to be careful about the square root. Recall that we are assuming

$$∊\cos \alpha <x<x_0-∊\cos \alpha \text{and}\delta <<∊.$$

Lemma 3.1

On γ₊

$$F\left(z\right)=i{\left(\right(x_0-x\left)\right(x_1-x\left)\right)}^{-\frac{3}{2}}{x}^{\frac{1}{2}}+\mathcal{O}\left(\delta \right)$$

and on γ₋

$$F\left(z\right)=-i{\left(\right(x_0-x\left)\right(x_1-x\left)\right)}^{-\frac{3}{2}}{x}^{\frac{1}{2}}+\mathcal{O}\left(\delta \right).$$

Proof

This is a consequence of the branching of the square root function. Let

$$H\left(z\right)=\frac{z}{(z-x_0)(x_1-z)}=\frac{z(\overline{z}-x_0)(x_1-\overline{z})}{{\mid z-x_0\mid }^2{\mid x_1-z\mid }^2}$$

and

$$h\left(z\right)=z(\overline{z}-x_0)(x_1-\overline{z}).$$

We see that

$$h(x+i\delta )=x(x-x_0)(x_1-x)+i\delta (x^2-1)+\mathcal{O}\left({\delta }^2\right).$$

Recall that δ is replaced by −δ on γ₋ and that 0 < x < x₀ < x₁. So Re H(z) < 0 on both γ₊ and γ₋ while Im H(z) < 0 on γ₊ and Im H(z) > 0 on γ₋. Thus on γ₊

$$\begin{array}{cc}\hfill H{\left(z\right)}^{\frac{1}{2}}& =-i{\mid \frac{x}{(x-x_0)(x_1-x)}\mid }^{\frac{1}{2}}+\mathcal{O}\left(\delta \right)\hfill \\ \hfill & =-i{\left(\frac{x}{(x_0-x)(x_1-x))}\right)}^{\frac{1}{2}}+\mathcal{O}\left(\delta \right)\hfill \end{array}$$

while on γ₋

$$H{\left(z\right)}^{\frac{1}{2}}=i{\left(\frac{x}{(x_0-x)(x_1-x)}\right)}^{\frac{1}{2}}+\mathcal{O}\left(\delta \right)$$

Since

$$\begin{array}{cc}\hfill F\left(z\right)& =F\left(x\right)+\mathcal{O}\left(\delta \right)=\frac{1}{(x-x_0)(x_1-x)}H{\left(z\right)}^{\frac{1}{2}}+\mathcal{O}\left(\delta \right)\hfill \\ \hfill & =-\frac{1}{(x_0-x)(x_1-x)}H{\left(z\right)}^{\frac{1}{2}}+\mathcal{O}\left(\delta \right)\hfill \\ \hfill & =-\frac{1}{(x_0-x)(x_1-x)}\left(-i{\left(\frac{x}{(x_0-x)(x_1-x))}\right)}^{\frac{1}{2}}+\right)\mathcal{O}\left(\delta \right))\hfill \end{array}$$

the Lemma follows.

We also need to be careful about the orientation. The curve γ is oriented counter-clockwise. This means that the integration over γ₊ goes in the direction of x₀ to 0. We need to reverse its sign in order to write it in the conventional way.

$$\begin{array}{cc}\hfill {\int }_{{\gamma }_{+}}F\left(z\right)\mathit{dz}& =-{\int }_{∊\cos \alpha }^{x_0-∊\cos \alpha }F(x+i\delta )\mathit{dx}\hfill \\ \hfill & =-{\int }_{∊\cos \alpha }^{x_0-∊\cos \alpha }\frac{{\mathit{ix}}^{1∕2}\mathit{dx}}{{(x_0-x)}^{3∕2}{(x_1-x)}^{3∕2}}+\mathcal{O}\left(∊\right).\hfill \end{array}$$

We let x = x₀t and $\Delta =∊x_0^{-1}\cos \alpha$ and use δ << ∊ to obtain

$${\int }_{{\gamma }_{+}}F\left(z\right)\mathit{dz}=-{\int }_{\Delta }^{1-\Delta }\frac{{{\mathit{ix}}_0}^{3∕2}{t}^{1∕2}\mathit{dx}}{{(x_0-x_{0}t)}^{∕2}{(x_1-x_{0}t)}^{3∕2}}+\mathcal{O}\left(∊\right).$$

Now let

$$\tau =\frac{x_1}{x_0}>1.$$

We have

$${\int }_{{\gamma }_{+}}F\left(z\right)\mathit{dz}=-\frac{i}{{x_0}^{3∕2}}{\int }_{\Delta }^{1-\Delta }\frac{t^{1∕2}\mathit{dt}}{{(\tau -t)}^{3∕2}{(1-t)}^{3∕2}}+\mathcal{O}\left(∊\right).$$

We may let Δ → 0 in the lower limit, but not in the upper limit. So we now have

$${\int }_{{\gamma }_{+}}F\left(z\right)\mathit{dz}=-\frac{i}{{x_0}^{3∕2}}{\int }_0^{1-\Delta }\frac{t^{1∕2}\mathit{dt}}{{(\tau -t)}^{3∕2}{(1-t)}^{3∕2}}+\mathcal{O}\left(∊\right).$$ (3.4)

Here Δ = ∊x₀⁻¹ cos α. We may let δ → 0 and redefine Δ to be ∊x₀⁻¹.

We get the same value for the integral over γ₋. This is because the integrand is the negative of that in (3.4) but the orientation is reversed and so the two negatives cancel.

For any function g(t), continuously differentiable on the interval [0, 1], we have

$${\int }_0^{1-\Delta }\frac{g\left(t\right)}{{(1-t)}^{3∕2}}\mathit{dt}=2\frac{g\left(1\right)}{{\Delta }^{1∕2}}-2g\left(0\right)-2{\int }_0^1{(1-t)}^{-1∕2}{g}^{\prime }\left(t\right)\mathit{dt}+O\left({\Delta }^{1∕2}\right).$$

as can easilly be seen by an integration by parts.

We apply this to g(t) = t^1/2/(Γ − t)^3/2 as in (3.4). This yields

$$\begin{array}{cc}\hfill {\int }_{{\gamma }_{+}}F\left(z\right)\mathit{dz}& =\frac{-2i}{{(\tau -1)}^{\frac{3}{2}}{x}_0^{\frac{3}{2}}{\Delta }^{\frac{1}{2}}}\hfill \\ \hfill & +\frac{i}{x_0^{\frac{3}{2}}}\left({\int }_0^1{t}^{-\frac{1}{2}}{(\tau -1)}^{-\frac{3}{2}}+3t^{\frac{1}{2}}{(\tau -1)}^{-\frac{5}{2}}\mathit{dt}\right)+\mathcal{O}\left({∊}^{\frac{1}{2}}\right).\hfill \end{array}$$

We now take twice this quantity and add to it the results of (3.2) and (3.3),

$$\begin{array}{cc}\hfill {\int }_{\mid z\mid =1}F\left(z\right)\mathit{dt}=& {\int }_{\gamma }F\left(z\right)\mathit{dz}\hfill \\ \hfill =& \frac{4\mathit{iC}}{\sqrt{∊}}+2(\frac{-2i\sqrt{x_0}}{{(x_1-x_0)}^{-3∕2}\sqrt{∊}}\phantom{)}\hfill \\ \hfill & +\phantom{(}\frac{i}{{x_0}^{\frac{3}{2}}}{\int }_0^1{(1-t)}^{-1∕2}\left({(\tau -t)}^{-3∕2}{t}^{-1∕2}+3t^{1∕2}{(\tau -t)}^{-5∕2}\right)\mathit{dt})\hfill \\ \hfill & +\mathcal{O}\left({∊}^{1∕2}\right).\hfill \end{array}$$

We substitute the value for C from (3.2) and let ∊ → 0

$${\int }_{\mid z\mid =1}F\left(z\right)\mathit{dz}=\frac{2i}{{x_0}^{\frac{3}{2}}}{\int }_0^2{(1-t)}^{-1∕2}\left({(\tau -t)}^{-3∕2}{t}^{-1∕2}+3t^{1∕2}{(\tau -t)}^{-5∕2}\right)\mathit{dt}.$$

Finally, we evaluate this integral using Mathematica® and obtain

$${\int }_{\mid z\mid =1}F\left(z\right)\mathit{dz}=\left(\frac{2i}{{x_0}^{\frac{3}{2}}}\right)\frac{2\left(2\tau E[1∕\tau ]-(-1+\tau )K[1∕\tau ])\right)}{{(\tau -1)}^2\sqrt{\tau }}$$

where K and E are the complete elliptic functions of the first and second kind

$$\begin{array}{cc}\hfill K\left[m\right]& ={\int }_0^1{(1-{\mathit{mt}}^2)}^{-1∕2}{(1-t^2)}^{-1∕2}\mathit{dt}\hfill \\ \hfill E\left[m\right]& ={\int }_0^1{(1-{\mathit{mt}}^2)}^{1∕2}{(1-t^2)}^{-1∕2}\mathit{dt}.\hfill \end{array}$$

We now have

$$\begin{array}{cc}\hfill I& ={\left(\frac{2}{b}\right)}^{3∕2}\frac{1}{i}{\int }_{\Gamma }F\left(z\right)\mathit{dz}\hfill \\ \hfill & ={\left(\frac{2}{b}\right)}^{\frac{3}{2}}\frac{2}{{x_0}^{\frac{3}{2}}}\frac{2\left(2\tau E\left(\frac{1}{\tau }\right)-(\tau -1)K\left(\frac{1}{\tau }\right)\right)}{{(\tau -1)}^2\sqrt{\tau }}\hfill \\ \hfill & ={\left(\frac{2}{b}\right)}^{\frac{3}{2}}\frac{4{\tau }^{\frac{1}{4}}}{{(\tau -1)}^2}\left(2\tau E\left(\frac{1}{\tau }\right)-(\tau -1)K\left(\frac{1}{\tau }\right)\right)\hfill \end{array}$$ (3.5)

and

$$g_{\mathrm{NP}}=\frac{1}{4\pi h^2}{\int }_0^{\frac{d}{2}}\rho \mathit{Id}\rho$$ (3.6)

with

$$b=2\frac{\rho }{h}\cot \theta ,a={\cos }^2\theta +\frac{{\rho }^2}{h^2}$$ (3.7)

$$\begin{array}{cc}\hfill \tau & =\frac{x_1}{x_0}=\frac{1}{{x_0}^2}\hfill \\ \hfill x_0& =\frac{a}{b}\left[1-\sqrt{1-\frac{b^2}{a^2}}\right]\hfill \\ \hfill x_1& =\frac{a}{b}\left[1+\sqrt{1-\frac{b^2}{a^2}}\right].\hfill \end{array}$$ (3.8)

4 Limiting cases

We validate (3.5) by consider two limiting cases.

4.1 Expansion for Small d

We look for an expansion of g_NP under the assumption that $\frac{d}{h}$ is small and rederive (2.1) The dependence of x₀ on ρ is given in (3.8). The two-term Taylor expansion of x₀ as a function of ρ is

$$x_0=A\rho +B{\rho }^3+\mathcal{O}\left({\rho }^5\right)$$ (4.1)

with

$$A=\frac{\cos \theta \sin \theta }{h}\text{and}B=A^3-\frac{A}{h^2{\csc }^2\theta }.$$ (4.2)

Since

$$\tau =\frac{1}{{x_0}^2}$$

we have

$$\frac{1}{\tau }=A^2{\rho }^2+\mathcal{O}\left({\rho }^4\right)$$ (4.3)

and

$$\frac{1}{{(\tau -1)}^2}=\frac{1}{{\tau }^2}+\frac{2}{{\tau }^3}+\mathcal{O}\left({\rho }^8\right).$$ (4.4)

It is convenient to work with the quantity ρ²Γ, so we note, using (4.1)

$${\rho }^2\tau =\frac{1}{A^2}-\frac{2B}{A^3}{\rho }^2+\mathcal{O}\left({\rho }^4\right).$$ (4.5)

We start with

$$I={\left(\frac{2}{b}\right)}^{\frac{3}{2}}\frac{4{\tau }^{\frac{1}{4}}}{{(\tau -1)}^2}\left(2\tau E\left(\frac{1}{\tau }\right)-(\tau -1)K\left(\frac{1}{\tau }\right)\right).$$ (4.6)

Substituting the expression for b from (3.7) and for (Γ − 1)² from (4.4) we obtain, after some manipulation

$$I=\left({\left(\frac{h}{\cot \theta }\right)}^{\frac{3}{2}}\frac{4}{{\left({\rho }^2\tau \right)}^{\frac{3}{4}}}\frac{1}{\tau }+\mathcal{O}\left({\rho }^4\right)\right)\left(2\tau E\left(\frac{1}{\tau }\right)-(\tau -1)K\left(\frac{1}{\tau }\right)\right).$$

We now use the expansions (as given by Mathematica®)

$$\begin{array}{cc}\hfill E\left(t\right)& =\frac{\pi }{2}-\frac{\pi t}{8}+\mathcal{O}\left(t^2\right)\hfill \\ \hfill K\left(t\right)& =\frac{\pi }{2}+\frac{\pi t}{8}+\mathcal{O}\left(t^2\right).\hfill \end{array}$$

So

$$I={\left(\frac{h}{\cot \theta }\right)}^{\frac{3}{2}}\frac{4}{{\left({\rho }^2\tau \right)}^{\frac{3}{4}}}\left(\frac{\pi }{2}+\frac{\pi }{8\tau }+\frac{\pi }{\tau }\right)+\mathcal{O}\left({\rho }^4\right).$$

From the expression for ρ²Γ in (4.5), we derive

$$\frac{1}{{\left({\rho }^2\tau \right)}^{\frac{3}{4}}}=A^{\frac{3}{2}}(1+\frac{3}{2}\frac{B}{A}{\rho }^2+\mathcal{O}({\rho }^4\left)\right)$$

and this leads to

$$I=4{\left(\frac{h}{\cot \theta }\right)}^{\frac{3}{2}}{A}^{\frac{3}{2}}\left(\frac{\pi }{2}+\frac{\pi }{8\tau }+\frac{\pi }{\tau }+\frac{3B{\rho }^2\pi }{4A}\right)+\mathcal{O}\left({\rho }^4\right).$$

We now substitute for A and B using (4.2) and also for Γ⁻¹ using (4.3)

$$I={\sin }^3\theta \left(2\pi +\frac{3\pi }{2}\left(3{\sin }^2\theta -5{\sin }^4\theta \right)\frac{{\rho }^2}{h^2}\right)+\mathcal{O}\left({\rho }^4\right).$$

Substituting this into (3.6) and integrating, we again derive (2.1).

4.2 An expansion for θ near π/2

We show how (4.6) also gives the expansion of Section 2.2. We start with

$$x_0=\frac{b}{2a}\left(1+\frac{b^2}{4a^2}+\mathcal{O}\left({\left(\frac{b}{a}\right)}^3\right)\right).$$

From (3.7) we see that

$$a=1+\frac{{\rho }^2}{h^2}+{(\theta -\frac{\pi }{2})}^2+\mathcal{O}{(\theta -\frac{\pi }{2})}^4$$ (4.7)

$$b=-\frac{2\rho }{h}(\theta -\frac{\pi }{2})+\mathcal{O}{(\theta -\frac{\pi }{2})}^3.$$ (4.8)

So from (3.8) we have

$$x_0=\frac{b}{2a}\left(1+\frac{b^2}{4a^2}+\mathcal{O}{(\theta -\frac{\pi }{2})}^3\right).$$

Thus

$$\begin{array}{cc}\hfill \tau & =\frac{4a^2}{b^2}-2+\mathcal{O}{(\theta -\frac{\pi }{2})}^2\hfill \\ \hfill \frac{1}{{(\tau -1)}^2}& =\frac{1}{{\tau }^2}(1+\frac{2}{\tau }+\mathcal{O}{(\theta -\frac{\pi }{2})}^4)\hfill \end{array}$$ (4.9)

and

$$\frac{1}{\tau }\left(2\tau E\left(\frac{1}{\tau }\right)-(\tau -1)K\left(\frac{1}{\tau }\right)\right)=\frac{\pi }{2}+\frac{9\pi }{8\tau }+\mathcal{O}{(\theta -\frac{\pi }{2})}^4.$$

These expansions let us write (4.6) as

$$\begin{array}{cc}\hfill I& ={\left(\frac{2}{b}\right)}^{3∕2}\frac{4}{{\tau }^{3∕4}}\left((1+\frac{2}{\tau })(\frac{\pi }{2}+\frac{9\pi }{8\tau }+\mathcal{O}{(\theta -\frac{\pi }{2})}^4\right)\hfill \\ \hfill & =\frac{2^{7∕2}}{{\left(b^2\tau \right)}^{3∕4}}\left((1+\frac{2}{\tau })(\frac{\pi }{2}+\frac{9\pi }{8\tau })+\mathcal{O}{(\theta -\frac{\pi }{2})}^4\right).\hfill \end{array}$$

Using (4.8) and (4.9) we obtain a substitute for (4.1)

$$\frac{1}{{\left(b^2\tau \right)}^{3∕4}}=4^{-3∕4}{a}^{-3∕2}(1+\frac{3b^2}{8a^2})+\mathcal{O}{(\theta -\frac{\pi }{2})}^4.$$

This gives, in light of (4.7),

$$\begin{array}{cc}\hfill I=& 2\pi a^{-3∕2}+\frac{15}{8}\pi b^2{a}^{-7∕2}+\mathcal{O}{(\theta -\frac{\pi }{2})}^4\hfill \\ \hfill =& 2\pi {(1+\frac{{\rho }^2}{h^2})}^{-3∕2}-3\pi {(1+\frac{{\rho }^2}{h^2})}^{-5∕2}{(\theta -\frac{\pi }{2})}^2\hfill \\ \hfill & +\frac{15}{2}\pi \frac{{\rho }^2}{h^2}{(1+\frac{{\rho }^2}{h^2})}^{-7∕2}{(\theta -\frac{\pi }{2})}^2+\mathcal{O}{(\theta -\frac{\pi }{2})}^4.\hfill \end{array}$$

Finally, we integrate term-by-term.

$$\begin{array}{cc}\hfill g=& \frac{1}{4\pi h^2}{\int }_0^{d∕2}\rho I\left(\rho \right)d\rho \hfill \\ \hfill =& \frac{1}{4\pi h^2}(2\pi h^2(1-{(1+{\left(\frac{d}{2h}\right)}^2)}^{-1∕2})\phantom{)}\hfill \\ \hfill & -3\pi h^2\frac{1}{3}(1-{(1+{\left(\frac{d}{2h}\right)}^2)}^{-3∕2}){(\theta -\frac{\pi }{2})}^2\hfill \\ \hfill +& \phantom{(}\frac{15}{2}\pi h^2(\frac{2}{15}-\frac{2+5{(d∕2h)}^2}{15}{(1+{\left(\frac{d}{2h}\right)}^2)}^{-5∕2}{(\theta -\frac{\pi }{2})}^2)\hfill \\ \hfill +& \mathcal{O}{(\theta -\frac{\pi }{2})}^4\hfill \\ \hfill =& \frac{1}{2}(1-{(1+{\left(\frac{d}{2h}\right)}^2)}^{-1∕2})-\frac{3}{8}{(1+{\left(\frac{d}{2h}\right)}^2)}^{-5∕2}{\left(\frac{d}{2h}\right)}^2{(\theta -\frac{\pi }{2})}^2\hfill \\ \hfill +& \mathcal{O}{(\theta -\frac{\pi }{2})}^4.\hfill \end{array}$$

5 Numerical Confirmation

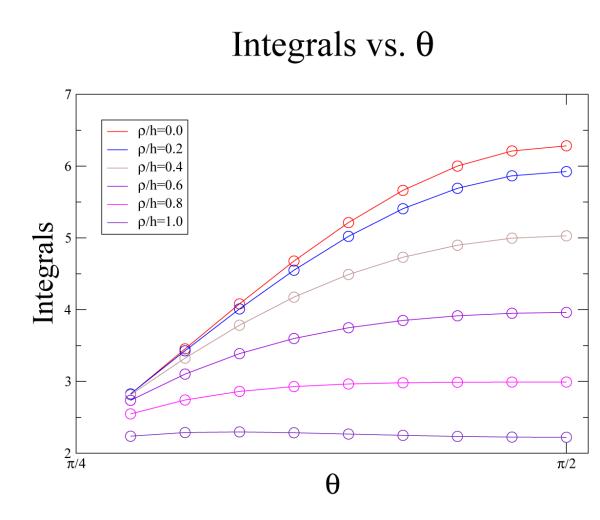
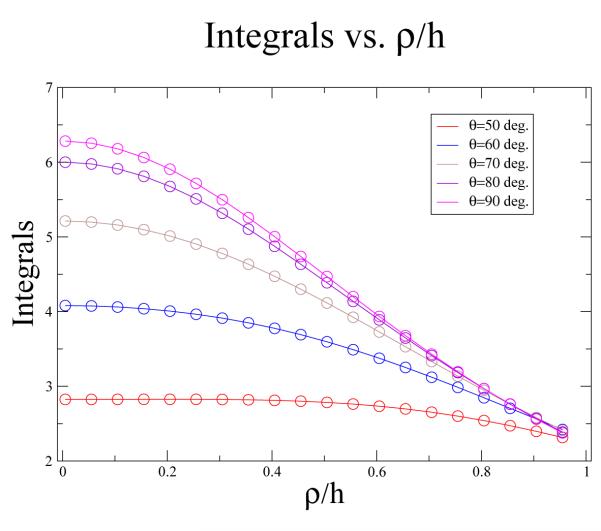
The result of (3.5) is further validated in this section with numerical integration of (3.1). In this original formulation, the integral depends on the ratio of ρ/h and on the value of θ. We analytically considered one limiting case for each of these quantities in the previous section. We consider these and other values for these quantities in this section using numerical methods. For fixed values of ρ/h, the numerical integration (solid lines) is shown with the results of the residue calculation (open circles) in Fig. 3 as a function of θ. Fig. 4 shows the numerical integration and residue results for fixed values of θ as a function of ρ/h. All corresponding values of the residue calculation and the numerical integration agree.

Figure 3.

Numerical integration of (3.1) (solid lines) and residue calculation of (3.5) (open circles) as a function of θ for fixed values of ρ/h: 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0.

Figure 4.

Numerical integration of (3.1) (solid lines) and residue calculation of (3.5) (open circles) as a function of ρ/h for fixed values of θ: 50, 60, 70, 80, and 90 degrees.

6 Conclusions

The accuracy of collimator efficiency is important for design and for quantitative reconstruction programs. Analytic forms obviate the need for numerical models, which do not readily offer insight into the interplay of collimator parameters. This paper approaches the problem by re-casting one of the integrals in terms of contour integration. This integration was completed, but the authors were unable to execute the second integral to yield a complete analytic solution. The result was studied for special cases with known outcomes for validation. Future efforts may be able to build on this validated result to find a complete analytic solution.