Abstract
Various computational models have been developed to transfer annotations of gene essentiality between organisms. However, despite the increasing number of microorganisms with well-characterized sets of essential genes, selection of appropriate training sets for predicting the essential genes of poorly-studied or newly sequenced organisms remains challenging. In this study, a machine learning approach was applied reciprocally to predict the essential genes in 21 microorganisms. Results showed that training set selection greatly influenced predictive accuracy. We determined four criteria for training set selection: (1) essential genes in the selected training set should be reliable; (2) the growth conditions in which essential genes are defined should be consistent in training and prediction sets; (3) species used as training set should be closely related to the target organism; and (4) organisms used as training and prediction sets should exhibit similar phenotypes or lifestyles. We then analyzed the performance of an incomplete training set and an integrated training set with multiple organisms. We found that the size of the training set should be at least 10% of the total genes to yield accurate predictions. Additionally, the integrated training sets exhibited remarkable increase in stability and accuracy compared with single sets. Finally, we compared the performance of the integrated training sets with the four criteria and with random selection. The results revealed that a rational selection of training sets based on our criteria yields better performance than random selection. Thus, our results provide empirical guidance on training set selection for the identification of essential genes on a genome-wide scale.
Introduction
As a minimal gene subset in organisms, essential genes are required for survival, development and fertility [1], [2]. Identifying such genes can aid in understanding the primary structures of complex gene regulatory networks in a cell [3]–[5], elucidating the relationship between genotype and phenotype [6], [7] and discovering potential drug targets in novel pathogens [8]–[10]. In addition, they can be useful in re-engineering microorganisms [11], [12], particularly for investigating the causes of human diseases [13], [14].
Prediction and identification of essential genes are done primarily by experimental and computational techniques. Experimental techniques randomly or systematically inactivate potential essential genes and assess their essentiality based on the effects on organisms [15]–[18]. However, in some organisms such as mammals, experimental techniques are time-consuming and expensive. In addition, the degree of gene essentiality varies under different growth conditions [6], [19]. For this reason, computational techniques are used, often in combination with experimental techniques, to both predict and identify essential genes. Known essential genes from various microorganisms provide instructional and training materials for computational studies. In addition, genome sequences obtained by high-throughput sequencing provide relevant information for investigating the minimal subset of genes in various organisms. Notably, recent development in bioinformatics has significantly advanced the computational tools and resources available to investigate essential genes.
Several prediction models have been developed to identify essential genes in silico. One of the simplest models utilizes known essentiality of homologous genes to predict new essential genes [20]–[23]. Although this model is generally reliable, two limitations have been observed. First, conserved orthologs between species account for a small portion of a genome [24]. Second, orthologs in distantly related species often exhibit differences in gene regulation and function [25], leading to a potential diversity of gene essentiality. To circumvent these limitations, researchers have developed feature-based models that can be used to distinguish essential genes from non-essential ones based on the presence of features similar to those of essential genes [26]–[30].
To improve the accuracy of feature-based machine learning methods, researchers have sought to determine special gene features (e.g., network topology feature, flux deviations, and domain enrichment) that significantly correlate with gene importance [26]–[33]. In addition to feature selection, training set selection is used as an alternative strategy to improve the accuracy of machine learning methods; however, training set selection is often ignored in the absence of sufficient data. Existing knowledge of a large number of essential genes in various microorganisms provides a great opportunity to investigate training set selection and thereby improve prediction of essential genes.
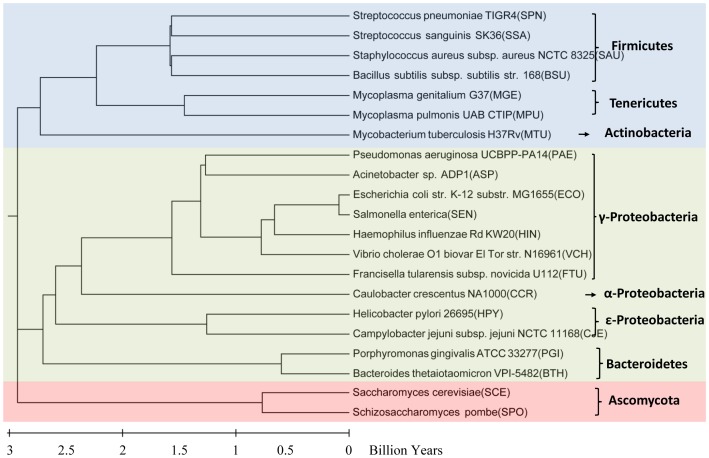
In the present study, a naïve Bayes classifier was applied initially to reciprocally predict essential genes among 21 species (Figure 1, Table S1). We found that the predictive accuracy based on different training sets varied significantly. We then demonstrated that this variation could be attributed to quality of training set, growth conditions, evolutionary distance, and lifestyle. Subsequently, we investigated the performance of incomplete and integrated training sets. Our results showed that at least 10% of the total genes were necessary to achieve optimum performance. We also demonstrated that integrated training sets were more stable and accurate compared to single sets. Finally, we validated the better performance of our selective four rules for training set selection by comparing with random selection.
Figure 1. Phylogenetic tree of the 21 species.
The divergence times of the 20 species were obtained from a public database TIMETREE [57] (Table S3).
Materials and Methods
Essential gene and gene sequences
The essential genes of 21 species (Table S1) were obtained from relevant studies, as well as the Online Gene Essentiality Database (OGEE) [34] and Database of Essential Genes (DEG) [35]. The cDNA and protein sequences of the 21 species were downloaded from the NCBI server (ftp://ftp.ncbi.nih.gov/genomes/). The homologous map and proteome sequences of 417 core species were downloaded from eggNOG 3.0 [36].
Features collection
We collected 15 features (see feature descriptions in Table 1) that are widely used in previous models. All 15 features are divided into six categories as following.
Table 1. Abbreviations and descriptions of selected features.
| Abbreviation | Description |
| mE | mRNA Expression level |
| mEF | mRNA Express Fluctuation |
| Age | gene origin age |
| DoT | gene domain type |
| DoC | gene domain conservation |
| DC | network topology feature, degree centrality |
| CCo | network topology feature, clustering coefficient |
| CC | network topology feature, closeness centrality |
| BC | network topology feature, betweenness centrality |
| PL | protein length |
| CAI | codon adaptation index |
| NP | number of paralogs for a target gene |
| NS | number of species which have at least a homology for a target gene |
| NEH | number of essential homolog genes in other species for a target gene |
| NNH | number of non-essential homolog genes in other species for a target gene |
Domain properties. Essential genes are associated with basic categories of biological functions or processes [37]. Therefore, essential genes may contain some shared domains. To identify the domain of each gene in the 21 species we investigated, we first downloaded the hidden Markov models (Pfam-A.hmm) of protein domains from the Pfam database [38], and then used the Hmmer software [39] to identify the protein domain of each gene. The corresponding domain type for each gene was defined as the feature DoT. The amino acid sites within protein domains are often more important and conserved than those in other parts. Therefore, we assumed that the conservation of protein domain is a reflection of gene essentiality, and the DoC of each gene was calculated according to the ratio of the conserved domain score and the domain length.
Protein–protein interaction (PPI) network. Network topology features have been used widely in previous studies. They indicated that essential genes tend to play topologically more important roles in protein interaction networks than non-essential genes. In our study, PPI data for the genes in 21 species were downloaded from the STRING Database [40]. Then, we used the NetworkX software package [41] to compute the four network topology features, i.e. DC, CCo, CC, and BC (see feature descriptions in Table 1).
Genomic sequence properties. Although protein length (PL) tends to become longer through evolution [42], different natural constraints might exist on the PL between essential genes and nonessential genes. The codon usage of essential genes suffers from more evolutionary constraints than non-essential genes. We used the CodonW [43] software package to calculate codon usage, i.e. CAI.
Homology properties. Duplicated genes are believed to often overlap in function and expression [44], and duplicates are always less likely to be essential than singletons [45]–[47]. An all-against-all BLAST search was conducted for the whole set of proteins in each of the 21 species to identify the paralogs with an E-value threshold of 10−20, and the number of paralogs for a target gene within each species was used as the feature NP. Four-hundred seventeen core organisms in the eggNOG database included all of the 21 species in our study. Therefore, we counted the number of species among the 417 core species that had at least one homologous gene for each target gene in 21 species (feature NS). The orthologous gene of an essential gene is highly likely to be essential as well [48]. Therefore, we calculated the numbers of essential and non-essential homologous genes, including those that are found in other species, for each target gene (NEH and NNH).
Phyletic gene age. Chen [46] showed that older genes (i.e. genes with earlier phyletic origin) are more likely to be essential than young ones. Age was calculated according to previously described methods [46], [49] and the target genomes of SCE and SPO were divided into five taxonomic groups, i.e. species typical, Ascomycota, Opisthokonta, Eukaryota, and cellular organisms.
Gene expression. mRNA expression data were obtained from Series GSE15352 [50] and GSE30025 [51] of the Gene Expression Omnibus (GEO) Database. The expression levels of essential genes are often higher and more stable than those of non-essential genes [52]. The average and variable coefficients of mRNA expression levels in all conditions were collected as predictors (i.e. mE and mEF).
Results and Discussion
Influences of different training sets on the predictive accuracy
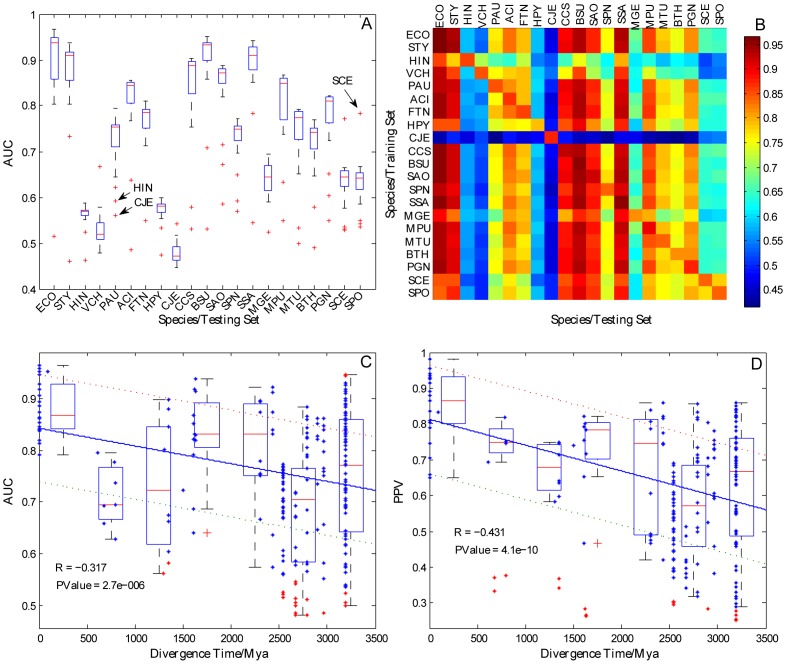
To investigate the manner and extent by which training set selection affects predictive accuracy, we trained and reciprocally predicted essential genes in 21 organisms by using naïve Bayes classifiers. The result are presented as a 21×21 AUC matrix M = (mij), where mij is the AUC score with ith species as a training set and jth species as a testing set.
Since the ratios of essential genes among organisms were different, and comparing the differences in AUC scores calculated based on the predictions from the same training set to different testing sets would not be meaningful. Therefore, we compared the AUC scores obtained from the same testing set and different training sets for each of the 21 species. Based on the AUC matrix, the variation of AUC scores from different training sets was displayed as boxplots (Figure 2A), and these variations were applied to determine the influence of different training sets on predictive accuracy. We found that the interquartile ranges (IQRs) of many species within testing sets were >0.03 (Table S2). ECO (E. coli) showed the largest IQR (0.091), demonstrating that the difference in predictive accuracy may exceed 9% when different species are selected as the training set.
Figure 2. Distribution of AUC scores among 21 species and the correlation between predictive accuracy and divergence time.
A) Variation in prediction accuracy from different training sets to the same testing set. Each boxplot displays the variation in AUC scores calculated from different training sets (in addition to the species on the X axis, the rest of the 20 species were used as the training set) relative to the same testing set (the species on the X axis). ‘+’ represents the outliers corresponding to the training sets that have significantly lower or higher predictive accuracy. B) Heatmap matrix of the influence of training sets on different species. Colors in each cell indicate AUC scores obtained when those species were used as the training set to predict the essential genes of the target 21 species including the speciesself. CJE shows the worst prediction performance when CJE was used as the training set. C) Correlation between AUC scores and divergence times. Stars refer to the AUC scores obtained from the organisms with the divergence time on the X axis, in which one species is used as a training set and the other was used as a testing set. Red stars refer to outliers that were discarded from the regression analysis. The regression line is indicated by a solid line, and error bars are indicated by dashes. The boxplot shows the variation in prediction per 500 millions of years. D) Correlation between PPV scores and divergence times.
Besides, some outliers were observed in the boxplots (Figure 2A), indicating that some training sets exhibited significantly lower or higher predictive accuracies than other sets. For example, the accuracy of SCE (S. cerevisiae) as the training set used to predict the essential genes of SPO (S. pombe) was significantly better than that of the other species. By contrast, use of HIN (H. influenza, AUC = 0.592), CJE (C. jejuni, AUC = 0.563), and MGE (M. genitalium, AUC = 0.621) as training sets exhibited significantly lower prediction accuracies than other species when PAU (P. aeruginosa) was used as the testing set. In summary, different training sets influenced the predictive accuracy significantly, and we explain these observed variations in the context of four factors discussed in detail below.
Quality of training set
To elucidate why some training sets exhibited significantly lower predictive accuracy than other species, we closely examined the heatmap of AUC scores (Figure 2B). We found that CJE, when used as the training set, exhibited the least performance among the predictive groups (each column as a group with the same testing set in Figure 2B). Although CJE (which belongs to ε-Proteobacteria) is distantly related to other species (Figure 1), we concluded that the extremely low AUC scores were a result of systematic biases in transposon mutagenesis (e.g., insertion-site preference, unsaturated insertion mutants, or polar effects) when essential genes in CJE were identified [53], [54]. A similar pattern was observed when HIN was used as the training set to predict essential genes in HPY, SCE and SPO. This is attributed mainly to the fact that the essential genes of HIN were obtained by integrating multiple sets of experimental data by bioinformatics methods. The poor accuracy of CJE and HIN demonstrated that the transferability of essentiality annotations between species was significantly affected by the quality of the training set. In general, the quality of essential genes identified by a genome-wide set of gene deletions was better than that identified by transposon mutagenesis, RNAi, and other methods. In subsequent experiments, CJE was removed from our study materials and the remaining 20 species were used as the training set or the testing set.
Difference in growth conditions
Papp [3] indicated that 18% to 34% of dispensable genes in SCE are not important under nutrient-rich conditions but are considered important under other conditions. Therefore, growth conditions may greatly affect predictive accuracy because of inconsistent essential gene sets in different media. For example, the growth conditions for the identification of essential genes in ECO and ACI (Acinetobacter sp. ADP1) were standard laboratory-rich (Luria-Bertani) media and minimal medium supplemented with succinate, respectively. Thus, many genes in ACI involved in the biosynthesis of important compounds are essential because these compounds are absent in minimal media. This difference in media accounts for a substantially higher percentage of essential genes in ACI (16%) than in ECO (7%). In our experiment, although ECO is more closely related to ACI than SSA (S. sanguinis), the prediction of ECO-ACI exhibited lower true positive rate (TPR = 0.60) than that of SSA-ACI (TPR = 0.63). This may be because the essential genes of SSA were identified in minimal medium, which is the same as that of ACI. Deng [30] removed 82 genes associated with biosynthesis from the ACI essential gene set. The refined data exhibited considerably better precision in predicting ECO essential genes. These results suggested that the growth conditions under which essential genes are defined in the training set should be determined because those conditions considerably affect the predictive accuracy of minimal gene subset.
Evolutionary distance between species
Deng [30] indicated that gene essentiality can be reliably predicted in a distantly related organism. However, the predictive accuracy of essential genes in closely related organisms is higher in general than that in distantly related organisms. To investigate the manner and the extent by which evolutionary distance affects predictive accuracy, we analyzed the correlation between AUC scores and divergence times (Figure 2C). The results revealed significant negative correlation between AUC scores and divergence times (R = −0.317, p = 2.7e–6). Moreover, we found that a greater evolutionary distance between organisms resulted in a larger variation in predictive accuracy.
To obtain a more general understanding of this negative correlation [55], we selected another parameter called positive predictive value (PPV), which represents the number of genes predicted and verified as essential, to assess predictive accuracy. The PPV scores were calculated by determining the proportion of true essential genes in the first 200 genes exhibiting the highest essentiality scores. By a similar method to that used for AUC matrix, the PPV matrix was then obtained to analyze the correlation between PPV scores and divergence times (Figure 2D). PPV scores showed a stronger negative correlation with divergence times than AUC scores (R = −0.431, p = 4.1e–10). The same patterns were observed in PPV scores calculated for the first 100, 300, and 400 genes (Table S4). Furthermore, we calculated the correlation between predictive accuracy and divergence times for each species used as the testing set (Table 2). Although all of the 20 species tested showed negative correlations, only those of HIN (−0.563), VCH (−0.685), HPY (−0.703), SPN (−0.495), MGE (−0.707), SCE (−0.818), and SPO (−0.850) were statistically significant. This result is likely attributable to the non-uniform divergence times between species.
Table 2. Correlation between predictive accuracy and divergence times for each species as the testing set.
| Species | R 1 | P-value2 | R 3 | P-value4 |
| ECO | −0.123 | 0.5944 | −0.153 | 0.5207 |
| STY | −0.084 | 0.7189 | −0.148 | 0.5342 |
| HIN | −0.563 | 0.0079 | −0.673 | 0.0011 |
| VCH | −0.685 | 0.0006 | −0.195 | 0.4099 |
| PAU | −0.358 | 0.1113 | −0.204 | 0.3886 |
| ACI | −0.072 | 0.7563 | −0.208 | 0.3781 |
| FTN | −0.264 | 0.2479 | −0.273 | 0.2437 |
| HPY | −0.703 | 0.0004 | −0.911 | 2.4E-8 |
| CCS | −0.098 | 0.6723 | −0.248 | 0.2915 |
| BSU | −0.248 | 0.2782 | 0.027 | 0.9095 |
| SAO | −0.350 | 0.1196 | 0.001 | 0.9971 |
| SPN | −0.495 | 0.0225 | −0.613 | 0.0041 |
| SSA | −0.267 | 0.2421 | −0.012 | 0.9583 |
| MGE | −0.707 | 0.0003 | −0.405 | 0.0769 |
| MPU | −0.211 | 0.3595 | 0.064 | 0.7878 |
| MTU | −0.294 | 0.1955 | −0.225 | 0.3397 |
| BTH | −0.309 | 0.1726 | −0.349 | 0.1310 |
| PGN | −0.255 | 0.2652 | −0.290 | 0.2147 |
| SCE | −0.818 | 6.0E-6 | −0.862 | 1.0E-6 |
| SPO | −0.850 | 1.1E-6 | −0.597 | 0.0055 |
Note: The first column indicates the species used as the testing set. R 1 refers to Pearson correlation coefficient between AUC scores and divergence times. P-value2 corresponds to the significance level of R 1. R 3 refers to Pearson correlation coefficient between PPV scores and divergence times. P-value4 corresponds to the significance level of R 3.
Difference in phenotype and lifestyle
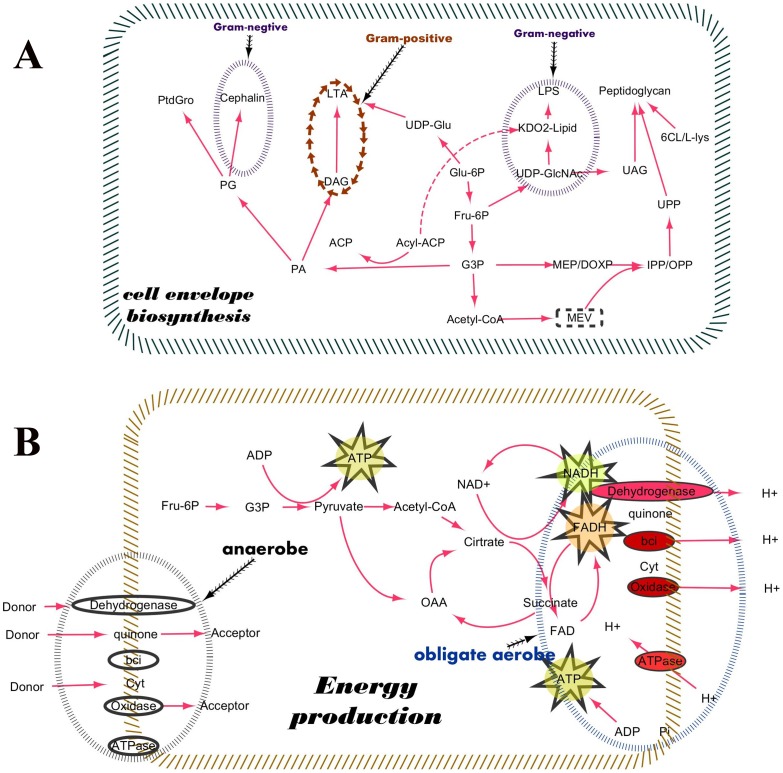
Essential genes are generally associated with three basic categories of essential functions or processes in organisms: maintenance of the cell envelope, energy production, and genetic information processing [37]. Apparent inconsistencies with this idea are observed between Gram-negative and Gram-positive bacteria in terms of cell wall biosynthesis (Figure 3A). Gram-negative bacteria contain an outer membrane with lipopolysaccharides (LPS), and many genes involved in LPS biosynthesis are essential genes. However, in Gram-positive bacteria, lipoteichoic acid (LTA) is present in their outer membrane, so the genes involved in LTA biosynthesis are essential. Different components of the cell wall or cell membrane correspond to various sets of essential genes; These results support the idea that the accuracy of prediction between species with similar cell wall structures is higher than that between species with different cell wall structures (i.e., Gram-positive or Gram-negative bacteria).
Figure 3. Difference in phenotype and lifestyle.
A) Pathway differences between Gram-positive and Gram-negative bacteria. These pathways include phosphoglycerolipid and glycerolipid metabolism, terpenoid backbone biosynthesis, peptidoglycan biosynthesis, and lipopolysaccharide biosynthesis. Bacteria are categorized as either Gram-negative or Gram-positive based on differences in their cell wall compositions. The greatest difference is that Gram-negative bacteria contain an outer membrane with lipopolysaccharides, whereas lipoteichoic acid is found in the outer membrane of Gram-positive bacteria. B) Pathway differences between anaerobic and aerobic bacteria. Bacteria possess an important respiratory chain for energy production and maintenance of redox balance. The electron transport chains between obligate aerobic and anaerobic bacteria contain several different electron donors and acceptors. Electrons can enter the chain at three levels: a dehydrogenase, a quinone pool, or a mobile cytochrome electron carrier, all of which correspond to successively lower Gibbs free energy changes.
The transferability of essentiality annotations depends greatly on the lifestyles of organisms. We found that the essentiality of electron transport chain components varies between obligate aerobic and anaerobic bacteria because they utilize different electron donors and acceptors (Figure 3B). In our prediction, SSA, which is an anaerobe, exhibited good performance (AUC score = 0.952) in predicting the essential genes of ECO, which is also an anaerobe, even though ECO is Gram-positive and SSA is Gram-negative. We mapped the genes to the KEGG pathway and found that the genes involved in energy production exhibited similar essentiality in SSA and ECO. For instance, the essentiality of many genes involved in electron transport chain components is consistent in the two bacteria. Similar lifestyles can decrease the discrepancy of essential gene distribution, thereby improving predictive accuracy.
The transferability of essentiality annotations between species is greatly affected by the quality of the training set, growth conditions, evolutionary distance, and lifestyle. In order to adequately improve predictive accuracy of the existing essential gene sets in new organisms, we next investigated the performance of incomplete training sets and integrated training sets.
Incomplete training set
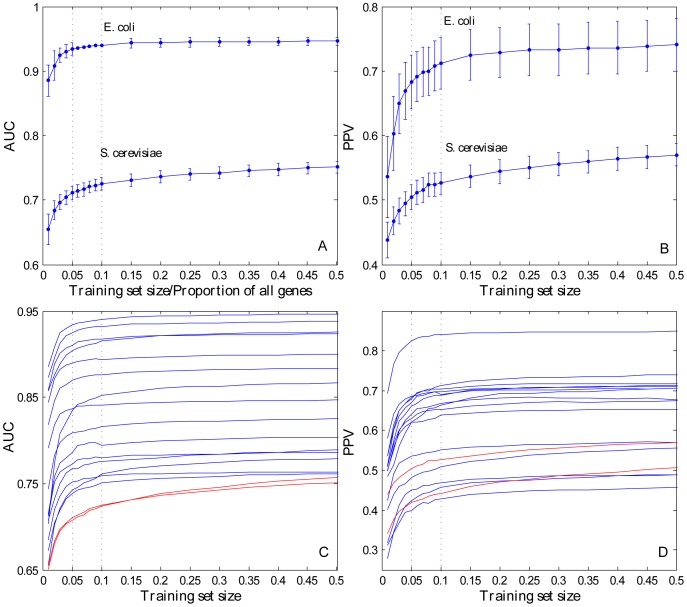
We sought to illustrate the influence of the size of a training set on essential gene prediction as follows. For species with known essential genes, 20% of the genes were randomly selected as the testing set. We gradually increased the size of the randomly selected training set from the remaining 80%. Then, we carried out the prediction and calculated AUC and PPV scores based on the training sets with different sizes. We obtained the AUC and PPV distributions and curves as well as the different sizes of training sets by simulating 1,000 replications (random selection of the training set and the testing set; Figures 4A and 4B; Table S5). The results showed that the predictive accuracy and robustness gradually improved as the size of the training set increased. In addition, the predictive accuracy improved rapidly in the previous phase (size <5%) and finally reached saturation after the size of the training set was 10% of the total genes (Figures 4C and 4D). We also found that the influence of the completeness of the training set in prokaryotes was weaker than that in eukaryotes. This result is consistent with that of a previous study in which the percentage of essential genes required to be included in the training sets in eukaryotes was reported to be twice that in prokaryotes for optimal performance [56].
Figure 4. Predictive performance with different sizes of training sets.
A) Distribution of AUC along with the different sizes of training sets in ECO and SCE. B) Distribution of PPV along with the different sizes of training sets in ECO and SCE. C) Mean curve of AUC along with the different sizes of training sets in all of the species (blue curve: 15 prokaryotes, red curve: 2 eukaryotes). D) Mean curve of PPV along with the different sizes of training sets in all species.
Integrated training sets
We investigated the integrated training set containing essential and non-essential genes from more than one species. In brief, we selected one species (e.g., ECO) as the testing set. Then, according to full enumeration, two (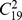 = 171), three (
= 171), three (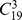 = 969), or four (
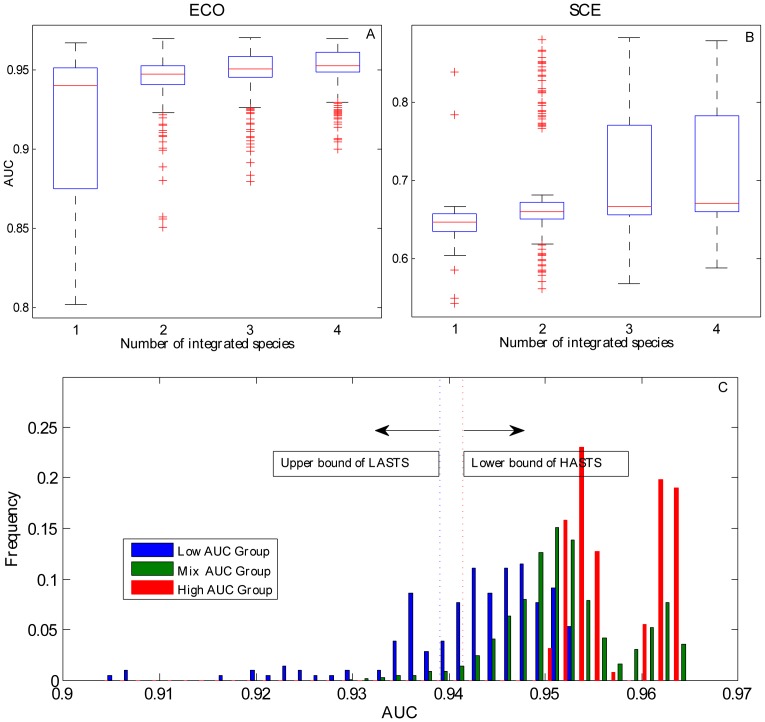
= 969), or four (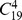 = 3876) species were chosen from the the rest of 19 species and integrated into a new training set. Subsequently, we used the new integrated training sets to construct a predictive model and compared its performance with the non-integrated training sets (the training set with only one species). Figures 5A and 5B showed the comparisons of AUC scores among the training sets (i.e., without integration, integrating two species, integrating three species, and integrating four species) when ECO and SCE were used as the testing set, respectively (for the remaining species as testing sets, see Figure S1). We observed that the prediction accuracy improved continually and significantly (t-test, p<0.01) with the number of integrated species increased in both species (i.e. ECO and SCE) used as the testing set. Similar results were obtained when other species were used as testing sets (Figures S1). We suggest that a complete and uniform essential gene set may account for the improved accuracy in the integrated training sets.
= 3876) species were chosen from the the rest of 19 species and integrated into a new training set. Subsequently, we used the new integrated training sets to construct a predictive model and compared its performance with the non-integrated training sets (the training set with only one species). Figures 5A and 5B showed the comparisons of AUC scores among the training sets (i.e., without integration, integrating two species, integrating three species, and integrating four species) when ECO and SCE were used as the testing set, respectively (for the remaining species as testing sets, see Figure S1). We observed that the prediction accuracy improved continually and significantly (t-test, p<0.01) with the number of integrated species increased in both species (i.e. ECO and SCE) used as the testing set. Similar results were obtained when other species were used as testing sets (Figures S1). We suggest that a complete and uniform essential gene set may account for the improved accuracy in the integrated training sets.
Figure 5. Performance of integrated training sets.
A) Comparison of the performance of non-integrated training sets with integrated training sets in ECO. The boxplot with X axle 1 indicates the AUC score distribution with non-integrated training sets. The boxplots with X axles 2, 3, and 4 indicate the AUC score distributions with the integrated training sets, where 2, 3, and 4 represent integration of 2, 3, and 4 species, respectively, out of the rest of the 19 species. B) Comparison of the performance of non-integrated training sets with integrated training sets in SCE. C) Comparison of the difference in diverse groups of integrated training sets. The blue histogram refers to low AUC group, the green histogram refers to mixed AUC group, and the red histogram refers to high AUC group. The blue dashed line indicates the upper bound of LASTS, and all training sets in LASTS have lower AUC score than this value. The red dashed line indicates the lower bound of HASTS, and all training sets in HASTS have higher AUC score than this value.
The integrated training set can also weaken the adverse effect of a training set exhibiting poor performance. For example, the AUC score of HIN-SSA is 0.781, which is remarkably lower than the accuracy of other training sets (0.851 to 0.941). Nevertheless, when we randomly integrated HIN with one, two, or three other species to predict the essential genes of SSA, the average AUC scores were 0.911, 0.924, or 0.928, respectively. This indicated that the predictive accuracy was improved by integrating HIN with other species. By contrast, the AUC score of SCE-SPO is 0.783, which is significantly higher than the accuracy of other training sets (t-test, p = 2.87E-12). The average AUC score was approximately 0.780 when SCE was integrated randomly with other species to predict the essential genes of SPO. The small predictive difference between the non-integrated and integrated training sets demonstrated that integrating training sets did not weaken the positive effect of training sets that exhibited excellent performance.
To further verify that integrated training sets are superior to non-integrated training set, we divided the corresponding 19 training sets (except the selected testing set) into two groups. The first group comprised nine training sets with AUC scores that exceeded a specific threshold and were defined as high AUC score training sets (HASTS). The second group comprised the remaining 10 training sets defined as low AUC score training sets (LASTS). We then selected four training sets from the HASTS and integrated them to carry out prediction. A distribution of AUC scores (high AUC group) was obtained by applying all combinations. Likewise, we established a low AUC group whose integrated training sets were obtained from the LASTS, and a mixed AUC group whose integrated training sets were obtained from both HASTS and LASTS. Figure 5C shows the distribution differences among low AUC group, mixed AUC group, and high AUC group (with ECO as the testing set). As expected, we observed that the high AUC group was significantly better than low and mixed AUC groups (t-test, p<1E-100). More importantly, although the low AUC group exhibited the worst performance, many predictions (158/210) in the low AUC group had higher AUC score than the specific threshold (0.939), which marks the best performance obtained using the non-integrated training sets. Conversely, few predictions in the high AUC group showed lower accuracy than the specific threshold (0.941).
We then compared the results of applying the four rules for good training sets described above with random selection of data sets for integration. First, we selected one species (e.g., ECO) as the testing set. Then, according to the four rules, four species (i.e. STY, PAU, BSU, and CCS, where STY is closely related to ECO) were selected for integration. All of the selected species are rod-shaped bacteria and their essential genes were obtained on nutrient-rich media. Four of them are gram-negative and facultative bacteria, and both PAU and BSU have very reliable essential gene sets. We used this integrated training set to perform predictions and obtained an AUC score which served as the threshold value. Subsequently, we randomly selected four data sets for integration and performed predictions on the same testing set (e.g., ECO). A p-value was then obtained as the proportion of 10,000 computer replications in which the simulated AUC scores exceed the threshold value. The distributions of the simulated AUC scores for all 20 species are displayed in Figure S2, and Table 3 shows the p-values for each species used as the testing set. All p-values were less than 0.05, demonstrating that selection of training sets based on the four rules yielded better performance than random selection.
Table 3. Performance of the integrated training sets under the four rules.
| Testing sets | Training sets | P-values |
| ECO | STY, PAU, BSU, CCS | 0.0080 |
| STY | ECO, PAU, BSU, FTN | 0.0037 |
| HIN | STY, PAU, SPO, SAO | 0.0024 |
| VCH | ECO, PAU, SPO, FTN | 0.0014 |
| PAU | VCH, CCS, ECO, FTN | 0.0011 |
| ACI | PAU, SSA, ECO, CCS | 0.0003 |
| FTN | VCH, PAU, ECO, BTH | 0.0048 |
| HPY | PAU, STY, ECO, VCH | 0.0013 |
| CCS | PAU, FTN, ECO, BTH | 0.0035 |
| BSU | SAO, SPN, ECO, CCS | 0.0022 |
| SAO | SPN, BSU, SCE, ECO | 0.0402 |
| SPN | SAO, HIN, ECO, SSA | 0.0095 |
| SSA | SAO, ACI, ECO, FTN | 0.0247 |
| MGE | MPU, SAO, ECO, HIN | 0.0017 |
| MPU | MGE, SAO, ECO, FTN | 0.0063 |
| MTU | SAO, HIN, ECO, CCS | 0.0034 |
| BTH | PGN, HIN, SCE, FTN | 0.0020 |
| PGN | BTH, PAU, ECO, SAO | 0.0030 |
| SCE | SPO, MGE, ECO, HPY | 0.0012 |
| SPO | SCE, MGE, ECO, HPY | 0.0147 |
Note: The first column indicates the species used as the testing set. The second column indicates the training sets selected according to the four criteria.
Conclusions
We applied a machine learning approach to predict and evaluate the essential genes reciprocally among and within 21 species whose genome-wide essentiality had been determined by experimental laboratory methods. Our results showed that selection of different training sets greatly influenced predictive accuracy. We analyzed the mechanism by which training set selection affected the transferability of essentiality annotation across organisms and developed four criteria for effective training set selection.
First, essential genes in the selected training set should be reliable. High-throughput gene disruption systems (e.g., transposon mutagenesis) could improve the efficiency of essential gene identification by permitting experimental validation, but the quality of the predicted essential gene set was definitely lower than that obtained using a genome-wide set of gene deletions. Therefore, determination of essential gene sets from databases or previous studies should be done with caution before using them. Second, the growth conditions under which the essential genes were defined in the training set selection should be identified. Gene essentiality is possibly a contextual property [6], and various growth conditions correspond to different essential gene sets. Thus, essentiality should be transferred across species under the same growth conditions. Third, the species used as the training set should be closely related to the target organism. Although Deng [30] reported that gene essentiality can be reliably predicted by using features trained and tested in a distantly related organism, our results revealed significant negative correlation between predictive accuracy and divergence times across organisms. For distantly related organisms, although few good predictions were occasionally obtained, a very large variation in predictive accuracy was observed. Fourth, organisms used as training set or prediction set should have similar phenotypes or lifestyles. We found that organisms exhibiting similar lifestyles or living in the same environment (e.g., extreme environments) may share similar essential gene sets.
We next investigated the influence of incomplete training sets on predictive accuracy within species. For organisms whose essential genes are partially identified, our results showed that the best performance in predicting the rest of the genes could be achieved when at least 10% of the total essential genes was used as training set.
Aside from incomplete training sets, we also investigated the performance of an integrated training set with multiple organisms. We found that predictions based on the integrated training set were more stable and accurate than those based on a singular training set. Furthermore, compared to random selection data sets for integration, better performance was obtained when the integrated data sets were selected according to the four criteria we determined.
Thus, our study provided valuable information regarding essential gene prediction. However, our research was performed in silico and focused only on bacteria and fungi. Further studies should be conducted to investigate the predictability of essential genes across more complex organisms, such as plants or animals.
Supporting Information
Fundamental information of the 21 species whose essential genes have been identified by different approaches. The information included the number of essential genes, morphological characters, experimental methods and so on.
(XLS)
Interquartile ranges of 21 species.
(XLS)
Divergence times among 21 species.
(XLS)
PPV matrices corresponding to the first 100, 200, 300, and 400 genes.
(XLS)
Mean and standard deviation of predictive accuracy with increasing training set size.
(XLS)
Performance of integrated training sets in the other species. The boxplot with X axle 1 indicates the AUC score distribution with non-integrated training sets. The boxplots with X axles 2, 3, and 4 indicate the AUC score distributions with the integrated training sets, where 2, 3, and 4 represent integration of 2, 3, and 4 species, respectively.
(PDF)
Distributions of the simulated AUC scores. Each frequency histogram shows the distribution of AUC scores obtained after 10,000 simulations. The red line indicates the AUC score generated by applying the four rules.
(PDF)
Acknowledgments
We are grateful to the members at the Bioinformatics Center of Northwest A&F University for many useful suggestions.
Funding Statement
The work was the project from National Natural Science Fund Program (31271917). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Itaya M (1995) An estimation of minimal genome size required for life. FEBS letters 362(3): 257–260. [DOI] [PubMed] [Google Scholar]
- 2. Kobayashi K, Ehrlich SD, Albertini A, Amati G, Andersen K, et al. (2003) Essential Bacillus subtilis genes. Proceedings of the National Academy of Sciences 100(8): 4678–4683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Papp B, Pal C, Hurst LD (2004) Metabolic network analysis of the causes and evolution of enzyme dispensability in yeast. Nature 429(6992): 661–664. [DOI] [PubMed] [Google Scholar]
- 4. Yu H, Greenbaum D, Lu HX, Zhu X, Gerstein M (2004) Genomic analysis of essentiality within protein networks. RNA 71: 817–846. [DOI] [PubMed] [Google Scholar]
- 5. Gerdes S, Edwards R, Kubal M, Fonstein M, Stevens R, et al. (2006) Essential genes on metabolic maps. Current opinion in biotechnology 17(5): 448. [DOI] [PubMed] [Google Scholar]
- 6. D'Elia MA, Pereira MP, Brown ED (2009) Are essential genes really essential? Trends in microbiology 17(10): 433–438. [DOI] [PubMed] [Google Scholar]
- 7. Dowell RD, Ryan O, Jansen A, Cheung D, Agarwala S, et al. (2010) Genotype to phenotype: a complex problem. Science 328(5977): 469–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Chalker AF, Lunsford RD (2002) Rational identification of new antibacterial drug targets that are essential for viability using a genomics-based approach. Pharmacology & therapeutics 95(1): 1–20. [DOI] [PubMed] [Google Scholar]
- 9.Cole S (2002) Comparative mycobacterial genomics as a tool for drug target and antigen discovery. European Respiratory Journal 20(36 suppl): :78s–86s. [DOI] [PubMed] [Google Scholar]
- 10. Barh D, Barve N, Gupta K, Chandra S, Jain N, et al. (2013) Exoproteome and Secretome Derived Broad Spectrum Novel Drug and Vaccine Candidates in Vibrio cholerae Targeted by Piper betel Derived Compounds. PloS one 8(1): e52773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Gibson DG, Glass JI, Lartigue C, Noskov VN, Chuang R-Y, et al. (2010) Creation of a bacterial cell controlled by a chemically synthesized genome. Science 329(5987): 52–56. [DOI] [PubMed] [Google Scholar]
- 12. RE C, BOTT T, EL M, MIR U, IFORNIA S, et al. (2007) Synthetic genome brings new life to bacterium. Science 18: 965. [Google Scholar]
- 13. Dickerson JE, Zhu A, Robertson DL, Hentges KE (2011) Defining the role of essential genes in human disease. PloS one 6(11): e27368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Georgi B, Voight BF, Bućan M (2013) From Mouse to Human: Evolutionary Genomics Analysis of Human Orthologs of Essential Genes. PLoS genetics 9(5): e1003484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Giaever G, Chu AM, Ni L, Connelly C, Riles L, et al. (2002) Functional profiling of the Saccharomyces cerevisiae genome. Nature 418(6896): 387–391. [DOI] [PubMed] [Google Scholar]
- 16. Roemer T, Jiang B, Davison J, Ketela T, Veillette K, et al. (2003) Large-scale essential gene identification in Candida albicans and applications to antifungal drug discovery. Molecular microbiology 50(1): 167–181. [DOI] [PubMed] [Google Scholar]
- 17. Cullen LM, Arndt GM (2005) Genome-wide screening for gene function using RNAi in mammalian cells. Immunology and cell biology 83(3): 217–223. [DOI] [PubMed] [Google Scholar]
- 18. Salama NR, Shepherd B, Falkow S (2004) Global transposon mutagenesis and essential gene analysis of Helicobacter pylori. Journal of bacteriology 186(23): 7926–7935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Fang G, Rocha E, Danchin A (2005) How essential are nonessential genes? Molecular biology and evolution 22(11): 2147–2156. [DOI] [PubMed] [Google Scholar]
- 20. Krasky A, Rohwer A, Schroeder J, Selzer P (2007) A combined bioinformatics and chemoinformatics approach for the development of new antiparasitic drugs. Genomics 89(1): 36–43. [DOI] [PubMed] [Google Scholar]
- 21. Kumar S, Chaudhary K, Foster JM, Novelli JF, Zhang Y, et al. (2007) Mining predicted essential genes of Brugia malayi for nematode drug targets. PloS one 2(11): e1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Holman AG, Davis PJ, Foster JM, Carlow CKS, Kumar S (2009) Computational prediction of essential genes in an unculturable endosymbiotic bacterium, Wolbachia of Brugia malayi. BMC microbiology 9(1): 243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Juhas M, Stark M, von Mering C, Lumjiaktase P, Crook DW, et al. (2012) High confidence prediction of essential genes in Burkholderia cenocepacia. PloS one 7(6): e40064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Bruccoleri RE, Dougherty TJ, Davison DB (1998) Concordance analysis of microbial genomes. Nucleic acids research 26(19): 4482–4486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Kim DU, Hayles J, Kim D, Wood V, Park HO, et al. (2010) Analysis of a genome-wide set of gene deletions in the fission yeast Schizosaccharomyces pombe. Nature biotechnology 28(6): 617–623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Seringhaus M, Paccanaro A, Borneman A, Snyder M, Gerstein M (2006) Predicting essential genes in fungal genomes. Genome research 16(9): 1126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Gustafson AM, Snitkin ES, Parker SCJ, DeLisi C, Kasif S (2006) Towards the identification of essential genes using targeted genome sequencing and comparative analysis. Bmc Genomics 7(1): 265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Acencio ML, Lemke N (2009) Towards the prediction of essential genes by integration of network topology, cellular localization and biological process information. BMC Bioinformatics 10(1): 290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Plaimas K, Eils R, König R (2010) Identifying essential genes in bacterial metabolic networks with machine learning methods. BMC systems biology 4(1): 56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Deng J, Deng L, Su S, Zhang M, Lin X, et al. (2011) Investigating the predictability of essential genes across distantly related organisms using an integrative approach. Nucleic acids research 39(3): 795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Estrada E (2006) Virtual identification of essential proteins within the protein interaction network of yeast. Proteomics 6(1): 35–40. [DOI] [PubMed] [Google Scholar]
- 32. da Silva JPM, Acencio ML, Mombach JCM, Vieira R, da Silva JC, et al. (2008) In silico network topology-based prediction of gene essentiality. Physica A: Statistical Mechanics and its Applications 387(4): 1049–1055. [Google Scholar]
- 33. Hwang Y-C, Lin C-C, Chang J-Y, Mori H, Juan H-F, et al. (2009) Predicting essential genes based on network and sequence analysis. Molecular BioSystems 5(12): 1672–1678. [DOI] [PubMed] [Google Scholar]
- 34. Chen W-H, Minguez P, Lercher MJ, Bork P (2012) OGEE: an online gene essentiality database. Nucleic acids research 40(D1): D901–D906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhang R, Ou HY, Zhang CT (2004) DEG: a database of essential genes. Nucleic acids research (suppl 1):D271. [DOI] [PMC free article] [PubMed]
- 36. Powell S, Szklarczyk D, Trachana K, Roth A, Kuhn M, et al. (2012) eggNOG v3. 0: orthologous groups covering 1133 organisms at 41 different taxonomic ranges. Nucleic acids research 2012 40(D1): D284–D289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Xu P, Ge X, Chen L, Wang X, Dou Y, et al. (2011) Genome-wide essential gene identification in Streptococcus sanguinis. Scientific reports 1.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Punta M, Coggill PC, Eberhardt RY, Mistry J, Tate J, et al. (2012) The Pfam protein families database. Nucleic acids research 40(D1): D290–D301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Finn RD, Clements J, Eddy SR (2011) HMMER web server: interactive sequence similarity searching. Nucleic acids research (suppl 2):W29–W37. [DOI] [PMC free article] [PubMed]
- 40.Szklarczyk D, Franceschini A, Kuhn M, Simonovic M, Roth A, et al. (2011) The STRING database in 2011: functional interaction networks of proteins, globally integrated and scored. Nucleic acids research (suppl 1):D561–D568. [DOI] [PMC free article] [PubMed]
- 41.Hagberg A, Swart P, S Chult D (2008) Exploring network structure, dynamics, and function using NetworkX. In: Los Alamos National Laboratory (LANL).
- 42. Lipman DJ, Souvorov A, Koonin EV, Panchenko AR, Tatusova TA (2002) The relationship of protein conservation and sequence length. BMC Evolutionary Biology 2(1): 20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Peden J (1997) CodonW. In: Trinity College.
- 44.Ohno S (1970) Evolution by gene duplication: London: George Alien & Unwin Ltd. Berlin, Heidelberg and New York: Springer-Verlag.
- 45. Gu Z, Steinmetz L, Gu X, Scharfe C, Davis R, et al. (2003) Role of duplicate genes in genetic robustness against null mutations. Nature 421(6918): 63–66. [DOI] [PubMed] [Google Scholar]
- 46. Chen W-H, Trachana K, Lercher MJ, Bork P (2012) Younger genes are less likely to be essential than older genes, and duplicates are less likely to be essential than singletons of the same age. Molecular biology and evolution 29(7): 1703–1706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Woods S, Coghlan A, Rivers D, Warnecke T, Jeffries SJ, et al. (2013) Duplication and Retention Biases of Essential and Non-Essential Genes Revealed by Systematic Knockdown Analyses. PLoS genetics 9(5): e1003330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Wang S, Sim TB, Kim Y-S, Chang Y-T (2004) Tools for target identification and validation. Current opinion in chemical biology 8(4): 371–377. [DOI] [PubMed] [Google Scholar]
- 49. Wolf YI, Novichkov PS, Karev GP, Koonin EV, Lipman DJ (2009) The universal distribution of evolutionary rates of genes and distinct characteristics of eukaryotic genes of different apparent ages. Proceedings of the National Academy of Sciences 106(18): 7273–7280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Strassburg K, Walther D, Takahashi H, Kanaya S, Kopka J (2010) Dynamic transcriptional and metabolic responses in yeast adapting to temperature stress. OMICS: A Journal of Integrative Biology 14(3): 249–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Jia X, He W, Murchie AI, Chen D (2011) The Global Transcriptional Response of Fission Yeast to Hydrogen Sulfide. PloS one 6(12): e28275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Jeong H, Oltvai ZN, Barabási A-L (2002) Prediction of protein essentiality based on genomic data. ComPlexUs 1(1): 19–28. [Google Scholar]
- 53. Stahl M, Stintzi A (2011) Identification of essential genes in C. jejuni genome highlights hyper-variable plasticity regions. Functional & integrative genomics 11(2): 241–257. [DOI] [PubMed] [Google Scholar]
- 54. Jacobs MA, Alwood A, Thaipisuttikul I, Spencer D, Haugen E, et al. (2003) Comprehensive transposon mutant library of Pseudomonas aeruginosa. Proceedings of the National Academy of Sciences 100(24): 14339–14344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Lobo JM, Jiménez-Valverde A, Real R (2008) AUC: a misleading measure of the performance of predictive distribution models. Global Ecology and Biogeography 17(2): 145–151. [Google Scholar]
- 56. Deng J, Tan L, Lin X, Lu Y, Lu LJ (2011) Exploring the optimal strategy to predict essential genes in microbes. Biomolecules 2(1): 1–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Hedges SB, Dudley J, Kumar S (2006) TimeTree: a public knowledge-base of divergence times among organisms. Bioinformatics 22(23): 2971–2972. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fundamental information of the 21 species whose essential genes have been identified by different approaches. The information included the number of essential genes, morphological characters, experimental methods and so on.
(XLS)
Interquartile ranges of 21 species.
(XLS)
Divergence times among 21 species.
(XLS)
PPV matrices corresponding to the first 100, 200, 300, and 400 genes.
(XLS)
Mean and standard deviation of predictive accuracy with increasing training set size.
(XLS)
Performance of integrated training sets in the other species. The boxplot with X axle 1 indicates the AUC score distribution with non-integrated training sets. The boxplots with X axles 2, 3, and 4 indicate the AUC score distributions with the integrated training sets, where 2, 3, and 4 represent integration of 2, 3, and 4 species, respectively.
(PDF)
Distributions of the simulated AUC scores. Each frequency histogram shows the distribution of AUC scores obtained after 10,000 simulations. The red line indicates the AUC score generated by applying the four rules.
(PDF)