Thermotaxis is a Robust Mechanism for Thermoregulation in Caenorhabditis elegans Nematodes

Abstract

Many biochemical networks are robust to variations in network or stimulus parameters. Although robustness is considered an important design principle of such networks, it is not known whether this principle also applies to higher-level biological processes such as animal behavior. In thermal gradients, Caenorhabditis elegans uses thermotaxis to bias its movement along the direction of the gradient. Here we develop a detailed, quantitative map of C. elegans thermotaxis and use these data to derive a computational model of thermotaxis in the soil, a natural environment of C. elegans. This computational analysis indicates that thermotaxis enables animals to avoid temperatures at which they cannot reproduce, to limit excursions from their adapted temperature, and to remain relatively close to the surface of the soil, where oxygen is abundant. Furthermore, our analysis reveals that this mechanism is robust to large variations in the parameters governing both worm locomotion and temperature fluctuations in the soil. We suggest that, similar to biochemical networks, animals evolve behavioral strategies that are robust, rather than strategies that rely on fine tuning of specific behavioral parameters.

Introduction

The ability to regulate body temperature (T_b) is essential for the survival of all animals. Endotherms, such as mammals and birds, can control T_b by adjusting their physiology (e.g., shivering and nonshivering thermogenesis, perspiration), their behavior (e.g., huddling, locating areas of more favorable temperatures), or both. However, ectotherms, including some reptiles and insects and all nematodes, rely solely on behavioral measures for the control of T_b and thus represent an opportunity to study such aspects of thermoregulation in isolation. It is unknown whether behavioral strategies for thermoregulation are robust to variations in the environment, or how temperature sensation drives behavior to maintain T_b within an optimal range. To address these questions, we developed a computational model of Caenorhabditis elegans thermotaxis from a detailed, quantitative analysis of behavioral responses to thermal gradients and used this model to investigate the ability of thermotaxis to regulate T_b and its robustness to genetic and environmental perturbation.

In the laboratory, spatial thermal gradients evoke two behavioral responses in C. elegans: thermotaxis (directed migration guided by changes in temperature) and isothermal tracking. Both behaviors exhibit significant plasticity in response to changes in the temperature at which adult animals are conditioned (T_c). For example, animals track narrow isotherms only within 1–2°C of T_c (Hedgecock and Russell, 1975; Mori and Ohshima, 1995; Ryu and Samuel, 2002; Luo et al., 2006). In their natural environments of soil and rotting vegetable matter (Hodgkin and Doniach, 1997; Barrière and Félix, 2005b; Kiontke and Sudhaus, 2006), C. elegans encounter a complex thermal environment in which temperature varies with time of day, distance from the surface, and across the seasons. Over the course of a day, soil temperature can vary by tens of degrees Celsius in these environments (Thorpe, 1974; Robinson, 1994; Chacko and Renuka, 2002). For several reasons, avoiding such considerable temperature fluctuations is likely to be important. First, many aspects of C. elegans physiology and behavior are known to be temperature sensitive, including growth rate (Byerly et al., 1976), lifespan (Lakowski and Hekimi, 1996), locomotion (Dusenbery et al., 1978; Dusenbery and Barr, 1980), and reproductive success (Anderson and Coleman, 1982; Gutteling et al., 2007; Harvey and Viney, 2007). Second, prolonged exposure to temperatures higher than the critical maximum temperature (CT_max) for reproduction, which for C. elegans is near 26°C (M. Ailion and J. H. Thomas, personal communication), is detrimental to survival. Third, minimizing deviations of T_b from the conditioned temperature is likely to be advantageous as physiological processes may be tuned to function efficiently near T_c. Because temperature variations decrease with depth, one strategy for both avoiding warm temperatures and moderating T_b is to burrow deep enough into the soil to be insulated from diurnal temperature variations altogether. Although this may serve as an effective strategy for thermoregulation, following it imposes a cost: limited access to oxygen. Thus, a behavioral mechanism that maintains T_b within a desired range without straying far from the soil surface is clearly desirable.

Here, we leverage comprehensive empirical studies of C. elegans thermotaxis to test the hypothesis that this behavior is an effective mechanism for maintaining T_b within a narrow range in soil, despite the complex spatiotemporal thermal landscape that this environment presents. To do this, we simulated the response of single worms to soil-like thermal environments. An appealing feature of our simulation is that all relevant parameters have been measured: there are no free parameters. We find that compared with a random walk, thermotaxis decreases exposure to temperatures warmer than the critical maximum for reproduction and minimizes deviations from T_c, while maintaining animals close to the soil surface. With respect to these outcomes, thermotaxis also outperforms simple strategies like isothermal tracking. We used the simulation to ask how robust these outcomes are to variations in environmental, behavioral, and genetic parameters. This analysis revealed the ability to maintain T_b below the critical maximum for reproduction was remarkably robust. These findings indicate that C. elegans thermotaxis is an effective strategy for thermoregulation and suggest that it is robust to both environmental and genetic perturbation in the evolutionary sense.

Materials and Methods

Nematode strains and culture.

Wild-type (N2, Bristol) worms were provided by the Caenorhabditis Genetics Center, thawed from frozen stock every 30–60 d, and cultivated with OP-50 Escherichia coli bacteria following standard procedures (Brenner, 1974). Unless indicated, we used synchronized populations of well fed young adult worms in all experiments. To avoid possible developmental effects of temperature, all worms were maintained at 20°C until the L4 larval stage and then transferred, if required, to plates at the desired temperature.

Thermal response assays.

Thermal gradients were generated across an aluminum plate (25 cm l × 12 cm w, 1.6 mm thick) using water-cooled thermoelectric (Peltier) devices (MCW50-T and MCW60-T VGA Coolers, Swiftech). A Peltier device was placed at each end of an aluminum plate and controlled by computer-programmable proportional-integral-derivative (PID) controllers (5C7–365 and 5C7–378, McShane). Feedback was provided by a thermistor (1 mm d × 3.2 mm l, TS91-170, McShane) in contact with the aluminum plate and in close proximity to the Peltier device, ensuring that each end of the plate was clamped at a fixed temperature. Rectangular Petri dishes (7.6 cm l × 5 cm w × 1 cm d, Lab Scientific) containing 15 ml of nematode growth medium (NGM) + 2% agar were placed on the aluminum plate and allowed to equilibrate (typically within 10 min), generating a linear thermal gradient across the agar surface. The position of the Petri dish on the aluminum plate and the settings of the temperature controllers were selected to achieve the desired gradient steepness and temperature at the center of the dish (T_start). Gradient and T_start were confirmed by measuring the temperature at the agar surface using a small thermistor (0.5 mm d × 2.2 mm l, TS91-196, McShane). Measurements assessing gradient linearity and accuracy of the thermal gradients are shown in supplemental Figure S1 (available at www.jneurosci.org as supplemental material).

When Petri dishes reached thermal equilibrium, ∼100–300 young adult worms were rinsed from culture plates into 1.5 ml centrifuge tubes, washed twice with ddH₂O, and transferred in suspension to a narrow (0.5 cm) starting zone at the center of the dishes. Between washes, worms were collected at the bottom of the tube by applying a brief (<3 s) pulse in a low-speed bench-top microcentrifuge. Worms were dispersed within the starting zone by gentle brushing of the worm suspension. Time 0 was set as the time when worms began crawling away from the starting zone, typically ∼2 min after transfer to the assay plate, and experiments were terminated after 10 min by killing worms in situ using chloroform vapor. The final position of each worm was marked and used to calculate a thermotaxis index, TI = (W − C)/(W + C), where W and C are the number of animals on the warmer and cooler sides of the assay plate, respectively. Images of each assay plate were scanned for archival purposes (Epson Perfection 1250). For statistical analyses, we used a Lilliefors test to confirm normality of TI distributions and a two-tailed t test to determine whether the mean of the distribution is significantly different from zero, accounting for multiple comparisons using the Bonferroni correction.

Video analysis of worm locomotion as a function of temperature.

We analyzed the movement of individual worms at constant temperature and in response to temporal temperature ramps with an automated video-based worm tracker described previously (Chalasani et al., 2007; Ramot et al., 2008). We used the tracker to measure three parameters (speed, mean run duration, and mean pirouette duration) and to test the hypothesis that thermotaxis is achieved by a biased random walk strategy. For each assay, we transferred ∼30–50 worms to an agar surface formed by adding NGM agar (5 ml) to a single-well chamber slide (LabTek II, Nalge Nunc International). The chamber slide was placed onto the surface of a custom temperature controller (see below) mounted on a dissecting microscope equipped with a macro zoom lens (Navitar). Worms were illuminated obliquely by a ring-light (19/32.5 mm, Schott Fostec), and movie capture began when most of the worms dispersed from their initial starting position.

We controlled the temperature experienced by worms during video capture using a mirror-polished aluminum block (8.3 cm l × 7.6 cm w, 0.6 mm thick, McMaster-Carr) that was in direct contact with a thermoelectric (Peltier) device (3 cm × 3 cm, TE Technology). Water circulated below the Peltier within a heat sink (Cygnus Technology), allowing direct contact between the top surface of the TEC and the aluminum block. To control temperature, we used a computer-programmable PID controller (5C7–378, McShane). Feedback to the controller was provided by a small thermistor (TS91-196) lightly embedded in the agar. The PID was programmed to maintain the feedback thermistor at a fixed temperature. To generate temperature ramps, custom-written software in MATLAB (The MathWorks) continuously monitored the temperature at the feedback thermistor and updated controller settings to produce ramp rates within a defined range. This arrangement produced linear temporal thermal gradients that were uniform across the entire agar surface (data not shown). We generated a record of the temperature imposed during each experiment by digitizing the output of the feedback thermistor (sample rate: 3 Hz). The temperature record was manually synchronized to the video stream; the time differential was always <1 s, corresponding to a maximum error of 0.02°C at the ramp rates used in our experiments.

Model of C. elegans thermotaxis: assumptions.

We developed a computational model of C. elegans thermotaxis based on the following eight assumptions: (1) worm locomotion is comprised of straight runs punctuated by abrupt turns (pirouettes); (2) run speed is a function of temperature; all runs at a given temperature have the same constant speed; (3) after a pirouette, all run orientations are equally probable; (4) on a thermal gradient, worms perform thermotaxis by modulating the durations of runs; (5) the probability distribution governing run durations is a function of temperature (T), the conditioning temperature (T_c), and the rate of temperature change (dT/dt); (6) run termination is governed by Poisson statistics: for every combination of T, T_c, and dT/dt, run durations are exponentially distributed; (7) Pirouettes are performed “in place”: the total displacement during a pirouette is negligible; and (8) pirouette durations are also exponentially distributed.

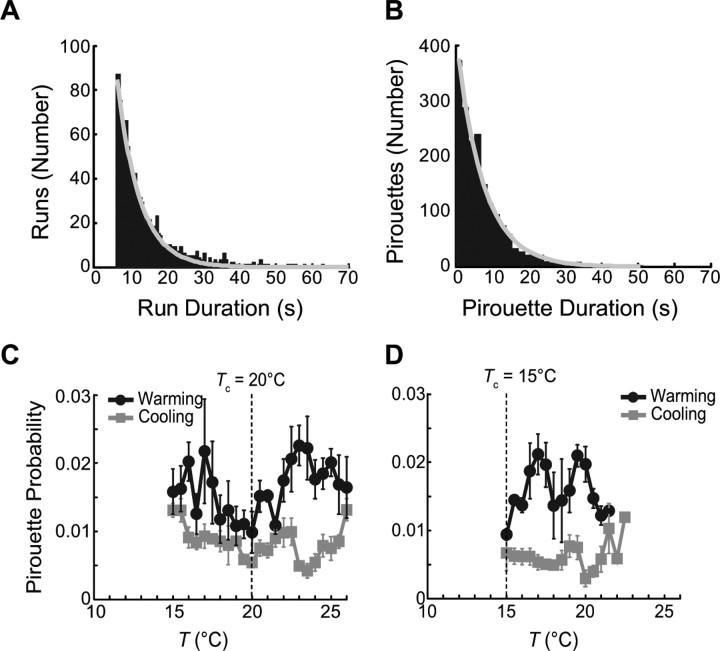
Although the assumptions above are an idealization of worm locomotion, a number of studies (Pierce-Shimomura et al., 1999; Ryu and Samuel, 2002; Zariwala et al., 2003; Luo et al., 2006; Clark et al., 2007) suggest that all are good approximations of C. elegans locomotion in general, and of its behavior in thermal gradients in particular. Furthermore, our analysis of worm locomotion at constant temperature and in temporal thermal gradients (Fig. 1) provides additional support for this view of worm thermotaxis. Consistent with a two-state model for worm locomotion, histograms of run and pirouette durations in isothermal environments were well fit by single exponentials (Fig. 1A,B). When subjected to temperature ramps, worms modulated turning rates in a manner that supports the hypothesis that a biased random walk model accounts for thermotaxis behavior (Fig. 1C,D). Matsuoka et al. (2008) have recently used a similar, although somewhat simplified, set of assumptions to generate Monte Carlo simulations of C. elegans behavior in linear thermal gradients.

Figure 1.

Worm movement is described by two states: runs and pirouettes. Run durations (A) and pirouette durations (B) are exponentially distributed at constant temperature. Data are pooled from experiments at 15°C (n = 3 assays), 20°C (n = 3), 22.5°C (n = 1), and 25°C (n = 3), and binned at 0.5 s intervals (runs) and 1.7 s intervals (pirouettes). Gray lines are exponential fits to the data (τ = 6.2 s and 7.4 s for runs and pirouettes, respectively). C, D, Warming above T_c increases pirouette probability. Pirouette initiation probability, P_ip, in response to warming (black circles) and cooling (gray squares) is plotted against temperature for worms conditioned at 20°C (C) and 15°C (D). Points are mean ± SEM (n = 3–5). At constant temperature (15, 20, and 22.5°C), P_ip was 0.008 ± 0.001.

Derivation and estimation of V_drift.

As previously demonstrated for bacteria (Lovely and Dahlquist, 1975), motion that satisfies the assumptions presented above is analogous to the diffusion of a particle drifting at constant velocity. Thus, the behavior of C. elegans in thermal response assays can be represented as a simple process of diffusion with drift. Framing thermotaxis in this manner allows the “macroscopic” measure TI, which we use to quantify the response of worm populations in thermal response assays, to be converted into a “microscopic” measure V_drift, the drift velocity of a single worm in a thermal gradient. Like TI, V_drift is a function of T, gradient steepness (∂T/∂z), and T_c. Below we develop a method for directly deriving from TI values the drift velocity V_drift of individual worms at different T, T_c, and gradient steepness conditions; we then use V_drift estimates to simulate the motion of individual worms in soil.

In natural environments, worms disperse freely in three dimensions; however, in thermal response assays the worms' motion is constrained in two dimensions. Because only the component of the worms' displacement in the direction of the gradient (x) contributes to TI, we can use the following familiar results for diffusion in one dimension to describe the distribution of the population of worms at time t:

V_drift is the worms' drift velocity up or down the gradient, and D is the diffusion coefficient, given by v_x²τα/2, where v_x is the component of the run speed in the x direction (denoted v in the remainder of the text, for simplicity), τ is the mean run duration, α is the ratio τ/(τ + τ_p), and τ_p is the mean pirouette duration (Lovely and Dahlquist, 1975; Berg, 1993). Thus, the standard deviation σ_x of the distribution of worms at time t is as follows:

Because v varies with temperature, σ_x is also temperature dependent.

At temperatures near T_c, worms track isotherms perpendicular to the thermal gradient for extended periods of time (Hedgecock and Russell, 1975; Mori and Ohshima, 1995; Ryu and Samuel, 2002; Luo et al., 2006). Thus, an additional factor must be included in Equation 3 to account for such isothermal tracking. In the thermal response assay, the x component of worms moving isothermally is zero. Such movement reduces the standard deviation of the worm distribution by a factor of (1 − f_track)^1/2, where f_track is the fraction of time (of the total time t) worms spend tracking isotherms. (Intuitively, tracking can be thought of as multiplying t, the time spent diffusing, by a factor of 1 − f_track.) Isothermal tracking behavior is active only within a narrow temperature range set by T_c. When T_c = 20°C, the range for isothermal tracking is centered at ∼20°C. The tracking range shifts with T_c, although the shift is incomplete; for example, worms cultivated at 25°C track isotherms near ∼24°C (Biron et al., 2006). Following Biron et al. (2006), we refer to the average temperature of isothermal tracks as T_s. Luo et al. (2006) found that ∼90% of isothermal tracks are observed within ±1°C of T_s, although other studies have reported tracking up to ∼2°C from T_s (Hedgecock and Russell, 1975; Mori and Ohshima, 1995; Ryu and Samuel, 2002). Luo et al. (2006) provide a useful quantification of isothermal tracking for worms cultivated at 20°C; they report the percentage of time spent by worms in isothermal tracking as a function of gradient steepness. We used these data to estimate f_track and thus account for isothermal tracking in thermal response assays; for any T_start within ±1°C of T_s, we assumed worms tracked isotherms for the percentage of time given by Luo et al. (2006). In an attempt to approximate the data reported by Biron et al. (2006) with a simple relationship, T_s was assumed to equal 20 + 0.8(T_c − 20).

From Equations 1 and 3, if x = 0 for all worms at t = 0, then TI at time t can be approximated by the following:

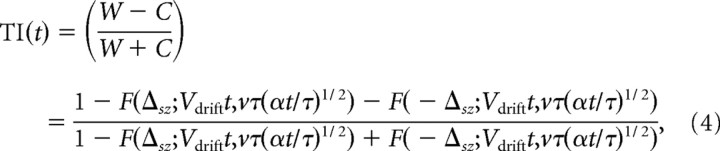where F(x;μ,σ) denotes the cumulative normal distribution with mean μ and standard deviation σ evaluated at x. Δ_sz is equal to 0.25 cm (half the width of the starting zone), and is included in the equation to account for the fact that worms found within the narrow 0.5 cm starting zone (−0.25 ≤ x ≤ 0.25) at the end of the experiment do not contribute to TI. Because t = 10 min (the duration of the assay), and experimental data for estimating v, τ, and α are available (to calculate v we assumed T = T_start for the duration of the assay), we can obtain the value of V_drift that satisfies Equation 4 for every TI measured in the thermal response assay. V_drift calculated in this manner provides the desired link between TI and the motion of worms in the simulated soil environment.

We used the MATLAB function fminsearch [which employs the simplex search method (Lagarias et al., 1998)] to find V_drift values that minimize the square difference between the TI calculated by Equation 4 and each of our experimental TI values. This approach provides an estimate of V_drift provided the following four assumptions are satisfied: (1) Unbounded dispersal along the direction of the gradient. In practice, worms cannot crawl beyond the ends of the assay plate (|x| < 3.8 cm). Because this limit was rarely reached in our 10 min assays, errors resulting from assuming unbounded dispersal are likely to be small. (2) All worms disperse from x = 0. In our experimental setup, worms were distributed within a 0.5 cm starting zone at the beginning of each experiment; i.e., at t = 0, x is in the range [−0.25 cm, 0.25 cm]. Assuming that the initial distribution had no bias in the x direction, deviations from this assumption are also expected to produce minor inaccuracies in our estimate of V_drift. (3) All worms begin moving at precisely the same time. In practice, worms begin dispersing as the transfer droplet dries, resulting in a range of start times. However, the variability in start times was small compared with the duration of the assay. (4) Worms move at a constant speed and respond with a fixed TI (and hence fixed V_drift) throughout the 10 min experiment. In thermal response assays, as worms disperse from the starting zone they experience a range of temperatures, and thus move with a range of speeds (which alters D) and respond with a range of TI values.

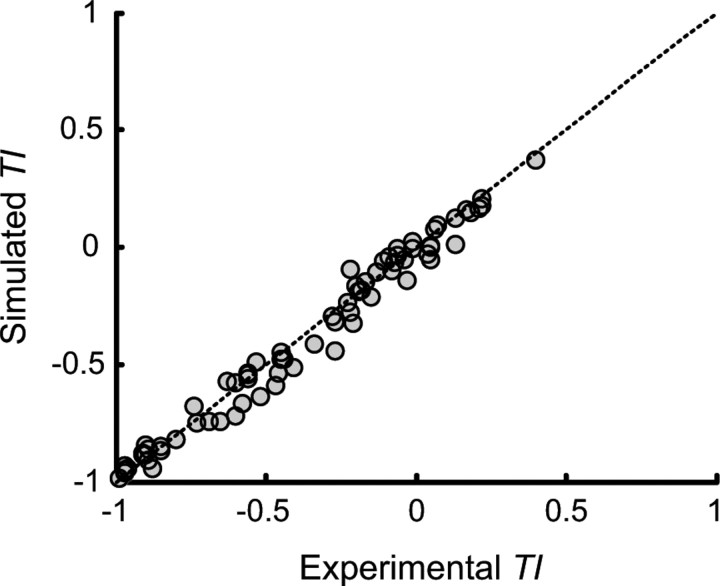
To confirm our derivation of V_drift and assess the magnitude of any errors resulting from the approximations discussed above, we asked whether worms diffusing with D = v²τα/2 and V_drift yield TIs that match experimental TI values. Our experimental data included TI values for 73 combinations of T_start, T_c, and gradient steepness. For each such combination, we applied the diffusion model and our estimate of V_drift derived from Equation 4 to obtain a predicted TI. Predicted TI values were computed by Monte Carlo simulation of 300 worms dispersing from a 0.5 cm starting zone at the center of a 7.6 cm plate. Worms were randomly distributed within the starting zone at time 0, and dispersed from the starting zone by randomly oriented runs whose durations were drawn from an exponential distribution (Fig. 1A). Run speed (v) varied with temperature as described in the following section. Runs were punctuated by pirouettes, whose durations were drawn from a second exponential distribution (Fig. 1B). During pirouettes the worms' speed was assumed to be zero. Superimposed on this isotropic diffusion was motion in the x direction at speed V_drift calculated using (Equation 4). T_c and T (and therefore v and V_drift) were updated for all worms at each time step of the simulation. Within ±1°C of T_c, worms initiated isothermal tracks with a probability derived from the data in Luo et al. (2006). Isothermal tracks could be initiated after both pirouettes and runs, and their duration was drawn from an exponential distribution with τ = 80 s (Luo et al., 2006). We computed the position of each worm at the end of 10 min of simulation, and counted all worms outside the starting zone to obtain a TI for the simulated thermal response assay. The simulations thus took into account all aspects of the thermal response assay, except for assumption 3 above. Simulated assays were repeated 40 times for each combination of T_start, T_c, and gradient steepness to obtain an average simulated TI value. We found that TIs simulated in this manner were tightly correlated with the experimental TIs used to derive V_drift (Fig. 2). The RMS error of simulated TIs versus experimental TIs was 0.06, and every simulated TI was within one standard deviation of its corresponding experimental TI (with one exception: at T_c = 15°C, T_start = 18°C, and gradient 1°C/cm, experimental TI was −0.97 ± 0.01, mean simulated TI was −0.93). Thus, although several of the assumptions associated with Equation 4 are imperfect, the model reproduces the original TI measurements with satisfactory fidelity.

Figure 2.

Simulated versus experimental TIs across all conditioning temperatures and gradients tested. The dotted line indicates experimental TI = simulated TI. R² = 0.98.

Simulation: general description and modes.

We used two complementary approaches to simulate the motion of C. elegans in soil. In one mode, we simulated the behavior of a population of worms by computing the mean depth of the population as a function of time, 〈z(t)〉. In the second mode, we modeled the stochastic motion of individual worms in the z direction. In both modes, at each time step i we computed the temperature T_i, temperature derivatives ∂T_i/∂t and ∂T_i/∂z, depth z_i or 〈z_i〉 (measured relative to the soil surface), and memory of temperature experience T_c,i. T_i was calculated from Equation 10 (see Results); ∂T_i/∂t and ∂T_i/∂z were calculated by differentiating Equation 10 with respect to either t or z. The simulation time step Δt was set to 1 s for all runs. Setting Δt to 0.5, 2, or even 5 s had no appreciable effect on the outcomes of the simulations (data not shown).

Computing depth (z or 〈z〉).

C. elegans thermotaxis is a function of T, T_c, and thermal gradient steepness, which vary continuously in the soil. V_drift, derived from experimentally measured TI values, provided the key measure for simulating thermotaxis in soil. At each time step i of the simulation, we estimated V_drift for T_i, T_c,i, and ∂T_i/∂z. ∂T/∂t was neglected because its amplitude never exceeded 0.0011°C/s, approximately an order of magnitude smaller than the minimal temporal stimulus reported to elicit a thermotaxis response in C. elegans (Clark et al., 2007). As V_drift values were measured with a resolution of 1–2°C for T, at three or four gradient values and at three T_c values, we used linear interpolation to assess the value of V_drift for any T_i and ∂T_i/∂z. To account for changes in T_c we defined three “regimes”: for T_c between 17.5 and 22.5°C, we used V_drift (TI) data obtained from worms cultivated at 20°C; for T_c < 17.5°C, we used data from worms maintained at 15°C, and for T_c > 22.5°C, we used data from worms grown at 23°C. We implemented hysteresis across a narrow range (0.2°C) when worms transitioned between T_c regimes.

In the population mode, Δ〈z_i〉, the change in depth of the population mean at step i, is given by the following:

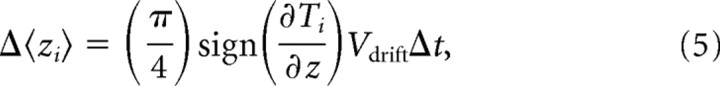where Δt is the size of the time step of the simulation. π/4 is a factor that corrects for using V_drift values obtained from two-dimensional thermal response assays to describe motion in three dimensions in soil. In simulations of constitutive migration up or down thermal gradients (see Fig. 6A), Δ〈z_i〉 equaled sign(∂T_i/∂z)v_wΔt or −sign(∂T_i/∂z)v_wΔt, respectively. For ∂T_i/∂z ≥ 0.1°C/cm, v_w equaled the average locomotion speed (supplemental Fig. S2, available at www.jneurosci.org as supplemental material). For ∂T_i/∂z < 0.1°C/cm, v_w = v[(dT_i/dz)/0.1].

Figure 6.

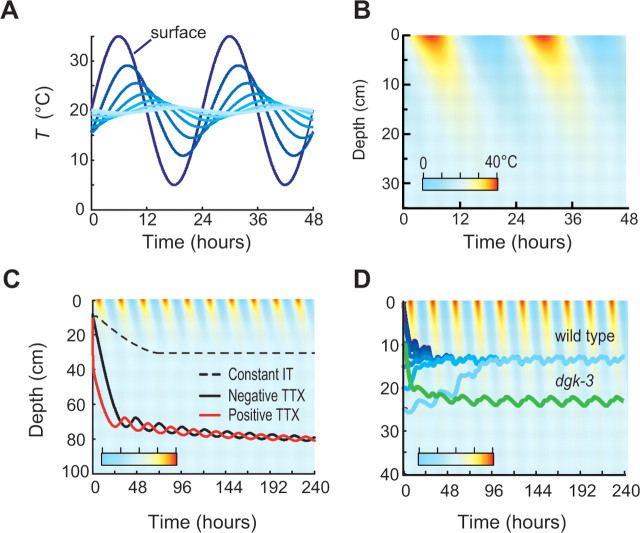
Spatiotemporal dynamics of temperature in soil-like environments and their effect on the distribution of worms using fixed and plastic thermotaxis strategies. A, Simulated variation in temperature as a function of time of day and distance from the soil surface. Smooth lines were calculated from Equation 10 using T_ave = 20°C, T_1/2 = 15°C, and z_d = 10 cm. Traces progress from dark blue (0 cm, surface) to light blue (35 cm) in 5 cm increments. B, Simulated heat map of the variation in temperature as a function of distance from the soil surface (ordinate) and time of day (abscissa). C, Constant isothermal tracking, positive and negative thermotaxis. Lines show the mean depth (relative to the soil surface) versus time of day of a simulated population of worms migrating either up or down the thermal gradient at all temperatures, or performing continuous isothermal tracking. D, T_c-dependent thermotaxis in wild-type (blue) and dgk-3 (green) worms. Mean depth versus time of day of a population of wild-type worms performing thermotaxis as measured in Figure 4. Shade indicates starting depth (same color scheme as in A). For all simulations, T_ave = 20°C, T_1/2 = 15°C, and z_d = 10 cm. Simulated behavioral responses in C and D are superimposed on a color image of temperature variation. Deep blue is 0°C, and red is 40°C.

In the single-animal mode, simulated worms stochastically transitioned between runs and pirouettes. Run and pirouette durations were drawn from exponential distributions. Pirouettes were assumed to generate zero displacement. Runs were associated with a randomly selected direction, such that the stochastic component of Δz_i was constant for each run and given by Δz_i = vΔtcos(cos⁻¹(1 − 2 × rand)) = vΔt(1 − 2 × rand), where rand is a pseudorandom number uniformly distributed between 0 and 1. Superimposed on this stochastic motion was the thermotaxis response given in Equation 5.

Updating T_c. T_c has been shown to follow an exponential time course after a shift to a new constant temperature (Biron et al., 2006). Thus, the change in T_c at time step i, ΔT_c,i, can be described by the following:

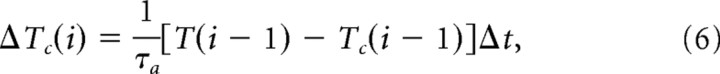where T(i − 1) and T_c(i − 1) are the temperature and T_c at time step i − 1, and τ_a is the time constant for adapting to a new T_c. Following Biron et al. (2006), we used different values of τ_a for T > T_c (τ_up) and for T < T_c (τ_down) (see Table 1).

Table 1.

Parameter values used for simulations

Parameter name	Condition	Value	Source
τup	T > Tc	1.6 h	Biron et al. (2006)
τdown	T < Tc	1.8 h	Biron et al. (2006)
Run duration, τ		13.4 s	This study
Pirouette duration, τp		6.7 s	This study

Modeling isothermal tracking.

During isothermal tracking, worms crawl in a direction, relative to the thermal gradient, that allows a constant temperature to be maintained. In the soil, this requirement can be expressed as follows:

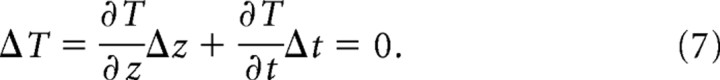Thus, during isothermal tracking, Δz_i is given by the following:

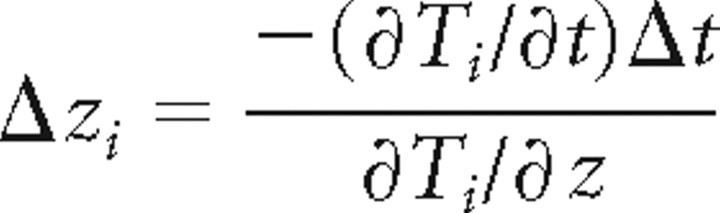In the soil, tracking is possible as long as the worm can move sufficiently rapidly to generate a rate of temperature change that equals or exceeds ∂T/∂t:

Constitutive isothermal tracking was modeled by assuming worms moved with Δz_i given by Equation 8 whenever the condition in Equation 9 was satisfied and as long as ∂T_i/∂z was greater than a threshold [set to 0.1°C/cm (see Luo et al., 2006)]; otherwise, they dispersed randomly (for the population mode, we assumed no change in mean depth when Equation 9 was not satisfied).

Parameter values.

Parameter values for mean run and pirouette durations and adaptation rates are given in Table 1, unless otherwise noted. Both mean run duration and mean pirouette duration displayed little, if any, temperature dependence. [Values measured at three constant temperatures were not significantly different from one another (one-way ANOVA p = 0.14 and p = 0.64 for run and pirouette durations, respectively, measured at 15, 20, and 25°C). Additionally, mean pirouette durations during thermal ramps were not significantly different from those measured at constant temperature (two-tailed t test, p = 0.53).] Run speed, in contrast, showed a quadratic dependence on temperature (supplemental Fig. S2, available at www.jneurosci.org as supplemental material). The idea that worm speed reaches a maximum between 20°C and 25°C, and declines at both cooler and warmer temperatures has been confirmed by several previous studies (Dusenbery et al., 1978; Dusenbery and Barr, 1980; Dusenbery, 1989). The fit to our data predicts worms would stop moving at temperatures <10.9°C and >33°C, in good agreement with experimental observations (Dusenbery and Barr, 1980; Dusenbery, 1989). Values for run speed were, therefore, computed from the fit to these data.

Values of τ_up and τ_down were measured by Biron et al. (2006) and are consistent with data from Hedgecock and Russell (1975) and Mohri et al. (2005). Values for v, τ, and τ_p were obtained from data collected using the video-based tracker (Fig. 1; supplemental Fig. S2, available at www.jneurosci.org as supplemental material). Our estimate of v is similar to a previously published value for worm speed (Pierce-Shimomura et al., 1999), although it is approximately one-half of another published value (Ryu and Samuel, 2002). Our measurement of τ is a factor of two smaller than previously reported mean run durations (Pierce-Shimomura et al., 1999; Ryu and Samuel, 2002; Luo et al., 2006), most likely because of a higher density of animals in our experiments, which resulted in undersampling of long runs (the tracking software did not track worms that came into contact with other worms). Thermal response assays were also performed at a relatively high density of worms (typically 200–300 per assay).

Initial conditions.

Three simulation parameters required initialization: the phase of the daily temperature variation, the starting depth and the initial T_c of the worms. Unless otherwise stated, all simulations began at t = 0 s, z = 10 cm, and T_c = T_ave (where T_ave is the average soil temperature). Increasing the initial depth delays the time required to converge on a constant depth (see Results), whereas varying initial T_c and t values had minimal effect on the quantitative results of the simulation and no effect on the qualitative results (data not shown).

Results

A comprehensive map of C. elegans thermotaxis

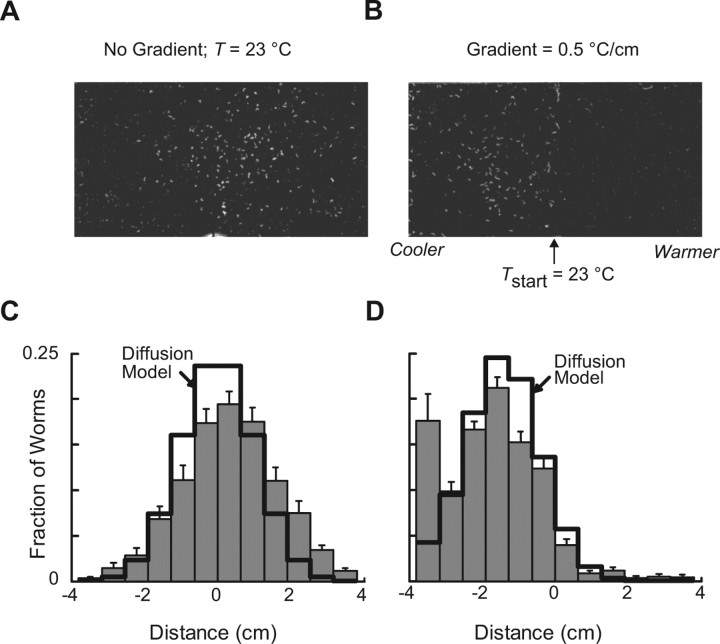
Although C. elegans thermotaxis has been the focus of a number of studies (Hedgecock and Russell, 1975; Ryu and Samuel, 2002; Yamada and Ohshima, 2003; Zariwala et al., 2003; Ito et al., 2006; Anderson et al., 2007; Clark et al., 2007), a comprehensive characterization of how thermotaxis varies with gradient steepness is lacking. We therefore mapped the response of worms to temperatures and thermal gradients that span the range of values likely to be encountered in soil-like thermal environments. To do this, we used a modified version of the thermal preference assay first described by Hedgecock and Russell (1975). In this assay, worms are conditioned at a temperature T_c, placed on a linear thermal gradient formed on an agar surface, and allowed to disperse for 10 min from a defined starting temperature, T_start. Under isothermal conditions, worms disperse from the starting zone at random; the distribution after 10 min is essentially Gaussian (Fig. 3A,C). In the presence of a thermal gradient, in contrast, worms bias their movement such that the final distribution resembles a Gaussian shifted toward colder temperatures (Fig. 3B,D). To quantify these distributions, we used a thermotaxis index, TI = (W − C)/(W + C), where W and C are the number of animals on the warmer and cooler sides of the assay plate, respectively. Thus, TI values greater than zero reflect migration toward warmer temperatures (positive thermotaxis), whereas values less than zero indicate migration toward cooler temperatures (negative thermotaxis). Values close to zero reflect conditions under which animals have no bias for either warmer or cooler temperatures. We selected this simple measure of thermotaxis to streamline data collection and analysis and facilitate comparison with previous studies that used the same metric (Hedgecock and Russell, 1975), and because, as shown below, this single value is sufficient to capture most, if not all features of the worms' distribution at the conclusion of the assay.

Figure 3.

Diffusion with drift captures the essential features of the response to spatial thermal gradients. A, B, Representative distributions of worms conditioned at 20°C and exposed to constant temperature (23°C) (A) or a 0.5°C/cm gradient (B) for 10 min. Images are scans of assay plates; bright white spots are worms. C, D, Average distributions of worms conditioned at 20°C and exposed to constant temperature (23°C) (C) or a 0.5°C/cm gradient (D) for 10 min. Gray bars are the mean ± SEM (n = 6 assays). Solid black lines were calculated from a simple diffusion with drift model, as described in Results.

How can a single TI value capture a seemingly complex thermotaxis response? C. elegans locomotion is composed of periods of forward movement (runs) interrupted by complex turns or reversals called “pirouettes” (Croll, 1975; Pierce-Shimomura et al., 1999; Tsalik and Hobert, 2003; Wakabayashi et al., 2004; Gray et al., 2005). Distributions of run and pirouette durations are well fit by single exponentials (Fig. 1A,B) (Pierce-Shimomura et al., 1999; Ryu and Samuel, 2002), suggesting that worm movement can be described by a simple, two-state model that is analogous to a random walk. To achieve thermotaxis, C. elegans extends runs in favorable directions (by suppressing pirouettes) and shortens unfavorably directed runs (Fig. 1C,D) (Ryu and Samuel, 2002; Zariwala et al., 2003; Clark et al., 2007). This strategy, which is also used by C. elegans to locate attractive chemicals (Pierce-Shimomura et al., 1999), is similar in many respects to the one responsible for bacterial chemotaxis (Berg and Brown, 1972).

Behaviors mediated by a biased random walk can be thought of as equivalent to diffusion with drift, provided a small set of formal assumptions are met (Lovely and Dahlquist, 1975). Because C. elegans thermotaxis satisfies this set of assumptions (see Materials and Methods), the distribution of worms exposed to a thermal gradient for time t can be approximated by a normal distribution with mean V_driftt and standard deviation (2Dt)^1/2, where V_drift is the drift velocity of worms in the thermal gradient, and D is the diffusion coefficient. The diffusion coefficient D is a function of the worms' speed, mean pirouette duration, and mean run duration. We measured all three parameters as a function of temperature (Fig. 1; supplemental Fig. S2, available at www.jneurosci.org as supplemental material). Given D, we now lack only V_drift to achieve a complete description of the distribution of worms at the end of the assay. As there exists a one-to-one correspondence between V_drift and TI, measuring TI is sufficient for reconstructing the entire worm distribution. (A detailed account of this derivation is given in Materials and Methods.)

In support of this theoretical argument, a diffusion-with-drift model which uses measured TI values to estimate V_drift reproduces the salient features of experimentally observed worm distributions in the absence and presence of a thermal gradient (Fig. 3C,D, solid lines). The model fails to account for the “edge effect” caused by the finite size of the assay plate (Fig. 3D). Nevertheless, the model is able to predict with reasonable accuracy the mean and standard deviation of the experimental distributions despite the fact that it does not make use of any information from the experimental distributions other than TI. Additional experimental support for our model comes from a study by Anderson et al. (2007), who showed that worm distributions at constant temperature are well fit by a simple diffusion model.

To ensure adequate representation of naturalistic thermal environments we measured TI for T_c and T_start values that span the physiological temperature range of C. elegans (15–26°C) and at thermal gradients likely to be experienced in soil-like thermal environments. In field measurements of temperature variation in soil, thermal gradients do not exceed 1°C/cm (Robinson, 1994). We systematically varied T_c between 15 and 23°C, T_start between 15 and 26°C, and thermal gradient between 0.3 and 1.5°C/cm, generating a comprehensive map of thermotaxis (Fig. 4). TI measurements are presented in the form of thermal response profiles, which consist of a set of TIs obtained by varying T_start while holding T_c and gradient steepness constant. Under isothermal conditions, TI values were consistent with simple diffusion and were not significantly different from zero (TI = 0.02 ± 0.03, n = 8 and 0.06 ± 0.07, n = 14 for T = 17°C and 23°C, respectively; T_c = 20°C).

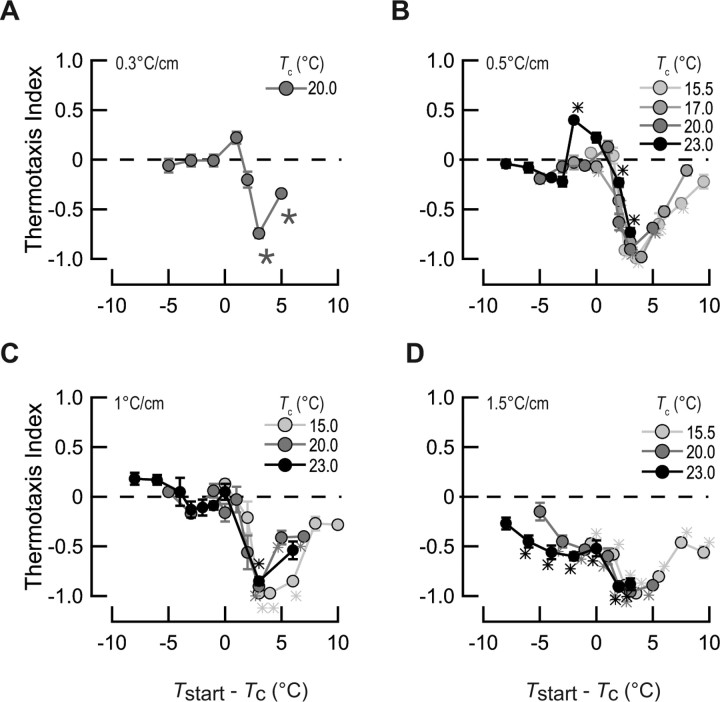
Figure 4.

Thermal response profiles as a function of T_c and gradient steepness. The thermotaxis index of wild-type (N2, Bristol) worms is plotted against T_start − T_c for gradients of 0.3°C/cm (A), 0.5°C/cm (B), 1.0°C/cm (C), and 1.5°C/cm (D). Points are mean ± SEM of at least six assays. Symbols correspond to different conditioning temperatures. *p < 0.01, significantly different from zero; two-tailed t test with Bonferroni correction.

Thermal response profiles were qualitatively similar for gradients between 0.3 and 1.0°C/cm (Fig. 4A–C). TI values were negative at starting temperatures warmer than T_c + 2°C and were not significantly different from zero at temperatures cooler than T_c + 2°C. [There was one exception: animals conditioned at 23°C and tested on a shallow gradient (0.5°C/cm) exhibited a positive TI value at T_c − 2°C.] Negative thermotaxis was maximal at ∼T_c + 3°C and became weaker at warmer starting temperatures. This decline is unlikely to reflect a disruption of the behavior by exposure to noxious temperatures, however, because it was evident both at starting temperatures within the physiological range and at temperatures that are not limiting for thermotaxis per se (for example, at T_start 23°C for animals conditioned at 15°C). Rather, it could indicate that thermotaxis has a limited operating range, which is set by T_c. Steep gradients (1.5°C/cm) evoked negative thermotaxis (TI < 0) at all starting temperatures, regardless of T_c (Fig. 4D). Consistent with previous reports of the effect of T_c on thermotaxis (Hedgecock and Russell, 1975; Mori and Ohshima, 1995; Ryu and Samuel, 2002; Yamada and Ohshima, 2003), a shift in T_c produced a corresponding shift in thermal response profiles. Thus, when plotted against the difference between T_start and T_c, thermal response profiles overlay remarkably well (Fig. 4).

In further support of the idea that thermotaxis is achieved by a biased random walk, worms conditioned at 20°C increased pirouette frequency in response to warming and decreased pirouette frequency in response to cooling above, but not below, T_c + 2°C (Fig. 1C). Much like the thermal response profiles (Fig. 4), this modulation of pirouette frequency peaked at ∼T_c + 3°C. Comparable results were obtained for worms conditioned at 15°C (Fig. 1D), and similar findings have been reported by Clark et al. (2007).

Modeling thermotaxis behavior in soil

Worms moving through soil experience a range of temperatures (T) and temperature changes resulting from both temporal temperature variations (∂T/∂t) and spatial thermal gradients present in the soil (∂T/∂z). Additionally, T_b and T_c vary continuously as they crawl, reflecting the animals' changing temperature experience. We used TI-derived V_drift values and empirical measurements of the parameters governing worm diffusion (speed, mean run duration, and mean pirouette duration) to explicitly simulate the motion of individual worms in soil. In this model, worms perform a random walk that is independent of the thermal gradient (diffusion) while moving up or down the gradient with speed V_drift that depends on T, T_c, and ∂T/∂z.

A temperature shift reactivates thermotaxis in food-deprived animals

Thus far, our empirical and analytical analysis has considered only the behavior of well fed worms. Prior work has suggested that food-deprived (starved) animals avoid T_c (Hedgecock and Russell, 1975; Mohri et al., 2005; Kodama et al., 2006; Kuhara and Mori, 2006), although this finding has been questioned (Yamada and Ohshima, 2003; Chi et al., 2007). We investigated the effect of depriving animals of food under two conditions: (1) constant temperature and (2) in the presence of a step change in temperature. Our goal was to determine the impact of neglecting feeding state in our simulations of soil-like thermal environments.

Animals deprived of food at constant temperature fail to respond to thermal gradients. This effect was evident after 2 h of starvation and reached a steady state after only 3 h (Fig. 5A). This effect was independent of gradient steepness (Fig. 5B).

Figure 5.

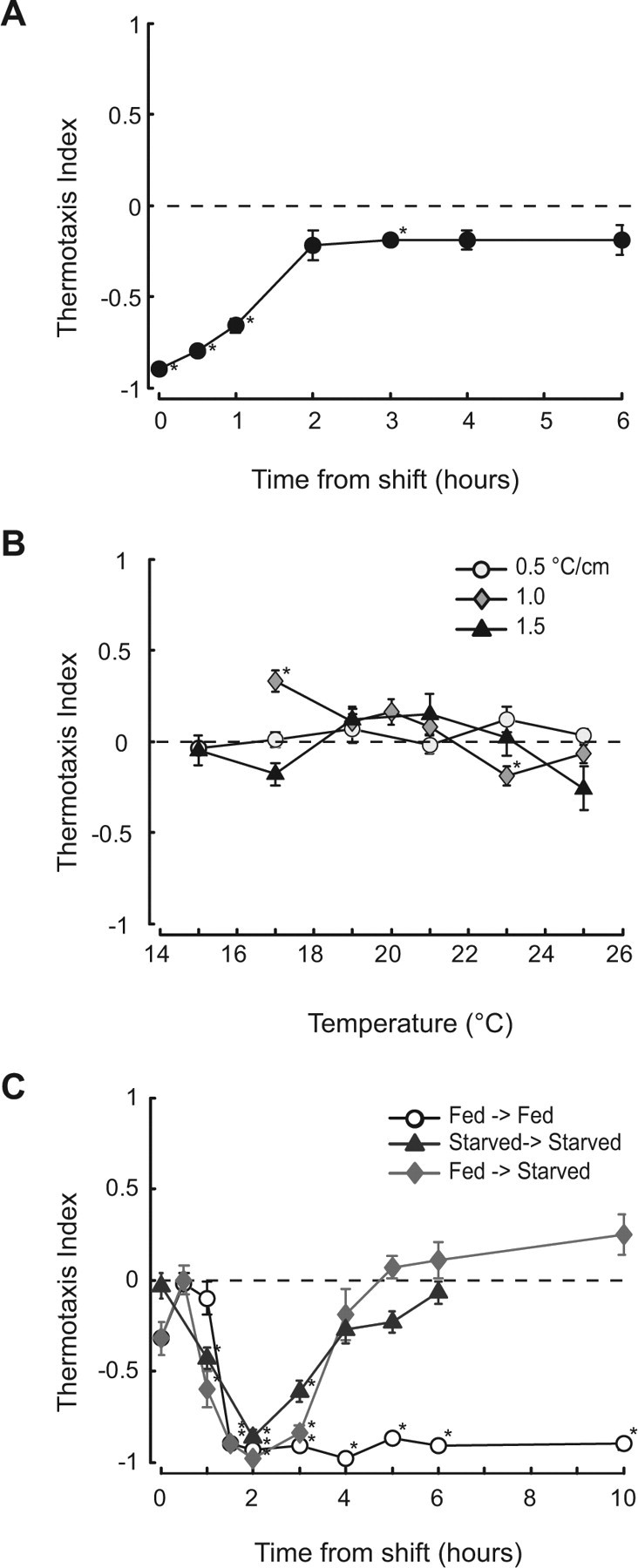
Thermotaxis is extinguished by starvation at constant temperature and reactivated by a temperature shift. A, Time course of starvation-induced extinction. Worms were deprived of food at 20°C for the time indicated and tested at T_start 23°C on 1°C/cm gradients. Points are mean ± SEM of six assays. T_c = 20°C. B, Thermal response profiles of worms deprived of food at 20°C for at least 5 h. Points are mean ± SEM of at least 8 assays. C, A temperature shift reactivates thermotaxis in worms cultivated at 20°C and shifted to 15°C for the time shown in the presence (circles) or absence (diamonds) of food. Reactivation was observed in animals starved for 3 h before the temperature shift (triangles). Similar results were obtained for animals starved for 15 h (data not shown). *p < 0.01, significantly different from zero; two-tailed t test, Bonferroni correction.

In contrast with controlled laboratory environments, temperature is continually changing in the natural environments of C. elegans and other free-living nematodes. To learn more about how temperature change affects thermotaxis, we measured responses to thermal gradients after a shift in cultivation temperature. We then tested whether such responses were different in well fed and food-deprived animals. Our experimental design was similar to that of Chi et al. (2007): we transferred well fed worms cultivated at 20°C to 15°C in the presence or absence of food for defined time periods, and measured their response to gradients at T_start 18°C. Based on the data in Figure 4, we predicted that (1) worms that had learned the new T_c of 15°C would migrate toward cooler temperatures, and (2) worms that had not learned the temperature would have TI values close to zero. Independent of the presence or absence of food at the new or old T_c, animals learned the new T_c within 1.5 h (Fig. 5C). Thus, bacterial food is not required to establish a new set point for negative thermotaxis.

In summary, these data show (1) that starvation at constant temperature eliminates negative thermotaxis; (2) that food is not required to reset the threshold temperature for negative thermotaxis; (3) that starved animals retain the ability to detect changes in ambient temperature and learn a new set point for negative thermotaxis; and (4) that worms exposed to temperature variations continue to perform thermotaxis in the absence of food. Thus, in an environment characterized by continuous temperature fluctuations, thermotaxis behavior is effectively independent of the presence or absence of food. As a result, it is possible to faithfully simulate thermotaxis in the soil while neglecting the availability of bacterial food or the worms' feeding state.

Spatiotemporal thermal variation in the soil

To simulate thermotaxis in nature, it was necessary to consider the dynamics of thermal variation in the soil. The temperature at the surface of the soil undergoes large daily fluctuations (Robinson, 1994; Chacko and Renuka, 2002) whose amplitude declines as the temperature wave penetrates the soil. Qualitatively similar spatiotemporal dynamics are also found in rotting fruit (Thorpe, 1974). We used the following equation (Dusenbery, 1989) to model soil temperature as a function of the time of day, t, and the distance from the soil surface, z:

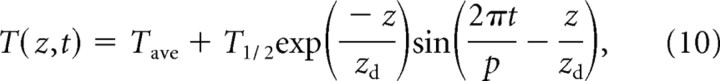where T_ave is the average soil temperature, T_1/2 is half the amplitude of the temperature variation at the surface, p is the period of the temperature variation, and z_d is the damping depth, or depth at which the amplitude of the temperature variation has decreased by a factor of e. Note that z_d is equal to $\sqrt{p{D}_{\text{s}}/\pi }$, where D_s is the thermal diffusivity of the soil; the value of D_s depends on soil moisture, soil porosity, and conductivity of the soil particles (Chacko and Renuka, 2002). The model provides a reasonable approximation of field measurements of circadian variation in soil temperature and its decline with depth (Robinson, 1994).

Figure 6, A and B, illustrates the daily variations in temperature that arise within 30 cm of the surface, assuming typical values for z_d = 10 cm and T_1/2 = 15°C (Dusenbery, 1989; Chacko and Renuka, 2002). Under these conditions, large temperature fluctuations and steep spatial thermal gradients arise near the surface. With increasing depth, both spatial and temporal gradients become shallower and the time of peak temperature is delayed. This is most evident in Figure 6B, which shows an image of temperature as a function of both time and depth.

Analysis of simple behavioral strategies

As a prelude to using our model to simulate the motion of worms performing thermotaxis in a soil-like thermal environment, we evaluated the outcomes of three simple strategies: (1) constitutive migration down thermal gradients (negative thermotaxis); (2) constitutive migration up thermal gradients (positive thermotaxis); and (3) constitutive isothermal tracking. All three simple strategies resulted in initial rapid movement deep into the soil (Fig. 6C), which slowed or ceased altogether as thermal gradients became shallower than the worms‘ threshold for initiating thermotaxis or isothermal tracking [set to 0.1°C/cm, as reported by Luo et al. (2006)]. These outcomes were not a consequence of specific parameter values, as qualitatively identical results were obtained for a range of initial conditions and locomotion speeds. (Speed could be increased by a factor of 100 or decreased by a factor of 10 relative to measured values without significantly altering the results.)

Both constitutive positive and negative thermotaxis steer worms away from the surface. Although this process slows as spatial gradients decline with depth, such simulations fail to converge on a stable average depth within 10 d (240 h). How does constitutive migration produce this result? An animal resting at constant depth will experience positive and negative thermal gradients for equal periods of time within a 24 h cycle, with transitions between positive and negative gradients occurring every 12 h (Fig. 6A,B). As animals move, however, they produce an additional motion-generated thermal stimulus because of spatial gradients present in the soil. Consider the case of a worm performing constitutive positive thermotaxis, moving toward warmer temperatures at all times. At night, when the soil surface is cool, this animal will move deeper into the soil. In so doing, the animal will delay the transition from a positive thermal gradient to a negative one, experiencing the transition later than it would if it had stayed in place (phase lag) (see Fig. 6B). The motion-generated stimulus maintains animals in a positive thermal gradient until they are so deep in the soil that gradients become very shallow and the thermotaxis drive declines. The motion-generated stimulus produced by a worm performing constitutive negative thermotaxis is similar, except that such an animal experiences the shift from positive to negative thermal gradients earlier than it would have by staying in place (phase lead).

Continuous isothermal tracking also leads worms away from the soil surface until the thermal gradients are too shallow to be detected. To track isotherms across time and space, worms must crawl along the spatial gradient in a direction that precisely offsets the temporal gradient they experience. In general terms, worms move away from the surface when the spatial and temporal gradients have opposing signs and toward the surface when spatial and temporal gradients have the same sign. Because of the nature of thermal variation in the soil, spatial and thermal gradients have opposing signs three-quarters of the time. Thus, isothermal tracking directs worms away from the surface three-quarters of the time and toward the surface only one-quarter of the time, resulting in net movement away from the surface. When the spatial gradients are too small to be detected, animals cease isothermal tracking and their average soil-depth remains constant (Fig. 6C). These unexpected results highlight the utility of computational tools in analyzing complex phenomena such as movement guided by a stimulus that varies across both space and time, where intuition alone may be insufficient.

Thermotaxis as a strategy for thermoregulation in the soil

Our experimental data show that wild-type worms: (1) move down thermal gradients at temperatures warmer than T_c + 2°C for a wide range of thermal gradient conditions, and (2) move down thermal gradients at most temperatures on steep gradients. Compared with the simple strategies considered above, what is the impact of this asymmetric, T_c-dependent thermotaxis strategy in soil-like thermal environments? Remarkably, thermotaxis produces movement that rapidly converges to oscillation within a narrow range of depths (Fig. 6D). Simulations converge on the same solution across a large range of initial depths. We hypothesized that the rate at which a new T_c is established plays an important role in thermotaxis. To test this idea, we simulated the behavior of dgk-3 mutants, which have been reported to form a new T_c more slowly than wild-type worms in response to increases in temperature. Measured values (Biron et al., 2006) for τ_up were 5.8 and 1.6 h for dgk-3 and wild type, respectively. Like wild type, simulations of dgk-3 mutants converge to an oscillation within a narrow range of depths. The final average depth is ∼1.5 times deeper than that of wild type, however (Fig. 6D). This result suggests that changes in a single gene are sufficient to direct soil nematodes to distinct zones in a common soil column.

To serve as an effective mechanism for thermoregulation, we postulated that thermotaxis should satisfy three criteria: (1) maintain body temperature below the critical maximum for reproduction or 26°C; (2) limit deviations from T_c; and (3) allow animals to remain relatively close to the soil surface. To evaluate the ability of asymmetric, T_c-dependent thermotaxis to meet these criteria, we simulated the behavior of individual animals and compared their performance with animals moving randomly. To simulate purely random motion, we set V_drift to zero and held all other locomotion and environmental parameters constant, except for average speed whose temperature dependence was determined empirically (supplemental Fig. S2, available at www.jneurosci.org as supplemental material). An example of a simulated worm performing thermotaxis is shown in Figure 7A1. Although the motion is inherently random, as expected from our simulation of the population mean (Fig. 6C), thermotaxis generally maintains the worm within a limited range of soil depths, ∼10–20 cm below the surface. Compared with random motion, which samples a larger range of depths, thermotaxis has the effect of significantly limiting the span of absolute temperatures and excursions from T_c experienced by the worm (Fig. 7B1,C1). To quantify this effect, we repeated the single-worm simulation 200 times and calculated the distributions of depths, temperatures, and deviations from T_c. We find that for three different values of average soil temperature (Fig. 7), animals performing thermotaxis are able to avoid warm (>26°C) temperatures and large (>2.5°C) deviations from T_c. In contrast, animals moving randomly consistently experience temperatures warmer than 26°C and are exposed to large deviations from T_c a greater fraction of the time. The distributions of worms performing thermotaxis suggest that thermotaxis allows animals to avoid the shallowest soil depths, where temperatures are most extreme and thermal fluctuations are greatest. Note that this strategy is in agreement with our three requirements for effective thermoregulation: avoidance of temperatures >26°C and of large deviations from T_c without resorting to burrowing deep into the soil and thus sacrificing access to oxygen.

Figure 7.

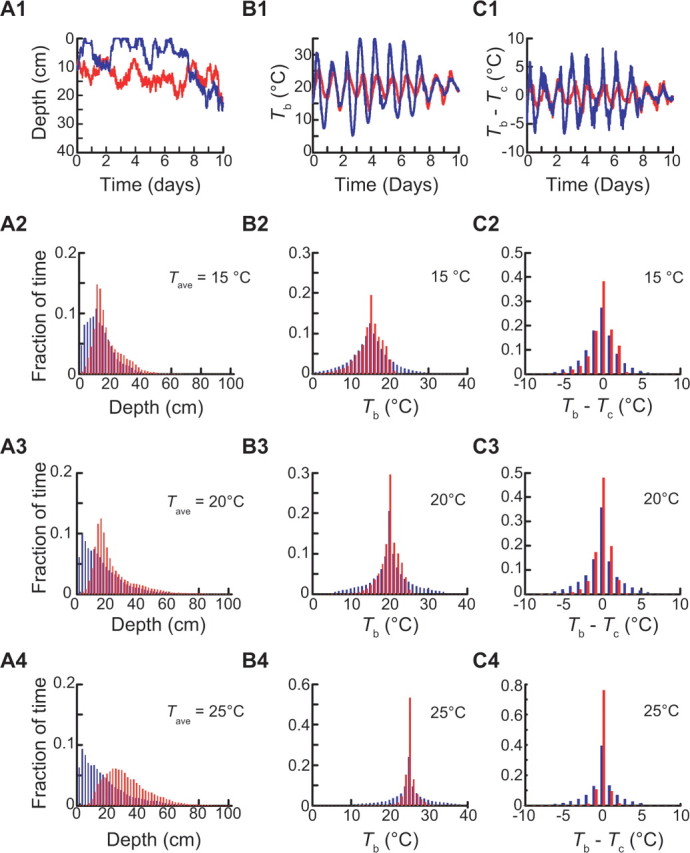
Thermotaxis outperforms a temperature-dependent random walk as a strategy for thermoregulation. Comparison of simulated worms performing asymmetric, T_c-dependent thermotaxis (red) or randomly exploring the soil environment (blue). Simulations of the random walk incorporated the empirical temperature dependence of average speed (see supplemental Fig. S2, available at www.jneurosci.org as supplemental material). Outcomes shown are soil depth (A1–A4), body temperature (B1–B4), and deviation from T_c (C1–C4). Traces in A1, B1, and C1 are for simulated single worms. The histograms in A2–A4, B2–B4, and C2–C4 are for 200 simulated worms for three values of T_ave, which are 15° (top), 20° (middle), and 25°C (bottom). T_c (t = 0) = 20°C, T_1/2 = 15°C, and z_d = 10 cm for all panels.

Robustness of thermotaxis

How robust are the outcomes of thermotaxis to variations in environmental conditions and to the accuracy of the measured parameters describing worm locomotion? In evolutionary terms, robustness is defined as the persistence of a trait subject to perturbations. Three types of perturbations are typically considered: noise, environmental change, and genetic change. Here, we focus on robustness to environmental and genetic change, using our computational model to evaluate the robustness to a wide range of perturbations. The effect of stochastic noise was not investigated. In addition to V_drift, our model is specified by eight parameters: three describing the soil environment (T_ave, T_1/2, and z_d) and five describing worm locomotion (τ_up, τ_down, v, τ, and τ_p; see Materials and Methods). We explored robustness to variations in environmental (soil) and worm locomotion parameters separately, reasoning that the first represents environmental change, produced by variations in climate or in composition of the soil resulting from seasonal variation or movement from one geographic region to another, whereas the second reflects genetic change among worm strains or the effect of a genetic mutation within a given strain.

To explore robustness to environmental change, in each simulation, two of the three environmental parameters were held constant, whereas the third was allowed to vary within a broad range. T_ave was allowed to vary between 15°C and 25°C, T_1/2 between 5°C and 20°C, and z_d between 5 and 15 cm. The parameters governing worm locomotion in these simulations were the empirically measured parameters used throughout this study (see Materials and Methods). This analysis reveals that when compared with a random strategy, thermotaxis is an effective means of regulating body temperature for a large range of environmental conditions (Fig. 8A). Thus, worms would not need to “retune” this mechanism to account for variations in daily weather, seasons, or habitats, a potentially useful feature of this strategy.

Figure 8.

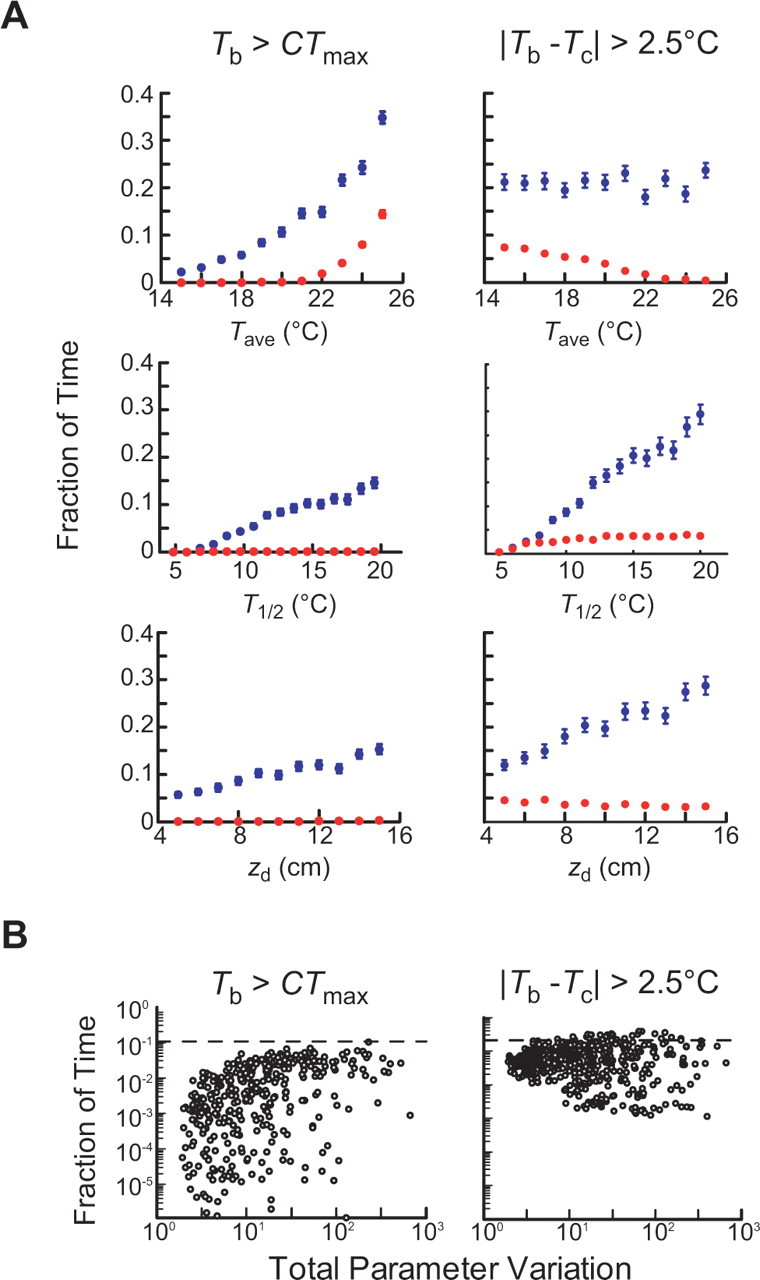
Robustness of thermotaxis to environmental and behavioral parameters. A, Mean fraction of time (out of 10 d) that simulated worms experienced T_b > CT_max (left) and |T − T_c| > 2.5°C (right) for different values of T_ave, T_1/2, and z_d. Red points are the mean ± SEM of 100 worms performing thermotaxis; blue points are means of 100 worms moving randomly. One parameter was varied while the other two were held constant. Initial values for T_ave, T_1/2, and z_d are 20°C, 15°C, and 10 cm, respectively. B, Fraction of time worms experienced T_b > CT_max (left) and |T_b − T_c| > 2.5°C (right) as a function of total variation in locomotion parameters. Each point is the average of 50 simulated worms; total of 500 altered systems were analyzed. CT_max = 26°C.

To explore the robustness of thermotaxis to variations in worm locomotion parameters, we adapted an approach first used by Barkai and Leibler (1997). All five locomotion parameters were allowed to vary (increase or decrease) by up to a factor of four. In addition, V_drift could be scaled (up or down) by up to a factor of four. Variations in individual parameters and in the V_drift scaling factor were randomly and independently generated, such that a set of parameter values altered in this manner yielded a single “altered system”. Following Barkai and Leibler (1997), total parameter variation k of each altered system was defined as follows:

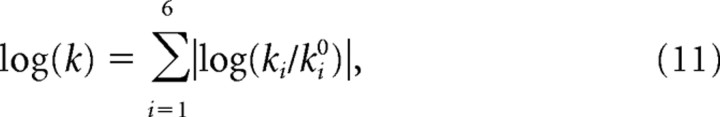where k_i are the altered parameters, and k_i⁰ are the measured (baseline) parameter values.

For each altered system, we simulated 50 worms moving through the soil (T_ave = 20°C, T_1/2 = 15°C, and z_d = 10 cm) using the altered parameters characterizing that system. We calculated the average fraction of time spent by these worms at T_b > 26°C and at |T_b − T_c| > 2.5°C for each such altered system. Thermotaxis successfully maintains body temperature below 26°C with high robustness to variations in locomotion parameters and V_drift (Fig. 8B). Despite variations of up to 2.5 orders of magnitude in parameter values, all altered systems exhibited superior performance to a random strategy and 99% of altered systems outperformed random motion by at least a factor of 2. In contrast, thermotaxis exhibited reduced robustness to variations in behavioral parameters with respect to limiting deviations from T_c (Fig. 8B). This result implies worms may forgo minimization of deviations from T_c to retain the ability to maintain body temperature below the critical maximum for reproduction.

Discussion

Behavioral strategies are critical for regulation of body temperature and shared by all animals. Thermoregulation has long been a subject of intense study, including studies of the evolution of thermal physiology and its adaptive value (e.g., Angilletta et al., 2002) and of the neural control mechanisms that coordinate thermoregulation in mammals (e.g., Romanovsky, 2007). A more recent focus has been analysis of the role that thermosensitive ion channels may play in thermoregulation and thermal physiology (e.g., Caterina, 2007). We used a computational approach to connect laboratory analysis of C. elegans thermotaxis to natural settings such as soil and showed that C. elegans can use thermotaxis to regulate T_b within limits favorable for reproduction in soil-like thermal environments. Compared with random movement and several alternative temperature-guided behaviors, the asymmetric, T_c-dependent thermotaxis performed by adult C. elegans is capable of maintaining T_b below CT_max for reproduction (26°C), limiting deviations from the worms' adapted temperature, and maintaining worms at relatively shallow depths which offer increased access to oxygen.

Soil temperature can vary dramatically not only during the course of a day, but also across seasons and between different geographic locations. In principle, survival and reproduction in the face of large daily temperature fluctuations could be achieved by behavioral strategies that are finely tuned to local environmental conditions. However, such strategies would require significant retuning during transitions between seasons, and would not permit animals to thrive in geographically diverse habitats. C. elegans appears to have adopted a different approach, using instead a behavioral strategy for thermoregulation that is highly robust to changes in environmental conditions. Such robustness suggests that this mechanism for thermoregulation should function across the wide range of conditions likely to be encountered in natural environments in a variety of distinct climates. Consistent with this prediction, C. elegans nematodes have been found in North America, Europe, Australia, and Hawaii (Barrière and Félix, 2005a).

Several aspects of C. elegans thermotaxis have been debated recently, including whether animals are capable of positive thermotaxis below T_c as well as negative thermotaxis above T_c. In principle, both abilities are needed to drive accumulation at T_c. We found that animals exhibit negative thermotaxis above T_c across a wide range of conditions, but only worms conditioned at 23°C and exposed to shallow (<0.5°C/cm) gradients exhibit positive thermotaxis. Although this finding agrees with Ito et al. (2006), who argued that positive thermotaxis occurs only in response to shallow linear gradients, the narrow range of conditions under which positive thermotaxis was detected begs the question of its importance in soil-like environments, which generate both shallow and steep spatial gradients. Based on our results, we suggest that positive thermotaxis plays a small role in the regulation of T_b and that thermotaxis is unlikely to be able to drive accumulation at T_c. Consistent with this idea, some groups have reported that worms fail to accumulate near T_c (Yamada and Ohshima, 2003; Anderson et al., 2007). We also show that steep temperature gradients (1.5°C/cm) always evoke negative thermotaxis. Because the thermal gradients produced in classical radial gradient assays appear to exceed 1.5°C/cm [see Mohri et al. (2005), their Fig. 1A], this new discovery implies that such assays test for the ability to perform negative thermotaxis and isothermal tracking. Thus, a mutant phenotype in this assay could arise from defects in negative thermotaxis, isothermal tracking, or in both behaviors.

Another area of controversy has been the nature of plasticity in C. elegans thermotaxis. Previous studies have assumed it reflects an association between T_c and a food-derived signal (Gomez et al., 2001; Mohri et al., 2005; Kodama et al., 2006; Kuhara and Mori, 2006). Direct tests of this idea have been conducted only recently (Biron et al., 2006; Luo et al., 2006; Chi et al., 2007 and this study). These recent studies and our data demonstrate that a new T_c can be learned in the absence of food. Because food is not required for plasticity, however, such plasticity cannot be the result of the formation of an associative memory between T_c and a food-derived signal.

Of the several aspects of C. elegans thermoregulation examined in this study, soil-depth was the only one that was sensitive to variations in the parameters governing thermotaxis. In particular, decreasing the rate at which a new T_c is established resulted in animals accumulating deeper in the soil. This result suggests that variations in genes controlling thermotaxis plasticity could allow coexisting nematode populations to distribute themselves without compromising thermoregulation. Indeed, it has been suggested that nematode genera are genetically programmed to preferentially reside at different depths (e.g., Boag and Yeates, 2004).

Regulation of T_b is robust to perturbations in the parameters governing worm locomotion and the amplitude of the thermotaxis drive. This unexpected result suggests that the most critical features of thermotaxis are its plasticity and the general form of the response, i.e., migration down gradients when T_b > T_c, rather than fine-tuned values of thermotaxis indices. It also implies that thermotaxis is an effective mechanism for thermoregulation in diverse nematode strains that inhabit soil-like thermal environments. Similar robustness exists in biochemical networks, including those controlling bacterial chemotaxis, metabolic networks, and developmental patterning (reviewed by Stelling et al., 2004). To the best of our knowledge, this is the first demonstration that a process like animal behavior also exhibits this property.