Abstract
Progressive stiffening of collagen tissue by bioapatite mineral is important physiologically, but the details of this stiffening are uncertain. Unresolved questions about the details of the accommodation of bioapatite within and upon collagen's hierarchical structure have posed a central hurdle, but recent microscopy data resolve several major questions. These data suggest how collagen accommodates bioapatite at the lowest relevant hierarchical level (collagen fibrils), and suggest several possibilities for the progressive accommodation of bioapatite at higher hierarchical length scales (fibres and tissue). We developed approximations for the stiffening of collagen across spatial hierarchies based upon these data, and connected models across hierarchies levels to estimate mineralization-dependent tissue-level mechanics. In the five possible sequences of mineralization studied, percolation of the bioapatite phase proved to be an important determinant of the degree of stiffening by bioapatite. The models were applied to study one important instance of partially mineralized tissue, which occurs at the attachment of tendon to bone. All sequences of mineralization considered reproduced experimental observations of a region of tissue between tendon and bone that is more compliant than either tendon or bone, but the size and nature of this region depended strongly upon the sequence of mineralization. These models and observations have implications for engineered tissue scaffolds at the attachment of tendon to bone, bone development and graded biomimetic attachment of dissimilar hierarchical materials in general.
Keywords: mineralization, bone, mineralized fibrils, mechanics of developing tissues, tendon-to-bone attachment, nanomechanics
1. Introduction
Progressive stiffening of collagen tissue by bioapatite mineral (‘bioapatite’) underlies much of musculoskeletal function and development. The spatial and temporal accommodation of bioapatite by collagen determines this stiffening and thus has important consequences for bone and for partially mineralized tissues that serve mechanical roles. Data for accommodation of bioapatite at the lowest levels of collagen hierarchical structure are now becoming available, although debate persists. Our objective, in this paper, is to apply this new nanostructural information, in conjunction with some recent nanoscale simulations of collagen mechanics, to develop estimates of the mechanical behaviour of partially mineralized collagen tissues. We then apply these models to interpret how partially mineralized tissues provide effective connection of tendon to bone.
Temporally, bioapatite accumulates on a collagen template during development to form mature bone [1]. Spatially, bioapatite increases from 0 vol% in tendon to 50 vol% in bone across the tendon-to-bone insertion site (the ‘insertion’) [2,3]. During development, bioapatite crystals may nucleate and grow in channels that arise in ‘gap regions’ at the terminations of tropocollagen molecules within collagen fibrils before accumulating on extrafibrillar surfaces, and possibly within ‘overlap regions’ (figure 1). However, studies have also demonstrated extrafibrillar mineral in the absence of intrafibrillar mineral [2]. Mineralization patterns of developing tissues may differ considerably from those of mature tissues.
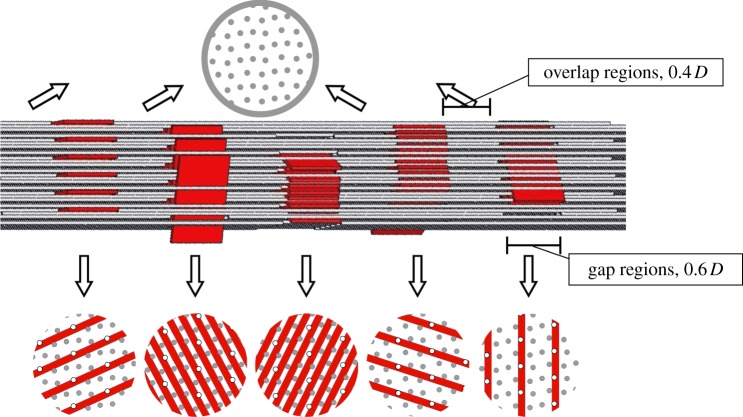
Figure 1.
Simplified steric model of the arrangements of tropocollagen molecules (grey) and bioapatite platelets (dark-shaded; red in online version) with a partially mineralized collagen fibril, adapted from [3]. Intrafibrillar bioapatite is known to accumulate in the gap regions (length 0.6 D, where D = 0.67 nm is the spacing between gap regions) that form at the termination of tropocollagen molecules (grey circles in cross sections: tropocollagen molecules that pass through the gap region in the cross section shown; hollow circles: tropocollagen molecules that terminate at the cross section shown). Bioapatite platelets can fit within the structure of the gap regions in five distinct orientations. The degree and manner to which bioapatite can accumulate within the remainder of the fibril (overlap regions of length 0.4 D is unknown). (Online version in colour.)
Our focus is prediction of how intrafibrillar and extrafibrillar mineralization stiffens collagen fibrils, fibres and tissues. We connected mechanical moduli across several hierarchical levels using homogenization methods that bound or estimate the degree to which bioapatite can stiffen tissue composed primarily of collagen and water. The coarsest of these methods involves mechanical responses of fictitious tissues obtained by arranging tissue constituents in parallel or in series. Increasingly accurate estimates and tighter bounds can be obtained by considering the arrangements of collagen, water and mineral.
A substantial body of literature focuses on estimates of bone biomechanics based upon inferred patterns of mineralization [4–7]. The science of relating the specific architecture of bone to its macroscale mechanical properties is quite mature, with solid tools and estimates in place for estimating anisotropic material properties [4,8], quantifying bioapatite–collagen interactions [9] and dissecting the key contributors to bone mechanics [10], dissecting failure mechanisms [11]. For the microscale features of bone, a host of technologies exist for relating patient-specific scans to individualized micro mechanical models [12–14].
This study adds to this literature in two ways. First, it quantifies mechanical implications of the most up-to-date nanostructural data for collagen/bioapatite morphology. Second, it extends to partially mineralized tissues. Five possible sequences of mineralization were studied to evaluate the range of bioapatite accrual patterns supported by the literature, ranging from nucleation initiating in gap regions, as may occur during bone development, to nucleation initiating outside fibrils, as may occur along the insertion. We quantified how combinations of intrafibrillar and extrafibrillar bioapatite stiffens collagen, and how the specific sequence of mineralization affects tissue-level mechanical responses. These tissue-level responses were then studied in the context of attachment of dissimilar materials and engineered grafts to surgically reattach tendon to bone.
1.1. Background: nanoscale physiology of bone
Tendon and bone have nearly identical hierarchical collagen structures ranging from the nano- to milliscale. Bone contains approximately 50 vol% bioapatite incorporated into and onto this structure. The insertion presents graded transitions in bioapatite, composition and meso-, but not in nanoscale organization of collagen. It also presents gradients in protein content [15–18]. The tendinous end transitions towards bone from aligned, predominantly (approx. 98%) type I collagen fibres to a fibrocartilaginous layer composed of types I, II and III collagen and the proteoglycan aggrecan. This transitions to mineralized fibrocartilage dominated by type II collagen, but with significant amounts of type X collagen and aggrecan. Beyond this is bone proper, with mineralized type I collagen. Although the insertion is classically defined as containing four zones, no sharp boundaries are evident between zones, and the transitional tissue is compositionally graded.
As a first-order simplification, we focus on type I collagen (‘collagen’), the main organic component of tendon, bone and the insertion. Collagen's nanoscale structure involves triple-helix collagen molecules, 300 × 1.5 nm diameter, that self-assemble into fibrils in a well-aligned but twisted and quasi-triclinic molecular packing [19]. Within fibrils, collagen molecules stagger with an axial period of D = 67 nm [20] that includes an overlap region (approx. 27 nm, or 0.4 D), and a gap region (approx. 40 nm, or 0.6 D) where one-fifth of triple-helix collagen molecules terminate (figure 1). Intermolecular spaces between triple-helix collagen molecules contain water and a small amount of non-collagenous proteins, including proteoglycans [21]. Collagen fibrils in tendons have a typical diameter of a few hundred nanometres and are decorated with proteoglycans, which form a matrix between fibrils. Fibrils assemble into fibres, fibres into fascicles and fascicles into tendon. We calculated mechanical properties at three levels. Fibril-level moduli (superscript fibril) represent moduli of fibrils and their internal components, and were based upon data from molecular models. Fibre-level moduli (superscript fibre) represent moduli of repeating unit cells incorporating fibres and materials including decorins that bind and cross-link fibrils. Tissue-level properties (no superscript) were derived by averaging over a measured collagen fibre orientation distribution. A complete list of nomenclature can be found in the electronic supplementary material.
Accommodation of bioapatite within collagen is only partially understood [22,23]. A beautiful model system for partially mineralized collagen is avian tendon [24], but unfortunately the mineralization patterns observed there seem to differ from those seen in mammalian bone [25]. In mature bone, bioapatite crystals appear predominately as thin plates with approximate dimensions 2.1 × 30 × 40 nm [26–29]. The 2.1 nm minimum dimension of its Bravais lattice is the most certain of these dimensions [25]. The Lm ≈ 30 nm c-axes of bioapatite crystals within gap regions align with the tropocollagen molecule axes. Atomic force microscopy studies [30,31] report bioapatite crystals with widths and lengths ranging from 30 to upwards of 200 nm. Recent work suggests that intrafibrillar bioapatite exists predominantly within end-to-end gaps between triple-helix collagen molecules, in five defined orientations; three distinct area fractions (α = {0.20, 0.28, 0.58}) of bioapatite are possible within a transverse cross section of a gap region filled to capacity with bioapatite (figure 1).
Volume fractions of bioapatite are central to estimates of stiffening. α = 0.58 corresponds to a tissue-level volume fraction of bioapatite ϕm ≈ 21%, based on the relationship 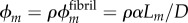 , where
, where 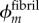 is the fibril-level volume fraction of bioapatite, and
is the fibril-level volume fraction of bioapatite, and 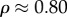 the area fraction of fibrils in mature tendon [32]. The precise amount of bioapatite in the intrafibrillar spaces of the overlap regions has not been established, but is bounded at 0.6 that of the gap regions; even with this maximum addition (ϕm ≈ 0.21(1 + 0.6) = 0.33), intrafibrillar bioapatite cannot account for the volume fraction of bioapatite present in fully mineralized bone. Consistent with this, extensive bioapatite is observed exterior to collagen fibrils [3]. The maximum volume fraction of bioapatite that can be accommodated by bone is therefore ϕm ≈ 0.41, if bioapatite cannot accrue in the overlap region, and ϕm ≈ 0.53 if it can. Both lie within the range reported for wet bone [4]. We explored the progressive stiffening of collagen by bioapatite within these constraints.
the area fraction of fibrils in mature tendon [32]. The precise amount of bioapatite in the intrafibrillar spaces of the overlap regions has not been established, but is bounded at 0.6 that of the gap regions; even with this maximum addition (ϕm ≈ 0.21(1 + 0.6) = 0.33), intrafibrillar bioapatite cannot account for the volume fraction of bioapatite present in fully mineralized bone. Consistent with this, extensive bioapatite is observed exterior to collagen fibrils [3]. The maximum volume fraction of bioapatite that can be accommodated by bone is therefore ϕm ≈ 0.41, if bioapatite cannot accrue in the overlap region, and ϕm ≈ 0.53 if it can. Both lie within the range reported for wet bone [4]. We explored the progressive stiffening of collagen by bioapatite within these constraints.
2. Material and methods
We modelled stiffening of collagen by bioapatite within gap regions, on the exterior of fibrils, and possibly within overlap regions. Our focus was prediction and bounding of the ways that bioapatite stiffens collagen. The stiffening was sensitive to the nanoscale structures and interactions of collagen and bioapatite. Although models exist for the structures of fully mineralized and non-mineralized collagen [3], the sequence of bioapatite accumulation during development and the bioapatite distributions within partially mineralized tissues at the insertion are not known [22]. We therefore studied the range of possibilities described below. The nanoscale mechanical interactions between bioapatite and collagen are not known, but are an area of focus by us and others. The interactions likely involve strong adhesion at low stress levels with little effect on tropocollagen mechanics, and sliding at higher stress levels [33]. In the absence of other information and as a first approximation, we model complete adhesion between collagen and bioapatite.
2.1. Models of the sequence of mineralization
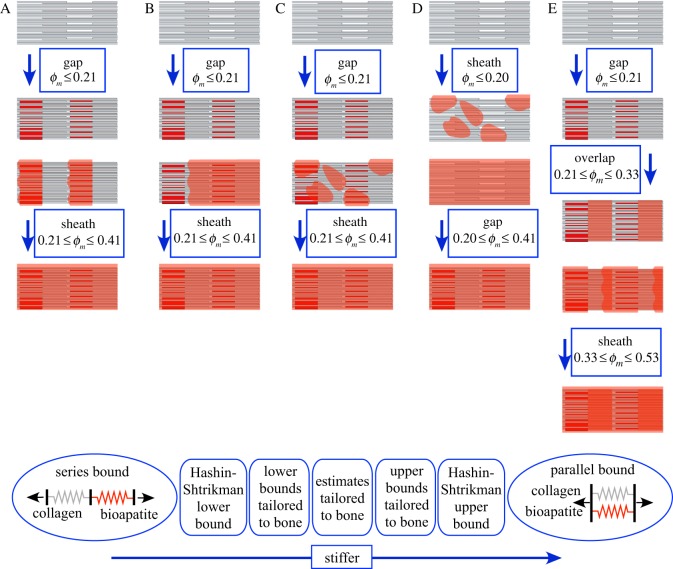
Five plausible sequences of mineralization were modelled (figure 2). Models began with unmineralized collagen fibrils (top row, figure 2), followed by prescribed bioapatite accumulation into gap regions, onto the exterior of collagen fibrils and within overlap regions:
— model A (‘gap-nucleated’) began with filling of gap regions (row 2, figure 2), and proceeded with extrafibrillar mineralization that initiated at the mineralized gap regions (row 3), then extended the entire length of the fibril (row 4). The first stage of mineralization (0 ≤ ϕm ≤ 0.21) involved inserting 2.1 nm thick and 30 nm high bioapatite platelets into the 0.4 D (40 nm) spaces between the C-terminus of one triple-helix tropocollagen molecule and the N-terminus of the next. Platelets were assumed to contact the N-terminus of one molecule and to extend 10 nm short of the C-terminus of the next. Bounds and estimates on stiffening by these platelets involved different spatial sequences of filling gaps, ranging from filling the maximum allowable space of one gap region before proceeding to the next (lower stiffness bound), to filling all gaps simultaneously with equal volumes of bioapatite (upper stiffness bound). The second stage (0.21 ≤ ϕm ≤ 0.41) involved formation of an extrafibrillar sheath from the N-terminus end of each gap region, past the C-terminus end, and then on to the next gap region. Model A is supported by observations of long bioapatite platelets spanning multiple collagen fibrils [3];
— model B (‘nucleation-inhibited’) began as in model A with filling of gap regions. Subsequently, nucleation of extrafibrillar bioapatite was treated as rare. Following nucleation, growth of extrafibrillar bioapatite along a nucleation front was promoted. This was modelled by a sheath that began at one point along the fibril then extended to encompass the entire fibril;
— model C (‘nucleation-promoted’) also followed model A for intrafibrillar mineralization. Thereafter, nucleation of small, randomly distributed patches of extrafibrillar bioapatite was promoted, but subsequent growth of these patches was suppressed;
— model D was analogous to model C, except that extrafibrillar bioapatite accrued prior to intrafibrillar bioapatite; and
— model E was analogous to model A, except that bioapatite was also allowed into the intermolecular spaces of the overlap regions. The sequence of bioapatite accrual in model E was (i) as platelets within the gap regions (0 ≤ ϕm ≤ 0.21); (ii) in an unknown structure within the overlap regions (0.21 ≤ ϕm ≤ 0.33, rows 2–3); and (iii) as an extrafibrillar ‘gap-nucleated’ sheath (0.33 ≤ ϕm ≤ 0.53, rows 3–5).
Figure 2.
Five possible models were considered for the sequence of accumulation of bioapatite within and upon collagen fibrils. Model A, the ‘gap region-nucleated model’, involved a filling to capacity of the gap regions followed by extrafibrillar bioapatite nucleating over the gap regions spreading along the fibril. Model B, the ‘external nucleation inhibited model’, involved a filling to capacity of the gap regions followed by extrafibrillar bioapatite emanating from a single nucleation site on each fibril. Model C, the ‘external nucleation promoted model’, involved a filling to capacity of the gap regions, followed by random accumulation of bioapatite on the exterior of fibrils, with no subsequent growth of these accumulations. Model D, the ‘internal nucleation inhibited model’, involved random extrafibrillar accumulations of bioapatite preceding the filling of gap regions. Model E was identical to model A, except that it included mineralization of the overlap regions following the filling to capacity of the gap regions and prior to extrafibrillar mineralization. Bottom panel: homogenization bounds that do not account for collagen and bioapatite architecture are broader than those that do. We used these models to generate bounds and estimates on the mechanics of fibrils. These bounds and estimates were then applied to bounds and estimates of fibre mechanics. (Online version in colour.)
2.2. Bounds and estimates for the stiffening of collagen
Bounds and estimates of stiffening by bioapatite are summarized here and presented in complete detail in the electronic supplementary material.
2.2.1. Stiffening of fibrils
For intrafibrillar mineralization, fibril-level longitudinal modulus bounds and estimates were assembled from structural arrangements of four types of regions: unmineralized collagen fibril within a gap region, modulus 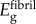 ; unmineralized collagen fibril within an overlap region, modulus
; unmineralized collagen fibril within an overlap region, modulus 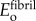 ; mineralized collagen fibril within a gap region modulus
; mineralized collagen fibril within a gap region modulus 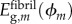 ; and mineralized collagen fibril within an overlap region modulus
; and mineralized collagen fibril within an overlap region modulus 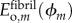 .
.
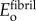 and
and 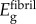 were estimated from ligament moduli reported by Stabile et al. [34], which, when scaled to the fibril level, yield Efibril ≈ 600 MPa. This is consistent with moduli found for fibre recruitment models of tendon mechanics [35]. The overlap regions (height 0.4 D) and gap regions (height 0.6 D) were taken to resist load in series, with the assumption that
were estimated from ligament moduli reported by Stabile et al. [34], which, when scaled to the fibril level, yield Efibril ≈ 600 MPa. This is consistent with moduli found for fibre recruitment models of tendon mechanics [35]. The overlap regions (height 0.4 D) and gap regions (height 0.6 D) were taken to resist load in series, with the assumption that 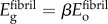 , where β ≈ 0.8, because the number of collagen molecules in the gap regions is four-fifths that of overlap regions (figure 1). Then, the total deformation of a fibril subjected to uniaxial loading was
, where β ≈ 0.8, because the number of collagen molecules in the gap regions is four-fifths that of overlap regions (figure 1). Then, the total deformation of a fibril subjected to uniaxial loading was 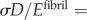
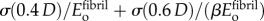 , where σ is engineering stress (tensile force divided by initial cross-sectional area). Thus
, where σ is engineering stress (tensile force divided by initial cross-sectional area). Thus
 |
2.1 |
Bioapatite crystals (Eha = 110 GPa) [36] incorporate into fibrils with the 30 nm c-axis in parallel with collagen molecules. Bioapatite is believed to replace water without otherwise altering collagen [2]. The modulus of a mineralized gap region was then a parallel summation:
| 2.2 |
where α(ϕm) = ϕmD/(ρLm) denotes the degree of stiffening by bioapatite.
Stiffening of collagen in overlap regions was modelled with the Hashin–Shtrikman (HS) bounds (see electronic supplementary material, equations (2.1)–(2.3)). HS bounds are the tightest bounds for an unstructured mixture, and were appropriate, because intermolecular spaces within overlap regions cannot accommodate a single Bravais lattice of bioapatite. These bounds involved estimates for moduli and volume fractions of collagen molecules, bioapatite and the largely aqueous matrix between fibrils. Using a density of 1.12 g cm−3 for tendon [37], approximately 1.3–1.4 g cm−3 for collagen [38], and 1.0 g cm−3 for the matrix yielded a volume fraction of collagen in tendon of approximately 30–40%. Adjusting for the volume fraction of fibrils in fibres (approximately the area fraction ρ = 0.80) suggests that fibrils contain 50 vol% of water/matrix and collagen molecules. Using the body temperature bulk modulus of water and Poisson ratio v = 0.499999 yielded E = 13 kPa [39] for this effective matrix. The modulus of the remaining material within an overlap region was estimated from the three-dimensional HS upper bound: matching this upper bound to 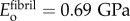 and taking v = 0.3, this was then estimated as
and taking v = 0.3, this was then estimated as 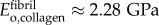 . Bioapatite accruing in the overlap regions replaced aqueous matrix and accrued according to
. Bioapatite accruing in the overlap regions replaced aqueous matrix and accrued according to 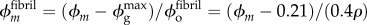 , whereas the fibril-level volume fraction of collagen remained at 50%; the volume fraction of aqueous matrix decreased as
, whereas the fibril-level volume fraction of collagen remained at 50%; the volume fraction of aqueous matrix decreased as 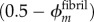 . The modulus of mineralized overlap regions was then taken as the three-dimensional HS lower bound (bioapatite embedded within a fibril lattice surrounded by aqueous matrix),
. The modulus of mineralized overlap regions was then taken as the three-dimensional HS lower bound (bioapatite embedded within a fibril lattice surrounded by aqueous matrix), 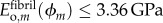 .
.
Fibril moduli were constructed from those of the above four regions. The upper bound involved adding equal volumes of bioapatite platelets to all gap regions simultaneously. Three types of regions were then combined in series: overlap regions, partially mineralized gap regions and unmineralized regions of gap regions representing space close to the C-termini of tropocollagen molecules that never mineralize. The lower bound was obtained by requiring that a single gap region be filled to the maximum level (area fraction αmax = 58%) before gap regions in the next gap region begin to accrue bioapatite.
In model E, after bioapatite platelets filled in the maximum allowable volume in gap regions, bioapatite was deposited in overlap regions. The upper bound fibril modulus involved adding bioapatite to all overlap regions simultaneously, and the lower bound involved filling a single overlap region entirely before adding bioapatite to the next.
2.2.2. Longitudinal stiffening of fibres
Linear response of fibres. Adjacent collagen fibrils were modelled as bound together with an extrafibrillar matrix (EFM, volume fraction 1 − ρ = 0.20) containing a relatively small amount of non-collagenous proteins that serve to bind adjacent collagen fibrils [31]. We neglected EFM contributions to longitudinal stiffness because its estimated modulus (EEFM ≈ 0.287 MPa, see electronic supplementary material) was small compared with that of collagen fibrils, but included it below in estimates of transverse moduli.
Bounds and estimates of stiffening involved accounting for extrafibrillar bioapatite in parallel with four types of possibly mineralized fibre segments: unmineralized gap regions, fully mineralized gap regions, unmineralized overlap regions (models A–D) and mineralized overlap regions (model E). Upper bounds on stiffening were estimated by modelling extrafibrillar bioapatite as thin sheaths around fibrils that grew radially increasing mineralization. Lower bounds were estimated by modelling extrafibrillar bioapatite as thick sheaths that grew longitudinally with increasing mineralization. Bounds and estimates for models A, B and E are included in the electronic supplementary material. Models C and D involved random accumulations of extrafibrillar bioapatite whose contributions were estimated using finite-element methods, as described below. A key feature of each of these models was a percolation threshold representing a critical bioapatite volume fraction at which stiffening by apatite rose rapidly from near the lower bounds to near the upper bounds.
Nonlinear response of fibres. Although our primary interest was linear approximations to collagen behaviour, mechanical measurements show sea cucumber dermal collagen fibres [40–43] and associated molecular dynamics (MD) models for fibrils [33] show significant nonlinearity at large strains. Although these MD simulations have not yet been validated directly, we believe that they represent the best estimates for the mechanics of type I mammalian collagen fibrils. We therefore studied the effects of mineralizing these fibres as a first effort at exploring the effects of nonlinearity given available data. As with the linear estimates, we note that the details of collagen–mineral nanoscale interactions are unclear at present and therefore model as a first approximation perfect adhesion between the two. Validation and modification of these MD results and identification of models of nanoscale collagen–mineral interactions are ongoing areas of research in our laboratories.
We studied the uniaxial relationship between engineering stress σ and engineering strain ε (ratio of fibril distension to initial fibril length) in a partially mineralized mammalian type I collagen fibril that, when unmineralized, followed the stress–strain relationship predicted by the MD simulations of [44], 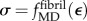 . Mineralization was taken to follow the scheme of model A. Because data for
. Mineralization was taken to follow the scheme of model A. Because data for 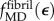 are available for only a single loading rate, viscoelastic effects could not be modelled. An effective nonlinear, continuum constitutive response of hydrated collagen within a fibril,
are available for only a single loading rate, viscoelastic effects could not be modelled. An effective nonlinear, continuum constitutive response of hydrated collagen within a fibril, 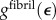 , was estimated from
, was estimated from 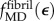 as follows. Collagen in the gap and overlap regions was idealized as identical continua. A uniaxial stress σ on the fibril was elevated to σ/0.8 in the gap regions owing to gaps between tropocollagen molecules. The total strain of a fibril was then the weighted sum of the strain
as follows. Collagen in the gap and overlap regions was idealized as identical continua. A uniaxial stress σ on the fibril was elevated to σ/0.8 in the gap regions owing to gaps between tropocollagen molecules. The total strain of a fibril was then the weighted sum of the strain 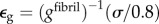 in gap regions and
in gap regions and 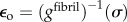 in the overlap regions:
in the overlap regions:
| 2.3 |
and
| 2.4 |
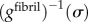 was calculated from equation (2.4) and a fifth degree polynomial fit to data for
was calculated from equation (2.4) and a fifth degree polynomial fit to data for 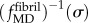 (dashed-dotted curve, figure 3a, blue in online version). The uniaxial constitutive response of partially mineralized fibres was estimated based upon gfibril(ε) (red solid curve, figure 3a) and upon methods analogous to those described above. Details are provided in the electronic supplementary material.
(dashed-dotted curve, figure 3a, blue in online version). The uniaxial constitutive response of partially mineralized fibres was estimated based upon gfibril(ε) (red solid curve, figure 3a) and upon methods analogous to those described above. Details are provided in the electronic supplementary material.
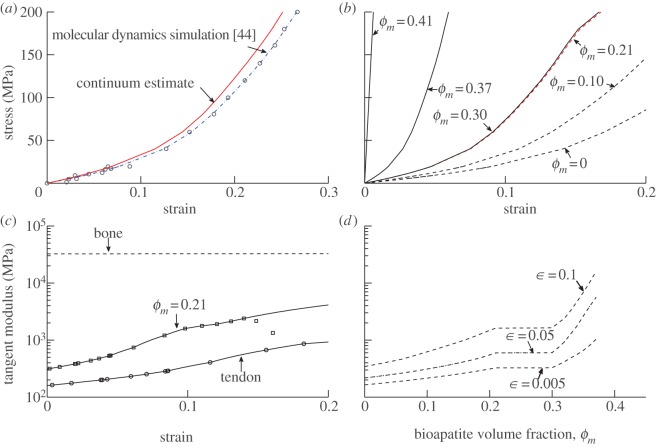
Figure 3.
Estimates of the nonlinear stress–strain response of individual collagen fibrils. (a) Stress–strain behaviour of collagen fibrils, based upon molecular dynamic simulations [44], and the estimated effective continuum constitutive response of collagen (solid line, red in online version). (b,c) These data for fibrils were used to make first-order estimates of the mechanics of fibres. Stiffening of fibres, following the mineralization scheme of model A, increased with increasing bioapatite volume fraction ϕm, but does so nonlinearly. As in the linear models, extrafibrillar bioapatite nucleating around the gap regions contributes little to longitudinal stiffness until the extrafibrillar bioapatite sheaths extend beyond the mineralized portions of the gap regions. (d) Tangential modulus of fibres, shown as a function of ϕm at several levels of strain, displays rapid stiffening for bioapatite volume fractions beyond the percolation threshold. (Online version in colour.)
2.2.3. Transverse stiffening of fibres and fibrils
Transverse (x2- and x3-direction, where the x1-direction parallels the fibre axis) properties of fibres and fibrils contribute to the axial moduli of tendon and bone. Fibres have a distribution of orientations, and estimating the axial moduli of tendon and bone involves integrating the full stiffness tensors of fibres over this distribution. Little data exist for rigorous estimates of these transverse properties, and even the simple estimates presented here required a number of assumptions. Fortunately, this ambiguity does not cloud interpretation of predicted moduli of partially mineralized tissues: these estimates are fully appropriate for tangent moduli of tendon and for tissue containing bioapatite volume fractions above the percolation threshold, and the transverse moduli of fibres have little contribution to the structural response of the insertion at bioapatite concentrations below the percolation threshold [45].
Transverse moduli for partially mineralized tissues were studied analytically using HS bounds, and using finite-element procedures described in §2.2.4. Details may be found in the electronic supplementary material.
2.2.4. Stochastic finite-element simulation for random bioapatite accumulation
Finite-element analysis was used for Monte Carlo simulations of random accumulations of extrafibrillar bioapatite (models C–E) and for estimating transverse moduli. The domain studied (figure 4) was a rectangular section of a compliant EFM (red) containing a hexagonal array of fibrils (volume fraction 0.8). Fibrils had a uniform diameter of 155 nm [46]. Fibrils were divided longitudinally into six pairs of overlap and gap regions; gap regions were divided into regions that could accept mineral (height Lm) and regions that could not (height 0.6 D − Lm). In simulations that allowed addition of randomly accruing bioapatite, fibrils were surrounded by sheaths of matrix elements that could be replaced with bioapatite (mesh not shown).
Figure 4.
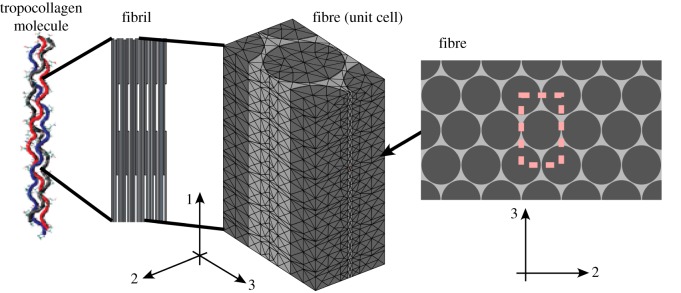
At the fibre level, some transverse and longitudinal moduli were estimated from finite-element simulation of the mechanical response of a representative unit cell. The unit cell shown with approximately 20 000 reduced integration tetrahedral elements was adequate for convergence of simulations of unmineralized collagen fibres. Significantly finer meshes discretized to allow sheaths of mineral were required for simulations of partially mineralized fibres. (Online version in colour.)
Periodic unit cell boundary conditions were applied to an eighth-space model. The three surfaces with outward normals in the positive 1-, 2- and 3-directions were constrained to maintain these normal directions, and to be free of shear traction, whereas the remaining three surfaces were constrained to have no shear tractions and no displacement in the direction of the surface normal. In each instance, one of the three faces with a positive outward normal was perturbed a prescribed amount, whereas the other two such faces were allowed to shrink inwards owing to Poisson contraction. The effective linear longitudinal and transverse moduli of the unit cell were determined from the forces necessary to sustain these isometric levels of stretch.
The EFM was approximated as isotropic, and fibrils were approximated as containing up to four transversely isotropic regions: gap regions with maximal intrafibrillar mineralization, unmineralized gap regions, mineralized overlap regions and unmineralized overlap regions. Poisson's ratios were set equal for each type of region: 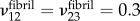 . The transverse and longitudinal moduli of these regions were as described above. The shear modulus was set to
. The transverse and longitudinal moduli of these regions were as described above. The shear modulus was set to 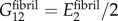 . Finite-element results showed effective moduli
. Finite-element results showed effective moduli 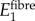 to be relatively insensitive to choices of
to be relatively insensitive to choices of 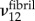 ,
, 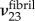 and
and 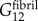 .
.
Simulations began with estimates of the effects of replacing unmineralized gap and overlap regions with mineralized gap and overlap regions within fibrils. Subsequent effects of extrafibrillar mineralization involved replacement at random of elements having the properties of EFM with elements having the properties of bioapatite. These Monte Carlo simulations were performed using standard techniques using scripts written in the Matlab environment in combination with Comsol finite-element analysis software. Careful convergence studies were performed. Models with no extrafibrillar mineralization could achieve convergence within 5% with as few as 20 000 quadratic, reduced integration tetrahedral elements (figure 4), whereas models with extrafibrillar mineralization required upwards of 100 000 elements.
2.3. Stiffening of tissues
The spatially varying tissue-level stiffness tensor C(x) was estimated at points x along the axis of a insertion from fibre-level moduli Cfibre(ϕm), published values for the spatial variation of ϕm(x), and published values of the spatial variation of the angular deviation s(x) that defined the circular orientation distribution of fibres according to a von Mises distribution [47]. Cfibre was assembled from spatially varying moduli estimates as described in the electronic supplementary material. Assuming a fibre distribution that is symmetric about the axis of the insertion, C(x) was calculated according to:
| 2.5 |
where θ is the inclination angle from the tendon-to-bone axis, R(θ) is a rotation from a coordinate system with the x1-direction oriented θ from the tendon-to-bone axis to the global coordinate system in which C(x) is defined, and 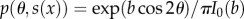 , in which b is the root of
, in which b is the root of 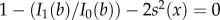 , I0(b) and I1(b) are the modified Bessel functions of order 0 and 1, respectively, and s is in radians.
, I0(b) and I1(b) are the modified Bessel functions of order 0 and 1, respectively, and s is in radians.
3. Results and discussion
3.1. Progressive stiffening of collagen fibres by bioapatite
Bioapatite increased the stiffness of collagen monotonically, but the degree of stiffening was sensitive to the sequence and structure of bioapatite accumulation. The effective nonlinear, fibril-level constitutive response gfibril(ε) of a hydrated collagen continuum was estimated from equation (2.4) and the data of [44]. The inverse of this function, (gfibril)−1(σ), followed these data closely (figure 3a, solid curve, red in online version). At the next hierarchical level, the fibre-level tangent stiffness of collagen increased linearly with straining, but never approached that of a nonlinear, fully mineralized fibre (figure 3b).
Mineralization according to model A stiffened such fibres monotonically (figure 3b,c). We note once more that while we can be confident of the responses at lower strains, the upper limits of these curves are highly uncertain, because the strain levels associated with permanent changes to collagen are not yet known, and those associated with slippage between collagen and bioapatite are even less certain (cf. [33,48]). Stiffening was less pronounced beyond ϕm = 0.21, the point at which gap channels became filled to capacity with bioapatite and intrafibrillar mineralization completed (figure 3d). For 0.21 < ϕm < 0.3, extrafibrillar sheaths extended over gap regions containing intrafibrillar mineral, yielding little additional stiffening (figure 3c,d). Significant stiffening was observed once more for ϕm > 0.3, as extrafibrillar sheaths extended over the overlap regions.
Trend lines in figure 3d do not converge at the stiffness of bone, because the levels of strain that must be accommodated just prior to percolation in this model are also high for input data to provide trustworthy constitutive estimates; extrapolating out would yield stiffnesses of a mineralized fibril that far exceed the moduli of bone. The high levels of strain in the compliant phase associated with the approach to percolation are evident in the curves associated with 0.21 < ϕm < 0.3. Here, the curves switch from concave up to concave down, associated with the slight reduction in stiffness of in the last datapoint of the Gautieri data, at a strain level approximately twice the average strain in the fibril. These predictions require validation to be trusted, especially because that single datapoint might represent either yield or numerical error. However, even with this uncertainty they highlight the amplification of strain that occurs in the approach to percolation and the importance of understanding the role of structural effects on the material response of a composite tissue.
Despite these limitations, it is useful to examine the relevance of the predictions to physiological levels of strain. One clear limit is the strain level at which fibrils and fibres begin to disassemble when loaded. The possible range of strains for disassembly is large, with estimates ranging from 0.07 to 0.5 [33]. These seem to be high values compared with the normal physiological range (a few percentage strain in bone, and up to 10% in tendon), but relating these measures to strain levels in vivo is premature because of the many unknowns including the level of pre-strain in fibrils and the heterogeneity in fibril strains that underlie the gradual recruitment of fibres during stretching. For load transfer across a region of tissue with a gradation in mineralization, a uniform tensile loading would be expected to induce a spectrum of strains in partially mineralized collagen fibrils based upon their degree of mineralization. Although further study is needed before nonlinear estimates such as these can be applied to model load transfer across a tendon-to-bone insertion site, the results provide an important baseline datapoint for ongoing study.
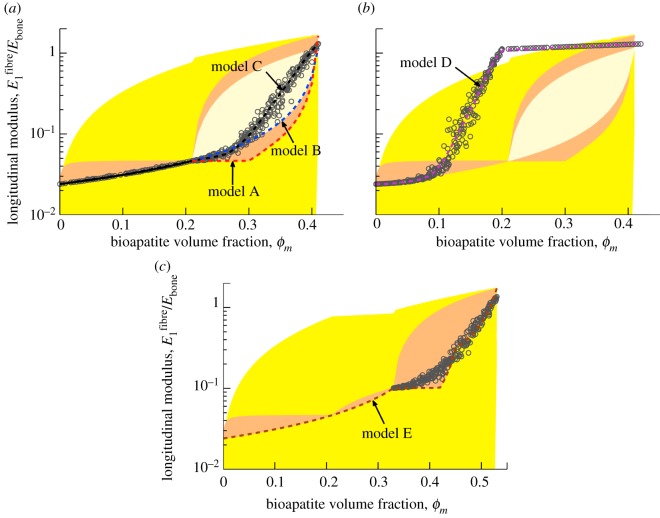
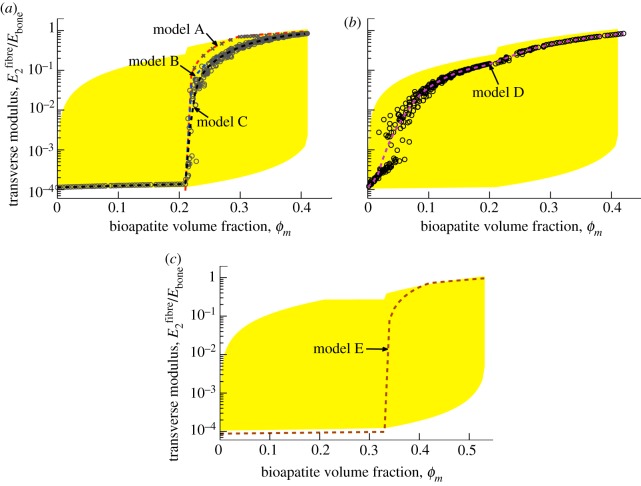
We next directed attention to linearized moduli to assess the five models of mineralization. The HS bounds (shaded region, figure 5; yellow in online version) formed a broad envelope for stiffening by bioapatite, with the lower bound extending beneath the lower cut-off of the graph. The HS upper bound displayed a slight ‘bump’ at ϕm = 0.21, where the composite considered shifted from a four-phase (mineralized gap regions, unmineralized gap regions, unmineralized overlap regions and EFM) to a five-phase composite (including extrafibrillar bioapatite). Incorporating microstructure into the bounds led to tighter bounds (darker shaded region, figure 5 orange in online version). For ϕm < 0.21 in models A–C (figure 5a), the upper bound required adding equal amounts of bioapatite to all gap regions simultaneously, resulting in relatively rapid initial stiffening and little stiffening thereafter, whereas the lower bound required adding bioapatite one gap region at a time, resulting in more gradual stiffening.
Figure 5.
Estimates of the fibre-level linear, longitudinal moduli. Shaded regions correspond to bounds described in the supplemental document. The broadest bounds are the HS bounds (lightly shaded, yellow in online version), truncated here because they extend several decades below the lowest estimate. The darker shaded regions (orange and tan in online version) represent ‘tighter’ bounds that are obtained by considering the details of the structure of collagen and bioapatite. (a) For models A–C, intrafibrillar mineralization precedes extrafibrillar mineralization. As motivated by the results of Monte Carlo simulations (circular markers, model C), the longitudinal moduli for models A and B were taken to follow lower bound estimates. (b) For model D, rapid stiffening occurs owing to extrafibrillar mineralization that precedes intrafibrillar mineralization (numerical results shown). (c) For model E, bioapatite accumulating in the overlap region leads to still greater stiffening of collagen fibrils. Circular markers represent numerical results for randomly distributed extrafibrillar bioapatite, as in model D. (Online version in colour.)
For models A–C, subsequent bioapatite accrued on the fibril exterior. The upper bound involved uniform sheaths of bioapatite that increased in thickness with increasing ϕm. The lower bound required either a sheath of bioapatite growing from one end of an infinitely long fibre (model B, light-shaded region) or periodically repeating belts growing from mineralized gap regions (model A, dark-shaded region, orange in online version). The upper bounds associated with models A and B differed, because the latter involved addition of extrafibrillar bioapatite to a homogenized, internally mineralized fibril, whereas the former incorporated the spatial distribution of bioapatite (equations in the electronic supplementary material).
For model E (figure 5c), an intermediate region existed in which bioapatite accrued within the overlap regions. Because bioapatite that exists in overlap regions is likely disorganized, three-phase (bioapatite, fibril, water) HS-type bounds were used.
The above bounds aided in the interpretation of the estimates of stiffening. For models A–C, the lower bound was the trendline for intrafibrillar mineralization: simulations with gap regions mineralized in random order (circles, figure 5a) followed the lower bound, as occurs with particle reinforced composites [49]. We note that random gap-by-gap mineralization is supported by the literature [22]. Thereafter, the three models diverged. Model A (extrafibrillar sheaths extending from gap regions) followed the series lower bound, with appreciable stiffening only after the sheaths extended beyond mineralized gap regions. The linear model reduced stiffening slightly at low ϕm relative to the nonlinear model. Model B (uniform sheath extended a single site) stiffened more rapidly as the sheath encompassed overlap regions at lower ϕm. Model C (random extrafibrillar additions) followed model B initially, but then stiffened rapidly towards the upper bound as a continuous network of mineralized EFM formed for ϕm beyond the percolation threshold. In all cases, the final modulus of a fibril exceeded the nominal modulus of Ebone = 20 GPa for cortical bone, indicating that the composite need not be fully dense with extrafibrillar bioapatite to reach this stiffness.
Model D (figure 5b, random extrafibrillar mineralization preceding intrafibrillar mineralization) followed models A–C until a percolation threshold, then stiffened beyond the four-phase HS bounds, as expected for a composite in which the stiff phase has a preferred alignment. Subsequent intrafibrillar mineralization yielded little stiffening.
Model E (figure 5c) included bioapatite in the overlap regions (0.21 ≤ ϕm ≤ 0.33). Stiffening here followed the HS lower bound, continuing the trend from the first region with little change in curvature, suggesting that stiffening is insensitive to whether gap versus overlap mineralize first. Thereafter, model E paralleled model A, except with a discontinuity in stiffening as the extrafibrillar sheaths extended over the different regions. Discontinuities disappeared for randomly accruing extrafibrillar bioapatite as in model C (circles, figure 5a).
The sequence of mineralization determined the nature of the mineralized structures that arose, and, in turn, the degree to which a specific volume fraction of bioapatite could stiffen a fibre. In each case, percolation was a key determinant of the degree of stiffening. Early formation of a sheath on a fibre's exterior (model D), as may occur in development, leads to significant stiffening at approximately one-third of the mineral volume fraction required if intrafibrillar mineralization precedes extrafibrillar mineralization (models A–C).
A number of other sequences of mineralization are possible in addition to those considered. Two important cases merit further discussion here, both relating to the possibility of bioapatite residing in the overlap regions, and uncertainty about its structure. First, how would a fibre behave if bioapatite accrued simultaneously and randomly in both gap and overlap regions? The likely answer is evident from data already presented: the results for model C indicate that the stiffening owing to random intrafibrillar accumulation would roughly follow that of the first two regimes of figure 5c, except that it would rise above that of the lower bounds to result in more rapid stiffening. Second, what if the mineral within the overlap regions is structured? A putative structure for bioapatite in the overlap regions has not yet been pinned down, but strong evidence exists that a connected structure is possible (cf. [29,50–52]). Structured bioapatite, especially if elongated along the axes of fibrils, would lead to a connected network and earlier percolation [53]. Following percolation, bioapatite would contribute almost as if it were added in parallel to the fibrils (cf. [54,55]) and, as observed from model D, would lead to a stiffening that would likely exceed the HS upper bound. Further characterization of the morphology of bipartite within the overlap regions is critically important.
Several important limitations must be borne in mind when interpreting these results. The first is the decomposition of fibrils into elastic matrix, bioapatite and hydrated collagen molecules that are not affected by surface interactions with bioapatite. This simplification would be expected to cause difficulty at very low levels of mineralization, but nevertheless enables a reasonable picture of how accrual of bioapatite in specified patterns stiffens collagen. The key is that uncertainty in the assumed properties and interactions are offset in the gap regions by only moderate levels of mineralization owing to the strong contrast in moduli: as gap regions fill with only a small fraction of bioapatite, the mechanics of the region becomes dominated by the bioapatite. The second is the nature of mineralization of the overlap regions. The structures and bioapatite/collagen interactions in this region are unknown. The third is validation: the absence of experimental data to validate the MD simulations upon which these estimates are based requires that nonlinear estimates be recognized as reliable only at smaller strain levels.
3.1.1. Stiffening transverse to a fibre axis
Transverse modulus estimates (figure 6a) were dominated by the EFM modulus at low levels of mineralization. Intrafibrillar mineralization had minimal (lower bound) stiffening effect, whereas extrafibrillar mineralization could lead to percolation more rapid than that observed for axial moduli. This was sharpest for model A, with a bioapatite network linking mineralized gaps of neighbouring fibres forming shortly after the onset of extrafibrillar mineralization. Formation of such bioapatite bridges is consistent with TEM observations [3]. Subsequent mineralization had a smaller stiffening effect. Model B predicted more gradual stiffening, because the percolated network surrounded both gap and overlap regions at the lowest levels of extrafibrillar mineralization. The random patterns of extrafibrillar bioapatite in model C resulted in further percolation delay. Model D (figure 6b) was analogous to model C but with extrafibrillar mineralization preceding intrafibrillar mineralization. The estimate for model E (figure 6c) was initially lower than the HS bounds, which are valid only for non-structured solids. Significant stiffening occurred only following extrafibrillar mineralization. We note that these observations might explain AFM measurements reporting a sharp mineralization front at the ligament-to-bone insertion: the models predict a sharp rise in transverse stiffness over a narrow range of the gradual rise in mineralization.
Figure 6.
Linear estimates of transverse moduli of fibres. Shaded regions (yellow in online document) are HS bounds. (a) For models A–C, intrafibrillar mineralization precedes extrafibrillar mineralization, and little stiffening occurs prior to the onset of extrafibrillar mineralization and the associated rapid percolation phenomenon. Percolation occurs more rapidly in the transverse direction than in the longitudinal direction, and some fibrils with intermediate degrees of mineralization may therefore be stiffer in the transverse direction than in the longitudinal direction. (b) For model D, rapid stiffening occurs due to extrafibrillar mineralization that precedes intrafibrillar mineralization (numerical results shown). (c) For model E, as with models A–C, little stiffening occurs prior to percolation. (Online version in colour.)
3.2. Progressive stiffening of collagenous tissues by bioapatite
We studied effects of gradations in bioapatite at the insertion. A compliant region between tendon and bone has been measured experimentally by tracking local strain between unmineralized and mineralized tissues [15]. This compliant tissue may serve to reduce stress concentrations [56] and is understood to arise from a trade-off between competing gradients of collagen organization and bioapatite [45]. The details of this zone are of interest, because the natural tissue is not regenerated following healing or surgical repair, and post-surgical failure rates reach 94% [57]. An important factor is surely that type II collagen in the insertion is expected to have mechanical properties that differ from type I collagen in bone and tendon. We hypothesized that, in addition to this, the nanoscale architecture of bioapatite accommodation is important for the spatial variation of stiffness along the insertion, and therefore investigated how the stiffness of a collagen fibril increases as bioapatite accumulates within and upon it, and as bioapatite links neighbouring fibrils. Results showed that the size of the compliant region, underestimated by previous methods, is highly sensitive to the way that mineral accrues on fibres across the insertion site.
The dominant factor in the size of this region is the onset of mineralization: this occurs at about the peak of disorganization in collagen at the insertion, and about halfway along its length (figure 7). The specific pathway by which bioapatite accumulates on the interior and exterior of a fibril can extend the width of the compliant zone. For model D, in which an extrafibrillar sheath of bioapatite forms around fibrils prior to mineralization of the fibril's interior, the rise in stiffness owing to bioapatite is relatively rapid. In all four of the other models, which we consider to be more likely candidates based upon our observations, the pattern of bioapatite accrual delays the rapid rise to the stiffness of bone, in some cases by delaying percolation to nearly 80% of the way from tendon to bone (figure 8). The minimum value of modulus predicted between tendon and bone is higher than that reported in [15], suggesting that other factors not considered, including a spatial gradient change in the collagen content, might play an additional role.
Figure 7.
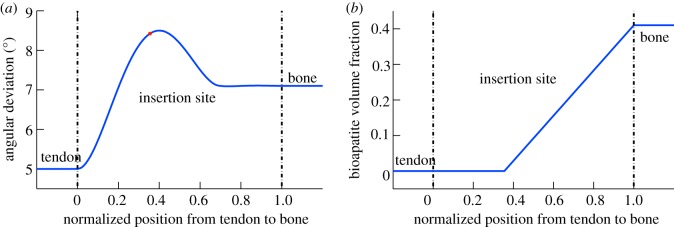
The spatially varying mechanical properties of the insertion were modelled based upon competing gradients in (a) organization of collagen fibres, and (b) bioapatite volume fraction. Disorganization of collagen fibres (increasing angular deviation) increases in the material between tendon and bone. The gradient in bioapatite volume fraction begins near the point of greatest disorganization (× symbol). The trendlines are based upon data described elsewhere [45]. (Online version in colour.)
Figure 8.
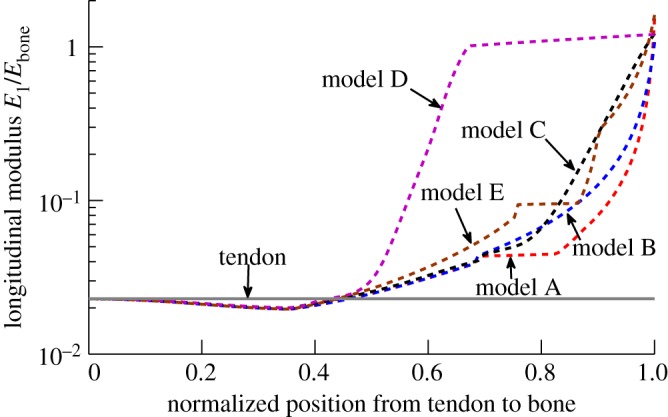
Tissue-level estimates of linear elastic moduli. The longitudinal modulus of tissue along the axis of the insertion is lower than that of either tendon or bone over a ‘compliant region’ within the insertion. The mineralization schemes most consistent with the literature serve to broaden this compliant region relative to model D. (Online version in colour.)
Results suggest that no modification of collagen properties by bioapatite owing to nanoscale interactions are needed to explain the stiffness of bone in terms of the properties of its constituents. Whereas many engineering polymer matrix nanocomposites are dominated in their behaviour by a stiffening and embrittlement that occurs at the polymer/nanoreinforcement interface, this might not occur in bone.
These results suggest that the pattern of mineralization that exists between tendon and bone may be tailored to maximize the size of a compliant band of tissue in healthy adults. Following both healing and repair surgery, the functionally graded tissue region and associated compliant zone are not regenerated, perhaps an important factor in the high rates of re-tear that occur [57]. Results presented here suggest that graft design can be optimized to account for this. We are currently pursuing this in our own laboratories through nanofibrous networks with gradations in bioapatite content [58] and orientation distribution [59] that mimic those of the insertion. Such nanofibrous electrospun mats are biocompatible, and can be tailored with cues for directed cell growth [59]. Although a wide range of mechanical properties are possible in this system, this study suggests that a fundamental rethinking of this approach is warranted involving stiffening and toughening over the entire range of spatial hierarchies [60,61]. Indeed, MD analysis has shown that microstructural details are key to constitutive and strength response of proteins, including hydrogen bond- and cross-link-driven unfolding mechanisms [62], and dissipative sliding of molecules [63]. While sacrificial bonds of bioapatite between mineralized collagen fibres [31] and the heterogeneity of such links [48,64] have long been known to be central to bone's toughness, the current results suggest an important role for the hierarchically derived stiffening of collagen by bioapatite, and suggest this as an important future direction for the design of scaffolds that guide post-surgical healing.
4. Conclusion
The nanoscale details of the accumulation of bioapatite on partially mineralized collagen fibrils are central to the fibril mechanics. Although the sequence and structure of mineralization are not yet known, reasonable estimates can be made. We presented models for a reasonable range of estimates and showed how these are important in the case of attachment of dissimilar materials. Mineralization sequences cited most frequently in the literature suggest that the nanostructure of collagen is optimized to accumulate bioapatite in a way that delays percolation. This in turn expands the size of the compliant region of partially mineralized tissue between tendon and bone and provides for a slower spatial gradient in tissue modulus, which has important ramifications in terms of macroscale stress transfer, and for cues to cells [65,66]. Nanostructurally based mechanical differences between developing and mature tissues may underlie poor healing outcomes in torn tendon-to-bone attachments [23,67]. In combination with observations that intermediate levels of mineralization are optimal for toughening of collagen [48], the current result that intermediate levels of mineralization might be distributed optimally across hierarchies to minimize stiffening motivate a picture of the insertion as an optimized, tough, compliant band.
Acknowledgements
Y.X.L. acknowledges a graduate fellowship from the Fannie Stevens Murphy Foundation.
Funding statement
This work was supported in part by the NSF (CAREER 844607), the NIH (R01 AR055580), and a joint NSF-NIH multiscale modelling grant (U01EB016422).
References
- 1.Schwartz A, Pasteris J, Genin G, Daulton T, Thomopoulos S. 2012. Mineral distributions at the developing tendon enthesis. PLoS ONE 7, e48630 ( 10.1371/journal.pone.0048630) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Glimcher MJ. 1987. The nature of the mineral component of bone and the mechanism of calcification. Instr. Course Lect. 36, 49–69. [PubMed] [Google Scholar]
- 3.Alexander B, Daulton TL, Genin GM, Lipner J, Pasteris JD, Wopenka B, Thomopoulos S. 2012. The nanometre-scale physiology of bone: steric modelling and scanning transmission electron microscopy of collagen–mineral structure. J. R. Soc. Interface 9, 1774–1786. ( 10.1098/rsif.2011.0880) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fritsch A, Hellmich C. 2007. ‘Universal’ microstructural patterns in cortical and trabecular, extracellular and extravascular bone materials: micromechanics-based prediction of anisotropic elasticity. J. Theor. Biol. 244, 597–620. ( 10.1016/j.jtbi.2006.09.013) [DOI] [PubMed] [Google Scholar]
- 5.Ji B, Gao H. 2006. Elastic properties of nanocomposite structure of bone. Compos. Sci. Technol. 66, 1212–1218. ( 10.1016/j.compscitech.2005.10.017) [DOI] [Google Scholar]
- 6.Oyen M, Ferguson V, Bembey A, Bushby A, Boyde A. 2008. Composite bounds on the elastic modulus of bone. J. Biomech. 41, 2585–2588. ( 10.1016/j.jbiomech.2008.05.018) [DOI] [PubMed] [Google Scholar]
- 7.Hamed E, Jasiuk I. 2012. Elastic modeling of bone at nanostructural level. Mater. Sci. Eng. Rep. 73, 27–49. ( 10.1016/j.mser.2012.04.001) [DOI] [Google Scholar]
- 8.Hellmich C, Ulm F-J. 2002. Micromechanical model for ultrastructural stiffness of mineralized tissues. J. Eng. Mech. 128, 898–908. ( 10.1061/(ASCE)0733-9399(2002)128:8(898)) [DOI] [Google Scholar]
- 9.Hellmich C, Barthélémy J-F, Dormieux L. 2004. Mineral–collagen interactions in elasticity of bone ultrastructure—a continuum micromechanics approach. Eur. J. Mech. A, Solids 23, 783–810. ( 10.1016/j.euromechsol.2004.05.004) [DOI] [Google Scholar]
- 10.Hellmich C, Ulm F-J, Dormieux L. 2004. Can the diverse elastic properties of trabecular and cortical bone be attributed to only a few tissue-independent phase properties and their interactions? Biomech. Model. Mechanobiol. 2, 219–238. ( 10.1007/s10237-004-0040-0) [DOI] [PubMed] [Google Scholar]
- 11.Fritsch A, Hellmich C, Dormieux L. 2009. Ductile sliding between mineral crystals followed by rupture of collagen crosslinks: experimentally supported micromechanical explanation of bone strength. J. Theor. Biol. 260, 230–252. ( 10.1016/j.jtbi.2009.05.021) [DOI] [PubMed] [Google Scholar]
- 12.Kim CH, Zhang H, Mikhail G, Von Stechow D, Müller R, Kim HS, Guo XE. 2007. Effects of thresholding techniques on microCT-based finite element models of trabecular bone. J. Biomech. Eng. 129, 481–486. [DOI] [PubMed] [Google Scholar]
- 13.Hellmich C, Kober C, Erdmann B. 2008. Micromechanics-based conversion of CT data into anisotropic elasticity tensors, applied to FE simulations of a mandible. Ann. Biomed. Eng. 36, 108–122. ( 10.1007/s10439-007-9393-8) [DOI] [PubMed] [Google Scholar]
- 14.Doube M, Kłosowski MM, Arganda-Carreras I, Cordelières FP, Dougherty RP, Jackson JS, Schmid B, Hutchinson JR, Shefelbine SJ. 2010. BoneJ: free and extensible bone image analysis in ImageJ. Bone 47, 1076–1079. ( 10.1016/j.bone.2010.08.023) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Thomopoulos S, Williams G, Gimbel J, Favata M, Soslowsky L. 2003. Variation of biomechanical, structural, and compositional properties along the tendon to bone insertion site. J. Orthop. Res. 21, 413–419. ( 10.1016/S0736-0266(03)0057-3) [DOI] [PubMed] [Google Scholar]
- 16.Waggett AD, Ralphs JR, Kwan AP, Woodnutt D, Benjamin M. 1998. Characterization of collagens and proteoglycans at the insertion of the human achilles tendon. Matrix Biol. 16, 457–470. ( 10.1016/S0945-053X(98)90017-8) [DOI] [PubMed] [Google Scholar]
- 17.Kumagai J, Sarkar K, Uhthoff HK, Okawara Y, Ooshima A. 1994. Immunohistochemical distribution of type I, II and III collagens in the rabbit supraspinatus tendon insertion. J. Anat. 185, 279. [PMC free article] [PubMed] [Google Scholar]
- 18.Fukuta S, Oyama M, Kavalkovich K, Fu FH, Niyibizi C. 1998. Identification of types II, IX and X collagens at the insertion site of the bovine achilles tendon. Matrix Biol. 17, 65–73. ( 10.1016/S0945-053X(98)90125-1) [DOI] [PubMed] [Google Scholar]
- 19.Orgel J, Irving TC, Miller A, Wess TJ. 2006. Microfibrillar structure of type I collagen in situ. Proc. Natl Acad. Sci. USA 103, 9001–9005. ( 10.1073/pnas.0502718103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fratzl P, Weinkamer R. 2007. Nature's hierarchical materials. Prog. Mater. Sci. 52, 1263–1334. ( 10.1016/j.pmatsci.2007.06.001) [DOI] [Google Scholar]
- 21.Miller A, Parker SB. 1984. Collagen: the organic matrix of bone [and discussion]. Phil. Trans. R. Soc. Lond. B 304, 455–477. ( 10.1098/rstb.1984.0040) [DOI] [PubMed] [Google Scholar]
- 22.Nudelman F, et al. 2010. The role of collagen in bone apatite formation in the presence of hydroxyapatite nucleation inhibitors. Nat. Mater. 9, 1004–1009. ( 10.1038/nmat2875) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Thomopoulos S, Genin GM, Galatz LM. 2010. The development and morphogenesis of the tendon-to-bone insertion—what development can teach us about healing. J. Musculoskelet. Neuronal Interact. 10, 35–45. [PMC free article] [PubMed] [Google Scholar]
- 24.Traub W, Arad T, Weiner S. 1989. Three-dimensional ordered distribution of crystals in turkey tendon collagen fibers. Proc. Natl Acad. Sci. USA 86, 9822–9826. ( 10.1073/pnas.86.24.9822) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pasteris JD, Wopenka B, Valsami-Jones E. 2008. Bone and tooth mineralization: why apatite? Elements 4, 97–104. ( 10.2113/GSELEMENTS.4.2.97) [DOI] [Google Scholar]
- 26.Pidaparti RMV, Chandran A, Takano Y, Turner CH. 1996. Bone mineral lies mainly outside collagen fibrils: predictions of a composite model for osternal bone. J. Biomech. 29, 909–916. ( 10.1016/0021-9290(95)00147-6) [DOI] [PubMed] [Google Scholar]
- 27.Lee DD, Glimcher MJ. 1991. Three-dimensional spatial relationship between the collagen fibrils and the inorganic calcium phosphate crystals of pickerel (Americanus americanus) and herring (Clupea harengus) bone. J. Mol. Biol. 217, 487–501. ( 10.1016/0022-2836(91)90752-R) [DOI] [PubMed] [Google Scholar]
- 28.Landis WJ, Moradian-Oldak J, Weiner S. 1991. Topographic imaging of mineral and collagen in the calcifying turkey tendon. Connect. Tissue Res. 25, 181–196. ( 10.3109/03008209109029155) [DOI] [PubMed] [Google Scholar]
- 29.Landis WJ, Song MJ, Leith A, McEwen L, McEwen BF. 1993. Mineral and organic matrix interaction in normally calcifying tendon visualized in three dimensions by high-voltage electron microscopic tomography and graphic image reconstruction. J. Struct. Biol. 110, 39–54. ( 10.1006/jsbi.1993.1003) [DOI] [PubMed] [Google Scholar]
- 30.Lees S, Prostak K, Ingle V, Kjoller K. 1994. The loci of mineral in turkey leg tendon as seen by atomic force microscope and electron microscopy. Calcif. Tissue Int. 55, 180–189. ( 10.1007/BF00425873) [DOI] [PubMed] [Google Scholar]
- 31.Fantner GE, et al. 2005. Sacrificial bonds and hidden length dissipate energy as mineralized fibrils separate during bone fracture. Nat. Mater. 4, 612–616. ( 10.1038/nmat1428) [DOI] [PubMed] [Google Scholar]
- 32.Goh KL, Holmes DF, Lu HY, Richardson S, Kadler KE, Purslow PP, Wess TJ. 2008. Ageing changes in the tensile properties of tendons: influence of collagen fibril volume fraction. J. Biomech. Eng. 130, 021011 ( 10.1115/1.2898732) [DOI] [PubMed] [Google Scholar]
- 33.Tang Y, Ballarini R, Buehler MJ, Eppell SJ. 2010. Deformation micromechanisms of collagen fibrils under uniaxial tension. J. R. Soc. Interface 7, 839–850. ( 10.1098/rsif.2009.0390) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Stabile KJ, Pfaeffle J, Weiss JA, Fischer K, Tomaino MM. 2004. Bi-directional mechanical properties of the human forearm interosseous ligament. J. Orthop. Res. 22, 607–612. ( 10.1016/j.orthres.2003.05.002) [DOI] [PubMed] [Google Scholar]
- 35.Raz E, Lanir Y. 2009. Recruitment viscoelasticity of the tendon. J. Biomech. Eng. 131, 1 11 001–1 11 008. ( 10.1115/1.3212107) [DOI] [PubMed] [Google Scholar]
- 36.Weiner S, Traub W, Wagner H. 1999. Lamellar bone: structure–function relations. J. Struct. Biol. 126, 241–255. ( 10.1006/jsbi.1999.4107) [DOI] [PubMed] [Google Scholar]
- 37.Ker RF. 1981. Dynamic tensile properties of the plantaris tendon of sheep (Ovis aries). J. Exp. Biol. 93, 283–302. [DOI] [PubMed] [Google Scholar]
- 38.Podrazky V, Sedmerova V. 1966. Densities of collagen dehydrated by some organic solvents. Cell. Mol. Life Sci. 22, 792–792. ( 10.1007/BF01897416) [DOI] [PubMed] [Google Scholar]
- 39.Dorsey N. 1940. Properties of ordinary water-substance in all its phases: water vapor, water, and all the ices. New York, NY: Reinhold Pub Corp. [Google Scholar]
- 40.Shen ZL, Kahn H, Ballarini R, Eppell SJ. 2011. Viscoelastic properties of isolated collagen fibrils. Biophys. J. 100, 3008–3015. ( 10.1016/j.bpj.2011.04.052) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Shen ZL, Dodge MR, Kahn H, Ballarini R, Eppell SJ. 2010. In vitro fracture testing of submicron diameter collagen fibril specimens. Biophys. J. 99, 1986–1995. ( 10.1016/j.bpj.2010.07.021) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shen ZL, Dodge MR, Kahn H, Ballarini R, Eppell SJ. 2008. Stress–strain experiments on individual collagen fibrils. Biophys. J. 95, 3956–3963. ( 10.1529/biophysj.107.124602) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Eppell SJ, Smith BN, Kahn H, Ballarini R. 2006. Nano measurements with micro-devices: mechanical properties of hydrated collagen fibrils. J. R. Soc. Interface 3, 117–121. ( 10.1098/rsif.2005.0100) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gautieri A, Vesentini S, Redaelli A, Buehler MJ. 2011. Hierarchical structure and nanomechanics of collagen microfibrils from the atomistic scale up. Nano Lett. 11, 757–766. ( 10.1021/nl103943u) [DOI] [PubMed] [Google Scholar]
- 45.Genin GM, Kent A, Birman V, Wopenka B, Pasteris JD, Marquez PJ, Thomopoulos S. 2009. Functional grading of mineral and collagen in the attachment of tendon to bone. Biophys. J. 97, 976–985. ( 10.1016/j.bpj.2009.05.043) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Derwin KA, Soslowsky L. 1999. A quantitative investigation of structure–function relationships in a tendon fascicle model. J. Biomech. Eng. 121, 598–604. ( 10.1115/1.2800859) [DOI] [PubMed] [Google Scholar]
- 47.Wagenseil J, Okamoto R. 2007. Modeling cell and matrix anisotropy in fibroblast populated collagen vessels. Biomech. Model. Mechanobiol. 6, 151–162. ( 10.1007/s10237-006-0019-0) [DOI] [PubMed] [Google Scholar]
- 48.Buehler M. 2007. Molecular nanomechanics of nascent bone: fibrillar toughening by mineralization. Nanotechnology 18, 295 102 ( 10.1088/0957-4484/18/29/295102) [DOI] [Google Scholar]
- 49.Genin GM, Birman V. 2009. Micromechanics and structural response of functionally graded, particulate-matrix, fiber-reinforced composites. Int. J. Solids Struct. 46, 2136–2150. ( 10.1016/j.ijsolstr.2008.08.010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Benezra Rosen V, Hobbs L, Spector M. 2002. The ultrastructure of anorganic bovine bone and selected synthetic hyroxyapatites used as bone graft substitute materials. Biomaterials 23, 921–928. ( 10.1016/S0142-9612(01)00204-6) [DOI] [PubMed] [Google Scholar]
- 51.Olszta MJ, Cheng X, Jee SS, Kumar R, Kim Y-Y, Kaufman MJ, Douglas EP, Gower LB. 2007. Bone structure and formation: a new perspective. Mater. Sci. Eng. Rep. 58, 77–116. ( 10.1016/j.mser.2007.05.001) [DOI] [Google Scholar]
- 52.Chen P-Y, Toroian D, Price PA, McKittrick J. 2011. Minerals form a continuum phase in mature cancellous bone. Calcif. Tissue Int. 88, 351–361. ( 10.1007/s00223-011-9462-8) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Bug A, Safran S, Webman I. 1985. Continuum percolation of rods. Phys. Rev. Lett. 54, 1412–1415. ( 10.1103/PhysRevLett.54.1412) [DOI] [PubMed] [Google Scholar]
- 54.Marquez JP, Genin GM, Zahalak GI, Elson EL. 2005a. The relationship between cell and tissue strain in three-dimensional bio-artificial tissues. Biophys. J. 88, 778–789. ( 10.1529/biophysj.104.041947) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Marquez JP, Genin GM, Zahalak GI, Elson EL. 2005b. Thin bio-artificial tissues in plane stress: the relationship between cell and tissue strain, and an improved constitutive model. Biophys. J. 88, 765–777. ( 10.1529/biophysj.104.040808) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Liu YX, Thomopoulos S, Birman V, Li J, Genin GM. 2011. Bi-material attachment through a compliant interfacial system at the tendon-to-bone insertion site. Mech. Mater. 44, 83–92. ( 10.1016/j.mechmat.2011.08.005) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Galatz LM, Ball CM, Teefey SA, Middleton WD, Yamaguchi K. 2004. The outcome and repair integrity of completely arthroscopically repaired large and massive rotator cuff tears. J. Bone Joint Surg. Am. 86, 219–224. [DOI] [PubMed] [Google Scholar]
- 58.Li X, Xie J, Lipner J, Yuan X, Thomopoulos S, Xia Y. 2009. Nanofiber scaffolds with gradations in mineral content for mimicking the tendon-to-bone insertion site. Nano Lett. 9, 2763–2768. ( 10.1021/nl901582f) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Xie J, Li X, Lipner J, Manning C, Schwartz A, Thomopoulos S, Xia Y. 2010. ‘Aligned-to-random’ nanofiber scaffolds for mimicking the structure of the tendon-to-bone insertion site. Nanoscale 2, 923–926. ( 10.1039/c0nr00192a) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Buehler M, Ackbarow T. 2007. Fracture mechanics of protein materials. Mater. Today 10, 46–58. ( 10.1016/S1369-7021(07)70208-0) [DOI] [Google Scholar]
- 61.Buehler M, Ackbarow T. 2008. Nanomechanical strength mechanisms of hierarchical biological materials and tissues. Comp. Methods Biomech. Biomed. Eng. 11, 595–607. ( 10.1080/10255840802078030) [DOI] [PubMed] [Google Scholar]
- 62.Ackbarow T, Sen D, Thaulow C, Buehler M. 2009. Alpha-helical protein networks are self-protective and flaw-tolerant. PLoS ONE 4, e6015 ( 10.1371/journal.pone.0006015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Buehler M, Yung Y. 2009. Deformation and failure of protein materials in physiologically extreme conditions and disease. Nat. Mater. 8, 175–188. ( 10.1038/nmat2387) [DOI] [PubMed] [Google Scholar]
- 64.Tai K, Dao M, Suresh S, Palazoglu A, Ortiz C. 2007. Nanoscale heterogeneity promotes energy dissipation in bone. Nat. Mater. 6, 454–462. ( 10.1038/nmat1911) [DOI] [PubMed] [Google Scholar]
- 65.Thomopoulos S, Marquez JP, Weinberger B, Birman V, Genin GM. 2006. Collagen fiber orientation at the tendon to bone insertion and its influence on stress concentrations. J. Biomech. 39, 1842–1851. ( 10.1016/j.jbiomech.2005.05.021) [DOI] [PubMed] [Google Scholar]
- 66.Thomopoulos S, Das R, Birman V, Smith L, Ku K, Elson EL, Pryse KM, Marquez JP, Genin GM. 2011. Fibrocartilage tissue engineering: the role of the stress environment on cell morphology and matrix expression. Tissue Eng. A 17, 1039–1053. ( 10.1089/ten.tea.2009.0499) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Smith L, Xia Y, Galatz LM, Genin GM, Thomopoulos S. 2012. Tissue-engineering strategies for the tendon/ligament-to-bone insertion. Connect. Tissue Res. 53, 95–105. ( 10.3109/03008207.2011.650804) [DOI] [PMC free article] [PubMed] [Google Scholar]