Flagellar dynamics of a connected chain of active, polar, Brownian particles

Abstract

We show that active, self-propelled particles that are connected together to form a single chain that is anchored at one end can produce the graceful beating motions of flagella. Changing the boundary condition from a clamp to a pivot at the anchor leads to steadily rotating tight coils. Strong noise in the system disrupts the regularity of the oscillations. We use a combination of detailed numerical simulations, mean-field scaling analysis and first passage time theory to characterize the phase diagram as a function of the filament length, passive elasticity, propulsion force and noise. Our study suggests minimal experimental tests for the onset of oscillations in an active polar chain.

1. Introduction

Eukaryotic cilia and flagella are whip-like, elastic microstructures that undergo oscillatory beating to drive processes such as locomotion [1], mucus clearance [2], embryogenesis [3] and directed cell migration [4]. While the molecular mechanisms that control ciliary beating remain incompletely understood, it is well established that sliding forces generated by dynein motors attached to the microtubule-based backbone of cilia play a crucial role [5]. Indeed, recent experiments on a reconstituted minimal motor-microtubule system by [6] demonstrate cilia-like beating suggesting that the interplay of elasticity and activity drives the oscillations.

In addition to understanding how these active structures work in nature, there is growing interest in designing artificial analogues. Artificial beating systems driven by external periodically varying electromagnetic fields have been synthesized [7], and theoretical calculations have suggested that swimmers can be constructed from gels that undergo time-dependent swelling/de-swelling transitions in response to an external forcing periodic stimulus [8] or an internal oscillatory chemical reaction [9]. However, developing internally driven structures capable of sustained beating patterns with controllable frequencies remains a subject of intense exploration.

In this study, we use simulations and theory to identify a different mechanism, involving no oscillating external fields or concentrations, that results in controllable, internally driven flagella-like beating or steady rotation. We consider microstructures comprised of tightly connected, polar, self-propelled units, which are geometrically constrained at one end by a clamp or a frictionless pivot. The tangentially directed compression forces arising from the self-propulsion cause a buckling instability, yielding periodic shapes and motions. The mechanism we study thus corresponds to the active analogue of the continuous buckling of a filament owing to follower forces, which refer to compressive forces that always act along the local instantaneous tangent to the filament, and thus ‘follow’ the filament as it moves in the ambient viscous medium.

The two-dimensional chain of connected, self-propelled particles that we envision may be realized in several experimental systems. First, Janus beads can propel themselves through self-diffusophoretic [10–12] or thermophoretic effects [13,14], whereas asymmetric granular discs or rods undergo directed motion on shake tables [15–17]. These individual propelled particles can be connected to form active filaments, either through face–face attractions or by passive tethers. A second route to obtain such active polar filaments is by using motility assays in which microtubule or actin filaments are propelled by surface-grafted molecular motors, with one end of the filament constrained by pinning to the surface or through optical trapping.

In the quasi-two-dimensional aqueous settings that we consider, the surface acts as a sink of momentum that cuts off long-range hydrodynamic interactions, allowing filament elasticity and active forces to control filament dynamics. Therefore, we do not include long-range hydrodynamic interactions in our model. Our findings are thus complementary to an independent study [18,19] conducted at the same time as ours, which uses non-local Stokesian hydrodynamics to examine a filament made active by a permanent distribution of stresslets along its contour and finds that induced secondary flows can generate autonomous filament motion. Although follower forces were first proposed by Euler [20–22] they have been rarely studied in the context of active filaments moving in a viscous medium. An exception to this is the elegant linear stability analysis by Sekimoto et al. [23] of elastic filaments animated by molecular motor proteins. They showed that, in the noise-free limit where fluctuations in the direction of the active forces on the filament can be neglected, oscillatory behaviour arises above a critical value of the active force. Here, we combine particle-based simulations, scaling analysis and first passage time calculations to determine the large-amplitude motions of an active filament as a function of the filament length, passive elasticity, propulsion force and the magnitude of fluctuations in propulsion directions. We find that linear analysis [23] is valid for short filaments in the zero-noise limit close to criticality. However, the nonlinear response leads to different scaling relations and meandering waves that resemble motions of long flagella [24] for long filaments or for strong active force densities. Importantly, we also combine extensive simulations and theory to identify the ability of noise to disrupt the emergent oscillations in these systems.

In §2, we describe the model, the computational implementation and the dimensionless parameters that govern system behaviour. Section 3.1 describes our dynamical simulation results in the limit of weak noise for anchored short filaments. We also present mean-field scaling arguments that enable us to obtain explicit expressions for the critical force f_c required to obtain oscillatory states as well as the frequency and wavelength of oscillations. In §3.2, we analyse the dynamics for very long filaments, or filaments that are subject to very high compressive force densities. We find that excluded volume interactions and the avoidance of self-contact results in looped shapes as well as a change in the frequency–activity relationship. We then explore the effect of noise in §3.3, where we identify the transition from steady, correlated oscillations to erratic, uncorrelated oscillations. A first passage time calculation based on transition state theory allows us to identify the critical noise level required to destabilize steady oscillations. We conclude in §4 by situating our work in the context of current research on active motile filaments.

2. Model

Our model for the active filament is a two-dimensional chain of connected, self-propelled, polar colloidal spheres. The chain (filament) has N such spheres each of diameter σ located at coordinates r_i (i = 1, … , N) interacting via harmonic potential with the equilibrium linker length being b, so that

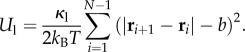The value of κ₁ is maintained at a value large enough that the actual distance between each polar particle is nearly b, making the chain nearly inextensible. Additionally, resistance to chain bending is implemented via a three-body-bending potential

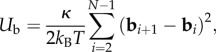where b_i = (r_{i – 1} – r_i)/|r_i – r_{i – 1}| is the unit bond vector that is anti-parallel to the local tangent and κ is the bending rigidity. The whole system moves in a fluid of viscosity μ, and the system is held at constant temperature T.

To enable active compressive forces to act on neighbouring spheres, we bias them to preferentially align with the instantaneous tangent vector. This is consistent with the interaction between a motor head and a filament in a motility assay, where attached motors walk and exert forces along the filament track, or self-propelled Janus spheres connected by face–face attractions, where the propulsion direction is normal to a face. The polar direction 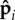for each sphere is biased to point along b_i by a harmonic potential

2.1

with κ_a controlling the magnitude of polarity fluctuations about the mean direction.

In the limit κ_a → ∞, the propulsion forces are perfectly aligned with the local tangent (the idealized follower-force scenario). This limit corresponds to an experimental system in which the chemical linkage between successive beads in the filament is tightly coupled to and parallel to the direction of the self-propulsion. Lower values of κ_a represent reduced coupling and thus result in a fluctuating polarity. This situation could arise either from thermal noise or from additional interactions, e.g. in the case of a microtubule–motor system, lateral interactions between the motor head and its neighbours could result in fluctuating polarity.

The dynamics of the filament is determined by the evolution of the sphere positions r_i and orientations 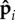, (i = 1, … , N) which we simulate using over-damped Brownian dynamics,

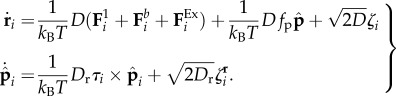2.2

Here, 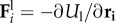, 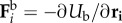and 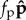are respectively the axial, bending and propulsion forces, 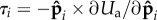is the torque arising from the angular potential, 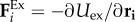is a pairwise excluded-volume repulsive force given by the Weeks–Chandler–Andersen (WCA) potential

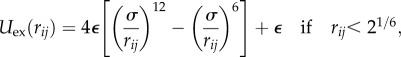and zero otherwise [25]. This pairwise interaction applies to all pairs of beads in close spatial proximity, including both nearest neighbours along the chain and those which are non-local in sequence. The translational and rotational diffusion constants D and D_r in our over-damped system satisfy the Stokes–Einstein relationship D_r = 3D/σ², and ζ and ζ^r are zero mean, unit variance Gaussian white noise forces and torques respectively, with covariances that satisfy

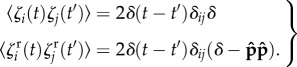2.3

As the viscous mobility of a sphere is isotropic, our simulations neglect differences in viscous resistance to normal and tangential modes of filament motion. We do not include hydrodynamic interactions between parts of the filament in our model; these can be neglected in the quasi-two-dimensional dense viscous systems we are motivated by due to screening resulting from confinement. In the limit of a single sphere, our model reduces to the over-damped description of a self-propelled particle, which undergoes a persistent random walk with mean instantaneous speed v_p = f_pD/k_BT, persistence length v_p/D_r and an effective diffusion coefficient .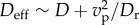

We define the arc-length parameter s in the range 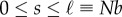to parametrize the coarse-grained position along the filament. Finally, we make the equations dimensionless by using σ and k_BT as basic units of length and energy, and σ²/D as the unit of time and we set ε = k_BT.

Simulations were initialized using a straight configuration with the filament vertically oriented along 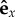, with all p_i initially along 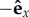. One end of the filament corresponding to s = ℓ was always free. The anchored end s = 0 was either clamped vertically or attached to a frictionless pivot with the filament free to rotate. The clamping was achieved by attaching the first particle at (s = 0) to a fixed point in space r₀ by a harmonic potential with the same properties as the binding potentials between the other particles in the filament. While the three-body-bending potential applied on r₁ has an equilibrium angle of π/2 between the bond vector r₁ – r₀ and .

3. Results

To investigate the dependence of filament behaviour on the system parameters, we performed simulations with filaments anchored according to clamped or pivoted boundary conditions for varying filament length ℓ, active force density f_p and angular stiffness. The angular stiffness parameter, κ_a, was varied from 0.1 to 20, to investigate situations from the noise-free idealized follower-force limit (κ_a → ∞) to the noise-dominated regime. For all simulations described here, we set the bending rigidity κ = 2 × 10⁴ to give a persistence length .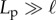

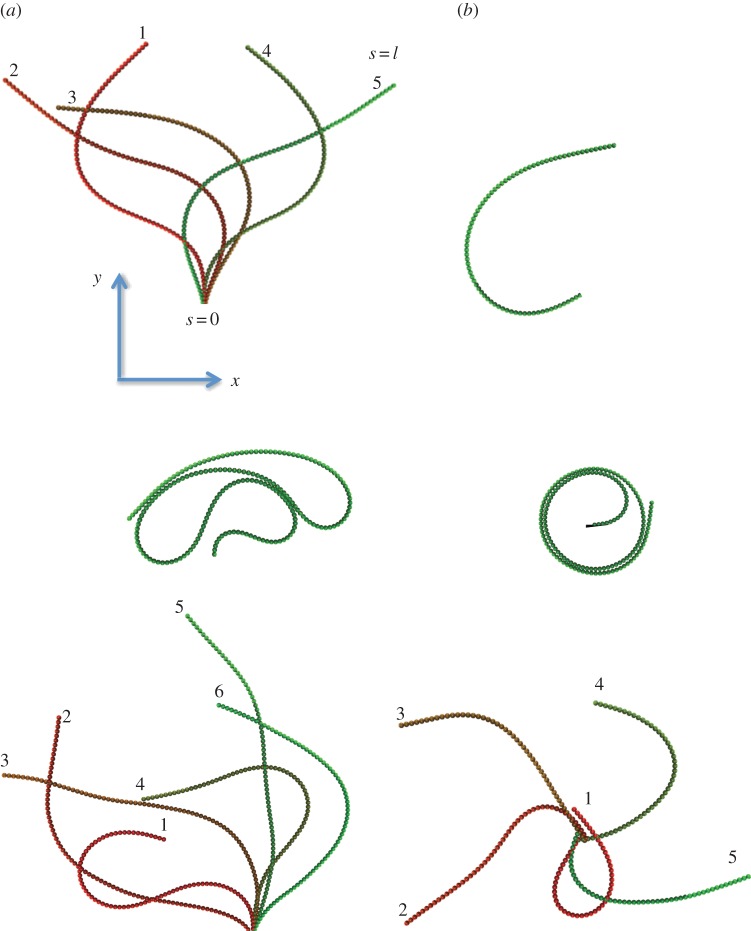
The images in figure 1 illustrate our main results. First, we find that for a given filament length, the straight filament configuration becomes unstable above a threshold propulsion force, and the system displays an oscillatory motion. The boundary condition at the anchored end dramatically changes the mode of oscillation. A clamped end results in flagella-like beating, whereas a pivoted end allows the filament to rotate freely, forming spiral shapes. Second, in the low noise limit, we observe a second critical length beyond which the beating and rotating shapes start to depend critically on the excluded volume interactions. Finally, above a threshold noise level, the system transitions from periodic oscillations to erratic motions. Thus, the noise-level provides an independent, experimentally accessible parameter with which to tune the filament behaviour.

Figure 1.

Overview of the dynamical shapes observed in simulations. The active force density is f_p, filament length is ℓ and the angular noise is parametrized by κ_a. (a) Shapes for a filament clamped at one end. (Top) Regular beating for short filaments, ℓ = 80 with weak angular noise κ_a = 20. The frequency of oscillations is controlled by f_p. (Centre) Self-contacting looped shapes observed for long filaments ℓ = 160 with weak noise κ_a = 20. Excluded-volume interactions alter the frequencies of oscillating and rotating shapes in this limit. (Bottom) For large angular noise, κ_a = 0.5, motions along the filament decorrelate, resulting in highly erratic shapes. (b) Spiral shapes for a filament with one free end and one end that can pivot. (Top) A weakly curved filament of ℓ = 50 rotating at constant frequency, typical of short filaments and weak noise κ_a = 20. (Centre) A rotating, tightly wound spiral typical of long filaments ℓ = 160 and weak noise κ_a = 20. (Bottom) Erratic rotation without a steady rotating shape or well-defined rotational frequency, typical of strong noise, κ_a = 0.5 for a filament with ℓ = 80. In all cases shown the active force density was f_p = 20. The value of bending stiffness is κ = 2 × 10⁴ in all figures in the article. Animations from typical simulations are provided in the electronic supplementary material. (Online version in colour.)

For the sake of simplicity, the simulations presented in the main text assumed local resistivity theory for the hydrodynamics and isotropic filament mobility. However, we have tested these approximations by performing additional simulations with (i) an anisotropic mobility (corresponding to a true slender body) and, (ii) non-local hydrodynamic interactions implemented using a coarse-grained fluid model called multiparticle collision dynamics [26] (see appendix C for details and results). While relaxing these approximations leads to quantitative differences in beating frequencies and the trajectories of filament material points, the dynamical behaviours and phase properties of the system remain qualitatively the same.

3.1. Dynamics for short filaments and weak activity

We first present results for the case of a clamped filament, with boundary conditions at the anchored end given by 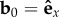, and r₀ = 0. The other end is force- and torque-free. For weak noise (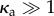), fluctuations in polarity along the filament are negligible, and the base state is a straight filament. The internal active forces act along the filament towards the clamped end, leading to compression. When the internal propulsion force f_p exceeds a critical value f_c, which depends on ℓ and κ_a, the filament buckles, in a manner similar to a self-loaded elastic filament subject to gravity. However, the post-buckled states are quite different (see electronic supplementary material, appendix A), because the direction of active force density follows the polarity vectors 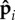and thus tends to point along the filament axis.

At fixed filament stiffness κ, and for f_p > f_c, we find that the magnitude of the polarization stiffness κ_a controls the long-time dynamics of the filament. In figure 2a, we show the local filament curvature as a function of time and arc length. For small values of κ_a (left), thermal diffusion controls the local orientation of 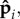and the propulsion activity is uncorrelated along the filament. In this regime, the filament dynamics is marked by transients resulting from the bending generated by the particle propulsion, but no coherent patterns. When κ_a is increased above a critical value 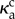, the polarities of the spheres align strongly with the local tangent. The resultant self-propulsion force is strongly correlated with the filament tangent and the filament oscillates with periodic, large-amplitude wavy motions (the plot on the right) that propagate from the proximal (clamped) end to the distal (free) end. This beating profile is very similar to that of flagella in eukaryotic cells, though the underlying physics differs fundamentally.

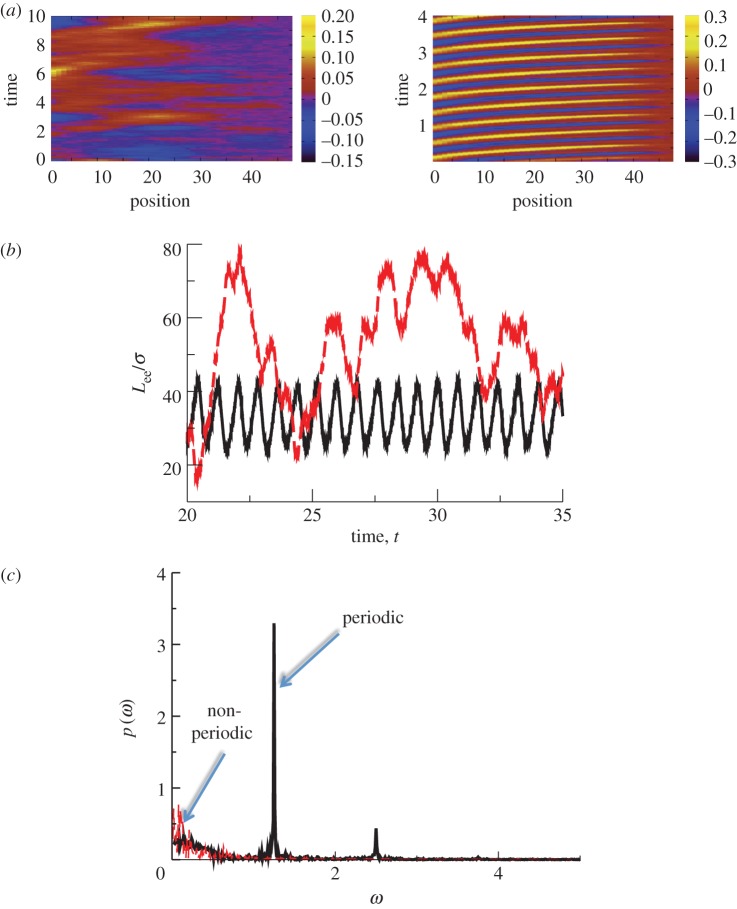
Figure 2.

(a) Plots of the local filament curvature as a function of time and the distance from the clamped end for a filament of length ℓ = 80 and active force density f_p = 20, for typical examples of non-periodic beating for angular force constant κ_a = 0.5 (left) and periodic buckling for angular force constant κ_a = 20 (right). (b) Length of the end–end vector L_ee as a function of time for periodic buckling (solid line) and non-periodic beating (dashed line). (c) Power spectral density of L_ee for filament length ℓ = 80, propulsion force f_p = 20, and angular force constant κ_a = 20 (periodic) and κ_a = 0.5 (non-periodic). (Online version in colour.)

We quantify the regularity of oscillations by measuring the length of the end–end vector 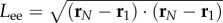, as a function of time, shown for two values of κ_a, 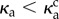and 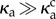, in figure 2b. While L_ee displays large variations in time for both values of κ_a because of the large propulsion force, the profile for 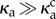is periodic, and its power spectral density shows a distinct frequency maximum (figure 2c).

To understand our numerical experiments and to obtain estimates for the critical buckling load and the frequency of ensuing oscillations in the periodic regime, we consider the noiseless limit κ_a → ∞, and coarse-grain the chain of spheres into a slender, elastic filament of length ℓ and bending stiffness κ. The force owing to the self-propulsion translates to a compressive force per unit length of strength f_p oriented anti-parallel to the local tangent vector. The resulting internal propulsion force 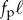deflects the tip by a small transverse distance leading to an effective filament curvature . Balancing moments about the base then yields 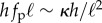and thence the critical propulsion force beyond which the straight filament is no longer stable,

3.1

The constant C₁ is, in principle, a function of κ_a (note that 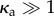still holds) and thus must be determined from simulations close to the critical point. For the particular case κ_a = 100, we find that 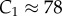(figure 3a). Thus a chain immersed in a viscous fluid cannot sustain a static buckled state and instead yields to oscillating, deformed shapes (see electronic supplementary material, appendix A).

Figure 3.

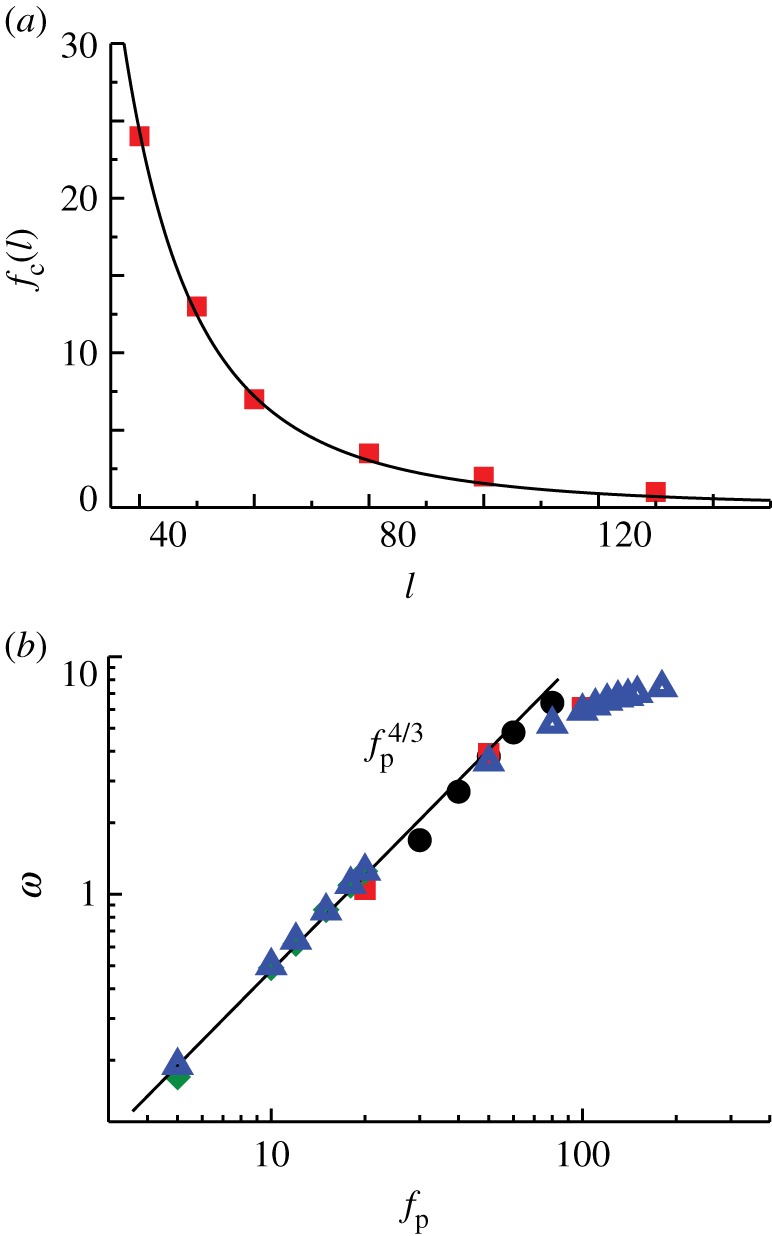
(a) Critical propulsion force 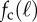for various filament lengths, at constant angular stiffness κ_a = 100. The solid line is 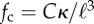with 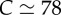, consistent with the theory (equation (3.1)). (b) The beating frequency of filaments as a function of propulsion force f_p for filament lengths ℓ = 40 (filled circles), ℓ = 50 (filled squares), ℓ = 80 (filled diamonds), and ℓ = 100 (filled triangles). The dashed line corresponds to the scaling law (equation (3.3)). Parameters are dimensionless as described in the text. For very long lengths, the filament becomes self-interacting resulting in a decrease in the exponent due to excluded-volume interactions. (Online version in colour.)

In the noise free limit, the constant C₁ (κ_a → ∞) can be exactly obtained from a stability analysis of the corresponding continuum mean-field equations. A systematic derivation of the full nonlinear equations governing the filament dynamics that builds on a local resistivity formulation relating filament bending to its velocity yields two coupled nonlinear equations for the tension in the filament T and θ, the angle the filament makes with e_x (see electronic supplementary material, appendix B). In this linear limit, the single dimensionless parameter that determines the existence and emergence of solutions is indeed the dimensionless number 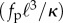. The linearized equations corresponding to the noise-free, mean-field version of model were considered earlier [23]. The critical value of the dimensionless parameter at onset of oscillations was determined to be 75.5, which closely matches the numerical value we obtain for κ_a = 100.

When 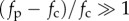and the straight filament is unstable, the characteristic length over which the active compression is accommodated

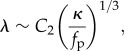3.2

is given by 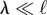. In the over-damped limit, all the energy supplied by the self-propulsion transforms first into elastic bending energy and is then dissipated viscously by the filament motion. In a time ω⁻¹, the energy dissipated viscously is the product of the force per unit length η_⊥λω, the characteristic deflection λ and the velocity ωλ. This dissipation has to balance the active energy input into the system owing to the self-propulsion f_pλ²ω, yielding η_⊥λ³ω² ∼ f_pλ²ω. Using equation (3.2), we obtain the oscillation frequency

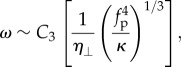3.3

which shows excellent agreement with our simulations for a range of active forces at constant ℓ. Simulations performed with anisotropic filament mobility with η_⊥ = 2η_|| instead of η_⊥ = η_|| yield qualitatively similar results (see electronic supplementary material, appendix C). However, comparing with the filament with isotropic mobility, the beating frequency is reduced roughly by half as predicted by equation (3.3) obtained from scaling arguments. For very high values of f_p (or equivalently for long filaments), we find that the frequency obeys a different scaling law, for reasons discussed in the next section.

The beating motions described above require a clamped boundary condition that prevents both rotation and translation. We next performed simulations for a filament moving about a frictionless, pivoting end at s = 0 such that r₀ = 0 but b₀ is unconstrained.

For small values of κ_a, and with the contour length ℓ and rigidity κ held fixed, the filament end–end length L_ee displays large irregular variations and the end–end vector L_ee undergoes irregular rotation about the fixed end—illustrated in figure 1c. Increasing the value of κ_a results in the active forces being increasingly correlated along the contour. The post-buckled filament now assumes that a steadily rotating bent shape and the value of L_ee does not vary in time (figure 1b).

The rotation frequency extracted from simulations by calculating the orientation of L_ee as a function of time is plotted in figure 4 as a function of f_p. When 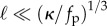, the filaments are short compared with the characteristic wavelength and do not overlap. Non-local interactions between segments of the filament can then be neglected and the steady rotational frequency varies with force in accord with equation (3.3). The shapes we obtain compare well with the experimental observed conformations in motility assays where filaments animated by underlying molecular motors encounter pinning sites (defects) and start to rotate [27]. While the scaling for the critical active density above which rotation occurs follows equation (3.1), the corresponding value of the dimensionless parameter C₁(κ_a) differs from that for the clamped case owing to the different boundary condition. For κ_a = 6, we obtain the value C₁ ∼ 36, which compares well with the value of 30.6 obtained in the mean-field noise-free limit [23].

Figure 4.

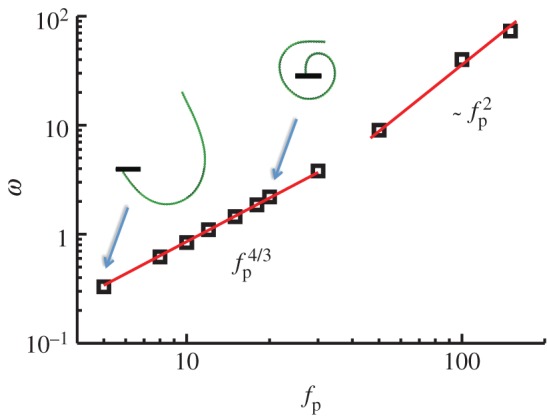
Frequency of steady rotation for a filament anchored at a pivot, with length ℓ = 160, angular force constant κ_a = 2 × 10², and bending stiffness κ_a = 2 × 10⁴. The snapshots illustrate typical shapes of the rotating filaments. For weak forcing, the filament is lightly coiled. As the force density increases, the filament starts to curve significantly almost closing in on itself. Finally for strong forcing (or equivalently for long filaments), the final stable rotating shapes are highly nonlinear, tightly wound coils and the frequency scaling deviates from the 4/3 power law. (Online version in colour.)

3.2. Self-avoidance modifies the steady frequency for strong activity or long filaments and modifies the resulting shapes

3.2.1. Clamped end

We now focus on the limit of strong activity 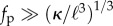or long filaments 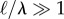for which large filament curvatures cause non-local segments to interact. For a clamped filament, these non-local interactions result in loopy curves with highly curved regions interspersed by relatively flat ones as shown in figure 1b.

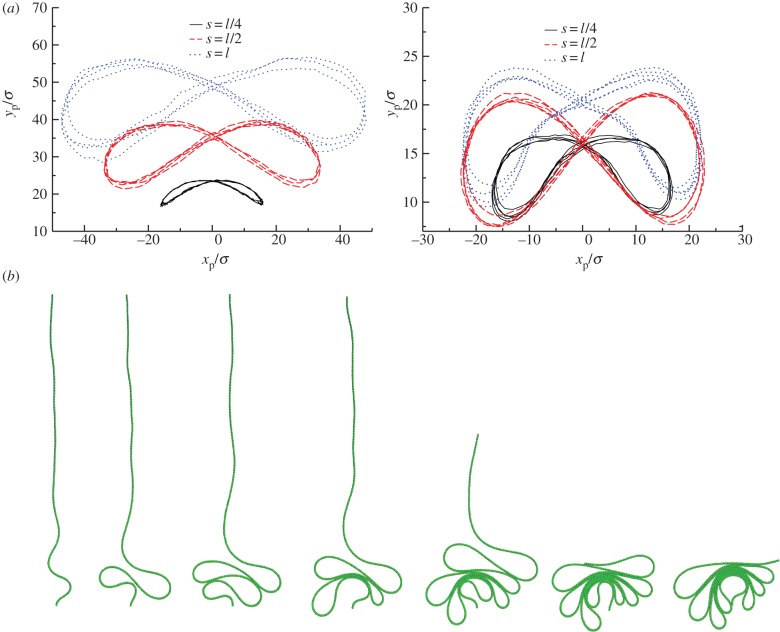
In figure 5, we compare the filament trajectories exhibited by non-interacting filaments with the self-interacting filaments. The length is held constant for the case illustrated, whereas the active force density is tuned to different values. For non-interacting filaments, material points on the filament execute closed trajectories resembling a figure-of-eight, as expected for an inextensible, non-interacting, oscillating filament. Points near the free end undergo larger deformations and thus larger amplitude oscillations when compared with points near the base. Increasing the force density to f_p = 50 yields dramatically different behaviours. First, the free end of the filament extends a greater distance in the vertical, downward direction owing to larger buckling. More importantly, trajectories exhibit significant self-interaction (compare, for instance, the locus of s = ℓ and s = ℓ/4 in the two cases) and oscillate with smaller frequencies. The frequency–activity response is characterized by a power law exponent different from that obtained for non-interacting filaments (equation (3.3)). This modification may arise due to additional energy dissipation resulting from excluded-volume interactions as two filaments slide past each other in close proximity. We also note that in a setting where hydrodynamic interactions are not screened, the frequency will be modified by anisotropic drag effects and direct fluid-mediated interactions between non-local parts of the filament (see electronic supplementary material, appendix C).

Figure 5.

Comparison between clamped filaments in the non-self-interacting case (small ℓ or small f_p) and the self-interacting case (large ℓ or large f_p). Trajectories of material points are shown for ℓ = 100 and varying force density f_p. (a) Left: results for f_p = 5 (non-interacting). The strength of the compressive forces are low enough that there is no interaction between segments separated along the filament contour by more than a few σ. (a) Right: a larger force density f_p = 50 (self-interacting) yields more curved and loopy structures. Note the dramatic change in the difference between trajectories for s = ℓ and s = ℓ/4. (b) A sequence of snapshots from a simulation in which an initially straight long filament buckles into a series of successively meandering loops. As time increases (moving right), we find that self-avoidance and bending control the number and lateral extent of the loops. Loops formed initially are trapped by those that form later. Eventually, most of the filament moves tangentially resulting in large parts of the filament undergoing lateral sliding. The first three snapshots from the left do not show the full length of the filament. (Online version in colour.)

Interestingly, the looped conformations we observe in the self-interacting case resemble the meandering waveforms seen in studies of quail spermatozoa [24], which have unusually long flagella. Meandering waveforms are also observed in a very viscous fluid or close to boundaries that resulted in increased local viscous resistivity such as near a coverslip. While the waveforms observed in experiments were almost static in relation to the field of view with bend propagation manifested as the forward movement of the flagellum through the static shape, in our simulations, because one end of the filament is clamped no such steady motion is possible. Thus, the loops that form first are continuously trapped by loops that form subsequently (figure 5b). An initially straight filament culminates in a tangle of continuously sliding looped structures with most of the filament moving tangentially.

3.2.2. Pivoted end

Changing the boundary condition at one end to a pivot yields tightly coiled, rotating structures as shown in figure 1b and figure 6b. At steady state, the final radius, R_c, decreases sharply with f_p; eventually bending of the coil is balanced by the lateral forces owing to excluded volume, resulting in a very slow decay with f_p. In figure 6a, we plot the radius of the coiled shapes and find an initial exponential decay with the active force f_p (red curve).

Figure 6.

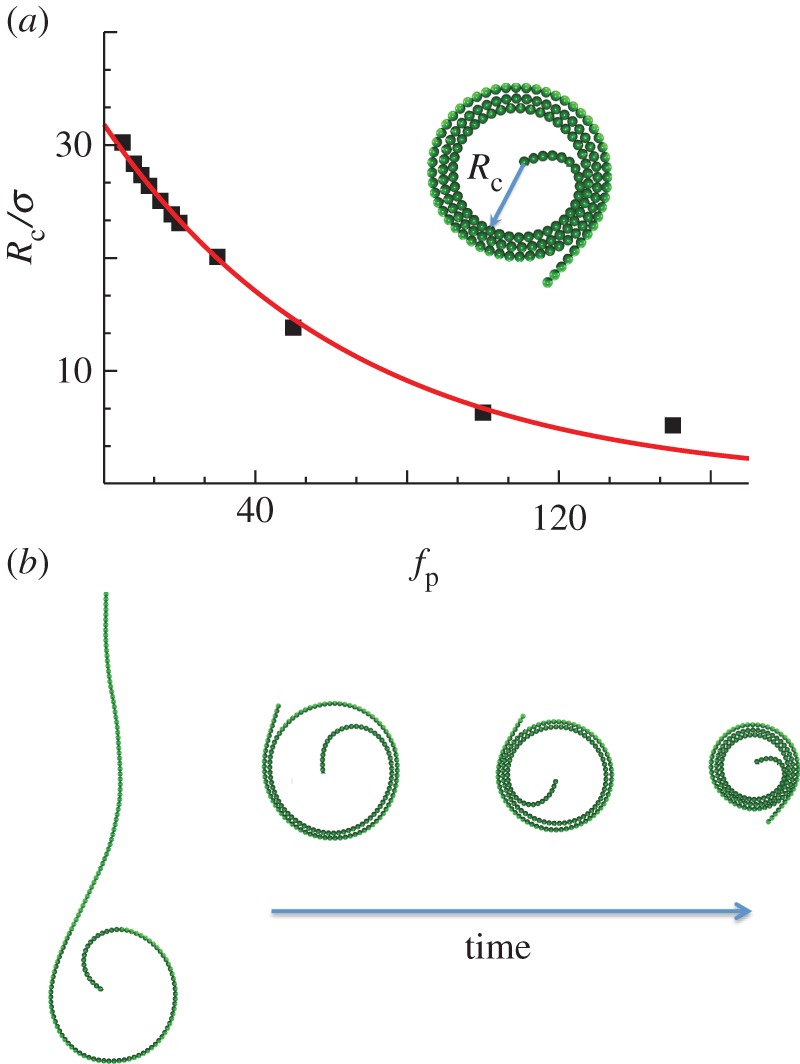
Radius R_c of the final coiled shape as a function of f_p for a filament with a pivoting end. The parameter values are ℓ = 160, κ_a = 2 × 10² and κ = 2 × 10⁴. The solid curve indicates a fit to an exponential decay. (b) Transient shapes for very large f_p as the filament coils and eventually undergoes steady rotation. (Online version in colour.)

Snapshots of the transient rotating shapes seen for long filaments (figure 3b) indicate multiple timescales in the coiling process. Initially, the filament curvature increases with a characteristic rate, until the free end closely approaches another region of the filament. Next, the remaining length is accommodated in concentric coils, whereas the curvature near the free end remains nearly constant. Once the entire filament is coiled, the curvature increases further, leading to a tightening of the coils, an increase in the number of coils, and a decrease in the coil radii. The filament behaves nearly as a rigid body, with negligible sliding between adjacent coils. The frequency of steady rotation depends strongly on excluded volume forces. For fixed ℓ, the frequency almost scales as 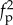(see figure 4 in the large f_p limit). When the same simulations were rerun without excluded-volume interactions, we obtained completely overlapping coils and a frequency that scaled as 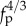, consistent with equation (3.3).

4. Correlation length of polarity controls dynamics for strong noise

In previous sections, we explored the dynamics of the active polar filament in the limit of small noise (large angular stiffness κ_a), where each 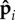points predominately along the filament and in the direction opposite to the local tangent. We now consider the response of connected self-propelled particles as a function of κ_a and active force density f_p. Figure 7 shows the phase diagrams for (i) clamped filaments and (ii) rotating filaments.

Figure 7.

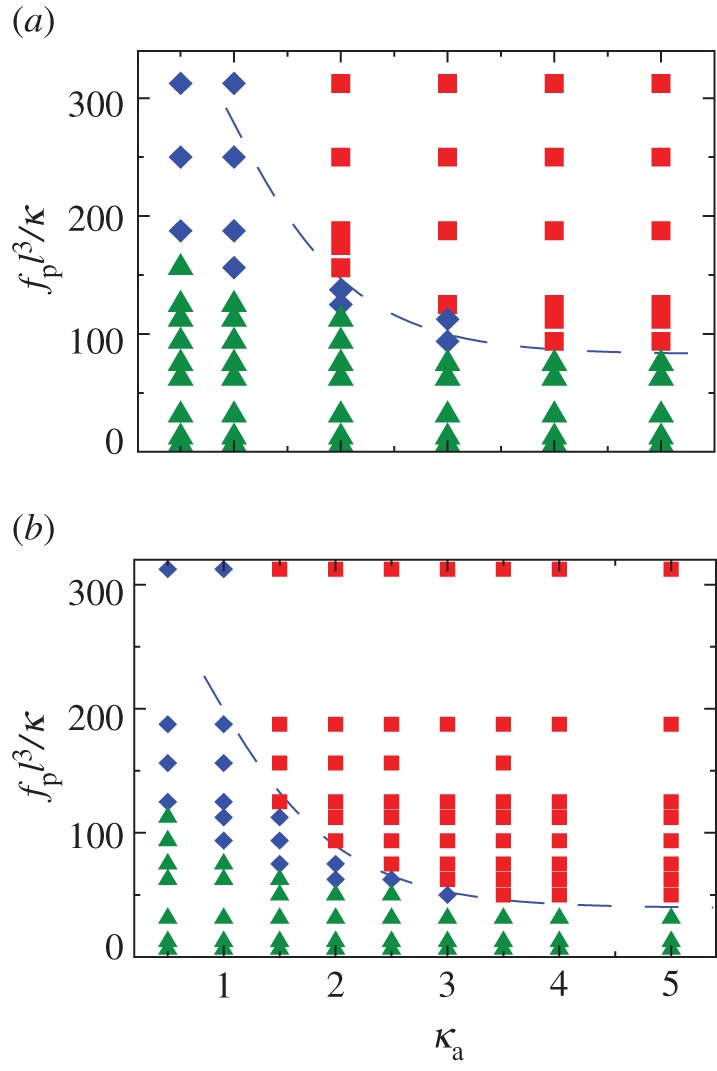
Phase diagram for (a) a clamped filament and (b) a rotating filament with bending stiffness κ = 2 × 10⁴. Triangles correspond to no beating, diamonds to irregular beating and squares to regular beating. The dashed curve (valid for 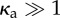) corresponds to equation (4.1). The constants A (obtained from the critical value of the active force at onset for 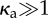) and B (determined by eye) are (a) (A, B) = (78, 80) and (b) (A, B) = (36, 70). (Online version in colour.)

As expected from the mean-field analysis in §3.1, for propulsion forces below the critical value f_p < f_c, we do not observe statistically significant beating (green triangles)—the straight configuration remains stable and variations in 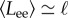owing to fluctuations of 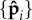are insignificant. The critical value of f_c that separates this regime from the unsteady (periodic as well as non-periodic) regime is a function of the passive filament elasticity (ℓ and κ) and κ_a. In the low noise limit, f_c tends to the values estimated in §3.1 from simulations.

Keeping κ_a fixed and increasing f_p to beyond the critical value renders the straight configuration unstable and results in persistent unsteady shapes. For small values of κ_a(≤1), we observe irregular beating. As κ_a is increased (κ_a > 1), the enhanced correlation of particle propulsion directions results in two trends—evident both for the clamped—shown in figure 7a—and pivoted—see figure 7b—cases. First, the critical propulsion force f_c to destabilize the straight configuration decreases, saturating to the continuum limit as κ → ∞. Second, the beating becomes periodic. Interestingly however, for any 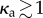, there persists a diminishing region of irregular beating between the stationary and periodic-beating regions. This region of irregular (or erratic) beating is characterized by variations in shape and the rates at which local curvatures change. As f_p increases at constant κ_a, we go from the no-beating regime (A) to an intermediate irregular beating regime (B) and finally to the regular beating regime (C). Note that the critical active force density that separates both transitions (A → B as well as B → C) depends on the passive filament elasticity (ℓ and κ) and also on κ_a.

To understand the mechanisms underlying these transitions, we adopt a simplified picture of the local dynamics and fluctuating forces generated by the self-propelled spheres. We separate f_p(s) into an average part and a rapidly fluctuating part: 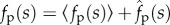. Significant fluctuations in filament conformations arise when orientations 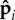escape from a favourable configuration (anti-parallel to the tangent) to an unfavourable configuration where the local contribution to the active force is negligible.

When κ_a ≤ 1 in the diffusion (noise)-dominated limit 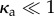, the active, polar spheres are very animated, reorienting themselves constantly on a rotary timescale 1/D_r. As κ_a is increased from unity with the force density held fixed, the enhanced correlation of 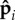results in two trends. First, at some value of κ_a, the force density becomes large enough to destabilize the straight configuration resulting in a regime characterized by erratic beating. In this regime, the mean active force density is large enough to cause buckling over the entire length of the filament ℓ and the orientation potential well has a depth large enough that few polar spheres reorient. Thus, with increasing κ_a, there is both an increasing spatial correlation of 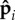along the filament and an increasing time over which the correlations are sustained. This irregular beating arises whenever the correlation time of propulsion directions, T_c, is shorter than the filament oscillatory timescale in the noiseless, perfectly aligned limit.

To estimate T_c, we use a first passage time calculation (see electronic supplementary material, appendix D). Treating the polarity as a continuous field p(s), we define ζ(s) to be the angle between the a local polarity vector and 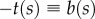, where t(s) is the tangent vector. We seek the characteristic time for a local patch of spheres to escape from a perfectly aligned configuration, in which they can drive filament compression, to a non-compressive configuration. Without loss of generality, we choose the latter to be a configuration in which the polarity vector and the local tangent are in the same direction (ζ = π), so that the forces are extensional and thus no compressive instabilities are possible. Rewriting the angular potential (equation (2.1)) as U_a(ζ) = κ_a(1 − cosζ), we find that the energy difference between the two configurations is U_a(π) − U_a(0) = 2κ_a. In the over-damped limit and for κ_a > 1, the orientations evolve diffusively, and the escape flux can be related to a frequency of crossovers or disrupting frequency. We estimate T_c using the steepest descent method [28] and ignore multiplicative factors, because our simulations are for constant diffusivities and temperature. The balance 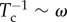provides a preliminary estimate for the activity separating irregular from regular beating:

This estimate however needs to be modified further. First, a non-zero critical density for buckling arises owing to the non-generic initial configuration. However, once buckled, the net force determines the beating, and the beat frequency is a function of f_p, not (f_p − f_c). Thus, the critical density should tend to the continuum noise-free limit. Second, the irregular beating behaviour requires that a critical number of motors escape from the well. Satisfying these conditions leads to the dimensionless estimate

4.1

Here A is a constant which ensures that the result reduces to the noise-free value and is thus not a fitting parameter. The constant B is a measure of the critical number of motors that need to reorient to disrupt beating and we estimate it by fitting to computational data. We interpret it as the minimal size of the patch (equivalently force) required to cause beating irregularities. While strictly valid for 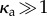, this expression—plotted as the dashed blue line in figure 7a,b—satisfactorily captures the shape of the boundary for κ_a > 1.

5. Conclusion and outlook

Our study suggests a simple proposal to mimic the beating of eukaryotic flagella. Rather than having motors that walk on adjacent filaments that are clamped at an end, we have shown that we can generate actively oscillating and rotating filaments using connected self-propelled particles. The frequency of oscillations and thereby the swimming speed and fluid forces can be controlled by varying the dimensionless parameters in our problem—the ratio of the chain stiffness to the polarity stiffness κ/κ_a, the scaled active force 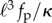, and the aspect ratio of the chain ℓ/σ, or equivalently the number of active particles. Furthermore, if the angular potential is written as 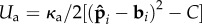, where 0 < C ≤ 1, thus introducing a preferred direction different from the local tangent, then the initial symmetry-breaking bifurcation is eliminated and the filament will always beat. All of these parameters, in principle, are accessible experimentally. In particular, recent efforts to manipulate connected passive colloids by electrical fields [29], microfluidics [30], lock-and-key type interactions [31] and heat [29] have been quite successful in yielding externally actuated filaments with controllable bending stiffness. Extension of such techniques using diffusophoretic Janus particles as templates should yield internally controlled self-propelling filaments, just as a small variation of the motility assay for rotating filaments [27], by clamping an end, will lead to beating. However, the quantitative experiments to check our predictions remain to be done.

The relationship between noise and beating patterns, a key aspect of our study, is relevant in several contexts. First, our analytical expressions for the oscillation or rotational frequency, critical buckling force, and beating wavelength can be of general use for estimating motor forces in over-damped filament-motor systems. While the microscopic analogue of κ_a in such systems requires further study, our theoretical estimate for the transition to steady beating suggests the magnitude of noise (equilibrium or non-equilibrium) that will disrupt stable dynamics in these systems. Second, devices have recently been developed [32] in which fluid is pumped and mixed by externally actuated biomimetic cilia with sizes approaching those of biological cilia. At this scale, advection and diffusion compete to determine mass transport. While pumping and mixing regimes are currently spatially separated [32], using an array of polar chains and tuning noise (e.g. by changing temperature to modify κ_a) could drive transitions from periodic (pumping) to erratic (mixing) regimes.

Motivated by quasi-two-dimensional systems in which particle motions are over-damped and hydrodynamic interactions are screened, we have focused on the roles of elasticity, local activity, local friction and noise in governing filament dynamics. In future work, we will study how the dynamics might change in the presence of long-range hydrodynamic interactions. Relatedly, Jayaraman et al. [18] observed autonomous motions in a noiseless active filament comprised force-free stresslet particles. Interestingly, in their model, the particles are not self-propelled in the manner that phoretic particles are, as individual particles are motionless when disconnected from the chain, and in contrast to our model they find that hydrodynamic interactions are essential for beating. The observation that self-generated periodic motions can arise from different fundamental driving forces suggests that they are a generic feature of internally active, slender filaments. In a broader context, in contrast to most studies of locomotion at low Reynolds number which prescribe the shape of the organism (typically as a slender filament with prescribed kinematics), here we prescribe the active forces locally, and calculate the resulting shapes. If the anchored end does not have infinite resistance the self-propelled particles will propel the whole chain, the study of which is a natural next step.

Funding statement

We acknowledge funding for this research provided by NSF-MRSEC-0820492 and the MacArthur Foundation (L.M.).