Photosynthetic light harvesting: excitons and coherence

Francesca Fassioli; Rayomond Dinshaw; Paul C Arpin; Gregory D Scholes

doi:10.1098/rsif.2013.0901

. 2014 Mar 6;11(92):20130901. doi: 10.1098/rsif.2013.0901

Photosynthetic light harvesting: excitons and coherence

Francesca Fassioli ¹, Rayomond Dinshaw ¹, Paul C Arpin ¹, Gregory D Scholes ^1,^✉

PMCID: PMC3899860 PMID: 24352671

Abstract

Photosynthesis begins with light harvesting, where specialized pigment–protein complexes transform sunlight into electronic excitations delivered to reaction centres to initiate charge separation. There is evidence that quantum coherence between electronic excited states plays a role in energy transfer. In this review, we discuss how quantum coherence manifests in photosynthetic light harvesting and its implications. We begin by examining the concept of an exciton, an excited electronic state delocalized over several spatially separated molecules, which is the most widely available signature of quantum coherence in light harvesting. We then discuss recent results concerning the possibility that quantum coherence between electronically excited states of donors and acceptors may give rise to a quantum coherent evolution of excitations, modifying the traditional incoherent picture of energy transfer. Key to this (partially) coherent energy transfer appears to be the structure of the environment, in particular the participation of non-equilibrium vibrational modes. We discuss the open questions and controversies regarding quantum coherent energy transfer and how these can be addressed using new experimental techniques.

Keywords: light harvesting, energy transfer, coherence, exciton

1. Introduction

The biological significance of photosynthesis is indisputable as it is necessary for nearly all life on the Earth. Photosynthesis provides chemical energy for plants, algae and bacteria, while heterotrophic organisms rely on these species as their ultimate food source. The initial step in photosynthesis involves the capture of energy from sunlight. Specialized pigment–protein complexes, called light-harvesting antenna complexes, have evolved for this purpose. The aim of this article is to discuss recent work on how ultrafast energy transfer occurs in light harvesting, in particular the role of coherence. This topic has been prominent in recent experimental and theoretical studies. Owing to the complexity of the processes being examined, there has been much discussion among researchers about what is being measured by recent experiments and what it means. We aim to describe and clarify the current issues.

Light-harvesting complexes are comprised chromophores, light-absorbing molecules, typically attached to a protein structure that holds them in place. Photosynthesis is initiated by the absorption of light by the chromophores, which excites the molecules from the ground state to an electronic excited state. The excited state of a molecule such as chlorophyll is short lived when compared with usual biological processes, relaxing to the ground state after about 6 ns when dissolved in de-oxygenated diethyl ether at ambient temperature and about 4 ns in vivo [1,2]. The singlet excited state lifetime of chlorophyll is reduced compared with the radiative lifetime largely owing to intersystem crossing, which yields triplet excited states of chlorophyll. This process occurs with around a 10 ns time constant [3,4]. Before the molecule(s) can relax, the electronic excitation must be ‘harvested’. That is, the excitation is transferred through space among the chromophores until it eventually reaches a reaction centre where it initiates charge separation. There is a wide variety of light-harvesting antenna structures in nature. They differ in the arrangements of chromophores, chromophore types (e.g. chlorophyll, bilins and carotenoids) and absorption spectra—light can be harvested from the blue wavelengths all the way to the near-infrared. Nevertheless, all antennae complexes are able to convert the photogenerated excitations to charge separation with very high efficiency [5]. Quantum efficiencies—the probability of converting an absorbed photon into a charge-separated state—depend on antenna size, light conditions and the organism. They are documented to be in the range of 50–90%. For instance, the light harvesting to charge separation efficiency is in the range of 84–90% for photosystem II of higher plants [6,7].

Recently, some work has stated that quantum coherence is essential for attaining the highly efficient light harvesting in photosynthesis. That is incorrect in our opinion, but there is certainly mounting evidence that coherence effects are involved in the dynamics—and therefore the mechanism—of ultrafast light-harvesting processes. The key to this efficiency is better understood as a balance between the ultrafast (femtosecond to picosecond timescale) transfer of electronic excitation within- and between-antenna complexes compared with the time for relaxation to the ground state and the scaling of the excitation diffusion time with the size of the antenna system. Many biophysical studies have therefore focused on elucidating the mechanism of this energy transfer [8–13].

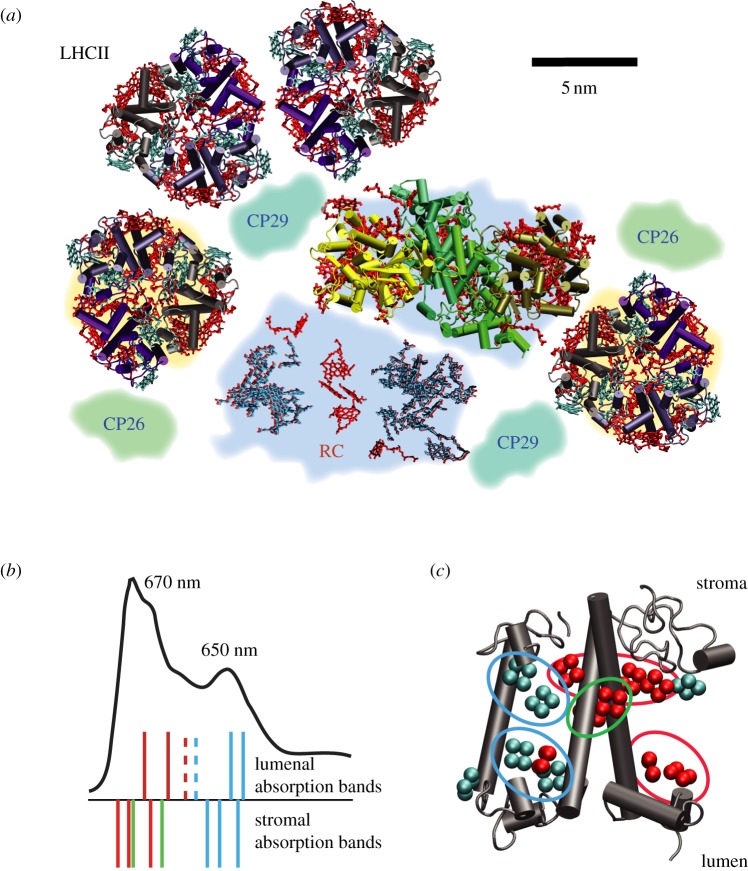
A plan of the organization of light-harvesting complexes around reaction centres in a thylakoid membrane is shown in figure 1. This is representative of higher plants or green algae [19]. The reaction centre, once photoexcited, initiates photosynthetic energy transduction via a series of electron transfer reactions. Specifically that involves excitation of the ‘special pair’ of chlorophylls in the centre of the red-coloured chlorophylls labelled RC. There we show the reaction centre from photosystem II, stripped of the protein scaffold in the lower part of figure 1a. Surrounding the reaction centres are major and minor chlorophyll-containing antenna complexes that bind, in total, about 200 chlorophylls per reaction centre. Light harvesting involves the absorption of sunlight by any of these chlorophyll chromophores and subsequent transfer through space of that electronic excitation to the special pair of a reaction centre.

The major light-harvesting complex shown in figure 1a is LHCII. It is seen as trimers of individual LHCII proteins. Each LHCII binds 15 chlorophylls and a typical absorption spectrum is shown in figure 1b. Chlorophyll a absorbs, on average, at 675 nm and chlorophyll b at 650 nm. Biophysicists work out the pathways and timescales of energy transfer among these chlorophylls. To do that, we need to map spectral signatures of the chlorophylls onto a structural model. It has been found that spectroscopic signatures often indicate coherently shared excitation over two or three chlorophylls (see §2). Such a coherently delocalized excitation is known as an exciton. This is indicated in figure 1b and correspondingly in the structural model of figure 1c. In this paper, we discuss the definition, detection and consequences of these bands of coherently shared excitations in light-harvesting complexes.

1.1. Energy transfer and the question of coherence

Transfer of electronic excitation energy in light-harvesting systems happens through the mechanism that is broadly known as resonant energy transfer (RET) [20–26]. Traditionally, this transfer has been assumed to happen in the Förster [27] limit of RET, where electronic excitations incoherently ‘hop’ between states localized on individual chromophores. The main justification for this description of energy transfer being the notion that electronic coherence between chromophores, that is, quantum superpositions of excited electronic states of different chromophores, is rapidly destroyed by the environment of the antenna molecules (specifically by stochastic energy fluctuations). These energy fluctuations derive from the interaction between electronic excitations of the chromophores and vibrational degrees of freedom of the environment, arising mainly from fluctuations in the protein and solvent surrounding the light-absorbing molecules. The physical fluctuations cause electrostatic fluctuations that modulate the transition energy of the embedded chromophores [28]. As we explain in §2, the subsistence of electronic coherence depends on the strength of the electronic coupling between chromophores. In light-harvesting antennae, these couplings can become significant because chromophores are densely packed to enhance the absorption cross section of the antenna. As a consequence, stable ‘excitons’ are commonplace in light-harvesting antenna and Förster theory is not generally valid. Furthermore, new evidence indicates that electronic coherence can survive in the biological environment for weaker electronic coupling than previously thought. Therefore, microscopic descriptions for RET mechanisms that go beyond Förster theory are needed to adequately describe light harvesting [29]. There has been a convergence of interest on these topics from different fields, and as a result of an influence of quantum optics research, these deviations from the Förster incoherent picture of energy transfer are now often referred to as non-trivial quantum effects in photosynthetic light harvesting. It is these effects that we discuss in this review.

Within a light-harvesting antenna, the concentration of chromophores, for example chlorophyll, can be as high as 0.6 M. This is likely to be the key optimization in light-harvesting complex ‘design’. As a consequence, the interchromophore separations are close—of the order of 10 Å centre-to-centre for the nearest neighbours. Electronic coupling scales quite steeply with distance (the inverse of chromophore separation cubed at long separations), therefore we find strong electronic interactions between chromophores in antenna complexes. Instances of strong coupling result in delocalized excited states or excitons, as foretold in figure 1. In this case, the electronic excited state is delocalized over two or more chromophores and the quantum-mechanical wave function has a particular pattern of amplitudes across the molecules. Formally, this means that the excitation is in a quantum superposition of the electronically excited states of different molecules or simply, in a state where there is electronic coherence among chromophores. Although not always present, delocalized excited states provide the most evident and widely available signature of quantum coherence in photosynthetic light harvesting, and probably the most important too. Excitons can extend over multiple chromophores [30–32] and can have a profound impact on the electronic structure and hence optical properties of the system as well as on energy transfer dynamics. Clear examples of excitons have been discovered in ensemble-averaged linear and nonlinear spectroscopy experiments [31–39] as well as single-molecule spectroscopy of LH2 from purple photosynthetic bacteria [40,41]. The latter have provided strong evidence for delocalized excited states immediately after the excitation of a single LH2.

The implications of delocalized excited states on energy transfer can be twofold. First, groups of strongly interacting chromophores can behave as effective donors and acceptors of excitation while transfer remains incoherent. This effect is captured by generalized Förster theory [42–45] that describes the incoherent transfer of energy between delocalized electronic states. In strongly delocalized systems, similar to J- and H-aggregates, exceptional enhancements of energy transfer rates, sometimes called ‘supertransfer’, are possible [46]. Additionally, a subtler quantum effect may take place. Rather than excitation ‘hopping’ between–possibly delocalized—states, excitation may delocalize over donor and acceptor states such that their relative phases evolve quantum coherently. This excitation transfer, which appears wave-like in a perfect periodic system, implies that different energy transfer pathways could be realized simultaneously altering transport properties through quantum interference [47–52]. Recent breakthrough experiments using two-dimensional electronic spectroscopy (2DES) have shown evidence of long-lived oscillatory features in the two-dimensional spectra of several light-harvesting complexes. This oscillatory behaviour had been first interpreted as a signature of quantum coherent evolution of superpositions of electronic states. We discuss later in §4 that vibrations also contribute to these oscillations, potentially playing a role in modulating electronic delocalization, so it is more accurate to speak of vibronic coherences. These non-trivial quantum effects could modify energy transfer dynamics to some extent.

The observations suggesting long-lived quantum-mechanical evolution of electronic coherences in photosynthetic antenna proteins have prompted a huge amount of theoretical research aiming at understanding how electronic coherence and in particular, quantum dynamics can be sustained in the complex biological environment. These theoretical studies are important because they explore whether coherences influence energy transfer dynamics, something not detected by the 2DES experiments. Several possible mechanisms supporting coherent dynamics have been identified. These include weak electron–vibration coupling, spatially correlated [49,53–56] environmental fluctuations at different chromophores and a slowly relaxing vibrational environment [57]. However, calculations so far indicate that environments at different chromophores are more or less independent [28,58]. The importance of the environment around the chromophores in light-harvesting complexes is indicated by the Stokes shift—the energy difference between the absorption and fluorescence maxima. The Stokes shift measures two times the ‘reorganization energy’, which tells us how strongly the electronic transitions of the chromophores are coupled to the environment. For LHCII the chlorophyll-a Stokes shift has been ascertained [59] to be approximately 110 cm^–1, which is notably reduced compared with chlorophyll-a in solution, which ranges from 135 to 200 cm^–1, depending on solvent polarity [60].

In many light-harvesting systems, the coupling of the electronic transitions to the environment, the reorganization energy mentioned earlier, is typically similar in magnitude to the electronic coupling between chromophores (the ‘dipole–dipole’ coupling that exchanges electronic excitation) [61,62]. This so-called ‘intermediate’ coupling regime makes solving energy transfer problems difficult, because all the energy scales are similar, so neither the electronic coupling (cf. Förster theory) nor the excitation-bath coupling (cf. Redfield theory) can be considered to be a small perturbation. Moreover, the typical timescale associated with equilibration of the protein and solvent environment of chromophores in response to electronic excitation is often comparable with the timescale of excitation dynamics, adding a further challenging aspect for theory [57,62,63]. In addition, strong coupling to selective vibrations, for example of intramolecular origin, are commonplace in molecular systems [64–66]. This means that non-equilibrium vibrational dynamics can actively participate in energy transfer and are likely to be underlying, at least partly, the observation of long-lived coherent dynamics [57,67,68]. These are the ingredients that need to be considered collectively in realistic theories for energy transfer in light harvesting, which will give the reader a feel of why this has been a difficult problem to investigate. Furthermore, given the complexity of any reasonable theory, the need for experimental insight is crucial.

The experimental findings have raised the question of whether coherent dynamics are significant for optimizing photosynthetic light harvesting. Though it has been recognized that delocalized donor and acceptors states may enhance transport in an incoherent transfer scenario [45,69–71], it is yet unclear whether exciton delocalization between acceptors and donors and the consequent coherent dynamics of excitations may provide a decisive advantage for light harvesting—although it is clear that the mechanism of energy transfer is modified. Furthermore, there is a current debate on whether coherent energy transport is present at all under natural sunlight illumination as opposed to laboratory conditions where lasers are used to expose femtosecond dynamics [72–74]. We discuss in §5 how the slowly relaxing vibrational environment of chromophores may be the key in allowing coherent energy transfer under sunlight excitation.

This review is organized as follows. In §2, we start by discussing how excited states delocalized over several spatially separated molecules can form and be sustained in a noisy environment. In §3, we discuss the regimes of energy transfer, from incoherent to coherent RET and the role of non-equilibrium vibrational dynamics in coherent exciton evolution. In §4, we describe the recent advances in 2DES as a tool to investigate quantum coherence in photosynthetic antennae. We critically discuss the evidence that experiments using this technique are providing electronic coherence. Finally in §5, we address the open question of whether quantum coherent energy transfer, as suggested by 2DES experiments, might be present under natural sunlight illumination and its possible relevance for efficient transfer, and discuss what we have learnt so far from 2DES experiments and future experimental directions.

2. Photosynthetic excitons

The exciton model was originally introduced to describe electronic excitations in solid-state materials. In the context of molecular systems, the model was adapted by Davydov [75,76] to treat excitations in molecular crystals. Building on the work of Davydov, the exciton model has been extended to describe the interaction of excitations in other molecular systems [77–79] and, in particular, the interaction of chromophores in photosynthetic antennae. One of the major differences between the understanding of excitons in the context of solid-state systems and molecular systems is the extent of delocalization of the excitation. Photosynthetic excitons are fairly localized; the typical delocalization length in the steady state only being two to four chromophores (with the notable exception of the chlorosome antenna), and in many cases the excited states can be approximated to be fully localized to one molecule [30,32].

When chromophores are photoexcited, they interact with each other by a coulombic interaction between their transition densities [23,80,81]. This coupling exchanges electronic excitation between molecules. At large separations between the chromophores, this interaction is a dipole–dipole coupling between transition dipole moments and the exchange of excitation is slow compared with dephasing and relaxation processes accompanying the Stokes shift, so excitation hops incoherently by the Förster mechanism. When the electronic coupling is large relative to the homogeneous line broadening (or equivalently, the reorganization energy) and electronic energy differences between the chromophores, then the interaction modifies the stationary states of the system relative to the isolated chromophores. The simple reason is that now we cannot differentiate where the excitation is, so the correct eigenstates are a linear combination of the possibilities. The key assumption of the molecular (Frenkel) exciton model in the context of photosynthetic systems is that the coulombic interaction between chromophores, is weak compared with the forces defining the electronic structure of the isolated molecules. Consequently, the electronic structure of individual chromophores is relatively unchanged by the interaction and the electronic states of single molecules remain a good basis to describe the state of the system (under the Born–Oppenheimer approximation). Formally, this means that the interaction leads to eigenfunctions of the modified Hamiltonian that are given by a linear combination of the eigenfunctions of the isolated chromophores.

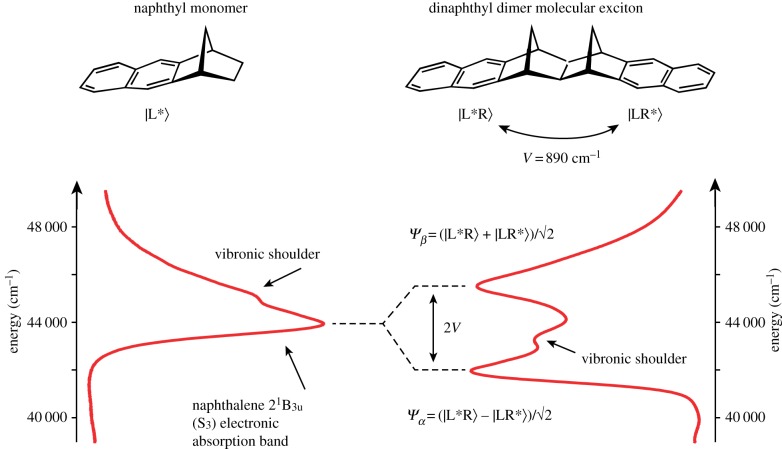
An example of a molecular exciton is shown in figure 2. The left-hand side of the figure shows the structure and absorption spectrum (in the spectral region of the third allowed singlet–singlet transition) of a naphthalene-type chromophore. On the right is a dimer held in fixed orientation by a norbornalog bridge. The electronic coupling is very strong, estimated to be about 890 cm^–1, and this coupling causes the excited electronic states of the dimer to be delocalized over both chromophores [82]. The two linear combinations of excitation being on the left or right chromophore define the phases of the excitation in each of the exciton eigenstates. These eigenstates are clearly observed as a splitting of the single absorption band from the monomer spectrum. The energy of this exciton splitting is twice the electronic coupling. Note that the vibronic shoulder is strongly evident only for one exciton state, which is because the symmetries of the two states differ, and hence the way they couple to vibrations is different.

2.1. The technical language of excitons

For a full description of the behaviour of excitons, it is not sufficient to describe how electronic states interact with each other. It is necessary to further describe how they interact with the surrounding environment. In particular, the interaction with the environment induces disorder in the system, by causing both heterogeneity and dynamical fluctuations in electronic parameters, which can greatly influence the extent of exciton delocalization and dynamics. Qualitatively it is evident that exciton splitting, similar to that shown in figure 2, will be obscured if the absorption bands are wider than the splitting. To understand what happens in this regime, we need more detailed models.

Of particular relevance is the interaction between electronic excitations and vibrational modes. Both the protein scaffold to which chromophores are attached and the solvent medium are usually modelled as a continuum of low-frequency vibrational ‘modes’ that interact with the electronic excitations. Additionally, molecular vibrations of the chromophores, including high-frequency modes, are also typically identified in the vibrational spectra of chromophores. The vibrational degrees of freedom are usually modelled as a collection of harmonic oscillators. Each of these vibrations is quantized, in analogy to the concept of phonon, the elementary quanta of vibrational excitation, in crystal lattices. Borrowing then the language from solid-state materials science, the interactions between the excitation and the vibrational degrees of freedom are often described as electron–phonon interactions [83]. Note, however, that phonons in the solid-state sense are not a sensible physical description of the fluctuations in solutions and complex environments, where the modes and their frequencies are continuously changing [84]. Nevertheless, the concept of phonons in the phenomenological sense has been valuable as a basis of models for energy transfer.

2.2. Electronic structure of excitons

In the simplest treatment of electronic excitations in light-harvesting systems, each chromophore labelled i is modelled as a two-level system with single electronic transition energy, E_i, the so-called site energy. The interaction between the transition dipole moments of two chromophores i and j is described by the electronic coupling parameter, V_ij. Within the single-excitation manifold, the basis for calculating the energies and wave functions for a system with N interacting chromophores is the Frenkel exciton Hamiltonian

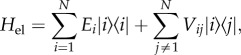2.1

where |i〉 denotes the state with chromophore i excited and all others in the ground state. Owing to the electronic interaction between chromophores, the eigenstates of the electronic Hamiltonian, H_el, also commonly known as Frenkel excitons, are delocalized among several molecules. This delocalization can have a profound effect in multi-chromophoric systems, creating new absorption bands and changing energy transfer dynamics.

To analyse dynamics that can involve quantum coherences, it is useful to describe the probabilities of different states being excited in terms of the density matrix. Off-diagonal terms contain information about superposition states (coherences in the quantum-mechanical sense). The general form of the density matrix ρ(t) describing the state of N chromophores at time t after photoexcitation is given by

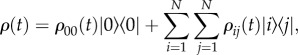2.2

where ρ₀₀(t) accounts for any losses that relax the system to the ground state |0〉, and ρ_ij(t) describes the populations (i = j) and coherences (i ≠ j) in the site basis. We note that coherences are basis dependent, that is, they depend on whether we choose to write the density matrix in terms of localized molecular states or exciton states. The term electronic coherence usually refers to coherence in the site-basis, while excitonic coherence denotes coherence in the electronic eigenbasis. While differentiating the site and excitonic basis is clear for a ‘pure’ state, recall that the density matrix is an average over the ensemble. Each member of the ensemble will be in a slightly different state, some excitons more localized than others. The details of this distribution will be hidden once the average is taken. For example, it is not obvious simply from inspection of the density matrix of a three-molecule system whether excitation is coherently shared among all three molecules or shared between pairs of molecules.

The LH2 complex, isolated from purple bacteria, is one of the most widely studied light-harvesting complexes provides clear evidence for delocalized excited states. Many experiments and calculations have shown how excitons can substantially change the electronic structure of an antenna as well as the energy transfer dynamics. The LH2 complex contains only one type of chromophore, the bacteriochlorophyll-a molecule. It is normally comprised eight or nine subunits circularly arranged, binding three bacteriochlorophylls each that give rise to two rings. In one ring, the B850 ring, there are 16 or 18 closely packed bacteriochlorophyll-a molecules; owing to their close mutual proximity and their preferential orientations, the coupling between these chromophores is strong, with the nearest neighbour coupling being approximately 300 cm^–1 [85]. In the B800 ring, there are eight or nine loosely spaced bacteriochlorophyll-a molecules where adjacent molecules have a 30 cm⁻¹ electronic coupling. The absorption of the B800 ring occurs at 800 nm, corresponding to the absorption of isolated bacteriochlorophyll-a molecules, while the B850 ring is red-shifted to 850 nm. This shift is in part a response to interactions between the chromophores and the protein; however, a significant contribution is owing to the strong coupling between molecules, which shifts the absorption resonance frequency to the new eigenenergy of the exciton [8,86]. The strength of electronic couplings and the associated level of exciton delocalization within the B800 and B850 rings can be clearly seen in the single-molecule fluorescence-excitation spectra of LH2 complexes. The spectra reveals a fundamentally different structure in the absorption bands around 800 and 850 nm, consistent with absorption of the B800 ring to populate localized excited states of the different bacteriochlorophyll-a molecules in the ring, while absorption of B850 ring populates exciton states delocalized over the entire ring [40,41]. In addition to changing the electronic landscape of the system, excitons in LH2 also change the energy transfer dynamics by setting up a gradient, which allows excitation to flow downhill from the high-energy B800 ring to the lower energy B850 ring.

The example of LH2 is not an isolated illustration of strong electronic coupling between chromophores modifying the electronic structure of a light-harvesting complex; exciton states are in fact common among light-harvesting proteins. Present in all higher order plants, the PSI complex has been shown to include sections of strongly coupled chlorophyll molecules [87]. Although the majority of dynamics in PSI do not rely on strongly coupled chromophores, it has been speculated that the presence of excitons may affect some of the more subtle steps, including the step involving trapping the excitation at the reaction centre [87]. Another example of strongly coupled chromophores is found in the light-harvesting machinery of some cryptophyte algae [30,88,89].

2.2.1. Sources of exciton localization

To understand in more detail delocalized excited states and when these can become significant for light harvesting, it is necessary to distinguish between two phenomena that, when strong in comparison with the magnitude of the electronic coupling, lead to localization of excitations. These are: (i) energetic disorder (heterogeneity of site energies) that results in localization of the eigenstates of the electronic Hamiltonian (equation (2.1)) and (ii) the electron–phonon coupling that induces dynamical localization of an initially delocalized photoexcited state.

Energetic disorder. In this case, localization is a consequence of the molecules having electronic transitions that are off-resonant. Generally speaking, the extent of delocalization of the eigenstates of H_el depends on the relative magnitude between the electronic coupling between molecules, V_ij, and the difference in site energies, ΔE = E_i–E_j. When transitions are near resonant, i.e. 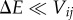Inline graphic , the eigenstates are largely delocalized between the molecules. In the opposite case of small electronic coupling, 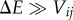, eigenstates are predominantly localized on single chromophores. Energetically detuned chromophores are commonplace in light-harvesting complexes. For example, differences in the local protein environment of otherwise identical molecules can give rise to differences in transition energies [90–94]. Slow environmental motions, for example conformational changes in the protein, cause random fluctuations in electronic parameters over long timescales (compared with the timescale of exciton dynamics), giving rise to what is known as static disorder. Some antenna complexes use a range of chomophore types, with distinctive transition energies, to further expand their spectral cross section for light absorption and/or engineer an energy funnel. Common examples of antennas containing different kinds of pigments are phycobilisomes from cyanobacteria and red algae, and the antenna proteins of cryptophyte algae, for example phycoerytherin 545 (PE545) and phycocyanin 645 (PC645).

The effect that energetic disorder has on exciton delocalization can be estimated, for instance, in the bacteriochlorophyll-a only B850 ring in the LH2 complex. While the eigenstates of a perfectly symmetric ring can delocalize over the entire molecular aggregate, disorder in site energies breaks the symmetry of the electronic Hamiltonian of the B850 ring, resulting in more localized excitonic states [31,32].

Electron–phonon coupling. The second and most important source of exciton localization is the unavoidable coupling between the electronic degrees of freedom of chromophores and the stochastic fluctuations in the surrounding environment. This means that although the eigenstates predicted by the bare Hamiltonian H_el (equation (2.1)) can be delocalized over several molecules, the environment will tend to destroy phase relations between the excited states of different molecules yielding an excited state that is more localized than that of an isolated system. This interaction induces the so-called dynamic disorder as it modulates electronic parameters on a timescale comparable to excitation dynamics.

The electron–phonon interaction is commonly assumed to be diagonal and given by

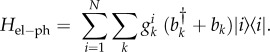2.3

The operators 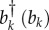Inline graphic are phonon operators that create (annihilate) a phonon mode of frequency ω_k, and 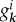is the coupling between the electronic transition and each mode. The effect of the environment in equation (2.3) can be interpreted as a dynamical modulation of transition energies of the molecules. Such dynamical modulation happens during energy transfer, shifting the energy of the molecules constantly in and out of resonance. The distribution of ‘phonon’ frequencies in the environment and their coupling to the electronic transitions of the chromophores is characterized by the spectral density, 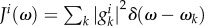Inline graphic , and the energy associated with equilibration of the environment after excitation is quantified by the reorganization energy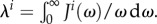

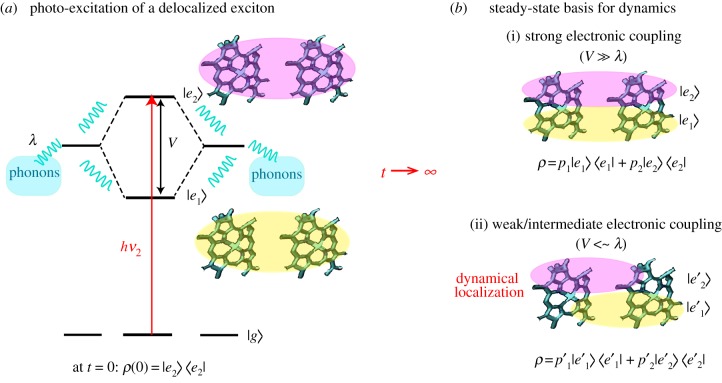
When electronic interactions are much stronger than the coupling to the environment, 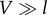Inline graphic , relaxation takes place between the excitonic states that diagonalize the electronic Hamiltonian H_el (equation (2.1)). In thermal equilibrium, the system is found in a statistical mixture of electronic eigenstates states, and therefore the excitation remains to some extent delocalized. This is illustrated for an electronic dimer consisting of two resonant molecules in figure 3. At t = 0, light excites the highest exciton (figure 3a) which is fully delocalized as the transition is assumed to obey the Franck–Condon principle of vertical transitions (phonon modes are unaltered immediately after the electronic transition). In the steady state (figure 3b), when the electronic system equilibrates with the phonon environment, the state of the electronic system is given as a classical mixture of excitonic states. In the very strong electronic coupling regime, these excitonic states correspond to the electronic eigenstates of H_el (figure 3b(i)).

Figure 3. — Dynamical localization in an electronic dimer. (a) At t = 0 light excites a fully delocalized electronic state. (b) The interaction with the phonon modes induces relaxation and dephasing, and the steady state of the system corresponds to a statistical mixture of electronic states. In the strong electronic coupling regime (i) the system is in a mixture of the fully delocalized excited states that diagonalize the electronic Hamiltonian (equation (2.1)). Otherwise (ii), the environment induces dynamical localization such that the excited states that diagonalize the density matrix in the steady state are more localized than the electronic eigenstates.

Away from the limit of very strong coupling, the electron–phonon coupling effectively renormalizes the basis in which the electronic system relaxes and the excitonic states that diagonalize the density matrix in the steady state are more localized than the electronic eigenstates (figure 3b(ii)). This phenomenon that is associated with polaron formation—an electronic state dressed by phonon modes—is referred to as dynamical localization [95–99]. Under very weak electronic coupling, 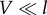Inline graphic , electronic states are fully dressed by the environmental phonons and the excitation is completely localized. In thermal equilibrium, individual chromophores are populated according to a Boltzmann distribution. The latter is the regime of validity of Förster theory.

2.3. Quantifying exciton delocalization

The importance of excitons in the light-harvesting function has motivated a considerable amount of research aimed at determining the degree of delocalization or ‘length’ of excitons. The delocalization length of a pure state, i.e. a well-known state, of the general form 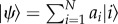Inline graphic describing the excited state of a molecular aggregate of N chromophores can be determined through the inverse participation (IPR) 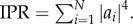The IPR ranges from 1 for a fully localized state to 1/N for a completely delocalized exciton. Calculation of the exciton size of the eigenstates of the bare electronic Hamiltonian (equation (2.1)) with the IPR is thus straightforward. The problem of determining the extent of delocalization of the excited electronic states is however much more complex when dealing with a system subjected to decoherence, that is, the loss of quantum coherence owing to interaction with the environment. Therefore, recently more sophisticated measures for delocalization have been explored.

The difficulty in quantifying exciton length under the electron–phonon coupling is, first of all, that the environment induces mixedness in the system. Even if the initial photoexcited state is well known (pure, i.e. described by a wave function), at later times the state of the system is generally described in terms of an ensemble of pure states in the density matrix formalism. Therefore, measures of exciton delocalization, for example the IPR, are not applicable. Furthermore, as mentioned in the previous section, dynamical localization results in relaxation in a basis that is more localized than the bare electronic eigenbasis.

To understand how mixedness comes into the picture when thinking about exciton delocalization, consider, for example, the strong electronic coupling limit. In the steady state, energy transfer can be described as incoherent transfer between electronic eigenstates (relaxation in this case, as internal conversion in molecular spectroscopy). However, even when the system has relaxed in the delocalized eigenbasis, the fact that the state of the system is mixed (with electronic eigenstates thermally populated) implies loss of electronic coherence in the sense that the magnitude of electronic coherences (off-diagonal elements of the density matrix in the site basis) are in general decreased [36,100,101].

In the quest for appropriate measures to quantify exciton delocalization under the electron–phonon coupling, researchers have recently applied concepts from the field of quantum information, namely entanglement, to multi-chromophoric energy transfer [102–106]. While claiming that entanglement itself is present in light-harvesting systems might not be the best way to think about excitons in the context of light harvesting [107], measures of entanglement are nevertheless useful to characterize the time evolution and spatial distribution of quantum correlations in molecular aggregates subjected to decoherence. They give a detailed picture of how excitation is delocalized and how coherent sharing of excitation evolves with time. Such measures are used to analyse the system's density matrix and capture the extent of delocalization of the basis in which the system relaxes and the environmentally induced loss of purity. The measures are able to characterize quantum correlations between distant chromophores going beyond traditional measures that only provide average delocalization lengths that do not correspond to any physical length.

3. Excitation dynamics and the regimes of energy transfer

The previous section introduced the concept of excitons in photosynthesis. In addition to assisting in interpretation of the linear absorption spectrum, the exciton model provides important tools for the understanding of the dynamics of an electronic excitation after photoexcitation, in particular, how an excitation migrates within an antenna and from an antenna to a reaction centre. In the first part of this §3.1, we overview the models used to describe the dynamics of a photosynthetic exciton. One of the major challenges in developing a consistent description of how an excitation migrates in a photosynthetic protein is that in many cases both the electronic coupling between chromophores and the coupling between the chromophores and the environment is significant and comparable. In the following section, we briefly describe the two limiting cases where well-developed models are available: Förster theory, which applies to the regime where coupling between the chromophores and the environment dominates, and Redfield theory which assumes strong electronic coupling between sites and allows for coherent oscillations of the populations at individual chromophore sites. In the second part (3.2), we describe how the interaction with phonons can affect the migration of an excitation in the intermediate regime where both electronic coupling between chromophores and the coupling to vibrational modes are significant.

3.1. Detailed explanation

The time evolution of the density matrix of the electronic system and phonon environment is given by the Liouville–von Neumann equation 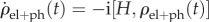Inline graphic , where 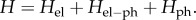The system's density matrix is obtained in the standard way by tracing out the degrees of freedom of the environment [108]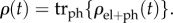

In the strong electron–phonon coupling regime (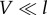 Inline graphic ), energy transfer is described by the theory of Förster RET. It corresponds to a second-order perturbation theory with respect to the electronic coupling and describes a classical ‘hopping’ of excitation between states localized on single chromophores. Within Förster theory, all coherences between sites are neglected leading to a master equation for the populations 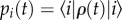Inline graphic only, in terms of the transfer rates k_ij from a site i to a site j (simply coupled rate equations)

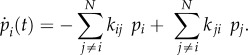3.1

When delocalized excited states become significant in light harvesting, theories that go beyond Förster are necessary to describe energy transfer. One natural extension of Förster theory is given by generalized Förster theory [42–45]. Here, excitation delocalizes within a domain of strongly interacting chromophores but not between different domains. It is assumed that within a domain excitation thermalizes (in a delocalized basis) much faster than any interdomain transfer. These delocalized excitons then behave as effective donors and acceptors of electronic excitations for transfer between different domains of chromophores. Populations of these new donors/acceptors evolve according to a rate equation similar to equation (2.3). Generalized Förster theory is usually applied to model energy transfer between different molecular aggregates, such as between the B800 and B850 rings in the LH2 [43,69] and intercomplex transfer, e.g. the LH2 to LH2 transfer [109].

Both Förster-type incoherent RET mechanisms described above neglect any coherence between donors and acceptors (either sites or delocalized states) justified by a weak electronic coupling between them. However, within an antenna protein, electronic couplings can be sufficiently large (in comparison with the coupling to the environment) to allow excitation to be coherently shared among donors and acceptors during energy transfer. In this case, exciton transport cannot be fully described by rate equations involving populations only but rather involves coherent evolution of excitation. This means that coherences, i.e. the off-diagonal elements of the density matrix, oscillate with well-defined phases. Unlike the case of diffusive incoherent transport, there is no basis in which the electronic density matrix is diagonal at all times.

Coherent exciton evolution implies that both electronic and exciton (eigenstate) coherences exhibit oscillatory behaviour. On the other hand, it may or may not manifest as significant coherent oscillations in the time evolution of populations. In particular, while coherent exciton dynamics implies coherent evolution of site populations, coherence-to-population exciton transfer may not be so significant as to lead to coherent evolution of electronic eigenstate populations. For instance, in the purely coherent regime eigenstate populations do not evolve in time while site populations coherently oscillate. Here, we refer to coherent energy transfer as a transport where coherent excitation dynamics take place. In other words, we mean transport where populations of chromophores (i.e. site basis) oscillate coherently, even when the energy of the system may not oscillate. This is to distinguish from purely incoherent excitation transfer. We note that the site basis can be meaningful if we remember that antenna proteins are not isolated but ultimately need to transfer energy to the reaction centre, which is sometimes coupled to a single molecule (e.g. in FMO chromophore ‘3’ couples to the reaction centre). Alternatively, coherent energy transfer has been defined as the regime, where electronic eigenstate populations show a coherent oscillatory evolution [110].

In order to illustrate how coherent exciton dynamics can accompany and possibly influence energy transfer, we consider the limit of strong electronic coupling (weak electron–phonon interaction). In this regime, energy transfer can be described by the well-known Redfield theory. Like Förster theory, Redfield theory is a second-order perturbation theory, this time with respect to the electron–phonon interaction. Furthermore, standard versions of Redfield theory make use of the Markovian approximation, which assumes that the environment equilibrates infinitely fast after an electronic transition from the ground to the excited state. Therefore, transfer of excitation happens from equilibrium phonon states [62]. Redfield theory is usually employed within the secular approximation, which guarantees positivity of the electronic density matrix. In this approximation, the density matrix describing the electronic degrees of freedom in the eigenstate basis 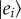Inline graphic of H_el evolves according to

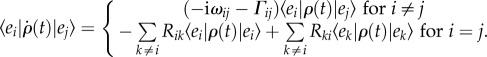3.2

Equation (3.2) shows that coherence between eigenstates oscillates with a frequency ω_ij = ɛ_i − ɛ_j proportional to the energy difference between the two excitons and that the environment induces dephasing of coherences at a rate Γ_ij. The environment also induces relaxation between (delocalized) eigenstates at rate R_ij. Under this regime, coherences and populations are decoupled in the exciton basis. It thus appears at first glance that the mechanism of energy transfer in this regime has little difference from that described by generalized Förster theory. However, one fundamental distinction between the two is that in this case relaxation of excitons is accompanied by coherent evolution of exciton coherences. This translates into populations in the molecular (site) basis that oscillate coherently, which is not captured by Förster-type mechanisms. Therefore, under this regime of weak electron–phonon interaction, coherent excitation transfer is possible following a photoexcitation during a transient timescale that will be determined by how fast dephasing occurs.

Although Redfield theory can provide useful insights into how coherent dynamics can influence energy transfer, it is not generally valid. First, it relies on the assumption of weak coupling to the environment, and second it employs the Markovian approximation. In many light-harvesting antenna, electronic interactions lie in the challenging intermediate coupling regime, making perturbative treatments inappropriate to model energy transfer [61,62]. Furthermore, often the timescale of environmental relaxation is comparable to electronic dynamics, such that the Markovian approximation fails [57,62,63]. In this case, the environment cannot be assumed to react infinitely fast to electronic excitations, and therefore non-equilibrium phonon dynamics take place. The effect of this time-dependent equilibration of the environment will be particularly important when the coupling of the system to the environment is not weak. The relevance of the slow motion of the environmental degrees of freedom of chromophores has led to the development of theories for coherent energy transfer beyond the perturbative limit of Redfield theory and Markovian assumptions [99,111–115]. As we discuss next, non-equilibrium phonon dynamics can significantly alter energy transfer and the timescale of coherent energy flow in the photosynthetic antenna.

3.2. Coherent exciton dynamics and non-equilibrium phonons

Both the smooth continuous density of low-frequency vibrational modes, likely arising from the protein and solvent, and the discrete vibrational modes of intra- or intermolecular vibrations can participate in energy transfer out of equilibrium. In the former case, the low-frequency continuum part of the spectral density is characterized by a timescale τ_relax that determines how fast the environment relaxes to an equilibrium configuration. If 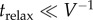Inline graphic , transfer can be assumed to happen from equilibrium phonon states, and consequently the Markovian approximation is valid. Otherwise, non-equilibrium phonon processes take place [62,63]. The second source of non-equilibrium phonon dynamics comes from discrete modes that strongly couple to the system [64–68,116–118]. One way of capturing such phonon dynamics is to explicitly include them as part of the system under study while the rest of the phonon modes can be treated as the (possibly in equilibrium) environment [116,118].

Much interest has been focused on the influence of a slowly relaxing environment associated with the smooth part of the spectral density on coherent exciton dynamics. Studies have shown that such an environment can protect quantum coherence and hence support coherent energy transfer for longer times than environments inducing purely Markovian exciton evolution [57]. The timescale of relaxation τ_relax also determines the timescale of environmental correlations [62] during which the environment has a memory of the previous state of the system. Hence, during τ_relax phase relations of electronic states that have been destroyed by the environment can be reintroduced to the system, thus sustaining quantum coherence. Non-Markovian exciton dynamics are also expected when the electronic system couples to selective vibrations. Indeed, recent studies have found that discrete non-equilibrium vibrations that are resonant with differences in energy of electronic eigenstates can also sustain coherent dynamics for long timescales consistent with those reported in experiments [67,68]. Importantly, reference [67] has shown that in the presence of such resonant non-equilibrated discrete modes, coherent dynamics supports fast and directed (non-cascade) transfer of excitations towards acceptor chromophores in disordered antennas, providing a functional role for coherent dynamics in the system under study.

While many studies have investigated how non-equilibrium phonons can sustain coherent excitation dynamics, less attention has been paid to the possibility that the same mechanism can support the creation of coherence and coherent energy transfer from an initial state with no superpositions between excitons. It is conceivable that such processes induce coherent dynamics even in the absence of initial exciton coherences. For example, within the weak coupling and Markovian approximations of Redfield-secular theory described by equation (3.2), coherent dynamics can be present if and only if there are coherences between electronic eigenstates initially (e.g. as generated by ultrafast laser pulse excitation). Otherwise, no oscillatory behaviour is present during energy transfer and dynamics are fully described by incoherent hopping of excitons. In a recent study, we have discussed how the time-dependent equilibration process of the low-frequency continuum of environmental modes can induce coherent energy transfer when the initial electronic state corresponds to an eigenstate of the electronic system [73]. Thus, coherent energy transfer can arise not only as a consequence of preparing the molecular aggregate in a coherent superposition of electronic eigenstates, but environment-induced coherent excitation dynamics are also possible.

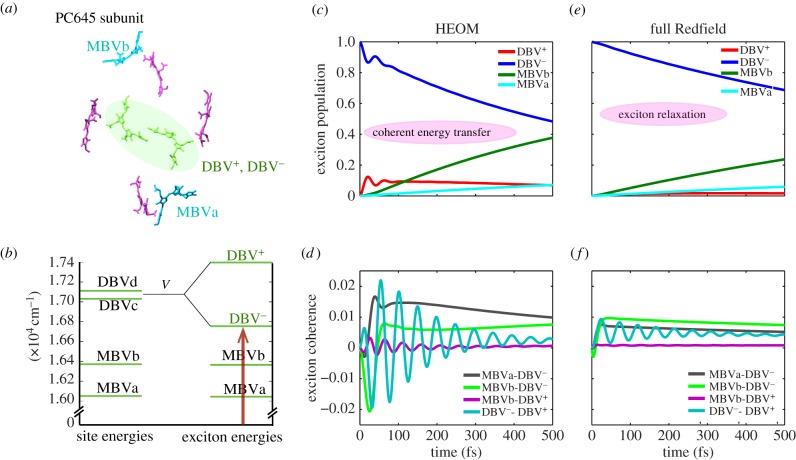
Figure 4 illustrates the emergence of excitonic coherence and coherent exciton evolution after excitation of an electronic eigenstate of a prototype system consisting of a subunit of the PC645 antenna protein (figure 4a) isolated from cryptophyte algae. The system is excited to the delocalized electronic eigenstate DBV⁻, which is optically active, such that no excitonic coherence is initially present. The time evolution of the state of the system is calculated using the non-perturbative, hierarchical equation of motion approach (HEOM) [111,119], which captures the time-dependent reorganization of the environment. Exciton populations show a transient oscillatory behaviour (figure 4c) and exciton coherences emerge and oscillate (figure 4d), revealing coherent energy transfer. When dynamics are calculated using the full-Redfield equation that is based on the assumption that the environment is always in thermal equilibrium (Markovian approximation), but which allows nevertheless population-to-coherence transfer, populations do not show any visible oscillatory behaviour (figure 4e) and the magnitude of exciton coherences (figure 4f) is much smaller than those predicted by the HEOM equations.

The emergence of environment-induced coherent excitation dynamics is a consequence of both an intermediate coupling to the environment and the time-dependent relaxation of the phonon modes. First, only in the very strong electronic coupling regime the system relaxes and thermalizes in the electronic eigenstate basis. Consequently, away from the regime of strong coupling, the environment induces coherences between electronic eigenstates. Second, correlations between the system and environment that form and evolve during the timescale associated with bath-relaxation time will induce non-Markovian exciton dynamics, and in turn protect phase relations of electronic states and sustain coherent energy transfer. It is therefore likely that the typical coupling to selective vibrations will also induce the emergence of coherent energy transfer from an initial state with no superpositions between excitons.

Coherent energy transfer from an initial eigenstate of the electronic system has immediate implications on our understanding of dynamical localization. As explained, environment-induced coherent energy transfer is partly a consequence of the system relaxing in a basis different from the one that diagonalizes the electronic Hamiltonian. This is essentially what we described in §2 as dynamical excitation localization owing to the environment, where in the steady state, excitations populate states that are more localized than electronic eigenstates. Thus, dynamical localization can in fact imply coherent energy transfer during a transient timescale after photoexcitation. The phenomenon of dynamical localization has been identified in LH2. As revealed by single-molecule excitation spectroscopy, excitation can be delocalized over the entire B850 ring after excitation [40,41]. However, it has been estimated that once the excitation thermalizes, the average exciton size ranges between two and four chromophores. What the results from reference [73] suggest, then, is that in LH2 the process of dynamical localization from an initially delocalized state can involve coherent evolution of electronic excitations.

4. Two-dimensional electronic spectroscopy

Elucidating the energy landscape and understanding excitation energy transfer dynamics in multi-chromophoric systems are significant challenges. Steady-state measurements, such as linear absorption, fluorescence, excitation anisotropy and circular dichroism, provide useful information on the electronic structure of these systems. Vibrational states can be investigated using stimulated resonance Raman spectroscopy [120]. However, congested spectra limit the amount of information that can be extracted from these measurements. Further information on both the energy landscape and the dynamics of the sample requires ultrafast optical measurement techniques.

This section first briefly describes optical techniques that have been used to measure energy transfer dynamics in photosynthetic proteins. Recent examples of experimental evidence for coherent exciton dynamics in photosynthesis are discussed, highlighting the challenges in clearly interpreting the dynamics observed in the experiments and presenting ways to approach these challenges.

4.1. Ultrafast spectroscopic measurements

In the most common ultrafast spectroscopic measurement, transient absorption spectroscopy, a laser pulse first excites (pumps) a sample and a time-delayed probe pulse monitors the dynamics. For a fixed delay between the pump and probe pulses, the spectrum of the probe pulse is measured after passing through a sample with and without the pump pulse first exciting the sample. From these two measurements, the differential absorption spectrum can be obtained. When one transition is bleached by exciting some fraction of the molecules out of the ground state, there are effectively fewer molecules left to absorb at that transition and there is a change in absorption at the corresponding probe frequency. As the excitation moves from one state to another, the peak of the bleach in the transient absorption spectrum shifts accordingly and the position of the excitation can be followed through the sample. Often this is done with a narrowband pump-pulse, where the wavelength is chosen to excite a single absorption band, and a broadband probe pulse monitors the spectrum of the excitation as it migrates to lower energy states [89]. Measurements of this type obtain information on the rates of decay of photoexcited populations.

Alternatively, a broadband pulse can excite a coherent superposition of multiple chromophore sites. Information on the coherences can then be observed in oscillations of the signal amplitude. The broadband-width pump pulse presents challenges in the interpretation of the data though, as many transitions are excited simultaneously and many energy transfer pathways contribute to the evolution of the signal amplitude as a function of pump-probe time delay.

2DES has emerged as an optical technique capable of creating and probing coherences while still preserving information on both the excitation and emission energies. In addition to elucidating typical optical properties of molecular systems, 2DES can distinguish homogeneous and in homogeneous broadening and detect correlations between excitonic states [121–127]. 2DES is similar to transient absorption spectroscopy, however two excitation pulses are used cooperatively to excite the sample followed by the third ‘probe-pulse’ which interacts with the sample after a time delay and initiates the radiation of a signal depending on the optical response of the sample. By controlling the delay between the two excitation pulses, information on the excitation energy is obtained in the data analysis and the resulting spectrum plots the optical response as a function of the excitation frequency and detection frequency for a given time delay. Inhomogeneous broadening, which results from chromophores in different protein environments that have varying transition energies (static disorder), elongates the spectrum in the diagonal dimension. Homogeneous broadening depends on system-bath interactions (dynamic disorder) and makes the spectral features become round. Thus, changes in the lineshape of the two-dimensional spectrum can indicate solvation dynamics and spectral diffusion.

4.2. Interpreting two-dimensional electronic spectra

Understanding a two-dimensional spectrum requires knowledge of the energy landscape of the system being measured and the ability to map signatures in a two-dimensional spectrum onto dynamics within that landscape [128–131]. A basic understanding of a two-dimensional spectrum can be achieved by treating one axis as the radiated four-wave mixing signal (or ‘emission’) axis and the other as the excitation axis. In this picture, a two-dimensional spectrum is a map correlating excitation and emission frequencies at a given probe delay. Figure 5 shows a sample two-dimensional spectrum for a model dimer system. Chromophores A and B are assumed to be coupled, non-degenerate chromophores with the exciton splitting shown. The exciton states α and β represent states delocalized over the two chromophores. These two states share a common ground state, and consequently excitation of one state bleaches the transition of the other. In the corresponding two-dimensional map, signals along the diagonal represent transitions where the excitation and emission frequency are the same. Off-diagonal signals correspond to transitions where the excitation and emission frequencies are different and represent correlations between the corresponding transitions absorbing and emitting at those frequencies.

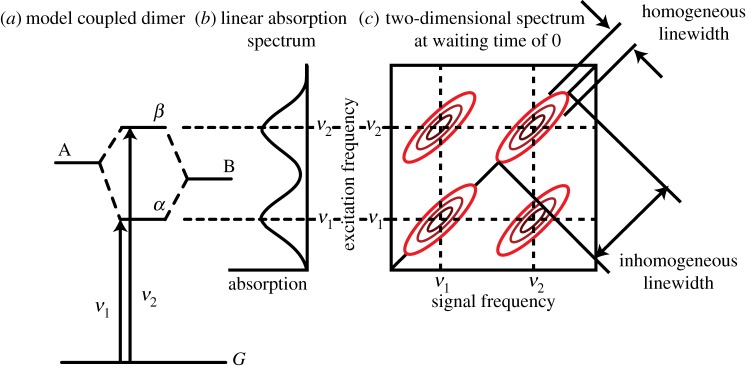
Figure 5. — (a) Energy level scheme for model dimer system formed between two different chromophores A and B with different transition energies. (b) Corresponding linear absorption spectrum for model dimer. (c) Two-dimensional spectrum of dimer system at 0 waiting time between the pump and probe pulses. The inhomogeneous and homogeneous linewidths are indicated by the diagonal and antidiagonal linewidths, respectively. Cross peaks appear because the states share a common ground state. (Online version in colour.)

At time zero, when the sample is probed before the system has evolved, correlations revealed as cross peaks in 2DES can indicate which transitions involve coupled changes in electronic structure. These states are sometimes referred to as possessing a common ground state. This can arise from electronic eigenstates that involve transitions between one or more common molecular orbitals [132]. For instance, excitation of any of the S₁, S₂ or S₃ states of naphthalene will bleach the other two transitions and that would be detected as cross peaks, because these transitions all derive from linear combinations of single excitations between two HOMOs and two LUMOs. Another example is exciton bands, where excitation of the state Ψ_α in figure 2 will bleach the transition to Ψ_β, and vice versa. The transitions in a vibronic progression will also be indicated by cross peaks.

Growth of the amplitude of a cross peak as a function of population time indicates energy transfer [123]. The position of the cross peak indicates which energy transfer pathway is involved. In addition, coherent superpositions of excitonic states appear as oscillations in the amplitudes of the cross peaks which decay as the coherence dephases. A coherent superposition of states evolves with a phase factor, which takes the form of Inline graphic where E_α and E_β correspond to the eigenenergies of the two states, α and β, in superposition. This leads to oscillations in the amplitude of the cross peaks in the two-dimensional spectrum, as shown in figure 6. Oscillations are observed for both exciton coherences and vibrational coherences [133–135]. Distinguishing between vibrational and electronic coherences in the evolution of a two-dimensional spectrum is currently a topic of investigation [136,137]; a task that is made more difficult by homogeneous and inhomogeneous broadening.

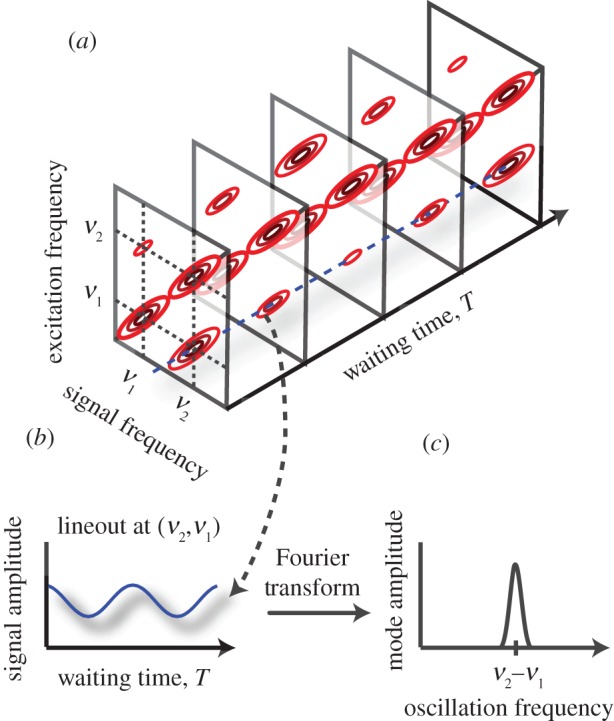
Figure 6. — (a) Evolution of the two-dimensional spectrum of the idealized dimer system of figure 5 with the waiting time, T. The amplitudes of the cross peaks oscillate at the difference frequency of the two states. (b) When analysing real data, lineouts are typically taken, plotting the signal amplitude as a function of waiting time at different positions in the two-dimensional spectrum. In this simple system, an oscillation of the cross-peak amplitude is observed at the difference frequency between the two states. (c) A Fourier transform of the signal amplitude gives a peak at the measured oscillation frequency. In general, this type of analysis helps to identify different contributions to the overall signal that is complicated by the presence of many states and vibrational modes typically accessible in 2DES measurements. (Online version in colour.)

The ability of 2DES to elucidate coherent dynamics in addition to population transfer is one of the features that make two-dimensional spectroscopy appealing. However, identifying the nature of coherences leads to oscillations in a two-dimensional spectrum has become a major topic of discussion in the field of two-dimensional spectroscopy.

4.3. Experimental evidence: electronic and vibrational coherence in photosynthetic light-harvesting proteins

Early reports exploring possible coherence of energy transfer dynamics in photosynthetic light-harvesting complexes came from pump-probe measurements of the Fenna–Mathews–Olson (FMO) complex from green sulfur bacteria and light-harvesting complexes LH1 and LH2 from purple bacteria [138,139]. This early work inspired many of the studies, both theoretical and experimental, described in this review. The current surge in interest stemmed from recent work employing 2DES to monitor the dynamics of excitations ensuing after photoexcitation of the FMO complex [140]. The way information is gathered in two dimensions by 2DES enabled a more detailed study of the dynamics in these complex systems. Three groups have reported the observation of oscillations in 2DES attributed to the coherent evolution of electronic excitations in photosynthetic proteins. Studies with the samples at cryogenic temperatures include the FMO complex from green sulfur bacteria, reaction centres from purple bacteria and the peripheral antenna complex LHCII from higher plants [53,140,141]. Studies have also been undertaken at room temperature [110,142,143]. This work has suggested that coherence may contribute to the functionality of light-harvesting proteins.

In our laboratory, we have studied the primary light-harvesting complexes isolated from cryptophyte algae. Particularly striking results have been attained for phycocyanin 645 (PC645), isolated from Chroomonas CCMP270. PC645 is a phycobiliprotein, a light-harvesting antenna protein found in the thylakoid lumen of cryptophyte algae, which contains eight bilins. PC645 contains three different types of bilins—two dihydrobiliverdins (DBV) with a peak absorption of 580 nm, two mesobiliverdins (MBV) with absorption peaks near 610 nm and four phycocyanobilins two with peak absorptions of 630 nm and two with peaks at 645 nm—covalently bound to a protein matrix [144]. The presence of three distinct types of chromophore increases the coverage of the solar spectrum available for photosynthesis by cryptophyte algae. From a spectroscopic perspective, this provides an opportunity to further quantify excitation dynamics in light-harvesting systems. While there is still significant spectral overlap of the different bilins, the different chromophores predominantly absorb light at different frequencies and allow a reasonably clear interpretation of dynamics as the information is more spectrally spread out. In PC645, the two DBV molecules that absorb on the blue side of the spectrum are positioned together at the centre of the protein and have an electronic coupling of 320 cm^–1.

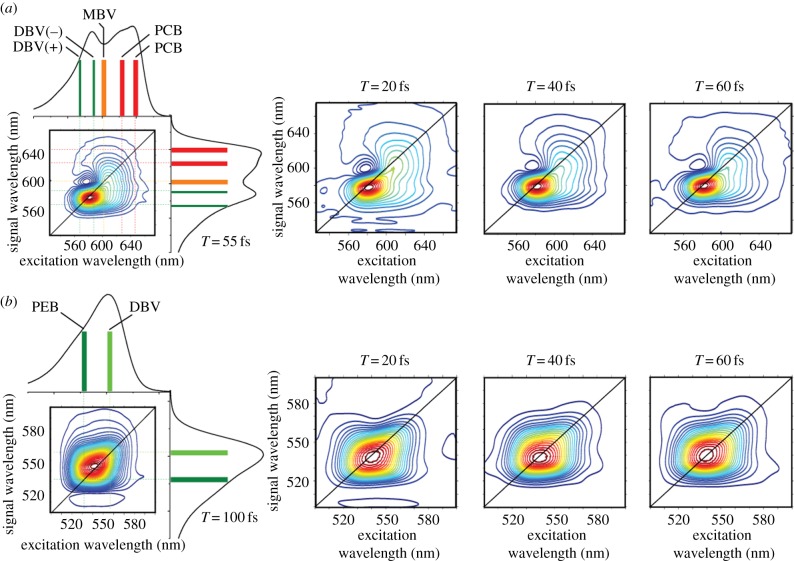
Figure 7 compares 2DES spectra recorded for PC645 (Chroomonas sp. CCMP270) and PE555 (Hemiselmis andersenii). These complexes contain different bilins but have a similar protein structure. Variations in the structure of the proteins among species include the fascinating ‘open’ versus ‘closed’ structures that have recently been discovered by the Curmi group [145]. In the open structure, the central PEB bilins of PE555 are held further apart than central DBVs of PC645, which has a closed structure. The ‘open’ antenna structure reduces the electronic coupling of the central dimer in PE555 considerably compared with the ‘closed’ structure of PC645. Possibly connected with the excitonic dimer, two-dimensional spectra of PC645 show interesting features. In particular, an off-diagonal cross peak that oscillates as a function of waiting time [142,146]. PE555, which has an ‘open’ structure, shows a fairly round spectrum without distinct cross peaks. The PE555 spectra also oscillate as a function of waiting time but the oscillations are assigned to vibrational wave packet oscillations.

There has been debate over the interpretation of the 2DES experiments. In particular, it has been argued that oscillations owing to vibrational coherences can appear very similar to electronic coherences in 2DES data [147,148]. In a typical photosynthetic protein, there are several vibrational modes accessible by stimulated Raman scattering. These modes lead to oscillations in pump probe and 2DES measurements at very similar frequencies to those reported to be exciton coherences. This has been a significant challenge in the interpretation of the ultrafast measurements.

For the purpose of discussion, here we distinguish two types of coherence—vibrational coherence and electronic coherence. Vibrational coherence here refers to pure nuclear wave packet motion induced by photoexcitation and is characteristic of resonance Raman active normal modes in the molecule on either the ground or excited electronic state. Electronic coherence here refers to the coherent excitation of two electronic states coupled by electronic interactions but uncoupled from any vibrational modes in the system. Assignment of the nature of the modes is critical to a meaningful interpretation of the results. In §4.4, we discuss models that begin to account for the coupling between electronic and nuclear degrees of freedom, probably present in real systems.

Turner et al. [136] took a systematic approach to identify and differentiate signatures of different types of coherences present in their 2DES data. They distinguished types of coherences in the three- versus the four-level system. The three-level system was modelled using a ground state, |g〉 and two electronic excited states, |α〉 and |β〉 assumed to be excitonic states of the system (e.g. model dimer). A coherent superposition between these two electronic states, signalled by the off-diagonal density elements 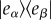Inline graphic , was considered to give rise to signatures associated with purely electronic coherence between electronic eigenstates. The four-level system was assumed to be the representative of a single chromophore (two-level system) with an additional vibrational level, |1〉, in both the ground and excited states. In this case, vibrational coherence was possible as either a ground-state vibrational wave packet, 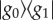Inline graphic or as an excited state vibrational wave packet, 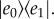The comparison of the expected dynamics of a three- and a four-level system provides a good test case for the simplest model of electronic or vibrational coherence. We note that this procedure for discriminating between electronic and vibrational coherences is really only valid in the strong electronic coupling limit.

Three distinct methods of distinguishing between oscillations from a three- and a four-level system in 2DES were identified in this work owing to the presence of the extra |g₁〉 state. Here, we describe one distinguishing feature identified in this work which relied on the ability that 2DES affords to manipulate the time ordering of laser pulses to extract information from a sample. This can be thought of in close analogy to NMR experiments where different pulse sequences can be used to identify different contributions to the signal. A significant difference between NMR and optical two-dimensional spectroscopy is that the optical excitation beams and signal beams in the optical case all have well-defined directions. As a result, for a given spatial geometry, different pulse sequences can be chosen simply by alternating the time ordering of the pulses in the different beams. In one pulse sequence, a photon echo sequence is achieved and referred to as the ‘rephasing’ spectrum. When the time ordering of the first and second pulses is reversed, the resulting spectrum is referred to as a ‘non-rephasing’ spectrum. The evolution of the cross peaks in the rephasing and non-rephasing spectra were predicted to behave differently for a three- and a four-level system. This happens because the presence of an additional vibrational level in the excited state of the four-level system opens several additional pathways capable of creating a coherence on the ground vibrational level.

The observation of oscillations owing to ground-state vibrational wave packet motion is then insensitive to the choice of pulse sequence. However, for the three-level system, there are a limited number of excitation pathways that create a coherence in the excited states and the observation of oscillations is sensitive to the pulse sequence. If the origin of the oscillations in the cross peak arise from a three-level system, then they will only occur in rephasing spectrum. By contrast, oscillations owing to stimulated Raman scattering will be observed in both rephasing and non-rephasing spectra [133,135,136,141,142,147,149,150]. Discerning this signature requires high-quality data because the non-rephasing signal is often significantly weaker than the rephasing signal. For example, a mode may appear above the noise level in the Fourier transform of the magnitude non-rephasing signal, while not appearing in the Fourier transform of the real non-rephasing signal owing to even minor errors in phasing. Conversely, a mode may appear artificially in the magnitude trace because of broad dispersive features centred on the diagonal which overlap the cross peak of interest. A mode may be present in the oscillations of a trace but hidden in the Fourier transformed data by the spectral overlap with features owing to a baseline or population decay that was not properly subtracted prior to performing the Fourier transform. These examples illustrate some of the difficulties that arise when assigning an oscillatory feature based on the absence of a mode in a noisy, weak signal. A careful statistical analysis of data is important when drawing conclusions from such analyses.

In the measured 2DES spectra for PC645, the oscillations of a cross peak observed below the diagonal were monitored. The oscillations were fit to a sum of eight damped cosine functions, identifying several oscillating components that contribute to the overall signal. The rephasing and non-rephasing contributions were separated and examined independently. Both components showed clear signs of oscillations, albeit similar in general, a Fourier transform of the separate components indicated two modes very close in frequency: 21 THz (700 cm⁻¹) and 26 THz (870 cm⁻¹). One of those frequency components was clearly visible in the rephasing trace while absent in the non-rephasing trace.

Further investigations were performed on PC645 using a related two-colour technique [151]. In these experiments, two pump beams excited the sample followed by a time-delayed probe beam to monitor the dynamics in a similar geometry as typical 2DES measurements. However, instead of using three broadband pulses to excite and probe all possible pathways, three narrowband pulses were used, two to excite and one to probe a limited number of specific pathways. This approach reduces the number of contributions to the overall signal and more clearly identify the signatures of coherences in PC645. In the reported results, the authors chose separated, non-overlapping spectra for the two excitation pulses. The choice of non-overlapping spectra ensures that signal measured in the chosen phase-matched direction is radiated by molecules left in a coherence after interacting with the two excitation pulses with no contribution from molecules left in a population. This technique can provide a direct measurement of the lifetime for a single coherence. Using this technique, Richards et al. [151] observed a coherence with a lifetime of 500 fs in PC645 at cryogenic temperatures. The laser central wavelengths were tuned such that the authors expected to excite a coherence between the DBV+ exciton state and the electronic excited state of one of the MBV bilins. In its presented form, however, the experiment did not distinguish between vibrational or electronic coherences, so it is difficult to clearly identify which coherence lifetime was measured. Similar to transient absorption spectroscopy with a narrowband pump—this technique has the potential to clarify the dynamics of individual coherences as the number of pathways contributing to the overall signal is significantly reduced.

Given the challenges of distinguishing coherences between electronic excited states from vibrational coherences in two-dimensional spectra, an alternative theory to the nature of the oscillations was recently proposed [152]. This work compared the spectrally integrated pump-probe response of a vibrational coherence in a system with a single excited electronic state to that of a coupled electronic dimer in the limit of an infinite bandwidth pump—infinite bandwidth probe experiment. In ultrafast pump-probe spectroscopy, excitation of a two-level electronic system with accessible vibrational levels on the ground and excited states, creates a vibrational wave packet which oscillates on either the ground or excited state manifold. For a single probe-pulse wavelength, the wave packet oscillations increase or decrease the probability of absorption or emission leading to oscillations in the pump-probe spectrum [153–155]. However, for a spectrally integrated measurement, the total probability for absorption or emission does not change and the oscillations in the pump-probe signal average to zero amplitude. By contrast, in a system with two excited electronic states that are in a coherent superposition, the evolution of two wave packets on the different electronic states depends on the relative accumulated phase of the excitation in each of the electronic states and does not spectrally average to zero. Through a careful analysis of the two cases, vibrational and excitonic coherence, the authors demonstrated that as the bandwidth of both pump and probe pulses are increased in a spectrally integrated pump-probe experiment, the oscillations due to a vibrational coherence should decay to zero linearly with the pump and probe pulse temporal durations, whereas the excitonic coherence should have residual oscillations. In principle, this technique can provide a relatively simple alternative approach to identify different modes present in the ultrafast spectroscopic measurements.

4.4. Towards more realistic models for vibronic coherence

We do not anticipate that coherences that are purely electronic act to promote energy transfer in light-harvesting complexes. In many of these systems, electronic transitions often couple strongly to selective vibrational modes whose frequencies match those of electronic energy gaps, and therefore a significant amount of mixing between electronic and vibrational degrees of freedom can occur [156]. This is the concept behind the famous Förster spectral overlap. Therefore, the frequency of oscillations in optical spectra may have a mixed vibronic origin rather than correspond to the purely electronic or purely vibrational frequencies [67,157]. Limitations of the simple exciton model in the presence of strong coupling to vibrational modes are well recognized [158,159].

Recently, a model was proposed by Tiwari et al. [148] attempting to address this issue in the context of prior experimental data, mainly focusing in the FMO data. They incorporated a non-adiabatic model to analyse the dynamics of a photoexcited electronic dimer system, where each pigment coupled to a discrete localized vibrational mode with a vibrational frequency matching the purely electronic exciton gap. In such a system, there is significant mixing between electronic and vibrational degrees of freedom. They focused on the behaviour of the system in the presence of the anticorrelated vibrational coordinate (a projection of the two localized vibrational coordinates) that delocalizes over the two pigments as it is the anticorrelated vibrations that shift the relative energy of the two chromophores, and therefore has an impact on the dynamics. With this model, they were able to reproduce many of the results reported in the experimental two-dimensional spectra including the suppression of the oscillation in the cross peaks of the non-rephasing spectrum reported in 2DES data on PC645. Their conclusion was that non-adiabatic coupling between the two chromophores led to coherent anticorrelated vibrational oscillations on the electronic ground state, which behaved differently from typical ground-state vibrational wave packets in the two-dimensional spectra.

Distinguishing the Tiwari model from the three-/four-level model described earlier requires even further improvement in the signal-to-noise ratio of the 2DES measurements. Taking another approach, we recently analysed broadband pump-probe experiments (PC Arpin et al. 2013, unpublished data). We clearly conclude that the oscillations in data recorded for several cryptophyte antenna complexes originate from the excited state manifold (electronic and vibration coherences), which is inconsistent with the Tiwari model for our excitation conditions in the experiment.

5. Coherent excitation dynamics: what it means for light harvesting

The experimental evidence of recent years indicating that energy transfer in several antenna complexes may involve quantum coherent evolution of electronic excitations has raised many questions. For example, what are the implications for light harvesting? At the heart of the scientific discussion has been the possibility that corrections to hopping transport by coherence effects, even if they are relatively subtle, may enhance light-harvesting function.

The main figure of merit in the numerous studies addressing the connection between coherent excitation dynamics and energy transfer performance has been the quantum yield, i.e. the probability that an absorbed photon results in a charge separation at a reaction centre [47]. Within this framework, optimal transport appears to lie in an intermediate regime of coupling to the environment, not too weak, where transfer is purely coherent, as to allow migration in heterogeneous systems, not too strong where the environment completely localizes excitation [111,160–162]. Although, in principle, transport in such an optimal regime may involve coherent dynamics, there is scant evidence that energy transfer involving this kind of mechanism is generally faster than transport in the incoherent limits of Förster and generalized Förster theories.

A possible scenario where coherent evolution may enhance transfer to acceptor sites is in the case of disordered antennae containing weakly coupled chromophores under the presence of coupling to non-equilibrium discrete vibrational modes, mentioned in §3 [67]. Yet, further studies are needed in order to clearly establish whether coherent exciton dynamics play any role in light harvesting and also whether it could be exploited in technological applications. In this direction, new performance measures and desired functionalities going beyond fast exciton transport should be investigated, as for instance the possibility of achieving control over energy transfer pathways [163].

On a more fundamental level, the observation of coherences under ‘laboratory conditions’ of light harvesting—that is, femtosecond laser excitation—has raised the question of to what extent such effects are relevant, or even present, in natural light harvesting [72–74,164]. After all, energy transfer is not initiated by coherent laser pulses in nature but by continuous incoherent sunlight. In the next section, we discuss how to think about energy transfer and coherent exciton dynamics under continuous and incoherent conditions of light harvesting.

5.1. How excitation conditions matter

The first difference between energy transfer dynamics initiated by coherent laser pulses versus incoherent sunlight, is that the degree of coherence of light will manifest in the photoexcited initial state. In this context, coherence of light refers to the presence of well-defined phase relationships between waves (or photon states in the quantized picture) at different frequencies. Thus, excitation with coherent light will, in general, give rise to a coherent superposition of energy states, whereas incoherent light will give rise to statistically independent excitations at different energies. That difference in excitation conditions can, in turn, lead to significantly different dynamics. Consider, for example, the case of an isolated molecule with fixed energy levels. It has been shown that a coherent pulse of light prepares the system in a coherent superposition of molecular eigenstates, and hence coherences evolve under unitary evolution. On the contrary, thermal incoherent light, such as sunlight, only populates a statistical mixture of eigenstates resulting in a stationary state that does not evolve in time, at least in the case of an isolated small molecule at low temperature [72,165]. Hence, it has been stated that thermal light not only does not induce coherent evolution but does not induce evolution at all.

Although this example nicely illustrates that coherent and incoherent light can induce very different molecular responses, it concerns an extremely idealized system that fails to capture well-known phenomena in real molecules, and thus does not provide any compelling evidence in favour or against the possibility of coherent dynamics in natural light harvesting. In particular, experiments dating back to the 1960s have shown that isolated molecules irradiated with continuous incoherent illumination exhibit a fluorescence yield smaller than unity owing to the occurrence of radiationless transitions between different electronic states [166–169]. This is evidence of incoherent illumination inducing dynamics even in isolated molecules. These dynamics are possible because in real molecules, electronic states couple to a continuum of vibrational modes rather than forming a discrete and static set of energy states. In this case, light does not excite eigenstates of the full electronic and vibrational degrees of freedom, and thus the photoexcited state is not stationary. In particular, vibrations allow resonances, and hence transfer between electronic states [168,169]. The same is true for multi-chromophoric antennae, where vibrational modes now include not only molecular vibrations but also those associated with protein and solvent.

Based on our premise that excitation dynamics happen under continuous incoherent light illumination, we are interested in answering the question of what are the mechanisms underlying these dynamics. Are coherent mechanisms at play or can energy transfer be fully modelled in terms of a classical rate equation where light incoherently populates electronic states that then incoherently transfer excitation to other states? Because of the incoherent nature of sunlight, we expect an incoherent population of electronic eigenstates [73,108]. Based on our discussion in §3, coherent exciton dynamics could be involved in energy transfer in this case under a regime of intermediate to strong electron–phonon coupling (i.e. under dynamical localization), and a slowly relaxing vibrational environment. Such regime is commonplace in light-harvesting systems and therefore it is likely that descriptions beyond hopping-like master equations are needed to adequately describe light harvesting.

Even though, as we have argued, a microscopic description of light harvesting under continuous illumination may often need to involve interactions associated with coherent (unitary) exciton evolution, there is a second issue that arises when discussing the relevance of coherent dynamics under continuous illumination (e.g. sunlight). That is, whether single realizations of the dynamics induced by the absorption of a photon are physically meaningful [72]. Furthermore, all possible realizations of the system could destructively interfere and destroy any quantum effects in the average dynamics [72,74,164].

Under constant pumping of excitation a multi-chromophoric system will reach a steady state shortly after illumination is turned on. However, such a steady state represents an ensemble of all possible individual realizations of the system. In each individual system, dynamical evolution still happens. In fact, energy transfer is in essence a dynamical process, where chromophores absorb light and then transfer the energy to other spatially separated molecules until excitation is trapped at a reaction centre or dissipated via fluorescence. Therefore, individual realizations of the dynamics should be physical. For example, in the steady state the rate of charge separation in a single reaction centre will be constant in time. But this does not mean that the reaction centre is continuously transferring an electron but, rather, that at stochastic intervals charge separation is established.

The difficulty in assigning a physical meaning to the dynamics that underlie the average steady state, for instance energy transfer subsequent to absorption of a photon, relies on the measurement problem in quantum mechanics [72]. Stochastic events during evolution such as photon absorption or emission are not well defined but only their detection is defined. Moreover, single realizations of the system only gain meaning in relation to the observation of such events. Then care needs to be taken when thinking about and assigning physical meaning to ultrafast exciton dynamics in continuous light harvesting. Nevertheless, dynamical evolution initiated by light, where quantum dynamics may underlie the mechanism of energy transfer at least transiently, does happen and, in principle, could be observable. Furthermore, in such a non-equilibrium transport scenario, coherent dynamics could play a role as long as transfer occurs faster than dephasing by the environment.

Recent work in our group has taken initial steps towards addressing some aspects of these questions from an experimental perspective by performing 2DES measurements of laser dyes using an incoherent light source (figure 8) that more closely mimics the solar radiation that drives photosynthesis in nature [170]. These experiments used the amplified spontaneous emission (ASE) from an unseeded laser amplifier. Much similar to sunlight, this stochastic light source does not have a well-defined phase relationship between different colours in the spectrum. Furthermore, while pulsed, the duration of the ASE pulses is much longer than the slowest photoexcited dynamics present in the samples studied and can be considered a continuous illumination source. The incoherent 2DES results produce many of the same features observed in the femtosecond experiments—somewhat surprising given the very different nature of the light sources used. Incoherent 2DES was proposed by Turner et al. [171] and built on prior experiments in the field of noisy light spectroscopy [172–176] where many of the nonlinear spectroscopies using femtosecond pulses have been reproduced in with incoherent sources capable of obtaining much of the same information.

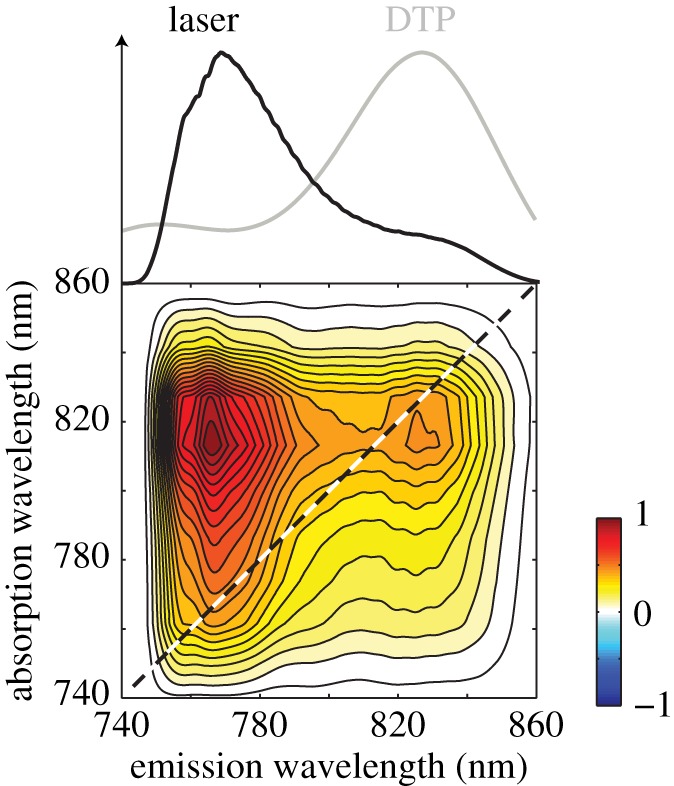
Figure 8. — Real part of the total two-dimensional spectrum of the carbocyanine dye 1,1′-diethyl-2,2′-tricarbocyanine perchlorate (DTP) in butanol measured with incoherent light at a waiting time of 100 fs. These measurements were made with the ASE of an unseeded laser amplifier, a light source with temporal properties more closely resembling sunlight than a femtosecond laser. Still, the two-dimensional spectrum looks qualitatively similar to those measured with femtosecond light sources, including a distinct cross peak between two transitions in a vibronic progression. The laser spectrum (black) and DTP absorption (grey) are plotted above. (Adapted from Turner *et al*. [170].)

There is work left to do to fully understand these new results gleaned from two-dimensional noisy light spectroscopy, but they suggest that the observed coherences are not a consequence of the properties of the light source used, but a consequence of the ways signals can be generated by nonlinear spectroscopy. In other words, the nonlinear optical experiments reveal information about the underlying Hamiltonian on the system rather than directly reflecting the dynamics of light-initiated energy transfer. This is a subtle but important point.

5.2. What we have learned from two-dimensional electronic spectroscopy and a wish list for new experiments

2DES has revealed oscillatory components in the ultrafast light induced dynamics of electronic excitations in photosynthetic light harvesting. A possible signature of long-lived quantum-mechanical evolution of electronic excitations, these results have opened a new research field aiming at elucidating the origin of these spectroscopic signatures as well as revising our current understanding of the microscopic mechanism for light harvesting. Unfortunately, the difficulty in interpreting the two-dimensional spectra of complex systems such as pigment–protein complexes has meant that the origin of these coherences—electronic, vibrational or mixed vibronic—is still an open question. But if these observations indeed indicate that coherent evolution of quantum superpositions of intermolecular electronic states are long lived, it means that two-dimensional spectroscopy has uncovered that, as opposed to common wisdom, the regime of energy transfer is such that unitary (quantum) evolution can be involved, at least partly, in electronic energy transfer.

Even if the origin of the experimental observations may not be clear, theoretical work that has not focused on the experiments but rather on microscopic theories for energy transfer are also an important piece in the puzzle to understand whether energy transfer may be coherent or not. Indeed vast numbers of theoretical studies have developed and applied a theoretical framework to investigate energy transfer in light-harvesting complexes. Using realistic parameters for electronic structure and the environment, researchers have shown that the regime of energies and coupling in pigment–protein complexes is such that coherent evolution can survive in the 0.1–1 ps timescale range (depending on temperature). Therefore, even when precise elucidation of oscillatory dynamics in the two-dimensional spectra is still being debated, this does not mean that electronic coherence is not involved in light harvesting.

In addition to what is known so far from two-dimensional spectroscopy and theoretical work, new experimental techniques are desirable to resolve some of the current issues where two-dimensional spectroscopy is limited. Here we mention two points. First, one of the big questions in the field is whether coherent dynamics are observed in experiments owing to the coherent and ultrafast nature of the excitation. In this direction, two-dimensional spectroscopy with incoherent light as proposed by Turner et al. [171] may provide a decisive tool to clarify whether coherent dynamics are only consequence of an ‘artificial’ excitation process or whether instead the characteristics of the pigment–protein complex allow such effects under solar-like light. Second, conventional spectroscopic techniques deal with ensembles of different complexes, and therefore the averaging over different complexes may obscure certain dynamical features. The single-molecule experiments related to those being developed by van Hulst and co-workers [177,178] will help reveal how individual complexes harvest light and the significance of static disorder. Recent theoretical work has suggested that three pulse photon echo techniques could be applied to single molecules to obtain the dynamics hidden by the ensemble average [179].

5.3. What we conclude for photosynthetic light harvesting

The most important conclusion that we can draw from the vast amount of work over recent years on coherence and coherent dynamics in light harvesting is that both the suggestions by experiments and predictions by theory are accumulating evidence that the mechanisms for energy transfer in light-harvesting involve quantum coherence. More surprisingly, exciton dynamics appears to be dictated, at least partly, by quantum unitary evolution. The significance of coherent dynamics for light-harvesting function is yet unclear and may be subtle, but these effects are likely to nevertheless alter the microscopic picture of energy transfer. Together, all this work is providing a detailed picture for how light-harvesting complexes function.

Funding statement

This work was supported by the Natural Sciences and Engineering Research Council of Canada, DARPA (QuBE) and the United States Air Force Office of Scientific Research (FA9550-13-1-0005).

References

1.Connolly JS, Janzen AF, Samuel EB. 1982. Fluorescence lifetimes of chlorophyll a: solvent, concentration and oxygen dependence. Photochem. Photobiol. 36, 559–563. ( 10.1111/j.1751-1097.1982.tb04416.x) [DOI] [Google Scholar]
2.Mullineaux CW, Pascal AA, Horton P, Holzwarth AR. 1993. Excitation-energy quenching in aggregates of the LHC II chlorophyll–protein complex: a time-resolved fluorescence study. Biochim. Biophys. Acta - Bioenerg. 1141, 23–28. ( 10.1016/0005-2728(93)90184-H) [DOI] [Google Scholar]
3.Bowers PG, Porter G. 1967. Quantum yields of triplet formation in solutions of chlorophyll. Proc. R. Soc. A Math. Phys. Eng. Sci. 296, 435–441. ( 10.1098/rspa.1967.0036) [DOI] [Google Scholar]
4.Peterman EJ, Dukker FM, van Grondelle R, van Amerongen H. 1995. Chlorophyll a and carotenoid triplet states in light-harvesting complex II of higher plants. Biophys. J. 69, 2670–2678. ( 10.1016/S0006-3495(95)80138-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Blankenship RE. 2002. Molecular mechanisms of photosynthesis. Oxford, UK: Blackwell Science Ltd. [Google Scholar]
6.Jursinic P, Govindjee 1977. Temperature dependence of delayed light emission in the 6 to 340 microsecond range after a single flash in chloroplasts. Photochem. Photobiol. 26, 617–628. ( 10.1111/j.1751-1097.1977.tb07541.x) [DOI] [Google Scholar]
7.Wientjes E, van Amerongen H, Croce R. 2013. Quantum yield of charge separation in photosystem II: functional effect of changes in the antenna size upon light acclimation. J. Phys. Chem. B 117, 11 200–11 208. ( 10.1021/jp401663w) [DOI] [PubMed] [Google Scholar]
8.Sundstrom V, Pullerits T, Van Grondelle R. 1999. Photosynthetic light-harvesting: reconciling dynamics and structure of purple bacterial LH2 reveals function of phyotosynthetic unit. J. Phys. Chem. B 103, 2327–2346. ( 10.1021/jp983722+) [DOI] [Google Scholar]
9.Van Grondelle R, Novoderezhkin VI. 2006. Energy transfer in photosynthesis: experimental insights and quantitative models. Phys. Chem. Chem. Phys. 8, 793–807. ( 10.1039/b514032c) [DOI] [PubMed] [Google Scholar]
10.Novoderezhkin VI, van Grondelle R. 2010. Physical origins and models of energy transfer in photosynthetic light-harvesting. Phys. Chem. Chem. Phys. 12, 7352–7365. ( 10.1039/c003025b) [DOI] [PubMed] [Google Scholar]
11.Scholes GD, Fleming GR, Olaya-Castro A, van Grondelle R. 2011. Lessons from nature about solar light harvesting. Nat. Chem. 3, 763–774. ( 10.1038/nchem.1145) [DOI] [PubMed] [Google Scholar]
12.Renger T, Müh F. 2013. Understanding photosynthetic light-harvesting: a bottom up theoretical approach. Phys. Chem. Chem. Phys. 15, 3348–3371. ( 10.1039/c3cp43439g) [DOI] [PubMed] [Google Scholar]
13.Cheng Y-C, Fleming GR. 2009. Dynamics of light harvesting in photosynthesis. Annu. Rev. Phys. Chem. 60, 241–262. ( 10.1146/annurev.physchem.040808.090259) [DOI] [PubMed] [Google Scholar]
14.Iwata S, Barber J. 2004. Structure of photosystem II and molecular architecture of the oxygen-evolving centre. Curr. Opin. Struct. Biol. 14, 447–453. ( 10.1016/j.sbi.2004.07.002) [DOI] [PubMed] [Google Scholar]
15.Nield J, Barber J. 2006. Refinement of the structural model for the photosystem II supercomplex of higher plants. Biochim. Biophys. Acta 1757, 353–361. ( 10.1016/j.bbabio.2006.03.019) [DOI] [PubMed] [Google Scholar]
16.Standfuss J, Terwisscha van Scheltinga AC, Lamborghini M, Kühlbrandt W. 2005. Mechanisms of photoprotection and nonphotochemical quenching in pea light-harvesting complex at 2.5 Å resolution. EMBO J. 24, 919–928. ( 10.1038/sj.emboj.7600585) [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Guskov A, Kern J, Gabdulkhakov A, Broser M, Zouni A, Saenger W. 2009. Cyanobacterial photosystem II at 2.9-A resolution and the role of quinones, lipids, channels and chloride. Nat. Struct. Mol. Biol. 16, 334–342. ( 10.1038/nsmb.1559) [DOI] [PubMed] [Google Scholar]
18.Schlau-Cohen GS, Calhoun TR, Ginsberg NS, Read EL, Ballottari M, Bassi R, van Grondelle R, Fleming GR. 2009. Pathways of energy flow in LHCII from two-dimensional electronic spectroscopy. J. Phys. Chem. B 113, 15 352–15 363. ( 10.1021/jp9066586) [DOI] [PubMed] [Google Scholar]
19.Croce R, van Amerongen H. 2011. Light-harvesting and structural organization of photosystem II: from individual complexes to thylakoid membrane. J. Photochem. Photobiol. B. 104, 142–153. ( 10.1016/j.jphotobiol.2011.02.015) [DOI] [PubMed] [Google Scholar]
20.Andrews DL, Curutchet C, Scholes GD. 2011. Resonance energy transfer: beyond the limits. Laser Photon. Rev. 5, 114–123. ( 10.1002/lpor.201000004) [DOI] [Google Scholar]
21.Renger T. 2009. Theory of excitation energy transfer: from structure to function. Photosynth. Res. 102, 471–485. ( 10.1007/s11120-009-9472-9) [DOI] [PubMed] [Google Scholar]
22.Scholes GD. 2003. Long-range resonance energy transfer in molecular systems. Annu. Rev. Phys. Chem. 54, 57–87. ( 10.1146/annurev.physchem.54.011002.103746) [DOI] [PubMed] [Google Scholar]
23.Andrews DL. 1989. A unified theory of radiative and radiationless molecular energy transfer. Chem. Phys. 135, 195–201. ( 10.1016/0301-0104(89)87019-3) [DOI] [Google Scholar]
24.Beljonne D, Curutchet C, Scholes GD, Silbey RJ. 2009. Beyond Förster resonance energy transfer in biological and nanoscale systems. J. Phys. Chem. B 113, 6583–6599. ( 10.1021/jp900708f) [DOI] [PubMed] [Google Scholar]
25.Van Grondelle R, Dekker JP, Gillbro T, Sundstrom V. 1994. Energy transfer and trapping in photosynthesis. Biochim. Biophys. Acta Bioenerg. 1187, 1–65. ( 10.1016/0005-2728(94)90166-X) [DOI] [Google Scholar]
26.Selvin PR. 2000. The renaissance of fluorescence resonance energy transfer. Nat. Struct. Biol. 7, 730–734. ( 10.1038/78948) [DOI] [PubMed] [Google Scholar]
27.Förster T. 1948. Zwischenmolekulare energiewanderung und fluoreszenz. Ann. Phys. 2, 55–75. ( 10.1002/andp.19484370105) [DOI] [Google Scholar]
28.Renger T, Klinger A, Steinecker F, Schmidt am Busch M, Numata J, Müh F. 2012. Normal mode analysis of the spectral density of the Fenna–Matthews–Olson light-harvesting protein: how the protein dissipates the excess energy of excitons. J. Phys. Chem. B 116, 14 565–14 580. ( 10.1021/jp3094935) [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Ishizaki A, Fleming GR. 2012. Quantum coherence in photosynthetic light harvesting. Annu. Rev. Condens. Matter Phys. 3, 333–361. ( 10.1146/annurev-conmatphys-020911-125126) [DOI] [PubMed] [Google Scholar]
30.Novoderezhkin VI, Doust AB, Curutchet C, Scholes GD, van Grondelle R. 2010. Excitation dynamics in phycoerythrin 545: modeling of steady-state spectra and transient absorption with modified Redfield theory. Biophys. J. 99, 344–352. ( 10.1016/j.bpj.2010.04.039) [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Jimenez R, Dikshit SN, Bradforth SE, Fleming GR. 1996. Electronic excitation transfer in the LH2 complex of Rhodobacter sphaeroides. J. Phys. Chem. 100, 6825–6834. ( 10.1021/jp953074j) [DOI] [Google Scholar]
32.Pullerits T, Chachisvilis M, Sundstrom V. 1996. Exciton delocalization length in the B850 antenna of Rhodobacter sphaeroides. J. Phys. Chem. 100, 10 787–10 792. ( 10.1021/jp953639b) [DOI] [Google Scholar]
33.Nagarajan V, Alden RG, Williams JC, Parson WW. 1996. Ultrafast exciton relaxation in the B850 antenna complex of Rhodobacter sphaeroides. Proc. Natl Acad. Sci. USA 93, 13 774–13 779. ( 10.1073/pnas.93.24.13774) [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Novoderezhkin VI, Razjivin VI. 1995. Excitation delocalization over the whole core antenna of photosynthetic purple bacteria evidenced by non-linear pump-probe spectroscopy. FEBS Lett. 368, 370–372. ( 10.1016/0014-5793(95)00663-T) [DOI] [PubMed] [Google Scholar]
35.Leupold D, Stiel H, Teuchner K, Nowak F, Sandner W, Ucker B, Scheer H. 1996. Size enhancement of transition dipoles to one- and two-exciton bands in a photosynthetic antenna. Phys. Rev. Lett. 77, 4675–4678. ( 10.1103/PhysRevLett.77.4675) [DOI] [PubMed] [Google Scholar]
36.Kuhn O, Sundstrom V. 1997. Pump-probe spectroscopy of dissipative energy transfer dynamics in photosynthetic antenna complexes: a density matrix approach. J. Chem. Phys. 107, 4154–4164. ( 10.1063/1.474803) [DOI] [Google Scholar]
37.Novoderezhkin V, Monshouwer R, van Grondelle R. 1999. Exciton (de)localization in the LH2 antenna of Rhodobacter sphaeroides as revealed by relative difference absorption measurements of the LH2 antenna and the B820 subunit. J. Phys. Chem. A 103, 10 540–10 548. ( 10.1021/jp9844415) [DOI] [Google Scholar]
38.Book LD, Ostafin AE, Ponomarenko N, Norris JR, Scherer NF. 2000. Exciton delocalization and initial dephasing dynamics of purple bacterial LH2. J. Phys. Chem. B 104, 8295–8307. ( 10.1021/jp000485d) [DOI] [Google Scholar]
39.Monshouwer R, Abrahamsson M, van Mourik F, van Grondelle R. 1997. Superradiance and exciton delocalization in bacterial photosynthetic light-harvesting systems. J. Phys. Chem. B 101, 7241–7248. ( 10.1021/jp963377t) [DOI] [Google Scholar]
40.Cogdell RJ, Gall A, Köhler J. 2006. The architecture and function of the light-harvesting apparatus of purple bacteria: from single molecules to in vivo membranes. Q. Rev. Biophys. 39, 227–324. ( 10.1017/S0033583506004434) [DOI] [PubMed] [Google Scholar]
41.Van Oijen AM, Ketelaars M, Kohler J, Aartsma TJ, Schmidt J. 1999. Unraveling the electronic structure of individual photosynthetic pigment–protein complexes. Science 285, 400–402. ( 10.1126/science.285.5426.400) [DOI] [PubMed] [Google Scholar]
42.Sumi H. 1999. Theory on rates of excitation-energy transfer between molecular aggregates through distributed transition dipoles with application to the antenna system in bacterial photosynthesis. J. Phys. Chem. B 103, 252–260. ( 10.1021/jp983477u) [DOI] [Google Scholar]
43.Scholes GD, Fleming GR. 2000. On the mechanism of light harvesting in photosynthetic purple bacteria: B800 to B850 energy transfer. J. Phys. Chem. B 104, 1854–1868. ( 10.1021/jp993435l) [DOI] [Google Scholar]
44.Scholes GD, Jordanides XJ, Fleming GR. 2001. Adapting the Forster theory of energy transfer for modeling dynamics in aggregated molecular assemblies. J. Phys. Chem. B 105, 1640–1651. ( 10.1021/jp003571m) [DOI] [Google Scholar]
45.Jang S, Newton M, Silbey R. 2004. Multichromophoric Förster resonance energy transfer. Phys. Rev. Lett. 92, 218301 ( 10.1103/PhysRevLett.92.218301) [DOI] [PubMed] [Google Scholar]
46.Scholes GD. 2002. Designing light-harvesting antenna systems based on superradiant molecular aggregates. Chem. Phys. 275, 373–386. ( 10.1016/S0301-0104(01)00533-X) [DOI] [Google Scholar]
47.Olaya-Castro A, Lee C-F, Fassioli Olsen F, Johnson NF. 2008. Efficiency of energy transfer in a light-harvesting system under quantum coherence. Phys. Rev. B 78, 085115 ( 10.1103/PhysRevB.78.085115) [DOI] [Google Scholar]
48.Cao J, Silbey RJ. 2009. Optimization of exciton trapping in energy transfer processes. J. Phys. Chem. A 113, 13 825–13 838. ( 10.1021/jp9032589) [DOI] [PubMed] [Google Scholar]
49.Fassioli F, Nazir A, Olaya-Castro A. 2010. Quantum state tuning of energy transfer in a correlated environment. J. Phys. Chem. Lett. 1, 2139–2143. ( 10.1021/jz100717d) [DOI] [Google Scholar]
50.Scholak T, Mintert F, Wellens T, Buchleitner A. 2010. Transport and entanglement. In Quantum efficiency in complex systems, part I: biomolecular systems (eds ER Weber, M Thorwart, U Würfel), pp. 1–38. Amsterdam, The Netherlands: Elsevier Inc. [Google Scholar]
51.Scholak T, De Melo F, Wellens T, Mintert F, Buchleitner A. 2011. Efficient and coherent excitation transfer across disordered molecular networks. Phys. Rev. E 83, 021912 ( 10.1103/PhysRevE.83.021912) [DOI] [PubMed] [Google Scholar]
52.Hossein-Nejad H, Olaya-Castro A, Scholes GD. 2012. Phonon-mediated path-interference in electronic energy transfer. J. Chem. Phys. 136, 024112 ( 10.1063/1.3675844) [DOI] [PubMed] [Google Scholar]
53.Lee H, Cheng Y-C, Fleming GR. 2007. Coherence dynamics in photosynthesis: protein protection of excitonic coherence. Science 316, 1462–1465. ( 10.1126/science.1142188) [DOI] [PubMed] [Google Scholar]
54.Nalbach P, Eckel J, Thorwart M. 2010. Quantum coherent biomolecular energy transfer with spatially correlated fluctuations. New J. Phys. 12, 065043 ( 10.1088/1367-2630/12/6/065043) [DOI] [Google Scholar]
55.Wu J, Liu F, Shen Y, Cao J, Silbey RJ. 2010. Efficient energy transfer in light-harvesting systems, I: optimal temperature, reorganization energy and spatial–temporal correlations. New J. Phys. 12, 105012 ( 10.1088/1367-2630/12/10/105012) [DOI] [Google Scholar]
56.Strümpfer J, Schulten K. 2011. The effect of correlated bath fluctuations on exciton transfer. J. Chem. Phys. 134, 095102 ( 10.1063/1.3557042) [DOI] [PMC free article] [PubMed] [Google Scholar]
57.Ishizaki A, Fleming GR. 2009. Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature. Proc. Natl Acad. Sci. USA 106, 17 255–17 260. ( 10.1073/pnas.0908989106) [DOI] [PMC free article] [PubMed] [Google Scholar]
58.Olbrich C, Strümpfer J, Schulten K, Kleinekathöfer U. 2011. Quest for spatially correlated fluctuations in the FMO light-harvesting complex. J. Phys. Chem. B 115, 758–764. ( 10.1021/jp1099514) [DOI] [PMC free article] [PubMed] [Google Scholar]
59.Hemelrijk PW, Kwa SLS, van Grondelle R, Dekker JP. 1992. Spectroscopic properties of LHC-II, the main light-harvesting chlorophyll a/b protein complex from chloroplast membranes. Biochim. Biophys. Acta Bioenerg. 1098, 159–166. ( 10.1016/S0005-2728(05)80331-7) [DOI] [Google Scholar]
60.Szalay L, Tombácz E, Singhal GS. 1974. Effect of solvent on the absorption spectra and Stokes’ shift of absorption and fluorescence of chlorophylls. Acta Phys. Acad. Sci. Hungaricae 35, 29–36. ( 10.1007/BF03159738) [DOI] [Google Scholar]
61.Scholes GD, Fleming GR. 2005. Energy transfer and photosynthetic light harvesting. Adv. Chem. Phys. 132, 57–129. ( 10.1002/0471759309.ch2) [DOI] [Google Scholar]
62.Ishizaki A, Calhoun TR, Schlau-Cohen GS, Fleming GR. 2010. Quantum coherence and its interplay with protein environments in photosynthetic electronic energy transfer. Phys. Chem. Chem. Phys. 12, 7319–7337. ( 10.1039/C003389H) [DOI] [PubMed] [Google Scholar]
63.Schröder M, Kleinekathöfer U, Schreiber M. 2006. Calculation of absorption spectra for light-harvesting systems using non-Markovian approaches as well as modified Redfield theory. J. Chem. Phys. 124, 084903 ( 10.1063/1.2171188) [DOI] [PubMed] [Google Scholar]
64.Doust AB, Marai CNJ, Harrop SJ, Wilk KE, Curmi PMG, Scholes GD. 2004. Developing a structure-function model for the cryptophyte phycoerythrin 545 using ultrahigh resolution crystallography and ultrafast laser spectroscopy. J. Mol. Biol. 344, 135–153. ( 10.1016/j.jmb.2004.09.044) [DOI] [PubMed] [Google Scholar]
65.Wendling M, Pullerits T, Przyjalgowski MA, Vulto SIE, Aartsma TJ, van Grondelle R, van Amerongen H. 2000. Electron-vibrational coupling in the Fenna–Matthews–Olson complex of Prosthecochloris aestuarii determined by temperature-dependent absorption and fluorescence line-narrowing measurements. J. Phys. Chem. B 104, 5825–5831. ( 10.1021/jp000077) [DOI] [Google Scholar]
66.Olbrich C, Strümpfer J, Schulten K, Kleinekathöfer U. 2011. Theory and simulation of the environmental effects on FMO electronic transitions. J. Phys. Chem. Lett. 2011, 1771–1776. ( 10.1021/jz2007676) [DOI] [PMC free article] [PubMed] [Google Scholar]
67.Kolli A, Reilly EJO, Scholes GD, Olaya-castro A. 2012. The fundamental role of quantized vibrations in coherent light harvesting by cryptophyte algae. J. Chem. Phys. 137, 174109 ( 10.1063/1.4764100) [DOI] [PubMed] [Google Scholar]
68.Chin AW, Prior J, Rosenbach R, Caycedo-Soler F, Huelga SF, Plenio MB. 2013. The role of non-equilibrium vibrational structures in electronic coherence and recoherence in pigment–protein complexes. Nat. Phys. 9, 113–118. ( 10.1038/nphys2515) [DOI] [Google Scholar]
69.Cheng Y, Silbey R. 2006. Coherence in the B800 ring of purple bacteria LH2. Phys. Rev. Lett. 96, 028103 ( 10.1103/PhysRevLett.96.028103) [DOI] [PubMed] [Google Scholar]
70.Jang S, Newton MD, Silbey RJ. 2007. Multichromophoric Förster resonance energy transfer from B800 to B850 in the light harvesting complex 2: evidence for subtle energetic optimization by purple bacteria. J. Phys. Chem. B 111, 6807–6814. ( 10.1021/jp070111l) [DOI] [PubMed] [Google Scholar]
71.Hossein-Nejad H, Curutchet C, Kubica A, Scholes GD. 2011. Delocalization-enhanced long-range energy transfer between cryptophyte algae PE545 antenna proteins. J. Phys. Chem. A 115, 5243–5253. ( 10.1021/jp108397a) [DOI] [PubMed] [Google Scholar]
72.Brumer P, Shapiro M. 2012. Molecular response in one-photon absorption via natural thermal light vs. pulsed laser excitation. Proc. Natl Acad. Sci. USA 109, 19 575–19 578. ( 10.1073/pnas.1211209109) [DOI] [PMC free article] [PubMed] [Google Scholar]
73.Fassioli F, Olaya-Castro A, Scholes GD. 2012. Coherent energy transfer under incoherent light conditions. J. Phys. Chem. Lett. 3, 3136–3142. ( 10.1021/jz3010317) [DOI] [PubMed] [Google Scholar]
74.Kassal I, Yuen-Zhou J, Rahimi-Keshari S. 2013. Does coherence enhance transport in photosynthesis? J. Phys. Chem. Lett. 4, 362–367. ( 10.1021/jz301872b) [DOI] [PubMed] [Google Scholar]
75.Davydov AS. 1948. Theory of absorption spectra of molecular crystals. Zhur. Eksptl. Teoret. Fiz. 18, 210–218. [Google Scholar]
76.Davydov AS. 1962. Theory of molecular excitons. [translated by M. Kasha and M. Oppenheimer, Jr.]. New York, NY: McGraw-Hill Book Company. [Google Scholar]
77.Kasha M. 1959. Relation between exciton bands and conduction bands in molecular lamellar systems. Rev. Mod. Phys. 31, 162–169. ( 10.1103/RevModPhys.31.162) [DOI] [Google Scholar]
78.Kasha M. 1963. Energy transfer mechanisms and the molecular exciton model for molecular aggregates. Radiat. Res. 20, 55–70. ( 10.2307/3571331c) [DOI] [PubMed] [Google Scholar]
79.Kasha M, Rawls HR, Ashraf El-Bayoumi M. 1965. The exciton model in molecular spectroscopy. Pure Appl. Chem. 11, 371–392. ( 10.1351/pac196511030371) [DOI] [Google Scholar]
80.Shipman LL, Housman DL. 1979. Forster transfer rates for chlorophyll a. Photochem. Photobiol. 29, 1163–1167. ( 10.1111/j.1751-1097.1979.tb07835.x) [DOI] [Google Scholar]
81.Krueger BP, Scholes GD, Fleming GR. 1998. Calculation of couplings and energy-transfer pathways between the pigments of LH2 by the ab initio transition density cube method. J. Phys. Chem. B 102, 5378–5386. ( 10.1021/jp9811171) [DOI] [Google Scholar]
82.Scholes GD, Ghiggino KP, Oliver AM, Paddon-Row MN. 1993. Through-space and through-bond effects on exciton interactions in rigidly linked dinaphthyl molecules. J. Am. Chem. Soc. 115, 4345–4349. ( 10.1021/ja00063a061) [DOI] [Google Scholar]
83.May V, Kuhn O. 2005. Charge and energy transfer dynamics in molecular systems, 2nd edn Weinheim, Germany: Wiley-VCH. [Google Scholar]
84.Stratt RM. 1995. The instantaneous normal modes of liquids. Acc. Chem. Res. 28, 201–207. ( 10.1021/ar00053a001) [DOI] [Google Scholar]
85.Read EL, Schlau-Cohen GS, Engel GS, Georgiou T, Papiz MZ, Fleming GR. 2009. Pigment organization and energy level structure in light-harvesting complex 4: insights from two-dimensional electronic spectroscopy. J. Phys. Chem. B 113, 6495–6504. ( 10.1021/jp809713q) [DOI] [PubMed] [Google Scholar]
86.Sauer K, Cogdell RJ, Prince SM, Freer A, Isaacs NW, Scheer H. 1996. Structure-based calculations of the optical spectra of the LH2 bacteriochlorophyll-protein complex from Rhodopseudomonas acidophila. Photochem. Photobiol. 64, 564–576. ( 10.1111/j.1751-1097.1996.tb03106.x) [DOI] [Google Scholar]
87.Yang M, Damjanović A, Vaswani HM, Fleming GR. 2003. Energy transfer in photosystem I of cyanobacteria Synechococcus elongatus: model study with structure-based semi-empirical Hamiltonian and experimental spectral density. Biophys. J. 85, 140–158. ( 10.1016/S0006-3495(03)74461-0) [DOI] [PMC free article] [PubMed] [Google Scholar]
88.Doust AB, Wilk KE, Curmi PMG, Scholes GD. 2006. The photophysics of cryptophyte light-harvesting. J. Photochem. Photobiol. A Chem. 184, 1–17. ( 10.1016/j.jphotochem.2006.06.006) [DOI] [Google Scholar]
89.Marin A, Doust AB, Scholes GD, Wilk KE, Curmi PMG, van Stokkum IHM, van Grondelle R. 2011. Flow of excitation energy in the cryptophyte light-harvesting antenna phycocyanin 645. Biophys. J. 101, 1004–1013. ( 10.1016/j.bpj.2011.07.012) [DOI] [PMC free article] [PubMed] [Google Scholar]
90.Freiberg A, Godik VI, Pullerits T, Timpmann K. 1989. Picosecond dynamics of directed excitation transfer in spectrally heterogeneous light-harvesting antenna of purple bacteria. Biochim. Biophys. Acta 973, 93–104. ( 10.1016/S0005-2728(89)80407-4) [DOI] [Google Scholar]
91.Wientjes E, Roest G, Croce R. 2012. From red to blue to far-red in Lhca4: how does the protein modulate the spectral properties of the pigments? Biochim. Biophys. Acta 1817, 711–717. ( 10.1016/j.bbabio.2012.02.030) [DOI] [PubMed] [Google Scholar]
92.Van Amerongen H, Valkunas L, van Grondelle R. 2000. Photosynthetic excitons. Singapore: World Scientific Publishing. [Google Scholar]
93.Fowler GJ, Visschers RW, Grief GG, van Grondelle R, Hunter CN. 1992. Genetically modified photosynthetic antenna complexes with blueshifted absorbance bands. Nature 355, 848–850. ( 10.1038/355848a0) [DOI] [PubMed] [Google Scholar]
94.Novoderezhkin VI, Palacios MA, van Amerongen H, van Grondelle R. 2005. Excitation dynamics in the LHCII complex of higher plants: modeling based on the 2.72 Angstrom crystal structure. J. Phys. Chem. B 109, 10 493–10 504. ( 10.1021/jp044082f) [DOI] [PubMed] [Google Scholar]
95.Silbey R, Harris RA. 1984. Variational calculation of the dynamics of a two level system interacting with a bath. J. Chem. Phys. 80, 2615–2617. ( 10.1063/1.447055) [DOI] [Google Scholar]
96.Meier T, Zhao Y, Chernyak V, Mukamel S, Introduction I. 1997. Polarons, localization, and excitonic coherence in superradiance of biological antenna complexes. J. Chem. Phys. 107, 3876–3893. ( 10.1063/1.474746) [DOI] [Google Scholar]
97.Silbey R. 2011. Description of quantum effects in the condensed phase. Procedia Chem. 3, 188–197. ( 10.1016/j.proche.2011.08.026) [DOI] [Google Scholar]
98.Yena T-C, Cheng Y-C. 2011. Electronic coherence effects in photosynthetic light harvesting. Procedia Chem. 3, 211–221. ( 10.1016/j.proche.2011.08.028) [DOI] [Google Scholar]
99.Kolli A, Nazir A, Olaya-Castro A. 2011. Electronic excitation dynamics in multichromophoric systems described via a polaron-representation master equation. J. Chem. Phys. 135, 154112 ( 10.1063/1.3652227) [DOI] [PubMed] [Google Scholar]
100.Grondelle R, Van Novoderezhkin V. 2001. Dynamics of excitation energy transfer in the LH1 and LH2 light-harvesting complexes of photosynthetic bacteria. Biochemistry 40, 15 057–15 068. ( 10.1021/bi0018943) [DOI] [PubMed] [Google Scholar]
101.Novoderezhkin VI, Rutkauskas D, van Grondelle R. 2006. Dynamics of the emission spectrum of a single LH2 complex: interplay of slow and fast nuclear motions. Biophys. J. 90, 2890–2902. ( 10.1529/biophysj.105.072652) [DOI] [PMC free article] [PubMed] [Google Scholar]
102.Fassioli F, Olaya-Castro A. 2010. Distribution of entanglement in light-harvesting complexes and their quantum efficiency. New J. Phys. 12, 085006 ( 10.1088/1367-2630/12/8/085006) [DOI] [Google Scholar]
103.Sarovar M, Ishizaki A, Fleming GR, Whaley KB. 2010. Quantum entanglement in photosynthetic light-harvesting complexes. Nat. Phys. 6, 462–467. ( 10.1038/nphys1652) [DOI] [Google Scholar]
104.Olaya-Castro A, Fassioli F. 2011. Characterizing quantum-sharing of electronic excitation in molecular aggregates. Procedia Chem. 3, 176–184. ( 10.1016/j.proche.2011.08.024) [DOI] [Google Scholar]
105.Whaley KB, Sarovar M, Ishizaki A. 2011. Quantum entanglement phenomena in photosynthetic light harvesting complexes. Procedia Chem. 3, 152–164. ( 10.1016/j.proche.2011.08.021) [DOI] [Google Scholar]
106.Smyth C, Fassioli F, Scholes GD. 2012. Measures and implications of electronic coherence in photosynthetic light-harvesting. Phil. Trans. R. Soc. A 370, 3728–3749. ( 10.1098/rsta.2011.0420) [DOI] [PubMed] [Google Scholar]
107.Tiersch M, Popescu S, Briegel HJ. 2012. A critical view on transport and entanglement in models of photosynthesis. Phil. Trans. R. Soc. A 370, 3771–3786. ( 10.1098/rsta.2011.0202) [DOI] [PubMed] [Google Scholar]
108.Breuer H-P, Petruccione F. 2002. The theory of open quantum systems. Oxford, UK: Oxford University Press. [Google Scholar]
109.Ritz T, Park S, Schulten K. 2001. Kinetics of excitation migration and trapping in the photosynthetic unit of purple bacteria. J. Phys. Chem. B 105, 8259–8267. ( 10.1021/jp011032r) [DOI] [Google Scholar]
110.Panitchayangkoon G, Hayes D, Fransted KA, Caram JR, Harel E, Wen J, Blankenship RE, Engel GS. 2010. Long-lived quantum coherence in photosynthetic complexes at physiological temperature. Proc. Natl Acad. Sci. USA 107, 12 766–12 770. ( 10.1073/pnas.1005484107) [DOI] [PMC free article] [PubMed] [Google Scholar]
111.Ishizaki A, Fleming GR. 2009. Unified treatment of quantum coherent and incoherent hopping dynamics in electronic energy transfer: reduced hierarchy equation approach. J. Chem. Phys. 130, 234111 ( 10.1063/1.3155372) [DOI] [PubMed] [Google Scholar]
112.Roden J, Eisfeld A, Wolff W, Strunz WT. 2009. Influence of complex exciton-phonon coupling on optical absorption and energy transfer of quantum aggregates. Phys. Rev. Lett. 103, 058301 ( 10.1103/PhysRevLett.103.058301) [DOI] [PubMed] [Google Scholar]
113.Nalbach P, Thorwart M. 2010. Multiphonon transitions in the biomolecular energy transfer dynamics. J. Chem. Phys. 132, 194111 ( 10.1063/1.3428385) [DOI] [PubMed] [Google Scholar]
114.Huo P, Coker DF. 2010. Iterative linearized density matrix propagation for modeling coherent excitation energy transfer in photosynthetic light harvesting. J. Chem. Phys. 133, 184108 ( 10.1063/1.3498901) [DOI] [PubMed] [Google Scholar]
115.Jang S. 2011. Theory of multichromophoric coherent resonance energy transfer: a polaronic quantum master equation approach. J. Chem. Phys. 135, 034105 ( 10.1063/1.3608914) [DOI] [PubMed] [Google Scholar]
116.Womick JM, Moran AM. 2011. Vibronic enhancement of exciton sizes and energy transport in photosynthetic complexes. J. Phys. Chem. B 115, 1347–1356. ( 10.1021/jp106713q) [DOI] [PubMed] [Google Scholar]
117.Nalbach P, Thorwart M. 2012. The role of discrete molecular modes in the coherent exciton dynamics in FMO. J. Phys. B At. Mol. Opt. Phys. 45, 154009 ( 10.1088/0953-4075/45/15/154009) [DOI] [Google Scholar]
118.Roden J, Strunz WT, Whaley KB, Eisfeld A. 2012. Accounting for intra-molecular vibrational modes in open quantum system description of molecular systems. J. Chem. Phys. 137, 204110 ( 10.1063/1.4765329) [DOI] [PubMed] [Google Scholar]
119.Shi Q, Chen L, Nan G, Xu R-X, Yan Y. 2009. Efficient hierarchical Liouville space propagator to quantum dissipative dynamics. J. Chem. Phys. 130, 084105 ( 10.1063/1.3077918) [DOI] [PubMed] [Google Scholar]
120.Kneip C, Parbel A, Foerstendorf H, Scheer H, Siebert F. 1998. Fourier transform near-infrared resonance Raman spectroscopic study of the a-subunit of phycoerythrocyanin and phycocyanin from the cyanobacterium Mastigocladus laminosus. J. Raman Spectrosc. 944, 939–944. () [DOI] [Google Scholar]
121.Hybl JD, Albrecht AW, Gallagher Faeder SM, Jonas DM. 1998. Two-dimensional electronic spectroscopy. Chem. Phys. Lett. 297, 307–313. ( 10.1016/S0009-2614(98)01140-3) [DOI] [Google Scholar]
122.Cundiff ST, Bristow AD, Siemens M, Li H, Moody G, Karaiskaj D, Dai X, Zhang T. 2012. Optical 2-D Fourier transform spectroscopy of excitons in semiconductor nanostructures. IEEE J. Sel. Top. Quantum Electron. 18, 318–328. ( 10.1109/JSTQE.2011.2123876) [DOI] [Google Scholar]
123.Lewis KLM, Ogilvie JP. 2012. Probing photosynthetic energy and charge transfer with two-dimensional electronic spectroscopy. J. Phys. Chem. Lett. 3, 503–510. ( 10.1021/jz201592v) [DOI] [PubMed] [Google Scholar]
124.Anna JM, Song Y, Dinshaw R, Scholes GD. 2013. Two-dimensional electronic spectroscopy for mapping molecular photophysics. Pure Appl. Chem. 85, 1307–1319. ( 10.1351/PAC-CON-12-10-21) [DOI] [Google Scholar]
125.Tokmakoff A. 2000. Two-dimensional line shapes derived from coherent third-order nonlinear spectroscopy. J. Phys. Chem. A 104, 4247–4255. ( 10.1021/jp993207r) [DOI] [Google Scholar]
126.Hochstrasser RM. 2007. Two-dimensional spectroscopy at infrared and optical frequencies. Proc. Natl Acad. Sci. USA 104, 14 190–14 196. ( 10.1073/pnas.0704079104) [DOI] [PMC free article] [PubMed] [Google Scholar]
127.Khalil M, Demirdoven N, Tokmakoff A. 2003. Obtaining absorptive line shapes in two-dimensional infrared vibrational correlation spectra. Phys. Rev. Lett. 90, 047401 ( 10.1103/PhysRevLett.90.047401) [DOI] [PubMed] [Google Scholar]
128.Mukamel S. 1995. Principles of nonlinear optical spectroscopy. New York, NY: Oxford University Press. [Google Scholar]
129.Cho M. 2008. Coherent two-dimensional optical spectroscopy. Chem. Rev. 108, 1331–1418. ( 10.1021/cr078377b) [DOI] [PubMed] [Google Scholar]
130.Mukamel S. 2000. Multidimensional femtosecond correlation spectroscopies of electronic and vibrational excitations. Annu. Rev. Phys. Chem. 51, 691–729. ( 10.1146/annurev.physchem.51.1.691) [DOI] [PubMed] [Google Scholar]
131.Abramavicius D, Palmieri B, Voronine DV, Sanda F, Mukamel S. 2009. Coherent multidimensional optical spectroscopy of excitons in molecular aggregates; quasiparticle versus supermolecule perspectives. Chem. Rev. 109, 2350–2408. ( 10.1021/cr800268n) [DOI] [PMC free article] [PubMed] [Google Scholar]
132.Turner DB, Hassan Y, Scholes GD. 2012. Exciton superposition states in CdSe nanocrystals measured using broadband two-dimensional electronic spectroscopy. Nano Lett. 12, 880–886. ( 10.1021/nl2039502) [DOI] [PubMed] [Google Scholar]
133.Nemeth A, Milota F, Mančal T, Lukeš V, Hauer J, Kauffmann HF, Sperling J. 2010. Vibrational wave packet induced oscillations in two-dimensional electronic spectra. I. Experiments. J. Chem. Phys. 132, 184514 ( 10.1063/1.3404404) [DOI] [Google Scholar]
134.Mančal T, Nemeth A, Milota F, Lukeš V, Kauffmann HF, Sperling J. 2010. Vibrational wave packet induced oscillations in two-dimensional electronic spectra. II. Theory. J. Chem. Phys. 132, 184515 ( 10.1063/1.3404405) [DOI] [Google Scholar]
135.Egorova D. 2008. Detection of electronic and vibrational coherences in molecular systems by 2D electronic photon echo spectroscopy. Chem. Phys. 347, 166–176. ( 10.1016/j.chemphys.2007.12.019) [DOI] [Google Scholar]
136.Turner DB, Wilk KE, Curmi PMG, Scholes GD. 2011. Comparison of electronic and vibrational coherence measured by two-dimensional electronic spectroscopy. J. Phys. Chem. Lett. 2, 1904–1911. ( 10.1021/jz200811p) [DOI] [Google Scholar]
137.Hayes D, Wen J, Panitchayangkoon G, Blankenship RE, Engel GS. 2011. Robustness of electronic coherence in the Fenna–Matthews–Olson complex to vibronic and structural modifications. Faraday Discuss. 150, 459–469. ( 10.1039/c0fd00030b) [DOI] [PubMed] [Google Scholar]
138.Chachisvilis M, Kuhn O, Pullerits T, Sundstrom V. 1997. Excitons in photosynthetic purple bacteria: wavelike motion or incoherent hopping? J. Phys. Chem. B 101, 7275–7283. ( 10.1021/jp963360a) [DOI] [Google Scholar]
139.Savikhin S, Buck DR, Struve WS. 1997. Oscillating anisotropies in a bacteriochlorophyll protein: evidence for quantum beating between exciton levels. Chem. Phys. 223, 303–312. ( 10.1016/S0301-0104(97)00223-1) [DOI] [Google Scholar]
140.Engel GS, Calhoun TR, Read EL, Ahn T-K, Mancal T, Cheng Y-C, Blankenship RE, Fleming GR. 2007. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 446, 782–786. ( 10.1038/nature05678) [DOI] [PubMed] [Google Scholar]
141.Calhoun TR, Ginsberg NS, Schlau-Cohen GS, Cheng Y-C, Ballottari M, Bassi R, Fleming GR. 2009. Quantum coherence enabled determination of the energy landscape in light-harvesting complex II. J. Phys. Chem. B 113, 16 291–16 295. ( 10.1021/jp908300c) [DOI] [PubMed] [Google Scholar]
142.Collini E, Wong CY, Wilk KE, Curmi PMG, Brumer P, Scholes GD. 2010. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature 463, 644–647. ( 10.1038/nature08811) [DOI] [PubMed] [Google Scholar]
143.Wong CY, Alvey RM, Turner DB, Wilk KE, Bryant DA, Curmi PMG, Silbey RJ, Scholes GD. 2012. Electronic coherence lineshapes reveal hidden excitonic correlations in photosynthetic light harvesting. Nat. Chem. 4, 396–404. ( 10.1038/nchem.1302) [DOI] [PubMed] [Google Scholar]
144.Wedemayer GJ, Kidd DG, Glazer AN. 1996. Cryptomonad biliproteins: bilin types and locations. Photosynth. Res. 48, 163–170. ( 10.1007/BF00041006) [DOI] [PubMed] [Google Scholar]
145.Harrop ASJ, et al. Submitted Evolution of cryptophyte light harvesting proteins: a structural switch that controls energy transfer. [Google Scholar]
146.Turner DB, Dinshaw R, Lee K-K, Belsley MS, Wilk KE, Curmi PMG, Scholes GD. 2012. Quantitative investigations of quantum coherence for a light-harvesting protein at conditions simulating photosynthesis. Phys. Chem. Chem. Phys. 14, 4857–4874. ( 10.1039/c2cp23670b) [DOI] [PubMed] [Google Scholar]
147.Christensson N, Milota F, Hauer J, Sperling J, Bixner O, Nemeth A, Kauffmann HF. 2011. High frequency vibrational modulations in two-dimensional electronic spectra and their resemblance to electronic coherence signatures. J. Phys. Chem. B 115, 5383–5391. ( 10.1021/jp109442b) [DOI] [PubMed] [Google Scholar]
148.Tiwari V, Peters WK, Jonas DM. 2013. Electronic resonance with anticorrelated pigment vibrations drives photosynthetic energy transfer outside the adiabatic framework. Proc. Natl Acad. Sci. USA 110, 1203–1208. ( 10.1073/pnas.1211157110) [DOI] [PMC free article] [PubMed] [Google Scholar]
149.Cheng Y-C, Fleming GR. 2008. Coherence quantum beats in two-dimensional electronic spectroscopy. J. Phys. Chem. A 112, 4254–4260. ( 10.1021/jp7107889) [DOI] [PubMed] [Google Scholar]
150.Butkus V, Zigmantas D, Valkunas L, Abramavicius D. 2012. Vibrational vs. electronic coherences in 2D spectrum of molecular systems. Chem. Phys. Lett. 545, 40–43. ( 10.1016/j.cplett.2012.07.014) [DOI] [Google Scholar]
151.Richards GH, Wilk KE, Curmi PMG, Quiney M, Davis JA. 2012. Coherent vibronic coupling in light-harvesting complexes from photosynthetic marine algae. J. Phys. Chem. Lett. 3, 272–277. ( 10.1021/jz201600f) [DOI] [PubMed] [Google Scholar]
152.Yuen-Zhou J, Krich JJ, Aspuru-Guzik A. 2012. A witness for coherent electronic vs vibronic-only oscillations in ultrafast spectroscopy. J. Chem. Phys. 136, 234501 ( 10.1063/1.4725498) [DOI] [PubMed] [Google Scholar]
153.Fragnito HL, Bigot J-Y, Becker PC, Shank CV. 1989. Evolution of the vibronic absorption spectrum in a molecule following impulsive excitation with a 6 fs optical pulse. Chem. Phys. Lett. 160, 101–104. ( 10.1016/0009-2614(89)87564-5) [DOI] [Google Scholar]
154.Pollard WT, Fragnito HL, Bigot J-Y, Shank CV, Mathies RA. 1990. Quantum-mechanical theory for 6 fs dynamic absorption spectroscopy and its application to nile blue. Chem. Phys. Lett. 168, 239–245. ( 10.1016/0009-2614(90)85603-A) [DOI] [Google Scholar]
155.Jonas DM, Fleming GR. 1995. Vibrationally abrupt pulses in pump-probe spectroscopy. In Ultrafast processes in chemistry and photobiology (chemistry in the 21st century series IUPAC) (eds El-Sayed MA, Tanaka I, Molin Y.), pp. 225–256. Oxford, UK: Blackwell Science. [Google Scholar]
156.Fulton RL, Gouterman M. 1961. Vibronic coupling. I. Mathematical treatment for two electronic states. J. Chem. Phys. 35, 1059 ( 10.1063/1.1701181) [DOI] [Google Scholar]
157.Christensson N, Kauffmann HF, Pullerits T, Mančal T. 2012. Origin of long-lived coherences in light-harvesting complexes. J. Phys. Chem. B 116, 7449–7454. ( 10.1021/jp304649c) [DOI] [PMC free article] [PubMed] [Google Scholar]
158.Heid CG, Ottiger P, Leist R, Leutwyler S. 2011. The S1/S2 exciton interaction in 2-pyridone·6-methyl-2-pyridone: Davydov splitting, vibronic coupling, and vibronic quenching. J. Chem. Phys. 135, 154311 ( 10.1063/1.3652759) [DOI] [PubMed] [Google Scholar]
159.Ottiger P, Leutwyler S, Köppel H. 2012. Vibrational quenching of excitonic splittings in H-bonded molecular dimers: the electronic Davydov splittings cannot match experiment. J. Chem. Phys. 136, 174308 ( 10.1063/1.4705119) [DOI] [PubMed] [Google Scholar]
160.Mohseni M, Rebentrost P, Lloyd S, Aspuru-Guzik A. 2008. Environment-assisted quantum walks in photosynthetic energy transfer. J. Chem. Phys. 129, 174106 ( 10.1063/1.3002335) [DOI] [PubMed] [Google Scholar]
161.Plenio MB, Huelga SF. 2008. Dephasing-assisted transport: quantum networks and biomolecules. New J. Phys. 10, 113019 ( 10.1088/1367-2630/10/11/113019) [DOI] [Google Scholar]
162.Caruso F, Chin AW, Datta A, Huelga SF, Plenio MB. 2009. Highly efficient energy excitation transfer in light-harvesting complexes: the fundamental role of noise-assisted transport. J. Chem. Phys. 131, 105106 ( 10.1063/1.3223548) [DOI] [Google Scholar]
163.Fassioli F, Oblinsky DG, Scholes GD. 2013. Designs for molecular circuits that use electronic coherence. Faraday Discuss. 163, 341–351. ( 10.1039/c3fd00009e) [DOI] [PubMed] [Google Scholar]
164.Mančal T, Valkunas L. 2010. Exciton dynamics in photosynthetic complexes: excitation by coherent and incoherent light. New J. Phys. 12, 065044 ( 10.1088/1367-2630/12/6/065044) [DOI] [Google Scholar]
165.Jiang X, Brumer P. 1991. Creation and dynamics of molecular states prepared with coherent vs partially coherent pulsed light. J. Chem. Phys. 94, 5833–5843. ( 10.1063/1.460467) [DOI] [Google Scholar]
166.Kistiakowsky GB, Parmenter CS. 1965. Effects of pressure on fluorescence and intersystem crossing in benzene vapor. J. Chem. Phys. 42, 2942–2948. ( 10.1063/1.1703267) [DOI] [Google Scholar]
167.Watts RJ, Strickler SJ. 1966. Fluorescence and internal conversion in naphthalene vapor. J. Chem. Phys. 44, 2423–2426. ( 10.1063/1.1727059) [DOI] [Google Scholar]
168.Bixon M, Jortner J. 1968. Intramolecular radiationless transitions. J. Chem. Phys. 48, 715–726. ( 10.1063/1.1668703) [DOI] [Google Scholar]
169.Englman R, Jortner J. 1970. The energy gap law for radiationless transitions in large molecules. Mol. Phys. 18, 145–164. ( 10.1080/00268977000100171) [DOI] [Google Scholar]
170.Turner DB, Arpin PC, McClure SD, Ulness DJ, Scholes GD. 2013. Coherent multidimensional optical spectra measured using incoherent light. Nat. Commun. 4, 2298 ( 10.1038/ncomms3298) [DOI] [PubMed] [Google Scholar]
171.Turner DB, Howey DJ, Sutor EJ, Hendrickson RA, Gealy MW, Ulness DJ. 2013. Two-dimensional electronic spectroscopy using incoherent light: theoretical analysis. J. Phys. Chem. A 117, 5926–5954. ( 10.1021/jp310477y) [DOI] [PubMed] [Google Scholar]
172.Morita N, Yajima T. 1984. Ultrahigh-time-resolution coherent transient spectroscopy with incoherent light. Phys. Rev. A 30, 2525–2536. ( 10.1103/PhysRevA.30.2525) [DOI] [Google Scholar]
173.Beach R, Hartmann S. 1984. Incoherent photon echoes. Phys. Rev. Lett. 53, 663–666. ( 10.1103/PhysRevLett.53.663) [DOI] [Google Scholar]
174.Asaka S, Nakatsuka H, Fujiwara M, Matsuoka M. 1984. Accumulated photon echoes with incoherent light in Nd³⁺-doped silicate glass. Phys. Rev. A 29, 2286–2289. ( 10.1103/PhysRevA.29.2286) [DOI] [Google Scholar]
175.Tomita M, Matsuoka M. 1986. Ultrafast pump-probe measurement using intensity correlation of incoherent light. J. Opt. Soc. Am. B 3, 560–563. ( 10.1364/JOSAB.3.000560) [DOI] [Google Scholar]
176.Ulness DJ. 2003. On the role of classical field time correlations in noisy light spectroscopy: color locking and a spectral filter analogy. J. Phys. Chem. A 107, 8111–8123. ( 10.1021/jp0222494) [DOI] [Google Scholar]
177.Hildner R, Brinks D, van Hulst NF. 2010. Femtosecond coherence and quantum control of single molecules at room temperature. Nat. Phys. 7, 172–177. ( 10.1038/nphys1858) [DOI] [Google Scholar]
178.Hildner R, Brinks D, Nieder JB, Cogdell RJ, van Hulst NF. 2013. Quantum coherent energy transfer over varying pathways in single light-harvesting complexes. Science 340, 1448–1451. ( 10.1126/science.1235820) [DOI] [PubMed] [Google Scholar]
179.Dong H, Fleming GR. 2013. Three-pulse photon echo of finite numbers of molecules: single-molecule traces. J. Phys. Chem. B 117, 11 318–11 325. ( 10.1021/jp402768c) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C1] 1.Connolly JS, Janzen AF, Samuel EB. 1982. Fluorescence lifetimes of chlorophyll a: solvent, concentration and oxygen dependence. Photochem. Photobiol. 36, 559–563. ( 10.1111/j.1751-1097.1982.tb04416.x) [DOI] [Google Scholar]

[RSIF20130901C2] 2.Mullineaux CW, Pascal AA, Horton P, Holzwarth AR. 1993. Excitation-energy quenching in aggregates of the LHC II chlorophyll–protein complex: a time-resolved fluorescence study. Biochim. Biophys. Acta - Bioenerg. 1141, 23–28. ( 10.1016/0005-2728(93)90184-H) [DOI] [Google Scholar]

[RSIF20130901C3] 3.Bowers PG, Porter G. 1967. Quantum yields of triplet formation in solutions of chlorophyll. Proc. R. Soc. A Math. Phys. Eng. Sci. 296, 435–441. ( 10.1098/rspa.1967.0036) [DOI] [Google Scholar]

[RSIF20130901C4] 4.Peterman EJ, Dukker FM, van Grondelle R, van Amerongen H. 1995. Chlorophyll a and carotenoid triplet states in light-harvesting complex II of higher plants. Biophys. J. 69, 2670–2678. ( 10.1016/S0006-3495(95)80138-4) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C5] 5.Blankenship RE. 2002. Molecular mechanisms of photosynthesis. Oxford, UK: Blackwell Science Ltd. [Google Scholar]

[RSIF20130901C6] 6.Jursinic P, Govindjee 1977. Temperature dependence of delayed light emission in the 6 to 340 microsecond range after a single flash in chloroplasts. Photochem. Photobiol. 26, 617–628. ( 10.1111/j.1751-1097.1977.tb07541.x) [DOI] [Google Scholar]

[RSIF20130901C7] 7.Wientjes E, van Amerongen H, Croce R. 2013. Quantum yield of charge separation in photosystem II: functional effect of changes in the antenna size upon light acclimation. J. Phys. Chem. B 117, 11 200–11 208. ( 10.1021/jp401663w) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C8] 8.Sundstrom V, Pullerits T, Van Grondelle R. 1999. Photosynthetic light-harvesting: reconciling dynamics and structure of purple bacterial LH2 reveals function of phyotosynthetic unit. J. Phys. Chem. B 103, 2327–2346. ( 10.1021/jp983722+) [DOI] [Google Scholar]

[RSIF20130901C9] 9.Van Grondelle R, Novoderezhkin VI. 2006. Energy transfer in photosynthesis: experimental insights and quantitative models. Phys. Chem. Chem. Phys. 8, 793–807. ( 10.1039/b514032c) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C10] 10.Novoderezhkin VI, van Grondelle R. 2010. Physical origins and models of energy transfer in photosynthetic light-harvesting. Phys. Chem. Chem. Phys. 12, 7352–7365. ( 10.1039/c003025b) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C11] 11.Scholes GD, Fleming GR, Olaya-Castro A, van Grondelle R. 2011. Lessons from nature about solar light harvesting. Nat. Chem. 3, 763–774. ( 10.1038/nchem.1145) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C12] 12.Renger T, Müh F. 2013. Understanding photosynthetic light-harvesting: a bottom up theoretical approach. Phys. Chem. Chem. Phys. 15, 3348–3371. ( 10.1039/c3cp43439g) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C13] 13.Cheng Y-C, Fleming GR. 2009. Dynamics of light harvesting in photosynthesis. Annu. Rev. Phys. Chem. 60, 241–262. ( 10.1146/annurev.physchem.040808.090259) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C14] 14.Iwata S, Barber J. 2004. Structure of photosystem II and molecular architecture of the oxygen-evolving centre. Curr. Opin. Struct. Biol. 14, 447–453. ( 10.1016/j.sbi.2004.07.002) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C15] 15.Nield J, Barber J. 2006. Refinement of the structural model for the photosystem II supercomplex of higher plants. Biochim. Biophys. Acta 1757, 353–361. ( 10.1016/j.bbabio.2006.03.019) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C16] 16.Standfuss J, Terwisscha van Scheltinga AC, Lamborghini M, Kühlbrandt W. 2005. Mechanisms of photoprotection and nonphotochemical quenching in pea light-harvesting complex at 2.5 Å resolution. EMBO J. 24, 919–928. ( 10.1038/sj.emboj.7600585) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C17] 17.Guskov A, Kern J, Gabdulkhakov A, Broser M, Zouni A, Saenger W. 2009. Cyanobacterial photosystem II at 2.9-A resolution and the role of quinones, lipids, channels and chloride. Nat. Struct. Mol. Biol. 16, 334–342. ( 10.1038/nsmb.1559) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C18] 18.Schlau-Cohen GS, Calhoun TR, Ginsberg NS, Read EL, Ballottari M, Bassi R, van Grondelle R, Fleming GR. 2009. Pathways of energy flow in LHCII from two-dimensional electronic spectroscopy. J. Phys. Chem. B 113, 15 352–15 363. ( 10.1021/jp9066586) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C19] 19.Croce R, van Amerongen H. 2011. Light-harvesting and structural organization of photosystem II: from individual complexes to thylakoid membrane. J. Photochem. Photobiol. B. 104, 142–153. ( 10.1016/j.jphotobiol.2011.02.015) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C20] 20.Andrews DL, Curutchet C, Scholes GD. 2011. Resonance energy transfer: beyond the limits. Laser Photon. Rev. 5, 114–123. ( 10.1002/lpor.201000004) [DOI] [Google Scholar]

[RSIF20130901C21] 21.Renger T. 2009. Theory of excitation energy transfer: from structure to function. Photosynth. Res. 102, 471–485. ( 10.1007/s11120-009-9472-9) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C22] 22.Scholes GD. 2003. Long-range resonance energy transfer in molecular systems. Annu. Rev. Phys. Chem. 54, 57–87. ( 10.1146/annurev.physchem.54.011002.103746) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C23] 23.Andrews DL. 1989. A unified theory of radiative and radiationless molecular energy transfer. Chem. Phys. 135, 195–201. ( 10.1016/0301-0104(89)87019-3) [DOI] [Google Scholar]

[RSIF20130901C24] 24.Beljonne D, Curutchet C, Scholes GD, Silbey RJ. 2009. Beyond Förster resonance energy transfer in biological and nanoscale systems. J. Phys. Chem. B 113, 6583–6599. ( 10.1021/jp900708f) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C25] 25.Van Grondelle R, Dekker JP, Gillbro T, Sundstrom V. 1994. Energy transfer and trapping in photosynthesis. Biochim. Biophys. Acta Bioenerg. 1187, 1–65. ( 10.1016/0005-2728(94)90166-X) [DOI] [Google Scholar]

[RSIF20130901C26] 26.Selvin PR. 2000. The renaissance of fluorescence resonance energy transfer. Nat. Struct. Biol. 7, 730–734. ( 10.1038/78948) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C27] 27.Förster T. 1948. Zwischenmolekulare energiewanderung und fluoreszenz. Ann. Phys. 2, 55–75. ( 10.1002/andp.19484370105) [DOI] [Google Scholar]

[RSIF20130901C28] 28.Renger T, Klinger A, Steinecker F, Schmidt am Busch M, Numata J, Müh F. 2012. Normal mode analysis of the spectral density of the Fenna–Matthews–Olson light-harvesting protein: how the protein dissipates the excess energy of excitons. J. Phys. Chem. B 116, 14 565–14 580. ( 10.1021/jp3094935) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C29] 29.Ishizaki A, Fleming GR. 2012. Quantum coherence in photosynthetic light harvesting. Annu. Rev. Condens. Matter Phys. 3, 333–361. ( 10.1146/annurev-conmatphys-020911-125126) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C30] 30.Novoderezhkin VI, Doust AB, Curutchet C, Scholes GD, van Grondelle R. 2010. Excitation dynamics in phycoerythrin 545: modeling of steady-state spectra and transient absorption with modified Redfield theory. Biophys. J. 99, 344–352. ( 10.1016/j.bpj.2010.04.039) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C31] 31.Jimenez R, Dikshit SN, Bradforth SE, Fleming GR. 1996. Electronic excitation transfer in the LH2 complex of Rhodobacter sphaeroides. J. Phys. Chem. 100, 6825–6834. ( 10.1021/jp953074j) [DOI] [Google Scholar]

[RSIF20130901C32] 32.Pullerits T, Chachisvilis M, Sundstrom V. 1996. Exciton delocalization length in the B850 antenna of Rhodobacter sphaeroides. J. Phys. Chem. 100, 10 787–10 792. ( 10.1021/jp953639b) [DOI] [Google Scholar]

[RSIF20130901C33] 33.Nagarajan V, Alden RG, Williams JC, Parson WW. 1996. Ultrafast exciton relaxation in the B850 antenna complex of Rhodobacter sphaeroides. Proc. Natl Acad. Sci. USA 93, 13 774–13 779. ( 10.1073/pnas.93.24.13774) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C34] 34.Novoderezhkin VI, Razjivin VI. 1995. Excitation delocalization over the whole core antenna of photosynthetic purple bacteria evidenced by non-linear pump-probe spectroscopy. FEBS Lett. 368, 370–372. ( 10.1016/0014-5793(95)00663-T) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C35] 35.Leupold D, Stiel H, Teuchner K, Nowak F, Sandner W, Ucker B, Scheer H. 1996. Size enhancement of transition dipoles to one- and two-exciton bands in a photosynthetic antenna. Phys. Rev. Lett. 77, 4675–4678. ( 10.1103/PhysRevLett.77.4675) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C36] 36.Kuhn O, Sundstrom V. 1997. Pump-probe spectroscopy of dissipative energy transfer dynamics in photosynthetic antenna complexes: a density matrix approach. J. Chem. Phys. 107, 4154–4164. ( 10.1063/1.474803) [DOI] [Google Scholar]

[RSIF20130901C37] 37.Novoderezhkin V, Monshouwer R, van Grondelle R. 1999. Exciton (de)localization in the LH2 antenna of Rhodobacter sphaeroides as revealed by relative difference absorption measurements of the LH2 antenna and the B820 subunit. J. Phys. Chem. A 103, 10 540–10 548. ( 10.1021/jp9844415) [DOI] [Google Scholar]

[RSIF20130901C38] 38.Book LD, Ostafin AE, Ponomarenko N, Norris JR, Scherer NF. 2000. Exciton delocalization and initial dephasing dynamics of purple bacterial LH2. J. Phys. Chem. B 104, 8295–8307. ( 10.1021/jp000485d) [DOI] [Google Scholar]

[RSIF20130901C39] 39.Monshouwer R, Abrahamsson M, van Mourik F, van Grondelle R. 1997. Superradiance and exciton delocalization in bacterial photosynthetic light-harvesting systems. J. Phys. Chem. B 101, 7241–7248. ( 10.1021/jp963377t) [DOI] [Google Scholar]

[RSIF20130901C40] 40.Cogdell RJ, Gall A, Köhler J. 2006. The architecture and function of the light-harvesting apparatus of purple bacteria: from single molecules to in vivo membranes. Q. Rev. Biophys. 39, 227–324. ( 10.1017/S0033583506004434) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C41] 41.Van Oijen AM, Ketelaars M, Kohler J, Aartsma TJ, Schmidt J. 1999. Unraveling the electronic structure of individual photosynthetic pigment–protein complexes. Science 285, 400–402. ( 10.1126/science.285.5426.400) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C42] 42.Sumi H. 1999. Theory on rates of excitation-energy transfer between molecular aggregates through distributed transition dipoles with application to the antenna system in bacterial photosynthesis. J. Phys. Chem. B 103, 252–260. ( 10.1021/jp983477u) [DOI] [Google Scholar]

[RSIF20130901C43] 43.Scholes GD, Fleming GR. 2000. On the mechanism of light harvesting in photosynthetic purple bacteria: B800 to B850 energy transfer. J. Phys. Chem. B 104, 1854–1868. ( 10.1021/jp993435l) [DOI] [Google Scholar]

[RSIF20130901C44] 44.Scholes GD, Jordanides XJ, Fleming GR. 2001. Adapting the Forster theory of energy transfer for modeling dynamics in aggregated molecular assemblies. J. Phys. Chem. B 105, 1640–1651. ( 10.1021/jp003571m) [DOI] [Google Scholar]

[RSIF20130901C45] 45.Jang S, Newton M, Silbey R. 2004. Multichromophoric Förster resonance energy transfer. Phys. Rev. Lett. 92, 218301 ( 10.1103/PhysRevLett.92.218301) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C46] 46.Scholes GD. 2002. Designing light-harvesting antenna systems based on superradiant molecular aggregates. Chem. Phys. 275, 373–386. ( 10.1016/S0301-0104(01)00533-X) [DOI] [Google Scholar]

[RSIF20130901C47] 47.Olaya-Castro A, Lee C-F, Fassioli Olsen F, Johnson NF. 2008. Efficiency of energy transfer in a light-harvesting system under quantum coherence. Phys. Rev. B 78, 085115 ( 10.1103/PhysRevB.78.085115) [DOI] [Google Scholar]

[RSIF20130901C48] 48.Cao J, Silbey RJ. 2009. Optimization of exciton trapping in energy transfer processes. J. Phys. Chem. A 113, 13 825–13 838. ( 10.1021/jp9032589) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C49] 49.Fassioli F, Nazir A, Olaya-Castro A. 2010. Quantum state tuning of energy transfer in a correlated environment. J. Phys. Chem. Lett. 1, 2139–2143. ( 10.1021/jz100717d) [DOI] [Google Scholar]

[RSIF20130901C50] 50.Scholak T, Mintert F, Wellens T, Buchleitner A. 2010. Transport and entanglement. In Quantum efficiency in complex systems, part I: biomolecular systems (eds ER Weber, M Thorwart, U Würfel), pp. 1–38. Amsterdam, The Netherlands: Elsevier Inc. [Google Scholar]

[RSIF20130901C51] 51.Scholak T, De Melo F, Wellens T, Mintert F, Buchleitner A. 2011. Efficient and coherent excitation transfer across disordered molecular networks. Phys. Rev. E 83, 021912 ( 10.1103/PhysRevE.83.021912) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C52] 52.Hossein-Nejad H, Olaya-Castro A, Scholes GD. 2012. Phonon-mediated path-interference in electronic energy transfer. J. Chem. Phys. 136, 024112 ( 10.1063/1.3675844) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C53] 53.Lee H, Cheng Y-C, Fleming GR. 2007. Coherence dynamics in photosynthesis: protein protection of excitonic coherence. Science 316, 1462–1465. ( 10.1126/science.1142188) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C54] 54.Nalbach P, Eckel J, Thorwart M. 2010. Quantum coherent biomolecular energy transfer with spatially correlated fluctuations. New J. Phys. 12, 065043 ( 10.1088/1367-2630/12/6/065043) [DOI] [Google Scholar]

[RSIF20130901C55] 55.Wu J, Liu F, Shen Y, Cao J, Silbey RJ. 2010. Efficient energy transfer in light-harvesting systems, I: optimal temperature, reorganization energy and spatial–temporal correlations. New J. Phys. 12, 105012 ( 10.1088/1367-2630/12/10/105012) [DOI] [Google Scholar]

[RSIF20130901C56] 56.Strümpfer J, Schulten K. 2011. The effect of correlated bath fluctuations on exciton transfer. J. Chem. Phys. 134, 095102 ( 10.1063/1.3557042) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C57] 57.Ishizaki A, Fleming GR. 2009. Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature. Proc. Natl Acad. Sci. USA 106, 17 255–17 260. ( 10.1073/pnas.0908989106) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C58] 58.Olbrich C, Strümpfer J, Schulten K, Kleinekathöfer U. 2011. Quest for spatially correlated fluctuations in the FMO light-harvesting complex. J. Phys. Chem. B 115, 758–764. ( 10.1021/jp1099514) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C59] 59.Hemelrijk PW, Kwa SLS, van Grondelle R, Dekker JP. 1992. Spectroscopic properties of LHC-II, the main light-harvesting chlorophyll a/b protein complex from chloroplast membranes. Biochim. Biophys. Acta Bioenerg. 1098, 159–166. ( 10.1016/S0005-2728(05)80331-7) [DOI] [Google Scholar]

[RSIF20130901C60] 60.Szalay L, Tombácz E, Singhal GS. 1974. Effect of solvent on the absorption spectra and Stokes’ shift of absorption and fluorescence of chlorophylls. Acta Phys. Acad. Sci. Hungaricae 35, 29–36. ( 10.1007/BF03159738) [DOI] [Google Scholar]

[RSIF20130901C61] 61.Scholes GD, Fleming GR. 2005. Energy transfer and photosynthetic light harvesting. Adv. Chem. Phys. 132, 57–129. ( 10.1002/0471759309.ch2) [DOI] [Google Scholar]

[RSIF20130901C62] 62.Ishizaki A, Calhoun TR, Schlau-Cohen GS, Fleming GR. 2010. Quantum coherence and its interplay with protein environments in photosynthetic electronic energy transfer. Phys. Chem. Chem. Phys. 12, 7319–7337. ( 10.1039/C003389H) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C63] 63.Schröder M, Kleinekathöfer U, Schreiber M. 2006. Calculation of absorption spectra for light-harvesting systems using non-Markovian approaches as well as modified Redfield theory. J. Chem. Phys. 124, 084903 ( 10.1063/1.2171188) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C64] 64.Doust AB, Marai CNJ, Harrop SJ, Wilk KE, Curmi PMG, Scholes GD. 2004. Developing a structure-function model for the cryptophyte phycoerythrin 545 using ultrahigh resolution crystallography and ultrafast laser spectroscopy. J. Mol. Biol. 344, 135–153. ( 10.1016/j.jmb.2004.09.044) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C65] 65.Wendling M, Pullerits T, Przyjalgowski MA, Vulto SIE, Aartsma TJ, van Grondelle R, van Amerongen H. 2000. Electron-vibrational coupling in the Fenna–Matthews–Olson complex of Prosthecochloris aestuarii determined by temperature-dependent absorption and fluorescence line-narrowing measurements. J. Phys. Chem. B 104, 5825–5831. ( 10.1021/jp000077) [DOI] [Google Scholar]

[RSIF20130901C66] 66.Olbrich C, Strümpfer J, Schulten K, Kleinekathöfer U. 2011. Theory and simulation of the environmental effects on FMO electronic transitions. J. Phys. Chem. Lett. 2011, 1771–1776. ( 10.1021/jz2007676) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C67] 67.Kolli A, Reilly EJO, Scholes GD, Olaya-castro A. 2012. The fundamental role of quantized vibrations in coherent light harvesting by cryptophyte algae. J. Chem. Phys. 137, 174109 ( 10.1063/1.4764100) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C68] 68.Chin AW, Prior J, Rosenbach R, Caycedo-Soler F, Huelga SF, Plenio MB. 2013. The role of non-equilibrium vibrational structures in electronic coherence and recoherence in pigment–protein complexes. Nat. Phys. 9, 113–118. ( 10.1038/nphys2515) [DOI] [Google Scholar]

[RSIF20130901C69] 69.Cheng Y, Silbey R. 2006. Coherence in the B800 ring of purple bacteria LH2. Phys. Rev. Lett. 96, 028103 ( 10.1103/PhysRevLett.96.028103) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C70] 70.Jang S, Newton MD, Silbey RJ. 2007. Multichromophoric Förster resonance energy transfer from B800 to B850 in the light harvesting complex 2: evidence for subtle energetic optimization by purple bacteria. J. Phys. Chem. B 111, 6807–6814. ( 10.1021/jp070111l) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C71] 71.Hossein-Nejad H, Curutchet C, Kubica A, Scholes GD. 2011. Delocalization-enhanced long-range energy transfer between cryptophyte algae PE545 antenna proteins. J. Phys. Chem. A 115, 5243–5253. ( 10.1021/jp108397a) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C72] 72.Brumer P, Shapiro M. 2012. Molecular response in one-photon absorption via natural thermal light vs. pulsed laser excitation. Proc. Natl Acad. Sci. USA 109, 19 575–19 578. ( 10.1073/pnas.1211209109) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C73] 73.Fassioli F, Olaya-Castro A, Scholes GD. 2012. Coherent energy transfer under incoherent light conditions. J. Phys. Chem. Lett. 3, 3136–3142. ( 10.1021/jz3010317) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C74] 74.Kassal I, Yuen-Zhou J, Rahimi-Keshari S. 2013. Does coherence enhance transport in photosynthesis? J. Phys. Chem. Lett. 4, 362–367. ( 10.1021/jz301872b) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C75] 75.Davydov AS. 1948. Theory of absorption spectra of molecular crystals. Zhur. Eksptl. Teoret. Fiz. 18, 210–218. [Google Scholar]

[RSIF20130901C76] 76.Davydov AS. 1962. Theory of molecular excitons. [translated by M. Kasha and M. Oppenheimer, Jr.]. New York, NY: McGraw-Hill Book Company. [Google Scholar]

[RSIF20130901C77] 77.Kasha M. 1959. Relation between exciton bands and conduction bands in molecular lamellar systems. Rev. Mod. Phys. 31, 162–169. ( 10.1103/RevModPhys.31.162) [DOI] [Google Scholar]

[RSIF20130901C78] 78.Kasha M. 1963. Energy transfer mechanisms and the molecular exciton model for molecular aggregates. Radiat. Res. 20, 55–70. ( 10.2307/3571331c) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C79] 79.Kasha M, Rawls HR, Ashraf El-Bayoumi M. 1965. The exciton model in molecular spectroscopy. Pure Appl. Chem. 11, 371–392. ( 10.1351/pac196511030371) [DOI] [Google Scholar]

[RSIF20130901C80] 80.Shipman LL, Housman DL. 1979. Forster transfer rates for chlorophyll a. Photochem. Photobiol. 29, 1163–1167. ( 10.1111/j.1751-1097.1979.tb07835.x) [DOI] [Google Scholar]

[RSIF20130901C81] 81.Krueger BP, Scholes GD, Fleming GR. 1998. Calculation of couplings and energy-transfer pathways between the pigments of LH2 by the ab initio transition density cube method. J. Phys. Chem. B 102, 5378–5386. ( 10.1021/jp9811171) [DOI] [Google Scholar]

[RSIF20130901C82] 82.Scholes GD, Ghiggino KP, Oliver AM, Paddon-Row MN. 1993. Through-space and through-bond effects on exciton interactions in rigidly linked dinaphthyl molecules. J. Am. Chem. Soc. 115, 4345–4349. ( 10.1021/ja00063a061) [DOI] [Google Scholar]

[RSIF20130901C83] 83.May V, Kuhn O. 2005. Charge and energy transfer dynamics in molecular systems, 2nd edn Weinheim, Germany: Wiley-VCH. [Google Scholar]

[RSIF20130901C84] 84.Stratt RM. 1995. The instantaneous normal modes of liquids. Acc. Chem. Res. 28, 201–207. ( 10.1021/ar00053a001) [DOI] [Google Scholar]

[RSIF20130901C85] 85.Read EL, Schlau-Cohen GS, Engel GS, Georgiou T, Papiz MZ, Fleming GR. 2009. Pigment organization and energy level structure in light-harvesting complex 4: insights from two-dimensional electronic spectroscopy. J. Phys. Chem. B 113, 6495–6504. ( 10.1021/jp809713q) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C86] 86.Sauer K, Cogdell RJ, Prince SM, Freer A, Isaacs NW, Scheer H. 1996. Structure-based calculations of the optical spectra of the LH2 bacteriochlorophyll-protein complex from Rhodopseudomonas acidophila. Photochem. Photobiol. 64, 564–576. ( 10.1111/j.1751-1097.1996.tb03106.x) [DOI] [Google Scholar]

[RSIF20130901C87] 87.Yang M, Damjanović A, Vaswani HM, Fleming GR. 2003. Energy transfer in photosystem I of cyanobacteria Synechococcus elongatus: model study with structure-based semi-empirical Hamiltonian and experimental spectral density. Biophys. J. 85, 140–158. ( 10.1016/S0006-3495(03)74461-0) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C88] 88.Doust AB, Wilk KE, Curmi PMG, Scholes GD. 2006. The photophysics of cryptophyte light-harvesting. J. Photochem. Photobiol. A Chem. 184, 1–17. ( 10.1016/j.jphotochem.2006.06.006) [DOI] [Google Scholar]

[RSIF20130901C89] 89.Marin A, Doust AB, Scholes GD, Wilk KE, Curmi PMG, van Stokkum IHM, van Grondelle R. 2011. Flow of excitation energy in the cryptophyte light-harvesting antenna phycocyanin 645. Biophys. J. 101, 1004–1013. ( 10.1016/j.bpj.2011.07.012) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C90] 90.Freiberg A, Godik VI, Pullerits T, Timpmann K. 1989. Picosecond dynamics of directed excitation transfer in spectrally heterogeneous light-harvesting antenna of purple bacteria. Biochim. Biophys. Acta 973, 93–104. ( 10.1016/S0005-2728(89)80407-4) [DOI] [Google Scholar]

[RSIF20130901C91] 91.Wientjes E, Roest G, Croce R. 2012. From red to blue to far-red in Lhca4: how does the protein modulate the spectral properties of the pigments? Biochim. Biophys. Acta 1817, 711–717. ( 10.1016/j.bbabio.2012.02.030) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C92] 92.Van Amerongen H, Valkunas L, van Grondelle R. 2000. Photosynthetic excitons. Singapore: World Scientific Publishing. [Google Scholar]

[RSIF20130901C93] 93.Fowler GJ, Visschers RW, Grief GG, van Grondelle R, Hunter CN. 1992. Genetically modified photosynthetic antenna complexes with blueshifted absorbance bands. Nature 355, 848–850. ( 10.1038/355848a0) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C94] 94.Novoderezhkin VI, Palacios MA, van Amerongen H, van Grondelle R. 2005. Excitation dynamics in the LHCII complex of higher plants: modeling based on the 2.72 Angstrom crystal structure. J. Phys. Chem. B 109, 10 493–10 504. ( 10.1021/jp044082f) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C95] 95.Silbey R, Harris RA. 1984. Variational calculation of the dynamics of a two level system interacting with a bath. J. Chem. Phys. 80, 2615–2617. ( 10.1063/1.447055) [DOI] [Google Scholar]

[RSIF20130901C96] 96.Meier T, Zhao Y, Chernyak V, Mukamel S, Introduction I. 1997. Polarons, localization, and excitonic coherence in superradiance of biological antenna complexes. J. Chem. Phys. 107, 3876–3893. ( 10.1063/1.474746) [DOI] [Google Scholar]

[RSIF20130901C97] 97.Silbey R. 2011. Description of quantum effects in the condensed phase. Procedia Chem. 3, 188–197. ( 10.1016/j.proche.2011.08.026) [DOI] [Google Scholar]

[RSIF20130901C98] 98.Yena T-C, Cheng Y-C. 2011. Electronic coherence effects in photosynthetic light harvesting. Procedia Chem. 3, 211–221. ( 10.1016/j.proche.2011.08.028) [DOI] [Google Scholar]

[RSIF20130901C99] 99.Kolli A, Nazir A, Olaya-Castro A. 2011. Electronic excitation dynamics in multichromophoric systems described via a polaron-representation master equation. J. Chem. Phys. 135, 154112 ( 10.1063/1.3652227) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C100] 100.Grondelle R, Van Novoderezhkin V. 2001. Dynamics of excitation energy transfer in the LH1 and LH2 light-harvesting complexes of photosynthetic bacteria. Biochemistry 40, 15 057–15 068. ( 10.1021/bi0018943) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C101] 101.Novoderezhkin VI, Rutkauskas D, van Grondelle R. 2006. Dynamics of the emission spectrum of a single LH2 complex: interplay of slow and fast nuclear motions. Biophys. J. 90, 2890–2902. ( 10.1529/biophysj.105.072652) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C102] 102.Fassioli F, Olaya-Castro A. 2010. Distribution of entanglement in light-harvesting complexes and their quantum efficiency. New J. Phys. 12, 085006 ( 10.1088/1367-2630/12/8/085006) [DOI] [Google Scholar]

[RSIF20130901C103] 103.Sarovar M, Ishizaki A, Fleming GR, Whaley KB. 2010. Quantum entanglement in photosynthetic light-harvesting complexes. Nat. Phys. 6, 462–467. ( 10.1038/nphys1652) [DOI] [Google Scholar]

[RSIF20130901C104] 104.Olaya-Castro A, Fassioli F. 2011. Characterizing quantum-sharing of electronic excitation in molecular aggregates. Procedia Chem. 3, 176–184. ( 10.1016/j.proche.2011.08.024) [DOI] [Google Scholar]

[RSIF20130901C105] 105.Whaley KB, Sarovar M, Ishizaki A. 2011. Quantum entanglement phenomena in photosynthetic light harvesting complexes. Procedia Chem. 3, 152–164. ( 10.1016/j.proche.2011.08.021) [DOI] [Google Scholar]

[RSIF20130901C106] 106.Smyth C, Fassioli F, Scholes GD. 2012. Measures and implications of electronic coherence in photosynthetic light-harvesting. Phil. Trans. R. Soc. A 370, 3728–3749. ( 10.1098/rsta.2011.0420) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C107] 107.Tiersch M, Popescu S, Briegel HJ. 2012. A critical view on transport and entanglement in models of photosynthesis. Phil. Trans. R. Soc. A 370, 3771–3786. ( 10.1098/rsta.2011.0202) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C108] 108.Breuer H-P, Petruccione F. 2002. The theory of open quantum systems. Oxford, UK: Oxford University Press. [Google Scholar]

[RSIF20130901C109] 109.Ritz T, Park S, Schulten K. 2001. Kinetics of excitation migration and trapping in the photosynthetic unit of purple bacteria. J. Phys. Chem. B 105, 8259–8267. ( 10.1021/jp011032r) [DOI] [Google Scholar]

[RSIF20130901C110] 110.Panitchayangkoon G, Hayes D, Fransted KA, Caram JR, Harel E, Wen J, Blankenship RE, Engel GS. 2010. Long-lived quantum coherence in photosynthetic complexes at physiological temperature. Proc. Natl Acad. Sci. USA 107, 12 766–12 770. ( 10.1073/pnas.1005484107) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C111] 111.Ishizaki A, Fleming GR. 2009. Unified treatment of quantum coherent and incoherent hopping dynamics in electronic energy transfer: reduced hierarchy equation approach. J. Chem. Phys. 130, 234111 ( 10.1063/1.3155372) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C112] 112.Roden J, Eisfeld A, Wolff W, Strunz WT. 2009. Influence of complex exciton-phonon coupling on optical absorption and energy transfer of quantum aggregates. Phys. Rev. Lett. 103, 058301 ( 10.1103/PhysRevLett.103.058301) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C113] 113.Nalbach P, Thorwart M. 2010. Multiphonon transitions in the biomolecular energy transfer dynamics. J. Chem. Phys. 132, 194111 ( 10.1063/1.3428385) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C114] 114.Huo P, Coker DF. 2010. Iterative linearized density matrix propagation for modeling coherent excitation energy transfer in photosynthetic light harvesting. J. Chem. Phys. 133, 184108 ( 10.1063/1.3498901) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C115] 115.Jang S. 2011. Theory of multichromophoric coherent resonance energy transfer: a polaronic quantum master equation approach. J. Chem. Phys. 135, 034105 ( 10.1063/1.3608914) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C116] 116.Womick JM, Moran AM. 2011. Vibronic enhancement of exciton sizes and energy transport in photosynthetic complexes. J. Phys. Chem. B 115, 1347–1356. ( 10.1021/jp106713q) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C117] 117.Nalbach P, Thorwart M. 2012. The role of discrete molecular modes in the coherent exciton dynamics in FMO. J. Phys. B At. Mol. Opt. Phys. 45, 154009 ( 10.1088/0953-4075/45/15/154009) [DOI] [Google Scholar]

[RSIF20130901C118] 118.Roden J, Strunz WT, Whaley KB, Eisfeld A. 2012. Accounting for intra-molecular vibrational modes in open quantum system description of molecular systems. J. Chem. Phys. 137, 204110 ( 10.1063/1.4765329) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C119] 119.Shi Q, Chen L, Nan G, Xu R-X, Yan Y. 2009. Efficient hierarchical Liouville space propagator to quantum dissipative dynamics. J. Chem. Phys. 130, 084105 ( 10.1063/1.3077918) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C120] 120.Kneip C, Parbel A, Foerstendorf H, Scheer H, Siebert F. 1998. Fourier transform near-infrared resonance Raman spectroscopic study of the a-subunit of phycoerythrocyanin and phycocyanin from the cyanobacterium Mastigocladus laminosus. J. Raman Spectrosc. 944, 939–944. () [DOI] [Google Scholar]

[RSIF20130901C121] 121.Hybl JD, Albrecht AW, Gallagher Faeder SM, Jonas DM. 1998. Two-dimensional electronic spectroscopy. Chem. Phys. Lett. 297, 307–313. ( 10.1016/S0009-2614(98)01140-3) [DOI] [Google Scholar]

[RSIF20130901C122] 122.Cundiff ST, Bristow AD, Siemens M, Li H, Moody G, Karaiskaj D, Dai X, Zhang T. 2012. Optical 2-D Fourier transform spectroscopy of excitons in semiconductor nanostructures. IEEE J. Sel. Top. Quantum Electron. 18, 318–328. ( 10.1109/JSTQE.2011.2123876) [DOI] [Google Scholar]

[RSIF20130901C123] 123.Lewis KLM, Ogilvie JP. 2012. Probing photosynthetic energy and charge transfer with two-dimensional electronic spectroscopy. J. Phys. Chem. Lett. 3, 503–510. ( 10.1021/jz201592v) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C124] 124.Anna JM, Song Y, Dinshaw R, Scholes GD. 2013. Two-dimensional electronic spectroscopy for mapping molecular photophysics. Pure Appl. Chem. 85, 1307–1319. ( 10.1351/PAC-CON-12-10-21) [DOI] [Google Scholar]

[RSIF20130901C125] 125.Tokmakoff A. 2000. Two-dimensional line shapes derived from coherent third-order nonlinear spectroscopy. J. Phys. Chem. A 104, 4247–4255. ( 10.1021/jp993207r) [DOI] [Google Scholar]

[RSIF20130901C126] 126.Hochstrasser RM. 2007. Two-dimensional spectroscopy at infrared and optical frequencies. Proc. Natl Acad. Sci. USA 104, 14 190–14 196. ( 10.1073/pnas.0704079104) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C127] 127.Khalil M, Demirdoven N, Tokmakoff A. 2003. Obtaining absorptive line shapes in two-dimensional infrared vibrational correlation spectra. Phys. Rev. Lett. 90, 047401 ( 10.1103/PhysRevLett.90.047401) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C128] 128.Mukamel S. 1995. Principles of nonlinear optical spectroscopy. New York, NY: Oxford University Press. [Google Scholar]

[RSIF20130901C129] 129.Cho M. 2008. Coherent two-dimensional optical spectroscopy. Chem. Rev. 108, 1331–1418. ( 10.1021/cr078377b) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C130] 130.Mukamel S. 2000. Multidimensional femtosecond correlation spectroscopies of electronic and vibrational excitations. Annu. Rev. Phys. Chem. 51, 691–729. ( 10.1146/annurev.physchem.51.1.691) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C131] 131.Abramavicius D, Palmieri B, Voronine DV, Sanda F, Mukamel S. 2009. Coherent multidimensional optical spectroscopy of excitons in molecular aggregates; quasiparticle versus supermolecule perspectives. Chem. Rev. 109, 2350–2408. ( 10.1021/cr800268n) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C132] 132.Turner DB, Hassan Y, Scholes GD. 2012. Exciton superposition states in CdSe nanocrystals measured using broadband two-dimensional electronic spectroscopy. Nano Lett. 12, 880–886. ( 10.1021/nl2039502) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C133] 133.Nemeth A, Milota F, Mančal T, Lukeš V, Hauer J, Kauffmann HF, Sperling J. 2010. Vibrational wave packet induced oscillations in two-dimensional electronic spectra. I. Experiments. J. Chem. Phys. 132, 184514 ( 10.1063/1.3404404) [DOI] [Google Scholar]

[RSIF20130901C134] 134.Mančal T, Nemeth A, Milota F, Lukeš V, Kauffmann HF, Sperling J. 2010. Vibrational wave packet induced oscillations in two-dimensional electronic spectra. II. Theory. J. Chem. Phys. 132, 184515 ( 10.1063/1.3404405) [DOI] [Google Scholar]

[RSIF20130901C135] 135.Egorova D. 2008. Detection of electronic and vibrational coherences in molecular systems by 2D electronic photon echo spectroscopy. Chem. Phys. 347, 166–176. ( 10.1016/j.chemphys.2007.12.019) [DOI] [Google Scholar]

[RSIF20130901C136] 136.Turner DB, Wilk KE, Curmi PMG, Scholes GD. 2011. Comparison of electronic and vibrational coherence measured by two-dimensional electronic spectroscopy. J. Phys. Chem. Lett. 2, 1904–1911. ( 10.1021/jz200811p) [DOI] [Google Scholar]

[RSIF20130901C137] 137.Hayes D, Wen J, Panitchayangkoon G, Blankenship RE, Engel GS. 2011. Robustness of electronic coherence in the Fenna–Matthews–Olson complex to vibronic and structural modifications. Faraday Discuss. 150, 459–469. ( 10.1039/c0fd00030b) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C138] 138.Chachisvilis M, Kuhn O, Pullerits T, Sundstrom V. 1997. Excitons in photosynthetic purple bacteria: wavelike motion or incoherent hopping? J. Phys. Chem. B 101, 7275–7283. ( 10.1021/jp963360a) [DOI] [Google Scholar]

[RSIF20130901C139] 139.Savikhin S, Buck DR, Struve WS. 1997. Oscillating anisotropies in a bacteriochlorophyll protein: evidence for quantum beating between exciton levels. Chem. Phys. 223, 303–312. ( 10.1016/S0301-0104(97)00223-1) [DOI] [Google Scholar]

[RSIF20130901C140] 140.Engel GS, Calhoun TR, Read EL, Ahn T-K, Mancal T, Cheng Y-C, Blankenship RE, Fleming GR. 2007. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 446, 782–786. ( 10.1038/nature05678) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C141] 141.Calhoun TR, Ginsberg NS, Schlau-Cohen GS, Cheng Y-C, Ballottari M, Bassi R, Fleming GR. 2009. Quantum coherence enabled determination of the energy landscape in light-harvesting complex II. J. Phys. Chem. B 113, 16 291–16 295. ( 10.1021/jp908300c) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C142] 142.Collini E, Wong CY, Wilk KE, Curmi PMG, Brumer P, Scholes GD. 2010. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature 463, 644–647. ( 10.1038/nature08811) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C143] 143.Wong CY, Alvey RM, Turner DB, Wilk KE, Bryant DA, Curmi PMG, Silbey RJ, Scholes GD. 2012. Electronic coherence lineshapes reveal hidden excitonic correlations in photosynthetic light harvesting. Nat. Chem. 4, 396–404. ( 10.1038/nchem.1302) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C144] 144.Wedemayer GJ, Kidd DG, Glazer AN. 1996. Cryptomonad biliproteins: bilin types and locations. Photosynth. Res. 48, 163–170. ( 10.1007/BF00041006) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C145] 145.Harrop ASJ, et al. Submitted Evolution of cryptophyte light harvesting proteins: a structural switch that controls energy transfer. [Google Scholar]

[RSIF20130901C146] 146.Turner DB, Dinshaw R, Lee K-K, Belsley MS, Wilk KE, Curmi PMG, Scholes GD. 2012. Quantitative investigations of quantum coherence for a light-harvesting protein at conditions simulating photosynthesis. Phys. Chem. Chem. Phys. 14, 4857–4874. ( 10.1039/c2cp23670b) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C147] 147.Christensson N, Milota F, Hauer J, Sperling J, Bixner O, Nemeth A, Kauffmann HF. 2011. High frequency vibrational modulations in two-dimensional electronic spectra and their resemblance to electronic coherence signatures. J. Phys. Chem. B 115, 5383–5391. ( 10.1021/jp109442b) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C148] 148.Tiwari V, Peters WK, Jonas DM. 2013. Electronic resonance with anticorrelated pigment vibrations drives photosynthetic energy transfer outside the adiabatic framework. Proc. Natl Acad. Sci. USA 110, 1203–1208. ( 10.1073/pnas.1211157110) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C149] 149.Cheng Y-C, Fleming GR. 2008. Coherence quantum beats in two-dimensional electronic spectroscopy. J. Phys. Chem. A 112, 4254–4260. ( 10.1021/jp7107889) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C150] 150.Butkus V, Zigmantas D, Valkunas L, Abramavicius D. 2012. Vibrational vs. electronic coherences in 2D spectrum of molecular systems. Chem. Phys. Lett. 545, 40–43. ( 10.1016/j.cplett.2012.07.014) [DOI] [Google Scholar]

[RSIF20130901C151] 151.Richards GH, Wilk KE, Curmi PMG, Quiney M, Davis JA. 2012. Coherent vibronic coupling in light-harvesting complexes from photosynthetic marine algae. J. Phys. Chem. Lett. 3, 272–277. ( 10.1021/jz201600f) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C152] 152.Yuen-Zhou J, Krich JJ, Aspuru-Guzik A. 2012. A witness for coherent electronic vs vibronic-only oscillations in ultrafast spectroscopy. J. Chem. Phys. 136, 234501 ( 10.1063/1.4725498) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C153] 153.Fragnito HL, Bigot J-Y, Becker PC, Shank CV. 1989. Evolution of the vibronic absorption spectrum in a molecule following impulsive excitation with a 6 fs optical pulse. Chem. Phys. Lett. 160, 101–104. ( 10.1016/0009-2614(89)87564-5) [DOI] [Google Scholar]

[RSIF20130901C154] 154.Pollard WT, Fragnito HL, Bigot J-Y, Shank CV, Mathies RA. 1990. Quantum-mechanical theory for 6 fs dynamic absorption spectroscopy and its application to nile blue. Chem. Phys. Lett. 168, 239–245. ( 10.1016/0009-2614(90)85603-A) [DOI] [Google Scholar]

[RSIF20130901C155] 155.Jonas DM, Fleming GR. 1995. Vibrationally abrupt pulses in pump-probe spectroscopy. In Ultrafast processes in chemistry and photobiology (chemistry in the 21st century series IUPAC) (eds El-Sayed MA, Tanaka I, Molin Y.), pp. 225–256. Oxford, UK: Blackwell Science. [Google Scholar]

[RSIF20130901C156] 156.Fulton RL, Gouterman M. 1961. Vibronic coupling. I. Mathematical treatment for two electronic states. J. Chem. Phys. 35, 1059 ( 10.1063/1.1701181) [DOI] [Google Scholar]

[RSIF20130901C157] 157.Christensson N, Kauffmann HF, Pullerits T, Mančal T. 2012. Origin of long-lived coherences in light-harvesting complexes. J. Phys. Chem. B 116, 7449–7454. ( 10.1021/jp304649c) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSIF20130901C158] 158.Heid CG, Ottiger P, Leist R, Leutwyler S. 2011. The S1/S2 exciton interaction in 2-pyridone·6-methyl-2-pyridone: Davydov splitting, vibronic coupling, and vibronic quenching. J. Chem. Phys. 135, 154311 ( 10.1063/1.3652759) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C159] 159.Ottiger P, Leutwyler S, Köppel H. 2012. Vibrational quenching of excitonic splittings in H-bonded molecular dimers: the electronic Davydov splittings cannot match experiment. J. Chem. Phys. 136, 174308 ( 10.1063/1.4705119) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C160] 160.Mohseni M, Rebentrost P, Lloyd S, Aspuru-Guzik A. 2008. Environment-assisted quantum walks in photosynthetic energy transfer. J. Chem. Phys. 129, 174106 ( 10.1063/1.3002335) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C161] 161.Plenio MB, Huelga SF. 2008. Dephasing-assisted transport: quantum networks and biomolecules. New J. Phys. 10, 113019 ( 10.1088/1367-2630/10/11/113019) [DOI] [Google Scholar]

[RSIF20130901C162] 162.Caruso F, Chin AW, Datta A, Huelga SF, Plenio MB. 2009. Highly efficient energy excitation transfer in light-harvesting complexes: the fundamental role of noise-assisted transport. J. Chem. Phys. 131, 105106 ( 10.1063/1.3223548) [DOI] [Google Scholar]

[RSIF20130901C163] 163.Fassioli F, Oblinsky DG, Scholes GD. 2013. Designs for molecular circuits that use electronic coherence. Faraday Discuss. 163, 341–351. ( 10.1039/c3fd00009e) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C164] 164.Mančal T, Valkunas L. 2010. Exciton dynamics in photosynthetic complexes: excitation by coherent and incoherent light. New J. Phys. 12, 065044 ( 10.1088/1367-2630/12/6/065044) [DOI] [Google Scholar]

[RSIF20130901C165] 165.Jiang X, Brumer P. 1991. Creation and dynamics of molecular states prepared with coherent vs partially coherent pulsed light. J. Chem. Phys. 94, 5833–5843. ( 10.1063/1.460467) [DOI] [Google Scholar]

[RSIF20130901C166] 166.Kistiakowsky GB, Parmenter CS. 1965. Effects of pressure on fluorescence and intersystem crossing in benzene vapor. J. Chem. Phys. 42, 2942–2948. ( 10.1063/1.1703267) [DOI] [Google Scholar]

[RSIF20130901C167] 167.Watts RJ, Strickler SJ. 1966. Fluorescence and internal conversion in naphthalene vapor. J. Chem. Phys. 44, 2423–2426. ( 10.1063/1.1727059) [DOI] [Google Scholar]

[RSIF20130901C168] 168.Bixon M, Jortner J. 1968. Intramolecular radiationless transitions. J. Chem. Phys. 48, 715–726. ( 10.1063/1.1668703) [DOI] [Google Scholar]

[RSIF20130901C169] 169.Englman R, Jortner J. 1970. The energy gap law for radiationless transitions in large molecules. Mol. Phys. 18, 145–164. ( 10.1080/00268977000100171) [DOI] [Google Scholar]

[RSIF20130901C170] 170.Turner DB, Arpin PC, McClure SD, Ulness DJ, Scholes GD. 2013. Coherent multidimensional optical spectra measured using incoherent light. Nat. Commun. 4, 2298 ( 10.1038/ncomms3298) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C171] 171.Turner DB, Howey DJ, Sutor EJ, Hendrickson RA, Gealy MW, Ulness DJ. 2013. Two-dimensional electronic spectroscopy using incoherent light: theoretical analysis. J. Phys. Chem. A 117, 5926–5954. ( 10.1021/jp310477y) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C172] 172.Morita N, Yajima T. 1984. Ultrahigh-time-resolution coherent transient spectroscopy with incoherent light. Phys. Rev. A 30, 2525–2536. ( 10.1103/PhysRevA.30.2525) [DOI] [Google Scholar]

[RSIF20130901C173] 173.Beach R, Hartmann S. 1984. Incoherent photon echoes. Phys. Rev. Lett. 53, 663–666. ( 10.1103/PhysRevLett.53.663) [DOI] [Google Scholar]

[RSIF20130901C174] 174.Asaka S, Nakatsuka H, Fujiwara M, Matsuoka M. 1984. Accumulated photon echoes with incoherent light in Nd³⁺-doped silicate glass. Phys. Rev. A 29, 2286–2289. ( 10.1103/PhysRevA.29.2286) [DOI] [Google Scholar]

[RSIF20130901C175] 175.Tomita M, Matsuoka M. 1986. Ultrafast pump-probe measurement using intensity correlation of incoherent light. J. Opt. Soc. Am. B 3, 560–563. ( 10.1364/JOSAB.3.000560) [DOI] [Google Scholar]

[RSIF20130901C176] 176.Ulness DJ. 2003. On the role of classical field time correlations in noisy light spectroscopy: color locking and a spectral filter analogy. J. Phys. Chem. A 107, 8111–8123. ( 10.1021/jp0222494) [DOI] [Google Scholar]

[RSIF20130901C177] 177.Hildner R, Brinks D, van Hulst NF. 2010. Femtosecond coherence and quantum control of single molecules at room temperature. Nat. Phys. 7, 172–177. ( 10.1038/nphys1858) [DOI] [Google Scholar]

[RSIF20130901C178] 178.Hildner R, Brinks D, Nieder JB, Cogdell RJ, van Hulst NF. 2013. Quantum coherent energy transfer over varying pathways in single light-harvesting complexes. Science 340, 1448–1451. ( 10.1126/science.1235820) [DOI] [PubMed] [Google Scholar]

[RSIF20130901C179] 179.Dong H, Fleming GR. 2013. Three-pulse photon echo of finite numbers of molecules: single-molecule traces. J. Phys. Chem. B 117, 11 318–11 325. ( 10.1021/jp402768c) [DOI] [PubMed] [Google Scholar]

PERMALINK

Photosynthetic light harvesting: excitons and coherence

Francesca Fassioli

Rayomond Dinshaw

Paul C Arpin

Gregory D Scholes

Abstract

1. Introduction

Figure 1.

1.1. Energy transfer and the question of coherence

2. Photosynthetic excitons

Figure 2.

2.1. The technical language of excitons

2.2. Electronic structure of excitons

2.2.1. Sources of exciton localization

Figure 3.

2.3. Quantifying exciton delocalization

3. Excitation dynamics and the regimes of energy transfer

3.1. Detailed explanation

3.2. Coherent exciton dynamics and non-equilibrium phonons

Figure 4.

4. Two-dimensional electronic spectroscopy

4.1. Ultrafast spectroscopic measurements

4.2. Interpreting two-dimensional electronic spectra

Figure 5.

Figure 6.

4.3. Experimental evidence: electronic and vibrational coherence in photosynthetic light-harvesting proteins

Figure 7.

4.4. Towards more realistic models for vibronic coherence

5. Coherent excitation dynamics: what it means for light harvesting

5.1. How excitation conditions matter

Figure 8.

5.2. What we have learned from two-dimensional electronic spectroscopy and a wish list for new experiments

5.3. What we conclude for photosynthetic light harvesting

Funding statement

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases