Alignment of crystal orientations of the multi-domain photonic crystals in Parides sesostris wing scales

Abstract

It is known that the wing scales of the emerald-patched cattleheart butterfly, Parides sesostris, contain gyroid-type photonic crystals, which produce a green structural colour. However, the photonic crystal is not a single crystal that spreads over the entire scale, but it is separated into many small domains with different crystal orientations. As a photonic crystal generally has band gaps at different frequencies depending on the direction of light propagation, it seems mysterious that the scale is observed to be uniformly green under an optical microscope despite the multi-domain structure. In this study, we have carefully investigated the structure of the wing scale and discovered that the crystal orientations of different domains are not perfectly random, but there is a preferred crystal orientation that is aligned along the surface normal of the scale. This finding suggests that there is an additional factor during the developmental process of the microstructure that regulates the crystal orientation.

1. Introduction

A three-dimensional periodic lattice known as a photonic crystal has attracted a considerable amount of attention for a few decades [1]. Photonic crystals have been studied because of the fundamental interest in the physical properties of light inside such materials [2], and many studies have been carried out to apply their capability of controlling the propagation of light to various applications such as low-threshold lasers [3,4] and photonic chips [5,6]. However, it is still difficult to fabricate photonic crystals with a period that is comparable to the wavelength of light. By contrast, some insects are known to possess naturally occurring photonic crystals for their colorations [7,8]; weevils are one such group of insects [9–14], and butterflies are another group that have been extensively studied. For example, some species of lycaenids (Callophrys rubi [15], Cyanophrys remus [16] and Callophrys dumetorum [17]) and papilionids (Parides sesostris [18] and Teinopalpus imperialis [19]) have been reported to have a photonic crystal structure inside their wing scales. These structures produce brilliant structural colours [20–24], which are presumably thought to serve as a tool for communication. It is quite interesting to learn how these natural photonic crystals develop and also to consider using them as a template for an inorganic photonic crystal that has a higher refractive index than biomaterials.

Exact identification of photonic crystal structures inside butterfly wing scales is a difficult task because of the complicated network topology. Recently, Michielsen & Stavenga [25] carefully compared cross-sectional images of the wing scales observed by transmission electron microscopy (TEM) with computer-generated patterns assuming several structural models. They concluded from the reasonable matching in the patterns that the photonic crystals of a wing scale have a gyroid-type structure [26], which is a type of cubic-structure group that consists of two interconnecting channels comprising different materials. This structural identification has been later confirmed by small-angle X-ray scattering using synchrotron radiation [27] and also by electron tomography [28].

The photonic crystals inside these wing scales are not a single crystal that spreads over the entire scale, but they are separated into many small domains with different crystal orientations. This multi-domain structure can largely affect the optical properties of the scale, because a photonic crystal generally has band gaps for different frequency ranges depending on the direction of propagating light. Hence, the wavelength of reflection can differ from domain to domain [29]. It has been reported for gyroid-type photonic crystals that band gaps appear for the frequency ranges along the three primary directions of the cubic crystal, [100], [110] and [111], corresponding to blue, green and violet or ultraviolet colours, respectively, with the structural parameters obtained for a butterfly [30,31]. In fact, the matte green scales of Cy. remus [16] and Ca. dumetorum [17,27] have been observed to consist of gleaming patches with different colours and intensities under an optical microscope. This appearance seems consistent with the multi-domain structure, where the exposed surfaces of domains are characterized by different Miller indices.

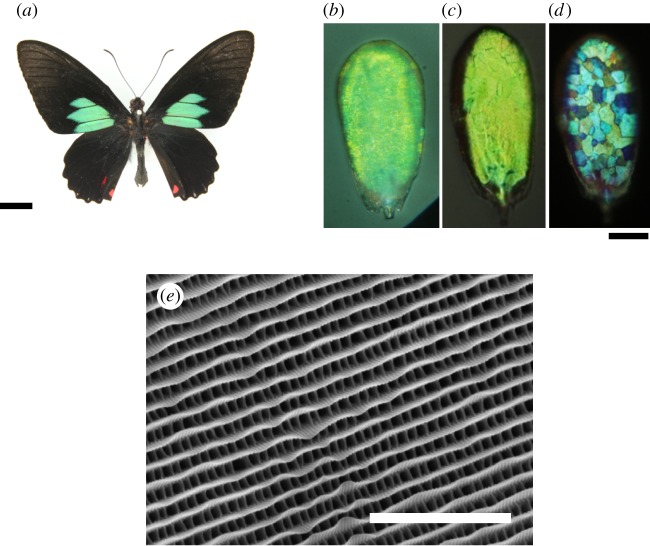
The emerald-patched cattleheart butterfly, P. sesostris, shown in figure 1a, is another species that has been reported to have a gyroid-type photonic crystal [25]. The scales of this butterfly produce a green structural colour in patches on the forewings. However, a simple microscopic observation poses a puzzle: the scale appears to be nearly uniformly green or yellow-green, as shown in figure 1b. This appearance seems to contradict the multi-domain structure of the photonic crystal that has been observed previously [22,30,31]. It has been reported that part of the scale structure, called a honeycomb, located above the photonic crystals has an optical property that suppresses iridescence [30]. In addition, Wilts et al. [31] reported that the honeycomb contains pigments that have a maximum absorbance of light at a wavelength of 395 nm. These pigments are considered to function as a spectral filter, which helps the scale appear as a uniform colour by absorbing light with shorter wavelengths. However, if the crystal orientations are random among the different domains, a large intensity variation in the green colour is still expected owing to the different band-gap frequencies.

Figure 1.

The emerald-patched cattleheart butterfly, Parides sesostris. (a) Dorsal side. (b–d) Single cover scale taken from the green patch of the forewing. The scale is observed under an optical microscope upside up without using polarizers (b), while it is observed upside down with a parallel (c) and crossed (d) polarizer and analyser. (e) SEM image of the surface of the cover scale. Scale bars: (a) 1 cm, (b–d) 25 μm and (e) 6 μm.

To reconcile these seemingly contradictory observations, we carefully investigated the structure of the wing scale of P. sesostris; the scale was thin-sectioned in three orthogonal planes and observed by TEM. In addition, the honeycomb part was removed to directly observe the exposed surface of the photonic crystal. We discovered a simple answer for the puzzle: the crystal orientations of the different domains are not perfectly random, but there is a preferred direction that orients the domains along the surface normal of the scale.

2. Material and methods

Specimens of the butterfly P. sesostris were purchased from an insect specimen supplier (Russel, Japan). The arrangements of the wing scales were observed by using a stereo microscope (Olympus SZX16). The scale morphology was investigated by scanning electron microscopy (SEM, Hitachi S-4800) and TEM (Hitachi H-7650). A small piece of the green patch on the dorsal side of the forewing was coated with Os using a Meiwaforsis Neoc osmium coater before SEM observation in order to increase electronic conductivity. For TEM observation, the sample was embedded in epoxy resin after a dehydration procedure using ethanol. The resin block was thin-sectioned to approximately 70 nm using an ultramicrotome.

To directly observe the top surface of the gyroid-type photonic crystal, the upper part of the scale (honeycomb) consisting of scale structures called ridges and crossribs was removed by using a pulled glass micropipette under an optical microscope (Olympus BX51). The glass pipette was precisely positioned and manipulated by using a manipulator (Narishige MMO-203). Gently touching the scale surface with the micropipette sometimes resulted in the removal of ridges and crossribs. This removal was later confirmed by using SEM.

A microscatterometer was used to examine the direction of reflected light from a single domain of the photonic crystal. The optical set-up for the microscatterometer was previously described in detail [32]. In brief, the back focal plane of the objective lens in the optical microscope (Olympus BX51) was observed by a CCD camera through a macro zoom lens, because the light intensity pattern from this plane is considered to be the far-field pattern of reflection. A high-power dry objective lens (Olympus MPLFLN100×, NA 0.9) was chosen to examine a single domain having a size of 5–10 μm. A small pinhole of 100 μm in diameter was placed on the plane of the field stop of the microscope, which resulted in an illumination spot size of approximately 2 μm in diameter on the sample. Another pinhole with a diameter of 50 μm was placed in the plane of the aperture stop of the microscope such that the epi-illumination was nearly collimated.

Computer graphics of the gyroid-type structure were created by using commercial software (Mathematica, Wolfram Research). It is known that the gyroid-type structure is approximately expressed by the following formula [26]:

2.1

where x, y and z are spatial coordinates; and a is the lattice constant of the cubic unit cell. A spatial position (x,y,z) satisfying the above inequality is filled with a biomaterial cuticle, while the rest of the region is air. Thus, the parameter t on the right-hand side directly relates to the volume fraction of the cuticle. This parameter was set to a previously reported value, t = −0.3 [25], which corresponds to a volume fraction of 0.40. In this coordinate system, the planes with constant x are parallel to the (100) plane of the photonic crystal. To model the surface morphologies with other Miller indices, the spatial coordinates were rotated. For example, the coordinate system was rotated to create a constant x′ plane parallel to the (110) surface as follows:

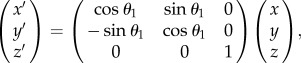2.2

where θ₁ is 45° (the angle between the [100] and [110] directions). When the (111) plane was investigated, a subsequent transformation was performed as follows:

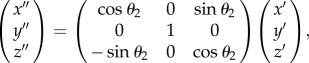2.3

where 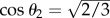holds for θ₂, which is the angle between the [110] and [111] directions. After this rotation, the (111) plane becomes parallel to the constant x″ planes. We investigated the surface morphologies of not only the three primary directions of the cubic crystal but other directions with large Miller-index values by using different rotation angles in the above coordinate rotations.

3. Results

In general, there are two types of scale layers on a butterfly wing: a layer of overlapping cover scales and a layer of underlying ground scales. On the forewings of P. sesostris, the brilliant green colour is due to the cover scales, which exist above the highly pigmented black ground scales. A cover scale is observed to be uniformly green or yellow-green, as shown in figure 1b, with typical sizes of 100 μm in length and 50 μm in width. When the scale is turned upside down and observed under epi-illumination, the reflection becomes more intense with a uniform yellow-green colour (figure 1c). On the other hand, under a crossed polarizer and analyser, an interesting tessellated pattern is observed (as shown in figure 1d) as previously reported [31,33]. However, the reflection intensity under the crossed polarizer and analyser is much weaker than under the parallel polarizer and analyser. Thus, we first focus our attention on the uniform yellow-green colour observed under natural polarization conditions. SEM reveals that there are longitudinal ridges on the scale surface, as shown in figure 1e. They are regularly spaced by about 0.8 μm. In addition, a type of structure called a crossrib [18] is observed; many crossribs connect adjacent ridges, and the separation between crossribs is 0.4–0.6 μm.

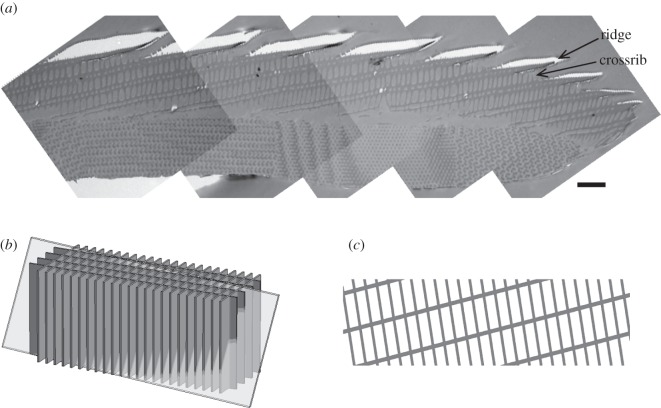
The cross section of the cover scale was observed using TEM, as shown in figure 2a. The upper layer consists of the ridges and crossribs, while the lower layer exhibits peculiar patterns corresponding to a photonic crystal. A two-dimensional section of a three-dimensional network can have a complicated pattern that depends on how it is sectioned, as reported previously [18,25,30,33]. Several different patterns in the lower layer confirm the multi-domain nature of the photonic crystal.

Figure 2.

Cross section of the cover scale. (a) Combined TEM images. Scale bar, 2 μm. (b) Cross-sectional images of the gyroid-type structure obtained by computer modelling. The images are calculated under the assumption that the [110] direction is nearly along the surface normal of the scale. The sectioning planes are specified by two angles α and β; we first consider the x′−y′ plane as the original sectioning plane (see figure 7b and equation (2.2) for the definitions of the coordinates), which has the normal vector n along the z′-axis. Next, the plane is rotated by an angle α with the axis of rotation along the x′-axis so that n is still in the y′−z′ plane, and the angle from the z′-axis is α. Finally, the plane is tilted such that n moves away from the x′-axis by an angle β, making the angle between the x′-axis and n to be β + 90°. The pairs of the two angles (α,β) are (−10°, 5°), (25°, 5°), (−128°, 5°) and (145°, 2°) in the images from left to right, respectively. The small value of β confirms that the [110] direction is nearly along the surface normal of the scale.

It is found that the upper layer is better characterized in a different sectioning plane, as shown in figure 3a, where the scale is sectioned nearly longitudinally. The upper layer looks like an oblique lattice; ridges are observed as oblique lines, and each ridge appears as double lines owing to the internal air voids inside it. A similar air-void structure has been previously reported for a different species of butterfly [34], because the ridges form as folds of the outer layer of the developing scale cuticle and the section is catching these folds partway down from their tops. Many crossribs are observed as vertical short lines between ridges. A simple rectangular lattice model is considered in figure 3b to interpret the observed oblique lattice pattern, which models the ridges with crossribs but not the very top part of the scale where only ridges exist. When it is sectioned nearly longitudinally and in a slightly inclined way, an oblique lattice pattern can be reproduced, as shown in figure 3c, which looks essentially similar to the observed pattern. Thus, the upper layer of the cover scale can be better modelled by a rectangular lattice.

Figure 3.

Longitudinal oblique section. (a) Longitudinal oblique section of the cover scale along the plane shown in (b). White regions above the ridges are due to abrasion between the scale and the resin. Scale bar, 2 μm. (b) Diagrammatic interpretation of the section shown in (a), showing the relationship of ridges and crossribs. A sectioning plane is illustrated that is nearly longitudinal along the ridges and slightly tilted. (c) Two-dimensional sectional image of the model along the plane of section diagrammed in (b).

Next, we removed the upper layer of the scale in order to directly observe the top surface of the gyroid-type photonic crystal. Figure 4 shows a scale with partially removed ridges and crossribs. Under a higher magnification, the cuticle networks can be directly observed, as shown in figure 5. As a simple analysis, we draw a set of three lines along the observed cuticle network at four positions on the micrograph and measure the angles between the three lines. For all the analysed positions, we found that one of the three angles is larger than the other two; the largest angle is 70–73°, while the other two are 50–55°. Because the directions of the three lines are different depending on the position, we can easily identify the boundaries between the different crystal domains that are indicated by the dotted white curves in figure 5. However, it should be emphasized that similar surface morphologies are observed for different domains. This observation leads us to hypothesize that planes with the same Miller indices are exposed on the surface, while the in-plane orientations of the domains are different with respect to one another, as schematically depicted in figure 6. Careful inspection of the micrograph reveals that the underlying cuticle network can be seen through the holes of the top cuticle network (see inset of figure 5). We analysed other SEM images obtained for different positions and different scales and found similar surface morphologies.

Figure 4.

Scanning electron micrograph of the cover scale. The ridges and crossribs are removed in the lower part, while they still remain in the upper part. Double-headed arrows indicate the z′-direction (see figure 7b and equation (2.2) for the definition of the coordinates). Scale bar, 10 μm.

Figure 5.

Scanning electron micrograph. The top surface of the gyroid-type photonic crystal structure is directly observed. At each of the four positions, a set of three lines is drawn along the directions of the observed cuticle network. The largest angle of the three angles between three lines is indicated by filled white circles (see figure 7b for interpretation). Dotted curves indicate the boundaries between different domains. Inset: a close-up image showing the underlying cuticle network through the holes of a network on the top (scale bar, 300 nm).

Figure 6.

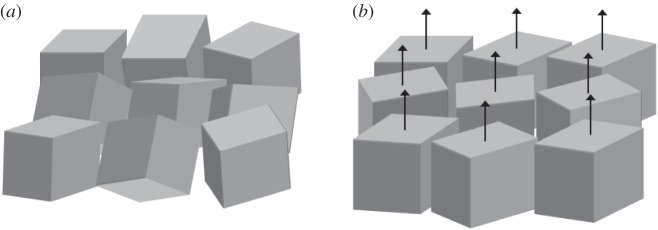
Schematic of multi-domain photonic crystals with different orientations: (a) a randomly oriented case and (b) a case where one crystal orientation is preferred along the surface normal.

4. Analysis

To identify the Miller indices of the top surface of the photonic crystal, the morphologies of the gyroid-type structure were examined by computer modelling. Figure 7 shows the surface morphologies of the three primary directions of the cubic lattice. They reflect symmetries along their directions; for example, threefold rotational symmetry is observed for the (111) plane in figure 7c. For both the (100) and (111) surfaces, we observe arrangements of holes that penetrate into the depth direction of the structure. On the other hand, part of the underlying cuticle network for the (110) surface is observed through the holes of the network on the top. This feature is consistent with the SEM observations (figure 5 inset). We estimated the angles between three lines that are drawn along the network in figure 7b. The largest angle is 70.6°, and the other two angles are 54.7°, which agree with those obtained experimentally. We theoretically examined surfaces with other Miller indices including larger values. However, the calculated surface morphologies did not match the observed relatively simple pattern.

Figure 7.

Morphologies of the gyroid-type photonic structure for the (a) (100), (b) (110) and (c) (111) surfaces obtained by computer modelling using equations (2.1)–(2.3). The calculated volume is set to have one period in the depth direction, while three periods are assumed for the in-plane directions, except for z″, where about two periods are assumed.

Next, we checked whether the textures of the photonic crystals observed in the cross section can be reproduced with the condition in which the [110] direction is along the surface normal. Figure 2b shows the computer-generated patterns by choosing in-plane orientations of the photonic crystal domains to reproduce the observed patterns with a slight tilt. This tilt is included to consider a slight variation of the [110] direction with respect to the surface normal and/or the tilt of the sectioning plane that may not be perfectly perpendicular to the scale. As reasonable matching is observed, we conclude that the [110] direction of the gyroid-type photonic crystal is preferred to be along the surface normal of the scale, although the crystal structure is separated into many domains. We investigated the in-plane orientations of different domains; the z′ directions of several domains are indicated by double-headed arrows in figure 4. However, these directions appear randomly oriented, and no clear preference is observed.

To investigate how precisely the [110] direction is along the surface normal, we examined the reflected light direction from single domains by using a microscatterometer. Measurements were carried out for a scale whose ridges and crossribs were removed. Figure 8a shows examples of the observed far-field pattern, where the results for three single domains are superimposed. The light spots are about two times larger than that of the specular reflection: the reflection from a single domain has an angular range of about 5–7°, whereas that of the specular surface is about 3°. This implies the existence of some imperfections in the photonic crystal or surface roughness that may affect the process of optical interference. The centres of the light spots observed for 13 single domains are shown in figure 8b. It is found that the angular distribution is about 20°, which is equivalent to a variation of 10° in the tilt angle of the [110] direction. This variation is smaller than the angles between the [110] and [111] directions and between the [110] and [100] directions, which are 35.3° and 45°, respectively.

Figure 8.

Far-field pattern of the reflections from single domains of the gyroid-type photonic crystal. (a) Superimposed image of the reflected light spots observed for three single domains. A scale whose ridges and crossribs were removed was examined. (b) Centre positions of the reflected light spots for 13 different domains. The circle edge corresponds to 64° from the optical axis of the microscope, while the dotted circle corresponds to 30°.

5. Discussion

We discovered that the crystal orientations of the different crystal domains of the wing scale of the butterfly P. sesostris are not perfectly random, but the [110] direction has a preference to be along the surface normal, whereas the in-plane orientations appear random. This fact naturally solves the puzzle of why the scale is observed to have a uniform colour despite the multi-domain structure. The green colour is consistent with the theoretical prediction from the photonic band-gap frequency, assuming a lattice constant a = 310 nm [31]. The previously suggested spectral filtering effect further serves to increase the spectral purity by absorbing the shorter wavelength part of the reflection band. Recently, Boden et al. [35] observed the (111) surface morphology in part of the exposed photonic crystal for this butterfly by using helium-ion microscopy. Their observations, however, were carried out by tilting the sample stage by 30–40°, taking advantage of its wide field of depth. Because this tilt angle is comparable with 35.3° between the [111] and [110] directions, our observations are not inconsistent with theirs.

It is known that the wing scale of P. sesostris has a strong polarization dependence [31,33]; the scale appears to have a tessellated pattern when it is observed from its underside with a crossed polarizer and analyser (figure 1d). This pattern indicates that the reflectance spectrum of the polarization-rotating component depends on the direction of the electric-field vector of the incident light with respect to the y′- and z′-axes (figure 7b). Because this study clarified the Miller indices of the exposed surface, detailed experimental and theoretical studies on the polarization-dependent reflectance are highly encouraged.

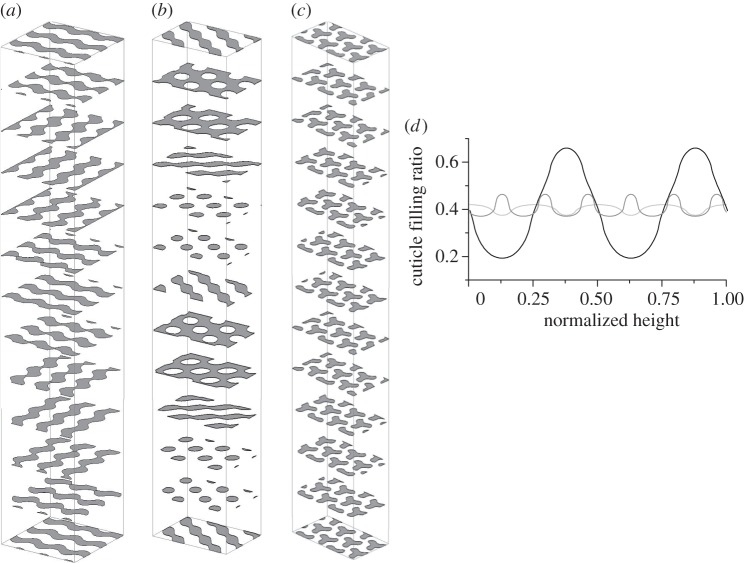
Pouya & Vukusic [36] reported for this butterfly that the filling ratio of the cuticle is adjusted to maximize the width of the photonic band gap. The choice of the [110] direction seems to be another optimization, as this direction is advantageous to increase the reflectance. Figure 9 shows two-dimensional sectional images at 13 different heights over one period along the [100], [110] and [111] directions. Along all three directions, the pattern of the cuticle and air gradually varies with height. However, the [110] direction is unique in the sense that the cuticle fraction largely varies because the pattern changes from air-rich polka dots to cuticle-rich polka dots (figure 9b). Along the other two directions, the cuticle fraction does not seem to vary as much. These features are quantitatively confirmed as the variations in the area filling ratio of the cuticle, as shown in figure 9d. The largest variation in the filling ratio means that the variation in the mean refractive index is also the largest. Thus, the [110] direction is suitable for increasing the reflectance of the photonic crystal with a finite thickness. Correspondingly, the ratio of the band-gap width to the middle frequency of this band-gap width is the largest in this direction among the three primary directions [30,31].

Figure 9.

Calculated two-dimensional cuticle patterns at 13 different heights along the three primary directions: (a) [100], (b) [110] and (c) [111]. (d) Filling ratio of the cuticle versus the normalized height along the three directions. Black, grey and light-grey curves are for the [110], [111] and [100] directions, respectively.

The unique properties of the [110] direction described above result in a characteristic pattern in the semi-frontal thin section of the scale; the gyroid-type structure appears as stripes with different grey levels at a coarse magnification, as shown in figure 10a. However, the stripes have differently detailed textures depending on the position, allowing us to easily identify the domain boundaries (figure 10b). These features can be understood from the large variation in the cuticle fraction along the [110] direction by analogy with a simple one-dimensional multi-layer system which appears as a broad stripe pattern in the semi-frontal thin section [37].

Figure 10.

Semi-frontal section of the cover scale. (a) A coarse observation. The gyroid-type photonic crystal appears as stripes with different grey levels. In the left bottom part, the ridges and crossribs are observed. The white rectangle indicates the part shown in (b). (b) A closer observation. The stripes have differently detailed textures depending on the position. Scale bars: (a) 5 μm and (b) 2 μm.

In contrast with P. sesostris, the ventral scales of Cy. remus and Ca. dumetorum are observed to consist of variously coloured patches with different intensities [16,17,27]. In these butterflies, the crystal domains are disjoint with each other, and the crystal orientations appear to be perfectly random. In fact, the reflectance spectra of these butterflies were reported to be reproduced by three spectral components that are thought to originate from the band gaps along three crystal orientations (fig. S7 in [27]). On the other hand, the reflectance spectrum of the papilionid butterfly T. imperialis was reported to be reproduced by mostly one component, similar to that of P. sesostris. Thus, it seems interesting to carefully check the photonic crystal orientations of the wing scales of T. imperialis. Several Parides species closely related to P. sesostris have green patches on their wings. However, the brightness and saturation of the green colours look different depending on the species. Thus, a comparative study of the microstructures may be beneficial to answer a deeper question as to how the structural colours with orientation-controlled photonic crystals have evolved.

Recently, Saranathan et al. [27] discussed the developmental process of the gyroid-type photonic crystal by expanding a previous study that suggested the role of the smooth endoplasmatic reticulum as a template for the structure [38]. This study suggests that there is an additional factor during development that controls the crystal orientations. Although the controlling mechanisms are unknown at present, the thickly developed layer of ridges with crossribs may be related to the mechanisms, as this feature is characteristic of P. sesostris (and of T. imperialis). In the scales of other butterflies, for example, Cy. remus and Ca. dumetorum, the large windows between the shallow ridges and the crossribs allow us to directly observe the underlying photonic crystals. Artificial photonic crystals produced by self-organizing processes often suffer from a multi-domain structure that makes their application difficult. Studying the developmental process of this butterfly may provide a solution to regulate the crystal orientations at least in one direction.

Funding statement

This work was supported by Grants-in-Aid for Scientific Research, no. 22340121 and no. 24120004, on Innovative Areas: ‘Engineering Neo-Biomimetics’ (Area no. 4402) from the Ministry of Education, Culture, Sports, Science, and Technology (MEXT).