Abstract
Organisms that are durophagous, hard prey consumers, have a diversity of tooth forms. To determine why we see this variation, we tested whether some tooth forms break shells better than others. We measured the force needed with three series of aluminium tooth models, which varied in concavity and the morphology of a stress concentrating cusp, to break a shell. We created functionally identical copies of two intertidal snail shells: the thicker shelled Nucella ostrina and the more ornamented Nucella lamellosa using a three-dimensional printer. In this way, we reduced variation in material properties between test shells, allowing us to test only the interaction of the experimental teeth with the two shell morphologies. We found that for all tooth shapes, thicker shells are harder to break than the thinner shells and that increased ornamentation has no discernible effect. Our results show that for both shell morphologies, domed and flat teeth break shells better than cupped teeth, and teeth with tall or skinny cusps break shells best. While our results indicate that there is an ideal tooth form for shell breaking, we do not see this shape in nature. This suggests a probable trade-off between tooth function and the structural integrity of the tooth.
Keywords: durophagy, tooth morphology, shell failure, rapid prototyping, biomechanics
1. Introduction
Teeth play an important role in the capture and processing of prey so it is not surprising that tooth morphology is closely correlated with diet. This relationship between tooth form and function is so strong that it is used to make inferences about the natural history of organisms. For example, Massare [1] used the observed relationships between the tooth morphologies and diets of marine mammals to define and infer feeding guilds of extinct marine reptiles. The broadest categories, which could be combined to generate additional guilds, consisted of: hard prey crushing organisms, organisms with piercing teeth to eat soft invertebrate prey and organisms with bladed teeth to cut through the flesh of large vertebrate prey. While these guilds are based on observed correlations between morphology and consumed prey, they do not explain why some morphologies are better at processing some prey items than others.
Models, both physical and mathematical, have been used to test tooth shapes associated with different feeding guilds. Based on observed tooth morphologies and general engineering principles, Evans & Sanson [2,3] generated ‘ideal’ cutting teeth. These theoretical teeth broadly reflected a diversity of mammalian teeth, both extinct and extant. In a more experimental context, the morphology of notched blades has been demonstrated to have a significant effect on the ease with which tough prey items are cut [4,5]. Similarly, the functional advantages of serrated teeth have been demonstrated when tearing through muscle [6]. The function of puncturing teeth has also been explored using models that varied in aspect ratio and taper, in order to compare bite forces and how different morphologies bend [7]. Physical models have also been employed to better understand how puncture and cutting performance differ between different extant and extinct shark tooth morphologies [8].
There has been some physical modelling of the performance of specific hard prey crushing dentitions—Schulp [9] used replicas of the crushing teeth of the mosasaur Carinodens belgicus to break potential prey items. By comparing the force needed to break the prey items with bite forces calculated based on jaw morphology, he demonstrated that soft-bodied prey, such as squid, were unlikely prey items for C. belgicus, and that hard-bodied organisms, such as sea urchins, arthropods, bivalves and gastropods, were more likely prey. However, the ability of the teeth to process hard-shelled prey very much depended on the shell thickness and morphology, as well as where forces were applied. Although this study clearly demonstrated the functional limitations of a single crushing tooth morphology, it does not explain the morphology of the C. belgicus crushing teeth, or why they were able to process some prey items, like whelk snails but not others, like winkle snails.
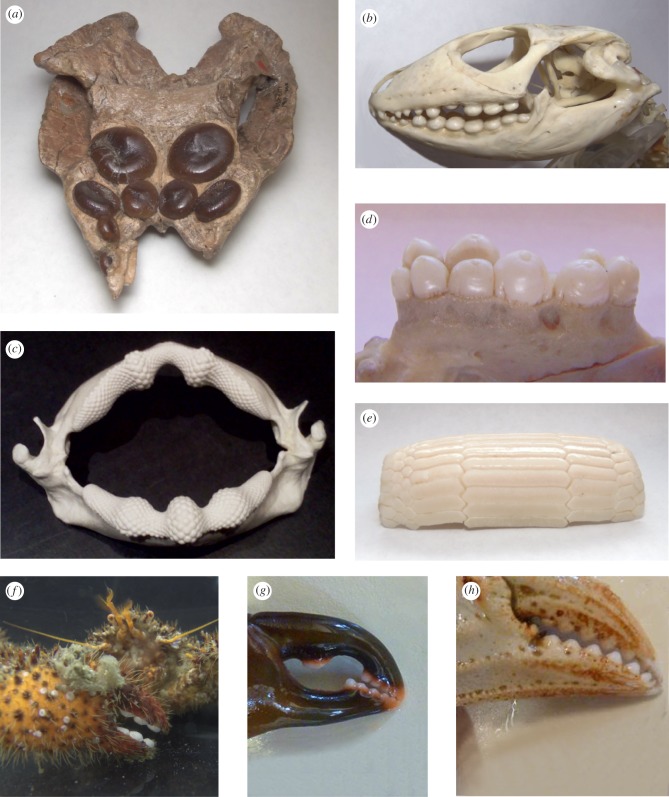
The literature of durophagy focuses on the defensive adaptations of the prey rather than the morphology of the crushing apparatus. Though this dentition is readily recognized in extant and fossil taxa, the precise morphology is variable and the implications of shape on performance are not understood. The teeth of durophagous organisms have been described as ‘flattened’ [10,11], ‘pavement-like’ [11,12], ‘molariform’ [11,13,14] and ‘pebble-like’ [14]. These terms lack precision and do not cover the diversity of morphologies seen in the hard prey crushing teeth of durophagous animals (figure 1). Crushing teeth can range from domed, to flat plates, and can be worn to the point of concavity. Additionally, durophagous teeth can have a range of different cusp morphologies which serve to concentrate forces and increase stress on the prey item.
Figure 1.
Diversity of durophagous tooth morphologies. (a) Placochelys placodonta † MB.R. 1765, (b) Dracaena sp. (lizard), (c) Rhina (guitarfish), (d) Anarrhichthys ocellatus (wolf eel), (e) Rhinoptera bonasus (stingray), (f) Acantholithodes hispidus (hairy crab), (g) Pugettia gracilis (graceful kelp crab), (h) Metacarcinus magister (Dungeness crab). (Online version in colour.)
The goals of this study are fourfold: (i) establish that rapid prototyping and computer numerical control milling can be used to generate repeatable performance data on crushing load by standardizing both tooth shape and prey morphology; (ii) determine the effect of crown concavity/convexity on the load needed to fracture prey; (iii) quantify the role of a centrally located stress concentrator on breaking load; and (iv) determine whether the optimal tooth shape is sensitive to subtle variations in the prey morphology. We can then use these results to discuss the implications of some extant and extinct crushing dentitions.
2. Material and methods
2.1. Tooth models
To isolate and test the performance of different aspects of tooth morphology, we created three series of models spanning a range of morphologies to reflect tooth morphologies seen in nature, as well as extreme morphologies. Model shapes were generated by rotating a section, from x = 0 to x = 1, of a parametric curve (equation (2.1)) about its y-axis
| 2.1 |
We varied different aspects of model morphology by changing two parameters: h, which controls the height of cusps projecting from the occlusal surface, and r, which controls how much of the occlusal surface the base of a projecting cusp covers. By setting h and r parameters to zero, we generated a tooth model with a flat occlusal surface, which we considered the ground state (model 0). Our first series consisted of five tooth models whose occlusal surface ranged from concave to convex (figure 2a). We achieved this by setting r approximately equal to the radius of the occlusal surface (r = 0.4) and then varied h from 0.5 to −0.5. For the second series, we compared model 0 to five models with central occlusal cusps of varying height (figure 2b). To create a small cusp in the middle of the occlusal surface, we set r = 0.1 and then varied the cusp height by changing h from 0.1 to 0.5. In our third set of tooth models, we varied the occlusal area covered by the base of a cusp of constant height (figure 2c). To do this, cusp height (h) was set to 0.25, and the width of the cusp base was varied from r = 0.35 to r = 0 (model 0). Milling tool paths were created from the model geometry with SprutCAM 7.0 and milled from round aluminium stock (6061 T6) on a Tormach mill with a 0.082 round carbide endmill. The end results are tooth models with bodies approximately 12.5 mm in diameter, with Young's modulus of 68.9 GPa, which is lower than Young's modulus reported for human enamel [15] or shark enameloid [16].
Figure 2.

Experimental model morphologies. (a) Convex–concave tooth model morphologies. (b) Tooth model morphologies with a cusp of varying height. (c) Tooth model morphologies with a cusp with a base of varying width.
2.2. Shell copies
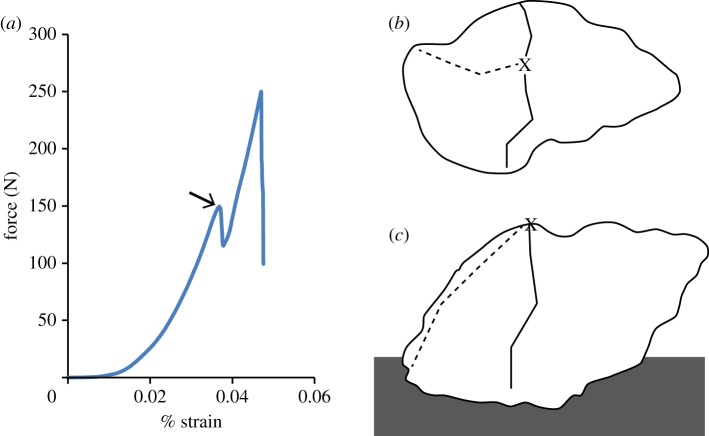
Because we were interested in testing only the effects of tooth morphology on crushing ability, we mass produced shells for testing using a rapid prototyper (ZPrinter 310, ZCorporation). This eliminated variation in shell material properties owing to the natural history of the individual and variation in covarying aspects of morphology. For example, opercular width is correlated with length but is not invariant with length. By printing the same shell multiple times, we ensured the exact same gross morphology. This leaves variation in microscale morphology, such as distributions of microfractures and inclusions that dictate the stochastic nature of failure. We tested two shell morphologies, based on data from computed tomography (CT) scans of intertidal gastropods (collected at Friday Harbor Labs, WA, USA) Nucella ostrina (figure 3a) and Nucella lamellosa (figure 3b), each demonstrating various adaptations to prevent crushing. By using CT data, we were able to accurately replicate the entire internal and external morphology of both shells in our copies. The relatively shorter spire in the N. ostrina specimen should be less prone to cracking, while the more developed ornamentation on N. lamellosa may provide increased structural support [17]. The N. ostrina shell also has thicker body whorl walls, which would make the shell sturdier. Surface data from each shell were generated from micro-CT scans and rendered in Amira (v. 5.2.2), then uploaded and scaled so that the shell height of each measured 25 mm (ZPrint v. 7.10.3-7). We printed shell replicas using zp150 high-performance composite powder and zb60 binding solution, and then hardened them with a misting of a saturated Epsom salt solution. In this way, we were able to generate two morphologically distinct sets of shell copies that behaved as brittle solids (figure 4a) with effectively identical material properties: Young's modulus of 314.977 ± 32.49 MPa and compressive strength of 4.54 ± 0.76 MPa. In contrast to real mollusc shells, our models lack a complicated microstructure, which functions to confound crack propagation in living molluscs. However, for the purposes of this study, we are focusing only on the force needed to initiate crack formation, not to propagate it.
Figure 3.
Snail shell prototypes. (a) A printed copy of Nucella ostrina in dorsal and lateral view. (b) A printed copy of N. lamellosa in dorsal and lateral view. (Online version in colour.)
Figure 4.
(a) Example of load versus strain curve demonstrating brittle failure. Strain was calculated based on the displacement of the tooth model. Arrow indicates point at which initial load of failure was measured. Common locations of crack formation as seen in (b) dorsal and (c) lateral view. Cracks most often formed radiating from the point of loading (indicated by an X) around the body whorl normal to the long axis of the shell (solid line). On some occasions, cracks would also radiate from the point of loading along the long axis of the shell towards the siphonal notch (dashed line). (Online version in colour.)
To determine that the rapid prototyper produced shells that would fail reproducibly, we printed and tested small batches of shells. To measure the force needed to break the shells, we attached the flat tooth model (model 0) to a moving 500 N load cell in a materials testing system (Synergie 100, MTS Systems Corporation), directly over a printed shell placed aperture down. The shells were positioned so that the tallest point of the body whorl was centred under the tooth model and were placed on a 5 mm, 60 durometer silicone rubber pad to reduce stress concentrations in the printed shell owing to interactions between the shell and platform. The tooth model was lowered directly onto the printed shell at a rate of 1.27 mm min−1. We found no difference between initial load to failure for shells from different batches (t-test; n = 5; p = 0.80271), so long as they were allowed to dry and set for at least 1 day before testing.
For both shell morphologies, fractures occurred in the main body whorl, at the point of loading and radiated out. The point at which crack initiation occurred was approximately 1.4 mm thick in N. lamellosa, and approximately 2.25 mm thick in N. ostrina. Cracks most often propagated around the circumference of the shell. Occasionally, cracks would also travel along the long axis of the shell, moving towards the siphonal notch (figure 4b,c). As a result of testing, shells were completely destroyed, as described by Zushcin et al. [18], and as would be expected from crushing predators.
2.3. Tests and analysis
Testing the various combinations of different tooth models and shell morphologies followed the same procedure as the batch testing. For each tooth model/shell combination, we tested 25 shells and measured the initial load of failure (F in N), defined as the first point at which the load dropped by 60% (figure 4a). The initial load of failure is an indicator of how much energy the predator needs to expend to break shells of different morphology, but the same size.
As the shells had different morphologies and were quite different in shell thickness, we also calculated the force to initiate crack propagation per unit volume (F/V in N cm−3) of each shell by dividing the initial load of failure by the volume of material that was used to make the shell. Nucella ostrina was slightly more voluminous (1.08 cm3) than N. lamellosa (0.83 cm3), reflecting the difference in shell wall thickness. The difference in volume can reflect a difference in energy invested in generating the shell, so the force per volume measurement will allow us to see how different shell architecture interacts with different tooth morphologies.
Both sets of data were log transformed to achieve a normal distribution. The interactions between shell and tooth morphology were compared for all three series of tooth models with a two-way ANOVA and post-hoc Tukey's tests in R.
3. Results
Average results and standard deviations for all tests are given in table 1. Across all tests, N. lamellosa required less force to initiate crack propagation than N. ostrina. The force to initiate crack propagation was significantly higher for N. ostrina shells than for N. lamellosa for all tooth models (two-way ANOVA: F1,240 = 1333.42, 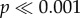 ) and the force normalized by volume followed a similar pattern for both shell morphs.
) and the force normalized by volume followed a similar pattern for both shell morphs.
Table 1.
Comparison of tooth model parameters and force of initial failure. Also reported are the radius of curvature of the occlusal surface of the tooth models, and force of initial failure scaled by both shell volume and by the cube root of volume, to estimate energy release.
| shape | h | r | radius of curvature | species | F (N) | ±s.d. | F/V (N m−3) | ±s.d. |
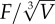 (N m−1) (N m−1) |
±s.d. |
|---|---|---|---|---|---|---|---|---|---|---|
| −2 | 0.5 | 0.4 | 0.4 | N. ostrina | 379.5724 | 53.72428 | 351.4559 | 49.7447 | 369.9588 | 52.363583 |
| N. lamellosa | 272.9533 | 28.76839 | 252.7346 | 26.6374 | 290.444 | 28.036758 | ||||
| −1 | 0.25 | 0.4 | 0.8 | N. ostrina | 319.3861 | 26.07399 | 295.7279 | 24.14258 | 311.2969 | 25.413603 |
| N. lamellosa | 57.84152 | 7.616884 | 47.63296 | 7.789641 | 61.54796 | 8.1048107 | ||||
| 0 | 0 | 0.4 | 0 | N. ostrina | 150.5768 | 14.28893 | 139.423 | 13.23049 | 146.7631 | 13.927032 |
| N. lamellosa | 61.73644 | 3.061052 | 74.38125 | 3.688014 | 65.69246 | 3.2572019 | ||||
| 1 | −0.25 | 0.4 | −0.8 | N. ostrina | 166.9758 | 18.94995 | 154.6072 | 17.54625 | 162.7467 | 18.469997 |
| N. lamellosa | 57.6576 | 2.697822 | 69.46699 | 3.250388 | 61.35226 | 2.8706967 | ||||
| 2 | −0.5 | 0.4 | −0.4 | N. ostrina | 142.7502 | 14.45487 | 132.1761 | 13.38414 | 139.1347 | 14.088765 |
| N. lamellosa | 51.25308 | 3.394624 | 61.7507 | 4.089908 | 54.53734 | 3.6121485 | ||||
| H1 | 0.05 | 0.1 | 1 | N. ostrina | 157.4508 | 12.03038 | 145.7877 | 11.13924 | 153.4629 | 11.72568 |
| N. lamellosa | 50.09194 | 7.678509 | 60.35174 | 9.251215 | 53.30179 | 8.170542 | ||||
| H2 | 0.15 | 0.1 | 0.333 | N. ostrina | 145.6952 | 15.94638 | 134.903 | 14.76517 | 142.0052 | 15.5425 |
| N. lamellosa | 47.41974 | 9.072596 | 57.13222 | 10.93084 | 50.45836 | 9.653961 | ||||
| H3 | 0.25 | 0.1 | 0.2 | N. ostrina | 125.9957 | 11.13195 | 116.6627 | 10.30736 | 122.8045 | 10.85001 |
| N. lamellosa | 50.75364 | 11.67119 | 61.14896 | 14.06168 | 54.00589 | 12.41908 | ||||
| H4 | 0.35 | 0.1 | 0.143 | N. ostrina | 103.0125 | 14.41341 | 95.38196 | 13.34575 | 100.4035 | 14.04836 |
| N. lamellosa | 48.52072 | 7.276258 | 58.4587 | 8.766576 | 51.62989 | 7.742515 | ||||
| H5 | 0.45 | 0.1 | 0.111 | N. ostrina | 96.04356 | 11.74515 | 88.92922 | 10.87514 | 93.61102 | 11.44768 |
| N. lamellosa | 36.6542 | 5.42367 | 44.16169 | 6.534542 | 39.00297 | 5.771215 | ||||
| R1 | 0.25 | 0.3 | 0.6 | N. ostrina | 145.9132 | 24.15595 | 135.1049 | 22.36662 | 142.2176 | 23.54414 |
| N. lamellosa | 54.38548 | 5.915001 | 65.52467 | 7.126507 | 57.87046 | 6.29403 | ||||
| R2 | 0.25 | 0.2 | 0.4 | N. ostrina | 123.2947 | 17.48208 | 114.1617 | 16.18711 | 120.1719 | 17.0393 |
| N. lamellosa | 44.44848 | 5.362634 | 53.55239 | 6.461005 | 47.2967 | 5.706268 | ||||
| R3 | 0.25 | 0.1 | 0.2 | N. ostrina | 116.0134 | 14.04102 | 107.4199 | 13.00095 | 113.0751 | 13.6854 |
| N. lamellosa | 51.09252 | 6.843818 | 61.55725 | 8.245564 | 54.36649 | 7.282365 | ||||
| R4 | 0.25 | 0.05 | 0.1 | N. ostrina | 107.1584 | 16.07942 | 99.22076 | 14.88835 | 104.4444 | 15.67217 |
| N. lamellosa | 38.93308 | 8.411486 | 46.90733 | 10.13432 | 41.42788 | 8.950487 | ||||
| R5 | 0.25 | 0.025 | 0.05 | N. ostrina | 78.03683 | 12.77552 | 72.25633 | 11.82919 | 76.06036 | 12.45195 |
| N. lamellosa | 31.6202 | 4.771286 | 38.09663 | 5.748537 | 33.6464 | 5.077026 |
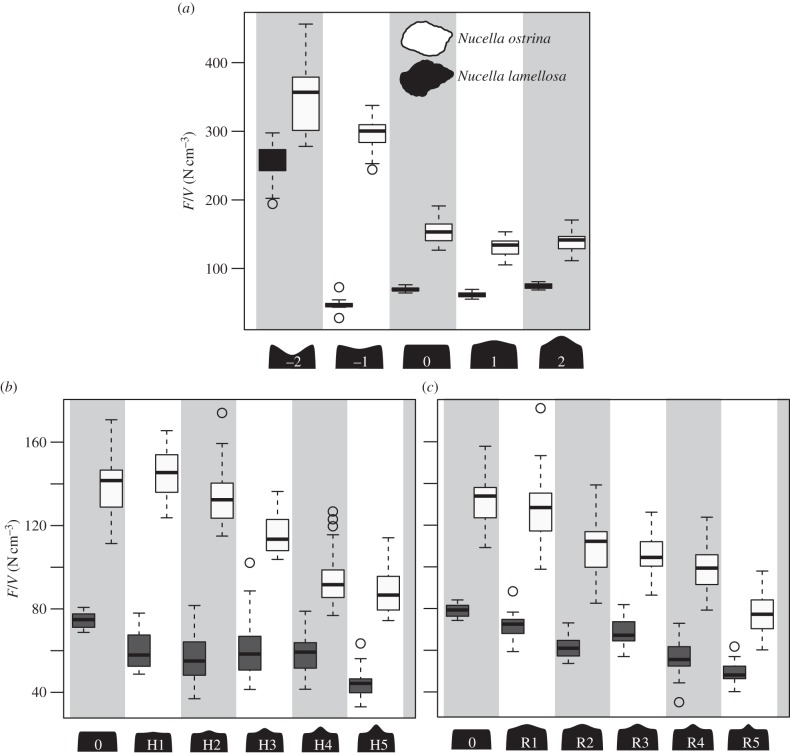
The force to failure normalized by shell volume for the first series of tooth models tested, where models varied by occlusal concavity and convexity, is illustrated in figure 5a. In addition to the difference between the shells, there were also significant differences in the force needed to initiate crack propagation between tooth model morphologies (two-way ANOVA: F4,240 = 292.76, 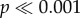 ), and significant interaction effects for the force measurements (two-way ANOVA: F4,240 = 73.91,
), and significant interaction effects for the force measurements (two-way ANOVA: F4,240 = 73.91, 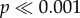 ). For N. ostrina, the two concave models (−2, −1) require significantly more force than the flat and two convex morphologies (0, 1, 2) to initiate crack propagation (
). For N. ostrina, the two concave models (−2, −1) require significantly more force than the flat and two convex morphologies (0, 1, 2) to initiate crack propagation (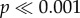 ). For N. lamellosa, by contrast, only the most concave tooth (−2) takes significantly more force (
). For N. lamellosa, by contrast, only the most concave tooth (−2) takes significantly more force (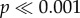 ). Significant differences (two-way ANOVA: F4,240 = 1128.5,
). Significant differences (two-way ANOVA: F4,240 = 1128.5, 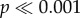 ) and interaction effects (two-way ANOVA: F4,240 = 400.8,
) and interaction effects (two-way ANOVA: F4,240 = 400.8, 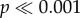 ) also existed when force of initial failure was normalized by volume; when adjusting for volume of shell material, all shell–tooth model interactions are significantly different (p < 0.05), except for the flat (0) and most convex (2) tooth in N. ostrina, and the flat tooth (0) (p < 0.05) and the shallow convex tooth (1) in N. lamellosa.
) also existed when force of initial failure was normalized by volume; when adjusting for volume of shell material, all shell–tooth model interactions are significantly different (p < 0.05), except for the flat (0) and most convex (2) tooth in N. ostrina, and the flat tooth (0) (p < 0.05) and the shallow convex tooth (1) in N. lamellosa.
Figure 5.
Comparison of F/V (in N cm−3) needed to initiate crack propagation in (a) convex–concave tooth models, (b) tooth models with cusps of varying heights and (c) tooth models with cusps with bases of varying widths. Boxplots demonstrate distribution of F/V for N. ostrina (white) and N. lamellosa (dark grey); heavy middle dashes indicate medians, the upper and lower edge of the box bound the second and third quartiles (25%) of the data, respectively, the whiskers indicate maximum quartile ranges, and circles represent outlying data points.
The effects of adding a stress concentrating cusp of varying heights on the force per volume needed to initiate crack propagation in both shell types are demonstrated in figure 5b. For both shells, there is a general trend of decreasing load to initial failure as cusp height increases, though this is more obvious in N. ostrina, and these trends hold true for the force normalized by shell volume. There are significant differences (two-way ANOVA: F5,288 = 85, 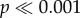 ) between the force needed by the different models to initiate crack propagation, as well as a significant interaction effect (two-way ANOVA: F5,288 = 16.03,
) between the force needed by the different models to initiate crack propagation, as well as a significant interaction effect (two-way ANOVA: F5,288 = 16.03, 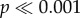 ), as well as for the force normalized by shell volume (two-way ANOVA: F5,288 = 85,
), as well as for the force normalized by shell volume (two-way ANOVA: F5,288 = 85, 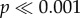 ; two-way ANOVA: F5,288 = 16.03,
; two-way ANOVA: F5,288 = 16.03, 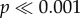 ). In N. ostrina, for both datasets, there is no significant difference between the flat tooth and the shortest two cusps (models 0, H1, H2), they differ from model H3, and a group formed by the tallest two cusps (H4 and H5) (
). In N. ostrina, for both datasets, there is no significant difference between the flat tooth and the shortest two cusps (models 0, H1, H2), they differ from model H3, and a group formed by the tallest two cusps (H4 and H5) (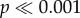 ). For N. lamellosa, the flat tooth (model 0) took significantly more force to initiate failure as well as initial force per volume (
). For N. lamellosa, the flat tooth (model 0) took significantly more force to initiate failure as well as initial force per volume (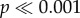 ) than any other tooth model to initiate crack propagation. There was no significant difference between the first four cusp heights (models H1–H4), all of which required an intermediate amount of force, as well as force normalized by volume, to initiate crack propagation and the fifth cusp height (model H5) took significantly less (
) than any other tooth model to initiate crack propagation. There was no significant difference between the first four cusp heights (models H1–H4), all of which required an intermediate amount of force, as well as force normalized by volume, to initiate crack propagation and the fifth cusp height (model H5) took significantly less (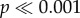 ).
).
Similarly, the patterns of initial force per unit volume needed to initiate crack propagation by cusps that taper to different degrees are illustrated in figure 5c. For both shell morphs, narrowing the cusp decreases the force as well as force normalized by shell volume needed to initiate crack propagation. For the force needed to initiate crack propagation in N. ostrina, the flat tooth and the widest cusp (models 0 and R1) formed a significantly distinct group (p < 0.01), as did models R2 and R3 (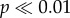 ), and R3 and R4 (p < 0.05), with the narrowest model (model R5) being significantly different from any other model (
), and R3 and R4 (p < 0.05), with the narrowest model (model R5) being significantly different from any other model (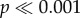 ). Similarly, for N. lamellosa the flat tooth model and the widest cusped model (models 0 and R1) were not statistically different from each other. All other models were significantly different (p < 0.05), except models R1 and R3. There was a similar pattern for N. lamellosa when force to crack propagation was normalized by shell volume (p > 0.05). For N. ostrina, however, the pattern differed. The flat model and widest cusp (models 0 and R1) still form a distinct group (p < 0.01), but model R1 is not statistically distinct from model R3. Finally, models R3 and R4 are not significantly different.
). Similarly, for N. lamellosa the flat tooth model and the widest cusped model (models 0 and R1) were not statistically different from each other. All other models were significantly different (p < 0.05), except models R1 and R3. There was a similar pattern for N. lamellosa when force to crack propagation was normalized by shell volume (p > 0.05). For N. ostrina, however, the pattern differed. The flat model and widest cusp (models 0 and R1) still form a distinct group (p < 0.01), but model R1 is not statistically distinct from model R3. Finally, models R3 and R4 are not significantly different.
4. Discussion
In cases such as this, investigating how changes in tooth and shell structures affect performance, rapid prototyping can be expedient in generating great quantities of experimental samples, while eliminating variation resulting from the natural history of the organism. The force needed to break mollusc shells can be highly variable, both within and between species [19]. This variation can be owing to differences in gross morphology, such as shell thickness and ornamentation, as well as microstructure, such as different shell composition and crystal orientation. This variability can make it difficult to ask specific morphological questions, as one cannot control for all of these variables. With rapid prototyping, by contrast, one can eliminate variation owing to natural history and can replicate experiments using the same morphology, and control how morphology changes.
We tested two intertidal snail shell morphologies: the thick-shelled, low-spired N. ostrina, and the thinner shelled, high-spired and more ornamented N. lamellosa. Both shell types broke in a similar manner for all tooth model morphologies, with thicker shells requiring more force, even when normalized against the volume of the shell. The similarity in breaking pattern also indicates that having a taller shell spire does not affect the specifics of failure. However, this may be owing to load placement on the shells, as tooth models were situated directly over the body whorl and were rarely in contact with the spire.
Concave teeth require more force to break shells than flat or convex teeth. This may be case dependent, however, as the body whorl of both shells fitted into the concavity of the concave tooth models, which increased the area of the tooth in contact with the shell and decreased the applied stress. Similarly, the most convex tooth had the least surface area in contact with the shells, and in N. lamellosa trials took statistically less force to break than any other model in the series. While it was not significantly different, a similar pattern can be seen in the interaction between the most convex tooth and the N. ostrina shell.
Adding a cusp to the flat tooth concentrated the force being applied to the shell, and reduced the force needed to break both shell morphs. For both shell morphologies, there is a general pattern of decreasing force as cusp height increases. This trend is most distinct in N. ostrina, while in N. lamellosa there is very little difference in the force needed to break the shell for intermediate cusp heights. As with the cusp height, both shell morphs demonstrated a similar pattern of decreasing force per volume to break as cusps become narrower.
Based on these data, the most effective tooth for breaking shells is flat or convex with a tall skinny cusp. The closest tooth to this ideal in nature may be the snail punching sculpin Asemichthys taylori which uses teeth with a high central cusp on its vomer to punch small holes in snail shells before swallowing them whole [20]. This shape will reduce the area being loaded and increase the stress on the shell for a given force, reducing the overall force needed to break the shell. Reducing the load needed to crush is clearly only part of the durophagy story though, because there are many different tooth morphologies in nature, and none fit this optimal shape. An explanation for the variation in tooth shape might in part be that not all hard prey is the same. Here, we showed that even relatively small differences in snail shell shape can have an effect on how much force is needed to initiate crack propagation. Hard prey spans a wide range of organisms, from the well mineralized and brittle, like sea urchins and decapod crustaceans, to tougher prey items, such as molluscs, which may reward different tooth shapes. Furthermore, it is intuitively clear that a high cusp is at greater risk of failure, so there is likely some trade-off between reducing the load needed to break the prey item and dissipating the load safely so the tooth does not fail.
In fact, different gnathostome lineages invest different amounts of energy when producing teeth. Some groups, such as sharks, create and regularly replace relatively simple teeth. Others, notably mammals, produce just a few sets of specialized teeth that are not replaced. This implies that the selective pressure to protect teeth from damage varies with phylogeny. The balancing act between damage to prey and tooth is well studied in mammals, especially those with bunodont dentition, such as humans or apes, where there is a wealth of literature on fracture mechanics. In these systems, enamel thickness and tooth size are aspects of the tooth that determine damage resistance, and food hardness is the prey's contribution to the damage equation [15,21–25].
This trade-off between function and damage control should be of less importance in animals that frequently replace teeth, such as reptiles or fish [23]. For example, the microstructure of tooth materials differs in non-mammals, with enamel crystals that are not arranged to deflect crack propagation [26]. Lawn et al. [25] extrapolate their findings to apply to sabre-toothed cats, as well as ‘crocodiles and many reptiles’ with conical teeth, so perhaps the puncturing case is well in hand. We suggest that looking at the stress distribution in crushing teeth would allow a direct measure of the risk of failure and, in a phylogenetic context, could be used to test the hypothesis that replacement rates affect risk tolerance in tooth design.
Acknowledgements
We thank E. Carrington and M. Dethier for loan of shells; T. Cox, T. Kleinteich and Ron Shahar for μCT work; and J. Grewal, V. Hoang and A. Vancil for assistance in laboratory.
Funding statement
This work was funded by NSF (IOS-1256602), the Stephen and Ruth Wainwright Endowed Fellowship, the Estes Grant, UW Bio Dept.
References
- 1.Massare JA. 1987. Tooth morphology and prey preference of Mesozoic marine reptiles. J. Vertebr. Paleontol. 7, 121–137. ( 10.1080/02724634.1987.10011647) [DOI] [Google Scholar]
- 2.Evans AR, Sanson GD. 2003. The tooth of perfection: functional and spatial constraints on mammalian tooth shape. Biol. J. Linnean Soc. 78, 173–191. ( 10.1046/j.1095-8312.2003.00146.x) [DOI] [Google Scholar]
- 3.Evans AR, Sanson GD. 2006. Spatial and functional modelling of carnivore and insectivore molariform teeth. J. Morphol. 267, 649–662. ( 10.1002/jmor.10285) [DOI] [PubMed] [Google Scholar]
- 4.Anderson PSL. 2009. The effects of trapping and blade angle of notched dentitions on fracture of biological tissues. J. Exp. Biol. 212, 3627–3632. ( 10.1242/jeb.033712) [DOI] [PubMed] [Google Scholar]
- 5.Anderson PSL, LaBarbera M. 2008. Functional consequences of tooth design: effects of blade shape on energetics of cutting. J. Exp. Biol. 211, 3619–3626. ( 10.1242/jeb.020586) [DOI] [PubMed] [Google Scholar]
- 6.Abler WJ. 1992. The serrated teeth of tyrannosaurid dinosaurs, and biting structures in other animals. Paleobiology 18, 161–183. [Google Scholar]
- 7.Freeman PW, Lemen CA. 2007. The trade-off between tooth strength and tooth penetration: predicting optimal shape of canine teeth. J. Zool. 273, 273–280. ( 10.1111/j.1469-7998.2007.00325.x) [DOI] [Google Scholar]
- 8.Whitenack LB, Motta PJ. 2010. Performance of shark teeth during puncture and draw: implications for the mechanics of cutting. Biol. J. Linnean Soc. 100, 271–286. ( 10.1111/j.1095-8312.2010.01421.x) [DOI] [Google Scholar]
- 9.Schulp AS. 2005. Feeding the mechanical mosasaur: what did Carinodens eat? Neth. J. Geosci. 84, 345–357. [Google Scholar]
- 10.Summers AP. 2000. Stiffening the stingray skeleton—an investigation of durophagy in mylobatid stingrays (Chondrichthyes, Batoidea, Myliobatidae). J. Morphol. 243, 113–126. () [DOI] [PubMed] [Google Scholar]
- 11.Wilga CD, Motta PJ. 2000. Durophagy in sharks: feeding mechanics of the hammerhead Sphyrna tiburo. J. Exp. Biol. 203, 2781–2796. [DOI] [PubMed] [Google Scholar]
- 12.Sasko DE, Dean MN, Motta PJ, Hueter RE. 2006. Prey capture behavior and kinematics of the Atlantic cownose ray, Rhinoptera bonasus. Zoology 109, 171–181. ( 10.1016/j.zool.2005.12.005) [DOI] [PubMed] [Google Scholar]
- 13.Mara KR, Motta PJ, Huber DR. 2010. Bite force and performance in the durophagous bonnethead shark, Sphyrna tiburo. J. Exp. Zool. Part A 313A, 95–105. ( 10.1002/jez.576) [DOI] [PubMed] [Google Scholar]
- 14.Mehta RS. 2009. Ecomorphology of the moray bite: relationship between dietary extremes and morphological diversity. Physiol. Biochem. Zool. 82, 90–103. (doi:1086/594381) [DOI] [PubMed] [Google Scholar]
- 15.Lucas P, Constantino P, Wood B, Lawn B. 2008. Dental enamel as a dietary indicator in mammals. Bioessays 30, 374–385. ( 10.1002/bies.20729) [DOI] [PubMed] [Google Scholar]
- 16.Whitenack LB, Simkins DC, Motta PJ, Hirai M, Kumar A. 2010. Young's modulus and hardness of shark tooth biomaterials. Arch. Oral Biol. 55, 203–209. ( 10.1016/j.archoralbio.2010.01.001) [DOI] [PubMed] [Google Scholar]
- 17.Vermeij GJ. 1977. The Mesozoic marine revolution: evidence from snails, predators and grazers. Paleobiology 3, 245–258. [Google Scholar]
- 18.Zushcin M, Stachowitsch M, Stanton RJ. 2003. Patterns and processes of shell fragmentation in modern and ancient marine environments. Earth-Sci. Rev. 63, 33–82. ( 10.1016/S0012-8252(03)00014-X) [DOI] [Google Scholar]
- 19.Zuschin M, Stanton RJ. 2001. Experimental measurement of shell strength and its taphonomic interpretation. Palaios 16, 161–170. () [DOI] [Google Scholar]
- 20.Norton SF. 1988. Role of the gastropod shell and operculum in inhibiting predation by fishes. Science 241, 92–94. ( 10.1126/science.241.4861.92) [DOI] [PubMed] [Google Scholar]
- 21.Berthaume M, Gross IR, Patel ND, Strait DS, Wood S, Richmond BG. 2011. The effect of early hominin occlusal morphology on the fracturing of hard food items. Anat. Rec. 293, 594–606. ( 10.1002/ar.21130) [DOI] [PubMed] [Google Scholar]
- 22.Lawn BR, Lee JJ-W. 2009. Analysis of fracture and deformation modes in teeth subjected to occlusal loading. Acta Biomater. 5, 2213–2221. ( 10.1016/j.actbio.2009.02.001) [DOI] [PubMed] [Google Scholar]
- 23.Lee JJ-W, Constantino PJ, Lucas PW, Lawn BR. 2011. Fracture in teeth—a diagnostic for inferring bite force and tooth function. Biol. Rev. 86, 959–974. ( 10.1111/j.1469-185X.2011.00181.x) [DOI] [PubMed] [Google Scholar]
- 24.Luke DA, Lucas PW. 1983. The significance of cusps. J. Oral Rehabil. 10, 197–206. ( 10.1111/j.1365-2842.1983.tb00113.x) [DOI] [PubMed] [Google Scholar]
- 25.Lawn BR, Bush MB, Barani A, Constantino PJ, Wroe S. 2013. Inferring biological evolution from fracture patterns in teeth. J. Theor. Biol. 338, 59–65. ( 10.1016/j.jtbi.2013.08.029) [DOI] [PubMed] [Google Scholar]
- 26.Sander PM. 2000. Prismless enamel in amniotes: terminology, function, and evolution. In Development, function and evolution of teeth (eds Teaford MF, Smith MM, Ferguson WWJ.), pp. 92–106. Cambridge, UK: Cambridge University Press. [Google Scholar]