Coherent Bragg nanodiffraction at the hard X-ray Nanoprobe beamline

Abstract

Bragg coherent diffraction with nanofocused hard X-ray beams provides unique opportunities for quantitative in situ studies of crystalline structure in nanoscale regions of complex materials and devices by a variety of diffraction-based techniques. In the case of coherent diffraction imaging, a major experimental challenge in using nanoscale coherent beams is maintaining a constant scattering volume such that coherent fringe visibility is maximized and maintained over the course of an exposure lasting several seconds. Here, we present coherent Bragg diffraction patterns measured from different nanostructured thin films at the Sector 26 Nanoprobe beamline at the Advanced Photon Source and demonstrate that with nanoscale positional control, coherent diffraction patterns can be measured with source-limited fringe visibilities more than 50% suitable for imaging by coherent Bragg ptychography techniques.

1. Introduction

Coherent hard X-rays focused to less than 100 nm provide unique opportunities for coherent diffraction imaging studies of nanoscale structure in materials [1]. In a Bragg geometry, nanofocused X-ray diffraction measurements can be made that are sensitive to strain, lattice rotation and other subtle structural variations in crystalline materials at high spatial resolution. Only regions of the sample within a small band of crystallographic orientations in the illuminated volume are selected, providing very high sensitivity to local structure and structural change [2]. By taking advantage of the wavefront coherence of the diffraction-limited nanofocused beam, the spatial resolution of scanning Bragg X-ray nanodiffraction measurements can be extended well beyond the beam size limit by employing ptychographic coherent diffraction imaging techniques [3–6]. Bragg ptychography uses iterative algorithms to invert multiple overlapping coherent nanodiffraction patterns into a self-consistent, high-resolution real-space image of a diffracting crystal, enabling the visualization of diffracting crystalline structure at the nanoscale. Because ptychography is based on the inversion of coherent diffraction patterns from well-defined, closely spaced regions of a crystal, the technique places extremely stringent requirements on beam coherence, positioning and stability in order to measure high-contrast coherent nanodiffraction suitable for image reconstruction.

Here, we discuss the instrument design elements and performance that enable the measurement of high-angle Bragg coherent nanodiffraction patterns with a sub-100 nm X-ray beam at the Hard X-ray Nanoprobe beamline at the Center for Nanoscale Materials and the Advanced Photon Source [7]¹. We present examples of coherent Bragg nanodiffraction patterns measured from different nanostructured thin films, we comment on the nature of the coherent diffraction observed from these films, and we demonstrate that the measured fringe visibility is source-limited and consistent with calculations of the expected degree of coherence.

2. Coherence, focusing and positioning at the Nanoprobe

Bragg ptychography with a nanofocused beam requires the measurement of overlapping coherent nanodiffraction patterns of a Bragg peak from well-defined volumes of a crystal. At the CNM/APS Nanoprobe Instrument (NPI), a ptychography technique known as Bragg projection ptychography (BPP) has been developed [3,8] that enables coherent diffraction imaging of crystalline thin films. BPP involves raster scanning a focused hard X-ray beam (approx. 35–85 nm FWHM) with a step size well below the focal spot size (approx. 15–30 nm step size) to assure significant point-to-point overlap of the film volumes sampled by the beam at each step. In all ptychography experiments, measuring high-contrast diffraction from a constant scattering volume is required for successful image reconstruction, along with accurate knowledge of the beam position.

The NPI uses a Fresnel zone plate (FZP) diffractive optic to focus 7–12 keV synchrotron X-rays to a nanoscale spot on the sample [7]. To achieve a nanoscale focus, the beamline was designed to operate with spatially coherent X-rays. The FZP is positioned at a distance of 74 m from the undulator X-ray source. The acceptance of the FZP matches the transverse coherence length of the incident X-rays in the vertical direction, as defined by the vertical source (approx. 25 μm FWHM Gaussian profile). This enables the use of FZPs with an acceptance of 100–160 μm depending on the operating energy and desired coherence. In the horizontal direction, the size of the X-ray source is s_h∼550 μm. Spatial filtering using a beam defining aperture positioned 40 m from the source is used to match the longitudinal coherence length in the horizontal direction to the zone plate acceptance. With a horizontal aperture size of approximately 13–25 μm, this provides symmetrical, spatially coherent illumination of the FZP and allows diffraction-limited focusing to a spot size as small as 35 nm (intensity FWHM). The Si (111) monochromator has a sufficiently small bandpass to provide longitudinally coherent illumination to the FZP. Further details as to the beamline and NPI design can be found in [9,10].

With an estimate of the source intensity profile at a given monochromatic photon wavelength, the degree of wavefront coherence propagating from the source can be calculated using the van Cittert–Zernike theorem [11–14]. From this formalism, a normalized complex coherence factor, μ₁₂, can be determined which describes the degree of spatial coherence in the wavefront as a function of the separation of two illuminated points. Figure 1 shows calculations of the magnitude of the complex coherence factor in the vertical direction of the FZP, |μ₁₂|_v, for two different photon energies, assuming a source with 25 μm FWHM vertical gaussian width, 74 m from the zone plate. On each plot, the dashed lines indicate the coherence factor at a point separation, Δy, corresponding to specific zone plate diameters used at the NPI. In both cases, the coherence factor at the zone plate is relatively high: μ₁₂=0.62 at 10 keV for a 133 μm FZP, and μ₁₂=0.79 at 9.5 keV for a 100 μm FZP. These two experimental conditions correspond to coherent diffraction measurements that will be discussed in the following section.

Figure1.

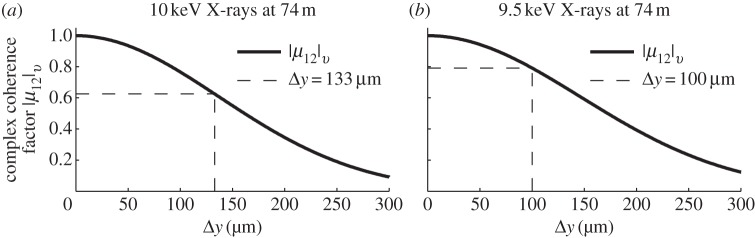
The value of the complex coherence factors in the vertical direction (|μ₁₂|_v) calculated at the plane of the NPI zone plate optic at 10 and 9.5 keV are shown in (a) and (b), respectively. Both calculations assume a 25 μm FWHM Gaussian intensity profile and a source-to-optic distance of 74 m. The curves shown are functions of Δy, the vertical separation of two points illuminated in the plane of the zone plate. The wavefront coherence at Δy= 133 μm and Δy=100 μm are indicated with dashed lines at the two energies. These values of Δy correspond to zone plate diameters used experimentally. The 133 μm diameter zone plate corresponds to a coherence factor of 0.62 at 10 keV, and at 9.5 keV, a 100 μm diameter zone plate corresponds to a μ₁₂ of 0.79.

The high degree of spatial coherence of the wavefront illuminating the zone plate at the NPI generated a nearly diffraction limited focus. Typical focusing optics used have outer zone widths ranging from 24 to 60 nm which correspond to diffraction-limited foci with 30–72 nm FWHM intensity profiles. A 35 nm FWHM focus has been demonstrated experimentally at the NPI [7]. Because the FZP is chromatic, focal lengths range from 20 to 30 mm, and convergence angles are typically between 0.2^° and 0.3^° (approx. 3–5 mrad) at the operating energies of the NPI.

Such tightly focused beams require a positioning system with nanometre scale resolution and stability that is robust to sample drift and instrument vibration through the duration of data acquisition. The NPI is equipped with an interferometric laser position tracking system that monitors the relative position of the FZP and sample and feeds position information back to a piezo-controlled optics stage. This system maintains registry between the FZP and sample in terms of relative position and relative beam angle, which together enable nanoscale stability and repeatability. The performance of the positioning system is demonstrated in figure 2, showing the laser tracking of the optic stage during a 50 nm commanded vertical displacement of the FZP with a 4 nm RMS stability. With the focused beams at the NPI, this level of positional control translates to a less than 10% RMS positional fluctuations, enabling diffraction patterns to be measured from a mostly fixed sample volume over the course of a typical 5–30 s exposure. Furthermore, typical step sizes of 15–30 nm used in BPP measurements can accurately be achieved. Over the course of a 1–2 h BPP scan at the NPI, the drift of the laser reference frame will be less than 4 nm, such that issues of beam position uncertainty that are known to seriously diminish the quality of ptychographic reconstructions [15] are minimized.

Figure2.

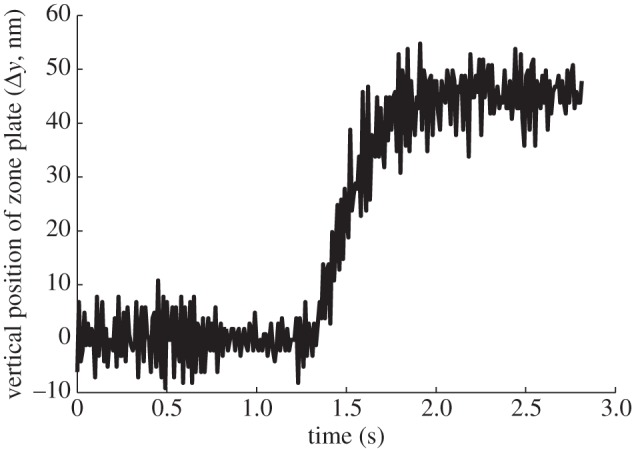
The position of the FZP optic as tracked by the laser interferometric feedback system at the NPI is shown here sampled at 1 kHz during the course of a single 50 nm displacement in the vertical direction relative to the sample. With a 4.0 nm RMS oscillation about the command value, reliable raster scans of the focused X-ray beam with step sizes down to less than 10 nm can accurately and reliably be achieved.

This level of precision will benefit any scanning probe measurement involving a nanofocused X-ray beam, but it is especially critical for Bragg coherent diffraction imaging experiments. Because of the complexity of the amplitude and phase distribution of the focused wavefront, beam motions of order of 10 nm that occur during the course of a fixed-point measurement reduce the visibility of intensity fringes diffracted from nanostructured samples. High-contrast diffraction patterns are needed for the reliable convergence of iterative ptychography algorithms, improving the resolution of the resulting image. Recently developed ptychography algorithms can accomodate diffraction patterns blurred by various sources of decoherence [16,17] and beam position uncertainty [15]; however, these approaches increase computation time and tend to impose stricter requirements on the overlap condition, increasing the dose on the sample. By analysing coherent diffraction patterns measured under different experimental conditions, we show that the coherence and positional control of the nanofocused beam allows for the measurement of coherent diffraction patterns with source-limited fringe visibility consistent with the expected complex coherence factor |μ₁₂| of the FZP illumination.

3. Coherent diffraction from nanostructured thin films

The NPI was used to measure symmetric Bragg coherent nanodiffraction patterns from three different epitaxial nanostructured thin films with distinct specular Bragg peak signatures in reciprocal space. Below, we discuss coherent Bragg diffraction at the NPI from an ‘ideal’ single-crystal thin film sample, we highlight two different ferroelectric thin films with nanoscale domain structure and we analyse the observed coherent diffraction patterns in terms of the structural characteristics of the crystalline films.

The basic characteristics of thin film Bragg coherent diffraction at the NPI are depicted schematically in figure 3, in which symmetric Bragg diffraction experiments from two different regions of a 65 nm single-crystal SiGe thin film are depicted. Figure 3a shows a schematic cross section of a flat section of the film in a horizontal scattering geometry with straight undistorted (001) lattice planes (vertical grey lines). Extending from the surface of the film is a set of 00L reciprocal space Bragg peaks (shown as dots) connected by the specular crystal truncation rod (CTR) oriented normal to the surface. In this experiment, the scattering plane is normal to the page along the horizontal direction (i.e. the incoming and diffracted X-ray beam direction vectors have one component into the page and one along x). The charge-coupled device (CCD) area detector in the experiment is indicated by the grey rectangle which approximates the field of view of the measurement in reciprocal space. Details of the SiGe film preparation, data collection at the NPI and imaging by BPP are given elsewhere [3]. Here, we focus on the qualitative properties of the nanodiffraction patterns measured from this sample to serve as an example of nanofocused diffraction from a homogeneous, high-quality crystal thin film.

Figure3.

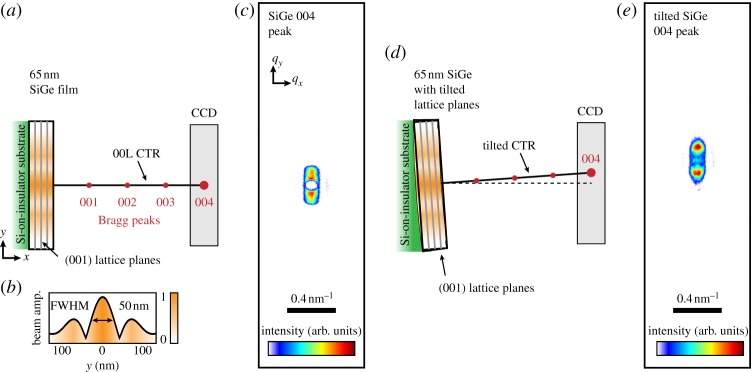
Schematics of a symmetric coherent nanodiffraction experiment in which two different regions of a 65 nm-thick epitaxial SiGe film grown on a silicon-on-insulator substrate were illuminated with nanofocused X-rays at the NPI are shown along with measured data. (a) A flat section of the film illuminated with the shaded beam profile shown in (b). (b) A calculation of an ideal focused X-ray profile at the NPI. In (a,d), the scattering plane is horizontal and normal to the page. The (001) lattice planes in the crystal films are depicted by the grey lines. The specular Bragg peak positions are depicted by circles along the crystal truncation rod (small circles indicate a forbidden SiGe reflection), and the measured 004 Bragg peak is shown in (c). A region of the film that was slightly tilted is depicted in (d) in which the 004 Bragg peak is displaced from the scattering plane, seen experimentally as a shift of the Bragg peak from the centre of the detector in (e). (Online version in colour.)

The focused X-ray beam defines a nanoscale volume within the film that Bragg diffracts. In figure 3b, a calculated 50 nm FWHM amplitude profile of an aberration-free NPI beam in the focal plane is depicted along with a corresponding amplitude colour scale. The shaded profile of the focused beam is superimposed on the thin film cross section to highlight the region of the film that diffracts at the Bragg condition, including the areas beneath the central focal envelop and first-order Airy fringes. The SiGe thin film in figure 3a has a CTR that is aligned with the scattering plane, and a single 004 Bragg peak in figure 3c was observed in the centre of the CCD detector field of view, as seen in figure 3c. The shape of this Bragg peak is characteristic of Bragg nanodiffraction from an ideal thin film illuminated with a high numerical aperture FZP [3,18]. The diffraction pattern features a Bragg intensity ‘stripe’ along q_y that is limited at its outer edges by the numerical aperture of the FZP and is eclipsed in the centre by the FZP beam stop. The width of the peak along q_x is related to the 65 nm thickness of the film. Figure 3d depicts 004 Bragg diffraction from a different region of the same SiGe film that is bent slightly from top to bottom. The bent lattice planes tilt the 00L Bragg peaks away from the horizontal scattering plane, such that the observed 004 Bragg peak is displaced from centre of the detector (figure 3e). In this case, the beam samples a continuum of slightly varying, tilted (001) lattice orientations that coherently interfere in the diffraction pattern. This distribution of illuminated lattice tilts slightly changes the intensity distribution of the Bragg peak, though its features still closely resemble the ‘ideal’ thin film case in figure 3c.

The examples in figure 3 demonstrate the characteristics of Bragg nanofocused diffraction from thin film crystals with an unchanging or gradually tilting lattice in the illuminated volume. However, the majority of thin films used for applications in nanoscience and nanotechnology are structurally heterogeneous at sub-beam length scales. Thus, multiple nanoscale regions of the film with different crystal characteristics are simultaneously illuminated and can interfere coherently when diffracting. In figure 4, we highlight two examples of epitaxial single crystal oxide ferroelectric thin films with nanoscale domains that produce distinct coherent interference patterns at Bragg peaks. Schematic representations of a 200 nm thick film of (001)_p BiFeO₃ grown on a (110) TbScO₃ single-crystal substrate and a 25 nm thin film of (001) PbTiO₃ grown on a (001) SrTiO₃ single-crystal substrate are shown in figure 4. The periodic domain structures depicted in the two films are governed by two different types of (001) lattice behaviour, discussed below. The details of sample preparation and NPI characterization are given elsewhere [19–21] and are summarized in table 1. In these examples, the domain sizes are such that isolating individual domains with a 40–80 nm focused X-ray beam is challenging. Multiple domains in the illuminated volume with slightly different crystal properties diffract coherently and produce distinct Bragg speckle patterns that can be used for coherent diffraction imaging by BPP.

Figure4.

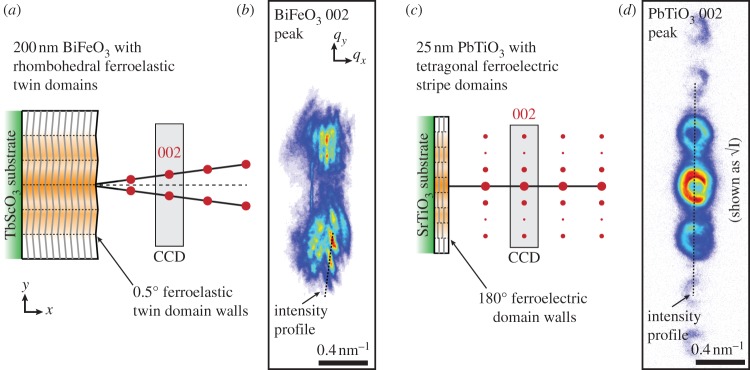
Examples of coherent nanodiffraction from domains of ferroelectric thin films are shown. A 200 nm-thick BiFeO₃ film grown epitaxially on TbScO₃ with multiple twin domains illuminated by the beam is shown in (a). The measured 002 Bragg peak in (b) was split because of the local lattice tilts. Measurements were also made of a PbTiO₃ thin film with ferroelectric stripe domains (d), shown schematically in (c). The alternating phase of the stripe domains decorated the measured 002 Bragg peak with satellite peaks that encode the phase and shape of the illuminated stripe domains. (Online version in colour.)

Table 1.

Summary of the experimental parameters for the BiFeO₃ and PbTiO₃ coherent nanodiffraction measurements. θ_Br is the symmetric Bragg angle, t_film is the film thickness, E_phot is the X-ray photon energy, s_v is the full width at half max undulator source size estimate used in the calculation of |μ₁₂|_v, count time describes the CCD detector exposure time, D_FZP is the diameter of the FZP, d_s is the distance from the undulator source to the FZP, |μ₁₂|_v is the calculated value of the coherence factor at a point separation corresponding to D_FZP and V is the observed fringe visibility.

	Bragg peak	θBr (°)	tfilm (nm)	Ephot (keV)	sv (μm)	count time (s)	DFZP (μm)	ds (m)	|μ12|v at FZP	Vobsqy at detector
BiFeO3	002	18.2	200	10.0	25	10.6	133	75	0.62	0.56±0.19
PbTiO3	002	18.4	25	9.50	25	10.0	100	75	0.79	0.73±0.11

At room temperature, BiFeO₃ is strongly ferroelectric. When grown as an epitaxial thin film, it can adopt a twin domain structure with corrugated (001) lattice planes that are tilted by approximately 0.5^° from the average surface plane with domains 30–100 nm in width, as depicted in figure 4a. The 200 nm BiFeO₃ film used in this study was oriented such that the twin domain walls were aligned with the scattering plane. In contrast to the tilted SiGe diffraction measurement, the distribution of lattice tilts in the illuminated volume, that spanned several domains, was much more diverse. As a result, a densely speckled split peak was observed at the 002 Bragg condition as shown in figure 4b, with maxima displaced from the scattering plane by an amount determined by the lattice tilts in the illuminated domains.

A comparison can be made with another room-temperature ferroelectric thin film system, a 25 nm epitaxial (001) PbTiO₃ thin film grown on (001) SrTiO₃ (figure 4c,d). This system differs from BiFeO₃ in terms of the coherent scattering mechanism and the observed diffraction pattern. The 25 nm thick PbTiO₃ thin film measured in this experiment had ferroelectric stripe domains modulated by the out-of-plane ionic displacements that drive local polarization in the film [22], introducing an alternating phase shift to the (001) lattice planes in each domain. As shown in figure 4d, the domain walls were again aligned with the scattering plane and each 00L Bragg peak was decorated with satellite peaks that encode information about the morphology and phase shift of the ferroelectric stripe domains illuminated by the beam (as opposed to lattice tilt).

By comparing nanodiffraction from all three thin film systems discussed above, we observe that coherent diffraction from systems with local crystalline nanostructure dominated by lattice tilt (as in SiGe and BiFeO₃) shifts the specular Bragg peaks away from the horizontal scattering plane. On the other hand, film systems with in-plane periodic density or diffracted phase (as in PbTiO₃) produce Bragg peaks in the scattering plane that are decorated by satellites. Thus, the images of these different film systems as reconstructed by BPP will convey different characteristics of the underlying thin film lattice [3,8]. However, successful image reconstruction by BPP is predicated on minimizing sources of decoherence in the experimental measurement, which can be estimated by analysing fringe visibility in Bragg nanodiffraction patterns. We note that in the examples above, the samples were designed such that the specular Bragg peaks of the substrate were separated from those of the film to enable the coherent diffraction from the film to be isolated in reciprocal space. In the SiGe sample, this was achieved by using a Si substrate that had a crystallographic offset of 0.3^° relative to the SOI. In the PbTiO₃ and BiFeO₃ samples, the epitaxial thin films had slightly different out-of-plane lattice parameters that enabled the measurement of thin film specular coherent Bragg peaks without interference from the substrates.

4. Coherence and fringe visibility

The magnitude of the complex coherence factor |μ₁₂| of a monochromatic wavefield originating from an incoherent source (for example a synchrotron) can be determined by measuring the fringe visibility in a far-field diffraction pattern from sharp, well-defined real-space objects. The fringe visibility V is given by

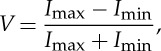4.1

where 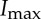and 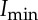are the observed intensities of a fringe at its peak and in an adjacent valley, respectively. In the case of a Young's double slit experiment involving diffraction from two separated ideal slits or pinholes, |μ₁₂|=V , as derived in references [11,12]. More recently, it has been shown that this relationship also holds for Bragg coherent diffraction patterns of compact nanocrystals with sharp facets illuminated with synchrotron X-rays [23]. Similarly, here we assume that |μ₁₂| in the vertical direction is equivalent to the fringe visibility along q_y in the coherent Bragg diffraction patterns measured from the ferroelectric thin film described above. This assumption is based on the fact that the domain walls in these systems are extremely thin (approx. 0.5 nm [19,24]), and their alignment with the scattering plane in both measurements created sharp interfaces in x, normal to the y direction. We further assume that the FZP behaves as an ideal lens and that the complex coherence factor in the plane of the wavefront illuminating the FZP is preserved upon focusing [25]. Finally, we assume that peak broadening owing to strain is minimal in these ferroelectric thin film domains and is not a significant factor in the observed fringe visibility.

We can therefore compare the visibility of the fringes along q_y in the coherent nanodiffraction patterns measured from BiFeO₃ and PbTiO₃ with calculations of |μ₁₂|_v at the FZP to evaluate the Nanoprobe as a coherent diffraction instrument. In the diffraction patterns shown in figures 3 and 4, the visibility along q_x depends on the horizontal coherence at the FZP, the transverse beam coherence and the sharpness of projected domain features that lie out of the scattering plane. Because this relationship is considerably more difficult to predict, we will focus on the analysis of the fringe visibility along q_y (V _qy) in the following discussion. We also note that the diffraction patterns from SiGe in figure 3 do not display strong fringes along q_y outside of the central Bragg peak envelope, and will therefore be excluded from the discussion. An analysis of fringe visibility along q_x in the SiGe experiment is presented elsewhere [3].

As summarized in table 1, the measurement of BiFeO₃ was done at a photon energy of 10 keV with a 133 μm zone plate and the PbTiO₃ diffraction pattern was measured at 9.5 keV with a 100 μm diameter FZP focusing optic. These two experimental conditions correspond to two different values of |μ₁₂|_v at the different energies and FZP diameters: |μ₁₂|_v=0.62 at 10 keV, and |μ₁₂|_v=0.80 at 9.5 keV, as shown in figure 1. These calculations of |μ₁₂|_v provide an estimate of the maximum expected fringe visibility in the two experiments. The fringes shown in figure 5 were extracted from the BiFeO₃ and PbTiO₃ coherent diffraction patterns in figure 4 along the dotted lines, which lie mostly along q_y. (Before line extraction, the diffraction patterns were background-corrected.) From the intensity profiles shown in figure 5, estimates of V _qy can be made for the two experimental conditions and were determined to be 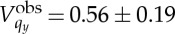for BiFeO₃ and 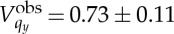for PbTiO₃ with error bars reported as one standard deviation (table 1). The difference in estimated error reflects the different number of fringes aligned along q_y in the coherent nanodiffraction patterns from the two films.

Figure5.

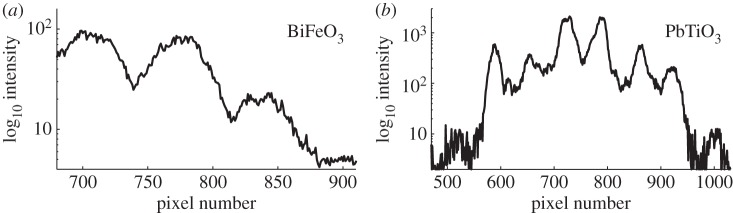
(a,b) Coherent diffraction fringe intensity profiles corresponding to the dotted lines in figure 4b,d are shown from which the visibility of the speckle pattern can be estimated.

The close agreement between 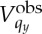and |μ₁₂|_v in both cases, differing by 8.6% on average, is plotted in figure 6. This indicates that the NPI can be used for coherent nanodiffraction measurements with nearly source-limited contrast. The 8.6% reduction of visibility includes imperfections in the beamline, in particular downstream of the beam-defining aperture, such as aberrations in the optics and the stabilization of the sample-to-optic reference frame. Because the measured visibility corresponds closely to the source-limited coherence factor, the calculated two-dimensional complex coherence factor at the FZP can be incorporated into the image reconstruction algorithms as a known correction [17], especially for cases considered partially coherent, V <0.7. This will improve algorithm convergence and will eliminate the need to treat the coherence function as an unknown when reconstructing images, reducing computation time.

Figure6.

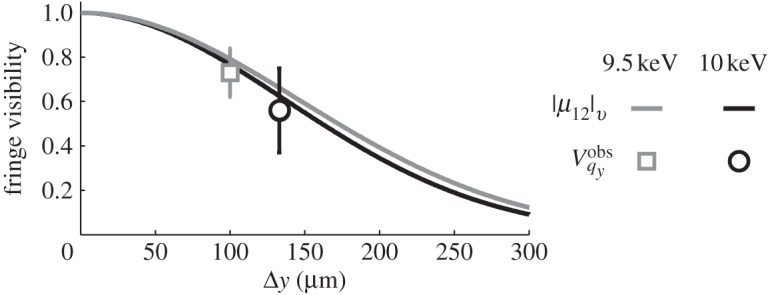
The fringe visibility determined from BiFeO₃ and PbTiO₃ coherent nanodiffraction patterns, collected at 10 and 9.5 keV with 133 and 100 μm diameter FZPs, respectively, are shown alongside calculated values the complex coherence factors |μ₁₂|_v for the two conditions.

5. Conclusion

Bragg coherent diffraction imaging with nanofocused beam provides a unique and powerful capability to study materials and devices with nanoscale functional features at lengths scales on the order of 10 nm and below. High spatial coherence and high accuracy and stability of the nanofocused X-ray beam with regard to the sample, as implemented in the Hard X-ray Nanoprobe, are required to ensure that the beam samples a constant volume over the course of the exposure. Here, we have given examples of coherent nanodiffraction from three different nanostructured single crystal thin film systems and demonstrated that the observed fringe visibility is nearly source-limited.

Coherent diffraction imaging techniques, for example X-ray BPP, can therefore be used to disentangle and spatially resolve various structural features relating to the physics of thin film heterostructures and devices that are otherwise difficult to extract by conventional reciprocal space analysis techniques. As such, coherent diffraction imaging implemented at instruments, for example the Hard X-ray Nanoprobe, provides new opportunities for non-destructive, in situ studies of nanoscale structural phenomena and transformations in advanced materials.

Funding statement

This work, including use of the the Center for Nanoscale Materials and the Advanced Photon Source, was supported by the U. S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract no. DE-AC02-06CH11357. S.O.H., M.J.H., C.M.F. and P.H.F. were supported by U.S. DOE, Basic Energy Sciences, Materials Sciences and Engineering Division.