Using Multidimensional Mutual Information to Prioritize Mammographic Features for Breast Cancer Diagnosis

Abstract

The goal of this study was to demonstrate that information theory could be used to prioritize mammographic features to efficiently stratify the risk of breast cancer. We compared two approaches, Single-dimensional Mutual Information (SMI), which ranks features based on mutual information of features with outcomes without considering dependency of other features, and Multidimensional Mutual Information (MMI), which ranks features by considering dependency. To evaluate these approaches, we calculated area under the ROC curve for Bayesian networks trained and tested on features ranked by each approach. We found that both approaches were able to stratify mammograms by risk, but MMI required fewer features (ten vs. thirteen). MMI-based rankings may have greater clinical utility; a smaller set of features allows radiologists to focus on those findings with the highest yield and in the future may help improve mammography workflow.

Introduction

Mammography is the most widely used imaging modality for breast cancer diagnosis. The efficacy of mammography depends on radiologists’ interpretative skills and integration of mammographic features into accurate assessments. The Breast Imaging Reporting and Data System (BI-RADS) lexicon standardized the terminology used to describe mammographic features for estimating the risk of breast cancer and making management recommendations^1–3. However, BI-RADS does not make explicit recommendation as to which features should be prioritized in risk assessment and decision making ⁴. The absence of a priority recommendation presents an opportunity to develop feature ranking algorithms to aid radiologists in gaining the knowledge of these features and choosing the most informative variables for accurate and efficient diagnosis. Radiologists in a busy practice would likely benefit from understanding the highest yield (most predictive) features in order to focus their attention in the most accurate and efficient manner.

Mutual information analysis has been widely used to rank features by quantifying the information that each feature provides for estimating the outcomes of interest ^{5, 6}. Prior studies have explored mutual information to identify diagnostically important mammographic features^7–9. However, these studies selected only the top-ranked features without considering dependency among features. The simple method of selecting the best individual features may fail to efficiently select the most informative group of mammographic features for breast cancer diagnosis due to the fact that the best two individual features are not always the two best ^10–12. In contrast, multidimensional mutual information analysis includes dependency in ranking for feature selection^13–17. Investigators have used multidimensional mutual information analysis to rank features from a mixture of mammographic features and some image processing features such as gray level or texture values extracted from mammograms ¹⁸. In this study, we aim to rank mammographic features exclusively for selecting the most informative features. We use mutual information analysis and Bayesian reasoning by considering dependency among features to inform decision makers which features would be most valuable in the diagnosis of breast cancer.

Materials and methods

The institutional review board of the University of Wisconsin Hospital and Clinics (UWHC) exempted this Health Insurance Portability and Accountability Act-compliant (HIPAA) compliant retrospective study from requiring informed consent.

Subjects

We collected data for consecutive mammography findings observed at UWHC between Oct 1, 2005 and Dec. 30, 2008. The database consisted of 9,986 mammographic findings for 6,440 patients. The mean age of the patient population was 53.43 years ± 12.74 (standard deviation). Demographic risk factors (age, personal history of breast cancer, family history of breast cancer, use of hormone replacement therapy, and a personal history of breast surgery) and mammographic features were described according to BI-RADS lexicon, and were prospectively catalogued by using a structured reporting system (PenRad Technologies, Inc., Buffalo, MN). Demographic risk factors were recorded by technologists; mammographic features were entered by radiologists. Eight radiologists interpreted the mammograms. All of them have 7–30 years of experience interpreting mammography, and meet the standards of the Mammography Quality Standards Act (MQSA) as qualified physicians in interpreting mammograms. The outcomes of interpretation were checked against MQSA audit requirements as well as national benchmarks^{19, 20}.

Features and the outcome of interest

In this study, we ranked mammographic features in the most clinically relevant manner possible. Specifically, we included demographic risk factors, which were typically available in clinical practice, in this experiment to take into account their effects on the rankings of mammographic features. As a result, the set of feature variables in the experiment consisted of five demographic risk factors (age, personal history of breast cancer, family history of breast cancer, hormone replacement therapy, and the personal history of breast surgery) and 27 variables of mammographic features (Table 1). We also included breast composition in the experiment since it is an important feature variable that confers breast cancer risk^21–24. In the following context, we use mammographic features to stand for those 33 feature variables without differentiation between demographic risk factors and variables of mammographic features.

Table 1.

Feature Variables Used in Our Study

Feature Variable	Instances
Age	<46, 46–50, 51–55, 56–60, 61–65, >65
Personal history of breast cancer	Yes, no
Family history of breast cancer *	None, minor, major
Surgery history of breast cancer	Yes, no
Hormone replacement therapy	Yes, no
Breast composition **	1, 2, 3, 4
Mass shape	Oval, round, lobular, irregular, missing
Mass stability	Decreasing, stable, increasing, missing
Mass margin	Circumscribed, ill defined, microlobulated, speculated
Mass density	Fat, low, equal, high, missing
Mass size	None, small (<3 cm), large (>3 cm)
Lymph node	Present, not present
Asymmetric density	Present, not present
Tubular density	Present, not present
Skin retraction	Present, not present
Nipple retraction	Present, not present
Skin thickening	Present, not present
Trabecular thickening	Present, not present
Skin lesion	Present, not present
Axillary adenopathy	Present, not present
Architectural distortion	Present, not present
Calcifications
Popcorn	Present, not present
Milk of calcium	Present, not present
Rod-like	Present, not present
Eggshell	Present, not present
Dystrophic	Present, not present
Lucent	Present, not present
Dermal	Present, not present
Round	Scattered, regional, clustered, segmental, linear ductal
Punctate	Scattered, regional, clustered, segmental, linear ductal
Amorphous	Scattered, regional, clustered, segmental, linear ductal
Pleomorphic	Scattered, regional, clustered, segmental, linear ductal
Fine linear	Scattered, regional, clustered, segmental, linear ductal

^*minor = non-first-degree family member(s) with a diagnosis of breast cancer, major = one or more first-degree family member(s) with a diagnosis of breast cancer.

^**1 = predominantly fatty, 2 = scattered fibroglandular, 3 = heterogeneously dense, 4 = extremely dense.

We matched mammography finding reports with the cancer registry at our institution’s Comprehensive Cancer Center, which served as the reference standard. The cancer registry achieves high collection accuracy because the reporting of all cancers is mandated by state law and checked using nationally approved protocols ²⁵. We considered a finding “malignant” if it was matched with a registry report of ductal carcinoma in situ or any invasive carcinoma. All other findings shown to be benign with biopsy or without a registry match within 365 days after the mammogram were considered “benign”. Our study used the finding’s status (malignant or benign) as the outcome.

Mutual information

Originating from Shannon’s information theory ⁶, mutual information (MI) of a variable v₁ with respect to the other variable v₂ is defined as the amount by which the uncertainty of v₁ is decreased with the knowledge that v₂ provides. The initial uncertainty of v₁ is quantified by entropy H(v₁). The average uncertainty of v₁ given knowledge of v₂ is conditional entropy H(v₁|v₂). The difference between initial entropy and conditional entropy represents therefore MI of v₁ with respect to v₂. MI is defined as follows:

$$\text{MI}(v_1;\hspace{0.17em}{v}_2)=H(v_1)-H(v_1|v_2)=\sum _{v_2}\sum _{v_1}p(v_1,\hspace{0.17em}{v}_2)\mathit{log}\hspace{0.17em}\frac{p(v_1,\hspace{0.17em}{v}_2)}{p(v_1)p(v_2)}$$

where p (v₁) and p (v₂) are the marginal probability of v₁ and v₂, and p(v₁, v₂) is their joint probability.

In the following context, we use MI(x₁; x₂) to stand for the information value that one mammographic feature x₁ provided for estimating the other mammographic feature x₂. We use single-dimensional mutual information SMI(x; y) to denote the information that one mammographic feature x provided for estimating the outcome y. SMI does not take into account dependency among features.

We use multidimensional mutual information MMI(x; y) to denote the information that one mammographic feature x provides for estimating the outcome y when dependency with other mammographic features is considered. We assess MMI by an algorithm that minimizes Redundancy among features while Maximizing Relevance to the outcome (mRMR)^{13–16, 26}. “Redundancy” is related to MI of features with each other, and “relevance” is defined as SMI of features with the outcome. Specifically, in this study, we use the following algorithm to rank most important mammographic features ²⁶.

1. We calculate SMI associated with each feature as relevance.

2. We compute MI between any pair of features for quantifying redundancy.

3. We choose the feature with the highest SMI as the most important one.

4. We select subsequent important features sequentially, such that each feature simultaneously maximizes its SMI and minimizes MI between the feature of interest and already selected features. Specifically, we choose the next most important mammographic feature x_i, i = 2, 3, 4, ⋯, that maximizes

   $$\text{SMI}(x_i;\hspace{0.17em}y)-\sum _{j<i}\frac{\text{SMI}(x_j;\hspace{0.17em}y)}{H(x_j)}\text{MI}(x_i;x_j)$$

   where H(x) represents the entropy of x. The feature x_j is one of important features selected ahead of x_i and y is the outcome. The computational complexity of this search method is O(n²).

Study design and statistical analysis

To calculate SMI of a feature with respect to the outcome, we first constructed a joint probability table of the feature and the outcome from our database. After we derived the probability of the outcome and the conditional probability of the outcome given the feature from the joint probability table, we calculated the corresponding entropy of the outcome and conditional entropy. We obtained SMI of each feature with respect to the outcome, and ranked all features according to SMI values.

To evaluate rankings according to SMI, we first defined feature sets by sequentially selecting the most informative features, one by one, in order of SMI values. Then, using 10-fold cross-validation, we trained and tested Bayesian networks (BN) using a tree augmented naïve Bayes algorithm on the set of sequentially selected features in Weka (Weka, version 3.6.4; University of Waikato, Hamilton, New Zealand) ²⁷. We chose a BN as our prediction method since it has a clear semantic interpretation of model parameters ²⁸. We constructed a receiver operating characteristic (ROC) curve based on estimated probabilities from the BN, and obtained the area under the ROC curve (AUC) as a measure of overall discriminating performance. We found the maximum value of AUC in this process. We compared AUC of different sets of features with the maximum AUC by using the DeLong method ²⁹, implemented in MATLAB software (MathWorks, Natick, MA). We used a P-value of .05 as the threshold for statistical significance testing to determine the difference between two AUC values. We also used “parsimony” to describe the performance of ranking approaches. We define parsimony here as the smallest number of the features needed to reach a performance level such that there is no significant difference of AUC as compared with the maximum AUC.

We then used a similar procedure to rank features using MMI approach. We first obtained relevance measure of each feature with respect to the outcome from SMI calculation. Then, we constructed joint probability tables for any pair of features from our database, and calculated MI values. We calculated MMI values for mammographic features by using mRMR algorithm and ranked features based on these MMI values.

Finally, using similar procedure of evaluating SMI rankings, we assessed the performance of MMI ranking approach. We first created feature sets with sequentially selected features, one by one, in order of MMI values and then trained BNs with those feature sets. After ROC curves were constructed with estimated probabilities from BNs, we calculated AUC values and implemented significance testing with the DeLong method. We also obtained parsimony of the MMI approach.

Results

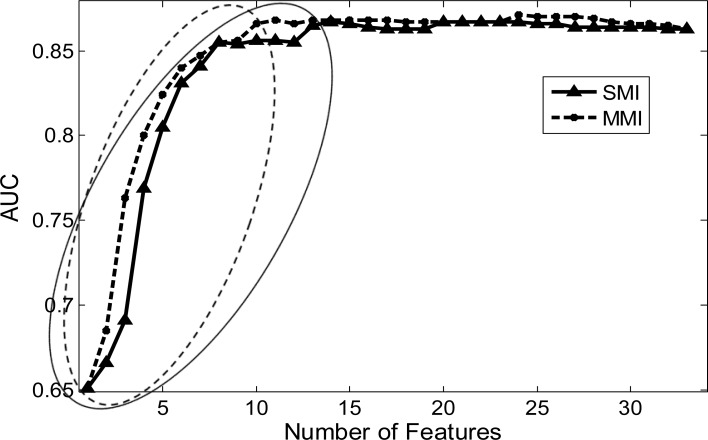
Both SMI and MMI could prioritize mammographic features. However, in terms of parsimony, MMI approach outperformed SMI. Specifically, when we calculated AUC values to evaluate SMI ranking results, we observed that AUC values increased as more features were included (solid curve in Figure 1). Parsimony was thirteen features for the SMI approach, which were needed to reach no significant difference of AUC as compared with the maximum AUC value (0.865 vs. 0.867, P-value = 0.432). For MMI ranking results, we observed that correspondent AUC values also increased as more features were included (dashed curve in Figure 1) while only ten features were needed to reach parsimony with no significant difference of AUC as compared with the maximum AUC value (0.866 vs. 0.871, P-value = 0.251).

Figure 1.

AUC changes with the number of selected features. Solid curve with triangle points, SMI; Dashed curve with star points, MMI. Triangle points in solid ellipse, parsimony features for SMI; Star points in dashed ellipse, parsimony features for MMI.

Maximum AUC values differed between SMI and MMI approaches. The maximum AUC value for SMI was not significantly larger than the AUC value obtained from a BN trained on the full set of all 33 features (0.867 vs. 0.863, P-value = 0.318) while the maximum AUC value for MMI was significantly larger than the AUC value of the full set of features (0.871 vs. 0.863, P-value = 0.039).

The rankings of mammographic features were different for SMI and MMI approaches. When we ranked features based on SMI values, we observed that mass margin and mass shape were the two most informative features for differentiating malignant from benign findings. When we ranked features based on MMI values, we observed that mass margin and mass density were the two most informative features while mass shape became the eighth most informative feature (Table 2). The change of the rankings occurred because the dependency between mass margin and mass shape was substantively more than that between mass margin and mass density. MI between mass margin and mass shape was 0.4292 while MI between mass margin and mass density was only 0.1737.

Table 2.

Ranking results based on SMI and MMI.

Feature Variable	SMI ranking	MMI ranking
Mass margin	①*	①
Mass shape	②	⑧
Mass density	③	②
Personal history of breast cancer (PHx)	④	③
Pleomorphic	⑤	④
Age	⑥	⑤
Mass stability	⑦	⑦
Fine linear	⑧	⑥
Mass size	⑨	33
Amorphous	⑩	13
Architectural distortion	⑪	⑨
Breast composition	⑫	12
Hormone replacement therapy	⑬	⑩
Family history of breast cancer	14	11
Surgery history of breast cancer	15	32
Punctuate	16	28
Round	17	18
Nipple retraction	18	14
Dystrophic	19	17
Skin thickening	20	24
Skin lesion	21	15
Axillary adenopathy	22	16
Skin retraction	23	27
Lymph node	24	26
Milk of calcium	25	19
Rod like	26	20
Trabecular thickening	27	29
Lucent	28	25
Eggshell	29	21
Dermal	30	22
Asymmetric density	31	30
Popcorn	32	31
Tubular density	33	23

^*Circles around the ranking numbers indicate parsimony features.

Discussion

Mutual information approaches (SMI and MMI) in general have the capability of determining the most informative mammographic features for breast cancer diagnosis. We find that multidimensional mutual information addresses the issue of dependency of features and may have the potential to assist radiologists in prioritizing predictive features in order to select the most parsimonious set of mammographic features with the highest predictive ability. Offering accurate breast cancer diagnosis to the ever-increasing number of women in need presents a great challenge because it demands both high sensitivity and high specificity. To ensure diagnostic accuracy, radiologists strive to provide reliable observations and assessments of routinely used mammographic features. On the other hand, to improve accuracy, radiologists are eager to garner additional features from other imaging modalities such as ultrasound and MRI for breast cancer diagnosis ^{30, 31} since they presume that the information from mammogram may be insufficient. Our results show that a BN trained with the whole set of those routinely used mammographic features demonstrates inferior performance as compared to the most parsimonious subset. The results of performance improvement with the most parsimonious subset are in concert with the objective of feature selection³². In summary, our study provides a fundamentally different strategy to help improve diagnosis accuracy by employing MMI approach to find a subset of the most important features for breast cancer diagnosis.

In a screening mammography program, accuracy is a high priority and efficiency is an important second goal. Identifying the most important features may help improve the efficiency of mammogram interpretation directly since radiologists can assess only these important features if they have this knowledge of mammographic features. In BI-RADS lexicon, there are many features routinely used to estimate breast cancer risk. SMI analysis demonstrated that thirteen features were needed to reach no significant difference of AUC as compared with the maximum AUC value. Performance analysis based on MMI reduced the number of important features to ten. Our study suggests that, in clinical practice, it appears that radiologists in our practice may have been equally accurate in their interpretations if they focused on less than one-third of routinely used mammographic features for breast cancer diagnosis. Assessing additional variables beyond important features does not improve accuracy. This suggestion of using a smaller set of important features for breast cancer diagnosis may help improve mammography workflow in the future.

Our results exhibit the importance of the dependency among features when we look for the most important features. Results of SMI analysis show that mass margin, mass shape and mass density are three most informative features in estimating the risk of breast cancer. However, in MMI analysis, we observe that mass margin is the most informative feature, mass density is the second most, and mass shape becomes the eighth most important feature (Table 2). This observation is in concert with clinical mammography interpretation; on mammography, a highly suspicious mass has an irregular shape with spiculated margins while a benign mass typically has a round shape with well-circumscribed margins. Hence, in MMI analysis, after mass margin is chosen at first, mass density instead of mass shape will be chosen as the second most important feature because mass density seems to contribute more “net” information than mass shape in estimating the risk of breast cancer. This observation suggests that in clinic mammography interpretation, radiologists should focus on the features having high mutual information with respect to the outcome and low mutual information with respect to other features.

Limitations and Future Work

There are several limitations to our study. First, our study focused on discussion of predictive accuracy associated with features but did not consider benefit and cost related to the decision. We plan to extend our study in this direction soon since cost-effectiveness analysis allows radiologists to compare the health gains that various decision of choosing the most important features can achieve. Second, our study used Bayesian networks to assess ranking results of mutual information analysis. A possible line of future research is to employ other prediction algorithms such as logistic regression, artificial neural network, or support vector machine for validating the validity of MMI rankings. Third, MMI addresses the issue of dependency among features but it does not guarantee the global optimization of feature selection. MMI belongs to the class of forward search methods in which one feature is selected at a time. At each step, each feature that is not already selected is tested for inclusion. It is difficult to search the whole feature space for these methods. However, although MMI is just an approximation method that obtains sub-optimal feature selection, it seems to be a practical way to achieve a high ranking accuracy with a low computation complexity. Finally, we generate the study findings based on the dataset from UWHC only. We plan to repeat our study on other datasets to ensure general validity of the study findings.

Conclusion

Our study demonstrates that SMI and MMI can be used to rank the relative importance of mammographic feature variables for breast cancer diagnosis. By considering dependency, MMI outperforms SMI in determining the smallest set of informative features with significantly more predictive performance than the entire feature set. In applications where addition of features incurs additional time or monetary cost, MMI may help reduce the cost of diagnostic testing. Moreover, MMI-based rankings may have greater clinical utility to the extent that a smaller set of features allows radiologists to focus attention sequentially on those findings with the highest yield.