Using Hierarchical Mixture of Experts Model for Fusion of Outbreak Detection Methods

Abstract

A wide variety of disease outbreak detection methods has been developed in automated public health surveillance systems. The choice of outbreak detection method results in large changes in performance under different circumstances. In this paper, we investigate how outbreak detection methods can be combined in order to improve the overall detection performance. We used Hierarchical Mixture of Experts, which is a probabilistic model for combining classification methods, for fusion of detection methods. Simulated surveillance data for waterborne disease outbreaks are used in this research to train and evaluate a Hierarchical Mixture of Experts model. Performance evaluation of our approach with respect to sensitivity-specificity trade-off and detection timeliness is provided in comparison with several other detection methods.

Introduction

The occurrence of infectious disease outbreaks results in high human and financial costs. The past decade has seen the emergence of diseases caused by previously unrecognized threats or the sudden appearance of known diseases in the environment. Since the probability of major infectious disease outbreaks is very high, their early detection is a crucial task in order to prevent or reduce the large spread of diseases. Automated public health surveillance systems monitor health data drawn from multiple sources, with the goal of detecting potential disease outbreaks rapidly and accurately.

When an outbreak occurs, the care-seeking infected population adds a signal to the background health utilization data. Screening large volumes of data, detecting changes in the number of infected people, and issuing alerts to draw an epidemiologist’s attention to anomalies are the roles of the outbreak detection process in automated public health surveillance systems. Surveillance systems analyse observed surveillance data (e.g. counts of Emergency Department visits) to detect significant changes from the expected data values. Typically, statistical outbreak detection algorithms monitor the surveillance ED visits time series and calculate the expected number of visits in a day. Then they compare this expected value with the observed value.

Recently, there has been a proliferation of outbreak detection algorithms in the field of syndromic surveillance. The choice of outbreak detection algorithm and its configuration can result in important variations in the performance of public health surveillance systems. However, there is little empirical evidence about which characteristics of syndromic surveillance systems determine their effectiveness in detecting outbreaks and it is not clear how public health practitioners should configure the systems in order to ensure effective outbreak detection. The performance evaluations have not kept pace with algorithm development. Evaluations are usually based on a single data set which is not publicly available, therefore, such evaluations are difficult to generalize or replicate. Furthermore, the performance of different algorithms is influenced by the nature of the disease outbreak. As a result of the lack of thorough performance evaluations, one cannot determine easily which algorithm should be applied under what circumstances.

There exists already a significant amount of work on fusion methods for outbreak detection, which focus on integrating predictions coming from multiple databases, or multiple sensors. However, little work has been invested so far in fusing currently available detection methods which work on a single stream of data (such as ER patient counts) but may have very different sensitivity, specificity, and timeliness. The objective of this work is to study how one can aggregate the predictions of several outbreak detection algorithms and to investigate whether this can enhance performance, compared to using single methods. We consider an outbreak detection task as a classification problem and outbreak detection methods as classifiers. Using Hierarchical Mixture of Experts (HME) model as a structure that aggregates the output of several classifiers and generates a single result, we combine the prediction of several widely used outbreak detection algorithms. In this study, as a background for comparison, we used the majority voting method to combine the prediction of several outbreak detection algorithms. Generally, the trade-off between missing outbreaks and generating false alarms is a challenging problem in the performance evaluation of detection methods. We evaluate the detection performance of both single and aggregated outbreak detection algorithms in terms of the sensitivity, specificity, and timeliness of detection.

The structure of this paper is as follows: in the Background section, we review outbreak detection methods and focus on some of the widely used detection algorithms that are employed in our study. Then we describe the majority voting method and HMEs for combining classifiers. In the Methods and Study Design section, first we describe the simulated surveillance data for waterborne disease outbreaks used in this study and then, we explain how the majority voting and HME methods are used to detect disease outbreaks. In the Results section, we evaluate the detection performance of our methods in comparison with other detection methods. This section is followed by discussion on the results. Concluding remarks and directions for future work are presented in the final section.

Background

Statistical outbreak detection methods

There are two main approaches for outbreak detection. One is based on regression modeling of surveillance data, the other is derived from probability-based process control charts which are widely used in monitoring industrial processes. Regression-based models usually use categorical variables to account for correlation and explain data features like seasonal and weekly trends. If the data history is short or counts are sparse, the adapted process control chart methods provide a better detection performance. These methods generally operate on a measure of how data vary from the baseline mean.

A set of widespread detection methods which were developed based on the process control chart concept are C-family detection algorithms ¹. The C1, C2, and C3, are adaptive algorithms developed in the Early Aberration Reporting System (EARS) by the Centre of Disease Control and Prevention (CDC). According to the Central Limit Theorem, which states that a series of means approaches a Gaussian distribution as the size of series increases, C-algorithms assume that the expected value of the time series for the given time t is the mean of the values observed during the baseline interval. If the difference between the observed value at a given time t and the mean of the baseline interval divided by the standard deviation of the baseline is bigger than a threshold, an unusual event is flagged and the possibility of a disease outbreak is signalled.

The C-algorithms are distinguished by the configuration of two parameters, the guardband and the memory. Generally, gradually increasing outbreaks can bias the test statistic upward, so the detection algorithm will fail to flag the outbreak. To avoid this situation, the C2 and C3 use a 2-day gap, called guardband, between the baseline interval and the test interval. Furthermore, C3 includes two recent observations, called memory, in the computation of test statistic of time t. In the EARS system, the length of the baseline interval used for the calculation of the expected value is 7 days; however, it can also be varied. All detection algorithms can be configured using varying alerting thresholds which result in different sensitivity and false alarm rates.

C-algorithms use a single baseline for both weekdays and weekends. However, most of the surveillance time series are affected by weekly patterns. This is because many health-care facilities have fewer visits during weekends and there is a sharp increase in the number of visits on Mondays which should not be considered as an outbreak. A revised version of C family algorithms that accounts for days of the week is W family algorithms. The W2 algorithm is a modified version of the C2 which takes weekly patterns of surveillance time series into account ². In the W2 algorithm, the baseline data is stratified to two distinct baselines: one for the weekdays, the other for weekends. The W3 algorithm includes 2 recent observations of each baseline and calculates the test statistic for time t based on the corresponding baseline.

The performance of outbreak detection algorithms is evaluated in terms of the sensitivity, specificity, and timeliness of detection. The sensitivity is the probability that a public health event of interest will be detected in the data given that the event really occurred. The specificity is the probability that no health event will be detected when no such event has in fact occurred ³. The timeliness is the proportion of saved time in the case that the outbreak is detected by the algorithm. Timeliness can be expressed as the proportion of saved time when an outbreak is detected relative to the onset of an outbreak. If an outbreak is detected, the timeliness of detection of the outbreak is computed as:

$$\mathit{timeliness}=1-\frac{t_{\mathit{detection}}-t_{\mathit{onset}}}{\mathit{outbreakDuration}}$$

where outbreakDuration is the number of days that the outbreak is continuing. The t_detection is the index of the day within the time series when the outbreak is detected and t_onset is the index of the day on which outbreak starts. The proportion of delay is subtracted from 1. Therefore, the higher value of the timeliness denotes the earlier detection of outbreak and the higher performance of the detection algorithm. Timeliness is equal to 1, if the outbreak is detected on the first day of occurrence. Timeliness is undefined when the outbreak is not detected. The sensitivity and timeliness are calculated per outbreak while the specificity is calculated per analysis interval ³.

Majority voting

Majority voting is an approach to combine prediction or classification methods. Assume that each classifier outputs a label for the instance i in the data set. The majority voting method finds the label which has been voted by the majority of the classifiers and outputs that label for the instance i. The predictions of different classifiers have equal weight in the unweighted majority voting method.

Hierarchical Mixture of Experts (HME)

In this section, we describe another method that aggregates the output of several learners for solving classification or regression problems and generating a single result. A Mixture of Experts is a structure in which the predictions of some learners (i.e. experts) are weighted based on the input variables and then combined to generate a single prediction. In this structure, if we have a set of K experts, a probabilistic combination is formed by

$$P(y|x)={\sum }_{k=1}^K{g}_k(x)P_k(y|x)$$

where P_k(y|x) is the probability of output y predicted by the kth expert and g_k(x) represents the input-dependent mixing coefficient for that expert. The mixing coefficients are also known as gating functions. The gating functions g_k(x) must satisfy the constraints of mixing coefficients, 0 ≤ g_k(x) ≤ 1 and Σ_kg_k(x) = 1⁴.

If we let each expert in the mixture be a mixture of experts itself, then this multilevel gating network leads to a more flexible structure, known as Hierarchical Mixture of Experts (HME) ⁵. HME follows the strategy of divide-and-conquer in statistics. This approach divides the input space into nested sequences of regions and fits simple hypotheses within these regions.

Learning the structure and adjusting the parameters of the HME are considered in a maximum likelihood framework. Jordan and Jacobs ⁵ apply the Expectation-Maximization algorithm (EM) for learning HMEs.

HMEs have previously been used successfully in time series analysis. For example, Jacobs and Jordan ⁶ developed a mixture of experts model for a speaker independent, four-class vowel discrimination problem in which the data formed two pairs of overlapping classes and different experts learned to concentrate only on one pair of classes. They compared this model with standard back propagation networks. and showed that the mixture of experts requires half as many epochs to reach the same error level. The idea behind this application is that if a training data set can be naturally divided into subsets that correspond to subtasks, using a combination of experts and a gating network that decides which expert should be used for each subset will reduce the interference. We hypothesise that the outbreak detection task follows this type of patterns as well.

Methods and Study Design

Simulated surveillance data

The simulated surveillance data that we used in this work was generated by the Surveillance Lab of McGill University using the Simulation Analysis Platform (SnAP) ⁷. They considered surveillance in an urban area to detect waterborne outbreaks due to the failure of a water treatment plant. In this simulation scenario, they varied two parameters for generating the outbreak signals: the duration of water contamination was varied over 6 values (72, 120, 168, 240, 360, 480) and the cryptosporidium concentration was varied in 3 levels (10⁻⁶, 10⁻⁵, 10⁻⁴). Each of these 18 scenarios was run 1000 times with random variation of other parameters. Then, these outbreak signals were superimposed on baseline data which was the count of people seeking medical help in the emergency departments of several Montreal hospitals for gastro-intestinal diseases over 6 years. The onset of the signal was randomly selected, relative to the baseline.

Evaluation set up

In order to aggregate the strength of several outbreak detection algorithms, we generated a data set including the prediction results of C1, C2, C3, W2, and W3 detection algorithms. The hypothesis is that information on whether or not in recent days an outbreak has been detected will improve the certainty of predictions in a surveillance system. To test this hypothesis, we added the prediction for 7 most recent days from W3 algorithm to the data set. Each instance i of the data represents a vector for outbreak prediction on day_i in our analysis, so the data contains 12 features. These features include the predictions of C1, C2, C3, W2, W3 for day_i and the predictions of W3 for day_i−7 to day_i−1. We create various training and testing data sets using the surveillance data with different levels of contamination.

Combining outbreak detection using simple voting

Assuming that a detection algorithm is a classifier of outbreak versus non-outbreak days, we can aggregate multiple outbreak detection algorithms using a combination of classifiers. The simple voting method computes the fraction of classifiers which are predicting an outbreak; if this fraction is above a threshold, it predicts an outbreak. A threshold of 0.5 corresponds to simple majority voting. In the experiments, we use C1, C2, C3, W2, and W3 as the base classifiers and vary the classification threshold between 0 and 1 so that the sensitivity of the detection is adjustable based on the desired level of false alarm rate. This trade-off is illustrated in the ROC curves.

HME for outbreak detection

In this work, focusing on constructing an HME structure to detect disease outbreaks, we use the predictions of statistical detection algorithms (C1, C2, C3, W2, W3) as the input of the Experts. The goal is to train a binary classifier which predicts whether there is an outbreak on a day or not. We developed several HME structures using different subsets of data and evaluated their performance in comparison with other outbreak detection algorithms. We assigned the threshold of the classification to 0.5 so that, for the day_i, if P(day_i ∈ outbreak) ≥ 0.5, then i is an outbreak day.

We used the Bayes Net Toolbox of Matlab^*1.07 software for HME structure written by Pierpaolo Brutti. The HME structure was learned from a batch training data set using desired number of iterations of the Expectation-Maximization (EM) algorithm. The architecture of the HME can be adjusted by choosing the number and the type of gating layers and experts. We used this set of procedures in Matlab to develop an HME for outbreak detection.

Results

In the first experiment that we ran, we used the predictions of C and W algorithms for 300 low contaminated time series to create the training set with 14538 instances. To evaluate the accuracy of developed model, we built a testing set from 90 time series that are not included in the training process (194040 instances). We used the training data to learn an HME structure with 5 gating levels and 32 experts in the lowest level of hierarchy. The performance of the learned model was evaluated in predicting the outbreaks of the testing set with 194040 instances. We varied the classification threshold of HME over a range between 0 and 1 to estimate the sensitivity-specificity trade-off. We also evaluated the majority voting algorithm on the testing data using a range of classification threshold.

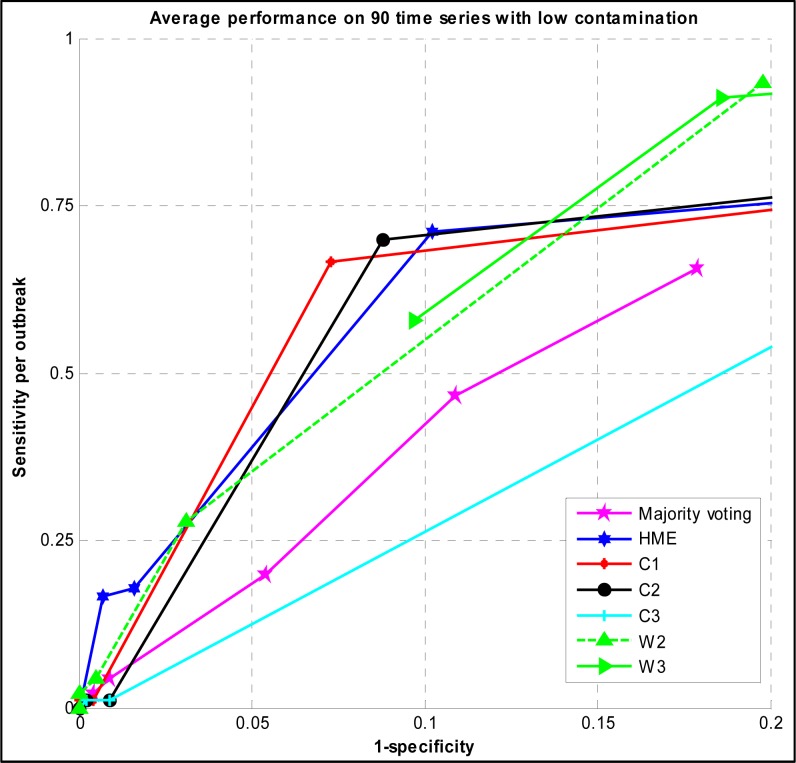
Figure 1 shows the trade-off between the sensitivity and the specificity of majority voting and the HME with different thresholds of classification. It also illustrates the ROC curves of C1, C2, C3, W2, and W3 detection algorithms with different alerting thresholds evaluated on the same testing time series.

Figure 1.

ROC curve of Majority voting, HME, C, and W family detection algorithms evaluated on low contamination surveillance time series

Focusing on upper left side of the ROC curves, the best sensitivity of the HME was 0.711 at the specificity of 0.898 and threshold of 0.4. At the best point of ROC of majority voting, the sensitivity was 0.2 and the specificity was 0.946.

In the second experiment, we used simulated surveillance time series with higher levels of contamination to create the training and testing data sets. Because the level of contamination of water affects the outbreak characteristics (e.g. outbreak duration, outbreak peak size, shape of the signal), therefore, the performance of different detection algorithms varies based on different outbreak characteristics among these contamination scenarios. We created a training set based on predictions of C and W family algorithms for 75 highly contaminated time series including 4494 instances and a testing set from untouched 30 time series containing 64680 instances.

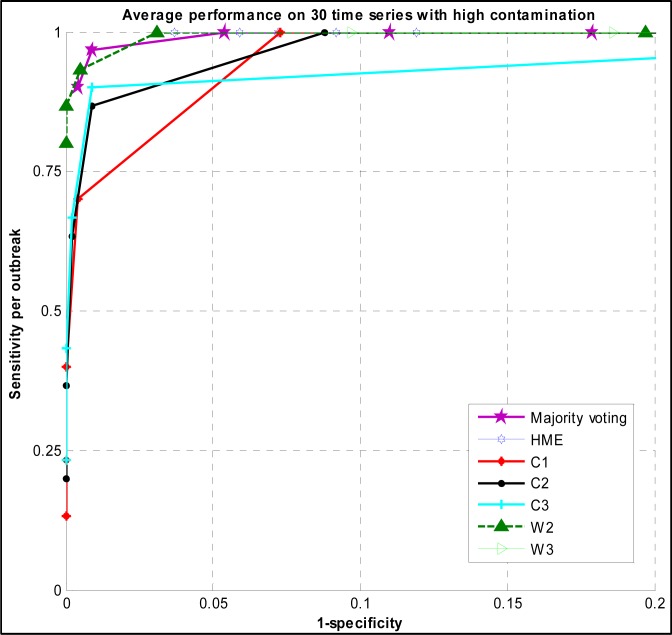
The ROC curves of majority voting and HME are shown in (Figure 2) using different thresholds. It also plots the ROC curves of C and W family algorithms evaluated on the same time series with high contamination.

Figure 2.

ROC curve of Majority voting, HME, C, and W family detection algorithms evaluated on high contamination surveillance time series

The sensitivity of majority voting was 1 when the specificity was 0.946. In contrast, the sensitivity of HME is 1 at the specificity of 0.963.

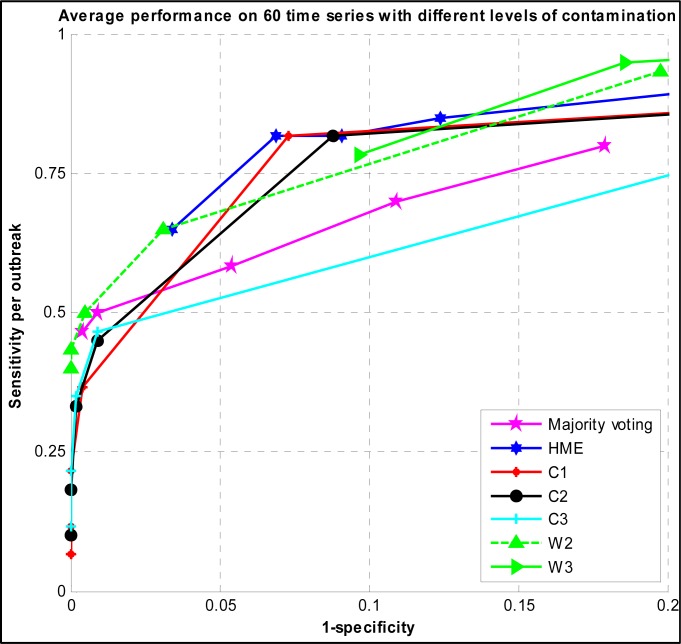
In the third experiment, we used time series with both high and low levels of contamination in order to have an overall view of the detection performance of algorithms. We built a training data set based on 150 time series and a testing set on 60 time series. Figure 3 shows the ROC curve of the developed HME and majority voting versus C and W family algorithms.

Figure 3.

ROC curve of Majority voting, HME, C, and W family detection algorithms evaluated on surveillance time series with both high and low levels of contamination

To assess the timeliness of developed methods versus C and W family algorithms, we evaluated the timeliness of algorithms when the specificity was set to 0.99. The false positive ratio obtained from this configuration was 1%. We chose this level of specificity because the alerting ratio of 1 in 100 days is a practical one for public health surveillance ⁸. We evaluated the timeliness testing on 3 types of simulated time series data: time series with low contamination, time series with high contamination, and time series with low and high contamination. The timeliness of the voting majority, HME, and C and W family algorithms with the specificity of 0.99 is summarized in (Table 1) for 3 testing data sets.

Table 1.

The timeliness of Majority voting, HME, and C W family detection algorithms with the specificity of 0.99

	Majority voting	HME	C1	C2	C3	W2	W3
Low contamination	1	0.5	0.143	0.143	0.143	0.534	0.917
High contamination	0.727	0.682	0.688	0.74	0.731	0.804	0.75
Mixed high & low contamination	0.727	0.773	0.685	0.731	0.731	0.796	0.75

In the first row of the table, the best timeliness belongs to majority voting, however, this comes with the sensitivity of 0.044 which is lower than the sensitivity of other algorithms. In the second row, W2 has the best timeliness of detection. The best timeliness of detection over the mixed testing data was obtained by W2, however, the timeliness of the developed HME is very close to the best timeliness.

Discussion

The experimental results show that the detection performance of the developed HME algorithm in terms of sensitivity and specificity is higher than simple majority voting algorithm. So it is valuable to build an HME to aggregate different predictions rather than using simple majority voting algorithm.

The results also show that the detection performance of C and W algorithms is dependent on the outbreak characteristics (i.e. contamination level) and there is no one single algorithm that always outperforms other methods under different circumstances. Although the detection methods behave with various performance levels, the developed HME algorithm is competitive to the best detection algorithm in all three experiments and the level of contamination of surveillance time series does not influence the relative performance of the HME. Hence, the developed detection algorithm based on HME is more robust under different circumstances.

Conclusion

In this paper, we proposed to combine various outbreak detection methods for the purpose of improving the overall detection performance in surveillance systems. We described a framework based on HMEs that can be employed for this method fusion. In addition, we used a majority voting strategy as a simpler alternative for aggregating detection methods. Our experimental evaluation of these two approaches to method fusion does not seem to provide improvement over the best detection methods for the particular surveillance scenarios used in this paper. However, HME outperforms most algorithms tried in our experiments.

In the developed models, we used the predictions of C and W family detection algorithms, however, the models can be extended to consider the predictions of other detection algorithms, like Negative binomial CUSUM and Poisson Regression. We intend to do this extension in future, because these methods may provide more diversity of predictions.

We developed the aggregating methods based on temporal surveillance data. We plan to extend our work to consider difference sources of surveillance data, like spatiotemporal surveillance data to detect outbreak event in several regions. We can also use other sources of surveillance data, like school and work absenteeism rates and others.

In the developed HME, the predictions of detection algorithms were fed to all the experts of the structure. The model can be altered by assuming that each detection algorithm is an expert in the HME architecture and its vote is weighted based on determinants of detection performance (e.g. outbreak characteristics, desired false alarm rate).