Optimized Dual Threshold Entity Resolution For Electronic Health Record Databases – Training Set Size And Active Learning

Abstract

Clinical databases may contain several records for a single patient. Multiple general entity-resolution algorithms have been developed to identify such duplicate records. To achieve optimal accuracy, algorithm parameters must be tuned to a particular dataset. The purpose of this study was to determine the required training set size for probabilistic, deterministic and Fuzzy Inference Engine (FIE) algorithms with parameters optimized using the particle swarm approach. Each algorithm classified potential duplicates into: definite match, non-match and indeterminate (i.e., requires manual review). Training sets size ranged from 2,000–10,000 randomly selected record-pairs. We also evaluated marginal uncertainty sampling for active learning. Optimization reduced manual review size (Deterministic 11.6% vs. 2.5%; FIE 49.6% vs. 1.9%; and Probabilistic 10.5% vs. 3.5%). FIE classified 98.1% of the records correctly (precision=1.0). Best performance required training on all 10,000 randomly-selected record-pairs. Active learning achieved comparable results with 3,000 records. Automated optimization is effective and targeted sampling can reduce the required training set size.

Introduction and Background

Duplicate medical records (i.e., multiple records belonging to a single patient) are associated with operational inefficiencies, potential patient harm and liability^1–3. Consider the case of two records for the same patient, one of which indicates a severe drug allergy. A physician working with the alternate record may unknowingly prescribe a fatal drug.

Entity resolution (or de-duplication) is the process of identifying duplicate records. First, various methods are used to quantify similarity between identifiers in the records (i.e., name, date of birth, social security number, etc.). Scores are then combined by an entity resolution algorithm. In most studies algorithms are set to identify a single threshold (match/non-match). However, in order to achieve optimal accuracy, algorithms can be implemented to identify two thresholds (separating the dataset into definite matches, a set of questionable cases to be reviewed manually, and definite non-matches)⁴.

In the majority of recent studies manual review has been considered unacceptably expensive. Thus, the main focus of research has been on single threshold algorithms⁴. To further minimize human effort, most studies have concentrated on automated (unsupervised) entity resolution approaches, such as the deterministic and probabilistic methods^4,5. These methods still require parameter tuning which is usually done manually by an entity resolution expert based on “trial and error” with the local data^6,7. Thus, it is impossible to conclude whether an optimal set of parameters has been chosen in the implementation.

Several recent studies have suggested optimization as an alternative to manual setting of algorithm parameters^6,8. Optimization is a computational process that searches for the optimal set of parameters, by iteratively evaluating candidate parameters with respect to algorithm performance on a (manually-reviewed) training set. In the case of Electronic Health Records (EHRs) databases the cost of a single error may be so high that it dwarfs the cost of human labeling for both a training set and questionable cases (e.g., a missed allergy resulting in the prescription of a fatal drug)⁹. In previous work we demonstrated that setting parameters by optimization reduced the number of questionable cases assigned to manual review for common entity resolution algorithms¹⁰. Best performance was noted for the Fuzzy Inference Engine (FIE) algorithm (a deterministic rule based algorithm) which identified 76% of the duplicate records (without false positives) and assigned the remainder to manual review after optimization on a training set of 10,000 records.

This study aimed to 1) establish the necessary training set size for optimizing common entity resolution algorithms to two thresholds; and 2) to determine whether training set and questionable cases can be minimized by active learning. That is, by sampling only the most informative cases to human labeling^11–13. We focused on two deterministic approaches - the simple deterministic and the rule-based, Fuzzy Inference Engine, and a probabilistic Expectation Maximization (EM) approach.

Methods

Overview

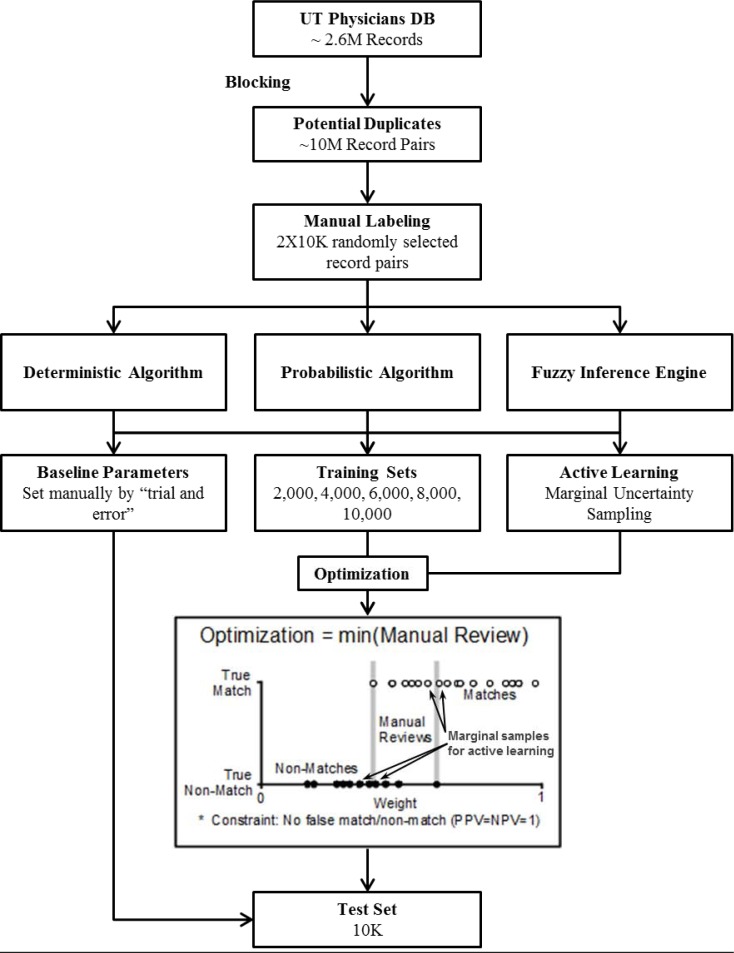
After cleaning and standardizing the data we used blocking to limit the search space of potential duplicates (Figure 1). We reviewed 20,000 randomly-selected record pairs (10,000 training and 10,000 test) ¹⁰. For each algorithm, we defined a baseline set of parameters based on previous literature and preliminary experimentation with the data⁷. We then set parameters using particle swarm optimization¹⁴ (for a detailed description see 10). We ran optimization using training sets of increasing size (2,000, 4,000, 6,000, 8,000, 10,000). We also used a simple active learning strategy in which we sampled 25 record pairs closest to the thresholds (i.e., the record pairs that were likely to be most helpful to define the distinction between matches and non-matches). We started with a random sample of 2,000 records and then sampled for 25 iterations. Algorithms were tuned for two thresholds (matched/manual review/unmatched) aiming to minimize the size of manual review set, under the constraint that there would be no false classification (i.e., PPV=NPV=1). We repeated optimization five times. Algorithm performance was evaluated against the test set of 10,000 record pairs and we report the averaged results.

Figure 1.

Study design

Data preparation and block search

We retrieved data from the University of Texas Health Science Center at Houston’s clinical data warehouse which contained 2.61 million distinct records (including duplicate records). We used eight fields: first name, middle name, last name, date of birth, social security number, gender, primary address and primary phone number. We removed stop-words (i.e., Mr., Ms., rd., etc.) and punctuation. Missing or invalid data fields were set to null¹⁵. We standardized names using a lookup table¹⁶. We removed invalid social security numbers based on the instructions published in the social security website¹⁷. To limit the search space of potential duplicates we used a blocking procedure, whereby, we identified potentially duplicate record pairs if they matched on: first and last names; first name and date of birth; last name and date of birth; or SSN (to increase recall of the blocking search we encoded names using Soundex)¹⁸. This process generated approximately 10 million distinct potential duplicate record-pairs.

Training and test set generation

We randomly selected 20,000 record-pairs (10,000 training set and 10,000 test set). We used a stepwise review process as described in detail in ¹⁰. In brief, two reviewers reviewed each record-pair. Reviewers were instructed to decide whether the available identifiers were sufficient in order to ascertain match status. Then, they were requested to assign a match or non-match status only if they would have been comfortable with a computer making the same assertion automatically. If there was any disagreement between the reviewers, or if one of the reviewers thought it was impossible to assert match status, the records were forwarded to an evaluation by four independent reviewers. At this stage, pairs that were not assigned a match/non-match status unanimously (or by three reviewers when the fourth reviewer was uncertain), went to further review by open discussion of the entire review panel (six reviewers). Only 48 record-pairs could not be assigned by the four reviewers. These were assigned by consensus after looking for additional data (if available) in the patient records (10 matched, 38 non-matched).

Calculating similarity measures

To compare identifiers between the two records, we used the Levenshtein edit distance. This is defined as the smallest number of edits (e.g., insertions, deletions, substitutions) necessary to make one string equal to another¹⁸.

Algorithms: The simple deterministic algorithm

The simple deterministic algorithm was based on a summation of weights of similarity scores for eachidentifier¹⁸. We mapped the similarity scores linearly onto an interval between an upper bound (u) and a lower bound (l). In the baseline implementation u and l were set to 1 and (−1) respectively. Thus, a similarity score of 0.9 (edit-distance is on a scale of 0–1) was mapped to a weight of 0.8 and a similarity score of 0.1 was mapped onto (−0.8). Comparisons with a blank field were mapped to zero. By assigning negative weights to highly dissimilar fields we were able to penalize for considerable differences between fields. In the optimization phase, the possible intervals for l and u were optimized on the intervals of [−1,0] and [0,1] respectively. For example, an interval could be optimized to [−0.2, 0.6] meaning a high similarity score of the field supports a match more strongly (will add 0.6 to the total weight) than a low similarity score supports a non-match (will subtract 0.2 from the total weight). For example, phone number match is moderately indicative of a match status and phone number non-match is not indicative of non-match because it is common for a person to change phone numbers.

Fuzzy Inference Engine (FIE)

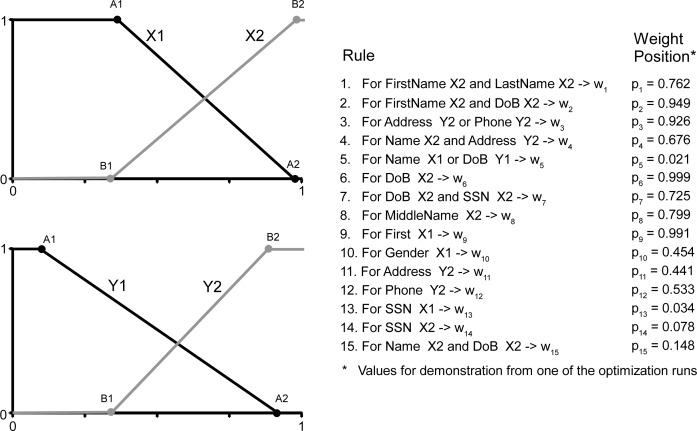
A fuzzy inference engine is a set of functions and rules that map similarity scores onto weights. FIE uses a combination of scores from several identifiers to calculate a weight, and is, in essence, a functional representation of a rule based system¹⁹. We defined four functions and 15 rules based on previous literature and preliminary experiments with the data (Figure 2)¹⁹. Each function takes a set of similarity scores and outputs a weight (ω_i). A rule maps similarity scores to different functions. If multiple scores are mapped with an OR condition, the maximum weight is returned. If an AND condition is used, the minimum weight is returned. The result is then multiplied by the rule’s position score (p) which represents whether a rule is used to support or negate a match status. Finally, the total weight of a record-pair is calculated by a weighted average.

$$\mathit{Weight}=\frac{{\sum }_i^{15}{w}_i\hspace{0.17em}·\hspace{0.17em}{p}_i}{{\sum }_i^{15}{w}_i}$$

Figure 2.

Fuzzy Inference Engine

For example, rule 3 will give a high score to cases where either the address or the phone number in two records are very similar, while rule 5 will penalize the total score if either the name or the date of birth are very dissimilar (Figure 2). For the baseline implementation we set A1 and A2 values to 0.05, B1 and B2 values to 0.95, position scores for rules strongly supporting a match status to 1 and 0 for rules with a weak support. In the optimization phase, the thresholds A1, A2 and B1, B2, the position score p and the final matching thresholds were optimized.

The probabilistic algorithm

We implemented the Expectation Maximization (EM) extension of the Fellegi-Sunter probabilistic algorithm²⁰. For each similarity measure, we defined a threshold (p_i) that maps it to either 0 or 1. Then, for each field, we calculated the probability that the field has the observed value given that the record-pair represents two different patients (u probability) and estimated the probability that it has the observed value given that the record-pair represents the same person (m probability)^7,21. We used the EM method - an iterative process designed to find the maximum-likelihood estimate of a the m probability, where the model depends on the unobserved actual match status (for a detailed description of the method see 20). For the baseline implementation we set p_i for mapping similarity measures based on previous literature and experiments with the data⁷. In the optimization phase p_i, and the thresholds for final match classification were optimized. Specifically, we did not optimize the m and u probabilities which were handled by the EM algorithm (i.e., we only optimized those parameters that would have otherwise been set manually). Parameters were set based on the training set and EM was performed on the test set (similar to ²²).

Optimization

Baseline parameters for each of the algorithms were set by an experienced analyst (M.J.B) based on experimentation with the data and baseline parameters reported in the literature to minimize the manual review set size while minimizing errors^7,18.

We chose the Particle Swarm Optimization, a stochastic global optimization technique, because it does not require an initial parameter estimation (all particles initialize randomly within the parameter space)¹⁴. We used a standard implementation of particle swarm as described in¹⁴. The parameters used in the optimization were 20 particles, a particle neighbor size of 2, and an acceleration constant of 2 for 5,000 iterations. We used the same parameters for optimizing all algorithms. Optimization was set to minimize the number of records requiring manual review under the constraint that the algorithm will have a precision of one (i.e., minimize the number of record-pairs that fall between two thresholds, while maintaining PPV=NPV=1).

Training sets sizes

We generated five distinct random samples for various training set sizes (2,000, 4,000, 6,000, 8,000 record pairs). We than used these training sets for optimization. For each of the training set samples, optimization was performed five times. We evaluated the performance on the test set (5 samples X 5 optimization runs) and averaged the results.

Active learning

For the active learning stage, we performed a preliminary optimization of the algorithms using a random sample of 2,000 record pairs. We used the remaining records (8,000) as a validation set. We evaluated the performance of the algorithms on the validation set as well as the test set. We used the run on the validation set to identify up to 25 of the record pairs on either side of the thresholds (up to a total 100 record-pairs, 1% of the record pairs available for sampling). We added these records to the training set, and repeated the optimization process. We reiterated this procedure for 25 cycles. We repeated optimization five times in each cycle. Sample size varied between the iteration, because there weren’t always 25 records to sample on either side of the thresholds. We report the averaged performance of the algorithms on the test set for each iteration.

Evaluation

Two-threshold algorithms were constructed to minimize errors as well as manual review set size. We, therefore, report error rates as false positive (FP) for cases classified as duplicate; false negative (FN) for cases classified as non-duplicates; and the size of the manual review set in percentage (of the 10,000 record pair test set) (Figure 1). We also report familiar metrics of recall and precision for duplicate records.

Results

Of the 20,000 manually reviewed record-pairs 1215 (6.08%) pairs were found to match (602 and 613 matched pairs in the training and test sets respectively).

Baseline performance

The baseline implementation of all algorithms were characterized by zero errors on the test set. However, manual review sizes were high and ranged from 10.5% (probabilistic), 11.6% (deterministic), and 49.6% (FIE). Recall for matched record pairs was highest for the deterministic approach (0.54) (Table 1).

Table 1.

Performance metrics for various training set sizes and active learning

Training set size	Performance metric	Deterministic		FIE		Probabilistic
		Avg	Stdev	Avg	Stdev	Avg	Stdev
0 (Baseline)	Match recall	0.54		0.12		0.20
	Match precision	1.0		1.0		1.0
	Match errors (FP)	0.0		0.0		0.0
	UnMatch errors (FN)	0.0		0.0		0.0
	Manual review	11.6%		49.6%		10.5%
2,000	Match recall	0.79	0.20	0.94	0.05	0.74	0.16
	Match precision	0.986	0.25	0.971	0.05	0.986	0.21
	Match errors (FP)	7.0	6.2	16.9	8.2	6.2	5.1
	UnMatch errors (FN)	13.2	5.4	9.4	3.7	7.4	3.9
	Manual review	1.9%	2.0%	0.4%	0.4%	2.0%	1.4%
4,000	Match recall	0.93	0.05	0.92	0.03	0.62	0.07
	Match precision	0.982	0.05	0.983	0.03	0.994	0.11
	Match errors (FP)	9.9	3.7	9.3	3.8	2.4	1.8
	UnMatch errors (FN)	8.3	5.7	5.6	4.4	7.0	2.9
	Manual review	0.7%	0.5%	0.7%	0.2%	2.5%	0.5%
6,000	Match recall	0.81	0.09	0.79	0.05	0.66	0.08
	Match precision	0.990	0.11	0.990	0.06	0.993	0.13
	Match errors (FP)	4.7	2.2	4.7	2.0	2.8	1.8
	UnMatch errors (FN)	5.4	2.6	1.6	1.6	5.4	2.0
	Manual review	1.9%	0.4%	1.8%	0.3%	2.3%	0.6%
8,000	Match recall	0.81	0.05	0.83	0.06	0.62	0.07
	Match precision	0.994	0.07	0.991	0.07	0.993	0.11
	Match errors (FP)	3.1	1.2	4.5	2.0	2.6	0.8
	UnMatch errors (FN)	4.2	2.5	0.9	0.8	4.4	2.6
	Manual review	1.7%	0.2%	1.6%	0.3%	2.6%	0.5%
10,000	Match recall	0.70	0.01	0.76	0.02	0.59	0.03
	Match precision	0.997	0.00	1.0	0.03	0.980	0.06
	Match errors (FP)	1.5	0.5	0.0	0.0	7.5	0.8
	UnMatch errors (FN)	1.6	0.5	0.1	0.3	1.2	0.4
	Manual review	2.5%	0.0%	1.9%	0.1%	3.5%	0.2%
Active learning 25 iterations (aprox. 3100)	Match recall	0.70	0.01	0.75	0.01	0.59	0.0
	Match precision	0.996	0.01	0.993	0.02	0.997	0.00
	Match errors (FP)	1.8	0.4	3.0	0.7	1.0	0.0
	UnMatch errors (FN)	1.4	0.9	0.0	0. 0	4	0.0
	Manual review	2.5%	0.05%	2.1%	0.13%	2.8%	0.01%

Two-threshold algorithms were constructed to minimize errors as well as manual review set size. We, therefore, report error rates as false positive (FP) for cases classified as duplicate; false negative (FN) for cases classified as non-duplicates; and the size of the manual review set in percentage (of the 10,000 record pair test set) (Figure 1). We also report familiar metrics of recall and precision for duplicate records.

Algorithm performance for various training set sizes

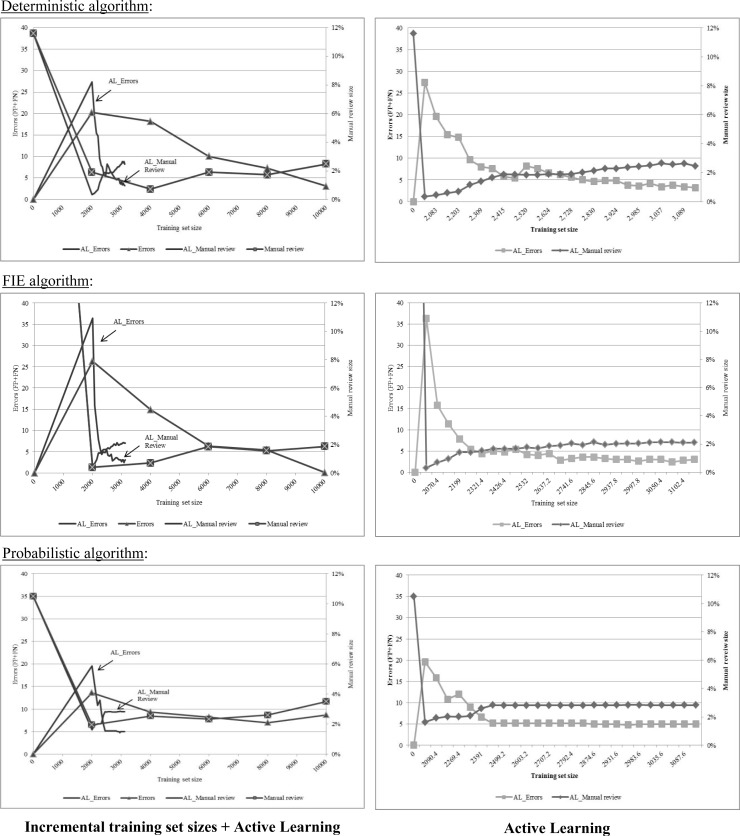
Optimization reduced the size of manual review sets (i.e., it increased the recall for both matched and unmatched record pairs) for all the algorithms (deterministic 11.6% vs. 2.5%; FIE 49.6% vs. 1.9%; and probabilistic 10.5% vs. 3.5% for baseline and 10,000 record pairs training set respectively). Best performance was noted for FIE with 10,000 record pairs which had a recall of 0.76 for matched record pairs, a precision of 1.0 (i.e., no false positive), and a manual review size of 1.9%. For the deterministic approaches (deterministic and FIE), the rate of errors decreased steadily with growing training set sizes. At the same time, the size of the manual review set increased, but was still considerably lower than the baseline implementation. For the probabilistic algorithm we did not note additional improvement in performance with training sets larger than 4,000 record pairs (Table 1, Figure 3).

Figure 3.

Manual review sizes and error rates for various training set sizes and active learning

The graphs on the left describe observed errors (left Y axis) and manual review set sizes in percentages (right Y axis) for varying training set sizes and for active learning (AL). The graphs on the right show active learning results (notice the different scale for the X axis only).

Algorithm performance following active learning

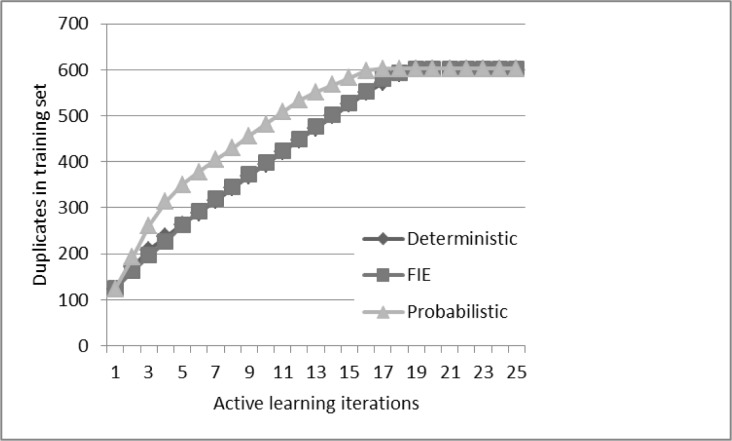
The deterministic algorithm achieved comparable performance to 10,000 record pairs after 22 iterations of active learning sampling (3089 record pairs). Using active learning for the probabilistic algorithm achieved better performance than random sampling (recall for matched records 0.59, one false positive and a manual review size of 2.8%). Best performance for active learning with the probabilistic algorithm was noted after seven iterations (2500 record pairs) and did not improve further. Using active learning for FIE achieved inferior performance than training with 10,000 record pairs and plateaued after 13 iterations (2742 record pairs) (Table 1, Figure 3). In all algorithms, training sets included all available duplicate records (602 of 10,000 record pairs) by the 19^th iteration (Figure 4).

Figure 4.

Duplicate records in the training set following active learning

Discussion

Performance of the deterministic approaches was dependent on the size of the training set. Best performance was noted with a training set of 10,000 record pairs. Using active learning, with as little as 2400 record pairs, improved the performance of the probabilistic algorithm beyond that seen with 10,000 randomly sampled record pairs. Active learning did not result in an improved performance for the deterministic approaches; however the size of the necessary training set was reduced considerably to approximately 3000 records. By the 19^th iterations, training sets generated by active learning included all the duplicate records from the original 10,000 record pair sample.

Our study has several limitations. First, the gold standard (i.e., training and test sets) was generated based on the same identifiers available to the algorithm. Ideally, the gold standard would be based on additional information (e.g., independent genealogic data, immunization records, physical identity verification)^23,24; which is particularly desirable if the available identifiers are insufficient for asserting whether two records match. This was not the case in our dataset. Only 48 of the 20,000 were difficult to classify based on the available data. However, it is possible that certain misleading cases were missed. For example, infant twins with very similar demographics that were considered the same person (Jayden and Jaylen Thompson, SSN 026-94-6788 and 026-94-789, and the rest of the identifiers are the same because they are twins), or a woman who married, and had changes and errors in all of her demographic data to the point she is considered two different entities. We estimate that the probability of such events, is extremely low (i.e., the product of the probabilities of errors in 7–8 data fields for the married woman, or the product of the probability of twins and the probability of twins having almost identical first names and SSN). In any case, the focus of this study was a comparison of the effect of varying training sizes on the performance of common algorithms and it is not expected to be influenced by minor inaccuracies in the gold standard.

A second limitation is that we used a narrow set of methods for the entity resolution task (i.e., a lenient blocking search, a limited set of similarity measures, specific implementations of the studied algorithms and a single optimization method). It is possible that other similarity measures or entity resolution algorithms could have resulted in better performance with smaller training sets^25–28. Further, we used the particle swarm optimization to avoid initial parameter estimation¹⁴. However, other optimization methods (e.g., genetic programing or lenient gradient descent) might have performed better^6,8. Third, our baseline parameters (no parameter optimization) may not have been optimal. We chose to include this baseline because it is common for institutions to manually tune entity resolution algorithms. Since particle swarm optimization does not require a starting parameter set to be defined, our choice of baseline parameters does not affect optimization (i.e., training set > 0). Lastly, we used a very basic method of marginal uncertainty sampling for active learning ¹¹. Active learning is often performed by sampling the most informative cases ¹¹. Since the optimization process is computationally expensive we sampled a range of cases without considering the added contribution of each individual case. More sophisticated active learning methods may perform better (i.e., decrease manual review without compromising precision)^12,13.

It is difficult to compare our results to previous studies. Entity resolution is highly data-dependent and varies with the frequency and complexity of duplicates, the identifiers available for comparison, and data quality factors such as missing values and error rates^15,28. Further, as opposed to single threshold entity resolution, the literature on two-thresholds with manual review of questionable cases is limited. Most studies have considered manual review too expensive and focused on automatic classification using a single threshold^4,29. Gu and Baxter, evaluated the probabilistic EM method using dual thresholds on several synthetic datasets. The manual review sizes they described are smaller than observed for our baseline implementation (ranging 3.9%–10%, depending on the rate and complexity of duplicate records). However, with a considerably lower precision (1–4 errors per 100 record pairs)²⁹. Similar results were described by Elfaky et. al. for a probabilistic algorithm using a synthetic dataset (5% manual review size, accuracy of 0.98)²². It is possible that our baseline parameter setting was not optimal. Alternatively, the difference in performance could have been the result of aiming to maximize precision even at the cost of recall. Also, possibly our dataset was more complex. In any case, following optimization our results were superior.

Performance improved steadily for the deterministic algorithms as the training set grew. At 10,000 record pairs FIE identified 76% of the duplicate records without false positives. The manual review set was still large (1.9% which would translate to approximately 190,000 record-pairs in our institution). It is possible that with a larger training set, the manual review set could be reduced further

Active learning reduced the number of labeled records required to achieve comparable results to using the entire training set (10,000 record pairs). For the probabilistic algorithm, training on an active learning based training set improved performance compared to training on all 10,000 records in the training set. However, this was not true for the deterministic approaches. A possible explanation is that by the 19^th iteration the active learning training sets have included all of the available duplicate records (602) in the dataset. Continuing to enrich the training set with examples of duplicate records might improve performance.

Several previous studies have evaluated active learning for entity resolution (single threshold). All reported achieving optimal performance (F-measures 0.97–0.98) after 100–200 samples^12,13,30. Unlike our experiment, these studies used active learning based on a committee of classifiers (using several decision trees or genetic algorithms to classify the unlabeled data, and then sampling cases the classifiers disagreed on) and sampled a single case at every iteration. Due to the computational complexity of the optimization process, we started the active learning experiment from a baseline of 2,000 record pairs, and sampled multiple cases in every iteration. Using a similar technique to those described in previous studies we likely could have reduced the size of the training set even further.

Manual review required six reviewers just over seven days for 20,000 record-pairs. Manual review of all questionable cases is a task of considerably larger magnitude (i.e., 190,000 record-pairs in our institution). However, the cost of such a review would arguably be much less than a single malpractice settlement due to fragmented information in duplicate records⁹. Further, reviewed questionable cases could be used to enrich the training set, similar to active learning¹⁸. Lastly, it is possible that supervised machine learning techniques would outperform the optimized deterministic and probabilistic algorithms^12,13,30.

Conclusions

Optimized entity resolution algorithms outperformed manual setting of algorithmic parameters for dual-threshold entity resolution. Algorithmic performance improved as optimization was performed on larger dataset. Active learning reduced the size of the required training set.