USING THE BIPARTITE HUMAN PHENOTYPE NETWORK TO REVEAL PLEIOTROPY AND EPISTASIS BEYOND THE GENE

Abstract

With the rapid increase in the quality and quantity of data generated by modern high-throughput sequencing techniques, there has been a need for innovative methods able to convert this tremendous amount of data into more accessible forms. Networks have been a corner stone of this movement, as they are an intuitive way of representing interaction data, yet they offer a full set of sophisticated statistical tools to analyze the phenomena they model. We propose a novel approach to reveal and analyze pleiotropic and epistatic effects at the genome-wide scale using a bipartite network composed of human diseases, phenotypic traits, and several types of predictive elements (i.e. SNPs, genes, or pathways). We take advantage of publicly available GWAS data, gene and pathway databases, and more to construct networks different levels of granularity, from common genetic variants to entire biological pathways. We use the connections between the layers of the network to approximate the pleiotropy and epistasis effects taking place between the traits and the predictive elements. The global graph-theory based quantitative methods reveal that the levels of pleiotropy and epistasis are comparable for all types of predictive element. The results of the magnified “glaucoma” region of the network demonstrate the existence of well documented interactions, supported by overlapping genes and biological pathway, and more obscure associations. As the amount and complexity of genetic data increases, bipartite, and more generally multipartite networks that combine human diseases and other physical attributes with layers of genetic information, have the potential to become ubiquitous tools in the study of complex genetic and phenotypic interactions.

1. Introduction

Genetic diseases and propensities have been at the center of the biomedical world for decades. From simple Mendelian diseases that obey the one-gene-one-phenotype paradigm, to complex genetic disorders, geneticists are working on developing novel methods to diagnose, treat, cure, and even prevent these diseases. At the center of prevention lie the information and education of patients on their personal genetic risk landscape. Because of the sheer number and complexity of genetic interactions within any given organism, and with its environment, genetic disorders and traits cannot be studied in isolation of one another or of external factors. The cascading effects of genomic mutations can extend to entire organisms, and having a global understanding of the ramifications of these mutations, including all the affected phenotypes and diseases, is becoming crucial. Two phenomena awlessly illustrate the underlying complexity of genetic variations: pleiotropy, when a single mutation affects several traits, and epistasis, when multiple mutations in distant parts of the genome have synergetic, usually non-linear, effects on a single phenotype. From a system’s biology perspective, the preferred visualization methods for these interactions are networks of human diseases and traits. Networks offer an intuitive representation of phenotypic and genotypic interactions, while at the same time allowing sophisticated quantitative statistical analysis of their intrinsic properties.

Although the concepts of epistasis and pleiotropy are over a 100 years old, they are widely under-appreciated due to their perceived rarity. State-of-the-art genome-wide association studies (GWAS) most often look for individual genes with large impacts on a single phenotype. The impact of genetic mutation cannot be studied in isolation, even if the attempt is to bridge the gap between a single gene and a single phenotype. Predictive elements, such as single nucleotides (SNPs), loci, genes, or entire biological pathways interact at all levels of granularity. The pervasiveness and strength of biomolecular interactions require a step back from reductionist biology and an acknowledgement of the importance of biological networks and pathways.

In this work, we propose to go beyond the gene as a unit of mutation, and use SNPs as a smaller unit, and biological pathways as a larger unit. We take a bird’s eye view of the effect of genetic mutations on human phenotypes. It is often arduous to distinguish between certain types of pleiotropy and epistasis. The effect of a single mutation rippling though a pathway can be confused with the combined effect of distinct mutations. We therefore decide to study these phenomena in unison. We propose to use bipartite networks made of both phenotypes and predictive elements, constructed with GWAS data and other publicly available genetic databases. These networks allow us to identify the pleiotropic and epistatic interactions at the system’s level. By studying several types of human phenotype networks (HPNs) based on predictive elements of different scales, we quantify the fundamental structural differences of these networks, as well as the amount of pleiotropic and epistatic information they contain. Finally, we magnify a specific phenotypic region of the HPN: the “glaucoma” region, which groups the disease and all its first and second neighbors. We offer a close up view of pleiotropic and epistatic interactions within a specific sub-network.

2. Background

In this section, we offer a cursory overview of the concepts of pleiotropy and epistasis. Furthermore, we define the fundamental concepts of HPNs, how they are constructed, and how they differ from one another (Section 2.2);

2.1. Concepts of Pleiotropy and Epistasis

Ludwig Platt and William Bateson first introduced the concepts of pleiotropy and epistasis, respectively, to explain observed inconsistencies in Mendelian inheritance and in the one-gene-one-phenotype paradigms.^1,2 To adapt with progress with genetics, the definition of pleiotropy has changed since it was first coined in 1910, and remains somewhat loose. A thorough history of pleiotropy in the past 100 year can be found in Stearns’ 2010 review.³ It refers to the general phenomenon in which a single gene dictates two or more seemingly unrelated phenotypic traits. In some cases, the definition is limited to a single mutation in a locus that affects multiple traits. It is however widely accepted that there is more than one type of pleiotropy. Grüneberg⁴ in 1938 correctly distinguished between two major types he called “genuine” and “spurious” pleiotropy. Genuine pleiotropy refers to a single locus responsible for the production of two distinct gene products, whereas spurious involves a single gene product utilized in two different ways. Furthermore, he distinguished a second form of spurious pleiotropy in which the single primary product initiates a cascade of events with different phenotypic consequences. Spurious pleiotropy can be said to perturb the biological pathways. Since then, more refined subdivisions have emerged. To help us navigate the various types of pleiotropy, Hodgking’s survey offers classifications, descriptions, and examples of seven types of pleiotropy⁵ (Table 1).

Table 1.

A classification of different types of pleiotropy. Adapted form Hodgkin’s study⁵

Type	Situation
Artefactual	Adjacent but functionally unrelated genes affected by the same mutation
Secondary	Simple primary biochemical disorder leading to complex final phenotype
Adoptive	One gene product used for quite different chemical purposes in different tissues
Parsimonious	One gene product used for identical chemical purposes in multiple pathways
Opportunistic	One gene product playing a secondary role in addition to its main function
Combinatorial	One gene product employed in various ways, and with distinct properties, depending on its different protein partners
Unifying	One gene, or cluster of adjacent genes, encoding multiple chemical activities that support a common biological function

Actual genetic mechanisms of pleiotropy are extremely diverse. Genuine pleiotropy encapsulates pleiotropy at the mRNA-processing level, multiple or overlapping loci reading frames, alternative splicing, and multifunctional proteins, to mention only a few. Spurious pleiotropy covers single loci mutations that produce deviation in the gene product affecting other genes or regulatory elements located further down the biological pathways. Indeed, new gene products may promote or repress the expression of other genes. They may initiate alternate gene-gene and protein-protein interactions and alternate mRNA and microRNA productions, which may in turn affect seemingly unrelated phenotypes. Pleiotropic genes offer a unique insight into the complexities of biomolecular interaction networks.

In epistasis, on the other hand, the phenotypic contribution of a gene and its gene products depends on the specific genotype of a locus at a different genomic position. From the origin of the word, “standing upon”, we can derive the modern definition of epistasis, or epistatic gene effects, in which the expression of an allele at one locus masks the expression of an allele at another locus.⁶ Epistasis is therefore usually the result of multiple genetic mutations at different loci. In this age of Genome-Wide Association Studies (GWAS), epistatic studies can be conducted at the genome level, quantitatively studying the masking and combined effect of single point mutations (SNPs).

Both epistasis and pleiotropy are exceptions to the one-gene-one-phenotype Mendelian rules of genetics. They are, however, far from being rare deviations.⁷ Epistasis and pleiotropy are ubiquitous inherent properties of biological systems, and they are necessary byproducts of biomolecular networks.⁸ Most phenotypes are the result of interactions between thousands of genes, as well as between genes and their environment. Because of the widespread connectivity within networks, the effects of a single mutation or variation can spread through thousands of gene-gene interactions, resulting in multiple phenotypes, or pleiotropy. The connections through which a variant’s effects propagate define the molecular basis for epistatic interactions and how they translate into an observed phenotype. Because of their close relatedness, it is not unreasonable to conclude that a similar set of quantitative tools can be applied to study both phenomena, sometimes simultaneously. In the present study, these tools are Bipartite Human Phenotype Networks.

2.2. Human Phenotype Network (HPN)

In recent years there has been a trend toward studying disease through network based analysis of various systems of connections between diseases. The result is the Human Disease Network (HDN). The nodes in the HDN represent human genetic disorders and the edges represent various connections between disorders, such as gene-gene or protein-protein interactions, to name only a few. The underlying connections of the HDN contribute to the understanding of the basis of disorders, which in turn leads to a better understanding of human disease.

One study by Goh, et al.,⁹ explored the Human Disease Network (HDN), limiting its analysis to the genes shared by different diseases. Another study by Li et al.¹⁰ traced the SNPs connecting disease traits. In 2009, Silpa Suthram et al.¹¹ found that when diseases were analyzed by disease-related mRNA expression data in combination with the human protein interaction network, there were significant genetic similarities between certain diseases, and some of the correlated diseases shared drug treatments, as well. This could help us target certain genes for treatment. In 2009, Barrenas et al.¹² further studied genetic architecture of complex diseases by doing a GWAS, and found that complex disease genes are less central than the essential and monogenic disease genes in the human interactome.

GWAS identify common genetic variants, such as SNPs, found in the genotype of different individuals in association with phenotypical traits. Using GWAS data, we extend the HDN to include not only diseases, but also general phenotypes, encompassing behavioral traits and physical attributes, such as hair color, and explore large portions of non-coding variations in the human genome. We call this more complete representation the Human Phenotype Network.¹³ We rely on the catalog of published GWAS maintained by the National Human Genome Research Institute (NHGRI) at the National Institute of Health (http://www.genome.gov/gwastudies/) as a primary source of phenotypic data. It aggregates studies that report SNP(s)-to-phenotype(s) and gene(s)-to-phenotype(s) associations. The NHGR catalog used in this study, downloaded in June 2013, reports 646 phenotypes associated with 2,000+ genes and 6,000+ SNPs.

Over 90% of risk-associated SNPs (raSNPs) identified by the GWAS fall outside of coding regions,¹⁴ stressing the requirement for a more global assessment of phenotypic associations. In this work we explore methods of building the HPN that go beyond previously mentioned gene-centric HDN approaches. An interesting side-effect of all the methods presented below is that before obtaining a HPN, the algorithm produces a bipartite network (see Section 3), which is the property that allows us to study the pleiotropic and epistatic information in the genetic association data. The HPN is obtained by projecting the bipartite network onto the phenotype space.

The following sections present our methods for building the HPNs based on different predictive elements. We start at the smallest predictive element, the SNP, then move on to SNP clusters, to genes, and finally to complete biological pathways. These offer varying density of the information contained with both the bipartite network and the projected HPN.

2.2.1. Genetic Variations based HPN

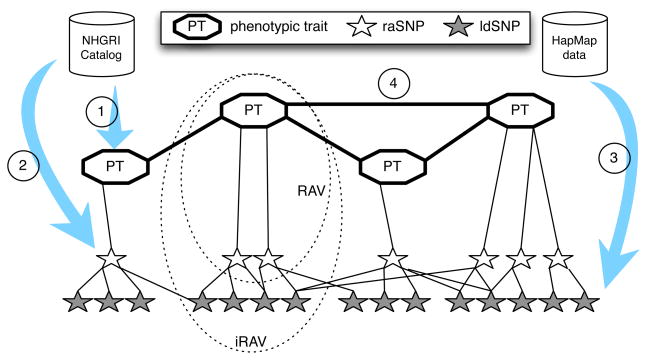
For each phenotype in the catalog (Fig. 1, Step 1), we define its risk-associated variome (RAV) as the complete set of its associated raSNPs (Step 2). To address the low genomic coverage provided by GWAS, we associate each raSNP with all SNPs found in linkage disequilibrium (ldSNPs) using the HapMap project data¹⁵ (Step 3). SNPs in linkage disequilibrium form clusters of variants that statistically tend to appear in the same patient.¹⁶ The HapMap project aims at building a repository of describing the common patterns found in human genetic variations (http://hapmap.ncbi.nlm.nih.gov/). The resulting imputed variome (iRAV) will allow us to establish connections between diseases/traits that share blocks, i.e. that have overlapping iRAVs (Step 4).

Fig. 1.

Step-by-step description of the method to obtain the HPN. The circled numbers correspond to the steps of the method description above.

iRAV-based HPN

In a previous study, we presented a model of iRAV-based HPN which included the phenotype-to-raSNPs association from GWAS, and added the HapMap project data to build clusters of variants for each phenotype (iRAVs).¹³ Phenotypes in the iRAV-HPN are linked when they share overlapping iRAVs. The algorithm (in Figure 1) produces a bipartite network of phenotypes and iRAVs.

RAV-based HPN

Linking phenotypes that share at least one raSNP, we build the RAV-PHPN. This approach is similar to that of Li et al.¹⁰ The phenotypes are linked based only on shared risk variants, i.e. overlapping RAVs, not including ldSNPs/iRAVs. This approach produces a HPN that is less dense than the iRAV-HPN, identifying fewer phenotype associations. The algorithm is similar to that described in Figure 1, omitting Step 3.

2.2.2. Gene-based HPN

Leveraging the gene(s)-to-phenotype(s) associations contained in the GWAS catalogue, we construct the gene-only based HPN (gHPN). Indeed, the GWAS catalog reports for each phenotype both the associated and the mapped genes in which the SNPs fall. This approach is analogous to that of Goh et al.⁹ To increase the genetic coverage of each phenotype, we use the Broad Institute’s GeneCruiser (genecruiser.broadinstitute.org) to identify the gene closest to a SNP, or for which SNPs fall in a known regulatory region. If this gene is not already associated with the SNPs phenotype, we include it in the study. This method increases the number of genes by 138, from 2,339 genes to 2,477. The algorithm is similar to that shown in Figure 1, omitting Step 3, and white star symbols are now genes, not raSNPs.

2.2.3. Biological Pathways based HPN

Expanding on the gHPN, we build a pathway-based HPN (pHPN).¹⁷ Biological pathways represent elaborate series of cascading biochemical reactions occurring within the cell, and possibly receiving external signals.¹⁸ Pathways govern all major cellular functions, such as cell cycle, cell respiration, and apoptosis (programmed cell death). Biochemical compounds, (e.g. nucleic acids, proteins, complexes and small molecules) participating in reactions form a network of biological processes and are grouped into pathways. KEGG Pathway (kegg.jp) is an open-access collection of manually curated and peer-reviewed pathway database, containing the structured information about the elements, enzymes, and genes (via their gene products) within many known pathways.

Relying on the gene(s)-to-phenotype(s) data used to construct the gHPN, genes were further linked to enriched pathways using KEGG. By building these associations, we were able to link phenotypes associated with genes involved in the same pathways in the pHPN. The algorithm is analogous to that in Figure 1, except that the white star symbols represent genes, and the grey stars are pathways.

3. Pleiotropy and Epistasis in the Bipartite HPNs

The HPN resulting from either method described in Section 2.2 can be represented as a mathematical object: a graph.¹⁹ In this work, the terms “graph” and “network” are used interchangeably. Formally, a network is a collection of nodes and edges connecting them. The degree, k, of a node is the number of edges incident upon the node. The average degree of the network is the average of all k. The degree distribution function, P(k), of the network describes the fraction of nodes within the network with degree k. The clustering coefficient (CC) of a network measures the degree to which nodes tend to form closely knit communities with a higher than average connectivity.²⁰ The CC of networks found in nature, in particular social and biological networks, show a higher degree of clustering than that observed in randomized networks of identical size. The average path length of a network (APL) represents the average of the minimum number of edges separating any two vertices. Finally, the network’s diameter is defined as the greatest distance between any pair of vertices.

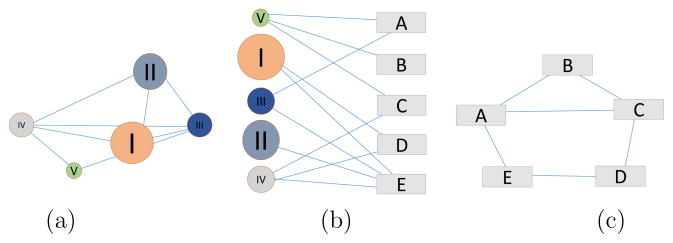
In our study, we start by building a bipartite network,²¹ consisting of two disjoint sets of nodes. The nodes are connected in such a way that the nodes of one set will have no connections between them, but can only be connected to nodes of the other set. The use of a bipartite network is natural when dealing with two different types of data sets (Figure 2b), in our case phenotypes (e.g. the rectangles) and RAVs, iRAVs, genes, or pathways (e.g. the circles). This type of network gives us three distinct degree distributions, one for each projection, and one for the bipartite network. Each degree distribution shows how many links each node has. Nodes in a projection of a bipartite network are connected if they share at least one node in the other group. This gives us the ability to see the interactions within each set.

Fig. 2.

Bipartite Network schematic. A bipartite network (b) made of 2 data sets the “circles”, and the “rectangles”. Projections in the “circle” space (a) and in “rectangle” space (c).

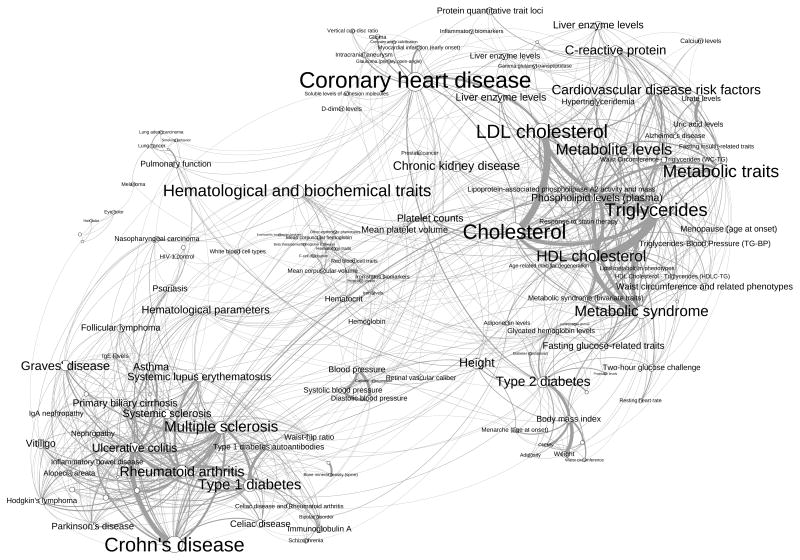
The data from the bipartite network can be projected onto either data space (Figure 2a, c). In both cases, the nodes are connected to one another through a vertex of the other space. By ignoring the different types of data, all network properties described above remain valid on the bipartite network (as a single data set network) and on either projection. We illustrate the iRAV-HPN resulting from the projection onto the phenotype space in Figure 3. In the context of this study, the qualitative nature of the projected HPN does not contain much information about the phenotypic pleiotropy and epistasis. Therefore, we only show one example of projected HPN to give a sense of the complexity of the data and the necessity for quantitative methods.

Fig. 3.

iRAV based Human Phenotype Network. In order to increase the readability, we have filtered out nodes with a degree smaller than 5 (i.e. connected to less than 5 other nodes), showing only 137 nodes (about 30%) and about 45% of the actual edges. To further facilitate the readability, we have manually merged a number of clearly redundant nodes. The nodes and labels sizes are proportional to the original degree of the phenotype (before filtering). The edge width is proportional to the number of overlapping iRAVs.

4. Characterizing and Quantifying Pleiotropy and Epistasis in the HPNs

Early studies have made use of network theory in studying both pleiotropy and epistasis. Global statistical properties of networks, such as the “shape” of the degree distribution and an above average CC place gene expression networks in the small-world²⁰ or scale-free¹⁹ family of networks.²² This indicates that most of the nodes (genes) in the network are of a low degree k. However, a small minority of the vertices are highly connected (hubs). Put in the context of the present work, a few genes have extensive pleiotropic/epistatic effects, but most genes only affect/are affected by a small number of phenotypes. The quantitative structural analyses of the protein interaction networks of model organisms have highlighted the importance of properties such as the diameter and the APL. Li et al.²³ determined that the diameter was ~ 4 – 5 edges, meaning that each gene in the genomes studied affected on average four or five proteins. This finding also corroborates the conjecture that pleiotropy and epistasis are confined to genomic modules, and cannot generally affect any pairs/set of loci in the genome.²⁴

In this work, we propose to use the information beyond the projected HPN, which is limited as it does not contain the actual interactions between the phenotypes and the predictive elements (SNPs, iRAVs, genes, or pathways). Instead, we will analyze the interactions between the two layers of the bipartite networks. Because of the density and complexity of the HPNs, the following section presents the results of a quantitative overview of pleiotropy and epistasis as properties of the entire network. In addition, Section 5 reports the clinical implications and the specific effects observed in a region of the HPNs centered on the “glaucoma” vertex and its neighboring phenotypes. The variable degrees of granularity offered by the different construction methods above result in slightly different definitions of pleiotropy and epistasis. The SNP level provides the most detailed degree, and it defines the strictest pleiotropy and epistasis: the same SNP is associated with multiple phenotypes, or a single phenotype is influenced by multiple SNPs, possibly shadowing each other’s effects. At the SNP-clusters level, we use the iRAV-HPN. The most common definition of pleiotropy and epistasis will be used on the gHPN, where the predictive elements are complete genes. Finally, at the highest level, we will study the pHPN and use biological pathways to quantify pleiotropy and epistasis. Admittedly, these interpretations of pleiotropy and epistasis may somewhat stray from the commonly accepted definitions, but they are in line with the loose nature of the phenomena, where both have sub-types that relate to all degrees of granularity.

Relying on the data in the bipartite HPNs, we calculate the number of phenotypes connected to each predictive element. We use the average connectivity of the predictive element as a proxy for measuring the global pleiotropy (Table 2). We also present the degree distribution of the of the predictive element subset, showing the effect of pleiotropy at each predictive element level (Figure 4). Inversely, the average epistatic effect of predictive elements on phenotypes can be calculated as the average degree of the phenotype subset in the bipartite HPN (Table 2). The degree distribution of the phenotype subset conveys the distribution of epistatic effects that different predictive elements have on the phenotypes (Figure 4).

Table 2.

Quantitative Properties of the different HPNs. (PT : phenotype, GE: predictive element.)

	RAV-HPN	iRAV-HPN	gHPN	pHPN
LCC size (%nodes)	295 (45%)	401 (62%)	430 (67%)	396 (61%)
#edges	932	2845	2556	40K
avg. degree / weighted	6.31 / 10.03	14.19 / 37.54	11.88 / 16.85	204.1 / 497.6
APL / diameter	3.7 / 10	2.96 / 8	2.96 / 6	1.48 / 3
avg. CC	0.58	0.59	0.57	0.79
modularity / communities	0.62 / 26	0.55 / 24	0.49 / 10	0.10 / 4
isolate vertices	351	245	216	250
avg. pleiotropy (#PT/#GE)	1.12	1.12	1.58	27.06
avg. epistasis (#GE/#PT)	11.11	285.64	6.07	5.69

Fig. 4.

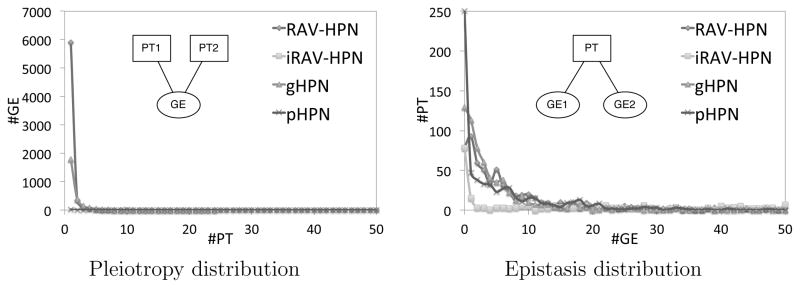
Pleiotropy and Epistasis Distributions. The pleiotropy distributions shows the distribution of the number of phenotypes (PT) for each predictive element, i.e. the distribution of predictive elements influencing multiple phenotypes (see inset). The epistasis distribution shows the number of predictive elements for each phenotype, i.e. the distribution of phenotypes ruled by multiple predictive element (see inset).

Both pleiotropy and epistasis distributions are right-skewed with a heavy tail, which denotes the presence of hubs. The pleiotropy distributions show that most predictive elements only influence a few phenotypes, however, a small minority of predictive elements influence a large number (50+) phenotypes. Similarly, the epistasis distribution depicts that most phenotypes can be associated with only a few predictive elements. However, a small number of phenotypes rely on the signaling of a large number of predictive elements. Although somewhat simplistic, these results are, for all models, in line with the findings of Featherstone et al.²² We acknowledge that the manner in which the average effects are computed may capture more than just the pleiotropic and epistatic effects. However, these results, due to the their ubiquity, reflect a biologically plausible property of the system. We run a full array of quantitative statistical analysis of the different HPNs, including the average pleiotropic and epistatic effects (Table 2).

As the models increase in granularity, the networks become denser with more edges, decreasing APL and diameter. This is to be expected: as the network has more connections, the distance between nodes decreases. The values agree with Li et al.²³ findings. The above average CC and the shape of the degree distributions (not shown here for space reasons) put the HPNs in the scale-free region of the network topology spectrum. Additionally, we note that the modularity and number of communities drops with increasing granularity and network density. The number of isolated nodes provides an insight into how many phenotypes have no detected genetic connection to any other phenotype. Finally, we see that the average pleiotropy remains relatively constant until we look at the pHPN, which biological pathways tend to affect ~ 27 phenotypes in average. Otherwise, predictive elements do not in general impact more than 1–2 phenotypes. This proves the necessity to apply a biologically relevant filter to the pHPN in order to extract the “backbone” of the network, containing the most relevant genetic influences.¹⁷ The average epistatic effect is also reasonably steady, except when ldSNPs are included in the iRAV-HPN. This is due to the fact that now both raSNPS and ldSNPs are directly associated to the phenotypes.

5. Clinical Implications: the Example of Glaucoma

As previously stated, each HPN differs in terms of the number of edges branching from each phenotype node. Moving from the gHPN to the pHPN provides a great deal more information, but the network itself becomes extremely complex and difficult to analyze visually. The pHPN can help to explain the shared etiology of glaucoma and other diseases by revealing a substantial number of interactions unseen in the gHPN. Ultimately, studying predictive elements from a global perspective, using networks, could contribute to novel discoveries in pleiotropic drug therapies.

The HPNs confirm well-known interactions, such as between glaucoma and blood pressure (BP). Studies have linked the two for years and drugs used to treat glaucoma, such as beta-blockers and alpha-adrenergic agonists,²⁵ are known to affect BP. In fact, patients with cardiovascular problems are advised against taking beta-blockers, a treatment for the high intraocular pressure (IOP) associated with glaucoma, because of its effect on heart rate and BP.²⁶ Moreover, many studies have shown that BP and ocular perfusion are important factors in the pathogenesis of glaucoma. For example, studies have linked increases in blood pressure to slight increases in IOP. Going further, the “Blue Mountains Eye Study” found that systemic hypertension was significantly associated with an increased risk of primary open-angle glaucoma (POAG), independent of the effect of BP on IOP. Systemic hypertension was the greatest risk factor for POAG.²⁶ Blood pressure is a first neighbor to Glaucoma in the pHPN, suggesting the validity of the model. They are linked by the umbrella pathways in cancer. Diabetes mellitus is another well-documented disease known to interact with glaucoma.²⁷ Type 1 diabetes is a direct neighbor and Type 2 diabetes is a second (indirect) neighbor. Type 1 diabetes and glaucoma are linked by the cell cycle and HTLV-I infection pathways. Type 2 diabetes and glaucoma share common gene: CDKN2B-AS. In the gHPN, on the other hand, Type 2 diabetes is a first neighbor, but Type 1 diabetes and blood pressure are only second neighbors to glaucoma. Additionally, the pHPN allows us to see connections that are not included in the gHPN, which could lead to new advances in treatments for the linked diseases. For instance, Alzheimers disease is a second neighbor of glaucoma. Both are neurodegenerative diseases and their similarities have recently begun to receive significant attention. Inoue et al. maintain that elevated levels of biomarkers for Alzheimers are more often found in patients with open-angle glaucoma (OAG) than in patients with cataracts.²⁸ In addition, Alzheimer’s and OAG share pathways such as cell death mechanisms (apoptosis), reactive oxygen species (ROS) production, mitochondrial dysfunction and vascular abnormalities.²⁹ Apoptosis of the neural ganglia cells is a major issue in glaucoma. In the gHPN, the link between Glaucoma and Alzheimers disease is not readily apparent by looking at the graph – it becomes a third neighbor. Another interesting link is to the “smoking behavior” phenotype, although this is only readily apparent in the pHPN where it is a first neighbor to glaucoma. The two share the umbrella pathways in cancer. Association studies have shown that smoking behavior is correlated with central corneal thickness in OAG and might also be a risk factor for POAG.³⁰

6. Conclusions & Future Work

The study of genetic diseases is progressing at an unprecedented pace, thanks to modern high-throughput sequencing technology and to the development of modeling techniques at the crossroads of bioinformatics and mathematics. Bipartite HPN models are capable of leveraging the massive amount of GWAS and other readily-accessible genetic data, and collapsing the information into a single, manageable source. The projection of the HPN helps analyze phenotypic interactions.^13,17 The overall structure of the connections between the layers of the bipartite HPN, on the other hand, allows us to estimate in a quantitative manner the pleiotropic and epistatic effect at a global level, for multiple types of predictive elements. Finally, by magnifying regions of the HPN, we are able to highlight previously documented phenotypic interactions, supported by genes and biological pathways evidence as a proof of concept. The bipartite HPNs are flexible, scalable, and intuitive models. HPNs are potentially useful to study phenotypic links, as well as uncover novel pleiotropy and epistasis effects at the single variation level, at the gene level, and all the way to the biological pathway. Future work will involve collapsing the multiple HPNs into an aggregated model. This step will however require the information to be filtered in a biologically sensible manner. Further refinements of the model will include the detection of different types of pleiotropy and epistasis. Finally, we are working on statistical and cross-validation approaches to validate the E&P significance.