Analyzing conformational dynamics of single P-glycoprotein transporters by Förster resonance energy transfer using hidden Markov models

Abstract

Single-molecule Förster resonance energy (smFRET) transfer has become a powerful tool for observing conformational dynamics of biological macromolecules. Analyzing smFRET time trajectories allows to identify the state transitions occuring on reaction pathways of molecular machines. Previously, we have developed a smFRET approach to monitor movements of the two nucleotide binding domains (NBDs) of P-glycoprotein (Pgp) during ATP hydrolysis driven drug transport in solution. One limitation of this initial work was that single-molecule photon bursts were analyzed by visual inspection with manual assignment of individual FRET levels. Here a fully automated analysis of Pgp smFRET data using hidden Markov models (HMM) for transitions up to 9 conformational states is applied. We propose new estimators for HMMs to integrate the information of fluctuating intensities in confocal smFRET measurements of freely diffusing lipid bilayer bound membrane proteins in solution. HMM analysis strongly supports that under conditions of steady state turnover, conformational states with short NBD distances and short dwell times are more populated compared to conditions without nucleotide or transport substrate present.

Introduction

Biochemical reactions catalyzed by proteins (enzymes), including the active transport of ions or small molecules across cellular membranes, are generally associated with cyclic conformational changes that are driven in the forward direction by a net gain in free energy generated by the conversion of substrate to product, or a coupled chemical reaction such as ATP hydrolysis. However, it is now widely recognized that random conformational fluctuations in protein machines can have a significant effect on the overall rate of enzymatic reactions. There is a large amount of high-resolution structural information available for many enzymes. However, to be able to relate crystallographic snapshots of protein machines trapped in different states of the reaction pathway, real-time trajectories of the entire stepwise changes are required. Identifying these steps, including potential intermediates and corresponding dwell times by monitoring single protein machines at work may finally reveal the mechanobiology of catalytic or transport processes.

Conformational changes can be monitored by intramolecular distance measurements between two reference positions on a single protein. Förster resonance energy transfer (FRET) between two specifically attached fluorophores is distance-dependent. Here, distances are calculated from the ratio of the fluorescence intensities of the spectrally distinct dyes. Single-molecule FRET (smFRET) data of freely diffusing proteins are often measured on a confocal microscope setup using time-correlated single photon counting for highest time resolution. To deduce conformational changes from smFRET time trajectories, data analysis methods like hidden Markov models (HMM) are applied. Specific measurement conditions, for example the spatial dependence of detected fluorescence intensities due to the three-dimensional Gaussian intensity distribution of the laser focus, require that HMM estimators have to be modified (one aim of this study). Then, improved analysis might enable the inference of conformational changes in single proteins and reveal the dynamics of the molecular machine.

A biochemically well characterized molecular machine is P-glycoprotein (Pgp), an ATP hydrolysis driven multidrug efflux pump that resides in the plasma membrane of animal cells where it functions to rid the cells of hydrophobic organic molecules such as environmental toxins and anti-cancer drugs [1–5]. Pgp belongs to the family of ATP binding cassette (ABC) transporters, the largest family of primary transport proteins with members found in all domains of life [6–8]. In bacteria and archaea, ABC transporters can function in the direction of both import and export whereas in eukaryotes, the proteins function exclusively as exporters [9]. ABC transporters share a common topology with two transmembrane domains (TMD) and two nucleotide-binding domains (NBD) each. In mammalian Pgp, the four domains are expressed as a single polypeptide in the order N-TMD1-NBD1-TMD2-NBD2-C with each of the two TMDs composed of a six membrane spanning α helix bundle. The interface of the two TMDs forms the drug binding site that shows affinity for a diverse group of molecules with sizes ranging from a few hundred (e.g. verapamil) to more than a thousand Daltons (e.g. cyclosporin A).

Crystal structures of nucleotide free and bound bacterial ABC transporters revealed two major conformations, an inward facing one, with the substrate binding site between the two TMDs exposed to the cytoplasm and an outward facing one, with the binding site for the transport substrate exposed to the periplasm or extracellular space (Fig. 1). It is generally assumed that efficient switching between the inward and outward-facing conformations is driven by binding and/or hydrolysis of two ATP molecules at the interface of the two NBDs. The detailed mechanism, by which ATP binding, hydrolysis and ADP/P_i release is coupled to the conformational switch and the concomitant transport of substrate is still not fully understood. In the case of mammalian Pgp, crystal structures are only available for the inward facing conformation, with the two NBDs separated by 30 Å [10, 11]. However, there is ample biochemical evidence that upon ATP binding, the two NBDs dimerize to form an 'ATP sandwich', a conformation in which nucleotides are bound at the two catalytic sites. Each nucleotide binding site is composed of amino acid sidechains contributed from both NBDs. Based on these data, models were proposed in which the two NBDs bind and hydrolyze ATP in an alternating fashion with the drug transport step coupled to ATP binding and/or hydrolysis and ADP/Pi release [5, 12–15].

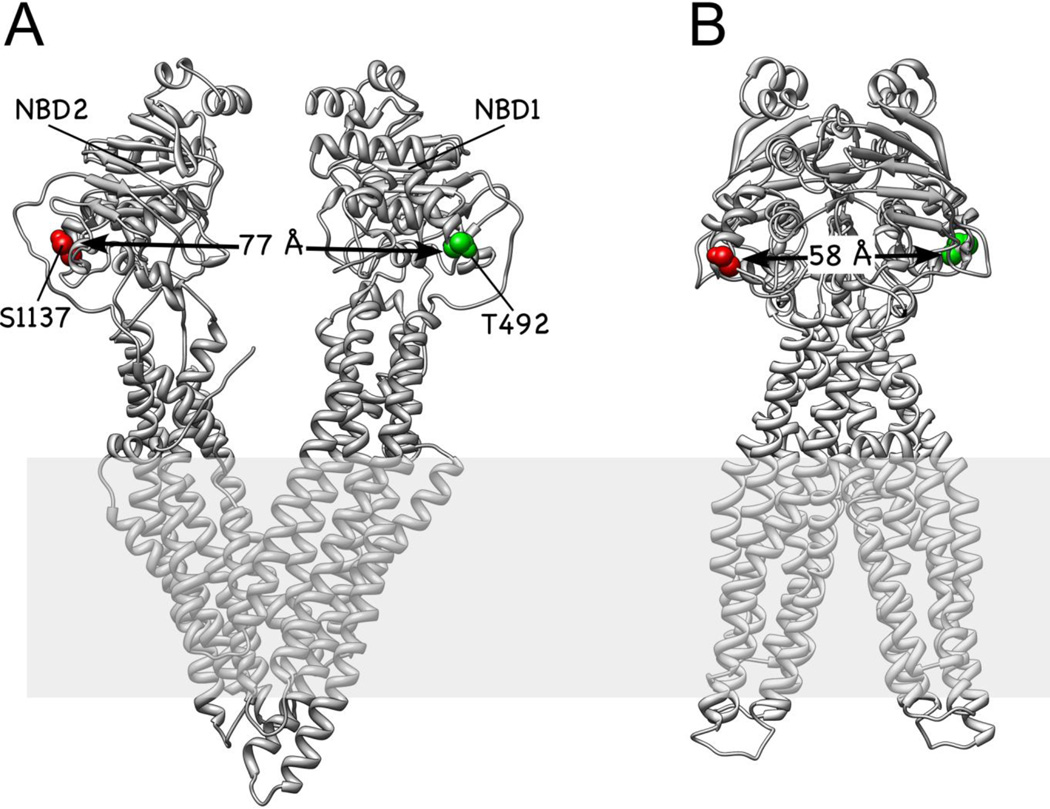
Figure 1.

Schematic of the experimental design. (A) Structural model of mouse Pgp crystallized in the inward facing, nucleotide-free conformation (3g5u). (B) Homology model of the two NBDs of Pgp in the outward facing conformation. For both conformations, the positions of T492 (green) and S1137 (red) are indicated in space fill. Modeling for panel (B) was completed using the outward facing conformation of Sav1866 (2hyd) as described [19]. (C) Confocal detection of freely diffusing FRETlabeled Pgp reconstituted in a liposome. Two laser foci are aligned for duty-cycle optimized alternating laser excitation with 488 nm and 594 nm. (D) Optical setup with two lasers triggered by an arbitrary waveform generator and synchronized TCSPC electronics for time-resolved single-molecule FRET recording.

To analyze the movements of the NBDs as a function of nucleotide and/or substrate binding, we had previously generated 2-D crystals of mouse and human Pgp and from an analysis of EM projection images, we could show that the NBDs undergo nucleotide/substrate dependent structural changes [16, 17]. More recently, we developed a FRET approach that allowed us to monitor changes in the distance between the NBDs under conditions of drug stimulated ATP hydrolysis in real time [18, 19]. FRET between two fluorophore molecules is distance-dependent and occurs in a range between 2 and 10 nm [20]. In our experimental design, the two fluorophores were attached to the two NBDs of Pgp reconstituted into a lipid bilayer (Fig. 1). We found that the ensemble-averaged ratios of donor/acceptor fluorescence did not vary strongly for the different biochemical conditions of drug transport, the 'vanadate-inhibited' state or the so called 'apo'-condition (in the absence of Mg-ATP and transport substrate). However, when conducting smFRET observations of single Pgp transporters during drug stimulated ATP hydrolysis, we found broad distributions of distances and fast distance changes which were assigned manually in the FRET time trajectories.

Single-molecule FRET was measured in solution on a confocal microscope to record individual time trajectories of Pgp conformations. Two pulsed lasers were used to excite the two fluorophores on a single Pgp independently, alternating within nanoseconds. Our duty cycle-optimized pulse sequence [21–23] allowed selection of those Pgp molecules that had one FRET donor and one FRET acceptor fluorophore bound, and ensured that more photons were counted for the FRET measurement than for the control of acceptor fluorophore being present at the single Pgp molecule. Using an enlarged confocal detection volume of about 10 fl (compared to the regular diffraction-limited size of about 0.5 fl) enabled prolonged observation times of Pgp reconstituted in liposomes. The diameter of the proteoliposomes varied between 50 to 150 nm according to negative-stain electronmicroscopic images [19] and resulted in mean diffusion times through the detection volume of about 30 ms, corresponding to photon burst lengths of 20 ms to 1000 ms. Due to the manual assignment of FRET levels in the photon bursts, the number of distinct states could not be determined with certainty. However, changes in consecutive FRET levels were found to be small and so only averaged dwell times of all assigned states could be obtained and compared for different biochemical conditions. Overall, the dwell time analysis indicated faster conformational changes of the NBDs during ATP-driven transport, i.e. in the range of 10 ms, compared to slower NBD fluctuations in the absence of hydrophobic compounds or in the 'vanadate-inhibited' state.

Some limitations of manual and possibly biased FRET level assignment can be reduced for FRET-labeled proteins or membrane transporters with an a priori knowledge of expected FRET levels. For example, we have studied F_oF₁-ATP synthase from E. coli with single-molecule FRET, and ATP-driven subunit rotation in this enzyme resulted in either 3 or 10 FRET levels in sequential order [24–27]. To confirm the manual analysis of F_oF₁-ATP synthase conformational transitions, a specific software-based HMM analysis was developed [28, 29]. HMM approaches for an unbiased and fast analysis of fluorescence intensity traces [30–32] or FRET time trajectories have been proposed, related to either time-binned data [33–36] as provided by EMCCD cameras or to single photon recording with picosecond time resolution for each photon [37–42]. Here we apply a HMM-based approach with modified estimators that account for the fluctuating intensities within a photon burst of freely diffusing single Pgp. To analyze the FRET time trajectories, a number of 2 to 9 different FRET levels were pre-selected for each HMM. HMM analyses yielded different FRET levels and dwell times depending on the biochemical conditions. An upper limit for the total number of FRET states could not be inferred, neither by HMM nor variational Bayesian [36] approaches. However, during ATP-driven drug transport, short-lived conformations with closely spaced NBDs of Pgp were found more often than for 'nucleotide-free' or 'vanadate-inhibited' conditions, supporting the mechanistic model of ATP hydrolysis in alternating sites on the two NBDs.

Materials and methods

Preparation of FRET-labeled Pgp proteoliposomes

Site directed mutagenesis of a cysteine less variant of Pgp (mouse Mdr3) for introducing pairs of cysteines for labeling with maleimide linked dyes and subsequent protein purification, labeling and preparation of proteoliposomes for single-molecule FRET analysis was done as described previously [19]. Briefly, the cysteine double mutant T492C/S1137C (TS mutant) was stochastically labeled with Alexa 488 and Atto 610. The protein was reconstituted to liposomes of a mixture of 19:1 phosphatidylcholine to phosphatidic acid with a 1:1739 protein/lipid ratio (w/w) to contain only a single Pgp per proteoliposome. Samples were diluted with charcoal-treated buffer (10 mM MOPS, 50 mM NaCl, 5 mM MgCl₂ pH 7.0) to achieve a maximum of one proteoliposome at any time in the confocal volume. Proteoliposomes were then incubated for 5 min at 37 °C with the conditions as follows: 'apo', 5 mM MgCl₂, no ATP, no substrate; 'verapamil', 5 mM MgSO₄, 1 mM ATP, 200 µM verapamil; 'vanadate-inhibited', 5 mM MgCl₂, 1 mM ATP, 200 µM verapamil, 237 µM sodium orthovanadate; 'cyclosporin', 5 mM MgCl₂, 1 mM ATP, 5 µM cyclosporin A.

Confocal single-molecule FRET measurements in solution

Our home-built microscope with expanded confocal detection volume of about 10 fl was described previously [19, 43]. Two lasers in duty cycle-optimized alternating fashion were used to excite the donor and acceptor fluorophores [21]. Briefly, Alexa488 was excited with a blue pulsed laser (PicoTa 490, up to 80 MHz repetition rate; Picoquant, Berlin, Germany) at 488 nm with 150 microwatts. The acceptor Atto610 was excited with an continuous-wave HeNe laser at 594 nm with 30 microwatts (Coherent), switched by an acousto-optical modulator. The alternating laser sequence was set for four blue laser pulses at a 16 ns interval with a 64 ps pulse duration, followed by a single 32 ns pulse of the HeNe laser 16 ns after the fourth blue pulse. Photons were detected between 497 and 567 nm (bandpass filter HQ 532/70; AHF, Tübingen, Germany) for Alexa 488 and wavelengths longer than 595 nm for Atto 610 (LP 595; AHF) by two avalanche photo diodes (SPCM-AQR 14; Perkin-Elmer). Recording of the photons was achieved by synchronized TCSPC electronics (SPC 153; Becker & Hickl, Berlin, Germany) in a computer for subsequent fluorescence lifetime analysis, fluorescence correlation spectroscopy, and FRET time trajectory analysis.

Single-Molecule FRET analysis

Photon bursts were automatically marked based on fluorescence intensity thresholds using the software 'Burst-Analyzer' [44]. Intensity time trajectories were binned to 1 ms time intervals. Photon bursts had to exceed 20 counts per ms (cpms) in the acceptor channel when directly excited with 594 nm, as well as 10 cpms in the FRET donor channel and 10 cpms in the FRET acceptor channel upon 488 nm excitation. A minimum burst duration threshold was set to 50 ms. Upper intensity thresholds of 150 cpms were applied for the three intenisty traces of FRET donor, acceptor, and directly excited acceptor. Background corrections of 4 or 3 cpms were subtracted for the FRET donor and acceptor intensities, respectively. Corrections of detection efficiencies and quantum yields were applied using the previously determined correction factor =0.79 for the donor detection channel [19]. Photon bursts were exported as time-binned intensity data with 1 ms time binning. Manual inspection of all selected photon bursts ensured that these thresholds were functional. Preliminary FRET analysis used FRET efficiency histograms consisting of each time bin of the photon bursts. Sets for each biochemical condition were compiled in one file for further analysis.

Hidden Markov model analysis

The sets of photon bursts were analyzed by HMMs with 2 to 9 states for each biochemical condition as well as for all conditions using software written in MatLab (MathWorks, Inc.). To find the minimum number of conformational states with an independent approach we implemented the software VBFRET [36] which uses a maximum evidence inference (i.e. Bayesian model selection) approach instead of maximum likelihood.

Results

We previously generated cysteine double mutants of mouse Pgp for ensemble and single molecule FRET measurements of fluorescently labeled transporters [19]. In these experiments, the cysteines located in the two NBDs were reacted stochastically with e.g. a mixture of Alexa488- and Atto610-maleimide for single-molecule FRET measurements. Fig. 1A,B show the positions of the two cysteines in the mutant 'TS' for the inward and outward facing conformations of Pgp (the outward facing conformation was modeled based on the crystal structure of the bacterial ABC transporter Sav1866 as described in the legend to Fig. 1). Fluorescently labeled Pgp retained drug stimulated ATP hydrolysis activity and was reconstituted in liposomes with diameters between 50 and 150 nm for smFRET experiments as described previously [19]. Preincubation at 37 °C with different buffers for four biochemical conditions (defined in Materials and Methods) and dilution of the Pgp-proteoliposomes in the respective buffers to less than 100 pM allowed single-molecule detection of freely diffusing transporters.

In the confocal microscope setup two laser foci (488 nm and 594 nm) were overlayed for duty-cycle optimized FRET and acceptor test (Fig. 1C). Switching of the lasers was controlled by an arbitrary waveform generator, triggering either 4 pulses of 488 nm or the acousto-optical modulator (AOM) by a 16 ns pulse of 594 nm in a 96 ns cycle (Fig. 1D). As the 594 nm laser was switched by a slow AOM with pronounced rising and decay times, only photons collected in the first 60 ns of the cycle were used for the intensity trajectories of FRET, and the last 36 ns were used to verify that the Pgp molecule in the confocal volume was labeled with an acceptor fluorophore.

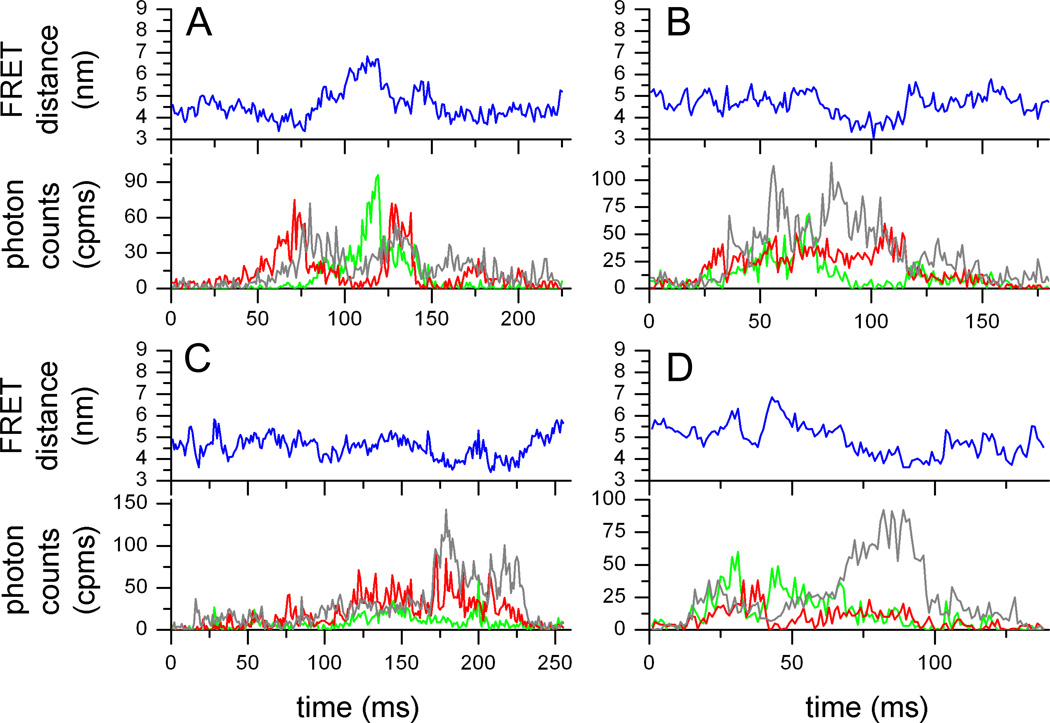
After background correction and given the detection efficiencies of our microscope setup, we used the previously determined correction factor =0.79 to obtain corrected intensities trajectories for FRET donor and acceptor. Shown in Fig. 2A–D are 4 photon bursts of FRET-labeled Pgp during ATP-driven cyclosporin A transport. Green and red traces are FRET donor Alexa488 and FRET acceptor Atto610, respectively. The gray trace shows the Atto610 fluorescence excited with 594 nm, i.e. the acceptor test. To generate the donor-acceptor distance trajectories (blue traces in upper panels) we applied a maximum-likelihood approach 'FRET-Trace' developed by G. Schröder and H. Grubmüller [45].

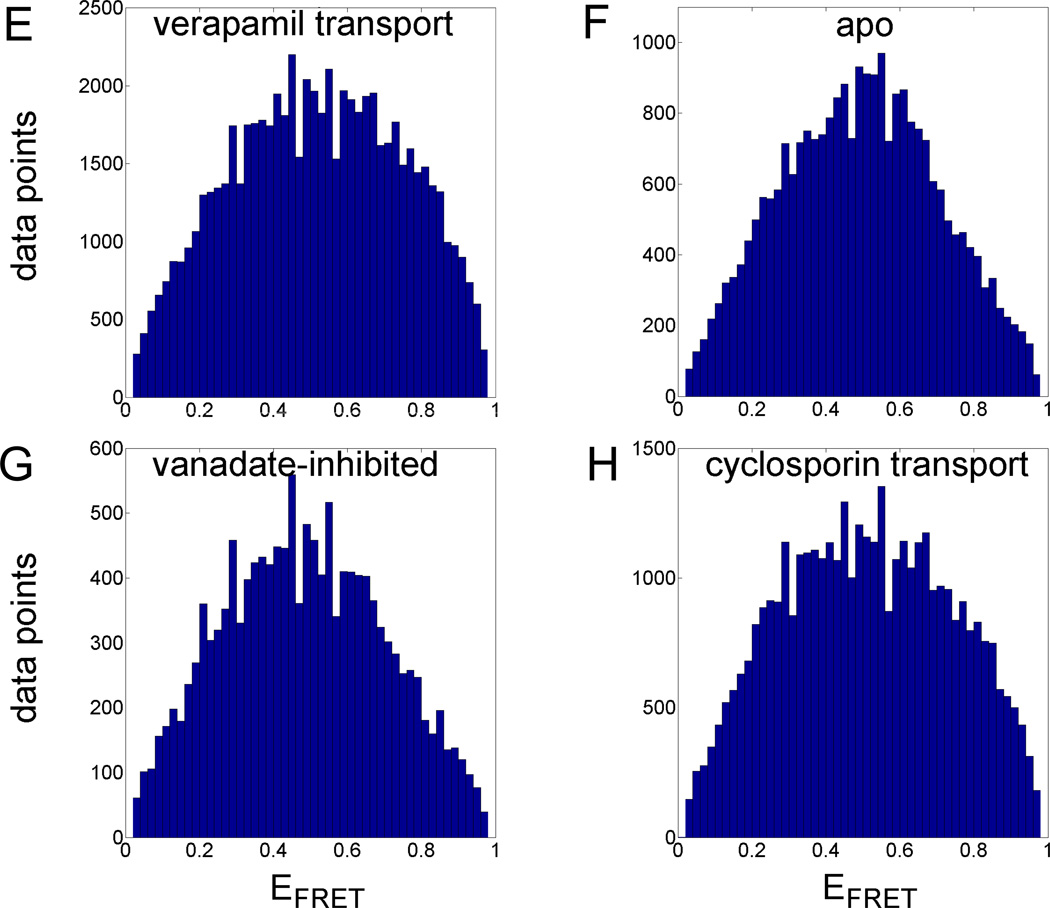
Figure 2.

Single-molecule FRET data of Pgp. (A–D) Time trajectories of single Pgp molecules during 'cyclosporin transport'. FRET donor fluorescence (Alexa 488) excited with 488 nm is shown in the lower panels as green time traces, with 1 ms time binning. FRET acceptor fluorescence (Atto 610) is shown as red trace. Intensities are backgound and detection efficiency corrected. Direct excitation of Atto 610 with 594 nm results in fluorescence intensities shown as grey time traces. Blue traces are the fluorophore distance trajectories calculated by maximum-likelihood estimation [45]. (E–H) FRET efficiency histograms for the four biochemical conditions plotting each time bin of the photon bursts. (E) 'verapamil transport', (F) 'apo', (G) 'vanadate-inhibited', (H) 'cyclosporin transport' (see Materials and Methods).

Before starting the HMM analysis we plotted FRET efficiencies calculated from the corrected fluorescence intensities of each time bin (1 ms) into histograms shown in Fig. 2E–H. The number of threshold-selected photon bursts varied for each biochemical condition despite similar total measurement times of 5 h with 15 min for each measurement before replacing the Pgp sample. Strict burst duration criteria of 50 ms length reduced the number of selected burst dramatically, because we looked for bursts exceeding the average diffusion time through the laser foci by a factor of two. For the 'apo' condition with no ATP and no drugs present we obtained 272 photon burst, for ATP-driven transport of verapamil 773 bursts, for ATP-driven transport of cyclosporin A 445 burst, and for the 'vanadate-inhibited' condition in the presence of ATP, Verapamil and VO₄³⁻ 147 bursts. Histograms of the FRET efficiencies indicated differences for the part with efficiencies E_FRET> 0.7. Both transport conditions have a higher relative number of these FRET efficiencies meaning either longer dwell times for these FRET levels or being more often populated compared to the 'apo' and 'vanadate-inhibited' conditions. However, the histograms displayed broad, unstructured E_FRET distributions indicating that describing the NBD dynamics of Pgp by a simple two-level system was not possible.

Hidden Markov models with new intensity-dependent estimators

To infer the number of FRET levels hidden in the photon bursts we applied the 'Bayesian approach to model selection' developed by J. E. Bronson et al. [36]. The authors had compared their analysis method with maximum-likelihood estimators and found significantly better recovery of the maximum number of states. They distribute their MatLab-based software VBFRET freely. We analyzed the data sets for each biochemical condition in two different ways. First, we analyzed burst by burst individually with VBFRET and found the maximum number of states to be 5 for the 'apo' condition and 4 for the other conditions (see Supplemental Fig. S1). The most likely number of states was 2 for all conditions for about 50 percent of the photon bursts. However, sorting the assigned FRET efficiencies in histograms did not result in well-separated populations of FRET efficiencies but showed a similar distribution as the time binned histograms in Fig. 2. We then merged all photon bursts for one condition and run VBFRET again. Now, the most likely number of states was 9 for all biochemical conditions, meaning that Pgp exhibited NBD movements with many different conformations.

How to describe such a transporter with many FRET levels, their transitions and the associated dwell times to reveal the mechanisms of drug transport? Here, the optimal number of conformational states in an experimental data set of time trajectories is identified using hidden Markov models (HMMs). Therefore, we briefly recapitulate the basic components of a HMM now.

A HMM requires a given number Q of hidden states S_i, which correspond to the absolute conformations but not the experimental FRET data, and transition probabilities k_ij from state S_i to state S_j, with _i,j=1,2,…,Q. Observables {x_t} are the experimental FRET efficiencies E_FRET, measured in each time bin t and calculated from the two intensity time trajectories I_D,t (from the donor fluorophore) and I_A,t (from the acceptor fluorophore) here:

$$x_t=\frac{I_{A,t}}{I_{A,t}+I_{D,t}}$$ (1)

However, to identify the hidden conformational state the intramolecular distance r_t between the two fluorophores is the only observable for the HMM. This intramolecular distance (FRET distance) is related to the FRET efficiency

$$x_t=\frac{R_0^6}{R_0^6+r_t^6}$$ (2a)

or

$$r_t=R_0{(\frac{1}{x_t}-1)}^{1/6}$$ (2b)

respectively. R₀ is the Förster radius for the given pair of FRET donor and acceptor fluorophores and corresponds to the distance for 50 % resonance energy transfer.

The detected intensities I_D,t and I_A,t depend not only on intramolecular distance, but also on the varying spatial position in the laser focus due to the three-dimensional Gaussian intensity distribution. Both contributions have to be separated. This is achieved by defining the ratiometric FRET efficiency x_t in eq. (1) and the sum intensity _t of acceptor and donor intensities for each time bin t in eq. (3):

$${\nu }_t=I_{D,t}+I_{A,t}$$ (3)

Note that x_t is related to the intramolecular fluorophore distances r_t between the dyes in each time bin, for example in each millisecond of the time trajectory, but the sum intensity ν_t is not directly used for determing the distance.

The experimental fluorescence intensities are considered independent Poisson variables [46]. Therefore, the observable x_t cannot be attributed one-to-one to a specific hidden state S_i (i.e. conformation i of Pgp in this study). Instead, a weighting factor w_it can be determined which specifies how likely x_t corresponds to state S_i, and w_it is called the a posteriori probability for state i at time t [47]. Vice versa, for a given state S_i possible values for x_t are distributed according to the probability density function f_i(x), which is called the emission function for state S_i. Because I_A,t and I_D,t are Poisson distributed, the probability density function of the FRET efficiency of a state i with characteristic values for a_i and b_i (i.e. the mean fluorescence intensity a of acceptor and b for the donor fluorophore for one specific position of the protein in the laser focus) is distributed according to a Beta law [48, 49]:

$$f_i(x|a_i,b_i)=\frac{1}{B(a_i,b_i)}{x}^{a_i-1}{(1-x)}^{b_i-1},x=\mathrm{0..1}$$ (4)

with a Beta function B comprising Gamma functions

$$B(a_i,b_i)=\frac{\mathrm{\Gamma }(a_i)\mathrm{\Gamma }(b_i)}{\mathrm{\Gamma }(a_i+b_i)}$$ (5)

The Beta distribution has an expectation value _i

$${\mu }_i=\frac{a_i}{a_i+b_i}$$ (6)

and a variance ${\sigma }_i^2$

$${\sigma }_i^2=\frac{a_i{b}_i}{{(a_i+b_i)}^2(a_i+b_i+1)}$$ (7)

With sum intensity _i = a_i + b_i, the variance is re-written as

$${\sigma }_i^2=\frac{u_i(1-u_i)}{{\nu }_i+1}$$ (8)

We approximate the Beta function with a Gaussian [33, 48]

$$f_i(x|{\mu }_i,{\sigma }_i^2)=\frac{1}{{(2\pi )}^{1/2}{\sigma }_i}\text{exp}(-\frac{{(x-{\mu }_i)}^2}{2{\sigma }_i^2})$$ (9)

This probability density function can now be used as the emission function for the FRET efficiency E_FRET. For normal distributed emission functions, estimators for _i and ${\sigma }_i^2$ have been deduced to learn these HMM parameters from the experimental FRET data [47, 50]. This is the 'standard case' for HMMs. The approximation for eq. (9) is achieved for sum intensities _t ≥ 20 counts per time bin (i.e. photon counts per ms), and several studies using immobilized FRET samples and EMCCD camera detection with time binning of tens of ms have been reported (reviewed in [51]).

However, all parameters characterizing a Markov state S_i have to be time independent in our case, especially the model parameters of the emission function _i and ${\sigma }_i^2$. The parameter _i for the FRET efficiency complies with this precondition. However, the variance ${\sigma }_i^2$ for the sum intensity ν_t does not fulfill this condition for measurements in solution. Here, the sum intensity ν_t changes with time as the labeled protein traverses the detection volume (see Fig. 2). For FRET time trajectories with fluctuating sum intensities ν_t and fast protein dynamics it is necessary to find an emission function which adopts a width at any time to the fluctuating intensities. In previous work we abandoned the approximation of a normal distribution and have used the Beta function as emission functions instead^{[27, 28]}. However, the numerical calculations resulted in a significant slowdown of the time-consuming learning algorithm and did not improve the accuracy of the results compared to the Gaussian approximation at high photon count rates [28, 48].

Here we propose and apply a different method based on the Gaussian approximation. The intrinsic time independent variance ${\sigma }_i^2$ for a Markov state i is additionally broadened in a time dependent manner only by the fluctuating sum intensity ν_t

$${\mathrm{\sigma ̃}}_{i,t}^2={\sigma }_i^2+{\sigma }_{x_t}^2\text{with}{\sigma }_{x_t}^2=\frac{{\mu }_i(1-{\mu }_i)}{{\nu }_t+1}$$ (10)

This modulated variance ${\mathrm{\sigma ̃}}_{i,t}^2$ is now time dependent itself, but can be implemented in the HMM formalisms using the knowledge of the actual sum intensities.

The general 'log likelihood' function L comprises the weighted sums of all emission functions f_HMM for the Q states

$$\text{log}L({\mu }_i,{\sigma }_i^2,w_{it}|\{x_t\})=\sum _{t=1}^T\sum _{i=1}^Q{w}_{it}\text{log}(f_{HMM}(x_t|{\mu }_i,{\sigma }_i^2))$$ (11)

with w_it being the contribution of the data point x_t on state i.

Using the normal distribution for the emission function f_HMM yields

$$\text{log}L({\mu }_i,{\sigma }_i^2,w_{it}|\{x_t\})=-\sum _{t=1}^T\sum _{i=1}^Q(\frac{w_{it}{(x_t-{\mu }_i)}^2}{2{\sigma }_i^2}+\frac{1}{2}\text{log}({\sigma }_i^2))$$ (12)

To obtain the estimators we calculate the derivations of equation (12) with respect to μ̂_i and ${\mathrm{\sigma ̂}}_i^2$. Setting these terms to zero results in the regular estimators [50, 52]

$${\mathrm{\mu ̂}}_i=\sum _{t=1}^T\frac{w_{it}{x}_t}{w_{it}}$$ (13)

and

$${\mathrm{\sigma ̂}}_i^2=\sum _{t=1}^T\frac{w_{it}{x}_i^2}{w_{it}}-{\mu }_i^2$$ (14)

Using the modified emission function with dynamic variance results in a changed 'log likelihood' function [53]

$$\text{log}L({\mu }_i,{\sigma }_i^2,{\sigma }_{x_t}^2,w_{it}|\{x_t\})=-\sum _{t=1}^T\sum _{i=1}^Q(\frac{w_{it}{(x_t-{\mu }_i)}^2}{2({\sigma }_i^2+{\sigma }_{x_t}^2)}+\frac{1}{2}\text{log}({\sigma }_i^2+{\sigma }_{x_t}^2))$$ (15)

Thus we obtain the modified estimator for the FRET efficiency

$${\mathrm{\mu ̂}}_i=\frac{\sum _{t=1}^T\frac{w_{it}{x}_t}{{\sigma }_i^2+{\sigma }_{x_t}^2}}{\sum _{t=1}^T\frac{w_{it}}{{\sigma }_i^2+{\sigma }_{x_t}^2}}$$ (16)

and the solely implicitly representable estimator for the variance

$$\sum _{t=1}^T\frac{w_{it}({(x_t-{\mu }_i)}^2-({\mathrm{\sigma ̂}}_i^2+{\sigma }_{x_t}^2))}{{({\mathrm{\sigma ̂}}_i^2+{\sigma }_{x_t}^2)}^2}=0$$ (17)

The roots of the continuous, one-parameter functions for ${\mathrm{\sigma ̂}}_i^2$ are found by iteration.

Finally, we implemented these modified emission functions and estimators for our HMM approach in the MatLab toolbox as provided by K. Murphy [54]. The weighting factors w_it were optimized iteratively using the forward-backward algorithm, because w_it depends on μ_i and _i, and vice versa (see [47] and references therein). Once all parameters have been optimized, it is possible to calculate a likelihood for a given state sequence. The most likely path of consecutive states which describes best the given data (known as the Viterbi path [55]) is that sequence, where the likelihood reaches a maximum.

With this modified HMM, the sum intensity fluctuations of the single-molecule FRET data are accounted for by dynamically adapted variances, so that HMMs can be applied to FRET data of single freely diffusing proteins and proteoliposomes. The photon bursts of FRET-labeled Pgp were analyzed with HMMs using 2 to 9 states S to obtain the likely FRET level for each state and transitions between the states.

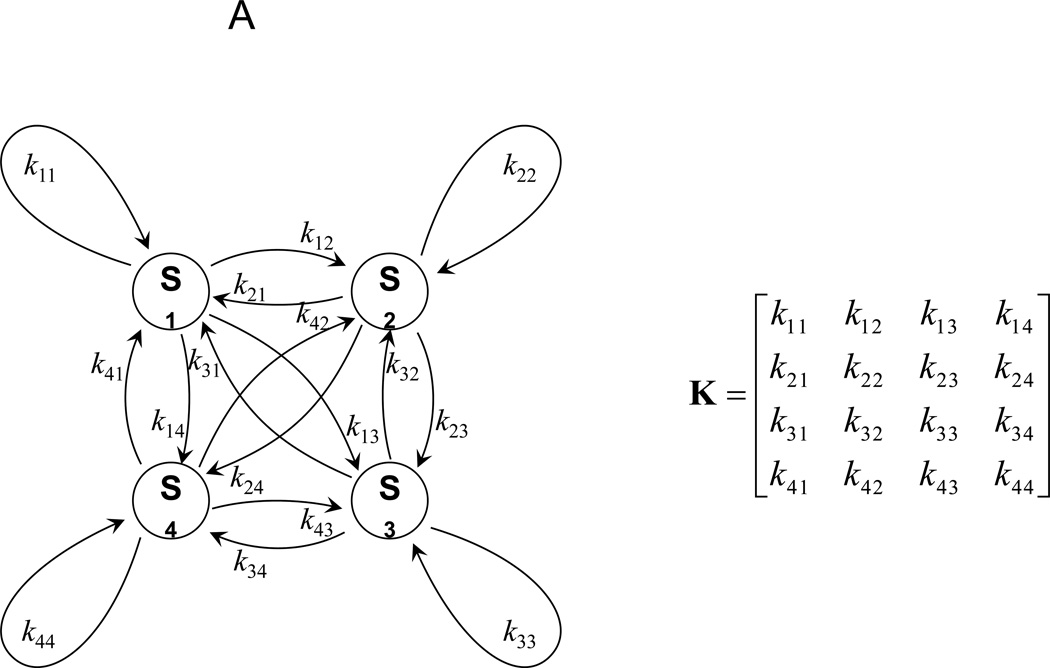
The 4-state HMM is shown in Fig. 3A, with states S₁, S₂, S₃ and S₄. Transition probabilities k_i,i yield the dwell time of state S_i, and k_i,j the transition probabilities from state S_i to S_j. All transitions are contained in the transition probability matrix K. The states and the dwell times for all HMMs with 2 to 9 states for the FRET-labeled Pgp are found in the Supplemental Tables 1 and 2.

Figure 3.

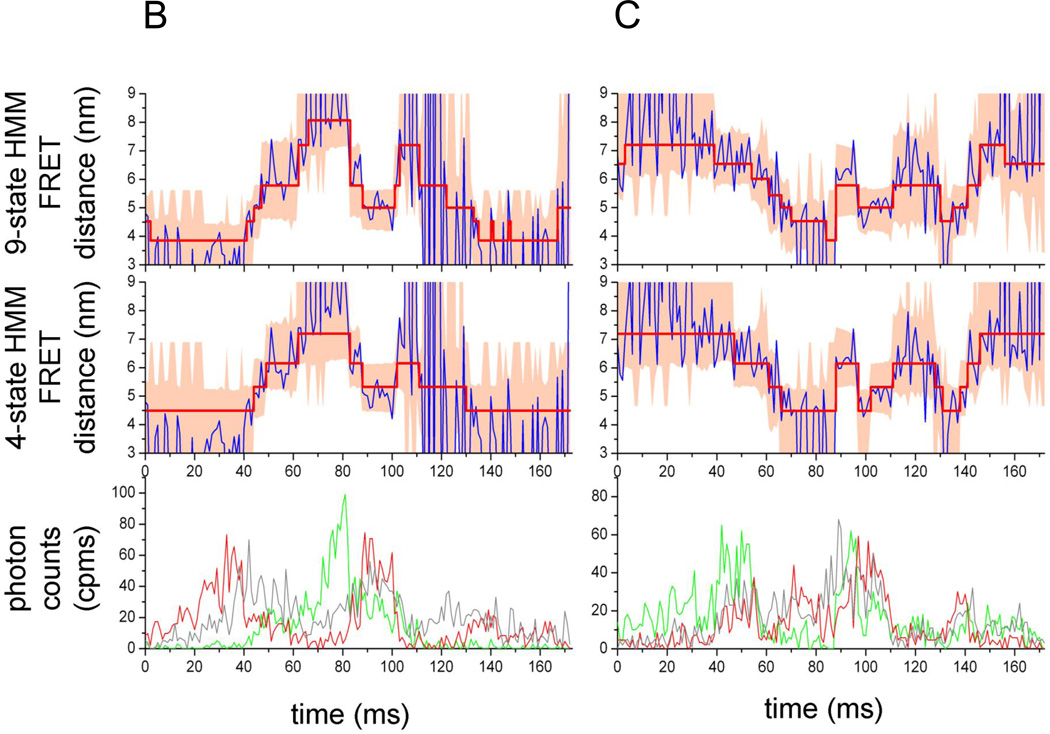
Hidden Markov model analysis of FRET-labeled Pgp. (A) 4-state HMM with transitions between four states S_i, with i= 1, 2, 3, 4, transition probabilities k_i,i and k_i,j, and the corresponding transition probability matrix K. (B, C) FRET state assignments by two HMMs in two photon bursts of FRET-labeled Pgp during 'cyclosporin transport' conditions. FRET donor fluorescence (Alexa 488) is shown in the lower panels as green time traces with 1 ms binning. FRET acceptor fluorescence (Atto 610) is shown as red trace. Intensities are backgound and detection efficiency corrected. Direct excitation of Atto 610 results in fluorescence intensities shown as grey time traces. In the middle and upper panels, the blue traces are the calculated FRET distances from FRET efficiencies E_FRET=I_A/(I_A+ I_D), with I_A, I_D, background and cross-talk corrected intensities of FRET acceptor or donor fluorophore, and, correction factor for the different detection efficiencies and quantum yields of the two fluorophores. FRET distances r_t were obtained per data point using E_FRET=_R0⁶ / (R₀⁶ + r_t⁶) according to the Förster theory of FRET [20]. Red lines with steps are the assigned FRET levels using a 4-state HMM (middle panels) or a 9-state HMM (upper panels), respectively. Light-red colored areas are the variance ( ²) limits for the assigned FRET levels using the new estimators that include the information of sum intensities of both fluorophores at each data point (eq. (10)).

Assignment of FRET levels based on a 4-state and a 9-state HMM, respectively, are depicted in Fig. 3B,C for two photon bursts of FRET-labeled Pgp during cyclosporin transport conditions. FRET donor intensity (green traces) and acceptor intensity (red traces) fluctuated strongly within the bursts. The corresponding FRET-based distance trajectories (blue traces in upper panels) showed the conformational changes of the NBDs. The 4-state HMM-assigned FRET levels (red lines with stepwise changes, middle panel) were calculated as distances, with sum-intensity, time dependent variances (shaded red areas in the panel); the corresponding results of the 9-state HMM were plotted in the panel on top. Apparently, the 4-state HMM did not match the very close NBD conformations with fluorophore distances less than 4 nm at the first 40 ms of the photon burst (Fig. 3B) when compared to the 9-state HMM. Similarly, the open conformations of the NBDs at times between 60 and 80 ms were matched better by the 9-state HMM. In Fig. 3C, the FRET distance trajectory of the NBDs showed transitions between 7 nm and about 4 nm in small increments. It was not obvious, which HMM was preferable. Other photon bursts can be found in Supplemental Fig. S2.

FRET level transitions for the four biochemical conditions

Next we plotted all assigned FRET state transitions for the two transport conditions 'verapamil' and 'cyclosporin', and the 'apo' and 'vanadate-inhibited' conditions. The FRET transition density plots in Fig. 4A–D resulted from the 4-state HMM, the plots in Fig. 4E–H from the 9-state HMM. The results of the other HMMs can be found in Supplemental Figs. S3 to S8. Learning the states was accomplished for each biochemical data set separately.

Figure 4.

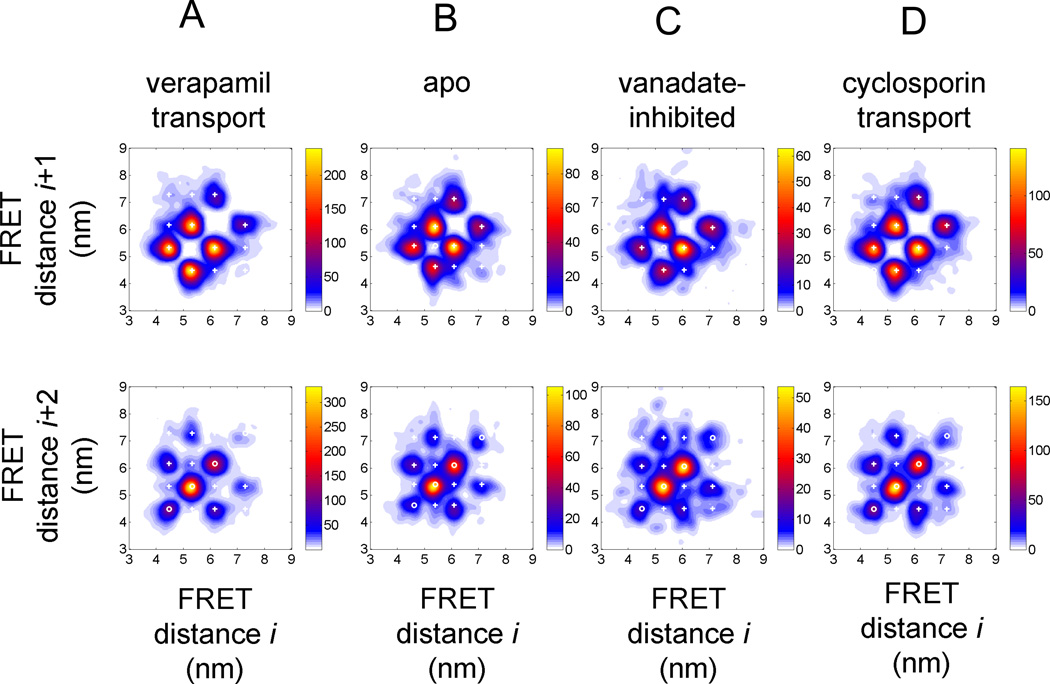
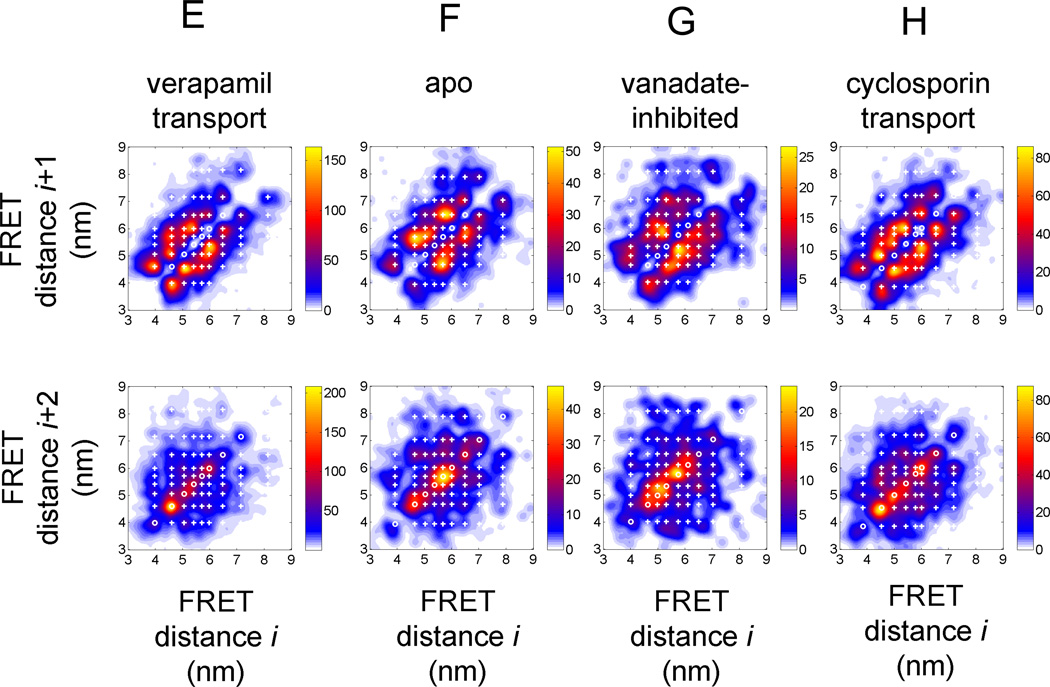
FRET transition density plots for HMM assigned FRET states in Pgp. (A–D) 4-state HMM results for the four biochemical conditions (A) 'verapamil transport', (B) 'apo', (C) 'vanadate-inhibited', (D) 'cyclosporin transport'. Upper row, FRET transitions between sequential FRET states S_i and S_i+1; lower row, FRET transitions between next but one FRET states S_i and S_i+2. (E–H) 9-state HMM results for the four biochemical conditions (E) 'verapamil transport', (F) 'apo', (G) 'vanadate-inhibited', (H) 'cyclosporin transport'. Upper row, FRET transitions between sequential FRET states S_i and S_i+1; lower row, FRET transitions between next but one FRET states S_i and S_i+2. Color map coding indicates minimal and maximal occurrences of FRET transitions for each plot.

The upper diagrams in Fig. 4 show transitions between neighboring assigned FRET distances, i.e. the transition from state S_i to state S_i+1. White crosses represent the HMM-learned most likely values for the states, whereas the normalized false-colored distributions were obtained from the assignment of these FRET states in each individual burst, i.e. from the experimental FRET trajectories and the subsequent recalculations of the FRET distances based on the intensity-weighted experimental photon counts in these states. Therefore, the experimental FRET distance distributions could deviate slightly. The lower diagrams summarized the assigned transitions between state S_i and the next but one state S_i+2.

At first, the FRET transition density plots based on the 4-state HMM looked very similar for all four distributions. The four FRET states were found at FRET efficiencies of 0.19, 0.38, 0.60, and 0.81 for the verapamil transport condition (calculated distances in Fig. 4A), at FRET efficiencies of 0.21, 0.40, 0.58, and 0.78 for the 'apo' condition, at FRET efficiencies of 0.21, 0.41, 0.60, and 0.81 for the 'vanadate-inhibited' condition, and at FRET efficiencies of 0.20, 0.39, 0.60, and 0.81 for the 'cyclosporin transport' condition.

The populations and transitions of these states are also similar as seen in the FRET transition density plots for the neighboring state transitions (Fig. 4A–D, upper row). For verapamil transport, the NBDs of Pgp showed 4 main transitions for fluorophore distances of 6.2 nm to 5.3 nm (and vice versa) and for 5.3 nm to 4.5 nm and back. The two other distances changes between 7.2 nm and 6.2 nm were assigned only to about 1/3 compared to the main transitions. Transitions between states that corresponded to distances changes larger than 1 nm were rarely assigned. The FRET state transitions found for 'cyclosporin' were very similar, with fewer transitions between the NBDs in an "open" conformation with fluorophore distances larger than 6.2 nm. For the 'apo' and the 'vanadate-inhibited' conditions, the transitions were not altered apparently. Eventually the transitions at large NBD distances slightly occurred more often compared to the transport conditions.

Minor differences in the NBD dynamics could be identified in the FRET transition density plots for transitions between next plus one states (Fig. 4A–D, lower row). During ATP-driven verapamil transport, the most often FRET state change is caused by back-and-forth movement starting from fluorophore distances at 5.3 nm. The position of the white circles in the figures indicated this oscillatory dynamics, with the data points on the diagonal of the plot. The other back-and-forth movements at 4.5 nm and 6.2 nm occurred less often, and an oscillatory movement from and to 7.2 nm was not found.

The other populated transitions in this FRET state S_i to S_i+2 plots from 4.5 nm to 6.2 nm or 6.2 nm to 4.5 nm indicate a stepwise opening or closing in small increments, i.e. two-step distance changes with less than 1 nm each. These transitions occurred more often than those between 7.2 nm and 5.3 nm and back. However, also small changes of the NBD distances were found for the conformational transitions from an open conformation to more closed one. For 'cyclosporin' transport and the 'apo' condition we noticed no significant changes with respect to the 'verapamil' transport condition. However, for the 'vanadate-inhibited' condition, the contribution of an oscillatory behavior at 6.2 nm became more pronounced and was observed as often as the back-and-forth movement from and to 5.3 nm.

The total number of assigned FRET states in the 4-state HMM for 'verapamil' were 5448 with 3921 intermediary states (in photon bursts with three or more FRET states) in 773 bursts, for 'apo' 1519 with 988 intermediary states in 272 bursts, for 'vanadate-inhibited' 862 with 571 intermediary states in 147 bursts, and for 'cyclosporin' 2879 with 1990 intermediary states in 445 bursts. For comparison, in the 9-state HMM the assigned FRET states for 'verapamil' were 6720 with 5190 intermediary states, for 'apo' 1632 with 1099 intermediary states, for 'vanadate-inhibited' 883 with 543 intermediary states, and for 'cyclosporin' 3603 with 2719 intermediary states. Increasing the number of states in the HMM from 4 to 9 did not result in assignment of many more states, with a maximum increase of less than 25% mainly for the 'verapamil' transport condition. The complete results of the various HMMs are found in Supplement Material.

The 9-state HMM assigned the FRET states also for smaller as well as larger distances (Fig. 4E–H). For example, for 'verapamil' transport the FRET efficiencies for the 9 states were found at 0.10, 0.20, 0.31, 0.43, 0.50, 0.58, 0.67, 0.78 and 0.90 (for comparison see Fig. 2E). Transitions for the shortest NBD distances from 4.5 nm to 4 nm and back were not assigned in the 4-state HMM, but in the 9-state HMM. Transitions for distances larger than 7 nm were rarely observed for 'verapamil' transport condition. A large variety of transitions with small distance changes less than 1 nm occurred between 5 nm and 6 nm. Also for the 'cyclosporin' transport condition, transitions between 4.5 and 4 nm were detected, and the relative amount of transitions between 7 nm and 8 nm was slightly higher. For the 'apo' condition, the FRET transition density plot for S_i to S_i+1 showed main transitions between 5.7 nm and 6.5 nm as well as between 4.6 nm and 5.7 nm, and the transitions at shorter NBD distances between 4 nm and 4.5 nm were rarely assigned. For the 'vanadate-inhibited' condition, the main transitions were found between 5.8 nm and 5.1 nm and back. However, the smaller number of assigned FRET states in total could limit the visibility of populations.

Comparing the next but one transitions of FRET state S_i to S_i+2 plots (in the lowest panels of Fig. 4E–H) revealed differences for the biochemical conditions. 'Verapamil' transport was associated mostly with oscillation at 4.5 nm, whereas the NBDs in 'apo' conditions moved back and forth at 5.7 nm, with a smaller population oscillating at 4.5 nm. 'Cyclosporin' transport was found often fluctuating at 4.5 nm. 'Vandate-inhibited' conditions corresponded to oscillation at 5.7 as well as 5 nm.

The corresponding FRET transition density plots for the HMMs with less than 4 states as well as with 5 to 8 states are provided as Supplemental Figs. S3 to S8. For HMMs with less than 4 states, differences in the FRET state transitions of the four biochemical conditions were indistinguishable. For HMMs with more than 4 states the differences described above for the 9-state-HMM slowly emerged, and the total numbers of assigned FRET states did not change by adding more states to the model.

Dwell times of assigned FRET states

Finally we compared the dwell times of the assigned FRET states for the four biochemical conditions using either the 4-state HMM or the 9-state HMM as before. The results are summarized in Fig. 5. For the 4-state HMM similar dwell times and dwell time distributions were found for all biochemical conditions. The white crosses mark the dwell times as learned by the HMM, and the false-colored, normalized plots showed the assigned FRET state dwell times in the experimental data sets. Dwell times ranged from 7.6 ms for state E_FRET = 0.6 for 'verapamil' transport to 14.4 ms for the state at E_FRET=0.21 for 'apo'. The dwell times calculated for the assigned experimental FRET states were found always longer (white curves) than the HMM-learned dwells. The mean dwell times for all biochemical conditions of states assigned by HMM ranged from 12 ms for 'verapamil' and 14 ms for 'cyclosporin' transport to 16 ms for 'vanadate-inhibited' and 16.5 ms for 'apo'.

Figure 5.

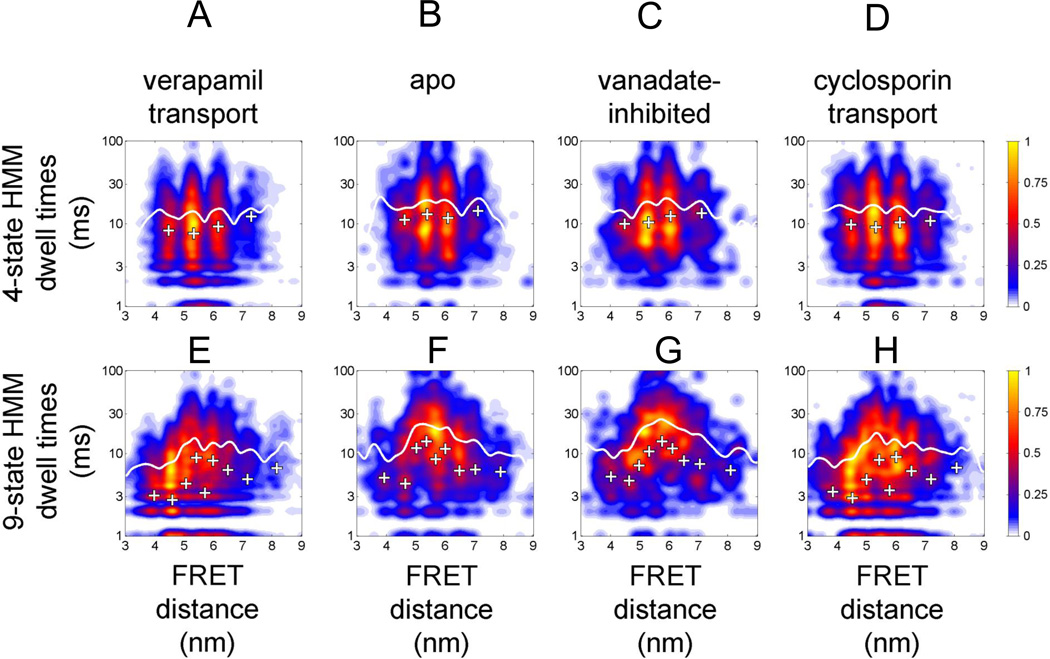
Dwell time distributions for assigned FRET states related to FRET distance. (A–D) 4-state HMM results for the four biochemical conditions (A) 'verapamil transport', (B) 'apo', (C) 'vanadate-inhibited', (D) 'cyclosporin transport'. (E–H) 9-state HMM results for the four biochemical conditions (E) 'verapamil transport', (F) 'apo', (G) 'vanadate-inhibited', (H) 'cyclosporin transport'. Note that the y axes (dwell times in ms) are plotted on a logarithmic scale. Color map coding indicates normalized occurrences for FRET transitions.

Differences of the NBD dynamics were revealed by the 9-state HMM. Both transport conditions for verapamil and cyclosporin were characterized by many dwells around 4.5 nm with short dwell times between 6 and 10 ms (or around 3 ms for the HMM-learned transitions, white crosses). In contrast, most dwells in 'apo' or 'vanadate-inhibited' conditions were found at 5.5 nm to 6 nm, with assigned long dwell times of about 20 ms (or 10 to 12 ms by the HMM). Results for the other HMMs with 2 to 8 states could be found as supplemental Figs. S9 to S11.

Discussion

Confocal single-molecule FRET measurements of the NBDs of mouse Pgp in liposomes had previously shown that this ATP-driven transporter exhibited large conformational changes of the NBDs during drug transport, but also in the absence of ATP or during 'vanadate inhibition'. Manual assignment of FRET levels unraveled faster NBD dynamics during drug transport than in the absence of ATP or inhibited by vanadate [18, 19]. In contrast to manual analyses of FRET levels and dwell times to study the catalytic processes in F_oF₁-ATP synthase[24, 25, 27, 56], an obvious number of FRET levels and a sequence of FRET levels associated with drug transport could not be assigned for Pgp by visual inspection.

Here, recording large data sets of FRET-labeled Pgp allowed selection of a sub-set of photon bursts with high mean count rates for both donor and acceptor fluorophores. Photon burst selection in 1-ms time-binned data was achieved computationally, using intensity thresholds of 20 counts per ms to define a photon burst, maximum count rates of 150 cpms for donor and acceptor to avoid analyzing proteoliposomes containing more than a single Pgp, minimum mean count rates of 10 cpms for both fluorophores, and a minimum photon burst length of 50 ms. From total data collection times of 5 h for each condition, we selected 773 bursts for 'verapamil' transport, 445 bursts for 'cyclosporin' transport, 272 bursts for 'apo' condition in the absence of ATP and drugs, and 147 bursts for 'vanadate-inhibited' condition. As the mean diffusion times of the FRET-labeled Pgp was 15 ms to 30 ms, a significant number of photon bursts with high count rates but shorter observation times were disregarded, and thereby diminished the sub-sets of single-molecule FRET data for the analysis.

The aim of this work was to establish software-based, unbiased FRET analysis methods to obtain the minimum number of FRET levels or NBD distances, respectively, associated with drug stimulated ATP hydrolysis by Pgp. Hidden Markov models (HMMs) have been suggested for the analysis of single-molecule FRET time trajectories and successfully applied to analyze surface-immobilized protein or nucleic acid conformations [33, 57, 58]. Therefore, EMCCD cameras were used with integration times (binning) of several tens of ms, for FRET trace recordings up to several seconds. Surface attachment of the samples yielded nearly constant sum intensities of FRET donor and acceptor fluorescence during the observation. However, monitoring freely diffusing proteoliposomes in a confocal setup resulted in strong fluctuations of the sum intensities of FRET dyes due to Brownian motion of the proteoliposomes, i.e. owing to arbitrary pathways through laser focus and detection volume.

HMMs relate experimental observables to a series of hidden conformational states S, which follow a Markov process with each state S_i+1 depending only on the previous state S_i, and transition probabilities between all states S_i to S_j. Each state is characterized by an emission function, i.e. a single FRET efficiency value plus a variance for E_FRET here. HMM relations of an experimental FRET efficiency to a state and a FRET efficiency change to a state transition are achieved using a maximum-likelihood approach by variation of the emission function parameters. HMMs require time-invariant parameters of the emission function, i.e. a constant FRET efficiency per state plus constant variance for each FRET efficiency. The FRET efficiency is a ratiometric value E_FRET=I_A/(I_A+I_D) from corrected photon count rates for donor (I_D) and acceptor (I_A). As the fluorescence intensities are Poisson distributed, photon count rates fluctuate, and deviations of the mean E_FRET are found characterized by a variance, which is time-invariant for the case of constant excitation power and constant detection efficiency of both fluorophores.

HMMs have to find change points in the experimental E_FRET time trajectories. For all HMM parameters, an underlying likelihood function delivers a measure for each data point to which state it will be assigned. HMM parameter values can be optimized based on the experimental data set using estimator functions. The HMM formalism allows the emission functions of the hidden states to overlap. Afterwards an assignment of each FRET data point to a state S is made.

Confocal single-molecule FRET data in solution, however, comprise spatial-dependent excitation power and detection efficiency, i.e. data depend on the actual position of the diffusing FRET-labeled protein in the detection volume. Therefore, each data point in time corresponds to a different variance, because smaller count rates result in stronger fluctuations of the ratiometric E_FRET, or an apparent broadening of the FRET level, respectively. Vice versa, higher count rates of a data point correspond to narrow fluctuations around the mean E_FRET. Therefore, the 'classical' HMM approach analyzing the E_FRET trace and applying "shot noise limited" variance for E_FRET has to be modified for solution data.

We propose to use the information of the actual fluorescence sum intensity ν_t=I_A,t + I_D,t at each data point to extend the variance as shown above in equation (10). The emission function comprises the time-invariant expectation value _i as model parameter for E_FRET of state S_i, and a new (to our knowledge) expectation value for the variance by combined ²_i, which is time-invariant for each state S_i, plus the time dependent, but defined in each data point by the sum intensities ν_t, component to obtain ²_i,t= _i·(1− _i)/( _t+1) in eq. (10). This emission function is approximated as a Gaussian. Thereby, for each data point x_t we have chosen the appropriate probability density function with a width defined by _t to match the experimental FRET data in solution. Finally, the modified estimators were implemented in the existing HMM loglikelihood formalism.

To test these modified estimators for the HMMs with FRET time trajectories we had generated Monte Carlo simulations of 3-state and 5-state systems previously [27–29]. We used low count rates (sum intensity limited to less than 20 cpms) and short dwell times of 10 ms or 20 ms, respectively, and included high background count rates as well as photobleaching of donor or acceptor [59, 60]. The HMM reassigned the FRET states and dwell times precisely. Smaller differences were found only in the dwell times after assigning FRET states and change points to the simulated FRET time trajectories by the Viterbi path of the HMM [55]. The assigned dwell times were about 50% longer than the learned dwells from the transition probability matrix. This phenomenon has been found in different HMM approaches for dwell times shorter than 20 ms [36, 40]. Depending also on the variance, the accuracy to determine the dwells, the reproducibility of the assigned FRET levels and the sensitivity to transitions dropped to less than 50%. Because our intensity-adjusted variance of FRET-labeled Pgp in solution are broader than for "shot noise limited" conditions of a surface-immobilized sample, the detected discrepancies of assigned longer dwell times and shorter learned values in Fig. 5 are as expected. Setting burst selection thresholds of 20 cpms and mean count rates of 10 cpms for FRET donor and acceptor was intended to ensure the applicability of the modified HMMs including the approximation of using Gaussians instead of Beta functions (see eq. (9)).

The minimum number of states for the HMM should be inferred by the Bayes Information Criterion (BIC). However, as shown also by others [36], the loglikelihood function often shows no maximum at the correct number of states but ends in a plateau with increasing number of states [28] resulting in possible over fitting of the data with too many states. Here, we also did not succeed in getting a distinct number of states for the NBDs of Pgp from the BIC. Therefore we applied the variational Bayesian expectation maximization approach by the software VBFRET [36]. If each photon burst of the Pgp FRET data was analyzed independently, about 4 to 5 states were inferred by VBFRET. However, the corresponding distributions of assigned FRET efficiencies were as broadened as the simple distributions obtained by adding each E_FRET data point into a histogram. Combining all photon bursts in a single data file and analyzing the number of states by VBFRET yielded 9 (the maximum allowed) states as the best solution. The conformational changes of the NBDs of Pgp appeared to occur in small increments, and fitting the experimental single-molecule FRET trajectories with many states was necessary. At least two states in the time trajectories were assigned for photophysical processes of the dyes only, because donor blinking and photobleaching as well as acceptor blinking and photobleaching were identified several times within the selected photon bursts.

Comparing the previously assigned dwell times and states of the NBDs of Pgp by manual inspection [19] with the HMM results presented here, a surprisingly good agreement was noticed. Manual assignment of a smaller data set found mean dwell times of less than 10 ms for 'verapamil' as well as 'cyclosporin' transport; long dwell times > 30 ms for 'apo' and 'vanadate-inhibited' conditions. For example, if we consider that in manual assignments several short FRET levels of a few ms might have been combined into one and recall the results from the 9-state HMM dwell times for transport conditions (see Fig. 5), we found that most transitions assigned now were associated with dwell times of 3 ms to less than 10 ms at NBD distances around 4.5 nm or high FRET efficiencies, respectively. This was exactly the result of the manual assignment. Vice versa, for 'apo' and 'vanadate-inhibited' conditions, we found dwell times of more than 10 ms for 3 or 4 states of the 9-state HMM around 5 nm to 6.5 nm. If manual assignment of FRET levels could not discriminate between these states, we would expect that the resulting combined dwell time would be longer, i.e. several times the 10 ms.

The here presented analysis adds to the emerging picture of Pgp operating as a highly dynamic molecular machine. For example, a recent EPR study revealed broad distributions of distances between the two NBDs, suggesting that the NBDs are able to sample open and closed conformations even in absence of nucleotides and transport substrate [61]. These findings are consistent with our earlier and the current smFRET study such that under the 'apo' condition, the majority of the FRET efficiencies between the two NBD linked dye molecules fluctuate corresponding to a range of distances of between 4.5 and 6.5 nm. Under active turnover, distances are generally shifted to smaller values, consistent with a larger population of transporters with closely associated NBDs, whereas in the 'vanadate-inhibited' state, the majority of transporters show the NBDs fluctuating between 5.2 and 5.8 nm, corresponding to the distance measured for the closed NBD conformation modeled after the outward facing bacterial ABC transporter (Fig. 1B). The presence of NBD distances significantly shorter than the ones measured for the closed NBD sandwich (mainly for the steady state turnover conditions), suggests that during the asymmetric hydrolysis step, the two residues used for site directed mutagenesis get even closer in a conformation not seen so far in crystal structures.

What are the structural basis and the functional rationale for the conformational flexibility of Pgp? It has been pointed out that Pgp contains an unusually large proportion of glycine residues in its transmembrane helices [61], a feature that may result in highly flexible TMDs and concomitant flexibility of the coupled NBDs. Pgp's relatively low affinity for ATP-Mg (compared to other transport ATPases such as P- or F-type pumps) [62, 63], probably contributes to the observed flexibility of the NBDs in that it allows multiple ATP binding and release events before a binding event can produce a conformation competent for hydrolysis. The relatively high activation energy for Pgp's ATP hydrolysis activity [63] means that only few of the conformational fluctuations have enough thermal energy to overcome the energy barrier of the transition state in one of the two catalytic sites. A unique feature of Pgp is the polyspecificity of its drug-binding pocket and it is possible that conformational flexibility in the TMDs is required for allowing Pgp to bind and transport such a structurally diverse group of substrate molecules.

Future improvements for HMM-based single-molecule FRET time trajectory analysis include better signal-to-background ratio using fluorophores with higher quantum yields but also prolonged observation times of single proteoliposomes as discussed [64]. One promising microfluidic approach to hold single FRET-labeled membrane proteins in solution within the confocal detection volume is the so-called 'Anti-Brownian electrokinetic trap' (ABELtrap) [65, 66], which extends the observation time to seconds. Long time trajectories with several complete transport cycles of ATP-driven Pgp will enhance the HMM state and transition assignment and will allow use of VBFRET for inferring the minimum number of states so that the most appropriate HMM could be found. From the current work and future studies with prolonged observation times, we can begin to piece together a comprehensive mechanistic model of the catalytic cycle of Pgp. These studies are ongoing in our laboratories.