Hidden Markov Model and Support Vector Machine based decoding of finger movements using Electrocorticography

Abstract

Objective

Support Vector Machines (SVM) have developed into a gold standard for accurate classification in Brain-Computer-Interfaces (BCI). The choice of the most appropriate classifier for a particular application depends on several characteristics in addition to decoding accuracy. Here we investigate the implementation of Hidden Markov Models (HMM)for online BCIs and discuss strategies to improve their performance.

Approach

We compare the SVM, serving as a reference, and HMMs for classifying discrete finger movements obtained from the Electrocorticograms of four subjects doing a finger tapping experiment. The classifier decisions are based on a subset of low-frequency time domain and high gamma oscillation features.

Main results

We show that decoding optimization between the two approaches is due to the way features are extracted and selected and less dependent on the classifier. An additional gain in HMM performance of up to 6% was obtained by introducing model constraints. Comparable accuracies of up to 90% were achieved with both SVM and HMM with the high gamma cortical response providing the most important decoding information for both techniques.

Significance

We discuss technical HMM characteristics and adaptations in the context of the presented data as well as for general BCI applications. Our findings suggest that HMMs and their characteristics are promising for efficient online brain-computer interfaces.

1. Introduction

Brain-Computer-Interface (BCI) oriented research has a principle goal of aiding disabled people suffering from severe motor impairments (Hoffmann et al., 2007; Palaniappan et al., 2009). The majority of research on BCI has been based on EEG data and restricted to simple experimental tasks using a small set of commands. In these studies (Cincotti, et al., 2003; Lee & Choi, 2003; Obermaier et al.,1999) information was extracted from a limited number of EEG channels over scalp sites of the right and left hemisphere.

Recently, studies have employed invasive subdural electrocorticogram (ECoG) recordings for BCI (Ganguly, K., & Carmena, 2010; Schalk 2010; Zhao et al. 2010; Shenoy et al. 2007). The ECoG is recorded for diagnosis in clinical populations, e.g. for localization of epileptic foci. The signal quality of ECoG recorded brain activity outperforms the EEG-data with respect to higher amplitudes and higher signal-to-noise ratio (SNR), higher spatial resolution, and broader bandwidth (0–500Hz) (Crone et al. 1998; Schalk 2010). Thus, ECoG-signals have the potential for improving earlier results of feature extraction and signal classification (Schalk, 2010).

While approaches have been made to correlate continuous movement kinematics and brain activity exploiting regression techniques (e.g. Wiener filter, Kalman filter and others: Dethier et al. 2011; Acharya et al. 2010; Ball et al. 2009; Kubanek et al. 2009; Liang & Bougrain, 2009; Pistohl et al. 2008), the Support Vector Machine (SVM) approach is established as a gold standard for deriving class labels in cases of a discrete set of control commands (Quandt et al. 2012; Liu et al. 2010; Zhao et al. 2010; Demirer et al., 2009; Shenoy et al. 2007). This is due to high and reproducible classification performance as well as robustness with a low number of training samples using SVM approaches (Guyon et al., 2002). However, depending on the individual problem, distinct properties of other machine learning methods may provide another viable BCI approach. Pascual-Marqui et al. (1995) and Obermaier et al. (1999) argued that brainstates and state transitions can explain components of observed human brain activity. Obermaier et al. applied HMMs in offline classification of non-invasive electroencephalographic (EEG) recordings of brain activity to distinguish between two different imagined movements. In support of the idea of distinct mental states, they reported an improvement of BCI classification results in subjects who developed a consistent imagination strategy resulting in more focused and reproducible brain activity patterns. The authors concluded that HMMs offer a promising means to classify mental activity in a BCI framework because of the inherent HMM flexibility in structural degrees of freedom and simplicity. Some studies however reveal unstable properties and less HMM robustness in high dimensional feature spaces. The latter point is critically related to small training sets leading to degradation in the classifiers ability (Lotte et al., 2007).

In this study we directly compare HMM and SVM classification of ECoG data recorded during a finger tapping experiment. This was done after a careful optimization of both classifiers – first, focusing on improvements of the features and secondly by introducing constraints to the HMMs reducing the amount of required training data. Additionally, the problem of high dimensional feature spaces is addressed by feature selection. It is known that feature extraction and selection have a crucial impact on the classifier performance (Pechenizkiy, M., 2005; Guyon, I. & Elisseeff, A., 2003). However, the exact effect on the decoding accuracy for given data characteristics and representations of information in time and space remains to be investigated. Poorly constructed feature spaces cannot be compensated by the classifier. However, an optimal feature space does not make the choice of the classifier irrelevant. A tendency toward unstable HMM behaviour as well as the different ways in which HMM and SVM model feature spaces was addressed with the ECoG data set.

Our hypothesis was that for ECoG classification of finger representations differences in performance between the two approaches would be due to the way features are extracted and selected and less influenced by the choice of the classifier. Here we demonstrate that constrained HMMs achieve decoding rates comparable to the SVM. We first provide an overview of how the data were acquired. We then review the analysis methods, involving feature extraction, HMMs and SVMs. Third, results on feature space setup and feature selection are evaluated. Finally, we discuss the decoding performance of the HMM classifier and directly compare it to the one-vs.-one SVM.

2. Material and methods

2.1 Patients, experimental setup and data acquisition

ECoG data were recorded from four patients who volunteered to participate (aged 18–35 years, right handed male). All patients received subdural electrode implants for pre-surgical planning of epilepsy treatment at UC San Francisco, CA, USA. The electrode grid was solely placed based on clinical criteria and covered cortical pre-motor, motor, somatosensory, and temporal areas. Details on the exact grid placement for each subject can be obtained from supplementary figures 1–4. The study was conducted in concordance with the local IRB-approved protocol as well as the declaration of Helsinki. All patients gave their informed consent before the recordings started. The recordings did not interfere with the treatment and entailed minimal additional risk for the participant. At the time of recording all patients were off anti-epileptic medications. They were withdrawn when they were admitted for ECoG monitoring.

The recordings were obtained from a 64-channel grid of 8 × 8 platinum-iridium electrodes with 1 cm centre-to-centre spacing. The diameter of the electrodes was 4 mm, of which a 2.3 mm were exposed (except for subject 4 who had a 16 × 16 electrode grid, 4 mm centre-to-centre spacing). The ECoG was recorded with a hardware sampling frequency of 3051.7 Hz and was then downsampled to 1017 Hz for storage and further processing. During the recordings patients performed a serial reaction time task in which a number appeared on a screen indicating with which finger to press a key on the keyboard (1 indicated thumb, 2: index, 3: middle, 5: little finger; the ring finger was not used). The next trial was automatically initiated with a short randomized delay of (335+/−36) ms after the previous key press (mean value for S1, session 1; others in similar range). The patients were instructed to respond as rapidly and accurately as possible, with all fingers remaining on a fixed key during the whole 6–8 min run. For each trial the requested as well as actually used finger was recorded. The rate of correct button presses was at or close to 100 % for all subjects. For classification trials were labeled according to the finger that was actually moved. Each patient participated in 2–4 of these sessions (table 1). Subjects performed slight finger movements requiring minimal force. Topographic finger representations extend approximately 55 mm along motor cortex (Penfield and Boldrey, 1937). The timing of stimulus presentations and button presses was recorded in auxiliary analogue channels synchronized with the brain data.

Table 1.

Number of recorded and rejected trials per subject, session and class (thumb/index finger/middle finger/little finger).

Subject #	Session #	Trials	Class Breakdown	# Rejected Trials (Breakdown)
S1	1	357	62/113/108/74	0 (0/0/0/0)
	2	240	33/90/72/45	1 (0/1/0/0)
	Total	587	95/203/180/119	1 (0/1/0/0)
S2	1	280	44/97/91/48	40 (5/13/13/9)
	2	308	51/103/111/43	0 (0/0/0/0)
	3	271	38/87/92/54	77 (13/23/26/15)
	4	273	32/88/88/65	41 (8/17/10/6)
	Total	1122	165/365/382/210	158 (26/53/49/30)
S3	1	234	54/70/70/40	114 (16/40/36/22)
	2	249	47/70/83/49	104 (15/31/38/20)
	Total	483	101/140/153/89	218 (31/71/74/42)
S4	1	359	57/113/116/73	6 (2/2/1/1)
	2	328	63/104/106/55	33 (6/11/11/5)
	Total	687	120/217/222/128	39 (8/13/12/6)

Due to clinical constraints, the time available for ECoG data acquisition is restricted providing a challenging dataset for any classifier. The number of trials for classification are listed in table 1. For pre-processing the time series was first high pass filtered using a cut-off frequency at 0.5 Hz as well as notch filtered around the power line frequency (60 Hz) using frequency domain filtering. The electric potentials on the grid were re-referenced to Common-Average-Reference (CAR).

Next, the time series were visually inspected for the remaining intervals and artefacts caused by the measurement hardware, line noise, loose contacts and sections with signal variations not explained by normal physiology were excluded from analysis. Channels with epileptic activity were removed since epileptic spiking has massive high frequency spectral activity and can distort informative features in this range. We also removed any epochs with spread of the epileptic activity to normal brain sites to avoid high frequency artefacts. The procedure was chosen to ensure comparability across subjects and sessions. Trial rejection was carried out without any knowledge of the corresponding class labels and in advance of any investigations on classification accuracies. Finally, the trials were aligned with respect to the detected button press being the response for each movement request.

2.2 Test Framework

The methods described in the following assemble an overall test framework as illustrated in figure 1. The classifier, being the main focus here, is embedded as the core part among other supporting modules including pre-processing, data grouping according to the testing scheme, channel selection and feature extraction. The framework includes two paths for training and testing data to ensure that no prior knowledge about the test data is used in the training process.

Fig. 1. Block diagram of the implemented test framework.

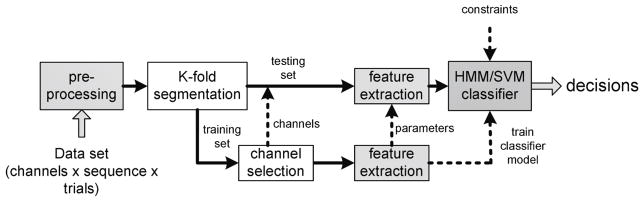
The decision for a particular class is provided by either SVM or HMM; in both cases they are exposed to an identical framework of pre-processing, channel selection and feature extraction

2.3 Feature Generation

Two different feature types have been extracted for this study. First, time courses of low-frequency components were obtained by spectral filtering in Fourier domain. These time courses were limited to a specific interval of interest around the button press containing the activation most predictive for the four classes. The chosen frequency range of the lowpass filter covers a band of low-frequency components that contain phase-locked event-related potentials (ERPs) and prominent Local Motor Potentials (LMP) (Kubanek, Miller, Ojemann, Wolpaw, & Schalk, 2009). These are usually extracted by averaging out uncorrelated noise over multiple trials (Makeig, 1993). Here we focus on single-trial analysis which may not reflect LMP activity (Picton et al., 1995). As a consequence, we will refer to this feature type as Low Frequency Time Domain (LFTD) features. Boundaries of time interval (length and location relative to the button press) and lowpass filter cut-off were selected by grid search for each session and are stated in the results. The data sampling was reduced to the Nyquist frequency.

Second, event-related spectral perturbation (ERSP) was measured using a sliding Hann-window approach (window length n_w = 260ms). For each window the square root of the power spectrum was computed by Fast Fourier Transform (FFT). The resulting coefficients were then averaged in a frequency band of interest. Taking the square root to obtain the amplitude spectrum assigned a higher weight to high frequency components compared to original power spectrum. The resulting feature sequence can be used as a measure for time-locked power fluctuation in the high gamma band neglecting explicit phase information (Graimann et al. 2004; Crone et al. 1998; Makeig, 1993). The time interval relative to the button press, the window overlap and exact low and high cut-off frequency of the high gamma band most discriminative for the four classes were selected by grid search. Resulting parameters for each session are stated in the results section.

A combined feature space including both, high gamma (HG) features as well as low-frequency time domain features (LFTD) was also evaluated. The ratio p of how many LFTD feature sequences are used relative to the number of HG sequences has been obtained by grid search. Subset selection beyond this ratio is described in the next subsection.

2.4 Feature Selection

General remarks on subset selection

Feature sequences were computed for all 64 ECoG channels giving 2×64 sequences in total. From these sequences a subset of size O has been identified, that contains the most relevant information about the finger labels. A preference towards certain channels is influenced by the grid placement as well as distinct parts of the cortex differentially activated by the task.

We tested several measures of feature selection such as Fisher’s Linear Discriminant Analysis (Fisher, 1936) and Bhattacharyya distance (Bhattacharyya, 1943) and found that the Davies-Bouldin (DB) Index (Wissel & Palaniappan, 2011; Davies & Bouldin, 1979) yielded the most robust and stable subset estimates for accurate class separation. In addition to higher robustness the DB Index computationally also represents the fastest alternative. The DB index substantially outperformed other methods for both SVM and HMM. Nevertheless it should be pointed out that observed DB subsets were in good agreement with the ranking generated by the normal vector w of a linear SVM. Apart from so-called filter methods such as the DB index, an evaluation of these vector entries after training the SVM would correspond to feature selection using a wrapper method (Guyon, I. & Elisseeff, A., 2003). Our study did not employ any wrapper methods to avoid dependencies between feature selection and classifier. This may have led to an additional bias towards SVM or HMM (Yu & Liu, 2004). Based on the DB Index we defined an algorithm, that automatically selects an O-dimensional subset of feature sequences as follows.

Davies-Bouldin Index

The index corresponds to a cluster separation index measuring the overlap of two clusters in an arbitrarily high dimensional space, where r ∈ ℝ^T is one of N sample vectors belonging to cluster C_i.

$${\mathbf{\mu }}_{\mathbf{i}}=\frac{1}{N}\sum _{\mathbf{r}\in C_i}\mathbf{r}$$ (1)

$$d_i=\frac{1}{N}\sum _{\mathbf{r}\in C_i}\Vert \mathbf{r}-{\mathbf{\mu }}_{\mathbf{i}}\Vert$$ (2)

$${\mathrm{R}}_{\text{ij}}=\frac{{\mathrm{d}}_{\mathrm{i}}+{\mathrm{d}}_{\mathrm{j}}}{\Vert {\mathbf{\mu }}_{\mathbf{i}}-{\mathbf{\mu }}_{\mathbf{j}}\Vert }\mathrm{i},\mathrm{j}\in {\mathrm{N}}^{+},\mathrm{i}\ne \mathrm{j}$$ (3)

Using the cluster centroids μ_i ∈ ℝ^T and spread d_i, Matrix R = {R_ij}_{i=1...Nc,j=1…Nc} contains the rate between the within-class spread and the between-class spread for all class combinations. The smaller the index, the less two clusters overlap in that feature space. The index is computed for all features available.

Feature selection procedure

Covering different aspects of class separation, we developed a feature selection algorithm based on the Davies-Bouldin Index taking multiple classes into account. The algorithm aims at minimizing the mutual class overlap for a subset of defined size O as follows. First, each feature sequence is segmented into three parts of equal length. The index matrix R measuring the cluster overlap between all classes i and j is then computed segment-wise for each feature under consideration. Subsequently all three matrices are averaged (geometric mean for a bias towards smaller indices) for further computing. The feature yielding the smallest mean index is selected, since it provides the best separation on average from one class to at least one other class. Second, for all class combinations the features corresponding to the minimal index per combination are added. Each of them optimally separates a certain finger combination. Next, features with the smallest geometric mean per class are added, if they are not part of the subset already. Finally, in case the predefined number of elements in the subset O admits further features, vacancies are filled according to a sorted ranking of indices averaged across class combinations per feature.

For each trial this subset results in an O-dimensional feature vector varying over time t ∈[0,T]. While this multivariate sequence was fed directly into the HMM classifier, the O × T Matrix O_t had to be reshaped into a 1× (T · O) vector for the SVM. The subset size O is obtained by exhaustive search on the training data. This makes the difference between both classifiers in data modelling obvious. While an HMM technically distinguishes between the temporal development (columns in O_t) and the feature type (rows in O_t), the SVM concatenates all channels and their time courses within the same one-dimensional feature vector. The potential flexibility of HMMs with respect to temporal phenomena substantially arises from this fact.

2.5 Classification

Hidden Markov Models

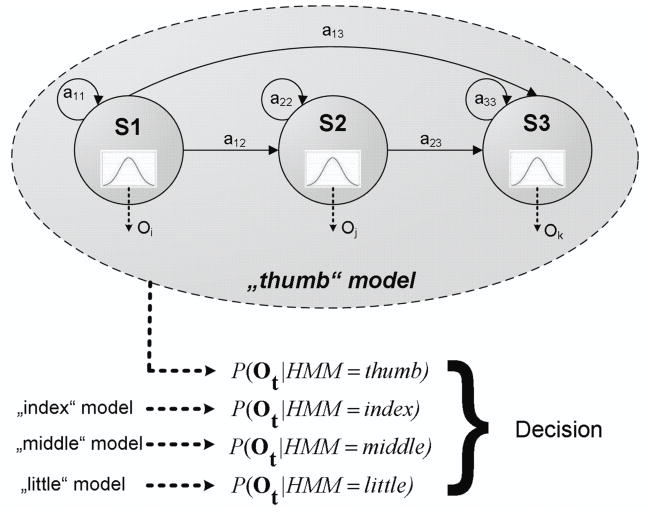
Arising from a state machine structure Hidden Markov Models (HMMs) comprise two stochastic processes. First, as illustrated in figure 2, a set of Q underlying states is used to describe a sequence of T O-dimensional feature vectors O_t. These states q_t ∈ {s_i}_i=1…Q are assumed to be hidden, while each is associated with an O-dimensional multivariate Gaussian M-mixture distribution to generate the observed features - the second stochastic process. Both, the state incident q_t as well as the observed output variable o_t at time t are subject to the Markov property – a conditional dependency only on the last step in time t−1.

Fig. 2.

An HMM structure for one class consists of Q states emitting multi-dimensional observations o_t at each time step. The state as well as the output sequence is governed by a set of probabilities including transition probabilities a_ij. To assign a sequence O_t to a particular model, the classifier decides for the highest probability P(O_t|model).

Among other parameters the state sequence structure and its probable variations are described by prior probabilities P(q₁ = s_i) and a transition matrix

$$\mathbf{A}={\{a_{ij}\}}_{i,j=1\dots Q}={\left\{P(q_{t+1}=s_j\mid q_t=s_i)\right\}}_{i,j=1\dots Q}.$$

A more detailed account on the methodological background is given by Rabiner (1989).

For each of the four classes one HMM had to be defined, which was trained using the iterative Baum-Welch algorithm with 8 Expectation-Maximization (EM) steps (Dempster et al., 1977). The classification on the test set was carried out following a maximum likelihood approach as indicated by the curly bracket in figure 2. In order to increase decoding performance the above standard HMM structure was constrained and adapted to the classification problem. This aims at optimizing the model hypothesis to give a better fit and reduces the amount of free parameters to deal with limited training data.

Model Constraints

First, the transition matrix A was constrained to the Bakis model commonly used for word modelling in automatic speech processing (ASR) (Schukat-Talamazzini, 1995). This model admits non-zero elements only on the upper triangular part of the transition matrix - specifically on the main as well as first and second secondary diagonal. Thus this particular structure implies only ‘loop’, ‘next’ and ‘skip’ transitions and suppresses state transitions on the remaining upper half. Preliminary results, using a full upper triangular matrix instead, revealed small probabilities, i.e. very unlikely state transitions, for these suppressed transitions throughout all finger models. This suggests only minor contributions to the signal characteristics described by that model. A full, ergodic transition matrix generated poor decoding performances in general. Recently, a similar finding was presented by Lederman and Tabrikian for EEG data (Lederman & Tabrikian, 2012). Given five states containing one Gaussian the unleashed model would involve 4·1235 degrees of freedom, while the Bakis model uses 4·1219 for an exemplary selection of 15 channels. The significant increase of decoding performance by dropping only a few parameters seems interesting with respect to the nature of the underlying signal structure and sheds remarkable light on the importance of feature selection for HMMs. An unleashed model using all 64 channels would have 4·20835 free parameters.

Model structure

Experiments for all feature spaces have been conducted in which the optimal number of states Q per HMM and the number of mixture distribution components M per state have been examined by grid search. Since increasing the degrees of freedom will degrade the quality of model estimation, high decoding rates have mainly been obtained for a small number of states containing only a few mixture components. Based on this search a model structure of Q = 5 states and M = 1 mixture components has been chosen as the best compromise. Note, that the actual optimum might slightly vary depending on the particular subject, the feature space and even on the session, which is in line with other studies (Obermaieret al., 1999, 2001a, 2001b).

Initialization

The initial parameters of the multivariate probability densities have been set using a k-means clustering algorithm (Duda et al., 2001). The algorithm temporally clusters the vectors of the O × T feature matrix O_t. The rows of this matrix were extended by a scaled temporal counter adding a time stamp to each feature vector. This increases the probability of time-continuous state intervals in the cluster output. Then, for each of the Q · M clusters the mean as well as the full covariance matrix have been calculated excluding the additional time stamp. Finally, to assign these mixture distributions to specific states, the clusters were sorted according to the mean of their corresponding time stamp values. This temporal order is suggested by the constrained forward structure of the transition matrix. The transition matrix is initialized with probability values on the diagonal that are weighted to be c-times as likely as probabilities off the diagonal. The constant c is being calculated as the quotient of the number of samples for a feature T and the number of states Q. In case of multiple mixture components (M>1) the mixture weight matrix was initialized using the normalized number of sample vectors assigned to each cluster.

Implementation

The basic implementation has been derived from the open source functionalities on HMMs provided by Kevin Murphy from the University of British Columbia (Murphy, 2005). This framework, its modifications as well as the entire code developed for this study were implemented using MATLAB R2012b from MathWorks.

Support Vector Machines

As gold-standard reference we used a one-vs.-one SVM for multi-class classification. In our study training samples come in paired assignments (x_i, y_i)_i=1…N, where x_i is a 1×(T·O) feature vector derived from the ECoG data for one trial with its class assignment y_i ={−1,1}. Equation (4) describes the classification rule of the trained classifier for new samples x. A detailed derivation of this decision rule and the rationale behind SVM-classification is given e.g. by Hastie et al. (2009).

$$F(\mathbf{x})=sgn\left(\sum _i{\alpha }_i{y}_{i}K\left({\mathbf{x}}_{\mathbf{i}},\mathbf{x}\right)+{\beta }_0\right)$$ (4)

The α_i ∈ [0,C] are weights for the training vectors and are estimated during the training process. Training vectors with weights α_i ≠ 0 contribute to the solution of the classification problem and are called support vectors. The offset of the separating hyperplane from the origin is proportional to β₀. The constant C generally controls the trade-off between classification error on the training set and smoothness of the decision boundary. The number of training samples per session (table 1) were in a similar range compared to the resulting dimension of the SVM feature space T · O (~ 130 – 400). Influenced by this fact, the decoding accuracy of the SVM revealed almost no sensitivity with respect to regularization. Since grid search yielded a stable plateau of high performance for C >1, the regularization constant was fixed to C = 1000. The linear kernel, that has been used throughout the study, is denoted by K(x_i,x). We further used the LIBSVM (http://www.csie.ntu.edu.tw/~cjlin/libsvm/) package for Matlab developed by Chih-Chung Chang and Chih-Jen Lin (Chang and Lin, 2011).

2.6 Considerations on testing

In order to evaluate the findings presented in the following sections a 5-fold cross-validation (CV) scheme was used (Lemm, 2011). The assignment of a trial to a specific fold set was performed using uniform random permutations.

Each cross-validation procedure was repeated 30 times to average out fluctuations in the resulting recognition rates arising from random partitioning of the CV sets. The number of repetitions was chosen as a compromise to obtain stable estimates of the generalization error, but also to avoid massive computational load. The training data was balanced between all classes to treat no class preferentially and to avoid the need for class prior probabilities. Feature subset selection and estimation of parameters of each classifier was performed only on data sets allocated for training in order to guarantee a fair estimate of the generalization error. Due to prohibitive computational effort the feature spaces have been parameterized only once for each subject and session and are hence based on all samples of each subject-specific data set. In this context preliminary experiments indicated minimal differences to the decoding performance (cf. table 2) when fixing the feature definitions based on the training sets only. These experiments used nested CV with an additional validation set for the feature space parameters

Table 2. HMM-decoding accuracies (in %) for parameter optimization on full data and on training subsets.

Accuracies are given for subject 1 - session 1. Parameter optimization was performed on the full dataset (standard-CV routine) as well as the training subset (nested-CV routine).

Parameter optimization on	LFTD	HG	LFTD + HG
Full dataset	80.7±0.3	97.9±0.1	98.4±0.1
Training subset	81.1±1.0	97.8±0.3	98.0±0.2

3. Results

3.1 Feature and channel selection

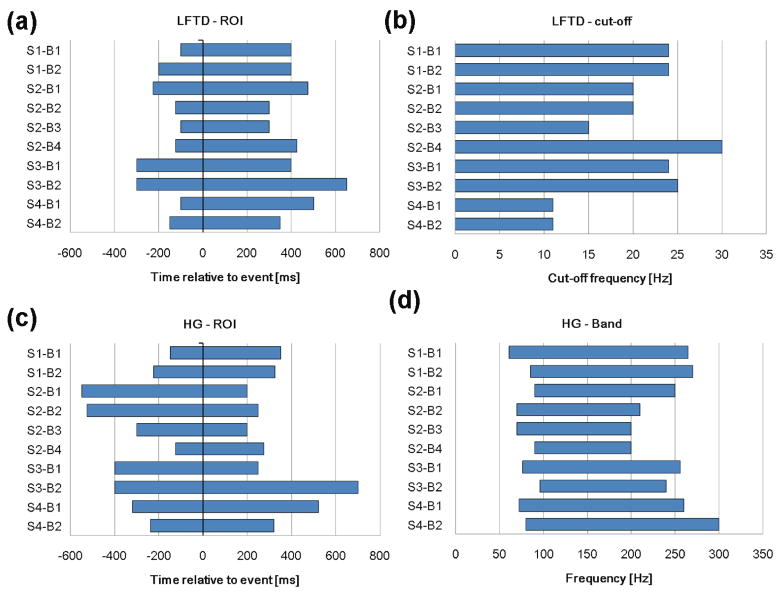
In order to identify optimal parameters for feature extraction a grid search for each subject and session was performed. For this optimization a preliminary feature selection was applied aiming at a fixed subset size of O = 8, which was found to be within the range of optimal subset sizes (cf. figure 6 and table 3). Results for all sessions are illustrated by the bar plots in figure 3. A sensitivity of the decoding rate has been found for temporal parameters such as location and width for the time windows (ROIs) containing most discriminative information about LFTD or HG features (figure 3a and 3c).

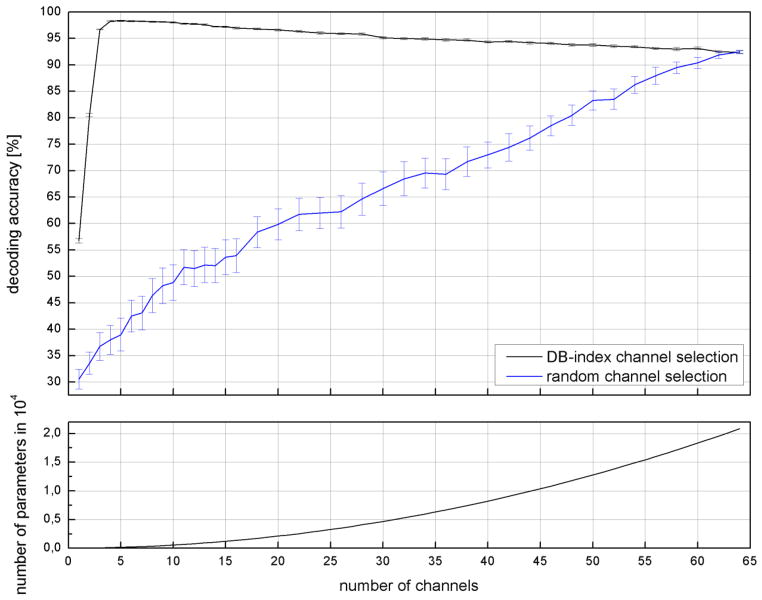
Fig. 6. Influence of channel selection on the decoding accuracy using high gamma features only (Subject 1, Session 1).

Changes in decoding accuracy when successively adding channels to the feature set applying either random or DB-index channel selection (top). Number of free parameters for each number of channels (bottom).

Table 3. Number of selected channels averaged across sessions.

The averaged number of selected channels and the corresponding standard derivations are given for all subjects and all feature spaces. For the combined space square brackets denote the corresponding breakdown into its components. The average is taken across all sessions and CV repetitions.

Subject	LFTD	HG	LFTD + HG
1	10.0±0.0	6.0±0.0	16.5±0.5 ([10.0±0.0]+[6.5±0.7])
2	6.5±1.9	7.3±2.1	12.8±3.4 ([7.0±4.5]+[5.8±1.5])
3	10.0±0.0	8.0±0.0	14.0±1.0 ([6.0±1.4]+[8.0±0.0])
4	10.0±0.0	6.0±1.4	16.0±0.7 ([9.5±0.7]+[6.5±0.7])

Fig. 3. Optimal parameters of both feature spaces for each subject and session.

(a) location and width of the time window (ROI) containing most discriminative information for LFTD features. (b) optimal high cut-off frequency for the spectral lowpass filter to extract LFTD features. (c) location and width of the time window (ROI) containing most discriminative information for HG features. (d) low and high cut-off frequency for the optimal HG frequency band.

Highest impact on the accuracy resulted for the HG ROI (mean optimal ranges: S1: [−187.5 337.5] ms; S3: [−400 475] ms; S4: [−280 420] ms). Further sensitivity is given for spectral parameters namely the high cut-off frequency for the LFTD lowpass filter and the low and high cut-off for the HG bandpass (figures 3b and 3d). For the former optimal frequencies ranged from 11–30 Hz and the optimal frequency bands for the latter lay all within 60 – 300 Hz –depending on the subject. There was hardly any impact on the decoding rate when changing the sliding window size and window overlap for the HG features. These were hence set to fixed values. According to these parameter settings, the mean number of samples T were 26.5 (subject 1), 21.3 (subject 2), 31 (subject 3) and 22 (subject 4).

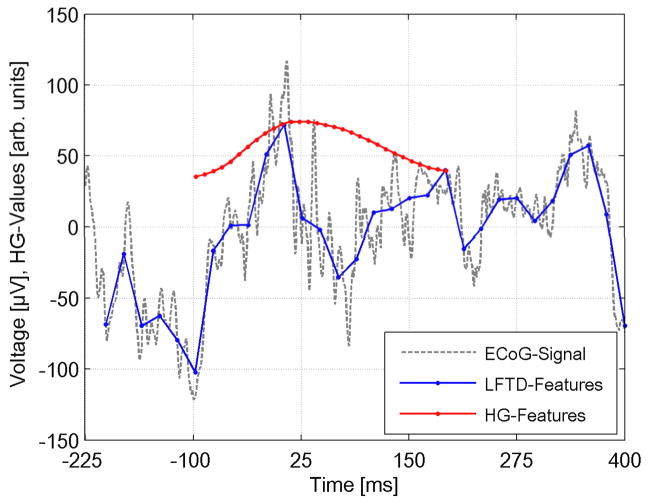
An example for the grid search procedure is shown in the supplementary figures 5–7. The plots show varying decoding rates for S1 session 1 within individual parameter subspaces. The optimal parameters illustrated in figure 3 represent a single point in these spaces at peaking decoding rate. Based on these parameters figure 4 illustrates a typical result for a LFTD and HG feature sequence extracted from the shown raw ECoG signal (S1, session 2, channel 23, middle finger). All feature sequences for this trial - consisting of the entire set of channels - are given in supplementary figure 8.

Fig. 4.

The dashed time course shows a raw ECoG signal for a typical trial (S1, session 2, channel 23, middle finger). The extracted feature sequences for LFTD (cut-off at 24 Hz) and HG (frequency band [85Hz, 270 Hz]) are overlaid as solid lines. Each HG feature has been assigned to the time point at the center of its corresponding FFT window.

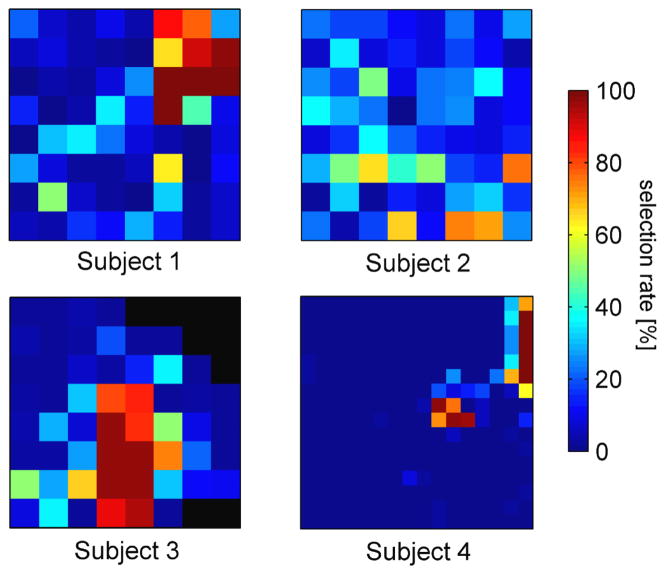
Using the resulting parameterization, subsequent CV runs sought to identify the optimal subset by tuning O based on the training set of the current fold. Figure 5 illustrates the rate at which a particular channel has been selected for each subject. It evaluates the optimal subsets O across all sessions, folds and several CV repetitions. Results are exemplarily shown for high gamma features. Full detail on subject specific grid placement and channel maps for LFTD and HG features can be found in supplementary figures 1–4.

Fig. 5. Channel maps for all four subjects.

The channels are arranged according to the electrode grid and coloured with respect to their mean selection rate in repeated CV-runs. Channels coloured in dark red tend to have a higher probability of being selected.

The channel maps reveal localized regions of highly informative channels (dark red) comprising only a small subset within the full grid. While these localizations are distinct and focused for high gamma features, informative channels spread wider across the electrode grid for LFTD features. This finding is in line with an earlier study done by Kubanek et al. (2009) and implies that selected subsets for LFTD features tend to be less stable across CV runs. Combined subsets were selected from both feature spaces. The selections indicated a preference for a higher proportion of LFTD features (Tab. 3). This optimal proportion was determined by grid search.

The optimal absolute subset size O was selected by successively adding channels to the subset as defined by our selection procedure and identifying the peak performance. For the high gamma case figure 6 shows a sharp increase in decoding performance already for a subset size below five. Performance then increases less rapidly until it reaches a maximum usually in the range of 6–8 channels for the HG features (cf. table 3 for detailed information on the results for the other features). This behaviour again reflects the fact, that a lot of information is found in a small number of HG sequences.

Increasing the subset size beyond this optimal size leads to a decrease in performance for both SVM and HMM. This coincides with an increase of the number of free parameters in the classifier model depending quadratically on the number of channels for HMMs (figure 6, bottom).

3.2 Decoding performances

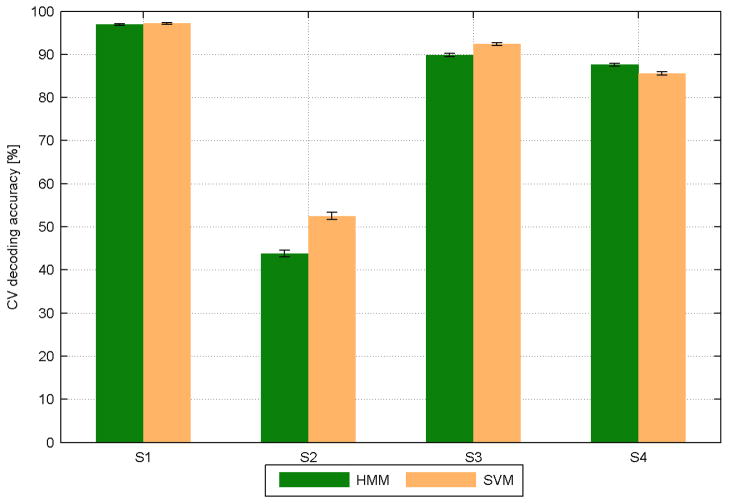
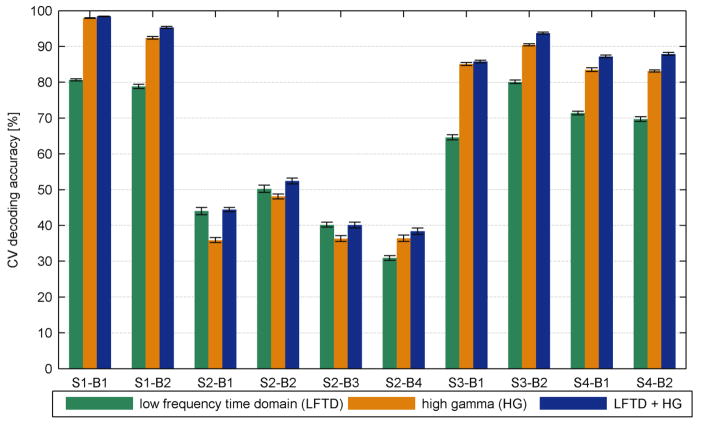
Based on the configuration of the feature spaces and feature selection, a combination space containing both LFTD and HG features yielded the best decoding accuracy across all sessions and subjects. Figure 7 summarizes the highest HMM performances for each subject averaged across all sessions and compares them with the corresponding SVM accuracies. Except for subject 2, these accuracies were close to or even exceeded 90% correct classifications. However, figure 8 shows that accuracies, obtained only from the HG space, come very close to this combined case implying that LFTD features contribute limited new information. Using exclusively time domain features decreased performance in most cases. An exception is given by subject 2 where LFTD features outperformed HG features. This may be explained by the wider spread of LFTD features across the cortex and the suboptimal grid placement (little coverage of motor cortex, supplementary figure 2). The channel maps show informative channels at the very margin of the grid. This suggests that grid placement was not always optimal to capture the most informative electrodes.

Fig. 7. Decoding accuracies (in %) for HMM (green) and SVM (beige) using LFTD+HG feature space (best case).

Average performances across all sessions are shown for all subjects (S1-S4) as a mean result of a 30×5 CV procedure with their corresponding error bars.

Fig. 8. Decoding accuracies (in %) for the HMMs for all feature spaces and sessions Bi.

Performances are averaged across 30 repetitions of the 5-fold CV procedure and displayed with their corresponding error bars.

Differences in decoding accuracy compared to the SVM were found to be small (table 4) and revealed no clear superiority of any classifier (figure 9). Excluding subject 2 the mean performance difference (HMM-SVM) was −0.53% for LFTD, 0.1% for HG and −0.23% for combined features. Accuracy trends for individual subjects are similar across sessions and vary less than across subjects (figure 9). Note, that irrespective of the suboptimal grid placement, subject 2 took part in four experimental sessions. Here, subject specific variables, e.g. grid placement, were important determinant of decoding success. Thus we interpret our results at the subject level and conclude that in three out of four subjects SVM and HMM decoding of finger movements led to comparable results.

Table 4. Final decoding accuracies (in %) listed for HMM (left) and SVM (right).

Accuracies for the Bakis model are given for each subject-session and feature space by its mean and standard error across all 30 repetitions of the cross-validation procedure. Additionally, for each subject and feature space the mean across all sessions as well as the mean loss in performance for LFTD and HG when using an unconstrained HMM is shown.

Subject-Session	HMM			SVM
	LFTD	HG	LFTD + HG	LFTD	HG	LFTD + HG
S1-B1 [%]	80.7 ± 0.3	97.9 ± 0.1	98.4 ± 0.1	85.8 ± 0.4	97.2 ± 0.2	98.3 ± 0.1
S1-B2 [%]	78.8 ± 0.6	92.4 ± 0.4	95.3 ± 0.3	84.9 ± 0.5	93.4 ± 0.4	96.1 ± 0.3
Mean[%]	79.8 ± 0.5	95.2 ± 0.3	96.9 ± 0.2	85.4 ± 0.5	95.3 ± 0.3	97.2 ± 0.2
Unconstrained model [%]	−3.1±0.5	−0.9±0.3	-	-	-	-
S2-B1 [%]	44.0 ± 1.0	35.9 ± 0.7	44.4 ± 0.6	51.4 ± 0.8	38.0 ± 0.8	55.7 ± 0.8
S2-B2 [%]	50.2 ± 1.0	48.1 ± 0.7	52.4 ± 0.8	55.5 ± 0.7	48.0 ± 0.6	60.2 ± 0.8
S2-B3 [%]	40.2 ± 0.7	36.3 ± 0.8	40.1 ± 0.8	49.6 ± 0.7	39.5 ± 0.9	51.5 ± 0.8
S2-B4 [%]	30.9 ± 0.7	36.4 ± 0.9	38.4 ± 0.9	39.1 ± 0.7	38.0 ± 1.0	42.7 ± 0.9
Mean[%]	41.2 ± 0.9	39.2 ± 0.8	43.8 ± 0.8	48.9 ± 0.7	40.9 ± 0.9	52.5 ± 0.9
Unconstrained model [%]	−2.2±0.9	−0.4±0.8	-	-	-	-
S3-B1 [%]	64.6 ± 0.7	85.1 ± 0.4	85.8 ± 0.4	61.2 ± 0.7	85.4 ± 0.5	88.8 ± 0.4
S3-B2 [%]	80.1 ± 0.5	90.5 ± 0.3	93.7 ± 0.3	85.0 ± 0.4	91.4 ± 0.3	96.0 ± 0.3
Mean[%]	72.4 ± 0.6	87.8 ± 0.4	89.8 ± 0.4	73.1 ± 0.6	88.4 ± 0.4	92.4 ± 0.3
Unconstrained model [%]	−5.9±0.7	−2.5±0.4	-	-	-	-
S4-B1 [%]	71.4 ± 0.5	83.5 ± 0.5	87.2 ± 0.4	68.5 ± 0.6	82.1 ± 0.4	86.7 ± 0.4
S4-B2 [%]	69.7 ± 0.7	83.1 ± 0.3	87.9 ± 0.4	64.3 ± 0.6	82.3 ± 0.3	84.4 ± 0.4
Mean[%]	70.6 ± 0.7	83.3 ± 0.3	87.6 ± 0.4	66.4 ± 0.6	82.2 ± 0.3	85.6 ± 0.4
Unconstrained model [%]	−1.1±0.6	−3.1±0.5	-	-	-	-

Fig. 9. Differences in decoding accuracy (in %) for the HMMs with respect to the SVM reference classifier (HMM-SVM).

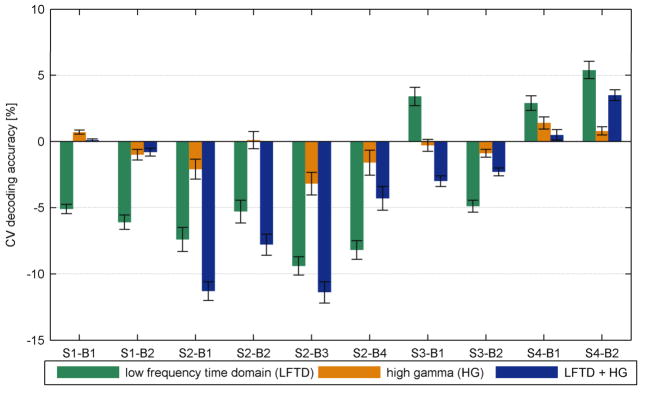
Results are displayed for all sessions Bi and feature spaces.

A clear superiority for SVM classification was only found for subject 2, for whom the absolute decoding performances were significantly worse than those of the other three subjects.

For the single spaces, LFTD and HG, Tab. 4 shows the mean performance loss for the unleashed HMM. That refers to a case wherein the Bakis model constraints are relaxed to the full model. For all except two sessions of subject 2 (full model had a higher performance of 0.2% for session 3 and 0.7 % for session 4), the Bakis model outperformed the full model. The results indicate a higher benefit for the LFTD features with up to 8.8% performance gain for subject 3, session 2. Higher accuracies were consistently achieved for feature subsets deviating from the optimal size. An example is illustrated for LFTD channel selection (subject 3, session 2) in supplementary figure 9. The plot compares Bakis and full model similar to the procedure in figure 6. While table 4 lists only the improvements for the optimal number of channels, supplementary figure 9 indicates that the performance gain may even be higher when deviating from the optimal settings. Finally, figure 10 illustrates the accuracy decompositions into true positive rates for each finger. The results reveal similar trends across subjects and feature spaces. While thumb and little finger provided least training samples, their true positive rates tend to be the highest among all fingers. An exception is given for LFTD features for subject 2. Equivalent plots for the SVM are shown in supplementary figure 10.

Fig. 10. Mean HMM decoding rates decomposed into true positive rates for each finger.

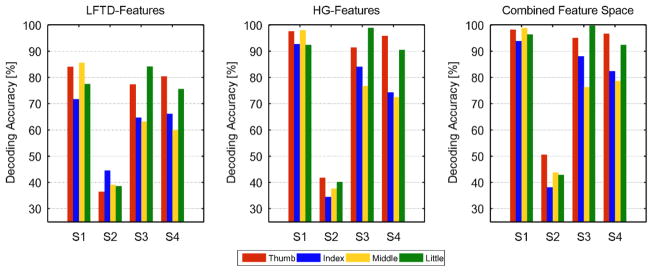
Results are shown for each feature space and averaged across sessions and CV repetitions.

For the classification of one feature sequence including all T samples the HMM Matlab implementation took on average (3.522 +/− 0.036) ms and the SVM implementation in C (0.0281 +/− 0.0034) ms. The mean computation time for a feature sequence was 0.2 ms +/− 2.1μs (LFTD), 1.72 ms +/− 37.9 μs (HG) and 1.79 ms+/− 20.0 μs (combined space). The results were obtained at an Intel Core i5-2500K @ 3,4 GHz, 16 GB RAM, Win 7 Pro 64-Bit, Matlab 2012b for 10 selected channels.

4. Discussion

An evaluation of feature space configurations revealed a sensitivity of the decoding performance to the precise parameterization of individual feature spaces. Apart from these general aspects, the grid search primarily allows for individual parameter deviations across subjects and sessions. Importantly, a sensitivity has been identified for the particular time interval of interest used for the sliding window approach to extract HG features. This indicates varying temporal dynamics across subjects and may favour the application of HMMs in online applications. This sensitivity suggests that adapting to these temporal dynamics has an influence on the degree to which information can be deduced from the data by both, HMM and SVM. However, our investigations indicate that HMMs are less sensitive to changes of the ROI and give nearly stable performances when changing the window overlap. As a model property the HMM is capable of modelling informative sequences of different length and rate. The latter characteristic originates from the explicit loop transition within a particular model. This means the HMM may cover uninformative samples of a temporal sequence with an idle state, before the informative part starts. Underlying temporal processes that may last longer or shorter are modelled by more or less repeating basic model states. Lacking any time-warp properties an SVM would expect a fixed sequence length and information rate, meaning a fixed association between a particular feature dimension o_i and a specific point in time t_i. This highlights the strict comparability of information within one single feature dimension explicitly required by the SVM. This leads to the prediction of benefits for HMMs in online applications where the time for the button press or other events may not be known beforehand. The classifier may act more robustly on activity that is not perfectly time locked. Imaging paradigms for motor imagery or similar experiments may provide scenarios in which a subject carries out an action for an unspecified time interval. Given that varying temporal extent is likely, the need for training the SVM for the entire range of possible ROI locations and widths is not desirable.

The SVM characteristics also imply a need to await the whole sequence to make a decision for a class. In contrast the Viterbi algorithm allows HMMs to state at each incoming feature vector how likely an assignment to a particular class is. In online applications this striking advantage provides prompter classification and may reduce computational overhead, if only the baseline is employed. There is no need to await further samples for a decision. Note that this emphasizes the implicit adaptation of HMMs to real-time applications: while the SVM needs to classify the whole new subsequence again after each incoming sample, HMMs just update their current prediction according to the incoming information. They do not start from scratch. The implementation used here did not make use of this online feature, since only the classification of the entire trial was evaluated. Another reason for the SVM being faster than the HMM is given by its non-optimized implementation in Matlab code. The same applies for the feature extraction. Existing high performance libraries for these standard signal processing techniques or even a hardware FPGA implementation may significantly speed up the implementation. The average classification time for the HMMs implies a maximal possible signal rate of about 285 Hz when classifying after each sample. Thus, in terms of classification, even with the current implementation real-time is perfectly feasible for most cases. More sophisticated implementations are used in the field of speech processing where classifications have to be performed at rates of up to 40 kHz.

Second, tuning the features to an informative subset yielded less dependency on the particular classifier for the presented offline case. Preliminary analysis using compromised parameter sets for the feature spaces as well as feature subset size instead, led to a higher performance gap between both classifiers. Adapting to each subject individually, a strict superiority was not observed for the HMMs versus the SVM in subjects 1 and 3. For subject 4 the HMM actually outperformed the SVM in all cases. Interestingly, this coincides with the grid resolution, which was twice as high for this subject, supporting the importance of the degree and spatial precision of motor cortex coverage. For subject 2 decoding performances were significantly worse in comparison with the other subjects. This is probably due to the grid placement being not optimal for the classification (supplementary figure 2). Figure 5 shows no distinct informative region and channels selected at a high rate are located at the outer boundary of the grid rather than over motor cortices. This hypothesis is further supported by decoding accuracies which are higher for LFTD than for HG features in subject 2. Since informative regions spread wider across the cortex for subject 2 (Kubanek et al. 2009), regions exhibiting critical high gamma motor region activity may have been located outside the actual grid.

While the results suggest that high feature quality is the main factor for high performances in this ECoG data set, two key points have to be emphasized for the application of HMMs with respect to the present finger classification problem. First, due to a high number of free model parameters feature selection is essential for achieving high decoding accuracy. Note, that the SVM exhibits less free parameters to be estimated during training. These parameters mainly correspond to the weights α. The number of these directly depends on the number of training samples. The functional relationship between features and labels even depends on the non-zero weights of the support vectors only. Thus, SVM exhibits higher robustness to variations of the subset size. Second, imposing constraints on the HMM model structure was found to be important for achieving high decoding accuracies. As stated in the methods, the introduction of the Bakis model does not substantially influence the number of free parameters. The subset size has a much higher impact (figure 6) on the overall number. Nevertheless, a performance gain of up to 8.8% per session or 5.9% mean per subject across all sessions was achieved for the LFTD features. This suggests that improvements may be less due to mere reduction of the absolute number of parameters, but also due to better compliance of the model with the underlying temporal data structure, i.e. the evolution of feature characteristics over time. For the LFTD space information is encoded in the signal phase and hence the temporal structure. The fact that the Bakis model constrains this temporal structure hence entails interesting implications. Higher overall accuracies for the HG space, along with only minor benefits from the Bakis model, indicate that clear advantages of model constraints mainly arise if the relevant information appears not as prominent in the data. This is further supported by a higher increase in HMM performance when not using the optimal subset size for LFTD features (cf. supplementary figure 9). This suggests that the Bakis approach tends to be more robust with respect to deviations from the optimal parameter setting.

Finally, it should be mentioned that the current test procedure does not fully allow for non-stationary behaviour. That means that the random trial selection does not take temporal evolution of signal properties into account. These might change and blur the feature space representation over time (Lemm, 2011). In this context and depending on the extent of non-stationarity, the presented results may slightly overestimate the real decoding rates. This applies for both, SVM and HMM. Non-stationarity should be addressed in an online setup by updating the HMM on-the-fly. Training data should only be used from past recordings and signal characteristics of future test set data remain unknown. While online model updates are generally unproblematic for the HMM training procedure, investigations on this side are still needed

5. Conclusions

For a defined offline case we have shown that high decoding rates can be achieved with both the HMM and SVM classifier in most subjects. This suggests that the general choice of the classifier is of less importance once HMM robustness is increased by introducing model constraints. The performance gap between both machine learning methods is sensitive to feature extraction and particularly electrode subset selection, raising interesting implications for future research. This study restricted HMMs to a rigid time window with a known event– a scenario that suits SVM requirements. This condition may be relaxed and classification improved by use of the HMM time-warp property (Sun et al., 1994). These allow for the same spatio-temporal pattern of brain activity occurring at different temporal rate.

By exploiting the actual potential of such models, we expect them to be individually adapted to specific BCI applications. The idea of adaptive online learning may be implemented for non-stationary signal properties.

Future research may encompass extended and additional model constraints for special cases, as successfully used in Automatic Speech Recognition (ASR), such as fixed transition probabilities or the sharing of mixture distributions among different states. Finally, incorporation of other sources of prior knowledge and context awareness may further optimize decoding accuracy.

Supplementary Material

jne475810suppdata.pdf

SI-Fig. 1. Grid placement for subject 1 and channel selection maps for both, LFTD and HG features. Suspected epileptic focus at posterior parietal-occupital.

SI-Fig. 2. Grid placement for subject 2 and channel selection maps for both, LFTD and HG features. No seizure focus has been delineated.

SI-Fig. 3. Grid placement for subject 3 and channel selection maps for both, LFTD and HG features. Suspected epileptic focus at left superior postcentral.

SI-Fig. 4. Grid placement for subject 4 and channel selection maps for both, LFT and HG features. Suspected epileptic focus at frontal eye field.

SI-Fig. 5. HMM performances for different lengths and locations of the LFTD ROI (subject 1 session 1). These and similar results for other subjects have been evaluated for optimizing the parameters of the feature space.

SI-Fig. 6 HMM performances for different lengths and locations of the HG ROI (subject 1 session 1). These and similar results for other subjects have been evaluated for optimizing the parameters of the feature space.

SI-Fig. 7. HMM performances for different lengths and locations of the HG frequency range (subject 1 session 1). These and similar results for other subjects have been evaluated for finding the optimal frequency band.

SI-Fig. 8. (a) Raw 64-channel ECoG signal for a typical trial (S1, session 2, middle finger). (b) Extracted LFTD feature sequence after lowpass filtering and downsampling. (c) Extracted HG feature sequence. Each HG feature has been temporally assigned to the time point at the center of its corresponding FFT window.

SI-Fig. 9. HMM performances varying number of channel for both, the Bakis and the unconstained HMM (subject 3 session 2). Error bars denote the uncertainty computed from several cross-validation runs.

SI-Fig. 10. Mean SVM decoding rates decomposed into true positive rates for each finger. Results are shown for each feature space and averaged across sessions and CV repetitions.