Abstract
In this work, we show that the asymmetrical distribution of mass at the surface of catalytic Janus swimmers results in the devices preferentially propelling themselves upward in a gravitational field. We demonstrate the existence of this gravitaxis phenomenon by observing the trajectories of fueled Janus swimmers, which generate thrust along a vector pointing away from their metallically coated half. We report that as the size of the spherical swimmer increases, the propulsive trajectories are no longer isotropic with respect to gravity, and they start to show a pronounced tendency to move in an upward direction. We suggest that this effect is due to the platinum caps asymmetric mass exerting an increasing influence on the azimuthal angle of the Janus sphere with size, biasing its orientation toward a configuration where the heavier propulsion generating surface faces down. This argument is supported by the good agreement we find between the experimentally observed azimuthal angle distribution for the Janus swimmers and predictions made by simple Boltzmann statistics. This gravitaxis phenomenon provides a mechanism to autonomously control and direct the motion of catalytic swimming devices and so enable a route to make autonomous transport devices and develop new separation, sensing, and controlled release applications.
Introduction
Synthetic swimming devices possess the ability to produce enhanced motion in a fluid environment, beyond the translations and rotations usually present due to Brownian phenomena. These devices have potential to function as targeted drug delivery systems, perform tasks such as minimally invasive surgery,1 and transport materials within microfluidic devices.2 Most devices currently capable of producing autonomous propulsion rely on asymmetrical decomposition of dissolved fuel molecules, catalyzed by an asymmetric distribution of catalyst at their surface. This process is thought to produce propulsion by a variety of mechanisms,3 including self-phoretic phenomena4 resulting from a localized concentration gradient, and bubble release5 where nanobubbles of oxygen detaching from the catalytic surface impart some of their momentum to the particle. Extensively studied examples of these devices include Janus spheres, where one hemisphere of a colloid is coated with a thin catalytic layer (usually platinum, see Figure 1)6,7 and also bimetallic nanorods, comprising two contacting solid cylindrical segments, one of which displays catalytic activity.8 Recently, simulations at a mesoscopic level have been used to model the propulsion, including self-thermophoresis9 and self-diffusiophoresis.9,10 Cordova-Figueroa et al.10 modeled Janus sphere swimmers as a motor particle that generates a nonuniform concentration distribution of reaction products via an asymmetric constant flux from the swimmer surface. The speed at which the swimmers moved was proportional to the flux or the square root of the flux depending on the flux rate, when the reaction products were otherwise not present in the surrounding medium.
Figure 1.
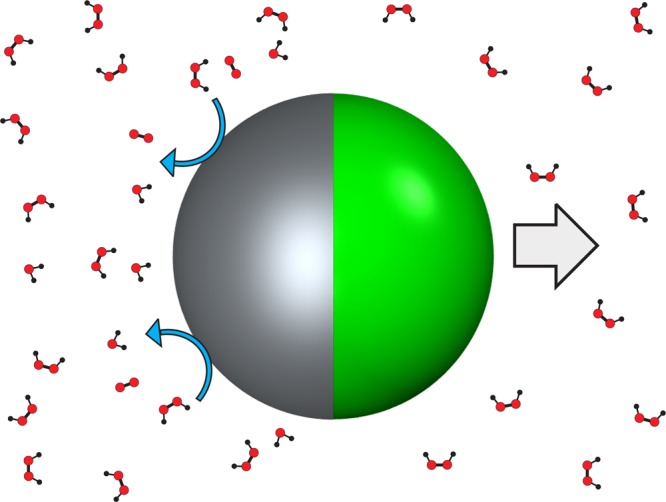
A Janus sphere consisting of a thin platinum coating on one hemisphere of a polymer bead. The asymmetric decomposition of H2O2 to water and oxygen is thought to produce propulsion through either a self-phoretic4 or nanobubble release mechanism.5
Recently, research has turned attention to the challenge of how to control the propulsive force such materials generate in order to perform useful tasks such as moving cargo within a microfluidic device. Achieving directional control has mainly been achieved by the incorporation of magnetic materials into the swimming device structure. To date, this approach has allowed Janus spheres, rods, and rolled up tubes (a third category of swimming devices which decompose fuel inside a tube causing bubbles to squirt from one end11), all to be steered by external magnetic fields, resulting in proof-of-concept cargo transport demonstrations.12−14 Speed modulation independent of direction control has also been achieved, for example using temperature15 or light stimuli.16 However, considerably less experimental attention has been given to the challenge of navigating swimming devices to a target with full autonomy, despite the fact that external field-based methods somewhat negate the benefits of the autonomous propulsion mechanism.17 The first experimental report suggesting the viability for full autonomy showed the slow accumulation of nanorod swimmers in high fuel concentration regions, an example of synthetic chemotaxis.18 In this scheme, autonomous velocity changes due to a spatial fuel concentration gradient resulted in statistical migration. We have also recently investigated an extension to this idea, showing that swimming devices containing responsive size-changing hydrogels can also perform chemotaxis by modulating their rotation rate in analogy to the run and tumble strategy used by bacteria.17
A survey of the literature also reveals that among these navigation strategies, surprisingly little or no attention has been given to controlling or measuring swimming devices’ behavior in three dimensions. The vast majority of observations and trajectory control demonstrations have instead focused on devices settled on or near a planar surface and, in general, not attempted to either measure or induce motion away from this plane. This omission appears significant; as in real-world applications, the ability to control motion in all three dimensions is likely to be essential. The only notable experimental example that has used an ability to control motion with respect to gravity is that of externally actuated and controlled helical swimming devices, which are deliberately angled upward as they swim, in order to resist gravitational sedimentation.19 Beyond this, the potential for gravity to exert and influence swimming device trajectories has been largely overlooked. There are two main reasons for this lack of attention. First, the most widely investigated autonomous swimmer type is bimetallic nanorods, made from dense solid metals which sediment rapidly and remain localized at the lowest interface. Second, while Janus spheres have been made from low density polymeric materials capable of remaining in suspension, there are some practical difficulties in measuring particle behavior in three-dimensions (3D) rapidly enough to quantify swimming behaviors. In addition, most two-dimensional (2D) microscopes are mounted to make observations in the xy plane. These issues are compounded by an implicit assumption of isotropic behavior contained in many theories and analysis for these device behaviors.5,6
This paucity of data was addressed to a limited extent by a study by Palacci et al., which used a 2D “sideways” microscope to study a propulsive-sedimented Janus sphere ensemble.20 The work concluded that increasing swimming velocity within the ensemble raises the effective temperature of the sedimented state, so that faster moving ensembles are distributed over a larger vertical distance above the interface. However the influence of gravity on individual swimmer trajectories was not reported, and effects due to the Janus sphere swimmers intrinsic mass asymmetry were not described. With concern to this later point, which is the focus of this current work, it has been shown that metallically coated Janus colloids undergoing Brownian rotation in water are statistically biased toward cap-down configurations due to their mass asymmetry.21 With a combination of this and our evidence that Janus spheres’ propulsion velocity vector points away from their platinum cap,22 a mechanism through which gravity can potentially orientate individual Janus swimmer trajectories emerges. This mechanism has also been retrospectively theoretically postulated to be capable of producing ensemble orientational ordering phenomena in the fully sedimented state described above;23 however, the required regime to observe this was not achieved in the initial experimental study.
In fact, in order to find examples where the role of mass asymmetry has been shown to effect “swimming” behavior, it is necessary to consider biological entities such as algae. Simple swimming algal cells have been shown to be able to navigate upward by virtue of an asymmetrical mass distribution alone, a phenomena termed “gravitaxis”.24−26 Although the mechanism for this phenomena was subject to debate, it is now established that these cells are simply bottom heavy, a feature which allows them to harness their ability to swim using flagella to consistently move upward. A key feature of this behavior is that it demonstrates that it is possible for such cells to show gravity-guided behavior without having a sophisticated gravity sensing mechanism to control their flagella. As autonomous sensing and response mechanisms are very challenging to implement in synthetic systems, this immediately suggests a useful new biomimetic approach to potentially add to the limited existing autonomous navigation strategies described above and so further motivates our work.
Here then, we systematically investigate the potential for low density (thin platinum coating on polystyrene colloid) spherical Janus swimmers6,17,22 to display a synthetic gravitaxis mechanism originating from the asymmetrical distribution of mass at their surface. We employ high-resolution fluorescence particle tracking to measure 3D trajectories for both propulsive and nonpropulsive devices in combination with “sideways” 2D tracking. We report and analyze the contributions of gravity to the trajectories for a range of particle sizes, selected so that the mass of the cap is expected to have a varying influence on the orientation of the particle with respect to gravity. This data reveals that the asymmetrical weight distribution can, for larger Janus swimmers, bias the orientation of the Janus swimmer with respect to gravity, resulting in significant gravitaxis where the synthetic devices autonomously swim upward via a simple “bottom”-heavy mechanism similar to that observed for some bacteria. We believe the future exploitation of these phenomena can lead to a wide range of new applications, including autonomous sorting and cargo transport.
Experimental Details
Materials
Unless stated, all materials were used as received. From Sigma-Aldrich, we obtained H2O2 puriss grade (30 wt%) and platinum wire, 0.25 mm (99.99%). We sourced green fluorescent Fluoro-Max polystyrene microspheres from Thermo Scientific, with a range of sphere radii (a = 0.95, 1.55, and 2.4 μm). We used water from an Elga Purelab Option filtration system (15 MΩ cm).
Swimmer Dispersion Preparation
We prepared our catalytic Janus spheres by spin coating a few drops of a 0.1 wt % dispersion of green fluorescent polymer microspheres in ethanol onto clean glass microscope slides. A 10 nm thick layer of platinum was evaporated onto the exposed hemisphere of the monolayer of microspheres under vacuum using a Moorfield (U.K.) Minilab 80 e-beam evaporator. Immediately prior to use, the Janus spheres were removed from the surface of the slides by first moistening one edge of a 1 cm square of microscope lens tissue. The edge of the lens tissue was then dragged over the surface of the slide several times, trapping the Janus spheres in the tissue fibers. To harvest the Janus spheres, the lens tissue was then immersed in 1.2 mL of water in a vial and shaken vigorously. We then diluted 1 mL of the dispersion with 1 mL of a 30 wt % solution of H2O2. The dispersion was then sonicated for 5 min and allowed to rest for a further 25 min. We have found that this method serves to “clean” and fully activate the catalytic surface of the Janus spheres, maximizing their swimming velocity. Before observing the swimmers under the microscope, an additional 1 mL of water was added to the dispersion to form a 10 wt % solution of H2O2. Fluorescence images measuring 170 × 170 μm in the (x,y) plane, with an observable depth of about 200 μm, showed a small number of widely separated particles; from this we estimate the final particle volume fraction of the swimming suspensions to be about 0.003%. By using such a low-volume fraction, we avoided introducing density fluctuations which are known to cause instabilities in swimming algal systems,26 resulting in downward flow.
Tracking Experiments in 2D
To observe swimmers in 2D along the (x, z) plane, we fixed a Nikon LV-EPILED microscope head vertically using a bespoke mounting bracket. The microscope head was fitted with a Nikon 20×, 0.45 N.A. objective and a Pixelink PL-B742F color video camera. We filled an oxygen plasma cleaned cuvette (4 × 1 × 0.1 cm) with the swimmer dispersion, and then located and focused on one or more swimmers under trans-illumination. A sequence of 1000 images (800 × 600 pixels) was recorded at 33 Hz with the vertical axis of the images parallel with the direction of gravity. During the recording of the image sequence, the focal position of the objective was adjusted as required to keep the swimmers in focus, appearing as a dark disc on a light background. Analysis of the images using a suite of algorithms6 written in Labview enabled us to extract the swimmer trajectories and a variety of statistical information.
Tracking Experiments in 3D
Tracking swimmers in 3D required a different approach. Swimmer suspensions were prepared as described and an oxygen plasma-cleaned cuvette filled with the suspension. The swimmers were observed in the fluorescence mode of a Nikon Eclipse LV100 microscope using the blue excitation band of a Nikon B2A filter cube. When in focus, the green fluorescent swimmers appear as solid bright discs on a dark background. However, when defocused above the swimmers, their diffraction pattern forms a bright ring, the radius of which is dependent upon magnification, sphere size, and the distance of the sphere from the focal plane of the objective.27 We recorded a sequence of 1000 images (730 × 730 pixels) using an Andor Neo camera at a frequency of 33 Hz. A second suite of algorithms written in Labview was used to analyze the images to find the x- and y-coordinates from the ring center and the z-coordinate from the ring radius (see the Supporting Information). To quantify the positional error of the 3D tracking technique, we examined a sequence of 50 images of a 1.9 μm sphere about 30 μm from the focal plane of the 20× objective. We found that noise in the image caused a z-positional error of ±25 nm, with a similar degree of error in the (x,y) plane. However, the detected intensity of the fluorescence light emitted by the particle drops as the distance of the spheres from the focal plane is increased. When the spheres are very far from the focal plane, the signal-to-noise ratio is too low to accurately track the spheres.27 Consequently, we tracked the 1.9 μm spheres over a maximum z-distance of about 100 μm and the 4.8 μm spheres over 150 μm. For most swimmers that we tracked this was not found to be a significant limitation.
Atomic Force Microscopy
TEM grids were attached to cleaned silicon wafers and these pieces were inserted into the evaporation chamber during platinum coating. The grids were carefully removed following coating, and a vertically calibrated Veeco Dimension AFM operating in tapping mode was used to record topographic data across the masked boundaries. After suitable software flattening, step heights were obtained from the 3D images using histogram analysis.
Results and Discussion
This paper is organized into three sections. First, we discuss the sedimentation behavior for Janus spheres, with one hemisphere coated with a thin layer of platinum, in pure water to allow us to determine the details of the mass distribution imparted by the catalytic coating and verify particle sizes and tracking procedures. Next, we report trajectories for the same Janus spheres following the addition of hydrogen peroxide fuel to the solution, causing them to undergo propulsion. Finally, we demonstrate a simple model that can be used to link the asymmetrical mass distribution of the Janus swimmers with their observed gravitational anisotropy.
Sedimentation Behavior
Figure 2 shows two 3d trajectories for representative spheres (a = 2.4 μm), with one sphere (blue trajectory) coated on one hemisphere with a nominally 10 nm thick platinum layer. In both cases, a systematic downward motion is observed, indicating the spheres are sedimenting due to their greater density than the surrounding aqueous medium. Qualitatively, it can be seen that over the same duration, the capped sphere is undergoing more rapid sedimentation due to the additional mass added by the platinum layer (ρPt = 21.45g cm–3). Table 1 summarizes the experimental sedimentation rates obtained from a linear fit to the z coordinate change with respect to time for spheres at the three sizes investigated in this study, both before and after coating with platinum (25 trajectories). For a dilute suspension, the rate of sedimentation of the uncapped spheres is characterized by the Stokes settling velocity
| 1 |
where a is the sphere radius, ρp is the sphere density, ρs is the density of the suspension medium, and g is the gravitational constant. Comparing our experimental data for uncapped spheres with this estimate (assuming the density of polystyrene is ρps = 1.05 g cm–3) gives good agreement, suggesting we are obtaining reasonable 3D tracks (Table 1).
Figure 2.
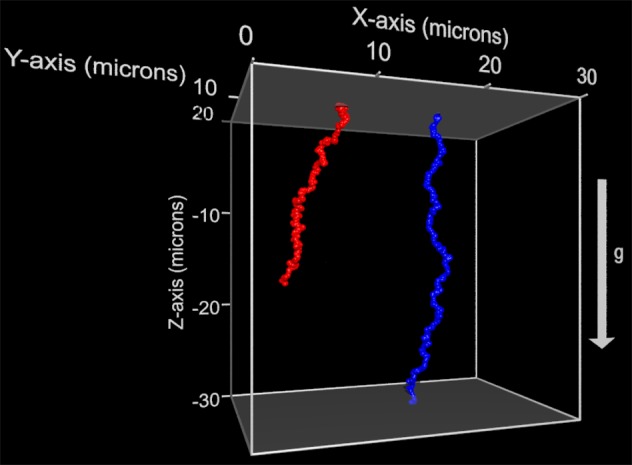
3D Trajectories for an uncapped (red) and capped (blue), a = 2.4 μm Janus sphere settling in water over a period of 30s.
Table 1. Theoretical and Experimental Sedimentation Velocity Dataa.
| sedimentation
velocity |
capped
sedimentation velocity |
experimental | |||
|---|---|---|---|---|---|
| radius, a (μm) | theoretical μm s–1 | experimental μm s–1 | theoretical μm s–1 | experimental μm s–1 | cap mass (pg) |
| 0.95 | 0.098 | 0.106 ± 0.016 | 0.316 | 0.193 ± 0.021 | 0.18 ± 0.03 |
| 1.55 | 0.262 | 0.215 ± 0.015 | 0.559 | 0.532 ± 0.020 | 0.85 ± 0.21 |
| 2.40 | 0.628 | 0.582 ± 0.014 | 1.115 | 1.008 ± 0.026 | 1.85 ± 0.35 |
Theoretical sedimentation data for the capped Janus spheres assumes an ellipsoid coating shape, as shown in Figure 6. Errors in the experimental values are the standard deviation of the mean values of 25 settling spheres. Experimental values for the total cap weight are also shown.
The effect of adding the thin platinum cap to our spheres can be approximated as an effective increase in ρp, resulting in an increase in vs. To predict the capped Janus particles, sedimentation velocity in this way consequently requires accurate knowledge of the additional mass added during the coating process. To estimate the added mass, first Atomic Force Microscopy was performed to find the mean step height for a partially masked flat silicon substrate coated with platinum in the same manner as the Janus swimmers. This verified the nominal thickness value provided by a quartz crystal oscillator during metal evaporation, returning a consistent value of 10.04 ± 0.6 nm. Using this thickness combined with a geometrical model for the cap shape allows the added mass and capped sphere stokes sedimentation velocity to be estimated. Initially we performed this calculation based on a uniform hemispherical overlayer; however, this gave poor agreement with the experimental data, considerably overestimating the sedimentation rate. Instead, a better, more physical model is used to describe the coating as an ellipsoidal shell overlayer, reaching a maximal thickness of 10 nm at the pole of the Janus particle and with 0 nm thickness at the equatorial boundary of the coated region (Figure 6). Sedimentation velocities estimated in this way give reasonable agreement (∼9% error) with experimental values, Table 1, although we note that the prediction is poor for the smallest spheres (∼30% error). The small radius of curvature of the smallest spheres may be causing a significant deviation from the cap weight predicted by the ellipsoidal layer model; however, despite this, the assumption of an ellipsoidal layer is far more accurate than that of a hemisphere. An ellipsoidal coating distribution is also consistent with the highly directional nature of the metal evaporation technique used to coat the colloids, which is known to cause shadowing effects.28 Consequently, in the later part of this paper we use a half-ellipsoid model for the asymmetric distribution of mass at the surface of the Janus particles.
Figure 6.
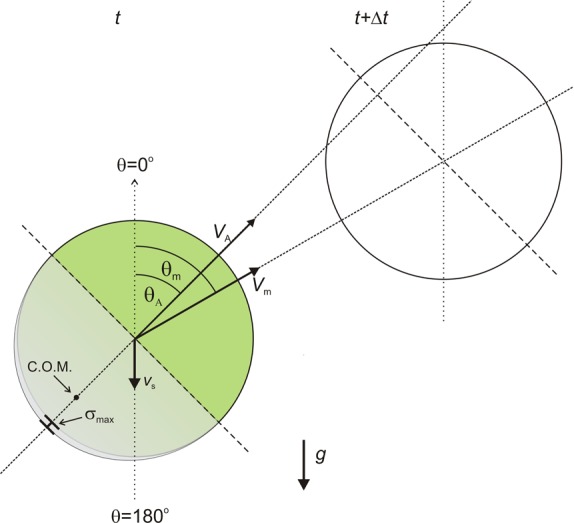
The mass of the catalytic cap, which reaches a maximum thickness σmax at the pole, introduces a gravitational energy cost to rotating the Janus spheres about its center and turning the center of mass (C.O.M.) from its lowest energy position at θ = 0°. We measured the instantaneous velocity (Vm) and direction (θm) from the 2D trajectories and corrected for the settling effect of gravity (vs), giving the actual values VA and θA.
Figure 2 also shows that the 3D tracks were obtained with sufficient resolution to accurately resolve the stochastic Brownian displacements that the colloids undergo by virtue of their small micrometer size. The magnitude of Brownian translational diffusion is quantified by the translational Diffusion coefficient, D = kBT/6πηa, where η is the suspension medium viscosity (water = 1 mPa s) and kBT is the thermal energy. A method to determine the diffusion coefficient from trajectory data is to calculate the mean-squared displacement, ΔL2, MSD, as a function of time step, which in the case of 3D trajectories is related to the diffusion coefficient by ΔL2 = 6DΔt.
We applied this analysis to the (x,y,z) trajectories for each sphere considered here in pure water (with the addition of a quadratic term to allow for the sedimentation velocity) and returned values for the diffusion coefficient which are consistent with those calculated based on the nominal particle sizes for all of the capped and uncapped particles (Table 2).
Table 2. Theoretical Rotational Diffusion Time and Theoretical and Experimental Diffusion Coefficients for the Capped and Uncapped Spheres at 20°C.
| radius | rotational time, τr | theoretical diffusion coefficient, D | experimental
diffusion coefficients |
|
|---|---|---|---|---|
| a (μm) | (s rad–2) | (μm2 s–1) | uncapped (μm2 s–1) | capped (μm2 s–1) |
| 0.95 | 5.325 | 0.226 | 0.205 ± 0.002 | 0.226 ± 0.004 |
| 1.55 | 23.130 | 0.139 | 0.157 ± 0.002 | 0.155 ± 0.003 |
| 2.40 | 85.864 | 0.089 | 0.092 ± 0.0001 | 0.093 ± 0.002 |
Propulsive Behavior
Having determined the nature of the cap mass and asymmetry for the Janus spheres under consideration, we now investigate their trajectories when fueled by aqueous hydrogen peroxide solutions, which should enable them to undergo propulsion. Figures 3 and 4 show representative 2D and 3D trajectories for the different sizes of Janus spheres considered. In order to establish that these Janus swimmers are in fact undergoing propulsion, we calculated the 2D MSD displacements in the xz plane for each trajectory as a function of time, which are expected to display an additional quadratic term due to propulsion
| 2 |
where v is the propulsion velocity.29 The average 2D propulsion velocities determined from the side on 2D trajectories for each sphere size are shown in Figure 5. As we have previously reported, diffusiophoretic theory suggests an inverse relationship between swimmer velocity and sphere radius (V ∝ 1/a),30 which gives a good fit to the experimental values. To further interpret the trajectory data, it is necessary to consider that the path followed by a given swimming Janus sphere will be determined by a combination of the magnitude of the propulsive velocity it generates, the rate of Brownian diffusion phenomena, and potentially any effect the asymmetrical mass distribution is exerting on the Janus spheres orientation. We have discussed the combined influence of the first two effects previously. Briefly, because the Janus spheres produce propulsion along a vector pointing away from the catalytic cap,22 their trajectories reflect the rate at which Brownian rotational diffusion alters their orientation. Rotational diffusion is characterized by rotational diffusion time
| 3 |
which characterizes the time it takes for loss of orientation to occur. The proportionality to a3 indicates that for larger particles, this rotational diffusion process is slower, Table 2, and therefore they are expected to show straighter trajectories. In consideration of the 2D trajectories (Figure 3), we can clearly see how this interplay of Brownian phenomena produces a change in swimmer trajectory character as a function of size. The a = 0.95 μm trajectories show most frequent changes of direction, while a = 2.4 μm trajectories show very little deviation over the tracking period. The interplay of rotational diffusion and propulsion velocity magnitude is most easily summarized by the mean path length, the product of τr, and the propulsion velocity, which provides an indication of the average length a given swimmer may be expected to travel in before changing direction. Good qualitative agreement is seen with the theoretically predicted mean-path length and the experimental trajectories (see Figure 3 caption). This interplay also determines the average distance a Janus sphere moves from the origin in a given time period: while we have seen that propulsion velocities scale as approximately 1/a, it is apparent that the difference in mean distance moved from the origin is actually very similar for a = 0.95 μm and a = 1.55 μm swimmers and only slightly reduced for a = 2.4 μm. This is because the greater propulsion velocity for the smaller-sized swimmers cannot result in a significantly greater travel distance at times longer than the rotational diffusion constant.
Figure 3.
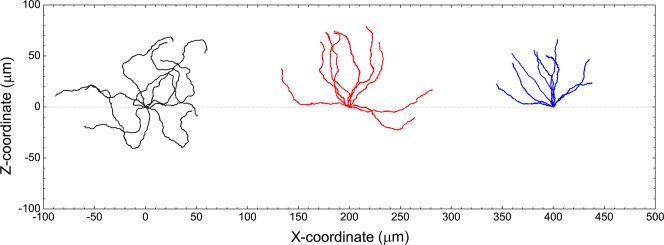
2D Swimming trajectories for representative Janus spheres observed in the (x,z) plane for a = 0.95 μm (black), a = 1.55 μm (red), and a = 2.4 μm (blue) spheres. The swimmers were suspended in a 10 wt % solution of H2O2. Predicted mean path lengths are 19, 59, and 151 μm, respectively. Gravity is acting downward along the z axis.
Figure 4.
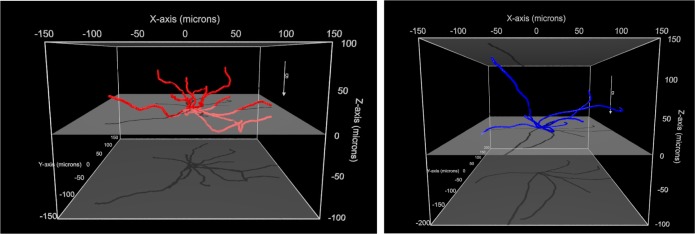
3D Swimming trajectories for representative Janus spheres; a = 1.55 μm (left) and a = 2.4 μm (right).
Figure 5.
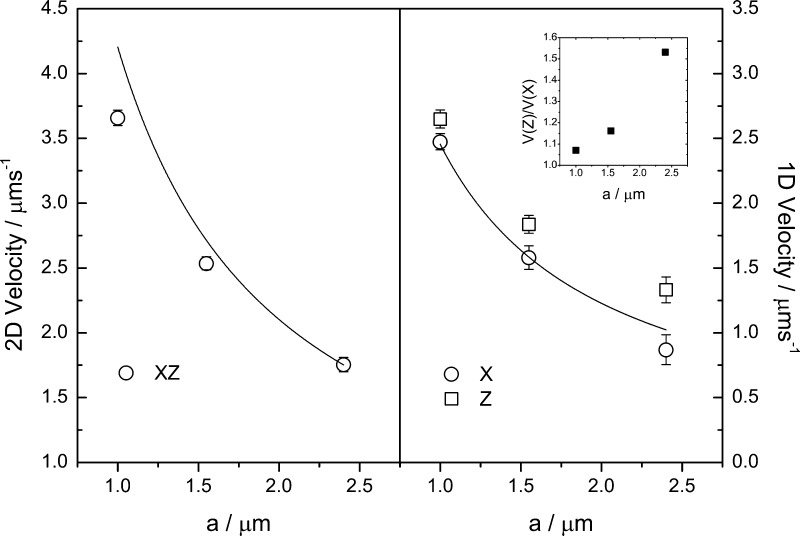
The relationship between swimmer velocity (2D) and sphere radius. (Left) Swimmer velocity in the (x,z) plane. The solid line is a fit to the data (see Ebbens et al.30). (Right) 1D Velocities along the x and z axes. Inset: ratio of velocity along the z axis (Vz) to the velocity along the x axis (Vx).
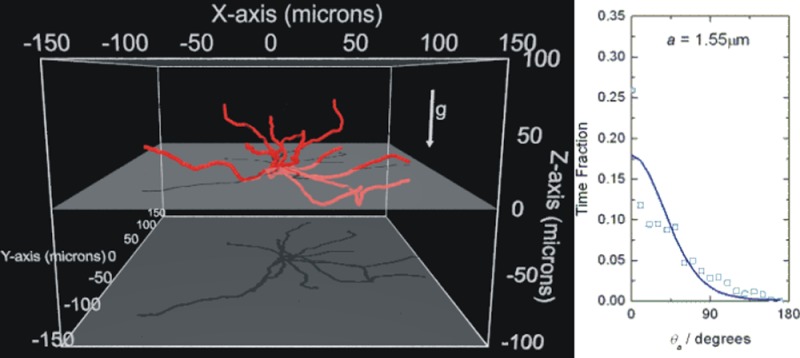
Finally, we consider the distribution of the trajectories with respect to the direction of gravity: qualitatively, it is apparent that the isotropy of motion in the z axis, in which gravity acts, is lost at larger particle sizes and replaced by a pronounced bias toward trajectories where the swimmers move upward (Figure 3). Examination of the larger-sized sphere trajectories in 3D (Figure 4) allows the isotropy along all axes to be assessed and makes it clear that isotropic behavior remains in the xy plane but is lost in the xz plane. The degree of gravitaxis was also quantified by determining the average 1D propulsion velocities resolved along the x and z axis, Figure 5. The ratio of these velocities assuming isotropic propulsion would be unity. However, at larger swimmer sizes, significantly higher velocities are seen in the z direction: the ratio Vz/Vx increases from 1.06 for a = 0.95 μm to 1.55 for a = 2.4 μm. Taken together, this data provides strong evidence that a synthetic gravitaxis mechanism is being turned on as particle size increases. On the basis of the mechanism described in the introduction, a qualitative explanation for this size dependency is that for larger particles, the platinum caps masses are both significantly larger (see Table 1) and are positioned further from the center of the Janus swimmer and so can generate an increasing torque to constrain the Brownian rotations of the particles, which are limited by the available thermal energy, kbT. In Gravitaxis Model, we elaborate this argument to build a simple model for the expected angular distribution for a freely rotating Janus sphere with an asymmetrical metallic cap and compare this prediction with our experimental data.
Gravitaxis Model
We can use Boltzmann statistics to build a simple numerical model for the expected azimuthal angle distribution, P(θA), of an asymmetrically platinum-coated Janus sphere. In order to do this, we require an expression for the energetic cost of rotating a given Janus sphere from its lowest energy position (θA = 0°) (Figure 6).
Using the additional mass values indicated by the experimental sedimentation data reported above, together with the ellipsoid model for the coating shape, we can use trigonometry to derive an expression for the additional gravitational energy required to rotate the particles to a given angle,
| 4 |
where m is the experimentally determined mass of the cap (Table 1) and l is the distance of the center of mass of the ellipsoidal shell from the center of rotation of the Janus spheres (see the Supporting Information). The expected residency time at a given angle is then given by
| 5 |
and the predicted normalized distribution over a given range of azimuthal angles is
| 6 |
In order to compare this predication with our experimentally observed data, we need a method to extract equivalent angular distributions from the Janus swimmer trajectories. The measured angle distributions across all successive Janus sphere steps for all the recorded 2D trajectories are shown in Figure 7. These plots clearly illustrate a strong upward bias in the measured translational step angles at larger sphere sizes. However, these measured angles are not directly comparable with the models output due to the constant sedimentation velocity experienced by each Janus sphere. As an illustration, an adjustment is required to allow for the case where, for example, a particle is measured to have moved upward, overcoming its tendency to sediment, requiring its actual orientation at the start of the observed trajectory step, θA, to have been angled even more steeply upward to overcome sedimentation (Figure 6). To generate a comparable experimental parameter from this data, we assume that θA at the start of each propulsive step is given by resolving the experimentally measured direction of travel velocity vector (Vm) and the downward acting constant sedimentation velocity determined experimentally above (trigonometry shows that in this case, the link between the two angles is θA = arctan[Vm sin(θm)/Vm cos(θm)–vs)]. Figure 8 compares the angle distribution predictions P(θA) with the actual corrected angular distributions obtained in this way <θA>, showing good agreement, particulary for the smaller two-sized swimmers. The slight deviation for the a = 2.4 μm spheres may be due to inhomogeneities in the platinum cap layer, which can introduce spin to the particle trajectories resulting in a higher population of high θA than predicted by the model. From the MSD of the trajectories, the mean angular velocities31 (ω) for the a = 0.95 μm, ω = 0.0002 rad s–1 and a = 2.4 μm, ω = 0.01 rad s–1 swimmers indicate that this is probably the case. However, this simple model clearly shows that the mass asymmetry possessed by larger Janus particles is sufficient to introduce appreciable gravitaxis behavior via the proposed mechanisms of biasing the Janus swimmers azimuthal angle toward cap-down configurations. To aid visualization of the effect of the platinum cap on each Janus sphere, we have also estimated the cant angles required to balance the sedimentation velocity and produce propulsion in the horizontal plane (i.e., 90° – θA). These are a = 0.95 μm, 3.0°; a = 1.55 μm, 11.8°; and a = 2.4 μm, 29.8° for swimmers producing the mean experimental propulsion velocities at those respective sizes. It is noticeable that the largest sphere requires an appreciable cant to produce horizontal progress, illustrating the magnitude of this additional factor that will to some extent reduce the amount of gravitaxis biasing observed for a given cap weight.
Figure 7.
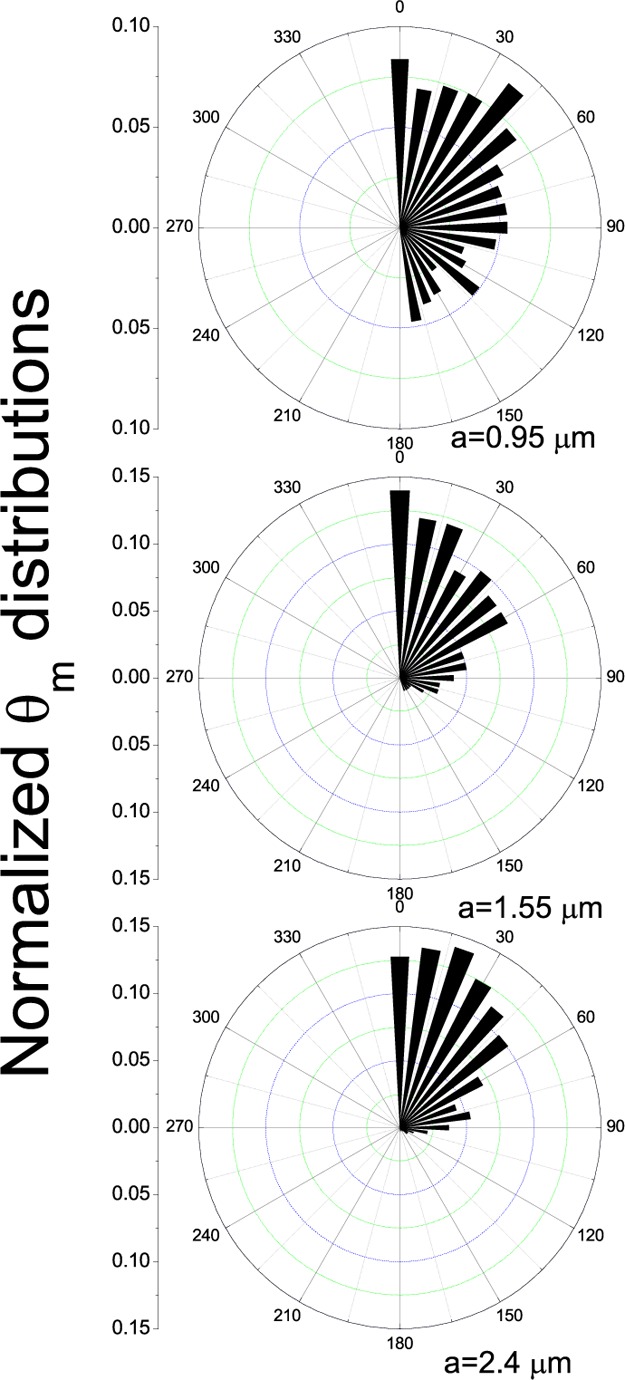
Normalized angle distribution for θm as a function of radius for all translational steps for each recorded 2D swimmer trajectory.
Figure 8.
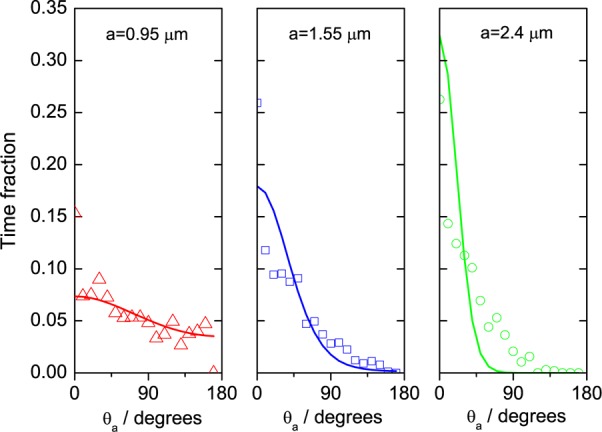
Scatter graphs showing the actual azimuthal angle, θa, derived by resolving the measured propulsion and sedimentation velocity vectors. Solid line is P(θa) estimated from a Boltzmann distribution for the gravitational energy cost for rotating a solid ellipsoid overlayer of platinum.
Conclusions
Our results clearly show that for catalytic Janus swimmers made from polystyrene, with radii of a = 1.55 μm and above, the effect of gravity acting on the thin (10 nm) hemispherical coating used to impart propulsion is sufficient to orientate the particles in a “cap down” configuration, causing them to display negative gravitaxis (i.e., a tendency to move upward). To our knowledge, this is the first example of gravitaxis being observed for autonomous synthetic swimming devices. The mechanism driving this effect is however equivalent to that present in gravitactic algae, which possess a comparable asymmetrical mass distribution. We have also tested a simple model capable of predicting the extent of gravitaxis for a given sphere size and coating mass, based solely on the gravitational energy required to lift the masses of the asymmetric caps to allow the colloid to change its azimuthal angle. This approach shows good agreement with our experimental data. In the process of developing this model, we have also shown how these larger Janus sphere swimmers are expected to have a significant difference between their azimuthal angle and subsequent observed step direction, for some orientations, due to their relatively large sedimentation velocities. This interplay will ultimately impose a limit for the achievable degree of negative gravitaxis in such devices. While our model indicates that an even higher degree of autonomous directional control can be achieved by increasing the coating mass (e.g., by increasing the coating thickness) and/or the swimmer size, there will be limits in both of these scenarios. Increasing coating mass will also increase the sedimentation rate which the propulsive velocities of the particles must exceed in order to be able to move upward, and increasing size also produces a reduction in intrinsic velocity as previously reported30 and confirmed again here. However, as an indication of the scope for gravitactic control beyond that reported here, a a = 1.55 μm particle with a nominally 50 nm thick coating is predicted to spend 85% of its time moving upward within 20 degrees of vertical and still be capable of producing a 1 μm s–1 translational rate despite having to overcome an increased sedimentation velocity.
As a result of these findings, we envisage that some new applications may be enabled by optimizing and exploiting this easily experimentally accessible gravitaxis behavior. For example, small scale cargo transport “lifts” could be constructed and made to switch between lifting and sedimenting by a changing stimuli such as fuel concentration.6 A similar scenario could be used to effect controlled release of active colloids from gravitational confinement. Additionally, new active separation methods may be possible, for example active and passive colloids are expected to separate vertically at an enhanced rate due to gravitactic propulsion, while the separation of differently sized swimmers, displaying differing amounts of gravitaxis, may also be envisaged. The new observations also open up the potential for some new emergent behavior in synthetic devices. For example it is well-known that algae produce flow patterns due to their gravitactic accumulation at the top surface of a fluid, which causes sinking and rising columns due to local densification.26 Our work shows that a similar behavior may be seen in synthetic devices. In addition, the potential influence of gravitaxis behavior on attempts to quantify the behavior of swimming devices in order to gain theoretical insights must also be considered. In the work here, we show that tracking the largest particles we considered in free solution using conventional microscopy in the xy plane alone would lead to their propulsion velocities being underestimated by almost a third. In conclusion, we hope that this study will lay the groundwork for future exploitation of and a greater attention to gravitational effects in catalytic swimming devices.
Acknowledgments
The authors thank Dr. Jonathan Howse for providing the 2D swimmer tracking algorithms and loan of a fluorescent filter. We also thank Dr Ehtsham U. Haq for recording the AFM data. We both thank the EPSRC for supporting this work via Dr Stephen Ebbens’ Career Acceleration Fellowship (EP/J002402/1).
Supporting Information Available
Additional information about our 3D tracking method and supplementary figures and videos as described in the text. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Supplementary Material
References
- Xi W.; Solovev A. a.; Ananth A. N.; Gracias D. H.; Sanchez S.; Schmidt O. G. Rolled-up magnetic microdrillers: Towards remotely controlled minimally invasive surgery. Nanoscale 2013, 5, 1294–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García M.; Orozco J.; Guix M.; Gao W.; Sattayasamitsathit S.; Escarpa A.; Merkoçi A.; Wang J. Micromotor-based lab-on-chip immunoassays. Nanoscale 2013, 5, 1325–31. [DOI] [PubMed] [Google Scholar]
- Ebbens S. J.; Howse J. R. In pursuit of propulsion at the nanoscale. Soft Matter 2010, 6, 726–738. [Google Scholar]
- Golestanian R.; Liverpool T.; Ajdari A. Propulsion of a molecular machine by asymmetric distribution of reaction products. Phys. Rev. Lett. 2005, 94, 1–4. [DOI] [PubMed] [Google Scholar]
- Gibbs J. G.; Zhao Y.-P. Autonomously motile catalytic nanomotors by bubble propulsion. Appl. Phys. Lett. 2009, 94, 163104. [Google Scholar]
- Howse J.; Jones R.; Ryan A.; Gough T.; Vafabakhsh R.; Golestanian R. Self-motile colloidal particles: From directed propulsion to random walk. Phys. Rev. Lett. 2007, 99, 8–11. [DOI] [PubMed] [Google Scholar]
- Ke H.; Ye S.; Carroll R. L.; Showalter K. Motion analysis of self-propelled Pt-silica particles in hydrogen peroxide solutions. J. Phys. Chem. A 2010, 114, 5462–7. [DOI] [PubMed] [Google Scholar]
- Paxton W. F.; Kistler K. C.; Olmeda C. C.; Sen A.; St Angelo S. K.; Cao Y.; Mallouk T. E.; Lammert P E.; Crespi V. H. Catalytic nanomotors: Autonomous movement of striped nanorods. J. Am. Chem. Soc. 2004, 126, 13424–31. [DOI] [PubMed] [Google Scholar]
- de Buyl P.; Kapral R. Phoretic self-propulsion: A mesoscopic description of reaction dynamics that powers motion. Nanoscale 2013, 1337–1344. [DOI] [PubMed] [Google Scholar]
- Cordova-Figueroa U.; Brady J.; Shklyaevabd S. Osmotic propulsion of colloidal articles via constant surface flux. Soft Matter 2013, 6382–6390. [Google Scholar]
- Sanchez S.; Solovev A. a.; Schulze S.; Schmidt O. G. Controlled manipulation of multiple cells using catalytic microbots. Chem. Commun. 2011, 47, 698–700. [DOI] [PubMed] [Google Scholar]
- Baraban L.; Makarov D.; Streubel R.; Monch I.; Grimm D.; Sanchez S.; Schmidt O. Catalytic janus motors on microfluidic chip: Deterministic motion for targeted cargo delivery. ACS Nano 2012, 6, 3383–3389. [DOI] [PubMed] [Google Scholar]
- Kagan D.; Laocharoensuk R.; Zimmerman M.; Clawson C.; Balasubramanian S.; Kang D.; Bishop D.; Sattayasamitsathit S.; Zhang L.; Wang J. Rapid delivery of drug carriers propelled and navigated by catalytic nanoshuttles. Small 2010, 6, 2741–7. [DOI] [PubMed] [Google Scholar]
- Fischer P.; Ghosh A. Magnetically actuated propulsion at low Reynolds numbers: Towards nanoscale control. Nanoscale 2011, 3, 557–63. [DOI] [PubMed] [Google Scholar]
- Balasubramanian S.; Kagan D.; Manesh K. M.; Calvo-Marzal P.; Flechsig G. U.; Wang J. Thermal modulation of nanomotor movement. Small 2009, 5, 1569. [DOI] [PubMed] [Google Scholar]
- Solovev A. a.; Smith E. J.; Bof’ Bufon C. C.; Sanchez S.; Schmidt O. G. Light-controlled propulsion of catalytic microengines. Angew. Chem., Int. Ed. 2011, 50, 10875–8. [DOI] [PubMed] [Google Scholar]
- Ebbens S. J.; Buxton G. a.; Alexeev A.; Sadeghi A.; Howse J. R. Synthetic running and tumbling: An autonomous navigation strategy for catalytic nanoswimmers. Soft Matter 2012, 8, 3077. [Google Scholar]
- Hong Y.; Blackman N.; Kopp N.; Sen A.; Velegol D. Chemotaxis of nonbiological colloidal rods. Phys. Rev. Lett. 2007, 99, 1–4. [DOI] [PubMed] [Google Scholar]
- Peyer K. E.; Tottori S.; Qiu F.; Zhang L.; Nelson B. J. Magnetic helical micromachines. Chem.–Eur. J. 2013, 19, 28–38. [DOI] [PubMed] [Google Scholar]
- Palacci J.; Cottin-Bizonne C.; Ybert C.; Bocquet L. Sedimentation and effective temperature of active colloidal suspensions. Phys. Rev. Lett. 2010, 105, 1–4. [DOI] [PubMed] [Google Scholar]
- Behrend C. J.; Anker J. N.; McNaughton B. H.; Brasuel M.; Philbert M. a.; Kopelman R. Metal-capped brownian and magnetically modulated optical nanoprobes (MOONs): A micromechanics in chemical and biological microenvironments. J. Phys. Chem. B 2004, 108, 10408–10414. [Google Scholar]
- Ebbens S. J.; Howse J. R. Direct observation of the direction of motion for spherical catalytic swimmers. Langmuir 2011, 27, 12293–6. [DOI] [PubMed] [Google Scholar]
- Enculescu M.; Stark H. Active colloidal suspensions exhibit polar order under gravity. Phys. Rev. Lett. 2011, 107, 058301. [DOI] [PubMed] [Google Scholar]
- Roberts a. M. Mechanisms of gravitaxis in Chlamydomonas. Biol. Bull. 2006, 210, 78–80. [DOI] [PubMed] [Google Scholar]
- Kam V.; Moseyko N.; Nemson J.; Feldman L. J. Gravitaxis in Chlamydomonas reinhardtii: Characterization Using Video Microscopy and Computer Analysis. Int. J. Plant Sci. (Chicago, IL, U.S.) 1999, 160, 1093–1098. [DOI] [PubMed] [Google Scholar]
- Kessler J. O. The Dynamics of Unicellular Swimming Organisms. Journal of the American Society for Gravitational and Space Research 1991, 4, 97–105. [PubMed] [Google Scholar]
- Peterson S. D.; Chuang H. S.; Wereley S. T. Three-dimensional particle tracking using micro-particle image velocimetry hardware. Meas. Sci. Technol. 2008, 19, 115406. [Google Scholar]
- Pawar A. B.; Kretzschmar I. Patchy particles by glancing angle deposition. Langmuir 2008, 24, 355–358. [DOI] [PubMed] [Google Scholar]
- Dunderdale G.; Ebbens S.; Fairclough P.; Howse J. Importance of particle tracking and calculating the mean-squared displacement in distinguishing nanopropulsion from other processes. Langmuir 2012, 28, 10997–11006. [DOI] [PubMed] [Google Scholar]
- Ebbens S.; Mei-Hsien Tu; Howse J. R.; Golestanian R. Size dependence of the propulsion velocity for catalytic Janus-sphere swimmers. Phys. Rev. E. 2012, 85, 020401(R). [DOI] [PubMed] [Google Scholar]
- Ebbens S.; Jones R.; Ryan A.; Golestanian R.; Howse J. Self-assembled autonomous runners and tumblers. Phys. Rev. E. 2010, 82, 6–9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.