Differential arrest and adhesion of tumor cells and microbeads in the microvasculature

Abstract

To investigate the mechanical mechanisms behind tumor cell arrest in the microvasculature, we injected fluorescently labeled human breast carcinoma cells or similarly sized rigid beads into the systemic circulation of a rat. Their arrest patterns in the microvasculature of mesentery were recorded and quantified. We found that 93% of rigid beads were arrested either at arteriole–capillary intersections or in capillaries. Only 3% were at the capillary–postcapillary venule intersections and in postcapillary venules. In contrast, most of the flexible tumor cells were either entrapped in capillaries or arrested at capillary or postcapillary venule–postcapillary venule intersections and in postcapillary venules. Only 12% of tumor cells were arrested at the arteriole–capillary intersections. The differential arrest and adhesion of tumor cells and microbeads in the microvasculature was confirmed by a χ² test (p < 0.001). These results demonstrate that mechanical trapping was responsible for almost all the arrest of beads and half the arrest of tumor cells. Based on the measured geometry and blood flow velocities at the intersections, we also performed a numerical simulation using commercial software (ANSYS CFX 12.01) to depict the detailed distribution profiles of the velocity, shear rate, and vorticity at the intersections where tumor cells preferred to arrest and adhere. Simulation results reveal the presence of localized vorticity and shear rate regions at the turning points of the microvessel intersections, implying that hemodynamic factors play an important role in tumor cell arrest in the microcirculation. Our study helps elucidate long-debated issues related to the dominant factors in early-stage tumor hematogenous metastasis.

1 Introduction

One major cause of cancer mortality is tumor metastasis through blood and lymphatic circulations. The steps in metastasis include local invasion of tissue where the tumor first forms, detachment from the primary tumor, intravasation to, arrest in, and extravasation from the circulation, and proliferation in distant organs (Chambers et al. 2002; Hedley and Chambers 2009; Talmadge and Fidler 2010). It is widely known that circulating tumor cells arrest in the microvasculature, but this arrest is not random. For example, breast cancer cells preferentially arrest in the small blood vessels of the lungs, the liver, the brain, and the bones (Disibio and French 2008), where the microvessels tend to be smaller, more curved, branched, and stretched. The underlying mechanisms responsible for this preferential arrest of cancer cells to distant organs are not well understood. Although both biochemical factors (seed and soil, e.g., cell adhesion molecules) (Fidler 2001, 2011; Gassmann et al. 2004; Kostenuik 2004; Fokas et al. 2007; Glinskii et al. 2005) and anatomical and mechanical influences (e.g., size restriction, stresses, and shear rates) (Weiss 1992; Ding et al. 2001; Mook et al. 2003; Steinbauer et al. 2003; Yan et al. 2010, 2012) have been found to play roles in tumor cell arrest and adhesion in the microvasculature, quantitative understanding of their contributions is poor.

In addition to specific cell adhesion molecules and the anatomical structure of the microvasculature at preferential metastatic tissues and organs, the mechanical properties of tumor cells (deformability or stiffness) also determine their degree of malignancy. Guck et al. (2005) and Koop et al. (1995) observed that tumor cells having a greater deformability are more invasive, malignant, and metastatic. Malignant (MCF-7) breast cells were found to have an apparent Young’s modulus significantly lower (1.4–1.8 times) than that of their nonmalignant (MCF-10A) counterparts (Li et al. 2008). More recently, Swaminathan et al. 2011 found that cancer cells with the highest migratory and invasive potential are five times less stiff than cells with the lowest migration and invasion potential.

Mechanical trapping due to size restrictions in the narrow part of the microvasculature, stiffness of tumor cells, blood flow patterns at microvessel branches and turns, and cell adhesion molecules expressed by circulating tumor cells and by the microvascular endothelial cells of target organs all play a role in tumor cell arrest and adhesion. However, how and how much each factor contributes to tumor cell arrest and adhesion in the microvasculature remain to be elucidated.

Therefore, the first objective of this study was to quantify the arrest and adhesion of malignant tumor cells (MDA-MB-231) and similarly sized rigid microbeads in the rat mesenteric microvasculature. Rigid microbeads served as a surrogate for stiff and nonmalignant cells without adhesion molecules at their surface. The arrest and adhesion patterns of rigid beads solely reflect the contributions from the anatomical/mechanical factors of the microvasculature and the hydrodynamic factors induced by blood flow since they are independent of biochemical interactions between circulating tumor cells and the endothelial cells forming the microvessel wall. In contrast, the arrest and adhesion patterns of MDA-MB-231 cells reflect the contributions from all the aforementioned factors. Comparison of the arrest and adhesion patterns of cells and beads can therefore indicate the relative contributions of each factor to tumor cell arrest and adhesion in the microvasculature.

The second objective of this study was to further investigate the mechanical mechanisms behind microvascular tumor cell arrest and adhesion. Based on the measured microvascular geometry and blood flow velocities in the microvessels, a numerical simulation was conducted to determine the distribution profiles of velocity, shear rate, and vorticity in the microvasculature. Comparison of these detailed profiles with the locations of tumor cell arrest and adhesion in the microvasculature can suggest how specific hemodynamic factors contribute to tumor cell arrest and adhesion.

To achieve our objectives, we directly injected tumor cells or beads into the rat systemic circulation via the carotid artery. Delivery at this location allowed significant amounts of tumor cells and beads to reach the microvasculature of the mesentery, a translucent thin tissue rich in microvessels. The mesentery was chosen for this study due to its need for minimal invasive preparation and its convenience for in vivo observation and image recording (Fu and Shen 2004; Shen et al. 2010; Liu et al. 2008). Arrest and adhesion patterns of tumor cells and beads in the rat mesentery were observed directly and quantified from recorded video images. In another group of animals, we injected smaller sized beads to determine the blood flow velocities in different microvessels of the mesenteric microvasculature where tumor cells and beads prefer to arrest and adhere. The measured blood flow velocities and microvascular geometry were then used in the numerical simulation to elucidate the effects of hemodynamic factors on tumor cell arrest and adhesion. The results from our study may suggest more efficient strategies to stop tumor metastasis by targeting preferential arrest and adhesion locations of tumor cells at different levels of malignancy.

2 Materials and methods

2.1 Experimental methods

2.1.1 Solutions and reagents

Mammalian Ringer solution was used for all dissections, perfusates, and superfusates (Cai et al. 2012; Shen et al. 2010; Fu and Shen 2004). Its pH was balanced to 7.4 by adjusting the ratio of HEPES acid to base. In addition, the perfusate solution injected into the carotid artery also contained bovine serum albumin (BSA) (A4378, Sigma-Aldrich, St. Louis, MO) at 10 mg/ml (1% BSA-Ringer solution).

Fluorescent polymer beads (10 µm diameter) were purchased from Duke Scientific Corp. (Palo Alto, CA). On the day of experiments, beads were suspended in 1% BSA-Ringer solution at a concentration of 5 million/ml, the same concentration as tumor cell perfusate. Separately, other fluorescent polystyrene microspheres (3 µm diameter, Phosphorex, Hopkinton, MA) were used to measure blood flow velocity. The excitation/emission wavelength for the fluorescent beads was 468/510 nm (green).

2.1.2 Tumor cell culture and labeling

Human breast ductal carcinoma (MDA-MB-231) cells were purchased from ATCC (Manassas, VA) and cultured in 75cm² plastic tissue culture flasks (Corning, NY) in DMEM medium (Sigma-Aldrich, St. Louis, MO) supplemented with 10% fetal bovine serum (Sigma, St. Louis, MO), 100 U/ml penicillin (Sigma-Aldrich, St. Louis, MO), and 100 mg/ml streptomycin sulfate (Sigma-Aldrich, St. Louis, MO). Cultures were maintained at 37 °C in a humidified atmosphere of 5% CO₂ and 95% air and subcultured every third day. Cells were cultured at 10⁶ cells/ml and allowed to reach confluence (>90 %) and routinely passaged using trypsin/EDTA (at a ratio of 1:4) (Earley and Plopper 2006). On the day of experiments, cells were collected by brief trypsinization, then counted and suspended in phosphate-buffered saline (PBS, Sigma-Aldrich, St. Louis, MO). To remove any remaining cell clumps, the cell suspension was filtered through a 40-µm nylon mesh. Then tumor cells were fluorescently labeled using 1 µM Calcein AM (Invitrogen, Eugene, OR) in serum-free medium for 30 min. The excitation/emission wavelengths for Calcein AM-labeled tumor cells were 490/525 nm (green). The final perfusate contained 5 million cells/ml in 1% BSA-Ringer solution. The cell survival rate was > 95% after fluorescence labeling, as determined by Trypan Blue exclusion (Sigma-Aldrich, St. Louis, MO). The cell diameter was measured as 14 ± 2 µm (SD, n = 20).

2.1.3 Animal preparation

All in vivo experiments reported in this paper were performed on female Sprague–Dawley rats (250–300 g, age 3–4 months), supplied by Hilltop Laboratory Animals (Scottdale, PA). All procedures were approved by the Animal Care and Use Committees at the City College of the City University of New York. The methods used to prepare rat mesenteries has been described in detail elsewhere (Fu and Shen 2004; Shen et al. 2010) and are summarized briefly here with emphasis on the special features of the current experiment. At the end of experiments the animals were euthanized with excess anesthetic. The thorax was opened to ensure death.

On the day of experiments, rats were first anesthetized with pentobarbital sodium given subcutaneously at an initial dosage of 65 mg/kg and additional 3 mg/dose as needed. After anesthetization, a PE50 tubing (Becton Dickinson, Franklin Lakes, NJ) was inserted into the left carotid artery in preparation for later injection of tumor cells or beads into arterial blood. The rat was then transferred to a tray and its body temperature maintained via a heating pad. A midline surgical incision (3–4 cm) was made in the abdominal wall. The mesentery was carefully taken out from the abdominal cavity and arranged on a glass coverslip, which formed the base of an observation platform, as previously described (Liu et al. 2008). The upper surface of the mesentery was continuously superfused by a dripper with mammalian Ringer solution at 35–37 °C, which was regulated by a controlled water bath and monitored continuously using a thermometer probe.

2.1.4 Intravital microscopy

The mesentery was observed by a Nikon Eclipse TE-2000 inverted microscope with a Super Fluor 20X/NA0.75 objective lens. The tissue was observed with either transmitted white light from a light pipe suspended above the preparation or with fluorescent light from an illumination system (a xenon lamp with monochromator FSM150Xe, Bentham Instruments, Reading, UK). The monochromator can generate light of wavelength from 200 to 700 nm. Here light of wavelength 468/490 nm was used to observe the fluorescently labeled beads and cells. The bead or tumor cell arrest process was monitored by a high-performance analog 10-bit XR/MEGA-10 ICCD camera (Stanford Photonics, PaloAlto, CA) and recorded on VCR tapes.

2.1.5 Tumor cell and microbead arrest and adhesion in microvasculature

Three milliliters of perfusate containing 5 million/ml tumor cells (~ 14 µm diameter) or beads (~ 10 µm diameter) were injected via the carotid artery toward the aorta in ~3 min. Simultaneously, the arrest of cells/beads in the mesenteric microvasculature was recorded for up to 3 h under bright field or fluorescent light. The recorded images were analyzed offline for cell/bead arrest and adhesion at the different locations of the microvasculature. In particular, analog video recordings were first converted into digital movies (640×480 µm/frame at 30 frames/s under medium/low video profile) via the Microsoft Media Encoder (Microsoft, Redmond, WA). Images of microvasculature with and without arrested cells/beads were taken by the Microsoft Live Movie Maker (Microsoft, Redmond, WA) from the digital movies, then analyzed by NIH Image-J for the diameters of microvessels and branching angles at the intersections, and the amount of arrested cells/beads in arterioles, at arteriole–capillary intersections, in capillaries, at capillary–postcapillary venule or postcapillary venule–postcapillary venule intersections, and in post-capillary venules. The percentage of arrested cells/beads at each specified location was calculated as the ratio of the number of arrested cells/beads at that location to the total number of arrested cells/beads in the examined microvasculature of each animal. In addition to being trapped at capillaries, we found that the rigid beads tended to adhere preferentially at arteriole–capillary intersections (Fig. 1A), while the flexible tumor cells tended to adhere at capillary or postcapillary venule–postcapillary venule intersections (Fig. 1B).

Fig. 1.

A Microbead adhesion at an arteriole–capillary intersection. “b” indicates the adherent bead; the branching angle θ is ~120° between the arteriole and the capillary. B Tumor cell adhesion at a postcapillary venule–postcapillary venule intersection. “c” indicates the adherent tumor cell. The branching angle θ is ~60° between the postcapillary venules. Red arrows indicate blood flow directions in the microvesssels

2.1.6 Determination of blood flow velocities in microvessels at intersections

To quantitatively determine the hemodynamic effects on tumor cell arrest and adhesion, especially at the intersections where cells/beads preferred to arrest, we used smaller fluorescent microspheres 3 µm in diameter to measure the blood velocity in the microvessels at the intersections in another group of animals. The smaller microsphere should induce less disturbance in blood flow. A small amount (~ 0.5 ml) of 5 million/ml microspheres in 1% BSA-Ringer solution was injected via the carotid artery each time; shortly after injection, microvessels at the corresponding intersections where cells or beads preferred to arrest were identified in the mesenteric microvasculature. The blood flow with moving microspheres in those microvessels was recorded by the video camera and converted into digital movies as described earlier.

To determine the blood flow velocity in the microvessel, the digital movie of 3 µm microsphere motion was first cut into clips in AVI format via the Microsoft Live Movie Maker and separated into frames via a free image manipulation program, GIMP (www.gimp.org). The positions of the centerline microsphere in a vessel in three sequent frames were measured using NIH Image-J to calculate the distances the microsphere moved; its velocity was obtained by dividing the distance by the time duration between adjacent frames. The centerline velocity in any one vessel was determined by averaging the velocities measured at two locations of that vessel at least 100 µm from intersections. Mean velocity in that vessel was then calculated using the correction 1/1.6 of the centerline sphere velocity (Liu et al. 2008; Baker and Wayland 1974).

2.1.7 Data analysis and statistics

All data are presented as mean ± standard deviation (SD) or otherwise specified. Data were analyzed for statistical significance using Student’s t-test. A χ² test was used to analyze the statistical significance of the distribution pattern of arrest/adhesion of tumor cells and microbeads in the microvasculature. Significance was assumed for probability levels of p < 0.05.

2.2 Numerical simulation

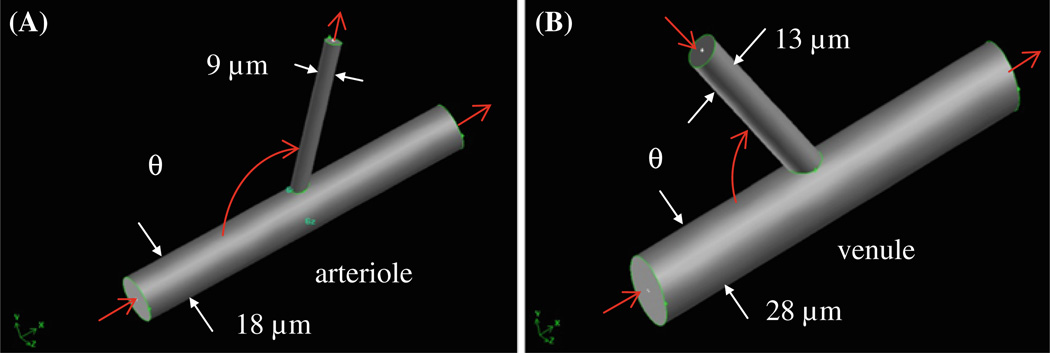
Based on the experimental observations in Fig. 1, a three-dimensional (3D) microvessel geometry for blood flow simulation at the intersections was constructed, as shown in Fig. 2. The intersection comprised a larger cylindrical tube (for either arteriole or postcapillary venule) and a smaller one for either capillary or postcapillary venule. The branching angle at the intersection, θ, was defined as the angle between the inlet side of the arteriole/postcapillary venule and the capillary (or postcapillary venule). Values for θ and the vessel diameters at intersections were determined from the experiments.

Fig. 2.

Branch geometry for simulations at A arteriole–capillary intersection; B capillary (or postcapillary venule)–postcapillary venule intersection. The mean diameter of and the mean blood flow velocity in each vessel are experimental results from Table 3. The branching angle θ (the angle between the inlet of arteriole/venule and the side vessel) is also from the measurement, ranging from 60° to 120°

Blood was considered as either a Newtonian fluid or a non-Newtonian fluid modeled by a Casson model. Blood flow was simulated using commercial computational fluid dynamics software ANSYS CFX 12.01 (ANSYS, Canonsburg, PA). The computational domain consisted of 3–3.2 million hexahedral elements for the geometry shown in Fig. 2. The convergence criterion for continuity and velocities was set as 1.0e–7. After solving for the velocity, we calculated vorticity Ω⃗, defined as Ω⃗ = ∇ × V⃗. Here ∇ is the gradient operator and V⃗ the velocity vector. We also determined the strain (or shear) rate tensor, defined as $\mathit{\epsilon }=\frac{1}{2}\left[\right(\nabla \overrightarrow{V})+{(\nabla \overrightarrow{V})}^T]$, where^T is the transpose operator.

In the simulation, the microvessel wall was taken as impermeable since the radial velocity across the vessel wall in a healthy vessel is approximately five orders of magnitude lower than the mean axial velocity. The mean velocity at the vessel entrance/exit was taken from the measured data. A no-slip boundary condition was applied along the microvessel wall. Flow was assumed to be steady as it is in the microvessels far from the heart; it was governed by the continuity and Navier–Stokes equations where the Reynolds number in the microvessel was on the order of 10⁻². Because the difference between the Newtonian and non-Newtonian fluids in the velocity and shear rate in most regions of these types of microvessels is negligible (Liu et al. 2008), blood was approximated as an incompressible and homogeneous Newtonian fluid with a density of 1,050 kg/m³ and an effective viscosity of 2.5 cP in the microvessels under study (Levenson et al. 1990; Liu et al. 2008). We also calculated the case for the non-Newtonian fluid by a Casson model (Levenson et al. 1990 and Liu et al. 2008) under the same geometry and velocity boundary conditions for the Newtonian fluid. The deviation between the non-Newtonian and Newtonian cases was less than 5% for the velocity, shear rate, and vorticity.

3 Results

3.1 Experimental results

3.1.1 Differential arrest and adhesion of tumor cells and beads in microvasculature

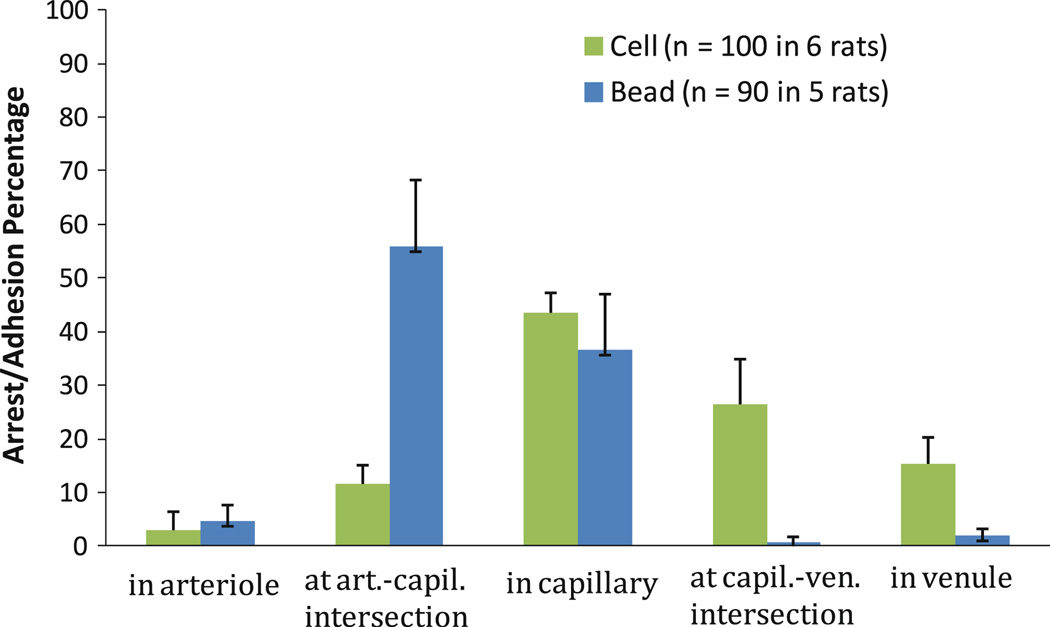
We successfully performed the tumor cell and bead arrest and adhesion experiments in six and five rats, respectively. In 10–25 s after injection via the carotid artery toward the aorta, tumor cells/beads started to be found in rat mesenteric microvasculature. After 1–3 h circulation, we found 100 arrested tumor cells in 6 rats and 90 arrested beads in 5 rats in the examined microvasculature. In addition to being trapped in capillaries, beads and cells preferred to arrest at the arteriole–capillary (Fig. 1A) or capillary (or postcapillary venule)–postcapillary venule (Fig. 1B) intersections. The distributions of the arrested tumor cells or beads at different locations of the microvasculature are shown in Fig. 3. Arrest and adhesion locations of tumor cells and those of beads were statistically significantly different (p < 0.001). That 43%of the tumor cells, 37% of the beads arrested in the capillaries, and 56% of beads at the arteriole–capillary intersections is due to mechanical trapping. However, a significant amount of tumor cells (42%) arrested either at the capillary (or postcapillary venule)–postcapillary venule intersections (27%) or in the postcapillary venules (15%), where there is no size restriction.

Fig. 3.

Histogram of arrest/adhesion locations of tumor cells and microbeads in mesenteric microvasculature (mean ± standard error). p < 0.001 (chi-squared test)

3.1.2 Diameters, branching angles, and blood flow velocities in microvessels at intersections

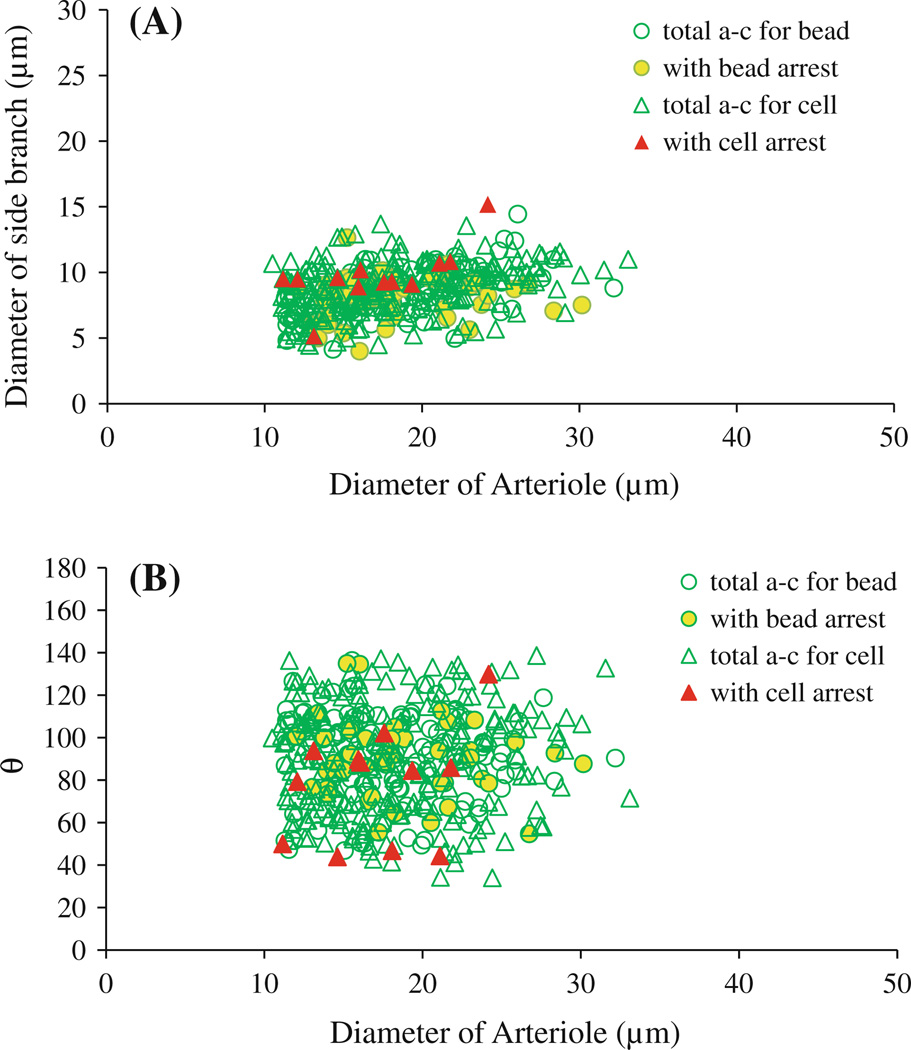
To further investigate the mechanical mechanisms behind this nontrapping tumor cell arrest/adhesion, we measured the diameters and branching angles of the microvessels at these intersections, as well as mean blood flow velocities. During our recording periods, nomeasurable changes were observed in the diameters and branching angles of the microvessels at these intersections. Figure 4 summarizes the diameter of the arteriole versus that of the side branch (mostly capillaries) (Fig. 4A) and the diameter of the arteriole versus branching angle θ (Fig. 4B) for the 395 arteriole–capillary (a–c) intersections examined in 11 rats. The diameters of microvessels and the branching angles at the a–c intersections in each rat are summarized in Table 1 (left column). The difference in the vessel sizes and branching angles between different rats is negligible (p > 0.1). Of 395 a–c intersections, only 62 had adherent cells/beads. The mean diameter of the arterioles at the 62 intersections was 18.4 ± 4.5 µm, and that of the side branches was 8.5 ± 1.9 µm. The mean branching angle θ was 86.3° ± 20.7°. These values have no significant difference from those of 395 examined intersections (p > 0.3). Out of 232 intersections examined in the 6 rats injected with the cells (open green triangles), cells were arrested in only 12 intersections (filled red triangles) (Fig. 4). In 163 intersections examined in the 5 rats injected with the beads (open green circles), beads were arrested in 50 intersections (filled yellow circles) (Fig. 4). Table 2 summarizes the vessel sizes and branching angles at the a–c intersections with adherent cells/beads in each animal (left column). There was no statistically significant difference in the vessel sizes and branching angles between the intersections with the adherent cells/beads and those without (p > 0.2) in the same animal.

Fig. 4.

Diameters and branching angles of microvessels at arteriole–capillary intersections with potential arrest of cells/beads. A Diameter of arterioles versus diameter of side branches (most of them are capillaries) at arteriole–capillary intersections. B Diameter of arterioles versus branching angle θ between arteriole and side branch. Empty green circles: total arteriole–capillary (a–c) intersections examined in five rats injected with beads; yellow filled circles: intersections with arrested beads. Empty green triangles: total arteriole–capillary intersections examined in six rats injected with tumor cells; red filled triangles: intersections with arrested cells

Table 1.

Microvessel diameters and branching angles at arteriole–capillary and side branch–postcapillary venule intersections examined in 11 rats

Rat no.	Arteriole–capillary intersection				Side branch–postcapillary venule intersection
	No. of intersections observed	Arteriole diameter (mean ± SD) (µm)	Capillary diameter (mean ± SD) (µm)	Angle (mean ± SD) (°)	No. of intersections observed	Venule diameter (mean ± SD) (µm)	Side branch diameter (mean ± SD) (µm)	Angle (mean ± SD) (°)
Group 1
1	46	17.9 ± 5.8	8.7 ± 1.9	92.9 ± 22.4	27	26.3 ± 6.3	12.8 ± 5.3	87.0 ± 21.3
2	45	19.6 ± 5.1	8.5 ± 1.8	85.1 ± 27.9	36	29.4 ± 6.9	13.4 ± 5.2	88.6 ± 18.7
3	33	20.2 ± 4.8	8.4 ± 1.6	87.4 ± 28.9	24	28.7 ± 6.6	14.8 ± 6.1	99.7 ± 24.7
4	43	18.1 ± 4.5	9.3 ± 1.6	83.0 ± 25.6	32	27.5 ± 6.3	12.9 ± 4.9	100.6 ± 20.1
5	40	16.4 ± 3.7	9.2 ± 1.8	87.6 ± 22.6	29	27.2 ± 5.8	13.3 ± 4.7	86.5 ± 16.2
6	25	14.2 ± 2.5	8.0 ± 2.2	99.4 ± 20.2	26	25.5 ± 7.7	12.7 ± 3.5	100.0 ± 15.5
Group 1 total	232	18.3 ± 4.8	8.8 ± 1.8	86.8 ± 25.9	174	27.6 ± 6.6	13.4 ± 4.9	92.8 ± 19.8
Group 2
1	34	18.3 ± 4.1	8.9 ± 1.9	90.6 ± 22.8	49	26.7 ± 7.7	12.2 ± 4.8	89.6 ± 27.0
2	24	17.8 ± 3.6	8.6 ± 1.6	91.1 ± 16.0	37	26.5 ± 7.4	13.4 ± 5.2	96.8 ± 31.2
3	27	18.4 ± 3.4	8.5 ± 1.3	89.6 ± 14.0	28	29.8 ± 9.4	14.4 ± 5.4	85.2 ± 29.4
4	37	19.2 ± 4.8	8.8 ± 1.5	88.3 ± 19.3	44	29.9 ± 10.9	13.9 ± 5.3	88.8 ± 27.2
5	41	16.8 ± 4.4	8.2 ± 1.4	94.1 ± 20.8	41	28.7 ± 10.4	14.1 ± 5.81	88.9 ± 24.7
Group 2 total	163	18.1 ± 4.3	8.6 ± 1.6	90.8 ± 19.5	199	28.2 ± 9.3	13.8 ± 5.3	89.9 ± 27.9
Groups 1 and 2 total	395	18.2 ± 4.7	8.7 ± 1.7	89.2 ± 23.1	373	27.9 ± 8.1	13.6 ± 5.1	91.3 ± 24.5

Group 1 injected with tumor cells and Group 2 with beads

Table 2.

Microvessel diameters and branching angles at arteriole–capillary and side branch–postcapillary venule intersections with adherent cells/beads

Rat no.	Arteriole–capillary intersection				Side branch–postcapillary venule intersection
	No. of intersections with adherent cell/bead	Arteriole diameter (mean ± SD) (µm)	Capillary diameter (mean ± SD) (µm)	Angle (mean ± SD) (°)	No. of intersections observed	Venule diameter (mean ± SD) (µm)	Side branch diameter (mean ± SD) (µm)	Angle (mean ± SD) (°)
Group 1
1	3	16.3 ± 4.0	9.9 ± 3.0	91.0 ± 40.0	3	28.4 ± 8.2	12.6 ± 4.3	90.3 ± 24.5
2	1	14.6	9.6	59.9	7	27.6 ± 4.2	12.5 ± 5.3	95.4 ± 14.1
3	2	17.0 ± 1.5	9.1 ± 0.3	68.2 ± 30.0	3	30.7 ± 1.5	17.5 ± 1.6	102.4 ± 21.7
4	3	17.7 ± 1.6	9.5 ± 0.6	91.6 ± 9.3	4	26.4 ± 7.5	13.0 ± 3.8	101.4 ± 18.2
5	3	18.3 ± 5.4	10.3 ± 0.7	69.8 ± 22.3	5	27.0 ± 5.4	13.5 ± 3.2	104.5 ± 15.0
6	0	N/A	N/A	N/A	5	27.9 ± 4.9	15.2 ± 2.6	100.9 ± 11.2
Group 1 total	12	17.1 ± 4.3	9.8 ± 2.2	78.2 ± 26.8	27	28.0 ± 5.8	14.2 ± 3.8	97.9 ± 17.8
Group 2
1	12	18.2 ± 4.3	6.6 ± 1.5	92.0 ± 17.8	1	21.9	12.5	120.4
2	8	19.7 ± 6.1	7.9 ± 2.1	91.6 ± 23.7	0	N/A	N/A	N/A
3	7	21.2 ± 4.7	8.5 ± 1.3	86.7 ± 19.3	0	N/A	N/A	N/A
4	12	19.4 ± 4.4	9.1 ± 0.4	86.6 ± 19.9	0	N/A	N/A	N/A
5	11	16.9 ± 2.8	9.4 ± 0.8	84.0 ± 14.0	0	N/A	N/A	N/A
Group 2 total	50	18.9 ± 4.5	8.1 ± 1.7	88.6 ± 18.4	1	21.9	12.5	120.4
Groups 1 and 2 total	62	18.4 ± 4.5	8.5 ± 1.9	86.3 ± 20.7	28	27.8 ± 4.6	14.1 ± 4.2	98.9 ± 18.0

Group 1 injected with tumor cells and Group 2 with beads

In another group of animals, we measured the mean blood velocity in the microvessels at the a–c intersections with similar size and branching angle. In 11 arterioles, the mean blood flow velocity was 2.24 ± 0.71 mm/s, and in 13 capillaries the velocity was 1.00 ± 0.43 mm/s (Table 3).

Table 3.

Microvessel diameter and mean blood flow velocity in microvessels at intersections where cells/beads arrested

Intersections	Diameter (µm) (mean ± SD)	Vmean(mm/s) (mean ± SD)
Arteriole–capillary intersection
Arteriole	18.4 ± 4.5 (n = 62)	2.24 ± 0.71 (n = 11)
Capillary	8.5 ± 1.9 (n = 62)	1.00 ± 0.43 (n = 13)
Side branch–postcapillary venule intersection
Postcapillary venule	27.8 ± 4.6 (n = 28)	0.99 ± 0.41 (n = 20)
Capillary or postcapillary venule	13.3 ± 4.2 (n = 28)	0.58 ± 0.21 (n = 17)

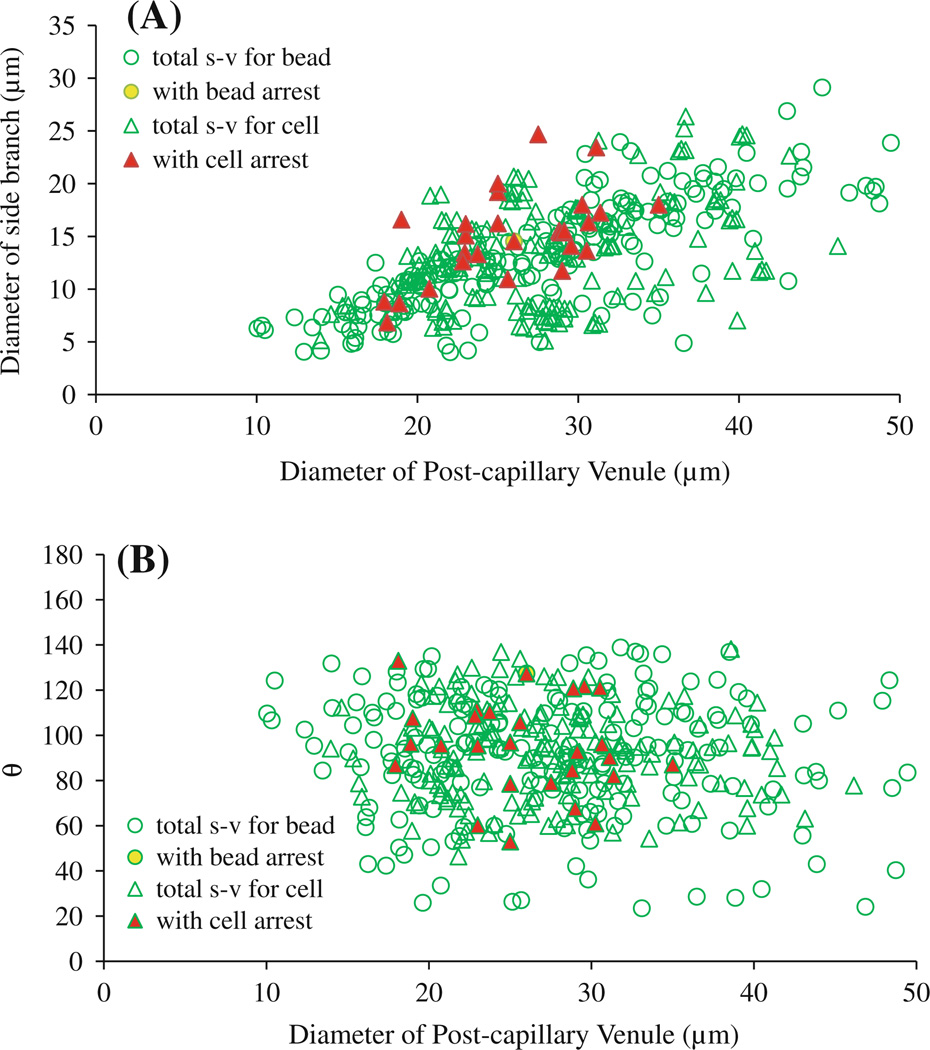
For side branch (capillary or postcapillary venule)–postcapillary venule (s–v) intersections, Fig. 5 summarizes the diameter of the postcapillary venule versus that of the side branch (Fig. 5a), and the diameter of the venule versus branching angle θ for 373 s–v intersections examined in 11 rats (Fig. 5b). Diameters of microvessels and the branching angles at the s–v intersections in each rat are summarized in Table 1 (right column). The difference in the vessel sizes and branching angles between individual rats was negligible (p > 0.1). Of 373 s–v intersections, only 28 had adherent cells/beads. The mean diameter of the postcapillary venules at 28 intersections was 27.8 ± 4.6 µm, and that of the side branches was 13.3 ± 4.2 µm. The mean branching angle θ was 98.9° ± 18.0°. These values have no significant difference from those of 373 examined s–v intersections (p > 0.2). Out of 174 intersections examined in the 6 rats injected with the cells (open green triangles), cells were arrested in 27 intersections (filled red triangles, Fig. 5). In 199 intersections examined in the 5 rats injected with the beads (open green circles), beads were arrested in only one intersection (filled yellow circle, Fig. 5). Table 2 summarizes the vessel sizes and branching angles at the s–v intersections with adherent cells/beads (right column). There was no statistically significant difference in the vessel sizes and branching angles between the intersections with the adherent cells/beads and those without (p > 0.2) in the same animal.

Fig. 5.

Diameters and branching angles of microvessels at capillary (or postcapillary venule)–postcapillary venule intersections with potential arrest of cells/beads. A Diameter of postcapillary venules versus diameter of side branches at capillary (or postcapillary venule)–postcapillary venule intersections.B Diameter of postcapillary venules versus branching angle θ between postcapillary venule and side branch. Empty green circles: total side branch–postcapillary venule (s–v) intersections examined in five rats injected with beads; yellow filled circles: intersections with arrested beads. Empty green triangles: total side branch–postcapillary venule intersections examined in six rats injected with tumor cells; red filled triangles: intersections with arrested cells

In another group of animals, we measured the mean blood velocity in the microvessels at the s–v intersections with a similar size and branching angle. In 20 postcapillary venules, the mean blood flow velocity was 0.99 ± 0.41 mm/s, and in 17 capillaries or postcapillary venules, the velocity was 0.58 ± 0.21 mm/s (Table 3).

3.2 Computational results

To elucidate the hydrodynamic mechanisms behind preferential cell/bead adhesion/arrest at microvascular intersections in addition to the mechanical trapping, we conducted a numerical simulation based on the measured geometrical and velocity data (Table 3 and Figs. 1 and 2) to calculate the distributions of the blood flow velocity, strain rate, and vorticity at the arteriole–capillary and side branch–postcapillary venule intersections.

3.2.1 Velocity profiles at intersections

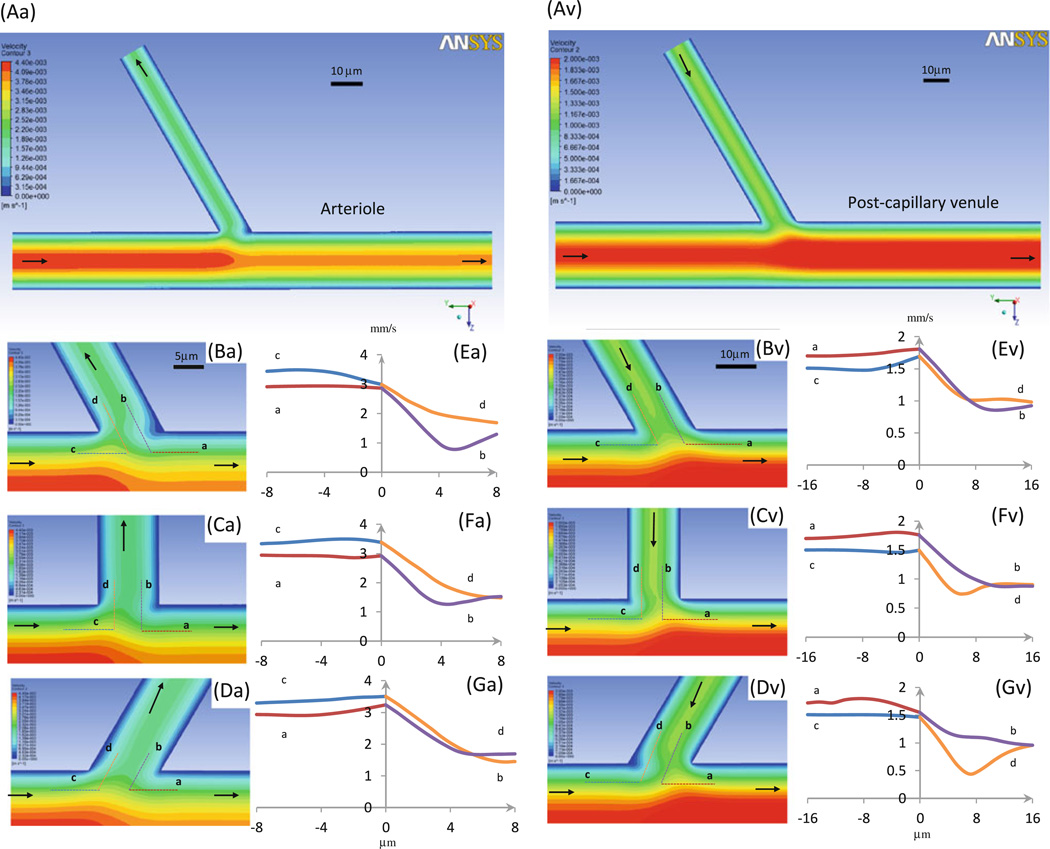
Figure 6 shows the velocity distributions at intersections of the arteriole–capillary (a–c, left panel) and side branch–postcapillary venule (s–v, right panel). Figure 6Aa, Av shows the global velocity contours in the midplane at the respective intersections. Figures 6Ba, Bv, Ca, Cv, Da, Dv are the detailed velocity contours at the midplane of the vessels near a–c or s–v intersections where the branching angle θ is 60°, 90°, and 120°, respectively. In less than 20 µm from the turning points in both vessels at the intersection, the flow becomes the parabolic Poiseuille flow. Figure 6Ea, Ev, Fa, Fv, Ga, Gv shows the velocity profiles along lines a (red), b (purple), c (blue), and d (orange), which are 1/4 vessel diameter from the respective vessel walls at the intersections (dotted lines in Figs. 6Ba, Bv, Ca, Cv, Da, Dv).

Fig. 6.

Velocity profiles in microvessels at intersections. Seven panels in left column: arteriole–capillary intersection; those in right column: side branch–postcapillary venule intersection. Aa and Av are velocity contour plots in midplane of vessels. Ba–Da and Bv–Dv are enlarged plots near intersectional region when branching angle θ is 60°, 90°, and 120°, respectively. Ea–Ga and Ev–Gv are detailed velocity profiles along dotted lines a (red), b (purple), c (blue), and d (orange) (in Ba–Da or Bv–Dv), which are 1/4 diameter distance from the vessel walls. Arrows: flow directions in microvessels

3.2.2 Strain (shear) rate profiles at intersections

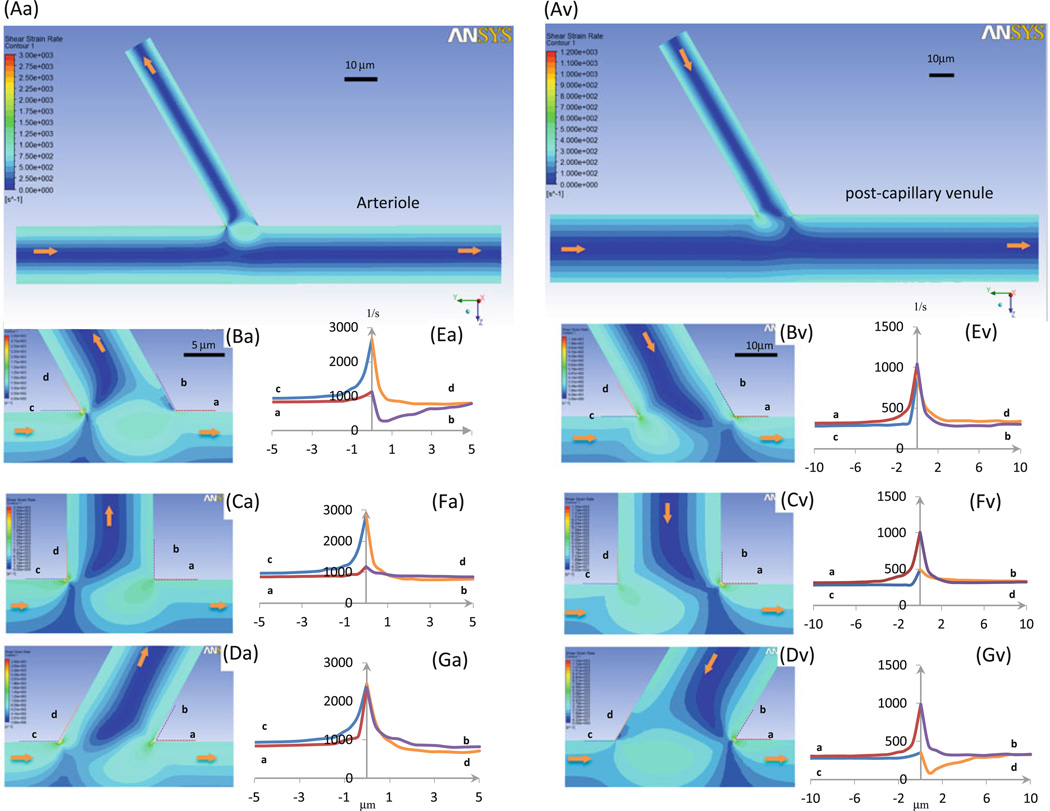
In Fig. 7, we plotted the strain (or shear) rate distributions in the midplane at intersections of the arteriole–capillary (a–c, left panel) and side branch–postcapillary venule (s–v, right panel). Figures 7Aa, Av are the overviews. Panels Ba, Bv, Ca, Cv, and Da, Dv show the details near the turning points of the intersections where the branching angle θ is 60°, 90°, and 120°, respectively. Figures 7Ea, Ev, Fa, Fv, Ga, Gv show the shear rate profiles along lines a (red), b (purple), c (blue), and d (orange), which lie along the vessel walls near the turning points at the intersections. The shear rate has a sudden increase at the inner turning points of both a–c (c, d lines) and s–v (a, b lines) intersections with the maximal strain rate just at the turning point. The sudden increase also occurs at the outer turning points (a, b lines for a–c intersections and c, d lines for s–v intersections). The magnitude of the shear rate increases with the intersection angle θ at a–c intersections and decreases with θ at s–v intersections. The shear rate can decrease to a magnitude lower than that at the straight part of the vessel wall near these outer turning points (Fig. 7Ea, Gv). Interestingly, there exist higher shear rate regions near the outer turning points at both intersections.

Fig. 7.

Strain (or shear) rate profiles in microvessels at intersections. Seven panels in left column: arteriole–capillary intersection; those in right column: side branch–postcapillary venule intersection. Aa and Av are strain rate contour plots in midplane of vessels; Ba–Da and Bv–Dv are enlarged plots near intersectional region when branching angle θ is 60°, 90°, and 120°, respectively; panels Ea–Ga and Ev–Gv are detailed wall shear rate profiles along dotted lines a (red), b (purple), c (blue), and d (orange) (in Ba–Da or Bv–Dv). Arrows: flow directions in microvessels

3.2.3 Vorticity profiles at intersections

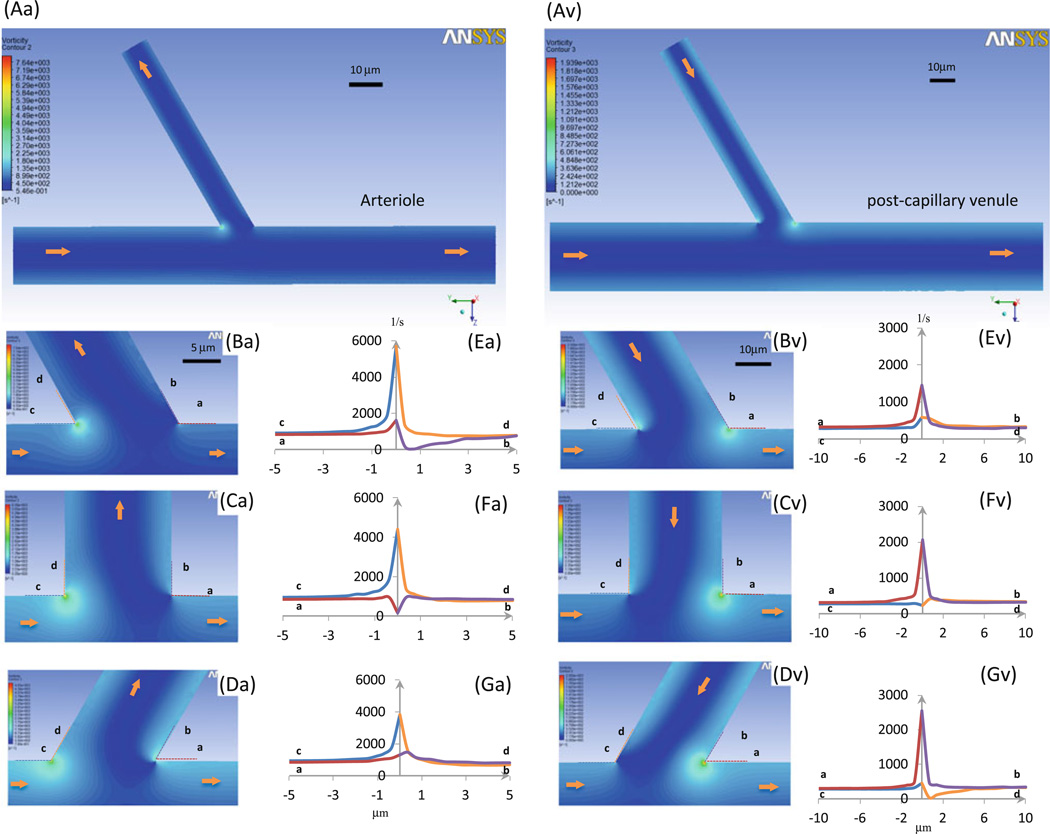
In Fig. 8 we plot the vorticity distributions in the midplane at the intersections of the arteriole–capillary (a–c, left panels) and the side branch–postcapillary venule (s–v, right panels). Figures 8Aa, Av are the overviews. Panels Ba, Bv, Ca, Cv, and Da, Dv show the details near the turning points of the intersections where the branching angle θ is 60°, 90°, and 120°, respectively. Figures 8Ea, Ev, Fa, Fv, Ga, Gv show the detailed vorticity profiles along lines a (red), b (purple), c (blue), and d (orange), lying along the vessel walls near the turning points at the intersections. We can see from Figs. 8Ba, Bv, Ca, Cv, and Da, Dv that the vorticity is highly localized near the turning points of the intersections. It peaks at the inner turning points: c, d lines for the a–c and a, b lines for the s–v intersections. The larger the branching angle θ, the smaller/larger the peak vorticity at the inner turning point for the a–c/s–v intersections. In contrast, the vorticity at the outer turning point either has a slight increase followed by a slight drop or a slight drop followed by a slight increase.

Fig. 8.

Vorticity profiles in microvessels at intersections. Seven panels in left column: arteriole–capillary intersection; those in right column: side branch–postcapillary venule intersection. Aa and Av are vorticity contour plots in midplane of vessels; Ba–Da and Bv–Dv are enlarged plots near intersectional region when branching angle θ is 60°, 90°, and 120°, respectively; Ea–Ga and Ev–Gv are detailed vorticity profiles at walls along dotted lines a (red), b (purple), c (blue), and d (orange) (in Ba–Da or Bv–Dv). Arrows: flow directions in microvessels

4 Discussion

In this study we quantified the arrest and adhesion patterns of malignant and flexible tumor cells and rigid beads of similar sizes in rat mesenteric microvasculature. Based on the measured microvascular geometry and blood flow velocities in the microvessels, we further performed a numerical simulation to elucidate the effects of hemodynamic factors on tumor cell arrest and adhesion. We found that 97% of rigid beads arrest in the microvasculature before they reach the postcapillary venules. Since the diameter of the rigid beads is ~10 µm, which is larger than the size of capillaries (diameter less than 10 µm), their arrest should be primarily due to the mechanical trapping. Because of the higher velocity (Fig. 6Ea–Ga) and vorticity (Fig. 8Ea–Ga) near the inner turning point at the arteriole–capillary intersection, the beads would be pushed into the capillary from the arteriole; 56% of the beads are stuck at the intersections and 37% can be washed further into the capillaries, while only 3% escape from the capillary trapping. In contrast, 42% of the flexible tumor cells (~ 14 µm diameter) escape from the capillary trapping. Of these cells, 27% arrest at the capillary (or postcapillary venule)–postcapillary venule intersections and 15% adhere at the walls of postcapillary venules with much larger diameter than tumor cells.

Although seed and soil theory describing specific biochemical interactions between circulating tumor cells and the host tissues/organs (Paget 1889; Fidler 2011; Langley and Fidler 2011; Schlüter et al. 2006; Gassmann et al. 2010; Kostenuik 2004; Fokas et al. 2007; Glinskii et al. 2005) and mechanical trapping mechanisms (Ewing 1928; Weiss 1992; Ding et al. 2001; Mook et al. 2003; Steinbauer et al. 2003) have been proposed for several decades, debates about which factor is dominant have not been resolved. Intravital video microscopy following systemic injection of eGFP-transfected rat colon cancer cells revealed that initial arrest of cancer cells in sinusoids of the liver was due to size restriction. Adhesion of cancer cells to endothelial cells at the microvessel wall was never found (Mook et al. 2003). In contrast, Glinskii et al. (2005) reported that following intravenous injection, a significant fraction of breast and prostate cancer cells escaped arrest in a lung capillary bed and successfully arrived at other organs. Antibodies targeting adhesion molecules at the tumor and endothelial cells inhibited cancer cell deposits in mouse lungs and bones by >90%. Schlüter et al. (2006) also found that colon carcinoma cells could pass microvessels without size restriction in rat liver, lung, intestine, skin, muscle, spleen, and kidney in vivo. Gassmann et al. (2009) later revealed that although a significant amount of metastatic colorectal cancer cells could be retained in liver sinusoids 5–7 µm in diameter, inhibition of integrins at the cancer cells significantly impaired cell arrest by 30–60%, suggesting that mechanical trapping and specific adhesion are not exclusive. Multiphoton microscopy was used to track cancer brain metastasis in vivo in blood microvessels deep in the mouse brain over minutes to months (Kienast et al. 2010). Tumor cells including lung carcinoma cells and melanoma cells were injected through internal carotid artery. It was found that in order to form brain metastases, it is necessary for the tumor cells to initially arrest in the microvasculature with similar sizes, especially at the vascular branch points.

Our in vivo observations over 1–3 h for the arrest and adhesion of flexible metastatic tumor cells and rigid beads with similar sizes in the microvasculature further quantify the contributions from mechanical trapping (size restriction), hydrodynamic factors (localized shear rate and vorticity), and interactions between tumor and endothelial cells. Our results indicate that mechanical trapping is responsible for almost all the arrest of rigid beads, the surrogates for nonflexible cells without cell adhesion molecules at their surfaces, and for about half of that of flexible tumor cells, while cell–cell interactions are responsible for the remaining half. As suggested by Slattery et al. (2005) and Yan et al. (2010, 2012), the shear stress distribution in the flow and its spatial gradients can modulate the interactions between circulating tumor cells and endothelial cells, resulting in more adhesion of tumor cells at a bent microvessel compared to a straight one.

Although no statistically significant difference was found in the branching angles between intersections with adherent cells and beads and those without, the inner turning angles at the intersections with the adherent cells and beads tended to be sharper, i.e., the branching angles were smaller at the a–c intersections and larger at the s–v intersections (Tables 1 and 2). As shown in Figs. 7 and 8, the sharper the turning angle, the larger the shear rate and the shear rate change, and the larger the vorticity near the inner turning point. These results further suggest that in addition to the enhanced shear rates and its gradients at the turning points of microvessel branches, the localized vorticity at these locations, especially at the inner turning points, should play a role in regulating cell–cell interactions, resulting in increased tumor cell adhesion at the branching intersections.

Although mesenteric tissue is not a typical site for breast cancer metastasis, it offers many advantages as a model, including minimal invasive preparation and continuous in vivo visualization of tumor cell arrest and adhesion over hours. In addition, local hydrodynamic factors in the mesenteric microvasculature, the activation of endothelial and tumor cells by these factors, and the specific cell adhesion molecules at tumor cells should be comparable to those target microvasculatures with even more complicated geometry. Therefore, we can use mesentery for identifying factors in tumor arrest and adhesion other than the specific cell adhesion molecules on the endothelial cells of the target organs.

Another important factor in tumor hematogenous metastasis is the deformability of the cancer cell. The more invasive, malignant, and metastatic the cancer cells are, the greater deformability they have (Koop et al. 1995; Guck et al. 2005; Li et al. 2008; Swaminathan et al. 2011). The flexibility of malignant tumor cells enables them to escape the mechanical trapping of the capillaries (similar to red blood cells) and circulate to all the tissues and organs, significantly increasing their capacity to elicit morbidity and mortality. However, if therapeutic agents that prevent circulating tumor cells from adhering to the vessel wall can be developed, it may be possible to inhibit tumor metastasis since cell arrest and adhesion is a necessary step for metastasis.

In summary, we have developed a direct in vivo visualization method to quantify the arrest and adhesion of flexible malignant breast cancer cells and similarly sized rigid beads in rat mesenteric microvasculature. Based on the measured geometry and blood flow velocities, we also performed numerical simulations to depict detailed distribution profiles of flow field velocity, shear rate, and vorticity at the intersections where tumor cells preferentially arrest and adhere. Our results help elucidate long-debated issues related to the dominant factors in early-stage tumor hematogenous metastasis.