Cortical graph smoothing : a novel method for exploiting DWI-derived anatomical brain connectivity to improve EEG source estimation

Abstract

The EEG source estimation problem consists of inferring cortical activation from measurements of electrical potential taken on the scalp surface. This inverse problem is intrinsically ill-posed. In particular the dimensionality of cortical sources greatly exceeds the number of electrode measurements, and source estimation requires regularization to obtain a unique solution. In this work we introduce a novel regularization function called cortical graph smoothing, which exploits knowledge of anatomical connectivity available from diffusion-weighted imaging. Given a weighted graph description of the anatomical connectivity of the brain, cortical graph smoothing penalizes the weighted sum of squares of differences of cortical activity across the graph edges, thus encouraging solutions with consistent activation across anatomically connected regions. We explore the performance of the cortical graph smoothing source estimates for analysis of the event related potential (ERP) for simple motor tasks, and compare against the commonly used minimum norm, weighted minimum norm, LORETA and sLORETA source estimation methods. Evaluated over a series of 18 subjects, the proposed cortical graph smoothing method shows superior localization accuracy compared to the minimum norm method, and greater relative peak intensity than the other comparison methods.

I. Introduction

The aim of every functional neuroimaging modality is to estimate neural activation in brain tissue. However, for all non-invasive imaging modalities (including fMRI, PET, SPECT, MEG, EEG), neural activation is not directly observed but rather indirectly inferred on the basis of some other physical measurement. Interpreting data from any such imaging modality relies upon an accurate forward model describing the chain of physiological and physical processes that connect brain activity to changes in the observed measurement. In particular, EEG signal is generated by electrical currents flowing throughout the head as a result of dipolar current sources inside cortical tissue. In this case the forward model consists of solving for the electrode voltages arising from a fixed set of dipole sources; this can be solved numerically given a description of the geometry and electrical conductivities of tissues in the entire head. Estimating brain activity requires inverting this forward model : i.e. finding the activity that matches the observed data when mapped under the forward model.

The EEG inverse problem is fundamentally ill-posed. Additionally, the number of electrodes is small compared to the number of degrees of freedom of brain activity. This implies that there are infinitely many possible configurations of current sources which match the observed data under the forward model, so that imposing some form of regularization is necessary in order to obtain a unique solution. Many commonly used regularization approaches are based on penalizing some measure of smoothness of the solution, such its Euclidean norm, or the norm of its gradient. A recent review of the EEG inverse problem including many different regularization methods is given in [1]. While such approaches lead to simple and tractable solutions, they are based on very generic assumptions about the underlying signal that do not exploit specific knowledge about the human brain.

Within the past 15 years, there has been significant progress in the development of methods utilizing diffusion-weighted imaging (DWI) for non-invasive imaging and reconstruction of white matter anatomical connectivity [2]. The water diffusion in dense white matter fiber bundles, also known as white matter fascicles, has been observed to be highly anisotropic with primary orientation along the fascicle direction [3], [4], due at least in part to cell membranes, axonal density and myelination [5]. This allows inference about the white matter structure and architecture by examination of the direction and magnitude of average water diffusion constrained by the white matter fiber bundles. The most common DWI technique has been diffusion tensor imaging (DTI), which describes the anisotropic diffusion at each voxel with a single tensor. It enables estimation of the major fascicle orientation and characterization of the white matter microstructure via diffusion parameters such as the fractional anisotropy (FA) and the mean diffusivity (MD).

Tractography [6], [7], [8], [9] can then be performed to track of the macroscopic water displacement along pathways from initial seed points, modeling the path of each fascicle as a sequence of steps taken along the path by considering the local diffusion information. Recently, approaches to characterize the whole brain connectivity have been investigated [10], [11]. These are based on dense sampling of tract streamlines in the white matter via whole brain tractography. The gray matter is then segmented into multiple parcels and the white matter connectivity between the parcels assessed. Particularly, the estimation of the connectome matrix enables description of the connectivity between each pair of parcels by a square symmetric matrix, in which the (i, j)^th element describes the connectivity strength between parcels i and j. Whole brain connectivity approaches and novel analysis methods based on graph theory have recently emerged as a major research area, including the Human Connectome Project [12].

In this paper, we develop a novel methodology that exploits the whole brain anatomical connectivity to constrain and improve the EEG source estimation. This work is motivated by the idea that as cortical activity is influenced by connectivity, connectivity knowledge should inform the prior information imposed by regularization. Our approach is based on the distributed-dipole formulation of the EEG forward problem, which involves discretizing the cortex into a large number of parcels, each of which is associated with a single unknown dipolar current source. We employ a triangulated mesh description of the cortical surface, so that each dipole source is associated with a small cortical surface patch. Crucially, both the EEG forward model and the connectome matrix are computed using these same cortical patches. By fusing the distributed dipole and connectome matrix, we may view the EEG inverse problem as one of estimating a function defined on the vertices of a weighted graph, where the edge weights of the graph are given by the connectome matrix elements. Interestingly, this viewpoint places EEG source estimation within the context of signal processing on weighted graphs [13], [14], [15]. Previous work by Phillips [16] exploited brain tissue geometrical knowledge and spatial adjacency of sources for EEG source estimation, but did not employ tractography.

The fundamental assumption underlying our approach is that strongly connected cortical regions will have similar activity. Our novel regularization functional, termed cortical graph smoothing (CGS), is formed by penalizing the squares of differences of source activity, summed over the edges of the connectome graph. We describe the interpretation of the CGS as acting by penalizing the derivatives of the activity treated as a function defined on the vertices of a weighted graph. We employ this CGS prior penalty with a quadratic data fidelity, yielding a variational approach with an analytic linear solution.

Evaluating the performance of source estimation on real data is complicated by the lack of ground truth. We address this by analyzing the source estimation results for an experimental setting where the location of expected activity is well known. In particular, we employ a motor task involving finger movements, where the origin of the motor potential is expected to be localized to a well defined region of the contralateral motor cortex. Our experimental results show quantitatively improved localization performance of the CGS compared to the widely used minimum norm approach.

We note that work using a different graph-based prior based on sparse approximation with graph wavelets, but employing similar methods for the EEG forward modeling and connectome graph construction [17], has been published previously. Our work in this paper extends the preliminary work in [18] on cortical graph smoothing by more extensive validation, comparison to alternative approaches, and by more principled selection of regularization constants.

II. Electrical Head Modeling

This current work has been developed in the context of ongoing research on constructing accurate numerical models of the physics of head electrical conduction for both EEG and event related potential (ERP) analysis [19]. The EEG signal consists of electric potentials on the scalp produced by current flowing throughout the head, arising from current sources within cortical tissue. These arise from microscopic synaptic currents following neurotransmitter release that are organized by the laminar structure of cortical tissue into macroscopic dipolar current sources, oriented perpendicular to the cortical surface.

A. Inhomogeneous Poisson Equation

The goal of the forward electrical model is to compute the scalp voltages arising from a given set of dipolar current sources. We ignore capacitive and inductive effects and consider the head to be a purely resistive medium, with a spatially varying isotropic conductivity σ(x, y, z). While some head tissues (especially skull and white matter) are known to have electrical conductivities which deviate from isotropic, we do not consider this extension here. In the isotropic case the current flux J⃗ is proportional to the electric field E⃗, so that J⃗ = σE⃗ = σ∇φ where φ(x, y, z) denotes the electric potential at each point in the head. Conservation of charge implies that ∇ · J⃗ = 0, so that φ satisfies the inhomogeneous Poisson equation

$$\nabla ·(\sigma \nabla \phi )=s,$$ (1)

with the no-flux boundary condition σ∇φ · n⃗ = 0 on the scalp surface, where n⃗ is the scalp surface normal vector, and where the scalar function s describes current sources or sinks. True dipolar current sources correspond to a limit case when a pair of a localized source and sink are brought infinitesimally close together; in practice during numerical solution, approximate dipole sources are described by setting s = 0 everywhere except at a pair of nearby voxels, where s is set to be positive on one, and negative on the other. Note that equation (1) is valid in the quasi-static limit, where current varies slowly enough so that contributions to the potential from both time-varying magnetic fields and capacitive effects are negligible. The EEG signal does not have appreciable frequency content above about 100 Hz, sufficiently low for the quasi-static approximation to apply.

B. Tissue Segmentation and Cortical Surface Partitioning

This work employs subject-specific head models constructed from individual anatomical T1 MR images. Both the configuration of the conductivity σ(x, y, z) and the locations of the distributed dipole sources are determined from a 3D map of head tissues. The conductivity σ is given by assuming a constant conductivity for each tissue type as shown in table I. The tissue conductivities were fixed based upon previous work and empirical measurements reported in the literature (see [20] for further references). This approach, sometimes referred to as a multi-shell or multi-compartment head model, depends on the ability to accurately segment head images into component tissue types. We construct subject-specific head models by acquiring and segmenting a high resolution (1 mm³ voxel) T1-weighted MRI image, classifying each image voxel as either air or one of the six following tissues: skull, scalp, cerebral-spinal fluid, gray matter, white matter or eyeball. This image segmentation problem is computed using the BrainK software package developed at the NeuroInformatics center [21].

TABLE I.

Conductivities of different head tissues, in Ω⁻¹m⁻¹

Scalp	Skull	CSF	GM	WM	Eyeball
0.44	0.018	1.79	0.25	0.35	1.5

An important feature of this work is that we make extensive use of a triangular mesh describing the outer cortical surface. This surface is defined as the interface between grey matter and cerebrospinal fluid, and is computed using the marching cubes algorithm for level surfaces. This yields two disconnected surface meshes, one for each hemisphere. The distributed dipoles we use are placed by partitioning these cortical meshes into a large number of approximately equal-sized patches, which we denote by Γ_i.

Each mesh was partitioned into patches using a spectral graph partitioning algorithm implemented as part of the CHACO software package [22]. This approach is based on partitioning the mesh dual graph, defined as the graph whose nodes are the mesh triangles and whose edges describe the the triangle adjacency relations (see [23] for a review of mesh partitioning). In this work we divide each hemisphere into 1200 patches, yielding patches of area roughly 85 mm². For each patch, we compute the patch center c_i and the outward facing normal vector n⃗_i. The choice of this number of patches was motivated by the application for EEG. For this application, patch sizes were chosen small enough to avoid any significant intra-patch heterogeneity of the surface normal vectors, which would invalidate the use of a single oriented dipole for each patch. We note that as the mesh partitioning is driven purely by the geometry of the cortical surface, the resulting patches are not constrained to correspond to standard anatomical regions of interest (in particular they are not subdivisions of Brodmann’s areas).

C. Leadfield Matrix

The distributed dipole formulation involves computing solutions to (1) for a large set of dipolar sources.

In this work we primarily employ a cortical surface-normal distributed dipole set, where we place the dipole sources j⃗_i at the patch centers c_i, and parallel to n_i so they are normal to the cortical surface. Choosing a finite number of source dipoles effectively discretizes the space of source currents. These dipoles then form a basis for the set of cortical sources we wish to estimate, i.e. we will consider only source current distributions of the form

$$J=\sum _{i}a(i){\overrightarrow{j}}_i.$$ (2)

We may consider J ∈ ℝ^Nd, where N_d is the total number of dipoles, to be the vector of coefficients in this expansion, i.e. J_i gives the activation of the i^th dipole.

We are interested in describing the forward model of the potential φ not at all points in space, but at the specific locations on the scalp where the EEG sensors are located. For a set of N_e electrodes, we let the vector ϕ ∈ ℝ^Ne denote the values of the potential at the electrode positions. Let ϕ⁽ⁱ⁾ ∈ ℝ^Ne be the potentials at the sensors for the solution to (1) when the i^th dipole is activated with unit current. As equation (1) is linear in φ, its solutions obey superposition, which implies that

$$\varphi =\sum _i{\varphi }^{(i)}{J}_i$$ (3)

are the sensor potentials for the solution when the dipole source current is described by J. This relationship can be compactly expressed as ϕ = KJ, where the N_e × N_d matrix K = (ϕ⁽¹⁾, … ϕ^(Nd)) is the leadfield matrix.

For completeness, we note that one may also form distributed dipoles without explicitly using the cortical surface. This is done by placing dipoles at N_d points on a regular 3D grid, restricted to lie within the grey matter. As the orientation of these volumetric dipoles is not fixed by the cortical surface normal, they are represented by an ordered triple of orthogonal dipole components in the x,y and z directions. By concatenating these three unknown coefficients at each dipole, one may define the current source vector J to be of length 3N_d, and then define a N_e ×3N_d leadfield matrix K so that the relation ϕ = KJ holds. In this work we employ the cortical surface-normal dipoles for the proposed cortical graph smoothing method. This dipole set was also used for the minimum norm, weighted minimum norm, and sLORETA comparison methods, while volumetric dipoles based on a regular 7mm 3D grid are used for the LORETA comparison method.

We solve the inhomogeneous poisson equation numerically with a finite-difference method on a 1mm³ grid, corresponding to the resolution of the T1-weighted MRI image. Our numerical solver is based on the alternating difference implicit (ADI) scheme, algorithmic details may be found in [20]. Using optimized GPU codes developed at the NeuroInformatics center, we were able to compute a subject specific leadfield matrix in 15 minutes using a 3-node subset of a GPU-enabled cluster employing 9 Nvidia Tesla M2070 GPU cards.

The locations of the electrodes are determined in a subject specific manner, based a the geodesic photogrammetry system described in [24]. Briefly, this system consists of multiple inward-facing cameras on fixed geodesic frame which the subject can sit inside of while wearing the electrode net. A point cloud of sensor positions can be determined from these multiple photographs, this point cloud is later registered with the scalp surface of the head to determine the electrode positions within the head model.

III. Connectome Graph Estimation

The cortical graph smoothing approach requires that the anatomical connectivity derived from DWI and the distributed dipoles be defined on the same space. We achieve this by using each subjects T1-weighted image to define a set of coordinates, and register each subject’s DTI to the corresponding T1-weighted image prior to further analysis. Following this, the various products of both images (namely the tract streamlines and the cortical surface) are naturally aligned. We note that each subjects connectome graph is computed using subject-specific T1 coordinates, in particular we do not perform registration onto a generic atlas T1 image.

A. Diffusion Tensor Estimation and Registration

We estimate diffusion tensors from the raw diffusion weighted images with a least square fitting procedure using the TEEM software package [25]. The transformation between the DTI space and the T1-weighted is estimated by registration of the mean diffusivity image to the T1-weighted utilizing the mutual information metric [26], well-suited for multi-modal image registration. [27]. The diffusion tensor field is then warped to the common space by utilizing log-Euclidean tensor interpolation. This prevents the interpolated tensors from experiencing the “swelling effect” which can be observed with conventional Euclidean tensor interpolation [28] and makes the estimated tensors larger than they should be.

B. Tractography

The cortical connectome is computed by using a large number of tract streamlines generated by tractography from the diffusion tensors. We consider the diffusion tensor field D warped to the common space so that the generated tracts are aligned to the meshes defining the cortical patches. We use a stochastic streamline tractography algorithm [29] that combines the speed and efficacy of deterministic decision making at each voxel with probabilistic sampling from the space of all streamlines. Our tractography method improves the simple streamlining through the use of tensor deflection [30], directional inertia, and stopping criterion inertia as described below.

We initiate tracts from seed voxels distributed densely throughout the white matter by choosing voxels with high fractional anisotropy (FA > FA_seed). This corresponds to voxels which contain mostly a single fascicle orientation, and therefore to voxels with reliable estimation of the fascicle orientation. A fixed number N_s of streamlines are initialized at stochastically sampled locations inside each seed voxel, and the tracts are constructed by stepping with subvoxel resolution through the tensor field. From a subvoxel location p^k, a new point along the streamline is identified by stepping with a fixed step size s in the direction υ^k+1: p^k+1 = p^k +υ^k+1s. The direction υ^k+1 of the streamline is calculated using a combination of the primary eigenvector and tensor deflection, while accounting for the previous direction υ^k of the streamline:

$${\upsilon }^{k+1}=\gamma {\upsilon }^k+(1-\gamma )(\delta {(D^{k+1})}^2{\upsilon }^k+(1-\delta )e^{k+1}),$$ (4)

where D^k+1 is the diffusion tensor at point p^k, e^k+1 is a normalized principal eigenvector of D^k+1, and γ and δ are the direction inertial momentum and the tensor deflection fraction, respectively.

Streamlines are terminated when the fractional anisotropy falls below a specified threshold, or when the tract bending angle exceeds a specified threshold. We avoid loss of connectivity due to local aberrations by incorporating a low-pass filter along the estimated pathway for the stopping criteria. To do so, we evaluate the trajectory FA F^k+1 and the trajectory angle θ^k+1 at step (k + 1) by:

$$\begin{array}{l}{F}^{k+1}=\alpha F^k+(1-\alpha )\text{FA}(D^{k+1})\\ {\theta }^{k+1}={cos}^{-1}(\beta cos({\theta }^k)+(1-\beta )e^{k+1}·v^{k+1}),\end{array}$$ (5)

where α and β are momentum parameters. We terminate the tractography whenever F^k+1 < FA_min or θ^k+1 > θ_max. Such a low-pass filtering and the use of tensor deflection enables better tractography in regions of crossing fibers.

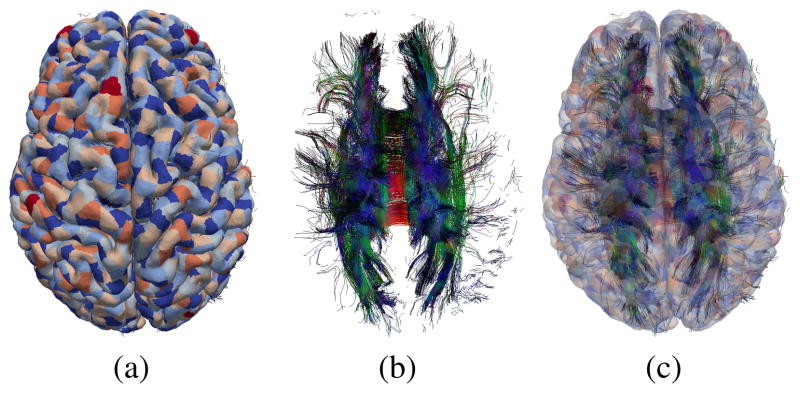
In table II we give the values of the tractography parameters used. In Figure 1 we illustrate the cortical surface mesh partitioned into patches and overlaid on a subset of corticocortical tracts.

TABLE II.

TRACTOGRAPHY PARAMETERS USED. DEFINITIONS GIVEN IN THE TEXT.

FAseed	Ns	s	γ	δ	α	β	FAmin	θmax
0.6	30	1/3 mm	0.5	0.5	0.5	0.5	0.2	30°

Fig. 1.

View of (a) cortical surface mesh (colored to distinguish patches), (b) selected tracts and (c) surface and tracts, superimposed.

C. Tract filtering and binning

The output of the tractography is a set of tract streamlines γ_k : [0, 1] → ℝ³, where 1 ≤ k ≤ N_tracts. In this work, we compute the connectome using only tract streamlines that directly connect cortex to cortex. For each tract γ_k, we compute $n_s^k$ and $n_e^k$, the cortical patches closest to the startpoint and endpoint, as

$$n_s^k=\underset{n}{\text{argmin}}d({\mathrm{\Gamma }}_n,{\gamma }_k(0)),n_e^k=\underset{n}{\text{argmin}}d({\mathrm{\Gamma }}_n,{\gamma }_k(1)),$$

where d(Γ_n, p) is the distance from a point p to the n^th cortical patch. The k^th tract is rejected as not corticocortical if either $d({\mathrm{\Gamma }}_{n_s^k},{\gamma }_k(0))$ or $d({\mathrm{\Gamma }}_{n_e^k},{\gamma }_k(1))$ exceed the distance threshold d_cthresh. Let I_cc be the set of cortical-cortical tract indices. We set d_cthresh =10mm, resulting in discarding on average 65% (stdev=6%) of the total tracts.

The anatomical connectome matrix A^tr ∈ ℝ^N_d,N_d is then computed explicitly as

$$A_{i,j}^{tr}=\frac{1}{N_s}\sum _{k:k\in I_{cc},(n_e^k,n_s^k)\in \{(i,j),(j,i)\}}\frac{1}{l({\gamma }_k)}$$ (6)

where l(γ_k) is the length of the k^th tract. We divide by l(γ_k) to counteract the bias towards longer tracts due to dense seeding throughout white matter, as the dense seeding implies that every physical tract would generate a number of tract streamlines in proportion to its length.

D. Hybrid Local / Nonlocal connectome matrix

The tractography-based connectome matrix A^tr described above is based entirely on white matter tract streamlines that can be resolved by DTI. However, local radial connections through the gray matter also exist that cannot be represented with diffusion-weighted imaging. Additionally, local short range “U-fibers” connections may connect gray matter regions through the white matter but are challenging to estimate with DTI at conventional resolution. These considerations motivate the inclusion of a local connectome matrix A^loc ∈ ℝ^N_d×N_d , derived purely from spatial adjacency of the cortical surface patches. Including this imposes prior belief that there exist local connections between regions that are not resolved by the long-range tractography. We form A^loc by setting $A_{i,j}^{\mathit{loc}}$ to be the length of the border (in mm) between the patches Γ_i and Γ_j . In particular, this sets $A_{i,j}^{\mathit{loc}}=0$ for non-adjacent patches.

We then form the hybrid local/nonlocal connectome matrix

$$A={\lambda }_{tr}{A}^{tr}+{\lambda }_{\mathit{loc}}{A}^{\mathit{loc}},$$ (7)

for non-negative regularization parameters λ_tr and λ_loc. These parameters will determine both the relative contribution of the tractography based and local connectomes, and the overall weight of the cortical graph smoothing penalty. A systematic procedure for determining them from observed data is described in section IV-A.

IV. CORTICAL GRAPH SMOOTHING

The source estimation problem at a single spatial timepoint consists of estimating source currents J ∈ ℝ^N_d given an observation of ϕ ∈ ℝ^N_e . A set of currents J will match the observed data if it satisfies ||KJ – ϕ||² = 0. Directly minimizing ||KJ –ϕ||² cannot yield a unique solution as the equation ϕ = KJ is underdetermined. Cortical graph smoothing employs a variational framework, where the desired source currents are given by the minimizer of ||ϕ–KJ||²+f_cgs(J). Here f_cgs : ℝ^N_d → ℝ is the CGS penalty function, which depends on the hybrid local/nonlocal connectome matrix A.

The CGS penalty is motivated by the hypothesis that connected brain regions should have similar activity. We impose this by penalizing squares of differences in activity between connected cortical patches. Additionally, as the edges of our connectome graph are weighted, we may scale the amount of the penalty incurred across any pair of patches by the strength of their connectivity. Specifically, given a weighted graph with edge weights a_i,j , we define

$$f_{\mathit{cgs}}(J)=\sum _{i~j}{a}_{i,j}{(J_i-J_j)}^2$$ (8)

with the sum taken over all pairs of connected vertices.

For simplicity, we reformulate (8) using the graph Laplacian matrix L, defined as follows. Given any symmetric adjacency matrix A, L is given by L = D–A, where D is the diagonal degree matrix with i^th element D_i,i = Σ_j A_i,j , i.e. the (weighted) degree of the i^th vertex. A relatively straightforward calculation [31] shows that J^T LJ = Σ_i,j a_i,j(J_i – J_j)², exactly the same as the CGS penalty. Using the hybrid local/nonlocal connectome matrix from (7), we may write f_cgs(J) = λ_trJ^TL^trJ +λ_locJ^TL^locJ, with the tractography-based and local graph Laplacians L^tr and L^loc defined accordingly. The CGS solution is defined by

$${\widehat{J}}_{\mathit{cgs}}(\varphi )=\underset{J}{\text{argmin}}{\Vert \varphi -KJ\Vert }^2+{\lambda }_{tr}{J}^T{L}^{tr}J+{\lambda }_{\mathit{loc}}{J}^T{L}^{\mathit{loc}}J.$$ (9)

As both the data fidelity and the prior penalty are quadratic in J, this problem has an analytic solution, linear in ϕ, given by

$${\widehat{J}}_{\mathit{cgs}}={(K^{T}K+{\lambda }_{tr}{L}_{tr}+{\lambda }_{\mathit{loc}}{L}_{\mathit{loc}})}^{-1}{K}^T\varphi .$$ (10)

Further intuition into the cortical graph smoothing can be gained by considering it as a penalty on a type of derivative of the source current J. If one considers the case of a connectivity graph corresponding to a regular 2-D grid, with each grid vertex connected with equal weight to its 4 nearest neighbors, the graph Laplacian L is exactly equal to the standard 5-point stencil for approximating the continuous Laplacian operator $-\mathrm{\Delta }=-(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2})$, so that Lf ≈ –cΔf for some constant c. Integration by parts shows

$$f^{T}Lf\approx c\int f\mathrm{\Delta }f\mathit{dxdy}=c\int {\mid \nabla f\mid }^2\mathit{dxdy},$$ (11)

if, for instance, lim_(x,y)→∞ f = 0 so that the surface terms may be ignored. These considerations show that the CGS penalty is analogous to more classical smoothing penalties on the spatial derivatives. Indeed, for the case when λ_tr = 0, the CGS penalty reduces to a purely local spatial smoothing.

A. Estimation of Regularization Parameters

The CGS method requires estimation of the regularization parameters λ_loc and λ_tr describing the relative importance of the local and nonlocal components of the graph. There is a very wide literature on criteria for estimating regularization constants, two common approaches being the L-curve analysis [32] and generalized cross validation [33]. Additionally, the restricted maximum likelihood (ReML) method provides another, statistically motivated approach for estimating regularization constants, which has been used previously for combining multiple weighting matrices for the weighted minimum norm approach for EEG source estimation [34], [35].

We have explored the use of generalized cross validation, but have found it to lead to overestimated parameters. We have instead pursued a modified L-curve approach. We first describe the L-curve method for determining a single regularization parameter for the variational problem

$$J^{\ast }(\lambda )=\underset{J}{\text{argmin}}{\Vert KJ-\varphi \Vert }^2+\lambda J^{T}LJ.$$ (12)

In this case, the L-curve is consists of the points defined by γ(λ) = (ρ(λ), η(λ)), where ρ(λ) = ||KJ^*(λ) − φ||² and η = J^*(λ)^T LJ^*(λ). This curve typically displays a characteristic L-shape, typically one chooses λ corresponding to the highest value of the curvature of γ.

For our problem, we first rescale the ρ and η axes before computing the curvature. We do this by setting ρ_s = ρ/ρ_max and η_s = η/η_max where ρ_max = lim_λ⃗∞ ρ(λ) and η_max = lim_λ⃗0 η(λ). We then define the (rescaled) curvature κ_s(λ) according to

$${\kappa }_s(\lambda )=\frac{{\rho }_s^{\prime }{\eta }_s^{″}-{\rho }_s^{″}{\eta }_s^{\prime }}{{({\rho }_s^{\prime 2}+{\eta }_s^{\prime 2})}^{3/2}}.$$ (13)

We have developed a modified L-curve procedure enabling estimation of multiple regularization constants. Similar in spirit to coordinate ascent, this approach proceeds by alternately fixing all regularization constants but one, then maximizing the curvature in terms of the single “active” regularization constant. We note that other authors have explored extensions of the L-curve to multiple parameters using alternative approaches: [36] constructs a multidimensional L-hypersurface and maximizes Gaussian curvature, while [37] relies on minimizing a simpler surrogate functional measuring distance from the L-hypersurface to a shifted origin.

We describe our modified L-curve approach for the case of N regularization constants λ⃗ = (λ₁, λ₂, …_N). For convenience, we write $\overrightarrow{{\lambda }_i^c}=({\lambda }_1,\mathrm{..},{\lambda }_{i-1},{\lambda }_{i+1},\mathrm{..}{\lambda }_N)$. The CGS solution (corresponding to N = 2) is given by

$$JJ(\overrightarrow{\lambda })={\left(K^{T}K+\sum _{i=1}^N{\lambda }_i{L}_i\right)}^{-1}{K}^T\phi .$$ (14)

The axes of the N separate L-curves are given by the univariate functions ${\rho }_i({\lambda }_i;\overrightarrow{{\lambda }_i^c})={\Vert KJ(\overrightarrow{\lambda })-\phi \Vert }^2$ and ${\eta }_i({\lambda }_i;\overrightarrow{{\lambda }_i^c})=J^T(\overrightarrow{\lambda })L_{i}J(\overrightarrow{\lambda })$. We define the rescaled ρ_s,i and η_s,i as above, and use them to define the curvature ${\kappa }_s({\lambda }_i,\overrightarrow{{\lambda }_i^c})$ as in (13). Given some initial values λ⃗⁽⁰⁾ for the regularization constants, we form the update step by choosing ${\lambda }_i^{(n)}$ to maximize ${\kappa }_s({\lambda }_i;{\overrightarrow{{\lambda }_i^c}}^{(n-1)})$. This optimization is performed numerically using a Quasi-Newton optimization algorithm (as implemented by the fminunc routine in MATLAB), which employs an exact analytic expression for the gradient of curvature ${\kappa }_s^{\prime }$. Details of this, depending on analytic formulae for the first three derivatives of η_i(λ) and ρ_i(λ), are given in Appendix A. An outline of the overall algorithm is shown in table III.

Table III.

Pseudocode for Modified L-curve algorithm

Initialize λ⃗(0)

n ← 0

repeat

for i = 1…N do

ρmax,i ← limt→∞ ρi(t)

ηmax,i ← limt→0 ηi(t)

$${\lambda }_i^{(n)}\leftarrow {\text{argmax}}_t{\kappa }_s(t;{\overrightarrow{{\lambda }_i^c}}^{(n-1)})$$

end for

n ← n + 1

until |λ⃗(n) − λ⃗ (n−1)| < ∊tol

We note finally that both the original and modified L-curve methods may be applied to a block of time series data φ(t_n) for n = 1…N_t, by setting ρ(λ) = Σ_n ||KJ^*(λ, t_n) − φ(t_n)||² and η(λ) = Σ_n J^*(λ, t_n)^T LJ *(λ, t_n), where J*(λ, t_n) is defined by 12 with φ = φ(t_n). This gives regularization constants that do not vary with time, that are well adapted for the data over the entire time window. We will use this approach for our later experimental results.

V. Experimental Validation

Evaluating the performance of any new source estimation method is challenging because of the lack of ground-truth knowledge of the true underlying cortical activity. One approach to evaluating source estimation performance is to examine the source estimates for an experimental paradigm where it is well established from prior neuroscience knowledge where the expected sources should be found.

In this work, we assess the performance of the proposed CGS method by investigating the quality of its estimated sources for a set of averaged event-related potentials (ERP’s) for a simple button-pushing task. A prominent feature of the ERP in this case is the motor potential (MP), a focal contralateral surface negativity occurring 10–180 ms before the recorded button press [38]. The MP is generated by activity in the motor cortex associated with hand movement, specifically in the “hand knob” which can be reliably identified in MRI imaging [39]. It is precisely this feature of the motor potential experimental paradigm which allows us to use the location of an identifiable anatomical feature (the hand knob) as a proxy for the unknown ground truth cortical activity in order to evaluate the quality of the source estimates. We thus expect source estimates for this motor ERP to show a salient, localized peak near the hand knob, during the expected time range. In particular, the relative intensity of this peak, as well as its distance from the hand knob, can be used as quantitative measures of algorithm performance.

We compare the source estimation results from CGS against a suite of comparison source estimation methods that are widely used, namely the minimum norm (MN), weighted minimum norm (WMN), low resolution electrical tomography (LORETA) and standardized low resolution brain brain electromagnetic tomography (sLORETA) approaches.

A. Motor potential task paradigm

In this study, collected at the University of Oregon, subjects had EEG acquired with a 256-channel HydroCel Geodesic Sensor Net (Electrical Geodesics, Inc.). Recordings were referenced to Cz, and bandpass filtered (0.1–100Hz) prior to being sampled at 250 Hz with a 16-bit ADC. During the study, subjects were asked to fixate on a visual crosshair, and then push a button with a single finger (right/left thumb/pinky) when the crosshair changed color. The finger conditions (RT,LT,RP,LP) were organized in separate blocks, data was collected for long enough ( 2 hrs) to ensure at least 100 trials per condition. Data presented in this work were collected on a set of 18 subjects.

Following collection, the data were bandpass filtered (pass-band 3–10 Hz) in order to accentuate the known spectral characteristics of the desired MP signal. Further postprocessing consisted of identification and removal via interpolation of bad channels, segmentation of the EEG based on timing of the recorded button press, and averaging over the extracted segments to generate the motor ERP.

B. Image data collection

The MR imaging was acquired on a Siemens Allegra MRI scanner. Our protocol includes a high-resolution 1 mm³ T1-weighted image used to construct the subject-specific head model for EEG source localization and to construct the cortical surface meshes. The T1 image was acquired with a matrix size of 256 × 256, 160 slices, TR=2500 ms and TE=4.38 ms. Our imaging protocol also includes a diffusion-weighted acquisition consisting of 10 unweighted (b = 0) images and 60 gradient weighted images at b = 700s/mm² with a matrix size of 128 × 128, 60 slices, 2 × 2 × 2mm³ cubic voxels, TR=10900 ms and TE=113 ms.

C. Evaluation of Source Estimates

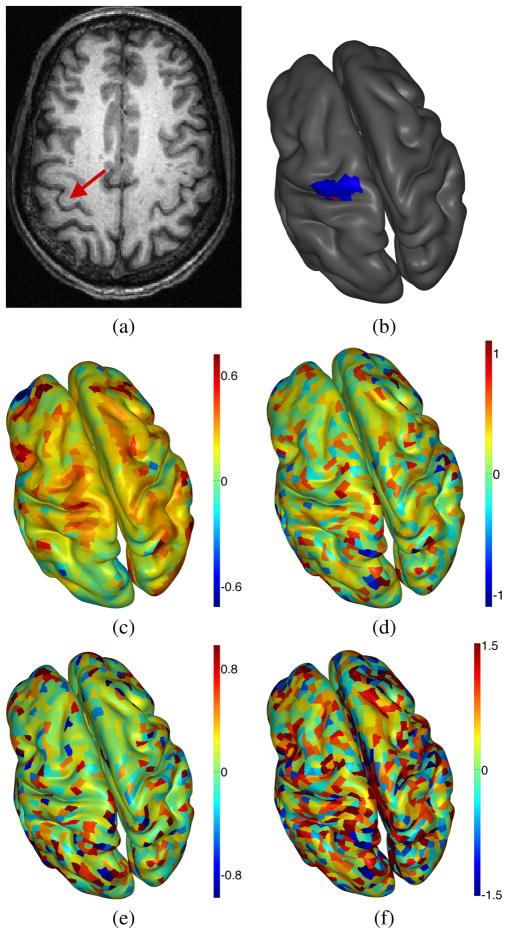
For both the proposed CGS and the comparison methods, we analyze source estimation performance by identifying the largest local maxima of the estimated current sources within a restricted region of both space and time. For the temporal window, we restrict our search for the peak activity to between 10 and 180 ms before the button press. The spatial restriction is described by a spatial region Ω^search near the hand knob, and is constructed as follows. We first determine a single voxel corresponding to the location of the hand knob by inspection of the T1 MRI image (see Figure 2(a) ), following the axial plane approach recommended in [39]. We then hand-select Ω^search for each hemisphere of each subject to consist of patches within the precentral gyrus, containing the closest patch to the hand knob. Over the 36 Ω^search sets defined in this work, the maximum distance from the patch closest to the hand knob was 32 mm (average 23.6 mm, std 3.2 mm). This process is illustrated in Figure 2 (a–b).

Fig. 2.

Comparison of source estimation results, for RP button press condition in a single subject: (a) axial MRI slice showing location of hand knob in left hemisphere, (b) inflated cortical surface showing cortical patch closest to hand knob (red) and hand segmented search region Ω^search (blue), (c) CGS, (d) MN, (e) WMN, (f) sLORETA. All source estimates are shown at −100ms. For (c)–(f), the color-scale is set so that the color-bar maximum is equal to 1.2 times the maximum absolute value of the source estimates within Ω^search. Note the clearer, more salient peak near the hand-knob for the CGS method.

For convenience, in the following we let X ∈ {CGS, MN, W MN, LORET A, sLORET A} index the different source estimation methods to be compared. Given the ERP time series φ(t_n), we compute (non time-varying) regularization constants for method X by using the modified L-curve method applied to all φ(t_n) from the time window defining Ω_search. We then compute time series of source current estimates J_X (t_n) by applying method X to each timepoint.

Let J_X (k, n) = (J_X (t_n))_k be the estimate for method X at dipole k and timepoint n. We say that J_X has a magnitude local spatial maximum at patch k at timepoint n if |J_X (k, n)| ≥ |J_X (r, n)| for all dipoles r adjacent to dipole k. For the methods employing the cortical surface-normal dipoles (CGS, MN, WMN and sLORETA), this adjacency relation is encoded by the local adjacency matrix A^loc detailed in section III-D, as r is adjacent to k iff A^loc(r, k) > 0. In contrast, for the LORETA method which employs a 3D grid of volumetrically defined dipoles, we use the standard 6-neighbor adjacency on the 3D grid.

For all methods, we first find the set of all magnitude local spatial maxima for all timepoints between 10 and 180 ms before the button press. For each such peak, we define the peak-RMS ratio ρ^rms(k, n) as |J_X (k, n)|/p(n), where $p(n)={\left(\frac{1}{N_d}{\sum }_k{J}_X{(k,n)}^2\right)}^{1/2}$. We then select k^* and n^* as the patch index and timepoint corresponding to the peak with the largest value of ρ^rms, so that k^* and n^* represent an estimate of the location and time of the peak MP source.

We use ρ^rms as a quantitative measure of the quality of the source estimate. For convenience, let ${\rho }_X^{\mathit{rms}}$ be the value of ρ^rms(k^*, n^*) at the identified peak of the rms-normalized source estimate for method X. Note that due to the normalization by the rms power p(n) which varies at each timepoint n, it may not necessarily be the case that |J_X (k*, n*)| ≥ |J_X (k, n)| for all n, k in the spatiotemporal search window.

Additionally, we compute the estimated localization error d^hk(k^*) to be the Euclidean distance from dipole k^* to the hand knob. Define $d_X^{hk}$ to be this distance for the source estimate given by method X. We will say that method A has better localization than method B, for a particular subject and task condition, if $d_A^{hk}<d_B^{hk}$. Note that for comparisons between methods using the same set of distributed dipoles (e.g. for comparisons amongst CGS,MN,WMN and sLORETA using the cortical surface-normal dipoles), ties may occur when the located peak dipole k^* is the same for both methods.

D. Results

For all of the source estimation methods considered, we have evaluated the hand-knob distance d^hk and the peak-RMS ratio ρ^rms, over a total of 72 different ERP’s (18 subjects under each of the 4 different finger task conditions). These results are shown in Table IV. In addition to tabulating the mean and median of these two quantitative measures, we indicate the number of times each comparison method performs better (e.g. higher ρ^rms or lower d^hk) or performs worse than the CGS method.

TABLE IV.

Summary of source estimation performance over 72 ERPs (18 subjects, 4 task conditions), as measured by the hand-knob distance d^hk and the peak-RMS ratio ρ^rms for the cortical graph smoothing (CGS), and comparison methods. Reported p-values are for the signed-rank test for the median of each method differing from the median of the CGS method.

	CGS	MN	WMN	LORETA	sLORETA
mean dkh	16.32	18.32	17.39	15.66	16.09
median dkh	16.84	18.45	17.23	15.31	15.68
# better/tied/worse than CGS (by dhk)	0/72/0	19/18/35	26/13/33	34/0/38	36/7/29
dhk SR test p-value (comparing to CGS)	1	0.00234*	0.158	0.504	0.613
mean ρrms	2.42	2.41	2.19	0.97	1.70
median ρrms	2.11	1.85	1.69	0.76	1.47
# better/tied/worse than CGS (by ρrms)	0/72/0	31/0/41	25/0/47	5/0/67	18/0/54
ρrms SR test p-value (comparing to CGS)	1	0.432	0.0156*	7.4e–13*	4.31e–06*

The CGS result gives lower hand-knob distance than the minimum norm method, and similar hand-knob distances to the remaining comparison methods. When compared against the MN method, CGS produced peak dipole locations that were as close or closer to the hand-knob location on 53 of 72 ERP’s, while against the other comparison methods CGS produced lower hand-knob distances roughly half the time. We have more carefully quantified this comparison by a series of Wilcoxon signed rank tests [40], to investigate whether the medians of the CGS and the comparison methods differ. As can be seen in Table IV, the CGS method produced statistically significantly lower hand-knob distance median than the MN (p=.002), whereas the difference between the CGS and the other comparison methods did not appear statistically significant.

Complementary results are seen for the comparison based on the peak-RMS ratio ρ^rms. In this case, the MN and CGS methods have similar median values for ρ^rms, while the CGS method performs significantly better than the WMN, LORETA or sLORETA methods. As measured by the signed-rank test, the statistical significance of the difference between CGS and the LORETA and sLORETA methods is especially strong. These results are important as the confidence and interpretability of an observed local peak is stronger if the peak is highly salient. Taken together, these two quantitative measures demonstrate that the CGS method is competitive with, and often superior to, several widely used source estimation methods.

We show source estimates from a single subject illustrating these differences in Figures 2 and 3, for the RP button press condition. In Figure 2, we display the CGS, MN, WMN and sLORETA source estimates at 100 ms before the button press. Additionally, we illustrate the point identified as the hand-knob location, and show the Ω^search region for the contralateral (left) hemisphere. For this ERP, these four methods all show a peak near the hand-knob. For visualization purposes, we chose the color-axis scaling such that the color-bar maximum is equal to 1.2 times the maximum absolute value of the source estimates within Ω^search. Accordingly, the peak near the hand-knob appears with similar coloring in all of these figures. Due to the color-axis scaling the comparison methods showing a low relative peak saliency (i.e. low ρ^rms) exhibit larger, “noisier” looking source estimates elsewhere on the cortical surface. In contrast, the peak for the CGS method appears much more salient than the surrounding activity than the other methods shown. While only a single ERP is shown due to space limitations, we have found this qualitative comparison typical across the rest of the data considered in this work. Finally, we note that these results are shown on inflated cortical surfaces for visualization purposes; the cortical inflation was not used for the computation of the source estimates.

Fig. 3.

LORETA source estimates, displayed at the volumetric dipole locations. (a) Locations of dipoles within Ω^search for volumetric dipole set (blue), and volumetric dipole closest to hand-knob (red); (b) Magnitude of LORETA source estimates. While this method does show a local maximum within Ω^search, observe that the peak is much less salient than for the CGS method.

Results for LORETA are displayed on the volumetric dipole set, where each volumetric dipole location is rendered as a single sphere, in Figure 3. While the results are somewhat harder to see visually than those displayed on the inflated cortical surfaces, LORETA does show a small local maximum within the volumetric Ω^search. However, the saliency of this peak is much lower than that of the CGS method, as is consistent with the significantly lower median value for ρ^rms observed for LORETA.

As the CGS approach employs the hybrid local/nonlocal connectome matrix, it is natural to ask which of these two components contribute most to the observed performance. We have explored this question by examining two restricted CGS methods, one employing only the local connectome (LOC-ONLY) and one employing only the tractography based connectome (TR-ONLY)². Results are given in table V. As can be seen, the LOC-ONLY method performs worse than CGS in terms of both localization error and saliency, by these measures the LOC-ONLY performance is similar to that of the WMN method. Interestingly, the TR-ONLY method shows a lower median localization error than CGS (though not statistically significant), but also a statistically significantly lower saliency. Taken together, these show that the tractography-based connectome is definitely an important contributor to the performance of the CGS method, but that both local and tractography-based components are important.

TABLE V.

Comparison of CGS to restricted CGS solutions using only local (LOC-ONLY) or only tractography-based (TR-ONLY) connectomes.

	CGS	LOC-ONLY	TR-ONLY
mean dkh	16.32	17.85	15.38
median dkh	16.84	17.89	16.25
# better/tied/worse than CGS (by dhk)	0/72/0	13/27/32	35/14/23
dhk SR test p-value (comparing to CGS)	1	0.018*	0.26
mean ρrms	2.42	2.13	1.93
median ρrms	2.11	1.98	1.53
# better/tied/worse than CGS (by ρrms)	0/72/0	27/0/45	27/0/45
ρrms SR test p-value (comparing to CGS)	1	0.0168*	0.0179*

VI. Conclusions

We have introduced a novel approach for EEG source estimation which uses a prior penalty on cortical activity based on anatomical connectivity derived from white matter fiber tractography. After constructing the cortical connectome graph with vertices identified with cortical patches, we defined a graph smoothing prior which penalizes the weighted sum of squares of differences in source activity across the edges of the graph. In combination with a quadratic data fidelity term, this penalty leads to a closed-form linear source estimate we call the cortical graph smoothing (CGS) method. We have illustrated its performance on estimating motor potential sources in a button-pressing task, and compared it to the minimum norm, weighted minimum norm, LORETA and sLORETA methods, employing quantitative measures of localization accuracy and peak saliency. We have found the CGS approach to give statistically significantly improved localization accuracy relative to the minimum norm, and equivalent localization accuracy to the remaining comparison methods. In contrast, the peak saliency is significantly greater for the CGS approach than all the comparison methods except the minimum norm, which shown similar saliency.

The benefits of combining the EEG source localization with the anatomical connectivity were demonstrated by utilizing connectivity matrices computed from DTI tractography. This model is well known to be an oversimplification of the white matter architecture. Particularly, DTI is unable to represent overlapping, interdigitated, fanning or crossing fascicles. Our framework could, however, be very easily extended to employ connectivities computed from tractography performed with other techniques proposed to overcome the limitation of DTI, such as Multiple fascicle models [41], [42], DSI [43], Q-Ball [44] or Constrained Spherical Deconvolution [7]. To the extent that the good performance of the CGS reflects correct representation of the underlying anatomical connectivity, we believe that the CGS approach should show improvement when based on connectome matrices utilizing more accurate tractographic methods. However, exactly how much improvement could be gained is an open question for further research.

Similarly, the underlying structure of the CGS is not dependent on the particular set of tissue segmentation and head model physics tools that were employed. While we have used proprietary, in-house tools specifically developed for the overall tissue segmentation and forward modeling workflow, there is no fundamental obstacle for many of these steps to be done with more openly available software (e.g. freesurfer ).

There are many opportunities for future research extending the CGS methodology described here. As the CGS estimate (10) uses scalp voltages ϕ defined at a single timepoint, it does not exploit temporal regularity of the underlying brain activation. In future work we will incorporate temporal smoothness into the CGS penalty by constructing a spatiotemporal connectome graph. The vertices of this augmented spatiotemporal connectome graph may be formed as the union of multiple copies of the vertex set, taking one such copy for each timepoint. In this way, the spatiotemporal vertices would be indexed by both cortical patch number and by timepoint. Edges of the spatiotemporal graph could be constructed by connecting each spatiotemporal vertex to its appropriate neighbors at the same timepoint, and in addition connecting each spatiotemporal vertex to the vertices representing its immediate temporal neighbors (i.e. the two vertices representing the same cortical patch, but at the previous and following timepoints). Using the same CGS approach with this augmented spatiotemporal graph would introduce a penalty on time derivatives of the source currents, yielding a joint spatiotemporal estimation procedure.

The CGS method described in this work used a purely corticocortical connectome graph. Ignoring subcortical structures, in particular the thalamus, gives an incomplete representation of brain connectivity. While the activation of subcortical structures does not directly contribute to observed EEG (as they lack the laminar organization necessary to generate coherent dipolar currents), it may influence cortical activity and thus indirectly affect the EEG. Incorporating such effects within the CGS framework will be considered in future work.

Finally, while the CGS penalty in this paper was used only for EEG analysis, the fundamental idea of exploiting anatomical connectivity to build source activity priors may be applied to other functional imaging modalities. Extending CGS to use with MEG would be very straightforward, a more interesting challenge would be to investigate its use for estimating fMRI activation.

APPENDIX A Computation Of Derivatives For L-Curve

Our optimization of the curvature function κ_s employs analytic formulae for derivatives of the L-curve coordinates ρ_i and η_i. Straightforward differentiation of (13) yields

$${\kappa }_s^{\prime }=\frac{({\eta }_s^{\prime 2}+{\rho }_s^{\prime 2})({\eta }_s^{\prime }{\rho }_s^{‴}-{\rho }_s^{\prime }{\eta }_s^{‴})-3({\eta }_s^{\prime }{\rho }_s^{″}-{\rho }_s^{\prime }{\eta }_s^{″})({\eta }_s^{\prime }{\eta }_s^{″}+{\rho }_s^{\prime }{\rho }_s^{″})}{{({\eta }_s^{\prime 2}+{\rho }_s^{\prime 2})}^{5/2}}$$ (15)

showing that ${\kappa }_s^{\prime }$ may be computed from the first three derivatives of ρ_s and η_s. Assuming i indicating the active constant λ_i is fixed, we write λ = λ_i, L = L_i, and H = Σ_j≠i λ_j L, so that the CGS estimate (as a function of the active constant λ) is J(λ) = (K^T K + H + λL)⁻¹K^T φ. We write N = (K^T K + H + λL)⁻¹. The L-curve coordinates are then η(λ) = J(λ)^T LJ(λ) and ρ(λ) = ||KJ(λ) − φ||².

We develop expressions for the unscaled derivatives ρ^(k), η^(k) for k = 1, 2, 3; scaled derivatives are then given by ${\rho }_s^{(k)}={\rho }_s^{(k)}/{\rho }_{\mathit{max}},{\eta }_s^{(k)}={\eta }_s^{(k)}/{\eta }_{\mathit{max}}$. As ρ (λ) = (KJ −φ)^T (KJ −φ) is dependent on λ only through J, we may compute

$$\begin{array}{l}{\rho }^{\prime }=2{(KJ-\phi )}^{T}K{J}^{\prime }\\ {\rho }^{″}=2{(KJ-\phi )}^{T}K{J}^{″}+2{(K{J}^{\prime })}^{T}K{J}^{\prime }\\ {\rho }^{‴}=6{(K{J}^{\prime })}^{T}K{J}^{″}+2{(KJ-\phi )}^T{J}^{‴}\end{array}$$ (16)

and

$$\begin{array}{l}{\eta }^{\prime }=2J^{T}L{J}^{\prime }\\ {\eta }^{″}=2{J^{\prime }}^{T}L{J}^{\prime }+2J^{T}L{J}^{″}\\ {\eta }^{‴}=6{J^{\prime }}^{T}L{J}^{″}+2J^{T}L{J}^{‴}.\end{array}$$ (17)

Completion of these expressions relies on computing derivatives of J = NK^T φ. Using the formula for differentiation of matrix inverse [45]

$$\frac{\partial Y^{-1}}{\partial x}=-Y^{-1}\frac{\partial Y}{\partial x}{Y}^{-1}$$ (18)

we see

$$\frac{\partial N}{\partial \lambda }=-\mathit{NLN}.$$ (19)

Repeated differentiation and use of 19 yields

$$\begin{array}{l}{J}^{\prime }=-{\mathit{NLNK}}^T\phi =-\mathit{NLJ}\\ J^{″}=2{\mathit{NLNLNK}}^T\phi =2{(NL)}^{2}J\\ J^{‴}=-6{\mathit{NLNLNLNK}}^T\phi =-6{(NL)}^{3}J\end{array}$$ (20)

Inserting the relations from (20) into (17) and (16) yields the desired closed-form expressions for ρ^(k) and η^(k).

We note finally that the full statements of these exact expressions involve multiple matrix multiplications. Naive left-to right matrix multiplication for these expressions can yield very inefficient computation. Additionally, explicitly forming the inverse matrix N is inadvisable for reasons of both numerical accuracy and computational efficiency. The actual scheme used to compute these expressions employed judicious use of order of matrix multiplication, saving of partial results, and use of Gaussian elimination in lieu of explicit forming and multiplying by N, to enable more efficient evaluation.

APPENDIX B PARALLEL TRACT COMPUTATION

Computing the whole-brain tractography as described in section III-B produces millions of tracts (mean N_tracts = 3.65×10⁶, stdev = 7.9×10⁵, averaged over 18 subjects), and is computationally demanding. With the parameters used in this work, the tractography required 2.5 days to complete when running on a single cpu core (2.6 GHz Intel Xeon). We have implemented a simple scheme for parallelizing this computation across multiple 12-core nodes of the ACISS system³ at the University of Oregon, a large heterogenous computational cluster consisting of approximately 200 nodes each of which have 12 or 36 cpu cores. We achieved this parallelism in two stages, first via a multithreaded implementation of the tractography capable of exploiting all 12 cores on a single node. We then achieved parallelism across nodes by dividing the binary mask image indicating the seed voxels into N pieces, running the multicore tractography in parallel on N separate nodes, and later combining the output tracts. For the results in this paper we used N = 50 nodes, giving an overall speedup of 600x relative to a single core, and allowing the tractography to complete in under 5 minutes.

APPENDIX C COMPARISON SOURCE ESTIMATION METHODS

For completeness, we briefly describe the details of the comparison source estimation methods used in this work. The MN, WMN and LORETA methods, as well as the proposed CGS method, can all be described as variational approaches using quadratic regularization. In particular, these methods all solve the minimization

$$J^{\ast }=\underset{J}{\text{argmin}}{\Vert \phi -KJ\Vert }^2+\lambda J^{T}WJ,$$ (21)

with linear solution

$$J^{\ast }={(K^{T}K+\lambda W)}^{-1}{K}^T\phi ,$$ (22)

and differ only in their choices for the matrix W.

This implies that optimal regularization constants for MN, WMN and LORETA can be determined by the (unmodified) L-curve method described in section IV-A, we have used this approach for all the results in this paper.

1. Minimum Norm: The minimum norm method (also known as ridge regression or Tikhonov regularization in the wider statistical literature) is given by taking W to be the identity matrix, so that the regularization term is simply proportional to the sum of squares of J.

2. Weighted Minimum Norm: The weighted minimum norm takes W to be diagonal, but with varying values so that the squares of different dipole sources may be weighted differently. While different weightings can be used, we follow the approach described in [1] with weights given by the reciprocal of the sum of squares of each dipoles projection onto the electrodes, i.e. $W_{j,j}={({\sum }_i{K}_{i,j}^2)}^{-1/2}$. This procedure is motivated by the desire to undo bias towards superficial sources, which is a known drawback of the minimum norm.

3. LORETA: The LORETA method [46] employs regularization based on the 3D discrete Laplacian operator, but also using lead-field matrix normalization as seen for the WMN. Because of this use of the 3D discrete Laplacian, LORETA is defined for volumetric dipoles and is not applicable to the cortical surface-normal dipole sets used elsewhere in this work. For LORETA, W = E^T D^T DE, where D corresponds to the Laplacian operator and E is a diagonal matrix corresponding to the lead-field matrix normalization. E is constant over triples of indices corresponding to each dipole. It be written using the Kronecker product as E = Ẽ ⊗ I₃, where the N_d×N_d diagonal matrix Ẽ is given by

   $${\stackrel{\sim }{E}}_{k,k}={\left(\sum _{i=1}^{N_e}\sum _{j\in \eta (k)}{K}_{i,j}^2\right)}^{-1/2},$$

   η (k) = {3k – 2, 3k – 1, 3k} are the indices for the x, y, z components of the k^th dipole, and K is the N_e × 3N_d lead-field matrix. Similarly, D is specified by D = D̃ ⊗ I₃ where D̃ is the matrix for the 3D discrete Laplacian operator employing a 7-point stencil.

4. sLORETA: The sLORETA approach [47] differs from the previous methods in that it is not given as the solution to a variational problem with quadratic regularization. Despite the similarity in name to LORETA, sLORETA is instead based on taking the result from the minimum norm solution, and standardizing each estimated dipole. This is done by dividing by the expected variance of the minimum norm estimates for each dipole, under the assumption that the unknown sources each have unit variance. The sLORETA estimate is given by $J_{\mathit{sloreta}}^{\ast }={ST}_{mn}\phi$, where T_mn = (K^T K + λI)⁻¹K^T is the linear estimator for the minimum norm solution. The standardization is performed by the diagonal matrix S given by $S_{i,i}=C_{i,i}^{-1/2}$, for C = T_mnK. For the sLORETA, we use the same regularization constant as was computed to be optimal for the minimum norm solution.