Abstract
A wide variety of cell biological and biomimetic systems use actin polymerization to drive motility. It has been suggested that an object such as a bacterium can propel itself by self-assembling a high concentration of actin behind it if it is repelled by actin. However, it is also known that it is essential for the moving object to bind actin. Therefore, a key question is how the actin tail can propel an object when it both binds and repels the object. We present a physically consistent Brownian dynamics model for actin-based motility that includes the minimal components of the dendritic nucleation model and allows for both attractive and repulsive interactions between actin and a moveable disk. We find that the concentration gradient of filamentous actin generated by polymerization is sufficient to propel the object, even with moderately strong binding interactions. Additionally, actin binding can act as a biophysical cap, and may directly control motility through modulation of network growth. Overall, this mechanism is robust in that it can drive motility against a load up to a stall pressure that depends on the Young’s modulus of the actin network and can explain several aspects of actin-based motility.
Keywords: actin, motility, ActA, self-assembly, self-diffusiophoresis
1. Introduction
Actin-based motility is ubiquitous in cell biology [1], and drives processes such as lipodial protrusion during cell crawling [2, 3], motility by the infectious bacteria Listeria monotocytogenes [4–6] and Shigella exneri [7, 8], transit of viruses through cells [9, 10], and trafficking of vesicles [11] and organelles [12]. In these examples, motility involves at least hundreds of actin filaments and requires a many-filament approach to understanding the physical mechanism underlying motility. Such a mechanism, known as the “self-diffusiophoretic” mechanism, has been suggested [13]. Through this mechanism, actin network growth leads to a concentration gradient, so that the actin concentration is higher behind the moving object than in front of it. This leads to motion of the object down the concentration gradient if the object is repelled by actin. However, it is known that actin binds to proteins on the moving object [8, 14, 15], leading to attractive interactions between the object and actin. The existence of attractions would appear to invalidate the self-diffusiophoretic mechanism. In this paper, we show that this is not the case, actin binding does not disrupt the self-diffusiophoretic mechanism at reasonable binding energies and densities. In addition, we find that if actin binding at the surface caps growing ends, it regulates motility by slowing network growth, rather than by resisting forward motion.
The biochemical components of actin-based motility have long been understood through the dendritic nucleation model [16, 17]. Although the full biochemistry of cell crawling by the dendritic nucleation model has many components, in vitro experiments have shown that only a few ingredients are essential to actin-based propulsion [18–21]. Actin polymerizes into filaments of F-actin by adding monomers of G-actin to the “barbed” ends of filaments. The protein Arp2/3 is activated near the object by actin-binding proteins such as ActA or WASP, and Arp2/3 in turn mediates branching of filamentous F-actin, creating additional growing barbed ends. Turnover is accelerated by cofilin, which severs actin filaments, generating additional barbed ends and enhancing disassembly. Further from the moving object, capping proteins halt barbed end growth and depolymerization occurs at the “pointed” ends of filaments. The result is a dynamic, branched actin network that polymerizes near the moving surface and disassembles at the trailing edge of the actin network (the end of the tail or rear of the lamellipodium). Altogether, these biochemical components lead to motion of the object [3, 16, 17]. The physical mechanism by which motion is generated is the subject of this paper.
Actin polymerization may occur within a moving object, such as during cell crawling, when it generates the lamellipodium, a branched actin network at the leading edge of the cell [3, 22]. Alternatively polymerization can occur outside the object, such as when Listeria grows a trailing actin network called the “comet tail” [4, 6, 23]. This has been demonstrated not only for biological objects such as the membrane at the leading edge of a crawling cell or a Listeria bacterium, but also for polystyrene beads [18, 21] and disks [24], oil droplets [25], and lipid vesicles [26, 27].
Many models have been proposed to explain actin-based motility, including the single-filament Brownian ratchet model [28–30], the continuum gel model [31, 32], and a variety of others [33–38]. Recently, it was suggested that the mechanism relies on the generation and maintenance of a steady-state F-actin concentration gradient [13]. Since polymerization activity is very high behind the moving surface and far lower elsewhere [17], there is a gradient of F-actin so that the actin concentration is higher behind the object than in front of it. A short-ranged repulsive interaction (for instance, due to excluded volume or screened Coulomb interactions) suffices to drive the object towards lower concentrations of F-actin, down the concentration gradient. According to this model, actin-based motility is an example of self-diffusiophoresis [13, 39], a phenomenon in which a particle generates around itself a concentration gradient that induces a steady-state, fluid flow which propels the particle [40–42].
However, the fact that F-actin not only repels the object but also locally attracts it at the sites of actin-binding proteins such as ActA or WASP [8, 14, 15] poses a major challenge to this model. Since the self-diffusiophoretic mechanism relies on repulsive interactions, these attractive interactions could, in principle, disrupt or destroy concentration-gradient-mediated propulsion. It is therefore important to investigate whether the many-filament model proposed in [13] is truly viable with actin-binding proteins such as ActA.
Here we extend the model of [13, 39] to include local binding interactions between the moving object (a disk) and actin. We find that binding interactions do not destroy the self-diffusiophoretic mechanism, and indeed, have little effect on motility up to reasonably large binding energies or binding site densities. In addition, binding interactions provide a novel mechanism for control of motility through the modulation of actin network growth. We show that the material properties of the F-actin network provide robustness against opposing loads even in the presence of actin binding to the object, consistent with experiments. Our simulations demonstrate that self-diffusiophoresis must exist in actin-polymerization-driven systems even if other phenomena [28–38] might come into play.
2. Methods and Model
Our Brownian dynamics simulations are similar to those in [13, 39], but they have been adapted to effectively model actin-based motility with specific binding between a motile disk and F- and G-actin subunits. As in [13, 39], some of the model parameters differ from experiments (see Table 1 for details) so that simulations can be completed within a reasonable time. However, in contrast to other simulated models [43–47], our model is physically consistent in that it conserves mass. This is important because the violation of mass conservation can lead to motility as an artifact.
Table 1.
Values of the parameters used in the simulations compared to those in experiments. All values listed are taken from in vitro experiments except for the ones marked with (*). All simulated parameters except for K+; K−; kC+; Kd; and ρActA were chosen to match those of previous studies [13, 39]. K+ was set by the additional polymerization constraint of aligning subunit polarization vectors (see Methods and Model); we decreased K− and kC+ to compensate for the reduced polymerization rate. ρActA was chosen to cover the experimental range of ActA densities, and also to explore the full range of behaviors of our model. ε was estimated from [81] which estimates 10–40 active binding sites per bacterium and a total bacterium binding energy of 10 kcal/mol (order 10 kBT per bacterium).
| Parameter | in vitro Exp. [ref] | Simulated |
|---|---|---|
| ℓp | 0.5–17.7 µM [90–94] | 0.1 µm |
| lave | 0.1–1 µm [95, 96]* | 0.1 µm |
| typical bead diameter | 0.2–2 µm [51] | 0.1 µm |
| viscosity (η) | 2.4 cP [51] | 2.4 cP |
| D = kBT/3πηa | 36.6 µm2/s | 36.6 µm2/s |
| K+ | 11.6 µM−1s−1 [17, 97] | 50 µM−1s−1 |
| K− | 0.3 s−1 [17, 97] | 2860 s−1 |
| [G-Actin] (initial) | 7 µm [20] | 600µM |
| [G-actin] (steady state) | 8.5 µM [65]* | 370µM |
| K+[G-Actin]/K− (initial) | 270 | 11 |
| Ka | ?µM−1s−1 | ~ K+ |
| Kd | 0.002 s−1 [98] | 2860 s−1 |
| [Arp2/3] | 0.1 µM [20] | 2.1 µM |
| Ka[Arp2/3]/Kd | N/A | 0.037 |
| KC+ | 8 µM−1s−1 [79] | — |
| KC− | 4· 10−4 s−1 [79, 99] | 0 s−1 |
| [Cap] | 0.1 µM [20] | — |
| kC+ = KC+[Cap] | 0.8 s−1 | 1570 s−1 |
| ρActA | 0.3–2.1 per 100 nm2 [56, 57] | 0–2.6 per 100 nm2 |
| ε | Few kBT [81]* | 0–16 kBT |
At the start of the simulations, a moveable disk of radius 10a and thickness a is placed at the center of the simulation box and actin subunits of diameter a are distributed randomly throughout the box. A small percentage of the actin subunits are initially joined together as dimers, whose barbed ends may polymerize to form F-actin filaments. Arp2/3 point particles are released from the back of the disk, facilitating additional network growth through side-on branching. Both the F-actin network and G-actin subunits interact with the disk through repulsive excluded volume interactions and short-ranged and localized attractive interactions with actin binding sites on the back of the disk. The binding sites attract actin to the disk, but unlike ActA and WASP in experimental systems [19, 48], do not enhance Arp2/3 or actin-polymerization activity. In order to simplify the analysis and obtain results for small system sizes, the disk is constrained to to move only in the z-direction, as shown in figure 1(a)-(b). Relaxing this constraint should not alter conclusions about the viability of motility, which is the subject of this paper. However, we fully expect that if we were allow the disk to move freely in all directions, our model would lead to the complicated trajectories observed and studied previously [49, 50], due to spatial fluctuations in the distribution of binding sites. The simulation takes place in a 40a × 40a × 80a box with periodic boundary conditions on all sides.
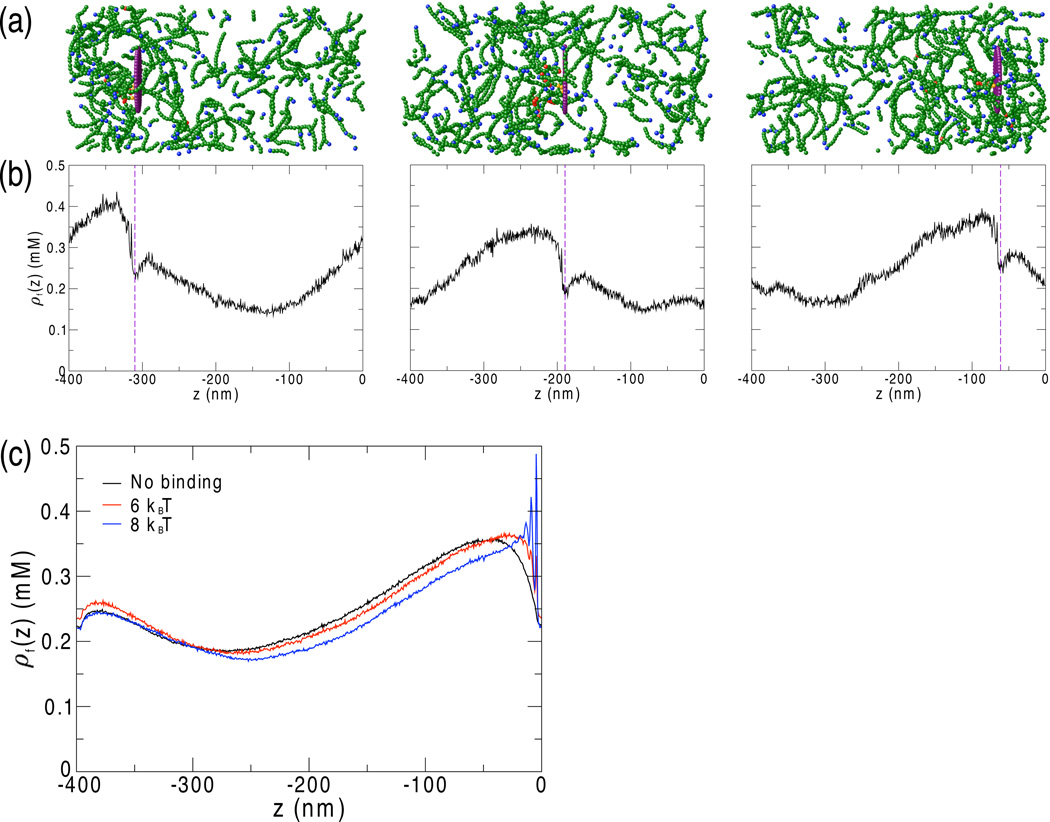
Figure 1.
(a) F-actin (green) accumulates behind the disk (purple). Pointed ends are shown in blue, bases of actin branches are shown in red, and subunits attached to the disk are shown in orange. For clarity, G-actin is not displayed. The system shown has 50 6 kBT binding sites randomly distributed on the back of the disk (ρActA = 0.64 per 100 nm2). Axes and scale match those of panel (b), below. (b) The F-actin concentration profile along the z-direction is potted at times corresponding to the snapshots shown above in (a). As described in [13], Arp2/3-mediated F-actin polymerization generates a concentration gradient of F-actin behind the disk. As the disk moves forward, F-actin continues to polymerize behind the disk so that the concentration gradient moves forward as well, maintaining the mechanism of motility. (c) In the center of mass frame of the disk, which is located at z = 0, the concentration gradient has a well-defined steady-state average that depends on the binding energy.
2.1. Units
We convert simulation units into physical units by taking the actin subunit length to be a = 5 nm and the diffusion coefficent to be D = 36.6 µm2/s. This gives a viscosity η = 2.4 cP, as measured experimentally in cell extracts [51], and a characteristic time scale τ = a2/D = 0.68 µs. Typically, we use time steps Δt = 0.68 ns and collect data for about 1 s.
2.2. Interactions
All actin subunits are diameter a spheres that interact with each other by a repulsive potential:
| (1) |
where rij is the center-to-center distance between subunits i and j, and KR = 100kBT/a2. A similar soft repulsion acts along the z-direction between actin subunits and the disk (except at the disk edge, where actin may be repelled in the x and y directions). F-actin subunits are bound to neighboring subunits through the bond potential:
| (2) |
where KB = 100kBT/a2. Thus, attractive bond forces are only felt for subunit separations of rij > a and are zero for rij ≤ a. Filaments and branches are given a stiffness by the bending potential [52]:
| (3) |
where KS = 100kBT, θi is an angle between the bond vectors b⃗hi, connecting neighboring subunits h and i, and b⃗ij connecting neighboring subunits i and j, and θ0 is the preferred bond vector angle. For filaments, bond vectors prefer to align, so θ0 = 0°. For branches, the subunits form y-shaped structures with filaments [13], at these “y-junctions,” the bond vectors connect at an angle of θ0 = 70° as observed in experiments [16, 22, 23, 53].
2.2.1. Interactions between actin and disk
In addition to the above interactions from [13, 39], we include specific binding interactions between binding sites on the back of the disk and actin subunits. To do this, we introduce a polarization unit vector, p̂i, for each subunit, i, that points to the “plus” pole of the subunit, thus, each subunit has a preferred spot on its surface for actin-binding site attractive interactions. The polarization vectors tend to align along the direction of the filament bond unit vectors, b̂i−1,i =b⃗i−1,i/|b⃗i−1,i| and b⃗i,i+1 = b⃗i,i+1/|b⃗i,i+1|, through the potential:
| (4) |
where KP = 50kBT and θP = 0°. Actin binding sites are randomly distributed on back of the disk and all actin subunits with the sites through the short-ranged, specific binding potential:
| (5) |
where riα = |r⃗α − r⃗i| is the center-to-center distance between the actin subunit i and binding site α. We vary the binding energy ε in our simulations. C = (σ/a)12−(σ/a)14 is a normalization factor for the binding energy scale. The length sets riα = a as the minimum of the binding potential. Binding site specificity is enforced through the angle, ψiα, which is the angle between p̂i and r⃗iα. The cutoff distance 2a for UA is chosen so that the spatial discontinuity in the energy is small. For riα < a, UA only acts to adjust ψiα. This is done in order to avoid extremely large repulsive forces that would otherwise exist for riα < a. In addition, actin subunits necessarily overlap with the disk when riα < a, and thus repel the disk through the potential in Eq. 1. Forces exerted on the binding sites are exerted on the motile disk.
2.3. Equations of motion
All actin subunits translate and rotate diffusively according to Brownian dynamics [54]. Thus, the evolution of the system is governed by coupled Langevin equations where each particle’s instantaneous velocity is determined by forces exerted by other subunits and thermal forces, F⃗:
| (6) |
| (7) |
and
| (8) |
| (9) |
The translational drag is ζ = 3πηa, and the rotational drag is ζp = πηa3, where η is the viscosity.
The disk is constrained to move only in the z direction. Thus, it undergoes translational diffusion and experiences forces due to interactions with actin through UA and a repulsive potential analogous to UR (Eq. 1). We take Ddisk = D/20.
Arp2/3 molecules are modeled as point particles that diffuse with diffusion coefficient DArp = D/20, which is small in order to localize them to near the back of the disk. We note, however, that our results are insensitive to the precise value of DArp. Arp2/3 particles are reected by disk, but do not exert forces on either the disk or actin.
2.4. Biochemistry
We include the basic components of the dendritic nucleation model [16, 17], as described in [13, 39]. Precise numbers for rate constants are given in Table 1.
A G-actin monomer polymerizes at an F-actin filament or branch barbed end if the two subunits are in contact (a − δr < rij < a), the G-actin subunit is aligned with the rest of the filament (| cos θi − cos θ0| < δθ0, θ0 = 0°), and the G-actin polarization vector points along the filament (|p̂i·b̂i−1,i − cos θP | < δθP , θP = 0°). Similarly, G-actin nucleates a branch along the side of a filament if satisfying these conditions (with θ0 = θP = 70°) with an F-actin subunit that has been tagged with Arp2/3. Arp2/3 tagging occurs when an Arp2/3 molecule comes into contact with an untagged F-actin subunit.
Polymerization proceeds in this manner until it is halted by capping, which stochastically occurs at the barbed end at rate kC+. To determine whether capping of a filament occurs at the current time step, we draw a random number, R, uniformly distributed over [0, 1], if R < kC+Δt, the filament is capped. Similarly, depolymerization (and debranching) occurs stochastically from the pointed end (or y-junction) at rate K− (Kd). A depolymerized G-actin monomer no longer interacts through the bond potential and is thus free to diffuse around the simulation box.
We use δr = 0.1a, δθ0 = 0.06, and δθP = 0.1 in our standard model, but the polymerization rate, K+, will depend on the precise choice of these parameters, especially δθ0 and δθP, as described in [13]. The intrinsic diffusion-limited polymerization and branching rates, K+ and Kb, respectively, are reduced by about a factor of 10 in our simulations as compared to [13, 39]. This is because we have introduced a polarization vector for each subunit and the polymerization rate depends on the tolerance, δθP, for deviation of the polarization vector direction. Thus, in order to obtain motility, we lowered the depolymerization, debranching, and capping rates (K−, Kd, and kC+, respectively) by a similar factor.
Finally, we note that actin dynamics in the bulk system (without a disk) agrees well with the mean field theory in [55]. Our results are therefore insensitive to the precise choice of constants KR,KB,KS, and KP, except for details described in [13].
3. Results
3.1. Specific binding does not inherently disrupt motility
The release of Arp2/3 from the back of the disk breaks the symmetry of the system and leads to the production of a branched network of F-actin behind the disk (figure 1(a)). We found motility over a broad range of binding site strengths, ε, and densities, ρActA (figures 1–2). The range of ρActA used in our simulations is wide enough to cover the physiological regime [56, 57] and to allow us to investigate the crossover behavior of our model. The values of these simulation parameters, as well as the values of other relevant physical variables, are listed in Table 1.
Figure 2.
(a) The velocity of the disk, vdisk vs. binding energy, ε. At small ε, vdisk is insensitive to the binding energy, but at higher ε, vdisk decreases as ε increases. ρActA is reported in number of binding sites per 100 nm2. (b) The dependence of vdisk on the density of binding sites, ρActA, depends on binding energy. For small ε (e.g., 2 kBT, black), vdisk is insensitive to ρActA. At higher ε (e.g., 6 kBT, 8 kBT, and 14 kBT, red, green, and blue, respectively), vdisk decreases as ρActA increases.
We find that the overall physical mechanism of motility is preserved in the presence of actin-binding sites on the disk. Each binding site is small and short-ranged, and can strongly bind an F-actin filament only when the filament's barbed end is aligned properly (Eq. 5). However, in general, this is not sufficient to overcome the repulsive excluded volume interaction between F-actin and the disk, so the disk is propelled forward on average (figure 1(a)). As in [13, 39], there is a gradient of F-actin such that the F-actin concentration, ρF, behind the disk is higher than the concentration in front (figure 1(a)-(b)). Since F-actin continually polymerizes near the back of the disk, the F-actin concentration gradient translocates with the disk as it moves forward (figure 1(b)). This leads to a steady-state F-actin concentration profile in the reference frame of the disk, as shown in figure 1(c).
Compared to the system without actin binding, the steady-state concentration profile exhibits steeper gradients in the z-direction, normal to the disk. Due to tighter actin binding as the disk-actin binding energy, ε, increases, the concentration gradient spans a narrower spatial range and the F-actin profile behind the disk decays more sharply.
3.2. Strong binding affects motility by modulating actin network growth
The translocation velocity, vdisk, depends on binding energy, ε, and binding site density, ρActA, in a surprising manner. Up to intermediate binding energies, ε, the translocation velocity, vdisk, is approximately constant. However, as shown in figure 2(a), for large ε, vdisk decreases with increasing ε. Additionally, as the binding site density, ρActA, increases, vdisk becomes more sensitive to ε. For instance, vdisk begins to decrease at smaller ε for ρActA = 1.3 sites per 100 nm2 (squares in figure 2(a)) than for ρActA = 0.32 or 0.64 sites per 100 nm2 (triangles and circles, respectively, in figure 2(a)).
Similarly, vdisk is insensitive to ρActA when either ρActA or ε is small (figure 2(b)). For example, for ε = 2kBT, vdisk ≈ 10 µm/s over the entire range of ρActA studied (black circles in figure 2(b)). In contrast, for large ε and ρActA, vdisk decreases as ρActA increases. We note that in our model, the density of activated Arp2/3 is the same for all binding ε and ρActA. Together, these results indicate that the translocation velocity is not determined by the total binding energy, . Instead, vdisk is primarily dependent on the individual binding site binding energy, ε, and is a weaker function of ρActA.
The dependence of vdisk on actin binding can be understood by considering F-actin polymerization kinetics behind the disk. In order to understand how polymerization is affected by actin binding, we measured the detachment rate, ωd, of barbed ends bound to the disk (figure 3(a)). ωd is the rate at which a barbed end interacting with a binding site moves or rotates away from the site so that either riα > 2a or cosψiα < 0 (see Eq. 5). In order to avoid artifacts from barbed ends that only weakly and transiently interact with the binding site for a few time steps, we only measure ωd for barbed ends that experience an interaction energy E > 0.1ε at some time during the attachment. Although this choice of E is arbitrary, the measured ωd is insensitive to E over the range 0.1ε < E < 0.5ε, indicating that essentially all barbed ends that experience some significant attraction will eventually fully bind to the binding site before detaching.
Figure 3.
a) Detachment rate, ωd (solid circles), decreases approximately as ω0εbe−cε/kBT (solid line) as the binding energy, ε, increases, where ω0 = 4420 s−1, b = 0.532, and c = 0.535. (b) The concentration, , of uncapped barbed ends not attached to the disk is approximately constant at small binding energies and decreases at larger binding energies. This mirrors the theoretical steady-state concentration of free barbed ends, , where ρb is the total (attached and unattached) uncapped barbed end concentration and ωa is the rate at which uncapped barbed ends attach to the disk. This theoretical estimate for is indicated by the solid line. ωa = 60 s−1 is a fitting parameter. Inset: Plot of the total barbed end concentration, ρb, which is insensitive to ε, remaining close to its ε = 0 value until large ε. (c) The measured velocity of the simulated disk, vdisk (dashed line), is correlated with the total production rate of F-actin, which is given by , where ρg is the steady-state G-actin concentration. Inset: ρg is insensitive to ε at small ε, but increases as ε and (and thus F-actin concentration, ρf ) decrease.
As expected for thermally activated processes [58, 59], ωd decays approximately exponentially with ε for large ε. Although the exact expression for ωd in our system is unknown, detachment rates are typically of the form ω0εbe−cε/kBT, where ω0 is an intrinsic detachment rate, and b and c are parameters [58, 59]. We fit this function to the data shown in figure 3(a) over the entire range of ε, and found the best fit with ω0 = 4420 s−1, b = 0.532, and c = 0.535.
These values roughly agree with the typical values of b ≈ 1 and c ≈ 1 found for escape processes along a single coordinate [58, 59]. The depressed value of the best-fit b may be due to local crowding of F-actin inhibiting the escape of barbed ends. The deviation of the best-fit value of c from c ≈ 1 is probably due to the effective dimensionality of detachment processes in our system. In particular, instead of traversing along just one coordinate such as z displacement in order to unbind, barbed ends can also unbind through rotations of their polarization vectors, p̂i, away from their respective binding sites. Additionally, barbed ends can sometimes detach from the disk by moving laterally in the x and y directions. Collectively, these effects increase the dimensionality of the escape process, leading to a slower than expected decay of ωd as a function of ε.
The decrease of the detachment rate ωd with increasing binding energy ε has important implications for actin network growth. When a barbed end is attached to the disk, it is sterically inhibited from polymerizing at its plus end by the excluded volume interaction between G-actin subunits and the disk. Thus, an attached barbed end is effectively capped until it detaches from the disk. We therefore examined the effect of binding energy on the total rate of F-actin polymerization, α, which is known to be closely linked to the translocation velocity of actin-based motility [13, 60].
The F-actin production rate is given by , where is the concentration of detached barbed ends, which are free to polymerize actin, and ρg is the concentration of monomeric G-actin. As shown in figure 3(b) (solid circles), the first variable, , depends on the attachment/detachment dynamics of barbed ends. These are governed by the kinetic rate equation
| (10) |
where ωa is the attachment rate of free barbed ends and ρb is the total concentration of barbed ends (i.e., the sum of attached and detached barbed end concentrations). In steady-state, , and is given by
| (11) |
figure 3(b) (solid line) shows the theoretical estimate for from 11 using ωd from figure 3(a), the simulated value of ρb at ε = 0, and a best-fit for ωa. Since barbed ends in our simulation are generated through Arp2/3-mediated branching, the total concentration of barbed ends, ρb, is insensitive to ε (inset to figure 3(b)). The agreement between the theoretical estimate and the simulation indicates that the assumption of constant ωa is reasonable, the rate at which barbed ends diffuse onto binding sites is insensitive to the strength with which they are bound. Thus, the decrease in ωd explains the observed behavior of as ε increases. When ωd/ωa ≫ 1, is unaffected by decreasing ωd. But when ε is large enough that ωd/ωa ≲ 1, further decreases in ωd are manifested by a marked decrease in , leaving fewer barbed ends free to polymerize new F-actin.
The inset to figure 3(c) shows the behavior of ρg, the other variable that determines α, the F-actin production rate. As ε increases, ρg increases because an increasing number of barbed ends are inhibited from polymerizing F-actin by attachment to the disk. However, since ≪ ρg, the F-actin production rate, α, is far more sensitive to variation in than in ρg. Combining K+, , and ρg, we determine α, as shown by the solid circles in figure 3(c). By overlaying the vdisk versus ε data (dashed line in figure 3(c)), we find a close correlation between α and vdisk, as expected [13, 60]. Thus, the entire dependence of vdisk on ε and ρActA (figure 2) can be explained by changes in the F-actin production rate resulting from barbed end attachment/detachment dynamics (figure 3).
3.3. Pressure-velocity relation
To better understand how specific binding affects the robustness of actin-based motility, we introduced an external load pressure, P, on the disk. As shown in figure 4(a), the attractive interactions between actin and the disk do not eliminate the ability of the disk to move under an opposing load, for various ε (different colored points), vdisk > 0 over a wide range of P. Moreover, similar to experiments in [61–64] and simulations in [39], we find that vdisk is insensitive to P at small loads. At larger P, as P increases, vdisk decreases until it reaches zero and the disk stalls at Pstall. In the inset to figure 4(a), we scale vdisk by the zero load velocity, v0, and pressures by the pressure, P1/2, when vdisk = v0/2, as described in [39, 62]. While the pressure-velocity curves collapse for small ε (black and red symbols), the curve is not universal for large ε (blue and brown symbols).
Figure 4.
(a) Velocity versus load pressure P. At small pressures, P, the disk velocity, vdisk ≈ v0, where v0 is the zero load velocity. As P increases, vdisk drops until the disk stalls (vdisk = 0) at the stall pressure, Pstall. Above Pstall, the disk is pushed backwards into the F-actin tail. Data is shown for disks with ρActA = 0.64 per 100 nm2 and binding energy ε = 0 (black), 2 kBT (red), 8 kBT (blue), and 11 kBT (brown). Inset: We rescale the vdisk by v0 and P by the pressure, P1/2, at which vdisk = v0/2, as in [39, 62]. For small ε, we obtain the expected rescaling. For large ε, we see the same qualitative pressure-velocity relation, but rescaling by P1/2 and v0 does not produce the same curves. (b) At small ε, Pstall is insensitive to ε. However, at larger ε,Pstall decreases as ε increases. Inset: F-actin concentration, ρf, vs. binding energy ε. At higher binding energies, ρf decreases with increasing ε.
As shown in figure 4(b), Pstall is insensitive to ε for ε ≲ 8 kBT. Above this binding energy, Pstall decreases, indicating that motility is less robust for very large binding energies ε. In our simulations, Pstall is of order 10−2 nN=µm2, much smaller than the experimental value [62, 64–66] of ≈ 1–10 nN/µm2. Our stall pressure, Pstall, also differs from the value observed in earlier simulations with a higher polymerization rate without actin binding to the disk [39], ≈ 0.1 nN/µm2.
Both of these observations can be explained by the behavior of the Young's modulus, Y, of the F-actin network. Y has been argued to govern the pressure-velocity relation for actin-based motility [38, 39]. Specifically, the actin network can continue to grow as long as the opposing load does not exceed its elastic modulus, which is on the order of 1–10 nN/µm2 [67] in experiments. In general, for a network of semiexible filaments,
| (12) |
where ℓp is the filament persistence length and ξm is the mesh size of the network [68, 69]. The mesh size depends on the concentration of F-actin, [68, 69]. In the inset to figure 4(b), we show that ρf is approximately constant for ε ≲ 8 kBT, and decreases dramatically above this binding energy. This is consistent with the dramatic decrease in the concentration, , of free barbed ends at large ε. Thus, the decrease in and consequent decrease in ρf due to increased actin binding is sufficient to explain the qualitative behavior of Pstall as a function of ε.
Eq. 12 provides a quantitative explanation of the difference between the three values of stall pressure. Assuming Y ≈ Pstall, we expect that the experimental stall pressure, , should be related to the simulated Pstall through appropriate rescaling of the persistence length and F-actin concentration:
| (13) |
This order of magnitude estimate is in good agreement with experiments [62, 64–66]. Moreover, it is clear that the agreement is not coincidental. Eq. 12 also predicts that our simulated Pstall should be lower than in previous simulations [39] by about a factor of due to the difference between the F-actin concentration, ρf, in our simulations and the F-actin concentration, , in [39]. Consequently, it is clear that in simulations with stiffer filaments and higher F-actin concentration in the tail, we would measure the experimentally observed value of stall pressure, as suggested in [39]. Simulations with higher stiffnesses and F-actin concentrations are too timeconsuming at current computational speeds, but nonetheless, with the parameters used in our simulations, we capture the underlying physics of actin-based motility.
4. Discussion
We have presented physically consistent simulations of actin-based motility in which self-assembly of an F-actin network stimulated by an object (a disk) propels that object forward through the creation of a steady-state actin gradient. In the case of a purely repulsive interaction between actin and the disk, the disk moves towards lower actin concentration, and continues to do so as it stimulates further F-actin polymerization through activation/release of Arp2/3 [13, 39] via the self-diffusiophoretic mechanism [40, 41], discussed further below. Here we have shown that this mechanism is viable even when actin binds to specific sites on the object. Note that in contrast to some other models [33, 35, 37] we do not require that the binding sites simultaneously allow for binding and polymerization. Indeed, our model assumes that the opposite is true - if a barbed end is bound, it cannot grow.
This assumption has consequences for the behavior as a function of binding energy, ε, and density of binding sites, ρActA. If either of these quantities is sufficiently low, then specific binding of actin to the disk has little effect on the velocity or stall pressure of the disk. However, if both are high enough, a large number of barbed ends remain bound to the disk, inhibiting polymerization. This decreases the network growth rate, , and thus the rate of forward motility, vdisk. Sufficient binding of barbed ends to the disk also decreases the concentration, ρf , of F-actin behind the disk, leading to a smaller Young's modulus, Y, and consequently, a depressed stall pressure, Pstall.
4.1. The self-diffusiophoretic mechanism is robust to specific binding of actin to the moving object
Based on Brownian dynamics simulations it was suggested that proteins such as ActA or WASP activate Arp2/3 and together catalyze polymerization of F-actin leading to the formation of a concentration gradient and that the repulsive interactions between F-actin and the disk therefore propel the disk forward, down the gradient [13, 39]. A major objection to this model is that it relies explicitly on repulsive interactions between F-actin and the disk, despite the fact that there are also significant attractive interactions due to actin-binding proteins like ActA or WASP [8, 14, 15, 25–27]. However, we have found that a concentration gradient can propel the disk forward even when actin binds to the disk. Such attractions do not disrupt the F-actin-gradient-driven mechanism of motility (figure 2). Furthermore, the observation of a steady-state F-actin concentration gradient in simulations agrees with several experiments [22, 61, 70, 71] showing an actin uorescence profile qualitatively similar to those shown in figure 1(b)-(c).
In a fluid environment, actin-gradient-driven motion could occur via self-diffusiophoresis [40–42]. Although we do not explicitly include fluid flow in our simulations, recent analyses demonstrate they can nonetheless accurately describe concentration-gradient-driven motility [72, 73]. A catalyst (Arp2/3) activated by an object (colloid/bacterium covered with ActA or WASP) stimulates the production of a chemical species (F-actin) near the surface of the object. Since this reaction only occurs locally, the concentration of this chemical species is non-uniform, so that it is higher behind the the object than it is elsewhere. This generates a steady-state fluid flow, whose precise nature is governed by the interaction of the chemical species with the object [40–42, 73, 74]. Since the catalyst is continually activated by the object, this concentration gradient persists in steady state, so that the object continues to move in this manner.
Our simulations show that this self-diffusiophoretic actin-based motility should not be disrupted by ActA- or WASP-mediated disk-actin attractions. However, in contrast to the prediction in [13], but in agreement with calculations in [75], we do not observe backwards motility when the strength (or density) of the attractive interactions is large. In both our Brownian dynamics simulations and the fluid dynamics calculation, polymerized actin cannot simultaneously pull the disk and move out of its way, so backwards motility cannot occur.
4.2. Novel mechanism of actin cytoskeleton control
Our results suggest a biophysical mechanism for control of actin-based motility. We find that at high enough concentrations or binding energies, actin-binding proteins can sterically inhibit polymerization. Specifically, in our model, actin-binding proteins on the disk directly attach to the barbed ends of F-actin filaments, preventing actin growth. If binding is weak, the attachment is transient, and thus its effect is limited by rapid F-actin detachment from the disk. On the other hand, if binding is strong, attachment is long-lived and detachment occurs infrequently, leading to stalled actin growth. This is consistent with the work of Co et al. [76], in which the authors studied beads coated with weak actin-binding N-WASP mutants. As in our model, the bead in their experiments moves more rapidly for weak-actin-binding N-WASP mutants.
The actin-binding protein cortactin, which also binds WASP and Arp2/3, has been shown to enhance the detachment of nucleated actin branches from surface-bound WASP. In turn, the branching rate, and thus overall rate of actin network growth is enhanced by cortactin up to a few tens of nanomolar concentrations [77, 78]. As a result, the speed of actin-based motility increases [78]. These effects can be explained in our model by supposing that cortactin decreases the actin-WASP binding energy, ε. This would lead to enhanced detachment of actin branches from the surface. By decreasing the duration of growing end attachments, cortactin should increase the concentration, , of free growing ends. The decrease in branching and motility at higher cortactin densities may be explained by the interplay between capping and branching [13, 55, 61, 79, 80], as follows. Since at high cortactin concentrations, barbed ends are released from N-WASP (thus “uncapping” the barbed ends), network growth is focused at filament ends rather than new branches, decreasing the amount of branching. This morphological change could decrease motility so that direct branch inhibition effects by cortactin, proposed in [78], may not be necessary. This idea could be tested experimentally by investigating systems with higher concentrations of capping protein. In these systems the concentration of cortactin required to inhibit branching should be higher than in the experiments in [78].
The primary difference between our model and the cortactin experiments is that cortactin, WASP, and actin bind with Arp2/3 at nascent branches, not at barbed ends. However, it has been shown that self-diffusiophoretic propulsion is insensitive to whether the disk interacts with the tips or sides of filaments [13]. Therefore, the experiments of [78] demonstrate that actin growth may be directly and physically regulated by actinbinding, consistent with our predictions.
Experiments such as those in [18, 51] that vary ActA surface density are more difficult to compare to our model because increasing ρActA stimulates additional actin polymerization in experiments. We have not included this detail in our model. As a result, our simulations do not capture the slight increase in velocity with increasing ρActA observed in the experiments. It would be straightforward to extend our model to capture this effect.
Several other models have considered competition between propulsive forces of actin polymerization and resistive forces due to binding interactions [26, 27, 30–32, 38, 44, 67, 81]. According to this idea, filaments that are not bound to the surface can grow and exert protrusive forces, while filaments that are bound to the surface exert a resistive force backwards. This competition has been suggested to lead to the intermittent velocity observed in actin-based motility of Listeria [14], beads [82], and vesicles [26, 27].
In contrast, we find that the actin-binding strength, ε, and concentration, ρActA, of actin-binding sites inuence motility (figure 2) by controlling the polymerization rate (figure 3), rather than exerting resistive pulling forces. We do observe an increase in internal stresses within the actin tail as ε increases (supplementary figure 1), but it is clear from figure 3 that polymerization rate is the primary control for velocity. In other words, we find that the direct effect on motility of actin binding by regulating the growth of the network (figure 3(b)-(c)) is more important than the indirect effect arising from tensile stress in the tail. However, while our tail is a branched network that can support some tensile stress, we have not included cross linking in our simulations, it is possible that once the elastic modulus of the tail is large enough, stresses in the tail could dominate the physics as predicted by the elastic gel model [31, 32, 67].
Our predictions for the effect of binding energy on propulsion speed can be tested directly in an experiment proposed in [13]. The idea is to to coat polystyrene beads not only with actin nucleators such as ActA and N-WASP but also with an actin-binding protein that does not promote branching. In this way, instead of varying surface concentration of ActA or N-WASP [18, 51, 61, 76] to study the effects of actin binding, one could vary the concentration of the second binding protein. This would directly test how actin binding inuences motility without the complication of simultaneously varying the rate of actin nucleation [13]. Our model's prediction for this experiment is shown by the data in figure 2(b).
4.3. Pressure-velocity relation
Our simulations demonstrate that the Young's modulus, Y, of the F-actin network is the most important factor in determining the stall pressure, Pstall. The Young's modulus is important because the self-diffusiophoretic mechanism propels the object forward until the concentration gradient required for motility is significantly deformed [39]. A significant deformation to the profile will only occur if the load pressure is greater than the strength of the F-actin network. This is consistent with previous work estimating both Y and Pstall to both be of order 1–10 nN=µm2 in experiments [38, 39, 62, 64–67].
In our simulations, the stall pressure is approximately two orders of magnitude smaller than it is in experiments, but this is due the short persistence length ℓp and the relatively low concentration, ρf, of F-actin filaments (which increases the mesh size, ξm). Together, these factors reduce Y below the experimentally observed value (Eqs. 12 and 13). Clearly, direct strengthening of the network through cross-linking should decrease ξm and increase Pstall [39, 68]. Additionally, our simulations reveal an alternative mechanism to control the robustness of actin-based motility. By increasing actin binding, the concentration of F-actin is decreased (figure 2), which in turn leads to a decrease in Pstall (figure 4(b)).
The overall pressure-velocity curve is in good agreement with several experiments that show a concave-down pressure-velocity curve [62–64]. Similarly, our model agrees with experiments showing that actin-based motility is insensitive to small opposing pressures [61–64]. In contrast to experiments in [62] and simulations in [39], the pressurevelocity curves at high binding energies in our simulations do not collapse onto a single curve when rescaled (inset to figure 4(a)). This is unsurprising because the F-actin network has fundamentally different material properties for different binding energies due to the change in ρf induced by varying ε and ρActA. By similar reasoning, we would expect that in AFM-based pressure-velocity experiments similar to those in [62], but with varying concentrations of cross-linking proteins (such as α-actinin [17]) would lead to several different pressure-velocity curves that do not collapse across different cross-linker concentrations (but would collapse when comparing experiments at the same cross-linker concentration).
4.4. Self-diffusiophoresis in filopodia
We propose that cofilin-driven filopodial retraction may constitute another biological realization of self-diffusiophoresis. It has been known for over a decade that the speed of filopodial protrusion and retraction are highly correlated with actin polymerization and myosin-driven retrograde flow [83]. More recently, cofilin, an actin disassembling protein has been implicated in filopodial retraction [84]. In particular, as the filopodium retracts, actin is depolymerized by cofilin at the tip of the filopodium. This is similar to the situation in bacterial chromosome segregation recently studied in [85]. Specifically, actin-like ParA filaments in the bacterial cytoskeleton can pull a chromosome by depolymerization of ParA subunits from the tips of filaments because chromosome-associated proteins are attracted to ParA. This works by a self-diffusiophoretic mechanism, depolymerization creates a ParA gradient, and the chromosome tends to move up this concentration gradient. Similarly, actin is thought to bind proteins at the tip of the filopodium [84], giving rise to an attractive interaction between actin and the filopodium tip. In this case, depolymerization of actin by cofilin could create the gradient necessary to drive filopodia tip retraction.
This idea could be tested by covering a polystyrene bead with actin-binding proteins from the filopodium tip complex and placing it in an F-actin solution. It is thought that proteins in this complex may enhance cofilin-mediated actin disassembly by phosphate release from ATP-F-actin [84] and thus could disassemble actin near the bead. Ideally, one would use Janus beads with one half covered with actin-binding proteins from the filopodium tip complex to eliminate the need for symmetry breaking. If actin and cofilin coordinate to drive filopodium retraction through self-diffusiophoresis, the bead should begin to move, and there should be a corresponding F-actin gradient of increasing concentration with distance from the bead.
4.5. Comparison of proposed mechanisms of actin-based motility
Many models have been proposed for motility, most notably Brownian elastic ratchet models [28–30], the elastic gel model [31, 32, 38] and an entropic model [86]. It is quite possible that barbed ends of individual filaments uctuate away from the surface and grow, as studied by Brownian ratchet models [28–30]. However, it was shown that the Brownian elastic ratchet mechanism does not predict the filament stiffness dependence of motility that is seen in Brownian dynamics simulations [13]. This is not surprising, since a single-filament picture is unlikely to capture motility, which is an emergent, collective phenomenon in the many-filament system.
One requirement for the self-diffusiophoretic mechanism to apply is that the actin filament density in the tail should be high compared to the average actin concentration in solution. If the actin filament density is sufficiently low, self-diffusiophoresis could be a weak effect and propulsion may be dominated by entropic effects [36, 86].
The elastic gel model is fully consistent with and complementary to the self-diffusiophoretic mechanism. In the case of a disk, the elastic gel model assumes that the propulsion speed is given by the polymerization speed, or the rate of production of F-actin. But the model does not explain why this is the case. In fact, this is true because of the self-diffusiophoretic mechanism. The elastic gel model focuses on a different issue - how stresses can build up in the tail to alter motility. We have not explored the motion of curved objects when actin tails are cross linked, but we would expect our mesoscopic model to capture the type of saltatory motion predicted by the macroscopic elastic gel model in that case [31, 32].
In addition to the above-mentioned models, many simulation models have been proposed and studied [43–47]. While these simulations have been instructive in many respects, it is crucial to note that none of them can yield any insight into the origin of motility. The models underlying these simulations [43–47] share the common property that single actin monomers cannot exert forces but actin filaments can. Such models are unphysical in that they violate mass conservation. Since the growing ends of filaments are concentrated behind the moving object, mass is created behind the moving object, thus unphysically creating new forces from nothing. These forces clearly lead to motility, so the violation of mass conservation has the serious consequence of generating motility as an artifact. Mechanisms underlying motility in real systems are much more subtle. Since concentration-gradient-driven motility emerges from our model, which conserves mass, it is a viable candidate for the mechanism of motility in real systems.
Self-diffusiophoresis is not only a viable candidate for the mechanism of motility, but also, it must exist in real systems. When an object is in the presence of a concentration gradient in a low Reynolds number fluid, diffusiophoresis necessarily occurs [42, 74]. In the case of actin-driven motility, it is obvious that a concentration gradient exists - the concentration in the actin comet tail is several orders of magnitude higher than the average concentration of actin in the system, so the concentration behind the moving object is substantially higher than the concentration in front [22, 61, 70, 71]. As a result, self-diffusiophoresis must occur.
Just because self-diffusiophoresis must occur, however, does not mean that it is necessarily the dominant mechanism underlying actin-driven motility. In order for self-diffusiophoretic motility to be dominant, it must lead to fluid flows that are not too slow compared to the scale of the velocity that is observed in experiments. An earlier estimate using Darcy's law [13] found that this is indeed the case. For the expected solute-generated pressure gradient, actin network permeability, and fluid viscosity, the F-actin concentration gradient could generate a fluid flow of up to 1 µm/s [13]. This is not too much larger than the 1 − 10 µm/min range of actin-based motility of Listeria [5, 14, 20, 50, 51, 67], viruses [9, 10], and ActA- or N-WASP-coated polystyrene beads [18, 21, 51, 61, 82], lipid vesicles [26, 27], and oil droplets [25].
Altogether, it is possible that a variety of physical phenomena may occur in real systems that are propelled by actin polymerization. The many models that have been proposed explore different facets of these phenomena. We reiterate, however, that statistical mechanical and hydrodynamic principles dictate that self-diffusiophoresis must occur [42, 74]. Mass-conserving, steady-state simulations here and in previous work [13, 39] suggest that self-diffusiophoresis is indeed the mechanism for actin-based motility. Moreover, a back-of-the-envelope calculation [13] suggests that it is a significant effect, of the right order of magnitude to explain motility. One would have to argue that self-diffusiophoretic flow is negligible in order to argue that another mechanism is instead responsible for actin-polymerization-driven motility.
5. Conclusion
We have found that self-diffusiophoresis, whereby an object generates and sustains a steady-state F-actin concentration gradient that propels it, can robustly provide actin-based propulsion, even in the presence of localized actin-binding sites. Actin-binding sites provide an additional mechanism of control, which could be used for diverse purposes ranging from transient physical capping to filopodial retraction. The self-diffusiophoretic mechanism is robust and stalls only against pressures exceeding the Young's modulus of the network. Since there is a steady-state actin concentration gradient, self-diffusiophoresis must occur.
Moreover, self-diffusiophoresis is potentially a mechanism for biological motility in other contexts because it is robust and relies on an ubiquitous feature of biological systems - the existence of concentration gradients. Recent experiments [87–89], have shown that diffusiophoresis can also provide precise spatiotemporal control. It has been suggested that chromosomal translocation in bacteria such as Caulobacter crescentus may rely on self-diffusiophoresis [85]. It remains to be seen whether filopodial retraction due to cofilin-driven actin depolymerization constitutes a similar example.
Supplementary Material
Acknowledgments
We thank C. P. Goodrich for helpful discussions in the early stages of this work and gratefully acknowledge the support of the National Science Foundation DMR-1104637 (EJB and AJL) and DMR-0520020 (EJB) and the National Institutes of Health NIGMS Glue Grant U54 GM64346 (KCL).
References
- 1.Pollard TP, Cooper JA. Actin, a central player in cell shape and movement. Science. 2009;326:1208–1212. doi: 10.1126/science.1175862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lauffenburger DA, Horwitz AF. Cell migration: A physically integrated molecular process. Cell. 1996;84:359–369. doi: 10.1016/s0092-8674(00)81280-5. [DOI] [PubMed] [Google Scholar]
- 3.Pollard TD, Borisy GG. Cellular motility driven by assembly and disassembly of actin filaments. Cell. 2003;112:453–465. doi: 10.1016/s0092-8674(03)00120-x. [DOI] [PubMed] [Google Scholar]
- 4.Tilney LG, Portnoy DA. Actin filaments and the growth, movement, and spread of the intracellular parasite Listeria monocytogenes . J. Cell Biol. 1989;109:1597–1608. doi: 10.1083/jcb.109.4.1597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Dabiri GA, Sanger JM, Portnoy DA, Southwick FS. Listeria monocytogenes moves rapidly through the host-cell cytoplasm by inducing directional actin assembly. Proc. Natl. Acad. Sci. USA. 1990;87:6068–6072. doi: 10.1073/pnas.87.16.6068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tilney LG, DeRosier DJ, Tilney MS. How Listeria exploits host cell actin to form its own cytoskeleton. I. formation of a tail and how that tail might be involved in movement. J. Cell Biol. 1992;118:71–81. doi: 10.1083/jcb.118.1.71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bernardini ML, Mounier J, d'Hauteville H, Coquis-Rondon M, Sansonetti PJ. Identification of icsA, a plasmid locus of Shigella exneri that governs bacterial intra- and intercellular spread through interaction with F-actin. Proc. Natl. Acad. Sci. USA. 1989;86:3867–3871. doi: 10.1073/pnas.86.10.3867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Egile C, Loisel TP, Laurent V, Li R, Pantaloni D, Sansonetti PJ, Carlier MF. Activation of the Cdc42 effector N-WASP by the Shigella exneri IcsA protein promotes actin nucleation by Arp2/3 complex and bacterial actin-based motility. J. Cell Biol. 1999;146:1319–1322. doi: 10.1083/jcb.146.6.1319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cudmore S, Cossart P, Griffiths G, Way M. Actin-based motility of vaccinia virus. Nature. 1995;378:636–638. doi: 10.1038/378636a0. [DOI] [PubMed] [Google Scholar]
- 10.Ohkawa T, Volkman LE, Welch MD. Actin-based motility drives baculovirus transit to the nucleus and cell surface. J. Cell Biol. 2010;190:187–195. doi: 10.1083/jcb.201001162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Taunton J, Rowning BA, Coughlin ML, Wu M, Moon RT, Mitchison TJ, Larabell CA. Actin-dependent propulsion of endosomes and lysosomes by recruitment of N-WASP. J. Cell Biol. 2000;148:519–530. doi: 10.1083/jcb.148.3.519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Boldogh IR, Yang HC, Nowakowski WD, Karmon SL, Hays LG, Yates JR, Pon LA. Arp2/3 complex and actin dynamics are required for actin-based mitochondrial motility in yeast. Proc. Natl. Acad. Sci. USA. 2001;98:3162–3167. doi: 10.1073/pnas.051494698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lee KC, Liu AJ. New proposed mechanism of actin-polymerization-driven motility. Biophys. J. 2008;95:4529–4539. doi: 10.1529/biophysj.108.134783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lasa I, Gouin E, Goethals M, Vancompernolle K, David V, Vandekerckhove J, Cossart P. Identification of two regions in the N-terminal domain of ActA involved in the actin comet tail formation by Listeria monocytogenes . EMBO J. 1997;16:1531–1540. doi: 10.1093/emboj/16.7.1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Machesky LM, Insall RH. Scar1 and the related Wiskott-Aldrich syndrome protein, WASP, regulate the actin cytoskeleton through the Arp2/3 complex. Curr. Biol. 1998;8:1347–1356. doi: 10.1016/s0960-9822(98)00015-3. [DOI] [PubMed] [Google Scholar]
- 16.Mullins RD, Heuser JA, Pollard TD. The interaction of Arp2/3 complex with actin: Nucleation, high affinity pointed end capping, and formation of branching networks of filaments. Proc. Natl. Acad. Sci. USA. 1998;95:6181–6186. doi: 10.1073/pnas.95.11.6181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pollard TD, Blanchoin L, Mullins RD. Molecular mechanims controlling actin filament dynamics in nonmuscle cells. Annu. Rev. Biomol. Struct. 2000;29:545–576. doi: 10.1146/annurev.biophys.29.1.545. [DOI] [PubMed] [Google Scholar]
- 18.Cameron LA, Footer MJ, van Oudenaarden A, Theriot JA. Motility of ActA protein-coated microspheres driven by actin polymerization. Proc. Natl. Acad. Sci. USA. 1999;96:4908–4913. doi: 10.1073/pnas.96.9.4908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yarar D, To W, Abo A, Welch MD. The Wiskott-Aldrich syndrome protein directs actin-based motility by stimulating actin nucleation with the Arp2/3 complex. Curr. Biol. 1999;9:555–558. doi: 10.1016/s0960-9822(99)80243-7. [DOI] [PubMed] [Google Scholar]
- 20.Loisel TP, Boujemaa R, Pantaloni D, Carlier MF. Reconstitution of actin-based motility of Listeria and Shigella using pure proteins. Nature. 1999;401:613–617. doi: 10.1038/44183. [DOI] [PubMed] [Google Scholar]
- 21.van Oudenaarden A, Theriot JA. Cooperative symmetry-breaking by actin polymerization in a model for cell motility. Nat. Cell Biol. 1999;1:493–499. doi: 10.1038/70281. [DOI] [PubMed] [Google Scholar]
- 22.Svitkina TM, Borisy GG. Arp2/3 complex and actin depolymerizing factor ADF/cofilin in dendritic organization and treadmilling of actin filament array in lamellipodia. J. Cell Biol. 1999;145:1009–1026. doi: 10.1083/jcb.145.5.1009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cameron LA, Svitkina TM, Vignjevic D, Theriot JA, Borisy GG. Dendritic organization of actin comet tails. Curr. Biol. 2001;11:130–135. doi: 10.1016/s0960-9822(01)00022-7. [DOI] [PubMed] [Google Scholar]
- 24.Schwartz IM, Ehrenberg M, Bindschadler M, McGrath JL. The role of substrate curvature in actin-based pushing forces. Curr. Biol. 2004;14:1094–1098. doi: 10.1016/j.cub.2004.06.023. [DOI] [PubMed] [Google Scholar]
- 25.Boukellal H, Campás O, Joanny JF, Prost J, Sykes C. Soft Listeria: Actin-based propulsion of liquid drops. Phys. Rev. E. 2004;69:061906. doi: 10.1103/PhysRevE.69.061906. [DOI] [PubMed] [Google Scholar]
- 26.Upadhyaya A, Chabot JR, Andreeva A, Samadani A, van Oudenaarden A. Probing polymerization forces by using actin-propelled lipid vesicles. Proc. Natl. Acad. Sci. USA. 2003;100:4521–4526. doi: 10.1073/pnas.0837027100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Giardini PA, Fletcher DA, Theriot JA. Compression forces generated by actin comet tails on lipid vesicles. Proc. Natl. Acad. Sci. USA. 2003;100:6493–6498. doi: 10.1073/pnas.1031670100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Peskin CS, Odell GM, Oster GF. Cellular motions and thermal fluctuations: The Brownian ratchet. Biophys. J. 1993;65:316–324. doi: 10.1016/S0006-3495(93)81035-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mogilner A, Oster G. Cell motility driven by actin polymerization. Biophys. J. 1996;71:3030–3045. doi: 10.1016/S0006-3495(96)79496-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mogilner A, Oster G. Force generation by actin polymerization II: The elastic ratchet and tethered filaments. Biophys. J. 2003;84:1591–1605. doi: 10.1016/S0006-3495(03)74969-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gerbal F, Noireaux V, Sykes C, Jülicher F, Chaikin P, Ott A, Prost J, Golsteyn RM, Friederich E, Louvard D, Laurent V, Carlier MF. On the ‘Listeria’ propulsion mechanism. Pramana. 1999;53:155–170. [Google Scholar]
- 32.Gerbal F, Chaikin P, Rabin Y, Prost J. An elastic analysis of Listeria monocytogenes propulsion. Biophys. J. 2000;79:2259–2275. doi: 10.1016/S0006-3495(00)76473-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dickinson RB, Purich DL. Clamped-filament elongation model for actin-based motors. Biophys. J. 2002;82:605–617. doi: 10.1016/S0006-3495(02)75425-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Carlsson AE. Growth velocities of branched actin networks. Biophys. J. 2003;84:2907–2918. doi: 10.1016/S0006-3495(03)70018-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dickinson RB, Caro L, Purich DL. Force generation by cytoskeletal filament end-tracking proteins. Biophys. J. 2004;87:2838–2854. doi: 10.1529/biophysj.104.045211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gholami A, Wilhelm J, Frey E. Entropic forces generated by grafted semiexible polymers. Phys. Rev. E. 2006;74:041803. doi: 10.1103/PhysRevE.74.041803. [DOI] [PubMed] [Google Scholar]
- 37.Zhu J, Carlsson AE. Growth of attached actin filaments. Eur. Phys. J. E. 2006;21:209–222. doi: 10.1140/epje/i2006-10061-9. [DOI] [PubMed] [Google Scholar]
- 38.Campàs O, Mahadevan L, Joanny JF. Actin network growth under load. Biophys. J. 2012;102:1049–1058. doi: 10.1016/j.bpj.2012.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lee KC, Liu AJ. Force-velocity relation for actin-polymerization-driven motility from Brownian dynamics simulations. Biophys. J. 2009;97:1295–1304. doi: 10.1016/j.bpj.2009.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Golestanian R, Liverpool TB, Ajdari A. Propulsion of a molecular machine by asymmetric distribution of reaction products. Phys. Rev. Lett. 2005;94:220801. doi: 10.1103/PhysRevLett.94.220801. [DOI] [PubMed] [Google Scholar]
- 41.Golestanian R, Liverpool TB, Ajdari A. Designing phoretic micro- and nano-swimmers. New J. Phys. 2007;9:126–133. [Google Scholar]
- 42.Jülicher F, Prost J. Generic theory of colloidal transport. Eur. Phys. J. E. 2009;29:27–36. doi: 10.1140/epje/i2008-10446-8. [DOI] [PubMed] [Google Scholar]
- 43.Carlsson AE. Growth of branched actin networks against obstacles. Biophys. J. 2001;81:1907–1923. doi: 10.1016/S0006-3495(01)75842-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Alberts JB, Odell GM. In silico reconstitution of Listeria propulsion exhibits nanosaltation. PLoS Biology. 2004;2:2054–2066. doi: 10.1371/journal.pbio.0020412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Burroughs NJ, Marenduzzo D. Nonequilibrium-driven motion in actin networks: Comet tails and moving beads. Phys. Rev. Lett. 2007;98:238302. doi: 10.1103/PhysRevLett.98.238302. [DOI] [PubMed] [Google Scholar]
- 46.Schreiber CH, Stewart M, Duke T. Simulation of cell motility that reproduces the forcevelocity relationship. Proc. Natl. Acad. Sci. USA. 2010;107:9141–9146. doi: 10.1073/pnas.1002538107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zhu J, Mogilner A. Mesoscopic model of actin-based propulsion. PLoS Comput. Biol. 2012;8:e1002764. doi: 10.1371/journal.pcbi.1002764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Welch MD, Rosenblatt J, Skoble J, Portnoy DA, Mitchison TJ. Interaction of human Arp2/3 complex and the Listeria monocytogenes ActA protein in actin filament nucleation. Science. 1998;281:105–108. doi: 10.1126/science.281.5373.105. [DOI] [PubMed] [Google Scholar]
- 49.Rutenberg AD, Grant M. Curved tails in polymerization-based bacterial motility. Phys. Rev. E. 2001;64:021904. doi: 10.1103/PhysRevE.64.021904. [DOI] [PubMed] [Google Scholar]
- 50.Shenoy VB, Tambe DT, Prasad A, Theriot JA. A kinematic description of the trajectories of Listeria monocytogenes propelled by actin comet tail. Proc. Natl. Acad. Sci. USA. 2007;104:8229–8234. doi: 10.1073/pnas.0702454104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cameron LA, Robbins JR, Footer MJ, Theriot JA. Biophysical parameters inuence actin-based movement, trajectory, and initiation in a cell-free system. Mol. Biol. Cell. 2004;15:2312–2323. doi: 10.1091/mbc.E03-12-0913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Rapaport DC. The art of molecular dynamics simulations. Cambridge: Cambridge University Press; 1995. [Google Scholar]
- 53.Blanchoin L, Amann KJ, Higgs HN, Marchand JB, Kaiser DA, Pollard TD. Direct observation of dendritic actin filament networks nucleated by Arp2/3 complex and WASP/Scar proteins. Nature. 2000;404:1007–1011. doi: 10.1038/35010008. [DOI] [PubMed] [Google Scholar]
- 54.Allen MP, Tildesley DJ. Computer simulation of liquids. USA: Oxford University Press; 1989. [Google Scholar]
- 55.Gopinathan A, Lee KC, Schwarz JM, Liu AJ. Branching, capping, and severing in dynamic actin structures. Phys. Rev. Lett. 2007;99:058103. doi: 10.1103/PhysRevLett.99.058103. [DOI] [PubMed] [Google Scholar]
- 56.Samarin S, Romero S, Kocks C, Didry D, Pantaloni D, Carlier MF. How VASP enhances actin-based motility. J. Cell Biol. 2003;163:131–142. doi: 10.1083/jcb.200303191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Footer MJ, Lyo JK, Theriot JA. Close packing of Listeria monocytogenes ActA, a natively unfolded protein, enhances F-actin assembly without dimerization. J. Biol. Chem. 2008;283:23852–23862. doi: 10.1074/jbc.M803448200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Risken H. The Fokker-Planck Equation. Berlin: Springer-Verlag; 1996. [Google Scholar]
- 59.Evans E, Ritchie K. Dynamic strength of molecular adhesion bonds. Biophys. J. 1997;72:1541–1555. doi: 10.1016/S0006-3495(97)78802-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Theriot JA, Mitchison TJ, Tilney LG, Portnoy DA. The rate of actin-based motility of intracellular Listeria monocytogenes equals the rate of actin polymerization. Nature. 1992;357:257–260. doi: 10.1038/357257a0. [DOI] [PubMed] [Google Scholar]
- 61.Wiesner S, Helfer E, Didry D, Ducouret G, Lafuma F, Carlier MF, Pantaloni D. A biomimetic motility assay provides insight into the mechanism of actin-based motility. J. Cell Biol. 2003;160:387–398. doi: 10.1083/jcb.200207148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Parekh SH, Chaudhuri O, Theriot JA, Fletcher DA. Loading history determines the velocity of actin-network growth. Nat. Cell Biol. 2005;7:1219–1223. doi: 10.1038/ncb1336. [DOI] [PubMed] [Google Scholar]
- 63.Prass M, Jacobsen K, Mogilner A, Radmacher M. Direct measurement of the lamellipodial protrusive force in a migrating cell. J. Cell Biol. 2006;174:767–772. doi: 10.1083/jcb.200601159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Heinemann F, Doschke H, Radmacher M. Keratocyte lamellipodial protrusion is characterized by a concave force-velocity relation. Biophys. J. 2011;100:1420–1427. doi: 10.1016/j.bpj.2011.01.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Abraham VC, Krishnamurthi V, Taylor DL, Lanni F. The actin-based nanomachine at the leading edge of migrating cells. Biophys. J. 1999;77:1721–1732. doi: 10.1016/S0006-3495(99)77018-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Marcy Y, Prost J, Carlier MF, Sykes C. Forces generated during actin-based propulsion: A direct measurement by micromanipulation. Proc. Natl. Acad. Sci. USA. 2004;101:5992–5997. doi: 10.1073/pnas.0307704101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Gerbal F, Laurent V, Ott A, Carlier MF, Chaikin P, Prost J. Measurement of the elasticity of the actin tail of Listeria monocytogenes . Eur. Biophys. J. 2000;29:134–140. doi: 10.1007/s002490050258. [DOI] [PubMed] [Google Scholar]
- 68.MacKintosh FC, Käs J, Janmey PA. Elasticity of semiexible biopolymer networks. Phys. Rev. Lett. 1995;75:4425–4428. doi: 10.1103/PhysRevLett.75.4425. [DOI] [PubMed] [Google Scholar]
- 69.Gardel ML, Shin JH, MacKintosh FC, Mahadevan L, Matsudaira P, Weitz DA. Elastic behavior of cross-linked and bundled actin networks. Science. 2004;304:1301–1305. doi: 10.1126/science.1095087. [DOI] [PubMed] [Google Scholar]
- 70.Watanabe N, Mitchison TJ. Single-molecule speckle analysis of actin filament turnover in lamellipodia. Science. 2002;295:1083–1086. doi: 10.1126/science.1067470. [DOI] [PubMed] [Google Scholar]
- 71.Soo FS, Theriot JA. Large-scale quantitative analysis of sources of variation in the actin polymerization-based movement of Listeria monocytogenes . Biophys. J. 2005;89:703–723. doi: 10.1529/biophysj.104.051219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Córdova-Figueroa UM, Brady JF. Osmotic propulsion: The osmotic motor. Phys. Rev. Lett. 2008;100:158303. doi: 10.1103/PhysRevLett.100.158303. [DOI] [PubMed] [Google Scholar]
- 73.Brady JF. Particle motion driven by solute gradients with application to autonomous motion: continuum and colloidal perspectives. J. Fluid Mech. 2011;667:216–259. [Google Scholar]
- 74.Anderson JL. Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 1989;21:61–99. [Google Scholar]
- 75.Alexander GP, Liu AJ. Self-diffusiophoresis in the advection dominated regime. Preprint. 2011 [Google Scholar]
- 76.Co C, Wong DT, Gierke S, Chang V, Taunton J. Mechanism of actin network attachment to moving membranes: Barbed end capture by N-WASP WH2 domains. Cell. 2007;128:901–913. doi: 10.1016/j.cell.2006.12.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Uruno T, Liu J, Li Y, Smith N, Zhan X. Sequential interaction of actin-related proteins 2 and 3 (Arp2/3) complex with neural wiscott-aldrich syndrome protein (N-WASP) and cortactin during branched actin filament network formation. J. Biol. Chem. 2003;278:26086–26093. doi: 10.1074/jbc.M301997200. [DOI] [PubMed] [Google Scholar]
- 78.Siton O, Ideses Y, Albeck A, Unger T, Bershadsky AD, Gov NS, Bernheim-Groswasser A. Cortactin releases the brakes in actin-based motility by enhancing WASP-VCA detachment from Arp2/3. Curr. Biol. 2011;21:2092–2097. doi: 10.1016/j.cub.2011.11.010. [DOI] [PubMed] [Google Scholar]
- 79.Carlsson AE, Wear MA, Cooper JA. End versus side branching by Arp2/3 complex. Biophys. J. 2004;86:1074–1081. doi: 10.1016/S0006-3495(04)74182-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Akin O, Mullins RD. Capping protein increases the rate of actin-based motility by promoting filament nucleation by the Arp2/3 complex. Cell. 2008;133:841–851. doi: 10.1016/j.cell.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Soo FS, Theriot JA. Adhesion controls bacterial actin polymerization-based movement. Proc. Natl. Acad. Sci. USA. 2005;102:16233–16238. doi: 10.1073/pnas.0507022102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Bernheim-Groswasser A, Wiesner S, Golsteyn RM, Carlier MF, Sykes C. The dynamics of actin-based motility depend on surface parameters. Nature. 2002;417:308–311. doi: 10.1038/417308a. [DOI] [PubMed] [Google Scholar]
- 83.Mallavarapu A, Mitchison T. Regulated actin cytoskeleton at filopodium tips controls their extension and retraction. J. Cell. Biol. 1999;146:1097–1106. doi: 10.1083/jcb.146.5.1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Breitsprecher D, Koestler SA, Chizhov I, Nemethova M, Mueller J, Goode BL, Small VJ, Rottner K, Faix J. Cofilin cooperates with fascin to disassemble filopodial actin filaments. J. Cell Sci. 2011;124:3305–3318. doi: 10.1242/jcs.086934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Banigan EJ, Gelbart MA, Gitai Z, Wingreen NS, Liu AJ. Filament depolymerization can explain chromosome pulling during bacterial mitosis. PLoS Comput. Biol. 2011;7:e1002145. doi: 10.1371/journal.pcbi.1002145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Brangbour C, du Roure O, Helfer E, Démoulin D, Mazurier A, Fermigier M, Carlier MF, Bibette J, Baudry J. Force-velocity measurements of a few growing actin filaments. PLoS Biol. 2011;9:e1000613. doi: 10.1371/journal.pbio.1000613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Abécassis B, Cottin-Bizzone C, Ybert C, Ajdari A, Bocquet L. Boosting migration of large particles by solute contrasts. Nat. Mater. 2008;7:785–789. doi: 10.1038/nmat2254. [DOI] [PubMed] [Google Scholar]
- 88.Palacci J, Abécassis B, Cottin-Bizonne C, Ybert C, Bocquet L. Colloidal motility and pattern formation under rectied diffusiophoresis. Phys. Rev. Lett. 2010;104:138302. doi: 10.1103/PhysRevLett.104.138302. [DOI] [PubMed] [Google Scholar]
- 89.Palacci J, Cottin-Bizonne C, Ybert C, Bocquet L. Osmotic traps for colloids and macromolecules based on logarithmic sensing in salt taxis. Soft Matter. 2012;8:980–994. [Google Scholar]
- 90.Käs J, Strey H, Bärmann M, Sackmann E. Direct measurement of the wave-vector-dependent bending stiffness of freely flickering actin filaments. Europhys. Lett. 1993;21:865–870. [Google Scholar]
- 91.Gittes F, Mickey B, Nettleton J, Howard J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 1993;120:923–934. doi: 10.1083/jcb.120.4.923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Isambert H, Venier P, Maggs AC, Fattoum A, Kassab R, Pantaloni D, Carlier MF. Flexibility of actin laments derived from thermal fluctuations. effect of bound nucleotide, phalloidin, and muscle regulatory proteins.factor stimulation. J. Biol. Chem. 1995;270:11437–11444. doi: 10.1074/jbc.270.19.11437. [DOI] [PubMed] [Google Scholar]
- 93.Götter R, Kroy K, Frey E, Bärmann M, Sackmann E. Dynamic light scattering from semidilute actin solutions: A study of hydrodynamic screening, filament bending stiffness, and the effect of tropomyosin/troponin-binding. Macromolecules. 1996;29:30–36. [Google Scholar]
- 94.Käas J, Strey H, Tang JX, Finger D, Ezzell R, Sackmann E, Janmey PA. F-actin, a model polymer for semiflexible chains in dilute, semidilute, and liquid crystalline solutions. Biophys. J. 1996;70:609–625. doi: 10.1016/S0006-3495(96)79630-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Podolski JL, Steck TL. Length distribution of F-actin in Dictyostelium discoideum. J. Biol. Chem. 1990;265:1312–1318. [PubMed] [Google Scholar]
- 96.Bailly M, Macaluso F, Cammer M, Chan A, Segall JE, Condeelis JS. Relationship between Arp2/3 complex and the barbed ends of actin filaments at the leading edge of carcinoma cells after epidermal growth factor stimulation. J. Cell Biol. 1999;145:331–345. doi: 10.1083/jcb.145.2.331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Pollard TD. Rate constants for the reactions of ATP- and ADP-actin with ends of actin filaments. J. Cell Biol. 1986;103:2747–2754. doi: 10.1083/jcb.103.6.2747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Blanchoin L, Pollard TD, Mullins RD. Interactions of ADF/cofilin, Arp2/3 complex, capping protein and profilin in remodeling of branched actin filament networks. Curr. Biol. 2000;10:1273–1282. doi: 10.1016/s0960-9822(00)00749-1. [DOI] [PubMed] [Google Scholar]
- 99.Schafer DA, Jennings PB, Cooper JA. Dynamics of capping protein and actin assembly in vitro: Uncapping barbed ends by polyphosphoinositides. J. Cell Biol. 1996;135:169–179. doi: 10.1083/jcb.135.1.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.