Abstract
We investigated how changes in outcome magnitude affect behavioral variation in human volunteers. Participants entered strings of characters using a computer keyboard, receiving feedback (gaining a number of points) for any string at least 10 characters long. During a “surprise” phase in which the number of points awarded was changed, participants only increased their behavioral variability when the reward value was downshifted to a lower amount, and only when such a shift was novel. Upshifts in reward did not have a systematic effect on variability.
Keywords: Human learning, Variability
When presented with novel activities, we must identify which behaviors or strategies lead to successful outcomes. In most cases, this is not a matter of identifying a single “perfect” action that always results in success; instead, many activities demand that behavior display an ongoing degree of variability. In this respect, mastery of a task consists not only of minimizing “errors” but also sustaining appropriate levels of variability in our actions (Stokes, 2001).
In behavioral paradigms, variability has often been characterized in terms of “operant response classes.” Rather than reinforcing a single discrete behavior, schedules instead reinforce those behaviors that belong to broad classes that vary along multiple dimensions, such as timing and response topography. The degree of variability of these various dimensions can also be shaped by feedback (Shahan & Chase, 2002).
Organisms can readily increase or decrease behavioral variability, whether responses are constrained to a narrow class (Davison & Baum, 2000) or widened to broad conceptual categories (Neuringer & Jensen, 2010). Indeed, behavioral variability seems not only inescapable but also often manifests at the precise levels appropriate to a given context; response variability not only adapts, but is also adaptive (Neuringer, 2002).
Experimental evidence suggests that strategic increases in variability precede the discovery of new problem-solving strategies. Greater variability during skill acquisition is associated with greater learning (Stokes et al., 2008). This pattern of “variability-as-path-to-discovery” is observed in children mastering grammatical rules (Bowerman, 1982), learning to solve arithmetic problems (Siegler & Jenkins, 1989), or acquiring novel concepts (Goldin-Measdow et al., 1993). Furthermore, children who use more strategies when first learning a task acquire the correct strategy more often than those with fewer initial strategies (Siegler, 1995). This is also seen in adults making novice-to-expert transitions in radiology (Lesgold et al., 1988) or cardiology (Johnson et al., 1981), where greater variability precedes acquisition of advanced diagnostic expertise. This makes modulating levels of variability central to exploration/exploitation strategies (March, 1991).
The increase in variability under extinction protocols is well-established (see Balsam et al., 1997, for a review), and this may simply be a basic principle of behavior. Natural selection plausibly favors mechanisms for generating variability in the face of failure, and such a mechanisms would have relevance to a wide range of problem domains (Neuringer, 2002). In studies of extinction, reported changes in behavior are often more quantitative than qualitative. Neuringer et al. (2001) report, for example, that although extinction increased the frequency of rare response sequences, relatively common sequences were still exhibited more often than their uncommon counterparts. In addition to extinction effects, intermediary levels of variability are observed when reinforcement is reduced without being entirely extinguished. Stahlman & Blaisdell (2011) report that variation in response form increases as the probability of reinforcer delivery is lowered, as well as when the magnitude of the reward is reduced or the delay to reward delivery is increased.
According to associative theories of Pavlovian conditioning, learning (and resulting changes in behavior) depends on surprising outcomes that are processes differently from the status quo (Kamin, 1969; Rescorla & Wagner, 1972; Wagner & Brandon, 1989). Surprising events (whether they be positive or negative) thus result in “prediction error” necessary to discovering causal relationships (Elsner & Hommel, 2004). This behavioral literature complements findings that valence-independent prediction error signals can be observed in the brain (Schultz, 2006; Wang & Tsien, 2011). A Pavlovian account of variability in response to novel events might thus begin by examining whether a prediction error might result in a shift in behavioral variability.
In practice, however, the simple ‘valence-independent’ symmetry of early prediction error models (in which unexpected reinforcement has an equivalent effect to an equally unexpected failure to obtain reinforcement) requires revision to accommodate experimental evidence. Even when outcomes are programmed using Pavlovian schedules, infrequent reinforcement corresponds to increased behavioral variability (Stahlman et al., 2010). When reinforcement is infrequent, the overall uncertainty is lower (because most trials are correctly predicted to be unreinforced); despite this, an increase in variability is observed. Whether or not trial-specific prediction errors play a roll, results such as these suggest that a degree of “induced variability” can be expected independent of whether the schedule directly reinforces “functional variability.”
Amsel’s frustration theory (Amsel, 1992) proposes a mechanism that may increase variability during extinction and other schedules with downshifted outcomes. If afferent feedback from formerly reinforced responses becomes aversive in extinction, then variants that do not produce this feedback will be negatively reinforced. Additionally, this “non-reward frustration” changes the general stimulus conditions, thus altering the relative strength of different responses and/or switching attention to different stimuli that might control different responses. Amsel’s account draws on a large body of experimental work (Killeen, 1994), and has been invoked to explain behavior in a wide range of species (Papini, 2002).
Surveying this literature suggests a variety of hypotheses. The classical prediction-error view might suggest that any uncued change in the explicit value of an outcome should impact variability; a more nuanced interpretation might suggest that only the initial (very unexpected) changes might have an effect, as subsequent changes come to be expected (and thus correspond to less dramatic prediction errors). On the other hand, an account that places special importance on downshifts in outcome value (such as Amsel’s frustration theory) might predict increased variability only in cases where the value of the outcome is reduced. It is also unclear whether extinction differs from more general downshift, so reducing an outcome’s value to zero might have an effect that is distinct from other reductions.
Because the literature has primarily emphasized the effects of low probabilities of informative feedback, we examined the effects of varying explicit reward magnitudes. In our experiment, participants generated arbitrary strings using a keyboard and were presented with different surprising changes in the value of response outcomes. After participants repeatedly earned points (delivered 10 at a time), they experienced one of three conditions: “Extinction” (where feedback was shifted to 0 points), “Downshift” (where feedback was shifted to 1 point), and “Upshift” (where feedback was shifted to 100 points). These shifts in point values were introduced unexpectedly and then, after a brief period, were revoked. We examined the response variability as a factor of this brief exposure to a surprising condition.
Method
Participants
Participants were 30 Barnard undergraduates (all female) who participated in the experiment to fulfill an Introductory Psychology class requirement.
Apparatus
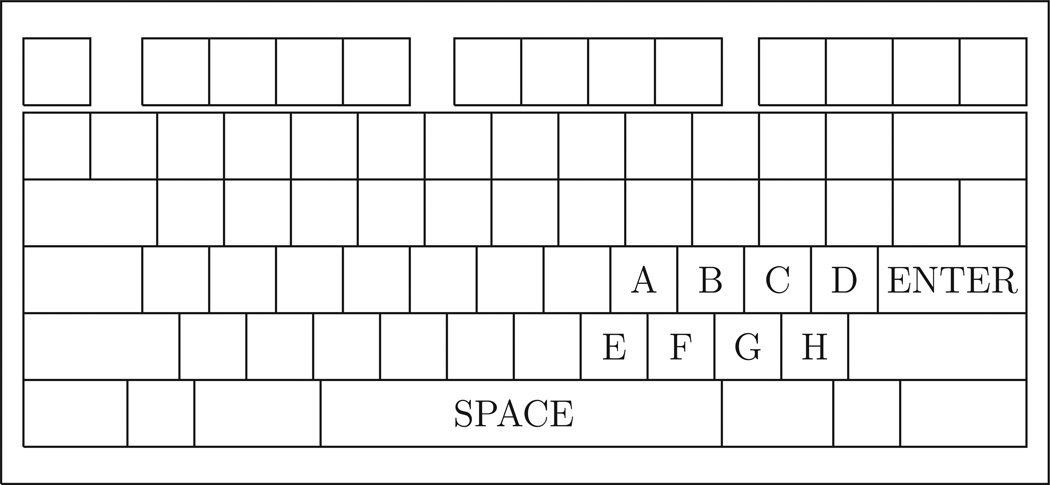
Participants made responses using a personal computer enclosed in a 1.5m×3.5m experimental room. Participants used a modified QWERTY keyboard, with all keys covered except for the Space key, the Enter key, and the eight characters in the string “kl;’m,./” (for clarity, denoted as ABCDEFGH), as depicted in Figure 1. The eight symbolic keys (that is, those other than the Enter and Space keys) are collectively referred to as the “Alpha” keys. Any keys unlabeled in Figure 1 were blocked from view and could not be used.
Figure 1.
Keyboard layout used in the experiment. Key letters are labeled A through H for clarity. Unlabeled keys were covered and could not be pressed.
The apparatus was identical to that used by (Stokes et al., 1999), where it is described in more detail.
Procedure
Participants were randomly assigned to three groups: Extinction, Downshift, and Upshift. These groups underwent identical training before beginning the experimental component of the experiment. Throughout the experiment, Participants were given feedback with “points” awarded on the computer screen, presented as black numbers in a white rectangle. Note that an explicit award of 0 points was distinct from receiving no feedback at all.
Training Component
Participants were instructed to earn points by pressing keys and to use the ten keys depicted in Figure 1; aside from these two statements, they were given no further verbal instruction, learning the remaining details of the task by trial and error. During training, each reinforcer was worth 10 points. Their responding was shaped in six stages, with each stage persisting until 10 reinforcers were collected, except where noted:
A blue rectangle was presented on screen. Reinforcement was delivered each time Enter was pressed.
A blue rectangle was presented on screen. After a press to any Alpha key, the upper-right corner of the rectangle turned white. Pressing Enter produced a reinforcer when the white corner was visible.
A red rectangle was presented on screen. The rectangle remained red until Space was pressed, which turned the rectangle blue. After any one press to an Alpha key, the blue rectangle’s white corner indicated that a reinforcer could be earned by pressing Enter.
Identical to (3), except that at least three Alpha key presses were required to make the white corner visible. Repeated responses to an Alpha key were counted toward this requirement.
Identical to (4), except that at least six Alpha key presses were required to make the white corner visible.
Identical to (5), except that at least ten Alpha key presses were required to make the white corner visible.
Identical to (6), with the exception that the white corner ceased to appear, so participants were no longer given an explicit cue indicating they had made a sufficient number of responses.
Experimental Component
In this component, the white corner never appeared, so participants were not given an explicit cue that they had made a sufficient number of responses. However, if their “response sequence” (the series of responses made between the initial Space response and the final Enter response) contained fewer than 10 Alpha key presses, the task went directly to presenting the red rectangle without providing feedback. As such, participants were still given a cue indicating that at least 10 Alpha responses were required. Beyond the requirement response sequences consisted of at least 10 Alpha responses, preceded by Space and followed by Enter, any combination of responses was permitted, including repeating the same Alpha key ten times. Reinforcement was not contingent on which Alpha responses were emitted.
In all three groups, participants made responses until 40 reinforcers had been earned. We will henceforth refer to this as “Phase 1” of the experiment. As in training, each reinforcer earned participants 10 points, so Phase 1 consisted of a total of 400 points earned.
Phase 2 of the experiment was the “Surprise Phase” and consisted of 10 consecutive reinforcers. In the Extinction group, participants were given an explicit reinforcer worth 0 points (although the requirement to emit at least 10 responses to receive explicit feedback was still in effect). In the Downshift group, participants received reinforcers worth 1 point. In the Upshift group, participants received reinforcers worth 100 points.
In Phase 3, participants returned to earning 10 points per reinforcer, as in Phase 1. This persisted for a total of 50 reinforcers, or 500 points. Across all phases, the experimental component consisted of as many trials as was necessary to earn 100 reinforcers.
Results
In order to compare the 10 reinforcers during Phase 2 with the 40 reinforcers in Phase 1 (and the 50 reinforcers in Phase 3), the history of responses was divided into “subphases” of 10 consecutive reinforcers apiece. From this point forward, “Phase 1” will refer to the 40 reinforcers in their entirety, whereas “Subphase 1-1” will refer to the first 10 reinforcers, “Subphase 1–2” to the second 10, and so forth; the same subdivision will be used for Phase 3.
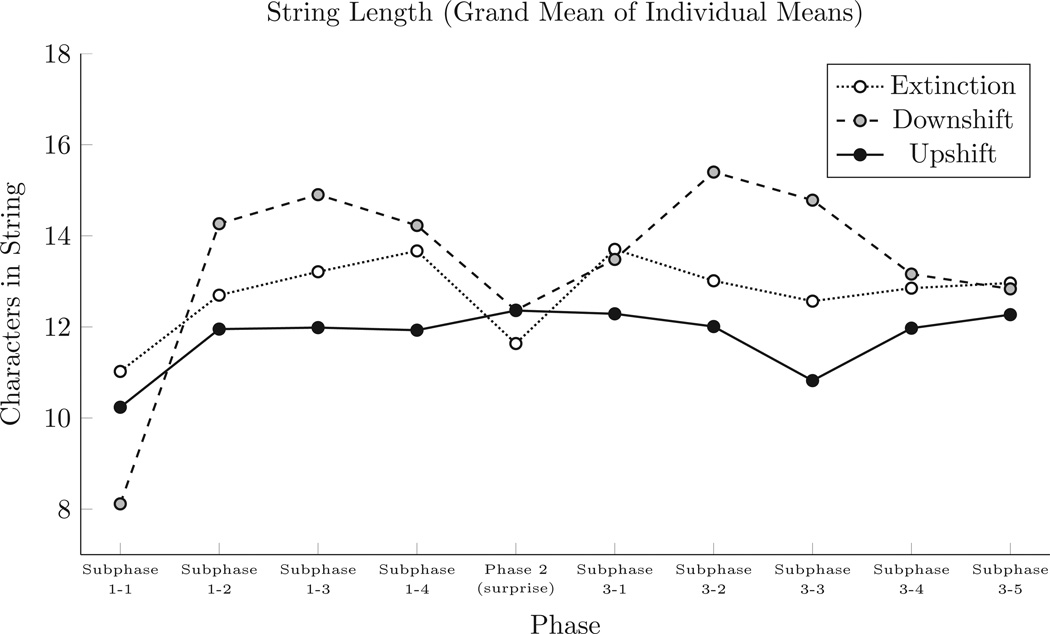
The mean length of response sequences emitted in each subphase was calculated for each participant. Figure 2 presents the grand mean (across participants) of those means. A mixed-model repeated-measures analysis of variance (ANOVA) was performed comparing the effect of subphase (within subjects) and condition (between subjects) on subjects’ mean string lengths. A significant effect was found for subphase (F(9,243) > 4.19, p < .0001). In a post-hoc Tukey test, Subphase 1-1 was found to be significantly different (p < 0.04) from all other subphases: Subjects had significantly shorter string lengths in Subphase 1-1 than in subsequent subphases of the experiment. Otherwise, no significant differences were found, including any effect resulting from the “surprise” manipulation.
Figure 2.
Mean length of strings entered via the keyboard during each phase. Means were calculated for each subject, and grand means were calculated from those means.
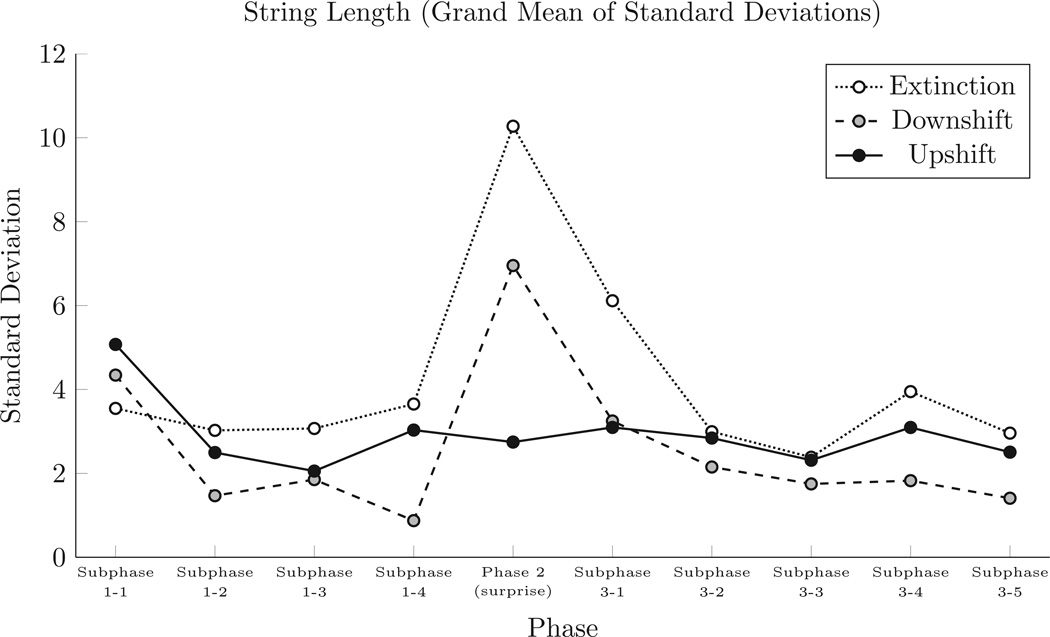
In addition to performing an analysis comparing the mean lengths in each subphase, we examined the mean of participant standard deviations for each subphase. Figure 3 shows these across-subject means of within-subphase standard deviations, and suggests a considerable increase in the variance during the surprise manipulation in the Extinction and the Downshift conditions, but no such change in the Upshift condition. We performed a mixed-model repeated-measures ANOVA comparing the effect of subphase (within subjects) and condition (between subjects) on subjects’ within-subphase standard deviations, and found a significant effect for subphase (F(9,243) > 10.5, p < .0001). We also found a significant interaction between subphase and condition (F(18,243) > 4.9, p < .0001). In a post-hoc Tukey test, we found that the Surprise Phase in the Extinction condition was significantly different (p < .002) than all other subphases, with the exception of Subphase 3-1. In the Downshift condition, the Surprise Phase was significantly different (p < .01) from all subphases except Subphase 1-1. Additionally, there was a significant difference (p < .03) between Subphases 1-1 and 1–4 in the Downshift condition. However, the only result from the Upshift condition was that Subphase 1-1 differed (p < .02) from all other subphases; its Surprise Phase was indistinguishable from any subphase apart from the first.
Figure 3.
Standard deviations of string lengths during each phase. SDs were calculated for each subject, and grand means were calculated from those SDs.
These results suggest that the surprise manipulation had a distinctive effect on responding, but only when the points awarded were unexpectedly reduced from their previous levels. The return to 10-point reward in Phase 3 had no discernible effect. However, an increase in the variance of length during the Surprise Phase might be independent of increased variability in the content of those strings.
To determine whether the content of the response strings changed as a result of the surprising manipulation in Phase 2, we compared strings in terms of “Levenshtein Distance” (Levenshtein, 1966). Levenshtein distance, described in detail in Appendix A, is a metric of the “edit distance” between two strings, which refers to the minimum number of discrete operations necessary to change one string into another.
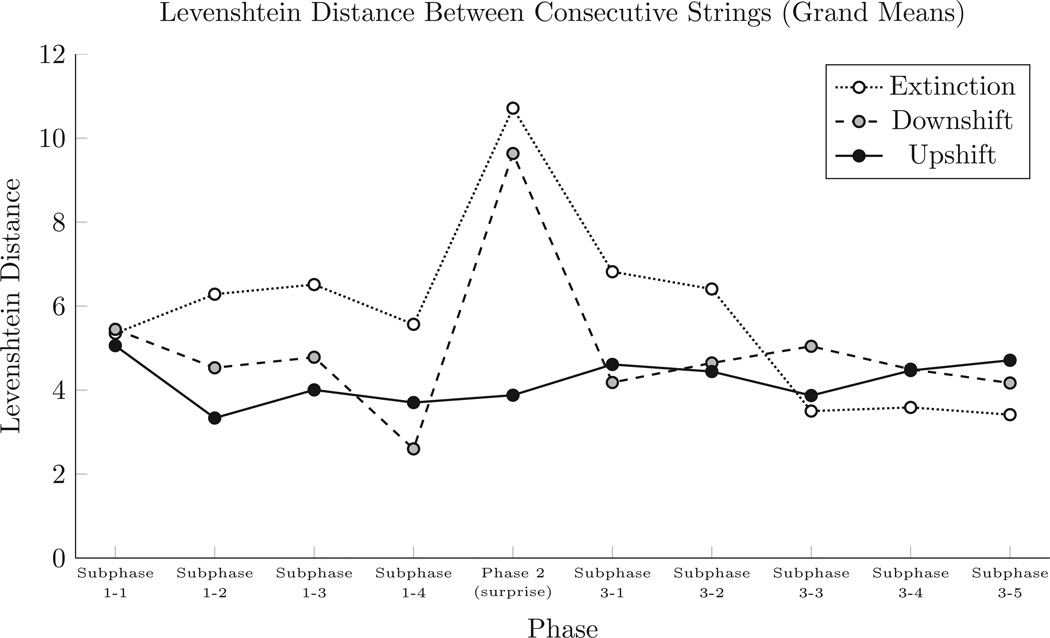
For each participant in each subphase, we calculated the Levenshtein distance between each consecutive pair of strings (first to second, second to third, etc.). We then computed the mean distance in each subphase as an overall estimator of how much participants varied their responses as each subphase progressed. Figure 4 presents these grand means of the within-subject mean Levenshtein distances for each subphase.
Figure 4.
Mean Levenshtein distance between consecutive strings during each phase. These distances were averaged for each subject, and grand means were calculated from those individual means.
As with string length, we performed a mixed-model repeated-measures ANOVA comparing the effects of subphase (within subjects) and condition (between subjects). We found a significant effect for subphase (F(9,243) > 5.6, p < .0001), as well as a significant interaction between subphase and condition (F(18,243) > 3.9, p < .0001). In a post-hoc Tukey test, we found significant differences in the Downshift condition: The Surprise Phase was significantly different from all other phases (p < .004). In the Extinction condition, the Surprise Phase differed significantly from Subphases 1-1, 1–4, 3-3, 3–4, and 3–5 (p < .05). All other subphase comparisons, including all comparisons from the Upshift condition, were non-significant.
In order to confirm that consecutive Levenshtein distances were representative of overall behavioral variability (as opposed to, for example, merely being the result of switching between two sequences), we calculated the average distance between all pairs of response strings (Pinheiro et al., 2005). The resulting means in phase 2 (μext = 14.00, μdown = 10.16, μup = 5.36) were similar to those in Figure 4, as were those in subphase 1–4 (μext = 9.07, μdown = 6.44, μup = 7.26) and subphase 3-1 (μext = 8.91, μdown = 5.69, μup = 6.64). The mean distance between pairs is a Hoeffding (1948) U-statistic of level 2, and as such its full statistical analysis is beyond the scope of this paper. To confirm that these differences were significant, a rank transformation of the means was performed, allowing ANOVA to be used as a robust nonparametric test (Conover & Iman, 1981). When applied to the data from Phase 2, the significant effect of the change in point value is confirmed by this nonparametric analysis (F(2,26) > 6.3, p < .006).
Discussion
We trained subjects to enter strings of responses, requiring only that these strings begin with Space, end with Enter, and consist of at least ten intervening Alpha key presses chosen from a bank of eight alternatives. Each sequence meeting these criteria was awarded 10 points in the first and third phases of the experimental component. Between these was a “surprise” phase, during which the number of points awarded was changed to one of three values: 0 (in the Extinction group), 1 (in the Downshift group), or 100 (in the Upshift group).
We observed that response variability increased during the surprise phase for the Extinction and Downshift groups, but not for the Upshift group. This is consistent with results showing that “unexpected downshifts” generally elicit variability, while also confirming that a surprising change in the rewards is not sufficient to do so. Additionally, the Upshift group also experienced a 10-fold downshift in the value of the reward at the end of the surprise phase, but this did not have any detectable impact on their behavior. This suggests that the unexpected nature of the initial downshift is an important characteristic of the manipulation, because it introduces a new kind of change to the participant’s learning history.
Unlike traditional extinction schedules, we did not withhold information from participants. Rather than use probabilistic reinforcement (e.g. Stahlman & Blaisdell, 2011; da Silva Souza et al., 2010) or outright extinction (Neuringer et al., 2001; Kinloch et al., 1981), our procedure was more akin to the “successive negative contrast” effects observed when outcomes unexpectedly worsen (Freidin et al., 2009). In our Extinction group, participants were given explicit feedback that ‘0 points’ were earned upon success, whereas they were given no feedback at all upon failure. Thus, the informative value of the feedback regarding whether each trial was correct was identical across conditions. It is inappropriate to interpret the point values of awarded by this feedback as corresponding to their “reinforcement value” in the classical sense, because number of points awarded was independent of how informative the feedback was about whether a string was deemed acceptable by the schedule.
Another benefit of the Alpha-sequence paradigm (previously described in Stokes et al., 1999) was that response strings had many degrees of freedom: Given 8 alpha keys, participants had over 1 billion ‘10-response’ strings to choose from. Tasks that constrain possible variability can be insensitive to differences in behavior, especially over short windows of time. This is why many extinction studies require hundreds or thousands of trials to obtain parametric estimates. Because of the combinatorial growth of possible strings, a sequence of discrete responses can easily entail much greater uncertainty than any single response sampled from a continuous multivariate space.
For example, spatial tasks (e.g. Stahlman & Blaisdell, 2011) constrain the range of behaviors judged to be “effective” because they only have a few dimensions along which to vary. Stahlman et al. (2010) report gradual shifts in the standard deviation of recorded behaviors on the order of at most 25%. By contrast, our reported variability changes were substantial: Our two downshifted groups at least doubled their standard deviations, doing so abruptly (Figure 3). We hesitate to directly compare the amount of variability we observed to those present in animal studies, but the increase in variability we observed appeared more acute and pronounced than the “induced variability” that arises in more constrained response paradigms.
The Levenshtein Distance provided a way to analyze these complex responses. As (Nickerson, 2002) points out, “variability” has several technical definitions. According to his classifications, Levenshtein Distance is a measure of compressibility, in contrast to more common measures of behavioral entropy (Neuringer, 2002). Entropy estimates require many observations, because estimators of entropy based on observed frequencies are biased, having error of approximately for k sequences and n observations (Roulston, 1999). Given a rule of thumb that bias can be kept small by requiring that n ≥ 5k, our Surprise phase did not consist of enough observations to obtain a reliable estimate, even in pairs of key-presses (for which k = 82 = 64). Consequently, entropy estimates were not appropriate, given the short duration of our manipulation. Contrastingly, the Levenshtein Distance reliably measures variability in arbitrarily long strings, a property exploited by computational biologists measuring mutation in genetic data (Gusfield, 1997). Future studies examining the effects of schedule- or prediction-error-induced variability can use this metric to complement findings from entropy-based metrics, as well as branch out to paradigms that are ill-suited to entropy estimation.
Recent studies suggests that Pavlovian learning about causal relationships is unlikely to be driven by mere contiguity, but instead depends on statistical contingency (Moore et al., 2009). According to this view, downshifted participants may have increased their variability in order to investigate the relationship between points and the input string. Such an account still does not eliminate the role of prediction error, however, because the Upshift group also experienced a tenfold downshift at the end of the surprise phase and did not change their behavior at that time. This suggests that increasing variability as a form of ‘hypothesis testing’ may depend on the relative unfamiliarity of the task conditions. This interpretation is compatible with a signal detection account of learning, in which the perceived degree of contingency between outcomes is modeled in psychophysical terms (Allan et al., 2008).
These results contribute to a growing literature examining how the properties of a conditioned stimulus are interpreted. For example, the information conveyed by a stimulus depends on the multiple layers of conditional probability used by an organism to build predictions (Bromberg-Martin et al., 2010). Any theory invoking ‘prediction error’ must thus account for the complexity of an organism’s prediction model. Similar results have been observed in studies comparing how different learning histories lead to distinctly different behaviors under an otherwise identical schedule (Stokes et al., 1999; da Silva Souza et al., 2010).
The interpretation that variability arises from primary drives, such as frustration (Amsel, 1992), suggests a very different underlying mechanism, wherein variability manifests explicitly as a component of an exploratory strategy (Freidin et al., 2009). According to this view, the dramatic effect in the downshift groups (as compared to the lack of any effect at all in the Upshift group) would not necessarily reflect changes in judgments of response dependency, but might instead point to framing effects: The 100-to-10 transition at the end of the surprise Upshift would constitute a return to the norm, rather than an aversive downshift in reward value. An important future direction in identifying these relationships will be to determine the degree to which learning mechanisms (and their resulting behavioral manifestations) depend on both the contingency detection and contextual outcome valence (Bromberg-Martin et al., 2010; Wang & Tsien, 2011).
In conclusion, we found that the way in which participants reacted to a surprising change in feedback depended on whether the change improved or worsened conditions. Although this result does not preclude a role for prediction error, it rules out the claim that any unexpected change is sufficient to induce variability. These results also rule out the claim that increased variability necessarily follows from downshifts, as the 100-to-10 point transition in the Upshift group did not result in a change in behavior. In our experiment, both the unexpected nature of the shift and its direction appeared to play a role. This emphasizes the importance of interpreting task cues not on their objective properties, but rather as they relate to an organism’s learning history.
Acknowledgments
The authors wish to thank Karen Zechowy and Jacqui Rick for their assistance in conducting this experiment. This work was supported by the National Institute of Mental Health Grant 5R01MH068073 awarded to Peter Balsam.
Appendix A
Levenshtein distance (Levenshtein, 1966) is a metric for measuring the “edit distance” between two strings of symbols. Put another way, it is a count of the smallest number of edits needed to switch from one string to the other.
Each edit is a discrete operation. Levenshtein distance counts three varieties of edit:
Insertion (“sit” → “skit” by inserting a “k”)
Deletion (“chat” → “cat” by deleting the “h”)
Substitution (“stale” → “stole” by replacing the “a” with an “o”)
Levenshtein distance is easily calculated using a dynamic programming algorithm (Gusfield, 1997). The following pseudocode describes an algorithm that calculates the distance between two strings s and t:
Algorithm 1.
How to calculate Levenshtein distance
 |
Below is an example comparing the strings “shout” and “scuttle” (minima in bold):
| Step 1: Setup | Step 2: First loop | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| s | c | u | t | t | l | e | s | c | u | t | t | l | e | ||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| s | 1 | s | 1 | 0 | |||||||||||||
| h | 2 | h | 2 | 1 | |||||||||||||
| o | 3 | o | 3 | 2 | |||||||||||||
| u | 4 | u | 4 | 3 | |||||||||||||
| t | 5 | t | 5 | 4 | |||||||||||||
Each position in the matrix compares the two strings up a certain letter. For example, the cell (2,2) compares the string “sc” to the string “sh.” The Levenshtein distance can easily be calculated by testing whether each additional letter increases or reduces the number of edits needed to match the strings.
First, the matrix d is initialized with starting values. Then, repeatedly looping through the columns of the table, the minimal path from one string to the other is traced by the bold values.
| Step 3: Ongoing | Step 4: Complete | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| s | c | u | t | t | l | e | s | c | u | t | t | l | e | ||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| s | 1 | 0 | 1 | 3 | 4 | 5 | s | 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ||
| h | 2 | 1 | 1 | 2 | 3 | 4 | h | 2 | 1 | 1 | 2 | 3 | 4 | 5 | 6 | ||
| o | 3 | 2 | 2 | 2 | 3 | 4 | o | 3 | 2 | 2 | 2 | 3 | 4 | 5 | 6 | ||
| u | 4 | 3 | 3 | 2 | 3 | 4 | u | 4 | 3 | 3 | 2 | 3 | 4 | 5 | 6 | ||
| t | 5 | 4 | 4 | 3 | 2 | 3 | t | 5 | 4 | 4 | 3 | 2 | 3 | 4 | 5 | ||
In other words, the minimum edit distance from “shout” to “scuttle” is 5 (substitute H for C, delete O, and insert T, L, and E).
Contributor Information
Greg Jensen, Columbia University.
Patricia Stokes, Barnard College & Columbia University.
Anthea Paterniti, Barnard College.
Peter Balsam, Barnard College & Columbia University.
References
- Allan LG, Hannah SD, Crump MJC, Siegel S. The psychophysics of contingency assessment. Journal of Experimental Psychology: General. 2008;137:226–243. doi: 10.1037/0096-3445.137.2.226. [DOI] [PubMed] [Google Scholar]
- Amsel A. Frustration theory. Cambridge: Cambridge University Press; 1992. [Google Scholar]
- Balsam P, Deich J, Ohyama T, Stokes PD. Origins of new behavior. In: O’Donohue W, editor. Learning and behavior therapy. Boston: Allyn and Bacon; 1997. pp. 403–421. [Google Scholar]
- Bowerman M. Starting to talk worse: Clues to language acquisition from children’s late speech errors. In: Strauss S, editor. U-shaped behavior growth. New York: Academic Press; 1982. pp. 101–145. [Google Scholar]
- Bromberg-Martin ES, Matsumoto M, Hikosaka O. Dopmaine in motivational control: Rewarding, aversive, and alerting. Neuron. 2010;68:815–834. doi: 10.1016/j.neuron.2010.11.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conover WJ, Iman RL. Rank transformations as a bridge between parametric and nonparametric statistics. The American Statistician. 1981;35:124–129. [Google Scholar]
- da Silva Souza A, Abreu-Rodrigues J, Baumann AA. History effects on induced and operant variability. Learning & Behavior. 2010;38:426–437. doi: 10.3758/LB.38.4.426. [DOI] [PubMed] [Google Scholar]
- Davison M, Baum WM. Choice in a variable environment: Every reinforcer counts. Journal of the Experimental Analysis of Behavior. 2000;74:1–24. doi: 10.1901/jeab.2000.74-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elsner B, Hommel B. Contiguity and contingency in action-effect learning. Psychological Research. 2004;68:138–154. doi: 10.1007/s00426-003-0151-8. [DOI] [PubMed] [Google Scholar]
- Freidin E, Cuello MI, Kacelnik A. Successive negative contrast in a bird: Starlings’ behaviour after unpredictable negative changes in food quality. Animal Behaviour. 2009;77:857–865. [Google Scholar]
- Goldin-Measdow S, Alibani MW, Church RB. Transitions in concept acquisition: Using the hand to read the mind. Psychological Review. 1993;100:279–297. doi: 10.1037/0033-295x.100.2.279. [DOI] [PubMed] [Google Scholar]
- Gusfield D. Algorithms on strings, trees and sequences: Computer science and computational biology. Cambridge: Cambridge University Press; 1997. [Google Scholar]
- Johnson PE, Duran AS, Hassebrock F, Moller J, Prietula M, Feltovich PJ, Swanson DB. Expertise and error in diagnostic reasoning. Cognitive Science. 1981;5:235–283. [Google Scholar]
- Kamin LJ. Selective associations and conditioning. In: Mackintosh NJ, Honig WK, editors. Fundamental issues in associative learning. Halifax: Dalhousie University Press; 1969. pp. 42–64. [Google Scholar]
- Killeen PR. Frustration: Theory and practice. Psychonomic Bulletin & Review. 1994;1:323–326. doi: 10.3758/BF03213973. [DOI] [PubMed] [Google Scholar]
- Kinloch JM, Foster TM, McEwan JSA. Extinction-induced variability in human behavior. The Psychological Record. 1981;59:347–370. [Google Scholar]
- Lesgold A, Rubinson H, Feltovich P, Klopfer RGD, Wang Y. Expertise is a complex skill: Diagnosing x-ray pictures. In: Chi MTH, Glaser R, Farr MJ, editors. The nature of expertise. Hillsdale, NJ: Erlbaum; 1988. pp. 311–342. [Google Scholar]
- Levenshtein VI. Binary codes capable of correcting deletions, insertions, and reversals. Soviet Physics - Doklady. 1966;10:707–710. [Google Scholar]
- March JG. Exploration and exploitation in organizational learning. Organization Science. 1991;2:71–87. [Google Scholar]
- Moore JW, Lagnado D, Deal DC, Haggard P. Feelings of control: Contingency determines experience of action. Cognition. 2009;110:279–283. doi: 10.1016/j.cognition.2008.11.006. [DOI] [PubMed] [Google Scholar]
- Neuringer A. Operant variability: Evidence, functions, and theory. Psychonomic Bulletin & Review. 2002;9:672–705. doi: 10.3758/bf03196324. [DOI] [PubMed] [Google Scholar]
- Neuringer A, Jensen G. Operant variability and voluntary action. Psychological Review. 2010;117:972–993. doi: 10.1037/a0019499. [DOI] [PubMed] [Google Scholar]
- Neuringer A, Kornell N, Olufs M. Stability and variability in extinction. Journal of Experimental Psychology: Animal Behavior Processes. 2001;27:79–94. [PubMed] [Google Scholar]
- Nickerson RS. The production and perception of randomness. Psychological Review. 2002;109:330–357. doi: 10.1037/0033-295x.109.2.330. [DOI] [PubMed] [Google Scholar]
- Papini MR. Pattern and process in the evolution of learning. Psychological Review. 2002;109:186–201. doi: 10.1037/0033-295x.109.1.186. [DOI] [PubMed] [Google Scholar]
- Pinheiro HP, de Souza Pinheiro A, Sen PK. Comparison of genomic sequences using the hamming distance. Journal of Statistical Planning and Inference. 2005;130:325–339. [Google Scholar]
- Rescorla RA, Wagner AR. A theory of pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement. In: Black AH, Prokasy WF, editors. Classical conditioning ii: Current research and theory. New York: Appleton-Century-Crofts; 1972. pp. 64–99. [Google Scholar]
- Roulston M. Estimating the errors on measured entropy and mutual information. Physica D: Nonlinear Phenomena. 1999;125:285–294. [Google Scholar]
- Schultz W. Behavioral theories and the neurophysiology of reward. Annual Review of Psychology. 2006;57:87–115. doi: 10.1146/annurev.psych.56.091103.070229. [DOI] [PubMed] [Google Scholar]
- Shahan TA, Chase PN. Novelty, stimulus control, and operant variability. The Behavior Analyst. 2002;25:175–190. doi: 10.1007/BF03392056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siegler RS. How does change occur? a microgenetic study of number conservation. Cognitive Psychology. 1995;28:225–273. doi: 10.1006/cogp.1995.1006. [DOI] [PubMed] [Google Scholar]
- Siegler RS, Jenkins E. How children discover new strategies. Hillsdale, NJ: Erlbaum; 1989. [Google Scholar]
- Stahlman WD, Blaisdell AP. The modulation of operant variation by the probability, magnitude, and delay of reinforcement. Learning & Motivation. 2011;42:221–236. doi: 10.1016/j.lmot.2011.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stahlman WD, Young ME, Blaisdell AP. Response variability in pigeons in a pavlovian task. Learning & Behavior. 2010;38:111–118. doi: 10.3758/LB.38.2.111. [DOI] [PubMed] [Google Scholar]
- Stokes PD. Variability, constraints, and creativity: Shedding light on claude monet. American Psychologist. 2001;56:355–359. [PubMed] [Google Scholar]
- Stokes PD, Lai B, Holtz D, Rigsbee E, Cherrick D. Effects of practice on variability, effects of variability on transfer. Journal of Experimental Psychology: Human Perception and Performance. 2008;34:640–659. doi: 10.1037/0096-1523.34.3.640. [DOI] [PubMed] [Google Scholar]
- Stokes PD, Mechner F, Balsam P. Effects of different acquisition procedures on response variability. Animal Learning & Behavior. 1999;27:28–41. [Google Scholar]
- Wagner AR, Brandon S. Evolution of a structured connectionist model of pavlovian conditioning (æsop) In: Klein SB, Mowrer RR, editors. Contemporary learning theory: Pavlovian conditioning and the status of traditional learning theory. Hillsdale, NJ: Erlbaum; 1989. pp. 149–189. [Google Scholar]
- Wang DV, Tsien JZ. Convergent processing of both positive and negative motivational signals by the vta dopamine neuronal populations. PLoS ONE. 2011;6:e17047. doi: 10.1371/journal.pone.0017047. [DOI] [PMC free article] [PubMed] [Google Scholar]