Stability of tibial defect reconstruction with fibular graft and unilateral external fixation: a finite element study

Abstract

Tibial defect is generally caused by high-energy injury, tumor, osteomyelitis, development deformity and bone non-union after internal fixation. This study was to determine stability of tibial defect reconstruction with fibular graft (FG) of different lengths by single free vascularized fibular graft (SFVFG) and double-barrel free vascularized fibular graft (DBFVFG). The left lower extremity of a male volunteer was scanned with computer tomography scanner. The contours of the tibia and fibula were extracted and the geometry of both bones rebuilt. From this intact model, the models of tibial defect reconstruction with fibular graft and external fixation were developed. Inter-fragmentary motion (IFM) and Von Mises stress on the fibular bone flap, and the locations of maximum Von Mises stress were introduced to quantify the biomechanical environment. Under the condition of the same graft length, the Von Mises stress value in DBFVFG group was 1.37 to 1.77 times higher than that in SFVFG group. When the length of graft was greater than 15 cm in the SFVFG group, the IFM exceeded 1 mm, but the IFM of the graft in the DBFVFG group was always less than 1 mm. The maximum Von Mises stress of models was frequently located at the second or third pin-bone interface. Thus, external fixation can provide a stable biomechanical environment for the reconstruction of tibial defect by both SFVFG and DBFVFG. The second or third pin-bone interface requires intensive care and that in the reconstruction of tibial defect by SFVFG, the graft length should not exceed 15 cm.

Introduction

Tibial defect is generally caused by high-energy injury, tumor, osteomyelitis, development deformity and bone non-union after internal fixation. For large tibial defect (the length of more than 5 cm), free vascularized fibular graft (FVFG) is the most common treatment modality [1-7]. Free vascularized fibular skin flap, which is rich in blood supply, can significantly shorten the union time, well fuse with the tibia and reconstruct the strength of the tibial grafting zone. However, this procedure has incidences of complications of up to 37-80% [3,4,8]. Bone non-union in the recipient and donor zones is the most common complication [3,9]. Hornicek et al. reported that of 945 patients, 17% experienced this complication [9]. The causes for non-union are multiple but the most important one is the disturbance of the mechanical environment in the grafting zone [10,11]. The mechanical environment is related to the length, cross section area and fixation mode of the grafting bone during reconstruction.

There are many methods to improve the environment in the bone-grafting zone. In clinical practice, FVFG in combination with external fixation is a commonly modality to reconstruct tibial defect, which allows for part of weight loading in an early stage following surgery to increase the union rate in FVFG. Other clinical studies also prove that the procedure is feasible [12-14].

FVFG includes single FVFG (SFVFG) and double-barrel FVFG (DBFVFG). DBFVFG can provide a large cross section area, thereby significantly increasing the stability following reconstruction. However, it is more invasive and may significantly reduce the strength of the donor zone with a high incidence of surgical complications. Up to date, no studies have investigated the effect of the length of the grafting fibula on the mechanical environment when using fibular graft in combination with external fixation to reconstruct the tibial defect. Thus, the selection of the two procedures is blind, which limits its clinical application.

In this study, using the limit element analysis, the effect of the grafting fibular length and modes on the stability was investigated by measuring the relative displacement of fracture fragments, the VonMises stress of the graft fibula and stress centralization.

Materials and methods

Construction of three-dimensional (3D) model

The left lower extremity of a 25-year-old male volunteer with a weight of 60 kg and height of 170 cm was scanned by a 16-slice computerized tomography (CT) scanner (Philips, Best, the Netherlands) with a range from knee joint to ankle joint, coronary scanning interval of 3mm, scanning pixel of 0.23 × 0.23 mm², scanning voltage of 120 KVP and current of 160 mA. The CT scanning data were imported into Mimics to construct the geometric model of the normal tibia and fibula.

On the basis of the normal geometric model, the 3D model of the tibial defect reconstruction with fibular graft was constructed. The length of the tibial defect was 5 to 20 cm and a model was added as long as if the length increased by 5 cm. The defect was filled with the fibula with the corresponding length. SFVFAG and DBFVFG models were constructed according to the graft mode.

The model of simplified external fixation was also constructed in the Mimics software with the diameter of the connecting rod of 12 mm and of the fixation needle of 5 mm. The fixation needle and connecting rod were connected as follow: 1. External fixation rod was at least 2 cm away from the skin; 2. Fixation needled was placed in the lateral leg at an angle of 40° with the longitudinal axis of the tibia and penetrated the contralateral cortex; 3. Distance of the first and fourth fixation needles was 2 cm to the knee and ankle articular facets; 4. Distance of the second and third fixation needles was 2 cm to the tibial osteotomy line.

Mesh generation

The tibial defect, fibular graft and external fixation were assembled in the Mimics software using the Boolean calculating. The model was exported in the iges format and then imported in the Hypermesh10.0 software for mesh generation. The mesh generation of the element was divided into 2 stages: first, the total model was generated using the 2 mm element, and then, the model binding site and potential stress centralization zone were further generated with the 1 mm element. The poor mesh was corrected manually.

Material parameters

Element attributes of all modes were set as the Solid Brick 8 node 185 type to better simulate the deformation of the stimulating model. All materials were assumed to be continuous, homogeneous, isotropic and linear elastic ones. With reference to literatures, the elastic module of the tibia and fibula was set 7.3 × 105 MP and the poisson ratio was 0.3 [15,16]. The external fixation apparatus was assumed to be made of the Ti-6Al-4V alloy and the elastic module was set 1.06 × 105 MP and the poisson ratio was 0.33 [17].

Limit element analysis

The model was introduced in the ANSYS v.11 software (ANSYS Inc, Houston, USA) for limit element operation. In this study, part of weight loading was assumed, i.e. the strength of the pressure was 1/4 of the body weight of the volunteer (150 N). The distribution ratio of the stress on the medial to the external condyle of tibia was 60:40. Contacts between fracture fragments and between the fracture and the fixation needle were designed as the frictional type. The limit element analysis was conducted using the MPC calculation. All nodes of the articular surface of the distal tibia were completely fixed with the degree of freedom of 0.

In nonlinear operation, the ANSYS software was used for automatic iteration and 28 equilibrium iterations were conducted for every analysis. The stress of the grafting fistula, relative displacement between fracture fragments and the stress centralization point of the whole limit element model were measured (Figure 1).

Figure 1.

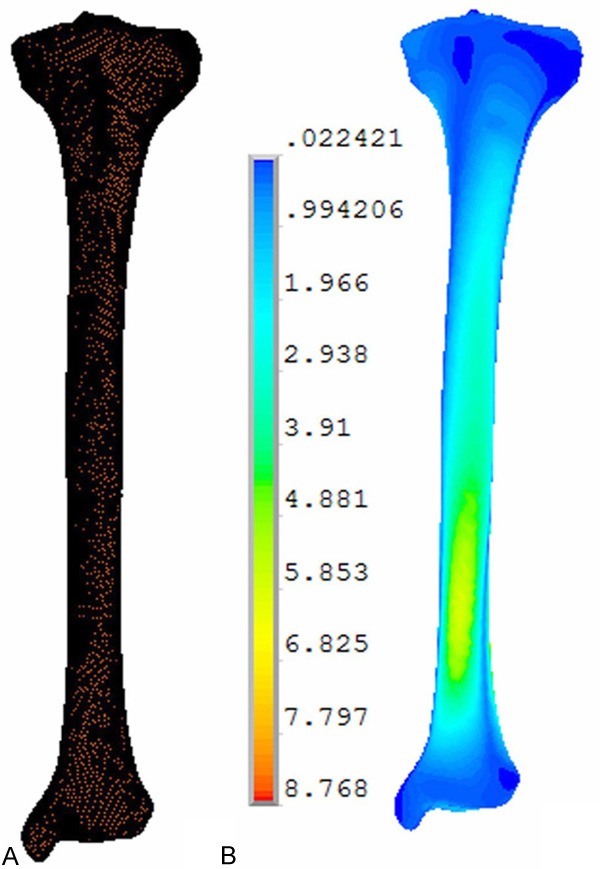
The limit element model of normal tibia. In nonlinear operation, the ANSYS software was used for automatic iteration and 28 equilibrium iterations were conducted for every analysis. The stress of the grafting fistula, relative displacement between fracture fragments and the stress centralization point of the whole limit element model of the normal tibia (A) and model verification results (B) were measured.

Results

Model verification

The normal tibial model contained 30,000 elements and 60,000 nodes (Figure 2A). In the normal tibia, the maximal Von Mises stress was 8.768 MPa and centralized in the distal 1/3 of the tibia (Figure 2), consistent with previous studies [18].

Figure 2.

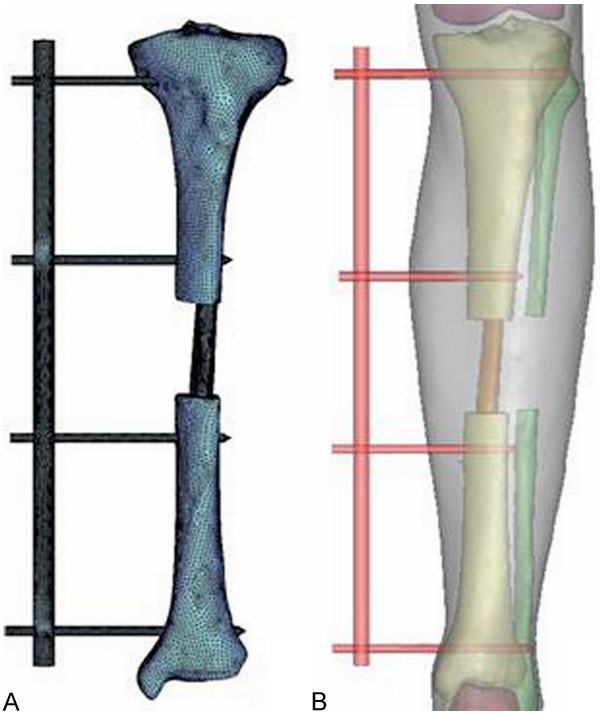
The limit element and three-dimensional model of using fibular. The limit element model (A) and three-dimensional model (B) of using fibular graft in combination with external fixation to repair the tibial defect. The normal tibial model contained 30,000 elements and 60,000 nodes (A). In the normal tibia, the maximal Von Mises stress was 8.768 MPa and centralized in the distal 1/3 of the tibia (A, B).

Comparison of the Von Mises stress in the graft bone zone

Comparison of the Von Mises stress in the graft bone zone was shown in Figure 3. The stress increased with the increase of the length of the grafting bone in both groups. In SFVFG, the Von Mises stress in 15 cm grafting bone was 2 times that in 5 cm grafting bone and the stress in 20 cm grafting bone was 2.31 times that in 5 cm grafting bone. In DBFVFG, the Von Mises stress in 20 cm grafting bone was 2.04 times that in 5 cm grafting bone. Under the same grafting bone, the Von Mises stress in the DBFVFG group was 1.37 to 1.77 times higher than that in the SFVFG group. Von Mises stresses in the fibular grafting zone in different grafting modes were shown in Figure 4.

Figure 3.

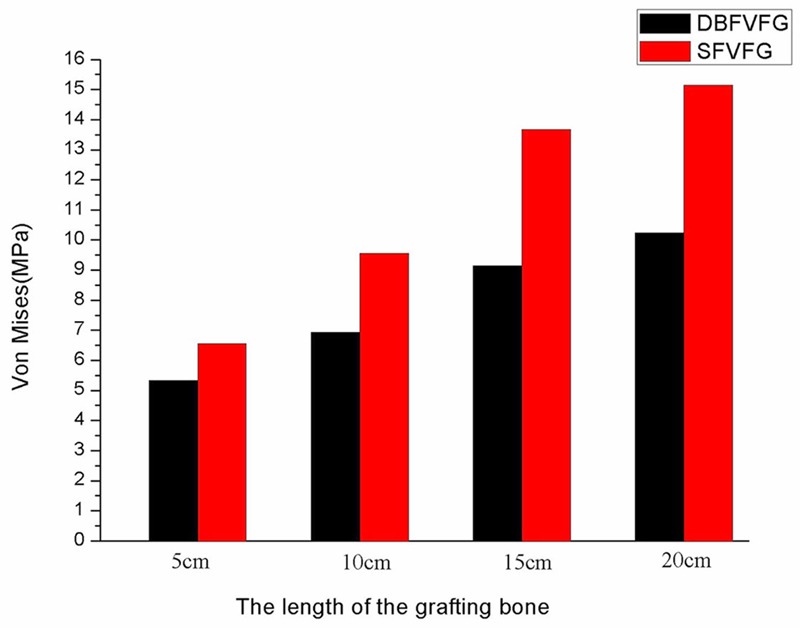
Von Mises stresses in the fibular grafting zone in different grafting modes. The stress increased with the increase of the length of the grafting bone in both groups. In SFVFG, the Von Mises stress in 15 cm grafting bone was 2 times that in 5 cm grafting bone and the stress in 20 cm grafting bone was 2.31 times that in 5 cm grafting bone. In DBFVFG, the Von Mises stress in 20 cm grafting bone was 2.04 times that in 5 cm grafting bone. Under the same grafting bone, the Von Mises stress in the DBFVFG group was 1.37 to 1.77 times higher than that in the SFVFG group.

Figure 4.

Von Mises stresses in the fibular grafting zone in different grafting modes. Cloud atlas of Von Mises stresses in the fibular grafting zone in different grafting modes (SFVFG: A: 5 cm; B: 10 cm; C: 15 cm; D: 20 cm; DBFVFG: E: 5 cm; F: 10 cm; G: 15 cm; H: 20 cm).

Inter-fragmentary motion (IFM) of the grafting fistula

IFM of the grafting fistula was determined via the displacement of the fistula (Figure 5). The displacement of the tibia increased with the lengthening grafting bone, regardless of the grafting mode. IFM in SFVFG was 1.13-2.45 times higher than that in DBFVFG. IFM of the grafting fistula exceeded 1 mm when the length of the grafting fistula was greater than 15 cm and it reached 2.22 mm when the length was 20 cm. In DBFVFG, IFM was 0.96 mm even if the length of the grafting fistula reached 20 cm.

Figure 5.

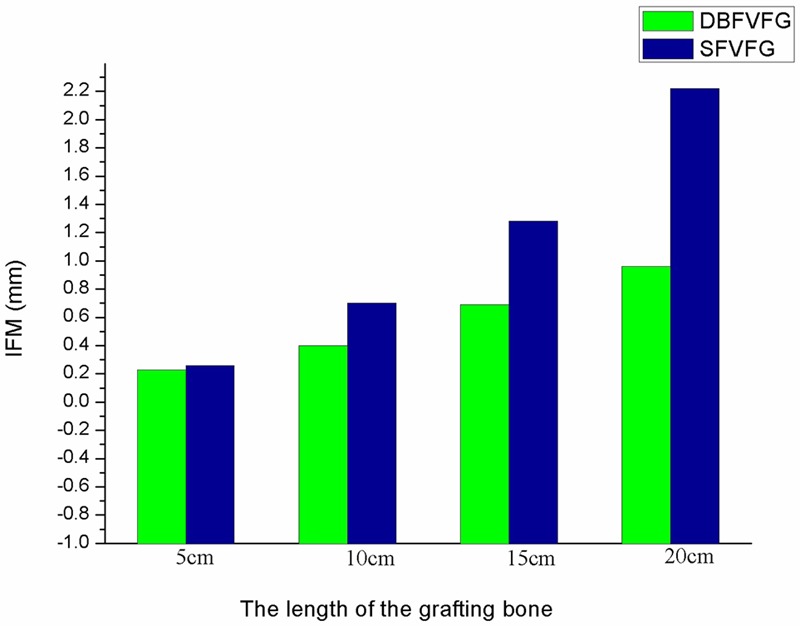
IFM of the fibular grafting zone under different grafting modes and different length of the grafting bone. IFM in SFVFG was 1.13-2.45 times higher than that in DBFVFG. IFM of the grafting fistula exceeded 1 mm when the length of the grafting fistula was greater than 15 cm and it reached 2.22 mm when the length was 20 cm. In DBFVFG, IFM was 0.96 mm even if the length of the grafting fistula reached 20 cm.

Stress centralization at the bone-pin interface

Under all models, the maximal Von Mises stress centralized at the bone-pin interface, frequently at the second and third interfaces, although the interface varied with the length of the grafting fistula. The maximal Von Mises stress was centralized as shown in Table 1.

Table 1.

Stress centralization at the bone-pin interface

Discussion

Restoration of large tibial defect is a clinical difficulty. Common treatment modalities included vascularized/no-vascularized bone autograft and allograft, prosthetic replacement or the combination [19-23]. In clinical practice, FVFG is commonly used to treat the tibial defect of more than 5 cm. Radius, rib, ilium and fibula can be used for the donor. FVFG is the most commonly used modality. It can provide the 26 cm high-density tubular bone cortex with fewer complications. Therefore, FVFG is the standard procedure for large tibial defect [24].

However, both SFVFG and DBFVFG require fixture to increase the stability. There are many fixtures such as intramedullary nail or plate screw for internal fixation and fixator, gypsum and brace for external fixation. It is generally thought that fibular graft in combination with external fixation can accelerate the union of the donor and graft bones and increase the union rate.

However, some studies reported a non-union rate of 11-32% when using autograft in combination with external fixation for treatment of tibial defect [25,26]. It is mainly due to insufficient blood supply and mechanical environment. Under the same weight loading situation, the displacement between fracture fragments and pressure distribution are the most important factors [26].

The effect of displacement between fracture fragments on fracture union has been investigated. Proper displacement can accelerate the fracture union via stimulating periosteal osteoblasts [27,28]. Animal experiments showed that fracture could well heal when the displacement was 0.2-1 mm [12,29-31]. Less than 0.5 mm displacement can promote the fracture union and more than 1 mm displacement can delay the union [32].

Animal and clinical studies proved that part of weight loading in the early stage following surgery can promote the union, stimulate the thickening of grafting bone and reinforced the strength and stability in the grafting zone [33]. However, complete weight loading can induce the disturbance of the mechanical environment in the grafting bone. Therefore, some studies used 150 N to simulate the part of weight loading [34].

This study indicates that under part of weight loading, SFVFG for tibial defect is associated with a less than 15 cm grafting bone and less than 1 mm displacement. Additionally, in DBFVFG, the displacement is always less than 1 mm even when the grafting bone reaches 20 cm in length. These results promote that selection of SFVFG or DBFVFG is based on the length of grafting fistula and DBFVFG is selected when the length is more than 15 cm.

Too high stress on the bone may cause fracture. In this study, the stress for 15 cm tibial defect was 2 times that for 5 cm tibial defect in SFVFG while the Von Mises stress did not significantly increase with the lengthening grafting bone in DBFVFG.

Too high Von Mises stress at the pin-bone interface often causes loosening of external fixation braces. In this study, the maximal Von Mises stress generally occurs at the second bone-pin interface in SFVFG but at the third bone-pin interface in DBFVFG. These results hint that second and third fixation needles should be emphasized to avoid loosening of the fixation needle post surgery when tibial defect is repaired by external fixation in combination with fibular graft.

In this study, the model was simplified from the following aspects: First, this study mainly investigates the preliminary stability of using fibular graft to treat tibial defect. Therefore, the effect of soft tissues and remnant fibula is disregarded in remodelling. This management is also applied by similar studies [34]. This study does not focus on changes in the mechanical status of individual sites. Hence, the fixation brace and needle are simplified during remodelling to ignore the effect of the screw on the model. Additionally, considering that the material property of the bone and the frictional coefficient are hard to determine, the continuous, homogenous, isotropic and linear elastic material is applied and the frictional coefficient is determined with reference to other studies. The limitation of model simplification should be taken into account when results of this study are used in clinical practice.

In conclusion, the grafting bone does not exceed 15 cm as can as possible in SFVFG in combination with external fixation to treat the tibial defect to avoid grafting bone fracture and non-union due to too high Von Mises stress and displacement between fracture fragments. Stability of the second and third fixation needles should be cared in placing external fixation brace and needle to avoid the loosening of the needle following surgery.

Disclosure of conflict of interest

None.