Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jan 27;4:3888. doi: 10.1038/srep03888

Concentration-dependent polyparameter linear free energy relationships to predict organic compound sorption on carbon nanotubes

Qing Zhao 1,2, Kun Yang 2,3, Wei Li 2,4, Baoshan Xing 2,a
PMCID: PMC3902440  PMID: 24463462

Abstract

Adsorption of organic compounds on carbon nanotubes (CNTs), governed by interactions between molecules and CNTs surfaces, is critical for their fate, transport, bioavailability and toxicity in the environment. Here, we report a promising concentration-dependent polyparameter linear free energy relationships (pp-LFERs) model to describe the compound-CNTs interactions and to predict sorption behavior of chemicals on CNTs in a wide range of concentrations (over five orders of magnitude). The developed pp-LFERs are able to capture the dependence of the ki on equilibrium concentration. The pp-LFERs indexes [r, p, a, b, v] representing different interactions are found to have a good relationship with the aqueous equilibrium concentrations of compounds. This modified model can successfully interpret the relative contribution of each interaction at a given concentration and reliably predict sorption of various chemicals on CNTs. This approach is expected to help develop a better environmental fate and risk assessment model.

Carbon nanotubes (CNTs) have attracted enormous interest since 19911. Due to their unique properties, they have promising applications in medical, material and environmental sciences. They can be used as superior sorbents to treat wastewater or act as a medicine carrier in drug delivery systems. These applications require knowledge on adsorption of organic compounds onto CNTs, which can help us better understand the environmental and health impacts of both CNTs and chemicals2. Developing rapid methods for predicting the sorption behavior of these compounds on CNTs is therefore important and urgently needed.

The pp-LFERs approach has been gaining more and more acceptance and application in the context of environmental chemistry and contaminant fate modeling3,4,5,6,7,8,9,10,11. It explicitly describes the contributions toward free energy change from multiple kinds of molecular interactions with both water and bulk phases of sorbent3. Recently, Xia et al. successfully applied this approach in predicting the adsorption of various chemicals onto CNTs, and 12 other nanomaterials at a low concentration9. Their approach is based on the fundamental forces of molecular interactions, and can be expressed as follows:

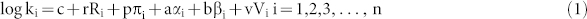graphic file with name srep03888-m1.jpg

where ki is the adsorbent-water distribution coefficient, n is the number of probe compounds, [Ri, πi, αi, βi, Vi] are the molecular descriptors of the ith probe compound. Ri is the excess molar refraction, πi is the polarity/polarizability parameter, αi and βi are the hydrogen-bond acidity and basicity respectively, and Vi is the McGowan characteristic volume. The regression coefficients [r, p, a, b, v] are defined as nanodescriptors that indicate the differential compound-CNTs interactions. The c is the regression constant.

However, up to now, most studies on pp-LFERs have been successfully applied only in a narrow and low concentration range of solute or in a situation that ki value did not varied significantly with solute concentrations (usually requires linear sorption isotherm). Those applications eliminate the well-known concentration effects of ki, which is in fact relevant for any sorbate that is capable of displacing water on naturally occurring adsorption sites. In real environments, organic compounds distribute in a wide range of concentrations and their sorption isotherms are often (if not always) found to be nonlinear. Xia et al. also suggested a concentration-dependency of pp-LFERs parameters for organic compound sorption to nanomaterials9, but the goal of their work was to characterize surface adsorption properties as a biologically relevant characterization metric to classify nanomaterial surfaces across nanoparticle types which specifically requires the lowest concentration to eliminate nonlinearity. Hence there is a great need to take concentration effect into consideration.

In this work, a set of 16 compounds (aqueous solubility Cs ranging from 0.135 to 80190 mg/L, Ri from 0.805 to 2.06, πi from 0.84 to 1.93, αi from 0 to 0.82, βi from 0.2 to 0.41, Vi from 0.775 to 1.585) for a multi-walled CNT with 8–15 nm outer diameter (MWCNT15) and 10 compounds (Cs ranging from 31.7 to 26300 mg/L, Ri from 0.871 to 1.43, πi from 0.92 to 2.42, αi from 0 to 0.82, βi from 0.1 to 0.47, Vi from 0.891 to 1.239) for a pristine MWCNT (P-MWCNTs), a graphitized MWCNT (G-MWCNTs), a carboxylated MWCNT (COOH-MWCNTs) and a hydroxylated MWCNT (OH-MWCNTs) were used to develop a new model (Supplementary Table S1). This model combines pp-LFERs parameters with aqueous equilibrium concentrations of compounds in order to identify and quantify the significant factors that govern the adsorption properties of CNTs in a wide range of concentrations. The selected compounds have diverse physicochemical properties and have been widely used as probing compounds for pp-LFER modeling. Xia et al. used 28 compounds (Ri ranging from 0.604 to 1.36, πi from 0.5 to 1.15, αi from 0 to 0.7, βi from 0.07 to 0.66, Vi from 0.775 to 1.324) to predict compounds' sorption on MWCNTs9. Our probing compound sets have comparable parameter [Ri, πi, αi, βi, Vi] value range with theirs. The number of compounds, from the quantitative structure-activity relationship (QSAR) viewpoint, may be a bit low, but does allow for the construction of a predictive model. Classic QSAR based on similar or even smaller sets of compounds has been successfully established and published elsewhere12,13,14.

Results

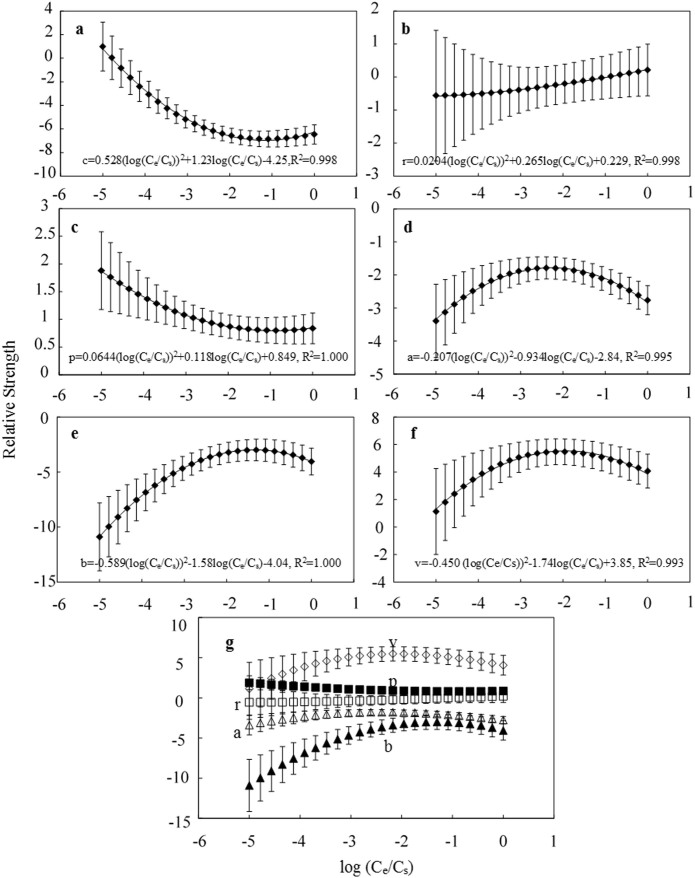
Supplementary Table S2 shows the correlation coefficient (R2), Root Mean Square Error of Calibration (RMSEC), cross-validated correlation coefficient (Q2CV) and cross-validated root mean square error (RMSECV) values of the pp-LFERs application in a wide range of concentrations (from −5 to 0 of log Ce/Cs, where Ce represents the equilibrium concentration and Cs is the solubility of the compounds) for MWCNT15. The difference between R2 and Q2CV did not exceed 0.315 and the Q2CV values were greater than 0.716, suggesting pp-LFERs can be applied well in all tested concentrations. Detailed description of R2, RMSEC, Q2CV and RMSECV is in Experimental Section. Careful analysis on pp-LFERs parameters of MWCNT15 with different equilibrium concentration Ce was further obtained in Figure 1. The London dispersion (v, 1.08 — 5.38) and the dipolarity/polarizability (p, 0.61 — 1.79) are two important molecular interactions. Hydrogen-bond basicity (b, −2.97 — −10.9) and hydrogen-bond acidity (a, −3.33 — −1.67) have negative values, which suggests that the sorbent surface has a weaker tendency to donate/accept protons to the probe compounds than water. These are consistent with Xia et al's work9. However, all the relative interaction strengths varied with Ce (The v, b and a increase with increasing Ce to reach a plateau and then decrease. The p decreases with increasing Ce.), which should be the results of the interactions among solute molecules, water molecules and the nanotube surface (Figure 2). In aqueous solution, water molecule can be either a hydrogen-bonding donor or accepter, which results in the competitive sorption with organic solutes at hydrophilic adsorption sites2. Water molecule can also compete with organic compounds on less hydrophilic adsorption sites17. Hence, at relatively low Ce, as there are plenty of sorption sites, chemical molecule will prefer to sorb on those sites with high energy18. With increasing Ce, solute molecule will gradually sorb on less energetic sites and the competing ability of water molecule on sorption sites will be relatively greater, which results in increasing of a, b and v. Meanwhile, as Ce increases, the sorption sites for solute molecule continue to decrease, which might then change the sorption manner of solutes molecule, from planar (that will occupy more sorption sites per molecule) to end by end (that will take fewer sorption sites per molecule)19. This will lead to the increase of v and decrease in p. As Ce continues to increase, there are not enough sites for sorption and the intermolecular interactions between solute molecules may increase, then a, b, v and p would be reduced. Moreover, all the pp-LFERs parameters and regression constant c were found to have a good relationship with log Ce/Cs. Shih and Gschwend developed a concentration dependent pp-LSERs model based on 14 organic chemicals sorption on activated carbon13. Their model indicated linear relationships between pp-LFERs parameters and log Ce/Cs (Equation 7 in their paper). This does not work for MWCNTs as shown in Figure 1, they are not linear. Also, linear relationship between pp-LFERs parameters and equilibrium concentration was not statistically significant via polynomial regression for MWCNTs (Supplementary information Section 2.2). In our study, a scaling factor Cs was introduced. Good quadratic polynomial regressions were obtained as suggested by P values of Normality and Constant Variance testing (>0.05) and the incremental P value (<0.001) (Supplementary Table S3).

Figure 1. Relative molecular interaction strengths on MWCNT15 varied with different log(Ce/Cs) values.

Figure 1

Open in a new tab

(a), regression constant (c); (b), regression coefficient r of the excess molar refraction (R); (c), regression coefficient p of the effective solute dipolarity and polarizability (π); (d), regression coefficient a of the effective solute hydrogen-bond acidity (α); (e), regression coefficient b of the effective solute hydrogen-bond basicity (β); (f), regression coefficient v of the McGowan characteristic volume (V). (g), Comparison of interaction strengths at different Ce. Error bars represent the standard errors of the regression analysis.

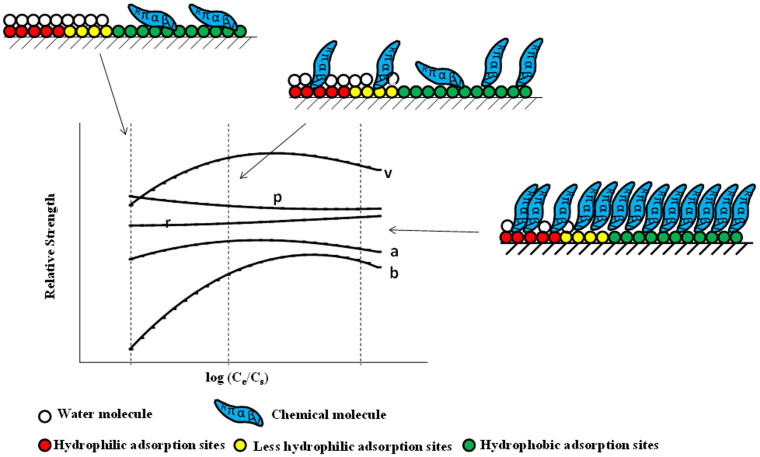
Figure 2. Schematic plot of adsorption of organic compounds on multiple sites on CNT surface at various concentrations.

Figure 2

Open in a new tab

At relatively low Ce, as there are plenty of sorption sites, chemical molecule will prefer to sorb on those sites that have high energy. With increasing Ce, solute molecule will gradually sorb on less energetic sites and the competing ability of water molecule on sorption sites will be relatively greater, which results in increasing of a, b and v. Meanwhile, as Ce increases, the sorption sites for solute molecule continue to decrease, which might then change the sorption manner of solutes molecule, from planar (that will occupy more sorption sites per molecule) to end by end (that will take fewer sorption sites per molecule). This will lead to the increase of v and decrease of p. As Ce continues to increase, there are not enough sites for sorption and the intermolecular interactions between solute molecules may increase, then a, b, v and p would be reduced.

A new model is therefore obtained as follows:

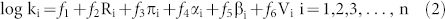graphic file with name srep03888-m2.jpg

 ƒ1 = 0.528(log(Ce/Cs))2 + 1.23log(Ce/Cs) − 4.25;

 ƒ2 = 0.0204(log(Ce/Cs))2 + 0.265log(Ce/Cs) + 0.229;

 ƒ3 = 0.0644(log(Ce/Cs))2 + 0.118log(Ce/Cs) + 0.849;

 ƒ4 = −0.207(log(Ce/Cs))2 − 0.934log(Ce/Cs) − 2.84;

 ƒ5 = −0.589(log(Ce/Cs))2 − 1.58log(Ce/Cs) − 4.04;

 ƒ6 = −0.450 (log(Ce/Cs))2 − 1.74log(Ce/Cs) + 3.85

where ƒ1, ƒ2, ƒ3, ƒ4, ƒ5, and ƒ6 are the quadratic functions of log Ce/Cs. The ƒ2, ƒ3, ƒ4, ƒ5, and ƒ6 describe the relative contribution of interaction strength from molecular force of lone-pair electrons, dipolarity/polarizability, hydrogen-bond acidity, hydrogen-bond basicity and hydrophobic interactions, respectively. For a given target compound, [Ri, πi, αi, βi, Vi] and Cs are constant. Thus the above equation only contains one unknown parameter Ce. According to equation (2), the concentration-dependent pp-LFERs model was successfully developed.

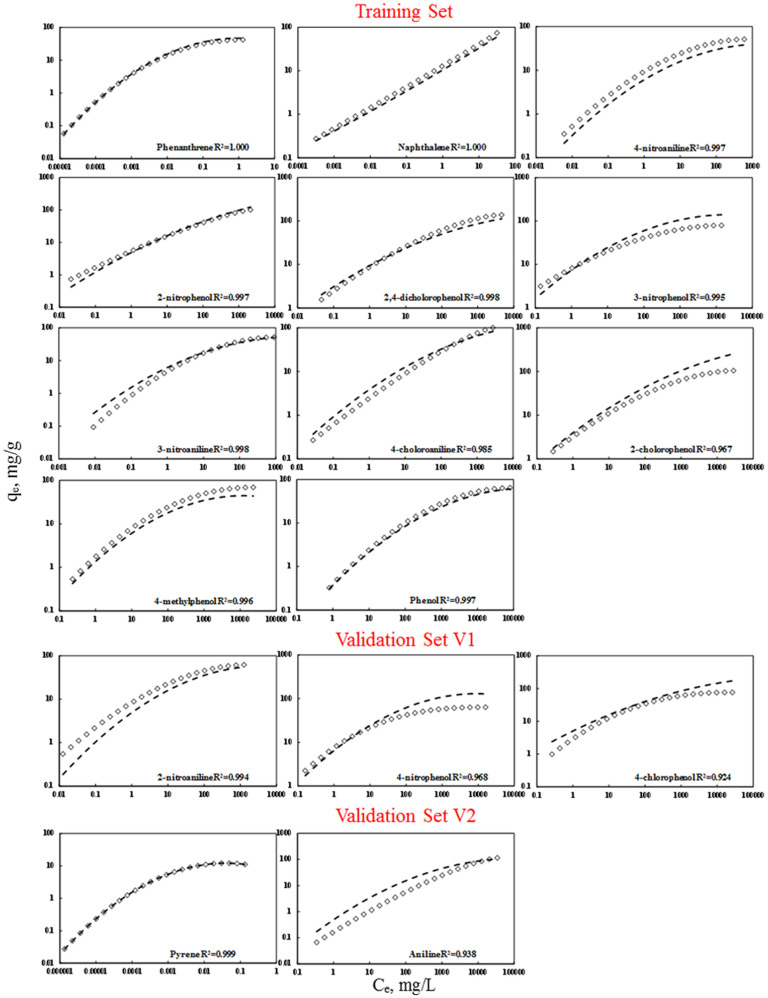
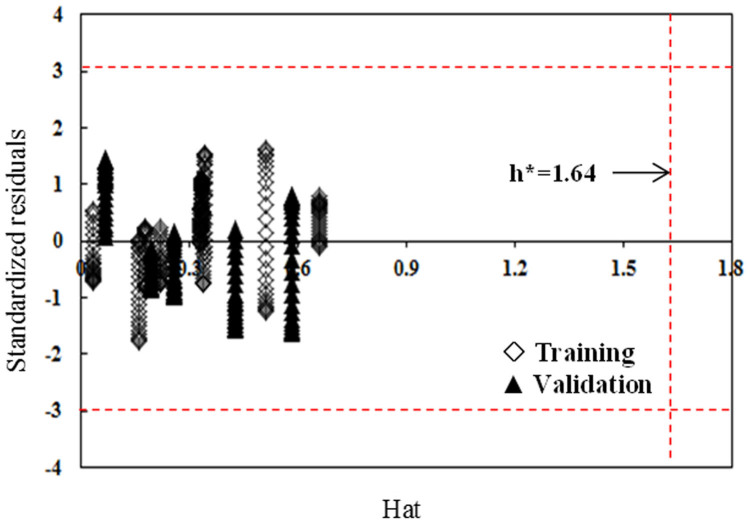
The prediction capability is evaluated through an initial two step development: first split the data into training and validation sets and then validate the data via internal and external certification4,9,12 (Supplementary information Section 2.3–2.5). In order to obtain appropriate validation, we split the data into the training and external validation set (Supplementary Table S4). First, we sorted 16 compounds based on decreasing maximum log ki value. Second, the data were split into three sets: pyrene and aniline which have the highest and the lowest log kimax value were grouped into the validation set V2 to represent the compounds that are not within the range of the training set. The rest 14 compounds were split into two sets: training set (T) and the validation set (V1). In order to ensure V1 set is evenly distributed within the range of log kimax value in training set, we utilized the following pattern of splitting: T-T-T-V1-T-T-T-V1-T-T-T-V1-T-T. The R2 (>0.967) and RMSEC (<0.201) of the internal validation suggest the good fit of the model. The Q2CV (>0.949) and RMSECV (<0.428) of the internal validation reveal the robustness of the predictive model (Supplementary Table S5). The R2 (>0.938) and RMSEC (<0.38) obtained from external validation indicate satisfactory predictivity for the external validation compounds (Supplementary Table S6). Figure 3 clearly shows the good predictivity for both training and validation sets. The applicability domain of the model was verified using a William plot (Figure 4). All the training and validation compounds in various equilibrium concentrations are within the chemical domain, suggesting that there are no outliers and the predictivity of the model is reliable. Using the same approach, we also built the models for P-MWCNTs, G-MWCNTs, COOH-MWCNTs and OH-MWCNTs. Good predictivity was obtained (Supplementary Figures S1–S4), which further validated the applicability of the new model.

Figure 3. Sorption isotherms of organic compounds on MWCNT15.

Figure 3

Open in a new tab

Open squares (Inline graphic) obtained from original reference; Dash lines (Inline graphic) predicted based on the modified pp-LFERs model.

Figure 4. Williams plot for verifying the applicability domain of the model under different equilibrium concentrations.

Figure 4

Open in a new tab

This figure clear showed no outliers of training and validation compounds and the predictivity of the model is reliable.

Discussion

Direct applications of this model have been described using MWCNT15 as an example. First, it can predict the adsorption of organic molecules onto MWCNTs at any given concentration, which is a critical process for MWCNTs in biological and environmental systems. Endocrine disrupting compounds (EDCs) and pharmaceuticals are trace organic contaminants that have been detected in aquatic environments. They can mimic or antagonize natural hormones, hinder metabolic processes, occupy hormone receptors, cause reproductive and development problems when consumed by humans and aquatic species20,21. The predicted logki for selected EDCs and pharmaceuticals was obtained by inputting solute descriptors and Ce/Cs value into the newly developed model (equation (2)). Good predictions were obtained compared to the data obtained from the literature (Figure 5a and Supplementary Table S7). The sorption of DNA-bases onto CNTs offers a remarkable set of technologically useful properties such as facilitation of CNT sorting, chemical sensing, and detection of DNA hybridization22. Based on the new approach, the adsorbent-water distribution coefficient ki which can be regarded as sorption affinity was calculated (Figure 5b). Nowadays, there are conflicting reports about sorption affinity of DNA-bases on CNTs. Xia et al. predicted the order of sorption affinity as follows: adenine > thymine > guanine > cytosine9. Johnson et al. and Gowtham et al. found the order as guanine > adenine > thymine > cytosine22,23. From Figure 5b, we can conclude that the sorption affinity order varied with Ce, the above reported orders can be found at different Ce ranges.

Figure 5. Application of modified pp-LFERs model.

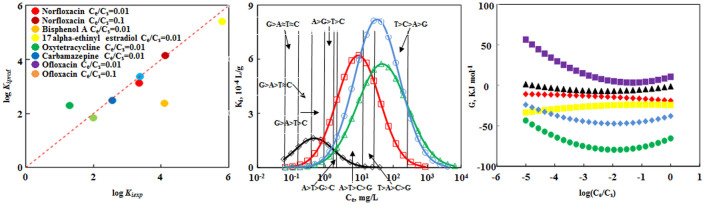
Figure 5

Open in a new tab

(a), Plot of predicted data of logKi (logKipred) vs experimentally measured data (logKiexp) of EDCs and pharmaceuticals sorption on MWCNT15 using the concentration dependent pp-LFERs. Dash line represents 1:1 line. (b), Predicted sorption affinity ki of four DNA bases at various equilibrium concentrations on MWCNT15, showing the often observed concentration-dependent sorption coefficients. 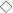Inline graphic Guanine (G) Inline graphic Adenine (A) Inline graphic Thymine (T) Inline graphic Cytosine (C) (c), Predicted sorption energy of Guanine on MWCNT15 at different equilibrium concentrations. Inline graphic Contributed by the excess molar refraction (R), Inline graphic Contributed by the effective solute dipolarity and polarizability (π), Inline graphic Contributed by the effective solute hydrogen-bond acidity (α), Inline graphic Contributed by the effective solute hydrogen-bond basicity (β), Inline graphic Contributed by the McGowan characteristic volume (V), and Inline graphicTotal sorption energy.

Secondly, this model can also explain the relative contribution of molecular-interface interactions varied with different equilibrium concentrations. Detailed calculation for relative contribution of interactions is illustrated in Supplementary Section 4.1. Figure 5c shows the predicted sorption energy of Guanine on MWCNT15. We can conclude that the main interactions are hydrophobic and π- π stacking interactions, consistent with several previous studies22,23,24. At low Ce (<0.000753 mg/L), the contributions followed an order: π-π stacking interaction > hydrophobic interaction > lone-pair electrons interaction > hydrogen-bond acidity interaction > hydrogen-bond basicity interaction. While at Ce > 0.000753 mg/L, hydrophobic interaction became the most dominant interaction.

Our new sorption model could open a quantitative way to establish a more accurate environmental fate and risk assessment model. It is important to note that this new approach might apply to other materials in addition to CNTs, since the original pp-LFERs approach was also found to be fit for additional nanomaterials (AgP, TiO2, ZnO, CuO, NiO, Fe2O3, SiO2, C60, nC60 et al.)9,25. In addition, environmental conditions (pH, ionic strength, temperature, dissolved organic matter) will greatly affect organic compound sorption on CNTs. For example, elevated pH generally increases ionization, solubility and hydrophilicity of ionizable organic chemicals and thus decreases their adsorption on CNTs26. At low ionic strength, an increase in salt concentration leads to a corresponding increase in attachment efficiency of CNTs27, which will then decrease organic compound sorption. Hence further studies should be addressed on modeling other nanomaterials and adsorbents under different environmental conditions by using this new approach.

Methods

Single solute adsorption isotherm data were obtained from our previous paper based on sorption isotherms17,28,29. For each compound, we used 24 different concentrations sorption data in order to compensate the mathematical identifiability issue caused by adding Ce into the model. The adsorbent-water distribution coefficient ki value (if not provided) was calculated according to the following equation:

graphic file with name srep03888-m3.jpg

where Q (mg g−1) is the equilibrium sorbed concentration; Ce (mg L−1) is equilibrium solution phase concentration. The physical/chemical properties including solubility (Cs) and the solute descriptors [Ri, πi, αi, βi, Vi] were obtained from corresponding references and the Absolv program in the ADME Suite software (Advanced Chemistry Development), separately (Table S1).

The correlation coefficient R2 and the root mean square error of calibration RMSEC were used as the two measures of the goodness of fit of model. They can be expressed as follows:

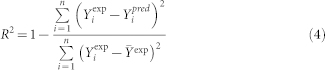graphic file with name srep03888-m4.jpg
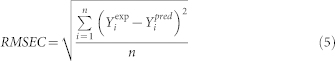graphic file with name srep03888-m5.jpg

where: Yiexp is the experimental value for the ith sample; Yipred represents predicted value for the ith sample; n is the number of samples.

The robustness of model was studied by internal cross validation using the CV-LOO (Cross-Validation Leave-One-Out technique). According to the CV LOO algorithm each compound from the data was removed, one at a time. Thus, n reduced models were calculated; each of these models was developed with the remaining n-1 compounds and used to predict the sorption coefficient of the removed compound. The cross-validated correlation coefficient Q2CV and cross-validated root mean square error RMSECV of prediction were calculated from equations below:

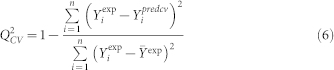graphic file with name srep03888-m6.jpg
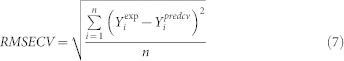graphic file with name srep03888-m7.jpg

The multiple linear regression analysis was conducted by using SPSS 18.0. Polynomial regressions between pp-LFER parameters and log Ce/Cs were run by Sigmaplot 11.0. Incremental Order Polynomial Regression program was used. It displays the regression equations for each order polynomial, starting with zero order and increasing to the specified order. According to the user guide of Sigmaplot, Normality and Constant Variance testing were employed for assumption checking for polynomial Regressions to ensure that: 1. The source population is normally distributed about the regression; and 2. The variance of the dependent variable in the source population is constant regardless of the value of the independent variables. Both of the tests were set at p = 0.05 to reject. This means if p computed by the test is greater than 0.05, the test passes. The F test statistical analysis was used to illustrate the ability of the independent variable in predicting the dependent variable. We used the incremental F value (Fincre) to gauge the increase in contribution of each added order of the independent variable in predicting the dependent variable. It is the ratio of regression variation from the dependent variable mean and residual variation about the regression curve. If Fincre is large, we can conclude that adding the order of the independent variables predicts the dependent variable significantly better than previous model. The first model that has a significant increase in the incremental F value is generally the best model to use. Because the R2 value increases as the order increases, we also need to use the simplest model that adequately describes the data.

The applicability domain of the developed model in various value of log Ce/Cs was verified by the leverage approach9 using the plot of standardized residuals versus leverages (hat diagonals), i.e. the Williams plot. If the standardized residual of a compound is greater than three standard deviation units (±3σ), the compound will be regarded as an outlier. The leverage of a compound is defined as

graphic file with name srep03888-m8.jpg

where xi is the descriptor vector of the considered compound and X is the descriptor matrix derived from the training set descriptor values. The warning leverage (h*) is defined as h* = 3(N + 1)/n, where N is the number of independent variables in the modified model (N = 5) and n is the number of training compounds (n = 11 in this study). If the leverage of the compound hi > h*, it suggests that the compound is very influential on the model.

Author Contributions

Q.Z. collected and analyzed the data, conceived, developed and validated the model. K.Y. and B.X. conceived the concentration-dependent model and contributed to data interpretation. W.L. collected the data and performed pp-LFERs calculation. All four authors involved in writing and revising the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep03888-s1.doc (1.7MB, doc)

Acknowledgments

This work was supported by NSFC (41201310, 41328003) and USDA-AFRI Hatch program (MAS 00978).

References

  1. Iijima S. Helical microtubules of graphitic carbon. Nature 354, 56–58 (1991). [Google Scholar]
  2. Yang K. & Xing B. S. Adsorption of organic compounds by carbon nanomaterials in aqueous phase: Polanyi theory and its application. Chem. Rev. 110, 5989–6008 (2010). [DOI] [PubMed] [Google Scholar]
  3. Nguyen T. H., Goss K. U. & Ball W. P. Polyparameter linear free energy relationships for estimating the equilibrium partition of organic compounds between water and the natural organic matter in soils and sediments. Environ. Sci. Technol. 39, 913–924 (2005). [DOI] [PubMed] [Google Scholar]
  4. Schuurmann G., Ebert R. U. & Kuhne R. Prediction of the sorption of organic compounds into soil organic matter from molecular structure. Environ. Sci. Technol. 40, 7005–7011 (2006). [DOI] [PubMed] [Google Scholar]
  5. Gotz C. W., Scheringer M., Macleod M., Roth C. M. & Hungerbuhler K. Alternative approaches for modeling gas-particle partitioning of semivolatile organic chemicals: Model development and comparison. Environ. Sci. Technol. 41, 1272–1278 (2007). [DOI] [PubMed] [Google Scholar]
  6. Endo S., Grathwohl P., Haderlein S. B. & Schmidt T. C. Compound-specific factors influencing sorption nonlinearity in natural organic matter. Environ. Sci. Technol. 42, 5897–5903 (2008). [DOI] [PubMed] [Google Scholar]
  7. Brown T. N. & Wania F. Development and exploration of an organic contaminant fate model using poly-parameter linear free energy relationships. Environ. Sci. Technol. 43, 6676–6683 (2009). [DOI] [PubMed] [Google Scholar]
  8. Zhu R. L. et al. Sorptive Characteristics of Organomontmorillonite toward Organic Compounds: A Combined LFERs and Molecular Dynamics Simulation Study. Environ. Sci. Technol. 45, 6504–6510 (2011). [DOI] [PubMed] [Google Scholar]
  9. Xia X. R., Monteiro-Riviere N. A. & Riviere J. E. An index for characterization of nanomaterials in biological systems. Nat. Nanotechnol. 5, 671–675 (2010). [DOI] [PubMed] [Google Scholar]
  10. Abraham M. H. Scales of solute hydrogen-bonding-their construction and application to physicochemical and biochemical processes. Chem. Soc. Rev. 22, 73–83 (1993). [Google Scholar]
  11. Abraham M. H. & Le J. The correlation and prediction of the solubility of compounds in water using an amended solvation energy relationship. J. Pharm. Sci. 88, 868–880 (1999). [DOI] [PubMed] [Google Scholar]
  12. Puzyn T. et al. Using nano-QSAR to predict the cytotoxicity of metal oxide nanoparticles. Nat. Nanotechnol. 6, 175–178 (2011). [DOI] [PubMed] [Google Scholar]
  13. Shih Y. H. & Gschwend P. M. Evaluating activated carbon-water sorption coefficients of organic compounds using a linear solvation energy relationship approach and sorbate chemical activities. Environ. Sci. Technol. 43, 851–857 (2009). [DOI] [PubMed] [Google Scholar]
  14. Puzyn T., Mostrag A., Falandysz J., Kholod Y. & Leszczynski J. Predicting water solubility of congeners: Chloronaphthalenes-A case study. J. Hazard. Mater. 170, 1014–1022 (2009). [DOI] [PubMed] [Google Scholar]
  15. Eriksson L. et al. Methods for reliability and uncertainty assessment and for applicability evaluations of classification- and regression-based QSARs. Environ. Health Perspect. 111, 1361–1375 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gramatica P. Principles of QSAR models validation: internal and external. Qsar Comb. Sci. 26, 694–701 (2007). [Google Scholar]
  17. Wu W. H., Chen W., Lin D. H. & Yang K. Influence of surface oxidation of multiwalled carbon nanotubes on the adsorption affinity and capacity of polar and nonpolar organic compounds in aqueous phase. Environ. Sci. Technol. 46, 5446–5454 (2012). [DOI] [PubMed] [Google Scholar]
  18. Zhang D. et al. Cosorption of organic chemicals with different properties: Their shared and different sorption sites. Environ. Pollut. 160, 178–184 (2012). [DOI] [PubMed] [Google Scholar]
  19. Yang K., Wu W. H., Jing Q. F., Jiang W. & Xing B. S. Competitive adsorption of naphthalene with 2,4-Dichlorophenol and 4-Chloroaniline on multiwalled carbon nanotubes. Environ. Sci. Technol. 44, 3021–3027 (2010). [DOI] [PubMed] [Google Scholar]
  20. de Rudder J., Van de Wiele T., Dhooge W., Comhaire F. & Verstraete W. Advanced water treatment with manganese oxide for the removal of 17 alpha-ethynylestradiol (EE2). Water. Res. 38, 184–192 (2004). [DOI] [PubMed] [Google Scholar]
  21. Comerton A. M., Andrews R. C. & Bagley D. M. Practical overview of analytical methods for endocrine-disrupting compounds, pharmaceuticals and personal care products in water and wastewater. Philos. T. R. SOC. 367, 3923–3920 (2009). [DOI] [PubMed] [Google Scholar]
  22. Johnson R. R., Johnson A. T. C. & Klein M. L. Probing the structure of DNA-carbon nanotube hybrids with molecular dynamics. Nano Lett. 8, 69–75 (2008). [DOI] [PubMed] [Google Scholar]
  23. Gowtham S., Scheicher R. H., Pandey R., Karna S. P. & Ahuja R. First-principles study of physisorption of nucleic acid bases on small-diameter carbon nanotubes. Nanotechnology 19 (2008). [DOI] [PubMed] [Google Scholar]
  24. Johnson R. R., Johnson A. T. C. & Klein M. L. The nature of DNA-base-carbon-nanotube interactions. Small 6, 31–34 (2010). [DOI] [PubMed] [Google Scholar]
  25. Xia X. R. et al. Mapping the surface adsorption forces of nanomaterials in biological systems. Acs Nano 5, 9074–9081 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Pan B. & Xing B. S. Adsorption mechanisms of organic chemicals on carbon nanotubes. Environ. Sci. Technol. 42, 9005–9013 (2008). [DOI] [PubMed] [Google Scholar]
  27. Saleh N. B., Pfefferle L. D. & Elimelech M. Aggregation kinetics of multiwalled carbon nanotubes in aquatic systems: Mesurements and environmental implications. Environ. Sci. Technol. 42, 7963–7969 (2008). [DOI] [PubMed] [Google Scholar]
  28. Yang K., Zhu L. Z. & Xing B. S. Adsorption of polycyclic aromatic hydrocarbons by carbon nanomaterials. Environ. Sci. Technol. 40, 1855–1861 (2006). [DOI] [PubMed] [Google Scholar]
  29. Yang K., Wu W. H., Jing Q. F. & Zhu L. Z. Aqueous Adsorption of Aniline, Phenol, and their Substitutes by Multi-Walled Carbon Manotubes. Environ. Sci. Technol. 42, 7931–7936 (2008). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep03888-s1.doc (1.7MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES