Experimental and finite element analysis of strains induced by axial tibial compression in young-adult and old female C57Bl/6 mice

Abstract

Axial compression of the mouse tibia is used to study strain-adaptive bone (re)modeling. In some studies, comparisons between mice of different ages are of interest. We characterized the tibial deformation and force–strain relationships in female C57Bl/6 mice at 5-, 12- and 22-months age. A three-gauge experimental method was used to determine the strain distribution at the mid-diaphysis, while specimen-specific finite element analysis was used to examine strain distribution along the tibial length. The peak strains in the tibial mid-diaphyseal cross-section are compressive and occur at the postero-lateral apex. The magnitudes of these peak compressive strains are 1.5 to 2 times those on the opposite, antero-medial face (a site often used for strain gauge placement). For example, −10 N force applied to a 5-months old mouse engenders a peak compressive strain of −2800 με and a tensile strain on the antero-medial face of +1450 με. The orientation of the neutral axis at the mid-diaphysis did not differ with age (p=0.46), indicating a similar deformation mode in young and old tibiae. On the other hand, from 5- to 22-months there is a 25% reduction in cortical thickness and moment of inertia (p < 0.05), resulting in significantly greater tibial strain magnitudes in older mice for equivalent applied force (p < 0.05). We conclude that comparisons of tibial loading responses in young-adult and old C57Bl/6 tibiae are facilitated by similar deformation pattern across ages, but that modest adjustment of force levels is required to engender matching peak strains.

1. Introduction

In-vivo mechanical loading models are used to study bone mechanoresponsiveness (Robling et al., 2001). A model that is increasingly used is murine axial tibial compression, whereby the lower leg of the mouse is loaded non-invasively through contacts at the foot and knee (De Souza et al., 2005; Fritton et al., 2005) (Fig. 1). Several investigators have used this approach and reported loading responses in both cortical and trabecular bone (Brodt and Silva, 2010; De Souza et al., 2005; Lynch et al., 2011, 2010; Moustafa et al., 2012; Silva et al., 2012; Sugiyama et al., 2012; Weatherholt et al., 2013; Willie et al., 2013).

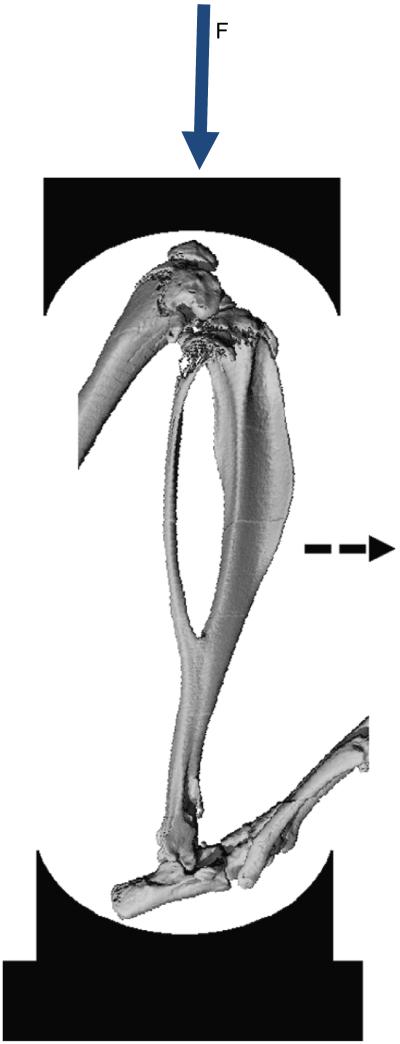
Fig. 1.

MicroCT image of bones of the mouse lower leg illustrating the axial compression setup. Force is applied at the knee. The tibia displaces downward and, due to its natural curvature, the midshaft displaces in the antero-medial direction (dashed arrow). (Fig. adapted from Christiansen et al. (2008).)

Because the bone response to loading is related to the local strain stimulus (Sugiyama et al., 2010), an understanding of the relationship between the applied axial force and the engendered tibial strains is critical. Our focus here is on the strains in the cortical bone. Tensile strains have been measured on the anteromedial surface of the diaphysis (Brodt and Silva, 2010; Christiansen et al., 2008; Fritton et al., 2005; Lynch et al., 2010; Main et al., 2010; Sugiyama et al., 2012; Weatherholt et al., 2013; Willie et al., 2013), the site most accessible to gauge placement. Further elaboration of spatial strain patterns have come from finite element analysis (Christiansen et al., 2008; Moustafa et al., 2012; Stadelmann et al., 2009; Willie et al., 2013) as well as experiments using multiple gauges placed around the tibial cross-section (Brodt and Silva, 2010; De Souza et al., 2005). These studies indicate that axial loading generates compression and bending in the middiaphyseal region, with a tension-to-compression strain gradient from the antero-medial to the postero-lateral aspect of the tibial cross-section.

The majority of tibial loading studies have been limited to young-adult (3–6 months) C57Bl/6 mice. Studies in older mice are important to examine the potential for loading-based approaches to modulate age-related bone loss. We recently reported a modest age-dependence between young and old BALB/c mice, with 5-months old mice being most responsive but 7-, 12- and 22-months old mice still exhibiting a significant anabolic cortical bone response to tibial loading (Brodt and Silva, 2010; Silva et al., 2012). Although we performed strain gauge measurements to characterize the strains at one or two sites on the tibial diaphysis, we did not perform a thorough analysis to assess possible differences in bending patterns or strain distributions with age. Lynch et al. (2011) reported that a difference in tibial curvature altered the force–strain relationship between 2- and 6-months old C57Bl/6 mice.

To extend the studies described above, we are examining cortical mechanoresponsiveness in young and old C57Bl/6 mice. In support of these studies, our objective here is to examine the effect of age on the force–strain relationships in the diaphysis of the mouse tibia during axial compression. We performed strain gauge measurements and finite element modeling of tibiae from mice aged 5, 12 and 22 months, ages that correspond to young-adult, middle-aged and old, respectively (Flurkey et al., 2007). We asked: does the bending pattern change with age? Do the force–strain relationships change with age? Does the strain distribution change with age?

2. Methods

2.1. Overview and baseline microCT

With approval from our institutional Animal Studies Committee, experiments were performed using female C57Bl/6 mice at age 5, 12 or 22 months (n=4−5 mice per group; Aged Rodent Colonies, National Institute of Aging, NIH). Upon arrival, mice were housed in our facility for 1 week and then euthanized by CO₂ asphyxiation. Bodies were stored at −20 °C and thawed at room temperature prior to use.

Baseline microCT scans of entire right lower legs were performed to capture bone geometry (70 kV, 114 μA, 100 ms integration time, 21 μm isotropic resolution; VivaCT 40, Scanco Medical). A suitable threshold to segment bone from background was selected by visual examination of representative samples from each age group, which yielded an average value of 214 mg HA/ccm, which was then applied to all samples. For cross-sectional analysis and subsequent strain measurements, the region of interest (hereafter referred to as the mid-diaphysis) was centered 5 mm proximal to the distal tibiofibular junction (TFJ), which is the mid-point of the region bounded by the proximal and distal TFJs and is the approximate location of peak strain (Christiansen et al, 2008; Stadelmann et al., 2009). Using the manufacturer’s analysis tools, we determined total (sub-periosteal) area, cortical area, cortical thickness, polar moment of inertia and tissue mineral density of the tibia, averaged over a 1 mm region centered at the mid-diaphysis. We also determined a measure of curvature, based on the perpendicular offset distance between the line of axial force and the centroid of the bone cross-section at the mid-diaphysis (Supplemental Fig. S1), similar to Main et al. (2010).

Results are shown as mean ± standard deviation. Age effects were determined by one-way analysis of variance (ANOVA) with a Tukey–Kramer post hoc test (Statview 5.0, SAS Institute). Differences between linear regression lines were evaluated by analysis of covariance, with Tukey tests for multiple comparisons (Zar, 1996). Significance level was set at 0.05.

2.2. Experimental strain measurement and neutral axis determination

We performed experimental strain analysis to assess force–strain relationships at each age. Throughout the manuscript ‘strain’ refers to normal strain in the axial direction. A three-gauge method was employed which allowed determination of the neutral axis of bending, i.e., line along which strain equals zero, at the middiaphysis (defined above).

After microCT scanning, tibiae were exposed by removal of surrounding muscle and three single-element strain gauges (C2A-06-015LW-120, Vishay Micro-Measurements) were attached to the postero-lateral (PL), antero-lateral (AL), and antero-medial (AM) surfaces of the mid-diaphysis, each aligned with the long (Z) axis of the bone (Fig. 2). The gauges were connected to a signal conditioning/amplifier system (SCXI-1001; National Instruments). Operation of the system was verified daily using a strain-gauged aluminum calibration beam. Specimens were kept moist using saline-soaked gauze. Hindlimbs were then placed in fixtures supporting the foot and knee which were attached to a servohydraulic materials testing machine (Instron Dynamite 8800). A pre-load of −0.5 N was applied, followed by cyclic axial loading at peak forces ranging from −3 to −11 N (2 N increments). The waveform consisted of triangle with load/unload rate of 80 N/s followed by 10 s rest between cycles. Strain gauge and force–displacement data were collected at 60 Hz (LabVIEW 8.2, National Instruments). Strain and force ranges were averaged over eight cycles for each force level. For each age group and gauge site, a force–strain relationship was determined using linear regression analysis. After measurements were complete, hindlimbs were re-scanned by microCT as described above to determine gauge locations.

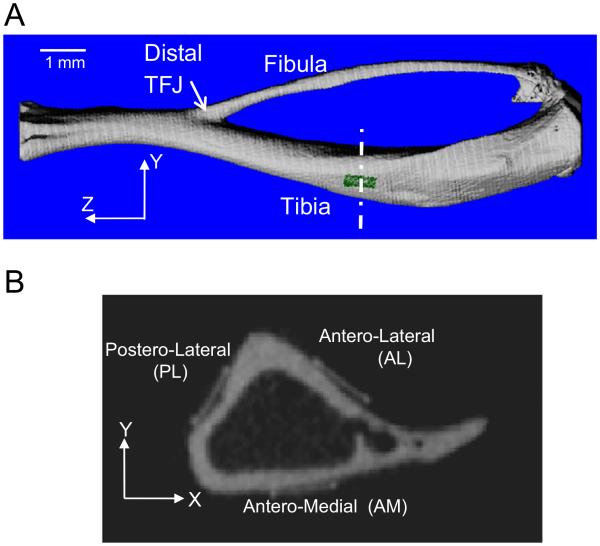
Fig. 2.

(A) 3D rendering of mouse tibia and fibula, illustrating longitudinal location of strain gauge (green) 5 mm from the distal tibiofibular junction (TFJ). (B) Grayscale microCT slice showing locations of the three strain gauges in the transverse cross-section of the tibial. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

To assess the direction of bending, the orientation of the neutral axis was determined from the experimental strain data and cross-sectional microCT images. We employed a graphical approach based on linear beam theory, adopted from Rizzo et al. (1998). Briefly, each pair of strain gauges is used to define a linear strain-position relationship. The points of zero strain on each line are connected to define the neutral axis (Fig. 3). We describe the neutral axis angle relative to the medial-lateral (M-L) anatomical axis, which is defined from the posterior surfaces of the tibial condyles (Fig. 4A). With the neutral axis determined, strain values at any point of interest (*) on the cross-section can be estimated by simple scaling:

$${∊}^{\ast }={∊}_{gauge}x{y}^{\ast }∕y_{gauge}$$

where ε* and ε_gauge are the strains at the point-of-interest and gauge-site, respectively; and y* and y_gauge are corresponding perpendicular distances from the neutral axis (Supplemental Fig. S2). Because the three-gauge analysis produces a unique solution, this scaling can be done from any gauge-site.

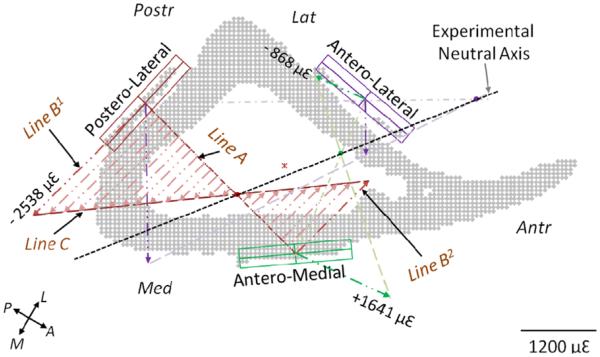
Fig. 3.

Determination of experimental neutral axis from strain data (shown is a 12-month sample; values shown correspond to 10 N force). Locations of strain gauges are identified on the cross-sectional microCT-based image. Mid-points of a gauge pair are connected with a line (Line A). Two line segments (Lines B¹ and B²) are drawn from the mid-points of the gauges, perpendicular to Line A, with lengths proportional to the recorded strain. Extrema of these two segments are connected with another line (Line C); the intersection of Line C with Line A is a point of zero strain, and thus lies on the neutral axis. Repeating these steps for another gauge pair determines a second point; these two points are sufficient to define the neutral axis. Repeating for the last gauge pair determines a third point, which also lies on the neutral axis. The anatomical directions are shown by the orthogonal axes (A:Anterior; P:Posterior; M:Medial; and L:Lateral).

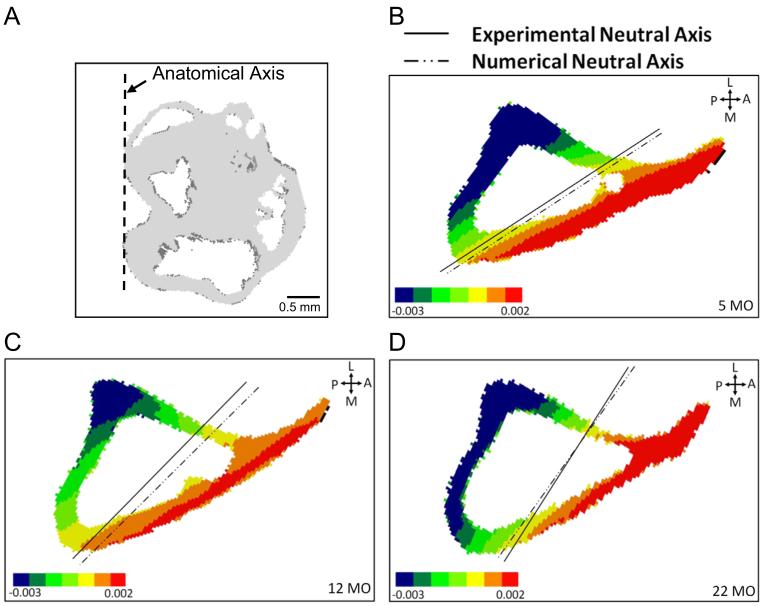
Fig. 4.

Neutral axis orientation predicted by FE model matches the experimental neutral axis. (A) Anatomical medial-lateral axis is determined from proximal tibial condyles. Axial (e_zz) strain gradient at mid-diaphyseal cross-section of representative FE models from (B) 5-month, (C) 12-month to (D) 22-month groups showing orientation of neutral axis. The experimentally determined neutral axis for each specimen is overlaid.

2.3. Specimen-specific finite-element modeling and analysis

Baseline microCT scans were segmented as described above and specimen-specific finite element models of each right tibia-fibula (n=4/group) were generated. We used the manufacturer’s (Scanco) Finite Element software, which employs a ‘voxel-conversion technique’ such that each bone voxel is represented by an 8-noded brick element (van Rietbergen et al., 1995). Each model was comprised of more than 6 × 10⁶ elements. Each model was rotated so that the centroids of the distal and proximal ends were aligned along the axial (Z) axis; we assumed that this axis corresponded to the experimental loading axis. After this transformation, we cropped the ends of the model (<0.5 mm from each end) with an X–Y plane to trim the irregularly shaped bone ends and provide flat surfaces for uniform application of boundary conditions (described below). We constrained the proximal fibula to remain attached to the tibia by filling the space between them with bone elements. Models were analyzed on two clustered workstations (HP Integrity rx2660). Computation time for each analysis ranged from 18 to 24 h.

Material properties were assumed to be linearly elastic, isotropic and homogenous. Poisson’s ratio was 0.3. The elastic modulus was chosen using back-calculation (van Rietbergen et al., 1995) based on a subset of six models (two from each age group) analyzed initially using a trial modulus value (10 GPa). For each gauge site and model we calculated the ratio between initial FE predicted and experimentally measured strain (Supplemental Fig. S3). The average of these ratios yielded a scaling factor that resulted in a modulus value of 20.7, 20.0 and 20.8 GPa for the three age groups. Because there was no obvious age effect, we chose a fixed value of 21 GPa for all subsequent analysis.

Boundary conditions were chosen to match the experimental conditions, and were adjusted to yield an accurate prediction of the neutral axis of bending. The set of nodes at the proximal most section of the model was fixed in all directions. At the distal end, we applied a −10 N force in the axial (Z) direction, and first fixed these nodes in the X- and Y-directions. Initial analysis revealed that the neutral axis at the mid-diaphysis did not match the experimentally determined neutral axis. Addition of a small (<0.5 N) force in the +Y-direction (lateral) caused a rotation of the neutral axis (Supplemental Fig. S4). Using an iterative approach we selected a final set of end forces of 0, 0.14 and −10 N in X, Y and Z directions, respectively, distributed equally over the proximal end nodes.

Our main outcome from the FE analysis was axial strain (e_ZZ). We calculated average strain values at sites corresponding to the strain gauges. To identify the exact gauge locations on the FE models, baseline scans were registered with scans taken with gauges attached. Locations for each gauge site were segmented from the baseline scans and identified on the finite-element model via a component labeling tool (Fig. 2A). Numerical results from the analyzed model were imported and periosteal elements corresponding to the surface area of each gauge site (0.38 mm × 0.50 mm) were segmented using a MATLAB program. The program used a simple ray-tracing algorithm to identify and segment surface voxels. An average for each gauge surface was calculated and compared with the experimental strain values. In addition to gauge-site strains, we evaluated peak tensile and compressive strains by computing the averages from the 100 elements in the mid-diaphyseal cross-section with the highest and lowest values of axial strain. Lastly, we visually examined the pattern of axial strain along the entire tibia to qualitatively assess strain gradients across the cross-section and along the length of the tibia.

3. Results

3.1. Bone area and cortical thickness decrease with age

Based on microCT analysis, cortical bone area and thickness at the tibial mid-diaphysis decrease with age in C57Bl/6 female mice, both of which contribute to a decrease in moment of inertia from 5 to 22 months (p < 0.05; Table 1). By contrast, age does not affect total area or the curvature of the tibia as measured by 3D offset. Thus, with age the overall tibial size and shape do not change, but bone is lost through cortical thinning. Age does not affect tissue mineral density.

Table 1.

Bone morphological parameters derived from microCT analysis (mean ± SD).

Age (month)	3D offset (mm)	Total area (mm2)	Bone area (mm2)	Avg. cortical thickness (mm)	Polar MOI (mm4)	Tissue mineral density (mg HA/cm3)
5	1.21 ± 0.14	1.51 ± 0.07	0.94 ± 0.04	0.194 ± 0.004	0.40 ± 0.04	1026 ± 11
12	1.33 ± 0.06	1.51 ± 0.10	0.83 ± 0.02a	0.178 ± 0.005a	0.36 ± 0.04	1038 ± 12
22	1.22 ± 0.25	1.48 ± 0.03	0.67 ± 0.04a,b	0.143 ± 0.013a,b	0.30 ± 0.02a	98 ± 56

^aDifferent from 5-months.

^bDifferent from 12-months; Tukey-Kramer test; p < 0.05.

3.2. Neutral axis of bending does not change with age

Both experimental and FE analysis indicated that the bending plane, as described by the orientation of the neutral axis, does not change significantly with age. Axial loading of the tibia generates compressive strain on the postero-lateral aspect of the tibia at the mid-diaphysis, and tensile strain on the antero-medial aspect (Figs. 4 and 5). Strain magnitude is greater on the compressive side than on the tensile side, consistent with a combined compression-bending loading mode, and the peak values occur at the postero-lateral apex of the cross-section. Based on the three-gauge approach, the neutral axis is oriented approximately 40° relative to the medial-lateral anatomical axis. The orientation of the neutral axis does not differ between 5-, 12- and 22-month age groups (5-month: 43.4 ± 7.7°; 12-month: 39.6 ± 2.5°; 22-month: 36.0 ± 7.8°; p=0.46). FE predictions of neutral axis orientation (overall average 40.4 ± 6.4°) matched well with experimental results (overall average 38.6 ± 5.4°) (Fig. 4).

Fig. 5.

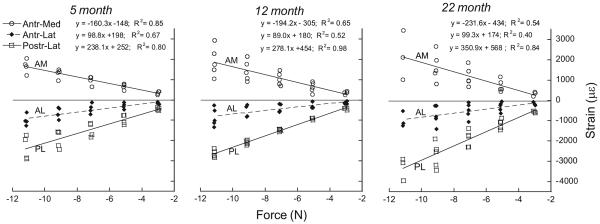
Experimental strain–force relationships determined for three age groups of C57Bl/6 female mice (n=4−5/group). Strain was measured using gauges placed at the mid-diaphysis at three periosteal locations (as shown in Fig. 2B). Data were fit using linear regression. Slopes for the AM and PL gauge locations increase with age.

3.3. Peak strains increase with age but strain distributions are similar across ages

With increasing age the magnitude of peak strain engendered by tibial loading increases. The force–strain relationship is linear (p < 0.005) at all sites and ages (Fig. 5). The strongest correlations were observed at the postero-lateral (PL) gauge site (r²=0.80−0.98), with moderately strong correlations at the antero-medial (AM) site (r²=0.54−0.85), and least strong at the antero-lateral (AL) site (r²=0.40−0.67). This finding may simply reflect the relative strain magnitudes at the three sites: |PL| > |AM| > |AL|.

The slope of the force–strain regression line differs significantly with age for the PL and AM gauge sites (p < 0.05), but not for the AL gauge site. For the slopes at the PL site: 5-month < 12-month < 22-month; for the slopes at the AM site, 5-month < 12-month and 22-month (p < 0.05). Accordingly, strain values were greatest in 22-month mice, intermediate in 12-month mice, and least in 5-month mice (Tables 2 and 3).

Table 2.

Strains at three mid-diaphyseal gauge sites for applied force of −10N (microstrain, mean ± SD).

Method	Antero-lateral gauge site			Antero-medial gauge site			Postero-lateral gauge site
	5 Month	12 Month	22 Month	5 Month	12 Month	22 Month	5 Month	12 Month	22 Month
Experimentala (strain gauge)	−826 ± 252	−678 ± 319	−864 ± 522	1453 ± 280	1640 ± 602	1886 ± 784	−2132 ± 526	−2329 ± 126	−2947 ± 684
Numericalb (FEA) 439	−893 ± 239	−1001 ± 431	−1228 ± 507	1216 ± 255	947 ± 439	1169 ± 525	−1957 ± 628	−2108 ± 658	−2637 ± 431

^aExperimental values were computed from individual regression lines for each specimen, then averaged; n=4–5.

^bNumerical values were computed from average surface strains at gauge locations for each model, then averaged; n=4–5.

Table 3.

Peak strains at the mid-diaphysis for applied force of −10N (microstrain, mean ± SD).

Method	Peak compression surface			Peak tension surface
	5 Month	12 Month	22 Month	5 Month	12 Month	22 Month
Experimentala (strain gauge)	−2816 ± 589	−3036 ± 412	−3506 ± 872	2051 ± 399	2980 ± 224	3194 ± 554
Numericalb (FEA)	−3133 ± 964	−2833 ± 988	−3656 ± 1575	1754 ± 615	1691 ± 515	1836 ± 650

^aExperimental values extrapolated from strain gauge sites to locations at maximal distance from neutral axis; n=4–5 specimens/group.

^bNumerical values were averaged over 100 elements at sites of peak compression and tension for each model; n=4.

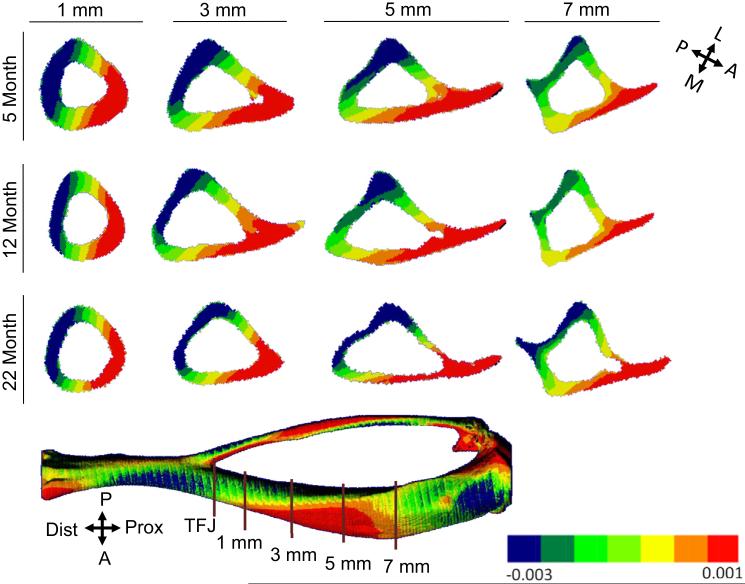
The strain distribution engendered by tibial compression does not differ qualitatively with age. Strain contour plots at different sections along the tibial length reveal a consistent pattern across age groups (Fig. 6; Table 4). At each section examined, the peak compressive magnitude is greater than the peak tensile strain, typically by a factor of 1.5–2. The peak values are comparable at sections 1, 3 and 5 mm from the TFJ, indicating that high values of strain occur throughout this region and there is no single section which has the highest strain across the range of ages we examined. Examination of strain contours at different sections illustrates changes in the neutral axis from distal to proximal. Near the distal TFJ, the neutral axis is oriented close to the medial-lateral axis, whereas at the mid-diaphysis the neutral axis is at approximately 40° to the medial-lateral axis. Thus, the locations of peak tension and compression shift along the length of tibia.

Fig. 6.

Transverse tibial cross-section from finite-element models from different age groups showing distribution of axial strain along the tibial length. The distributions are similar at the three ages. The orientation of the neutral axis can be approximated as a line passing through the zero strain contours (yellow). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 4.

FEA predicted peak compressive and tensile strains at different sections along the tibial diaphysis for applied force of −10N (microstrain, mean ± SD).

Distance from distal TFJ (mm)	Peak compression surface			Peak tension surface
	5 Month	12 Month	22 Month	5 Month	12 Month	22 Month
1	−3103 ± 1108	−3027 ± 1106	−2458 ± 450	2094 ± 829	1985 ± 996	1360 ± 399
3	−2830 ± 845	−2922 ± 835	−3187 ± 893	1663 ± 558	1539 ± 512	1704 ± 401
5a	−3133 ± 964	−2833 ± 988	−3656 ± 1575	1754 ± 615	1691 ± 515	1836 ± 650
7	−2147 ± 668	−2184 ± 669	−2669 ± 1231	1881 ± 664	1738 ± 635	1366 ± 362

Values were averaged over 100 elements at sites of peak compression and tension for each model; n=4.

^aSection corresponding to ‘mid-diaphysis’ as defined for this study.

4. Discussion

In vivo axial compression of the mouse tibia is used to study how bone responds to mechanical loading. Our objective here was to characterize the patterns of deformation and the tibial force–strain relationships in young, middle-aged and old C57Bl/6 mice. Our results indicate that the general size and shape of the tibia do not change from 5 to 22 months age, and thus the orientation of the neutral axis and the general strain distribution engendered by axial compression do not change with age. On the other hand, with aging there is cortical thinning and loss of bone area that result in greater tibial strain magnitudes in older mice for equivalent magnitude of compressive force.

The strain state engendered by axial tibial compression is spatially complex and therefore it can be difficult to compare across published studies. Nonetheless, there is consensus that tensile strains are engendered at the mid-diaphysis on the anterior-medial surface (Fig. 2B), often referred to as the ‘medial’ surface (Fritton et al., 2005; Lynch et al., 2011; Sugiyama et al., 2012; Weatherholt et al., 2013). (Note that one early report (De Souza et al., 2005) shows this incorrectly labeled as the lateral surface [see, Fig. 1].) Values of strain at this site are commonly reported, likely because of ease of gauge placement with minimal dissection which makes it amenable for in vivo application. For female C57Bl/6 mice aged 4–6 months, reported values of strain at this site (scaled to −10 N force) range from +1100 to +1950 με recorded in vivo (De Souza et al., 2005; Lynch et al., 2011; Main et al., 2010; Sugiyama et al., 2012; Willie et al., 2013), with comparable values (+1350 to +2040) recorded ex vivo (Moustafa et al., 2012; Weatherholt et al., 2013). Our average value of +1450 με for the 5-month group (Table 2) is in this range. Most studies report strains at the mid-point of the tibial length, slightly different from our ‘mid-diaphyseal’ section of interest which is 2–3 mm proximal to the mid-point. Our finite element results indicate that peak tensile strains differ by only ~100 με between these two sections (Table 4).

Strength of our study is the use of a three-gauge method to completely describe the cross-sectional tibial strain distribution at the mid-diaphysis. We determined that placement of three gauges at the mid-diaphysis is feasible and reliable, based on consistent position observed by microCT, and on force–strain linearity at each site (Fig. 5). Because the tibia is curved along its length, axial compression applied between the ankle and knee produces a combination of compression plus bending at the mid-diaphysis that results in a gradient from compression to tension. Based on an assumption of linearity, if the values of strain are known at three points on the cross-section, the complete (axial) strain state at that section is described which allows determination of the neutral axis. With this approach we find that the orientation of the neutral axis does not differ significantly between 5- and 22-months in C57Bl6 female mice.

The strain gauge sites did not correspond to sites of peak strain in the cross-section (Fig. 4), an observation with implications for study design and comparisons across studies. The peak strain magnitude at the mid-diaphysis occurs on the postero-lateral apex and is compressive, a finding consistent with recent finite element results (Moustafa et al., 2012; Stadelmann et al., 2009; Willie et al., 2013). Consequently, a description of tibial strain based on the tensile value at the antero-medial gauge site does not reflect the peak strain in the section. Our results indicate that the peak compressive strain magnitude is 1.5–2 times the magnitude at the antero-medial gauge site (Tables 2 and 3), similar to predictions of Willie et al. (2013). Thus, an in vivo loading study that reports application of peak strain of +1500 based on a single gauge may in fact be applying −2300 to −3000 elsewhere on the same section. Measures of bone’s anabolic response to loading are typically based on analysis of the entire cross-section, for example mineralizing surface per bone surface (MS/BS) for the entire periosteal perimeter. Accordingly, a more relevant description of the strain would include its peak value at the cross-section of interest. Notably, reports by others (Moustafa et al., 2012; Sugiyama et al., 2012) and unpublished data from our lab on C57Bl/6 mice indicate that the location of maximal bone formation at the mid-diaphysis corresponds to the site of peak compressive strain.

Because the strain state is not adequately described by a single value, it is difficult to fully match strain states in tibiae from mice across ages, genotypes or experimental conditions. We conducted the current study in preparation for in vivo experiments on mice of three ages. Our goal was to determine age-specific forces that produced matching strain magnitudes, and to confirm that the deformation pattern of the tibia did not change substantially from young-adult to old age. Based on observations noted above regarding peak strain and its association with bone formation, we decided to select force values that generated matching values of peak (compressive) strain determined by the three-gauge analysis, rather than matching the strain from any one gauge. Because our results indicate that peak strain increases with age (Table 3), different forces are needed to produce a strain match. For a target peak strain of −3000, the applied peak forces are −10.5, −10.0 and −9.0 N for 5-, 12- and 22-months old mice, respectively (Table 5). These force values satisfy our objective to match the peak compressive strain (within 100 με). On the other hand, the peak tensile strain values engendered by these forces match less well (810 με range); we attribute this to their location on the narrow anterior spine which has a highly variable shape (Fig. 6). Notably, at the postero-lateral gauge site, the selected force levels engender strains that match within 340 με, while at the commonly used antero-medial gauge site, the strain match is within 110 με. Thus, for the groups examined here, an equivalent match could have been achieved based on the antero-medial gauge site or the peak compressive site. This observation suggests that, while knowing the peak compressive value provides a more complete description of the local strain stimulus, strain matching across experimental groups can be done based on either the peak compressive strain or the antero-medial gauge-site strain.

Table 5.

Values of force (rounded to nearest 0.5 N) to engender target peak compressive strain of approximately −3000 με at the mid-diaphyseal periosteal surface in tibiae of 5-, 12-, and 22- month female C57Bl/6 mice.

Age (month)	Force (N)	Peak compressive periosteal strain (με)	Peak tensile periosteal straina (με)	Strain at postero-lateral gauge site (με)	Strain at antero- medial gauge site (με)
5	−10.5	−2970	2170	−2250	1540
12	−10.0	−3040	2980	−2330	1640
22	−9.0	−3080	2810	−2590	1650

Peak compressive and tensile values determined from regression lines of force vs. peak strain.

Gauge-site values determined from regression lines of force vs. gauge-site strain (Fig. 5).

^aPeak tensile values are observed on the anterior spine that extends from the cross-section.

Several limitation of our study should be noted. First, placement of three strain gauges on the small mouse tibia is technically challenging. Because of concerns about gauge interactions at such close distance, we confirmed in preliminary studies using samples from each age group that strain data recorded by an individual gauge was similar to data from that same gauge after two additional gauges were placed. Second, because the dissection required for placement of three gauges is invasive, it is not recommended for in vivo application. Third, some details about our findings may be limited to female C57Bl/6 mice at the ages examined. Mice from male C57Bl/6 and other inbred strains or mice carrying genetic mutations may have a different tibial structure and the location of the neutral axis as well as the site-specific force–strain relationships may differ from those reported here. Lastly, we had to iteratively adjust the loading conditions to match the neutral axis orientation by addition of a small lateral force. A similar adjustment was used in a FE study of the rat ulna (Kotha et al., 2004), and indicates that the experimental loading axis did not align perfectly with the longitudinal (Z) axis in the FE model.

In summary, using a combination of experimental and finite element analysis of strain, we described the strain state engendered by axial tibial compression in female C57Bl/6 mice at 5-, 12- and 22-months age. Application of three gauges at the mid-diaphysis was feasible and allowed for experimental determination of the neutral axis of bending and the value and location of the peak strain in the cross-section. The peak strains in the mid-diaphyseal cross-section are compressive and occur at the postero-lateral apex of the tibia. The magnitude of these peak values are 1.5–2 times those on the opposite, antero-medial site often used for strain gauge placement. The deformation pattern and orientation of the neutral axis do not differ with age. However, due to reduced bone area and moment of inertia, the strains engendered by a given applied force increase with age. We conclude that comparisons of bone responses to loading in young and old C57Bl/6 mice are facilitated by a similar deformation pattern across ages, but do require modest adjustment of force levels to engender matching peak strains.

Appendix A. Supplementary material

Supplementary data associated with this article can be found in the online version at http://dx.doi.org/10.1016/j.jbiomech.2013.10.052.