A Pulsed EPR Study of Amino Acid and Tetrahydropterin Binding in a Tyrosine Hydroxylase Nitric Oxide Complex: Evidence for Substrate Rearrangements in Formation of the Oxygen-Reactive Complex

Abstract

Tyrosine hydroxylase is a non-heme iron enzyme found in the nervous system that catalyzes the hydroxylation of tyrosine to form L-3,4-dihydroxyphenylalanine, the rate-limiting step in the biosynthesis of the catecholamine neurotransmitters. Catalysis requires the binding of three substrates: tyrosine, tetrahydrobiopterin and molecular oxygen. We have used nitric oxide as an O2 surrogate to poise Fe(II) at the catalytic site in an S=3/2, {FeNO}⁷ form amenable to EPR spectroscopy. ²H-Electron Spin Echo Envelope Modulation was then used to measure the distance and orientation of specifically deuterated substrate tyrosine and cofactor 6-methyltetrahydropterin with respect to the magnetic axes of the {FeNO}⁷ paramagnetic center. Our results show that the addition of tyrosine triggers a conformational change in the enzyme that reduces the distance from the {FeNO}⁷ center to the closest deuteron on 6,7-²H-6-methyltetrahydropterin from >5.9 Å to 4.4 ± 0.2 Å. Conversely, the addition of 6-methyltetrahydropterin to enzyme samples treated with 3,5-²H-tyrosine resulted in reorientation of the magnetic axes of the S=3/2 {FeNO}⁷ center with respect to the deuterated substrate. Taken together, these results show that the coordination of both substrate and cofactor direct the coordination of NO to Fe(II) at the active site. Parallel studies of a quaternary complex of an uncoupled tyrosine hydroxylase variant, E332A, show no change in the hyperfine coupling to substrate tyrosine and cofactor 6-methyltetrahydropterin. Our results are discussed in the context of previous spectroscopic and X-ray crystallographic studies done on tyrosine hydroxylase and phenylalanine hydroxylase.

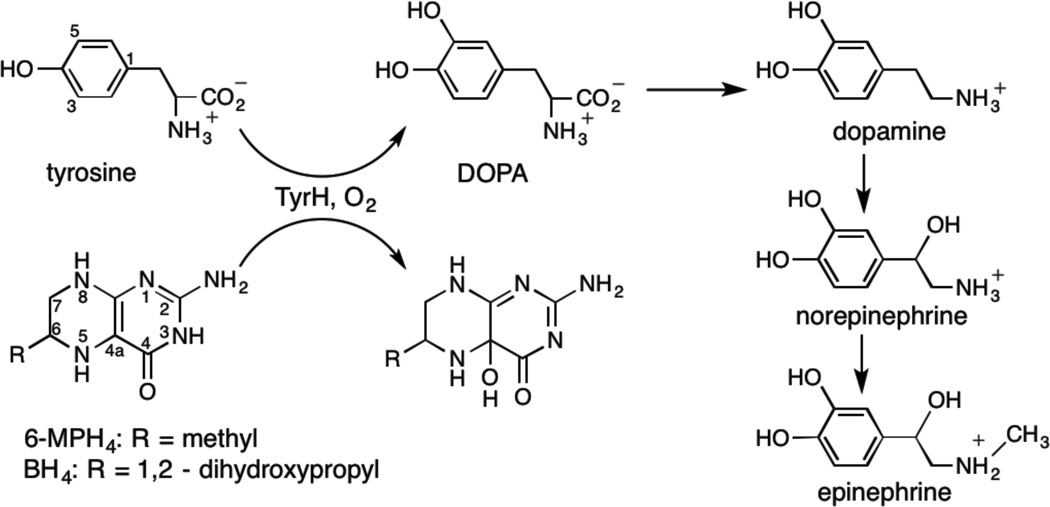
Tyrosine hydroxylase (TyrH) is a non-heme Fe enzyme found in the brain and adrenal gland of humans that catalyzes the hydroxylation of the amino acid L-tyrosine to form L-3,4 -dihydroxyphenylalanine (L-DOPA) ⁽¹⁾. This reaction is the rate-limiting step in the biosynthesis of the catecholamine neurotransmitters dopamine, epinephrine and norepinephrin (Scheme 1), making it vital to nervous system function. Mutations in TyrH have been associated with L-DOPA responsive forms of Segawa’s syndrome and Parkinson’s disease ^{(2, 3)}, and they have been implicated in bipolar affective disorder ⁽⁴⁾.

Scheme 1.

Hydroxylation reactions catalyzed by Tyrosine Hydroxylase

The chemical mechanism of tyrosine hydroxylation requires the binding of tyrosine (tyr), a tetrahydropterin, with tetrahydrobiopterin (BH₄) the physiological substrate, and O₂ to a catalytic site that houses an Fe(II) facially coordinated by the side-chains of two histidines and a glutamate ⁽⁵⁾. X-Ray crystallographic studies of TyrH are of Fe(III) forms of the enzyme and show that the metal ion is either 5- or 6-coordinate with the coordination sphere completed by water ligands ^{(6, 7)}. Detailed X-ray absorption and variable-temperature variable-field MCD spectroscopic studies have shown that tyrosine and BH₄ do not bind directly to the Fe(II), but that their binding leads to structural changes that result in the metal center transitioning from 6- to 5-coordinate ⁽⁸⁾. These changes at the catalytic site result in a ≥100-fold enhancement of O₂ reactivity with the Fe(II) and thus trigger the start of a two-step catalytic mechanism ^{(5, 8)}. The first step involves reaction of the Fe(II)-bound O₂ with BH₄ and leads to the hydroxylation of the C_4a carbon to yield 4a-hydroxy-biopterin (Scheme 1). In this reaction, BH₄ supplies two electrons for the heterolytic cleavage of the O-O bond leading to the formation of the hydroxypterin product and a Fe(IV)-oxo intermediate; the Fe(IV)-oxo species has been trapped for TyrH and characterized by Mössbauer spectroscopy ⁽⁹⁾. The second step of the catalytic mechanism involves attack of the Fe(IV)-oxo species on the phenol side chain of tyrosine to produce L-DOPA by electrophilic aromatic substitution ^{(10, 11)}.

Our understanding of the changes in protein structure that accompany the increased reactivity with oxygen once both substrates are bound is incomplete. In the case of TyrH, only structures of the inactive ferric enzyme are available, with and without bound dihydrobiopterin; these do not show any change in structure upon binding of this cofactor analog^{(6, 7)}. In contrast, fluorescence anisotropy analyses of TyrH have shown that the conformation of a mobile loop important for the coupling of BH₄ oxidation to the hydroxylation of tyrosine ⁽¹²⁾ is altered significantly upon binding of 6-methyl-5-deazatetrahydropterin, with a further smaller change when an amino acid is also bound ⁽¹³⁾. Structural data for the other two pterin-dependent, non-heme Fe aromatic amino acid hydroxylases, phenylalanine hydroxylase (PheH) and tryptophan hydroxylase (TrpH), provide some additional insight, since all three of these enzymes are thought to utilize the same catalytic mechanism ^{(14, 15)}. Comparison of the X-ray structures of the Fe(II) form of PheH without ligands to a binary complex with BH₄ showed no significant changes in protein structure upon pterin binding ⁽¹⁵⁾. Subsequent studies of a ternary complex of PheH treated with BH₄ and the slow amino acid substrates thienylalanine and norleucine showed that the addition of the amino acid induced a conformational change in the protein that tightened the structure about the Fe(II) site and reduced the distance between the metal ion and C_4a of BH₄ from 6.1 Å to 4.5 Å ⁽¹⁶⁾. The structure of the Fe(III) form of chicken TrpH similarly shows that two active site loops close in response to the binding of tryptophan and imidazole ⁽¹⁷⁾. However, there is no structure available of any aromatic amino acid hydroxylase with just the amino acid substrate bound, although hydrogen/deuterium exchange studies of PheH show that the phenylalanine does bind in the absence of a pterin ⁽¹⁸⁾.

In this paper, we present the results of an EPR spectroscopic study, using the pulsed EPR method of Electron Spin Echo Envelope Modulation (ESEEM), to determine the structural relationships between the paramagnetic Fe-center and the substrates tyrosine and 6-methyltetrahydropterin (6-MPH4) in enzyme-substrate complexes. A comparative study of a TyrH variant, E332A, is also presented; previous biochemical and spectroscopic studies have shown that this residue plays a role in the binding of the pterin cofactor and the successful coupling of tetrahydropterin oxidation to amino acid hydroxylation ^{(8, 19)}. We have used the approach developed by Salerno ⁽²⁰⁾ and broadly applied by Lipscomb and coworkers for EPR studies of non-heme Fe enzymes ^(21–23). Specifically, nitric oxide (NO) has been used as an O2 surrogate to allow EPR detection of the Fe(II) site by creating an S = 3/2, {FeNO}⁷ species ⁽²⁴⁾. For TyrH, the resulting EPR signals under the conditions of our measurements stem from the ms = ±1/2 Kramer’s doublet and show nearly axial spectra with effective g-values near g = 4 and g = 2. In addition to enabling EPR detection, the binding of NO blocks O2 binding to the active site allowing us to prepare samples with chemically active substrate and cofactor. Electronic structure calculations show that the g = 2.0 axis of the {FeNO}⁷ paramagnetic center lies within 5° of the Fe – NO bond⁽²⁵⁾ and that the Fe-NO bond is highly covalent with considerable double bond character. Taken together, these findings provide a structural reference point for interpreting our hyperfine couplings ^{(26, 27)}. Hoffman and coworkers combined this approach with 35 GHz ²H-ENDOR spectroscopy to characterize substrate binding to the active sites of naphthalene 1,2 dioxygenase and ACC oxidase ^{(28, 29)}. Following their lead, we used 9 GHz ²H-ESEEM spectroscopy to study the structural relationship between the {FeNO}⁷ center and substrate taurine in an alpha-ketoglutarate dependent hydroxylase, taurine dioxygenase ⁽³⁰⁾. An encouraging result from both the ENDOR and ESEEM studies was that the effective dipole-dipole distances derived from the anisotropy of the ²H hyperfine coupling agreed well with distances between Fe and the appropriate ligand protons as predicted from X-ray crystal structures. Furthermore, the measured orientations of the dipolar coupling vector with respect to the Fe-NO bond axis were in general agreement with chemical models for the catalytic mechanism.

Materials and Methods

6-Methyltetrahydropterin (6-MPH4) and 6-methylpterin were purchased from Schircks Laboratories (Jona, Switzerland). 6-(2-Hydroxy-1-methyl-2-nitrosohydrazino)-N-methyl-1-hexanamine (MAHMA NONOate), ethylenediamine tetraacetic acid (EDTA), L-tyrosine and glycerol were from Sigma-Aldrich (St. Louis, MO). L-3,5-²H2-Tyrosine and deuterium gas were from Cambridge Isotopes (Andover, MA). Potassium chloride and ferrous ammonium sulfate were from Fisher (Pittsburg, PA). All other chemicals were of the highest purity commercially available. Deuterated 6-MPH4 was synthesized by reduction of 6-methylpterin to the level of tetrahydropterin using deuterium gas, as previously described ⁽³¹⁾.

Wild-type TyrH was expressed in E. coli and purified as previously described⁽¹⁹⁾. To remove iron from the protein, the ammonium sulfate pellet at the end of the purification was resuspended in 5 mM EDTA, 200 mM Hepes, (pH 7.5), 10% glycerol and 0.1 M KCl, and incubated on ice for one hour. The enzyme solution was then dialyzed against the same buffer without EDTA and concentrated using Amicon Ultra-15 and Ultra-4 centrifugal filters (Millipore Corp., MA). The enzyme samples for ESEEM were brought to a final glycerol concentration of 30% (v/v) during the concentration stage. The iron content of the apo-enzyme was measured using a Perkin-Elmer AAnalyst600 atomic absorption instrument ⁽³²⁾. Typical iron content of an apo-enzyme preparation was ~0.1 equivalent.

Stock solutions of MAHMA NONOate were prepared in 0.01 M NaOH just before the experiment and were kept on ice. Concentrations of the MAHMA NONOate solutions were determined in 0.01 M KOH, using an ε₂₅₀ of 7.3 mM⁻¹cm^{−1 (33)}. Highly concentrated (~50 mM) stock solutions of tyrosine and 3,5-²H2-tyrosine were prepared at pH 10. Stock solutions of the protiated and deuterated 6-MPH4 were prepared in 2 mM HCl to prevent autoxidation until the sample was made anaerobic. Ferrous ammonium sulfate solutions were prepared fresh in 2 mM HCl. ESEEM samples were prepared inside an anaerobic cuvette at 25 °C. Apo-TyrH (0.9–1.2 mM) and tyrosine (1–1.7 equivalents for complexes containing tyrosine) were placed at the bottom of the cuvette. A ferrous ammonium sulfate solution (0.9 equivalent in ~10 µl) was placed on the lower neck of the cuvette. 6-MPH4 (~1.5 equivalents) and MAHMA NONOate solutions were either placed in the side arms or on the upper neck of the cuvette, for large and small volumes, respectively. Buffer conditions were 100 mM Mops (pH 7.0), 0.3 M KCl and 30% glycerol. The contents of the cuvette (a total volume of ~250 µl) were made anaerobic by the application of argon-vacuum exchange for at least 20 minutes. The anaerobic enzyme solution was then mixed with ferrous ammonium sulfate and incubated for 10 minutes. This was followed by mixing with 6-MPH₄ (if the complex was to contain 6-MPH₄). After a few minutes of incubation, MAHMA NONOate (~0.6 equivalent of the enzyme) at the upper neck of the cuvette was introduced to the enzyme-substrate mixture. After ~3 minutes, ~200 µl of the reaction mixture was quickly transferred to the quartz EPR tubes (4 mm OD, 707-SQ-250M, Wilmad, Buena, NJ) using a glass pipette and immediately frozen in liquid nitrogen. (The half-life of MAHMA NONOate is ~35 s under these buffer and temperature conditions (data not shown).) UV-Visible spectra collected at increasing concentrations of MAHMA NONOate showed that NO was saturating under the concentrations used.

EPR measurements were made on a Bruker E-680X spectrometer operating at X-band and equipped with a model ER 4118X-MD-X5-W1 probe that employed a 5 mm dielectric resonator. The temperature was maintained at 4.0 K using an Oxford Instruments liquid helium flow system equipped with a CF-935 cryostat and an ITC-503 temperature controller. ESEEM data were collected using a three-pulse (stimulated echo) sequence, 90°-τ-90°-T-90°, with 90° microwave pulse widths of 16 ns (FWHM). The tau values were chosen to suppress the hydrogen matrix contribution; due to short phase memory times they were restricted to less than 200 ns. An integration window of 24 ns was used to acquire the spin echo amplitude, and data set lengths were 512 points. A four-step phase cycling scheme was used to eliminate 2-pulse spin echoes and the DC offset voltage of the detection system from the data.

The deuterium contributions to the ESEEM spectra were elucidated using the ratio method and were performed using the analysis software of the Bruker Xepr program ⁽³⁴⁾. Three-pulse ESEEM data were collected for samples containing deuterated substrate or cofactor and matching reference samples containing the corresponding protiated substrate and/or cofactor. Both data sets were phase-corrected, and the real portion of each was normalized to one. The two normalized data sets were then divided, tapered with a Hamming window function and Fourier transformed. ESEEM spectra were obtained by taking the absolute value of the real part of the transforms. Because the 3-pulse ESEEM function is the sum of product terms for the two coherence transfer pathways that lead to formation of the stimulated echo ⁽³⁵⁾, this procedure is approximate and can give rise to cross-terms that appear as peaks in the FFT if the modulations are deep ⁽³⁶⁾. For the studies presented here, we found that the quotient deuterium spectra in the g = 2 region were free from such distortions, but that spectra in the g = 4 region, where deeper, overlapping modulations from coupled ¹⁴N and ¹H were observed, often contained spurious peaks. The resulting uncertainty in ²H-ESEEM amplitudes was considered in our analysis and will be discussed below.

Continuous wave EPR spectra were analyzed using the “pepper” module of EasySpin 4.0 ⁽³⁷⁾. The cw-EPR spectra observed for the various {FeNO}⁷ derivatives of TyrH showed nearly axial spectra with features near g = 4 and g = 2. These spectra were modeled using a standard approach for S = 3/2 transition ions with a spin Hamiltonian that consisted of a zero-field splitting term and an isotropic, or spin-only, electronic Zeeman term with g_o = 2.00 (Eqn. 1) ⁽³⁸⁾. For our simulations, we took D = 10 cm⁻¹ based on findings from EPR, magnetic

$$\widehat{H}=g_0{\beta }_e\underset{˜}{\widehat{S}}•\underset{˜}{H}+D[{\widehat{S}}_z^2-\frac{5}{4}+\frac{E}{D}({\widehat{S}}_x^2-{\widehat{S}}_y^2)]$$ [1]

susceptibility and Mössbauer studies of other non-heme Fe dioxygenases and {FeNO}⁷ model complexes ^{(21, 23, 26, 39)}. TyrH spectra were treated as composites of two paramagnetic species and were fit by varying the rhombic terms in the ZFS interaction, E/D, the strains in E, and the speciation of the paramagnetic centers. Fitting was restricted to the g = 4 region of the EPR spectrum and accomplished using the function “fminsearch” available in MATLAB (The Mathworks, Natick, MA).

Orientation selected ²H-ESEEM spectra were fit across the EPR spectrum using the “saffron” routine from EasySpin 4.0⁽⁴⁰⁾ for spectral simulation together with a combination of the MATLAB global optimization routines “patternsearch” and “fminsearch” for non-linear least squares optimization of the spin Hamiltonian parameters that describe the hyperfine interaction. These calculations were done for the S=3/2 electron spin system using the principal axis system (PAS) of the ZFS tensor as the reference frame and the values for D, E and g_o that were obtained from fitting the corresponding cw-EPR spectra. The deuterium hyperfine interaction was described by a spin Hamiltonian that included nuclear Zeeman, electron-nuclear hyperfine and nuclear quadrupole interactions,

$${\widehat{H}}_{hf}=-\frac{g_n{\beta }_n}{h}\underset{˜}{\widehat{I}}•\underset{˜}{H}+\underset{˜}{\widehat{S}}•\mathbf{A}•\underset{˜}{\widehat{I}}+\underset{˜}{\widehat{I}}•\mathbf{Q}•\underset{˜}{\widehat{I}}$$ [2]

where g_n = 0.8574 for ²H, β_n is the nuclear magneton, $\underset{˜}{\widehat{S}}$ and $\underset{˜}{\widehat{I}}$ are the electron and nuclear spin angular momentum operators, respectively, and [H̰] is the applied magnetic field. Because the deuterated tyrosine substrate and pterin cofactor are not coordinated to Fe, the measured ²H-hyperfine couplings were modeled with a through-space dipolar interaction described by

$$T=\frac{g_e{g}_n{\beta }_e{\beta }_n}{{\mathit{\text{hr}}}_{\mathit{\text{eff}}}^3}.$$ [3]

The resulting axial deuterium hyperfine tensor, with principal elements of (-T, -T, 2T), was rotated into the ZFS reference frame using a standard “zyz” Euler rotation scheme to obtain the 3×3 hyperfine coupling matrix, A, as denoted in Eqn. 2. The deuterium nuclear quadrupole interaction (nqi) was also constrained to have axial symmetry because the electric field gradient at the nucleus is dominated by the electrons of its sigma bond to carbon. The principal values of the nqi coupling tensor are then $\frac{e^{2}qQ}{4h}(-1,-1,2)$ and subsequent transformation to the ZFS axis system by an Euler rotation scheme yields the nqi coupling tensor, Q (Eqn. 2). Because both the hyperfine and the nuclear quadrupole interactions were constrained to axial symmetry, only the second and third Euler angles of the zy’z” rotation scheme will serve to reorient the tensors in the ZFS reference frame. As a result, our ²H-ESEEM simulations considered six adjustable parameters: the dipolar coupling strength, T; two Euler angles to orient the hyperfine tensor, β_hf and γ_hf; e²qQ/h, the quadrupole coupling constant; and two Euler angles, β_nqi and γ_nqi, to transform the nqi coupling tensor.

The ESEEM analysis described in the Results section below was based on a comparison of simulated and experimentally determined ²H spectra. To facilitate this comparison, the time domain output from the “saffron” (EasySpin) calculation was normalized to one and then treated with the same analysis procedure as described for our experimental data. Using this approach, it was possible to fit ²H-ESEEM peak amplitudes and lineshapes. The fitting procedure was based on minimizing χ² for each sample, where

$${\chi }^2=\sum _{i=1}^N\sum _{j=f\text{min}}^{f\text{max}}\frac{{(Y_{\mathit{\text{ij}}}^{\mathit{\text{calc}}}-Y_{\mathit{\text{ij}}}^{\text{exp}})}^2}{{\sigma }^2}$$ [4]

The sums of Eqn. 4 are taken over discrete ESEEM spectra, i, collected at “N” different magnetic field positions and across the ²H-ESEEM lineshape at each field position for frequency “bins” indexed from “fmin” to “fmax.” Typically, our analysis considered 5 – 6 ESEEM spectra collected at different field positions across the EPR spectrum. The indices for lineshape comparisons were determined from the individual spectra by selecting a span of 8 – 12 points that encompassed the ²H-ESEEM response. A constant value for the experimental standard deviation, σ = 0.1, was estimated from the noise typically observed over the 5–10 MHz range of our ESEEM spectra and was used for all of the fits. The overall quality of a fit for each sample was judged by normalizing Eqn. 4,

$${\chi }_{\nu }^2=\frac{{\chi }^2}{\mathit{\text{npts}}-L}$$ [5]

where npts was the total number of data points considered in the analysis and L was the number of parameters varied in the fitting procedure. For the calculations described in this paper, npts ranged from 55 to 65 and L = 6.

The errors in the spin Hamiltonian parameters that were derived from the fitting procedure described above are reported as ± one standard deviation. This corresponds to an increase in the best fit value, or minimum value, of ${\chi }_{\nu }^2$ by one. These standard deviations were estimated in two ways and the largest values obtained are reported along with the overall fitting results in Table 2. The first approach to estimating parameter errors was based on numerical calculation of the covariance matrix, C, using the Hamiltonian parameters that gave the best-fit value of χ^{2 (41, 42)}. The standard deviations were then given by the square roots of the diagonal elements of C. This approach assumes that the χ² function is quadratic near the minimum found for each parameter. In practice, we found that the minima in plots of χ² vs. T, β_hf and e²qQ/h were quadratic or cusp-like, and that the above procedure worked well for estimating the standard deviation in their values. The remaining three parameters, γ_hf, β_nqi and γ_nqi, showed individual χ² functions that were either edge-like or were characterized by shallow wells that were less than ${\chi }_{\nu }^2+1$ in depth. For these parameters, errors were also estimated directly from plots of χ² vs. individual parameter values and compared with those obtained from the covariance matrix. For these cases, the largest value determined for the standard deviation was reported in Table 2.

Table 2.

²H – ESEEM Analysis Results

sample	T (MHz)	reff (Å)	βhf(o)	e2qQ/h (MHz)	βnqi(o)	|γnqi−γhf|	${\chi }_{\nu }^2$
TyrH {2H-tyr}	0.18 ± 0.01	4.1 ± 0.1	26 ± 5°	0.27 ± 0.05	62 ± 12°	38 ± 20°	1.2
TyrH {2H-tyr, 6-MPH4}	0.12 ± 0.01	4.7 ± 0.2	94 ± 10°	0.34 ± 0.06	69 ± 10°	20 ± 80°	2.2
E332A {2H-tyr, 6-MPH4}	0.12 ± 0.01	4.7 ± 0.2	89 ± 9°	0.29 ± 0.05	44 ± 16°	14 ± 43°	1.2
TyrH {tyr, 2H-6-MPH4}	0.14 ± 0.01	4.4 ± 0.2	66 ± 5°	0.22 ± 0.06	70 ± 57°	26 ± 90°	1.2
E332A {tyr, 2H-6-MPH4}	0.14 ± 0.01	4.4 ± 0.2	65 ± 5°	0.20 ± 0.06	66 ± 60°	18 ± 90°	1.0
TyrH {2H-6-MPH4}	< 0.06	>5.9

Results

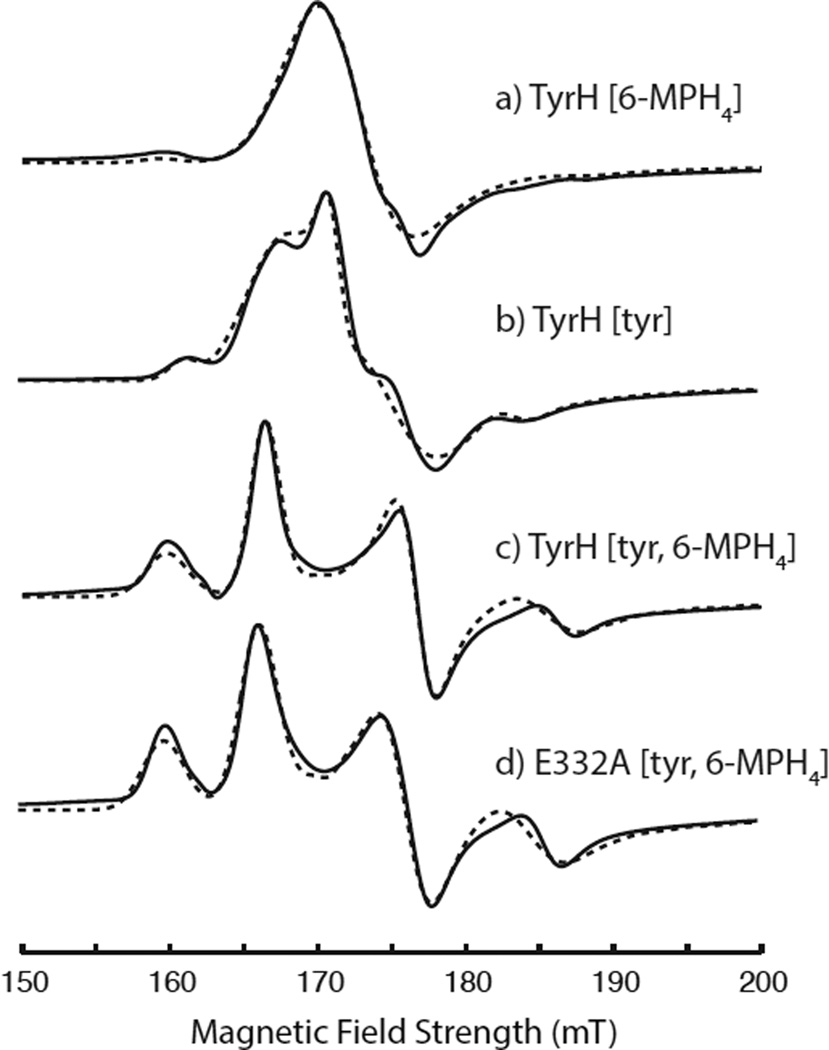
The cw-EPR spectra for all of the TyrH complexes studied showed nearly axial spectra with lineshape features near g = 4 and g = 2. As the g = 4 feature is most sensitive to changes in the symmetry of the zero field splitting interaction, it is the focus of Figure 1 where the experimental spectra are portrayed with solid lines. These spectra were analyzed using EasySpin as discussed above, and the results of the simulations are provided as dashed lines in Figure 1 and summarized by the spin Hamiltonian parameters given in Table 1. Corresponding full EPR spectra, showing both g=4 and g=2 regions, are provided in Figure S1 of the supplementary information. Figure 1a shows the cw-EPR lineshape in the g = 4 region for TyrH treated with 6-MPH₄ and NO. This spectrum is similar to that obtained for TyrH without added tyrosine or 6-MPH₄ (results not shown) in that a single broad feature centered at g = 4.00 characterized by |E|/D = 0 dominates the spectrum. For TyrH treated with tyrosine and NO (Figure 1b), the data were analyzed as a composite of two species, a majority species (91%) with |E|/D = 0.02 and a minority species characterized by |E|/D = 0.04. The cw-EPR lineshapes in the g = 4 region for the two quaternary complexes, wild type TyrH and the variant E332A treated with tyr, 6-MPH4, and NO are shown in Figures 1c and 1d, respectively. These spectra are nearly identical and show that two species are also present at 4.0 K: a majority species that represents about 60% of the {FeNO}⁷ sites with an |E|/D = 0.02 and a species that accounts for the remaining 40% of the EPR active sites characterized by an |E|/D = 0.05. Table 1 also shows that the strain, or spread, in E-values decreases modestly as substrates are added. This observation is in agreement with findings from the X-ray studies of PheH and TrpH where the protein structures were observed to “tighten” around the Fe(II) site as a result of substrate and cofactor binding ^{(16, 17)}.

Figure 1.

The g = 4 region of cw-EPR spectra collected for {FeNO}⁷ derivatives of TyrH treated with (a) 6-MPH₄, (b) tyr, (c) 6-MPH₄ plus tyr, (d) the E332A variant of TyrH treated with 6-MPH₄ plus tyr. The solid lines are the experimental spectra and the simulations performed using the parameters in Table 1 are shown with dashed lines. The experimental data were collected under the following conditions: microwave frequency, 9.68 GHz; microwave power, 0.0063 mW; field modulation amplitude, 0.8 mT; 10 kHz modulation frequency; time constant, 40 msec; sample temperature, 4.0 K.

Table 1.

Cw-EPR Parameters of Tyrosine Hydroxylase NO complexes

sample	% contribution	|E|/D	Estrain(MHz)
TyrH{6-MPH4}	95 5	0 0.025	7800 3700
TyrH{tyr}	91 9	0.017 0.043	6400 1900
TyrH{tyr, 6-MPH4}	63 37	0.020 0.050	1900 3700
E332A{tyr, 6-MPH4}	58 42	0.020 0.049	3200 4000

The results tabulated in Table 1 show that all of the paramagnetic centers being considered in this work are mixtures characterized by modest differences in |E|/D of 0.02 – 0.03. Previous EPR studies of coordinatively unsaturated {FeNO}⁷ model complexes have shown that changes in the rhombicity, |E|/D, of the ZFS interaction of 0.04 – 0.05 can arise from modest changes of 18° in Fe-NO bond angle brought about by steric crowding⁽⁴³⁾. It is also possible that differences in the orientation of the bound NO ligand with respect to rotation about the Fe-NO bond could lead to the observed speciation. A recent DFT study of the {FeNO}⁷ adduct of taurine: α-ketoglutarate dioxygenase reported two minima for the potential energy surface describing rotation about the Fe-NO bond with projections of the NO favoring alignment with the carboxylate oxygens of the glutamate ligand and bound α-ketoglutarate⁽²⁷⁾. Therefore, we chose to treat this speciation explicitly in our orientation-selective analysis of the ESEEM data, assuming that NO was coordinated to a unique position on Fe for each sample and that the speciation observed in the cw-EPR spectra arose from two conformations or rotamers present in frozen solution. In principle, treating two rotamers with a single set of Hamiltonian parameters for the purpose of defining the hyperfine interaction (Eqn. 2) is problematic as the values of γ_hf and γ_nqi for each rotamer should be distinct. In practice, it was found that the near axial nature of the paramagnetic centers, with a majority having |E|/D = 0.02, made our measurements less sensitive to γ_hf, and allowed us to approximate the spin Hamiltonian with single values for γ_hf and γ_nqi.

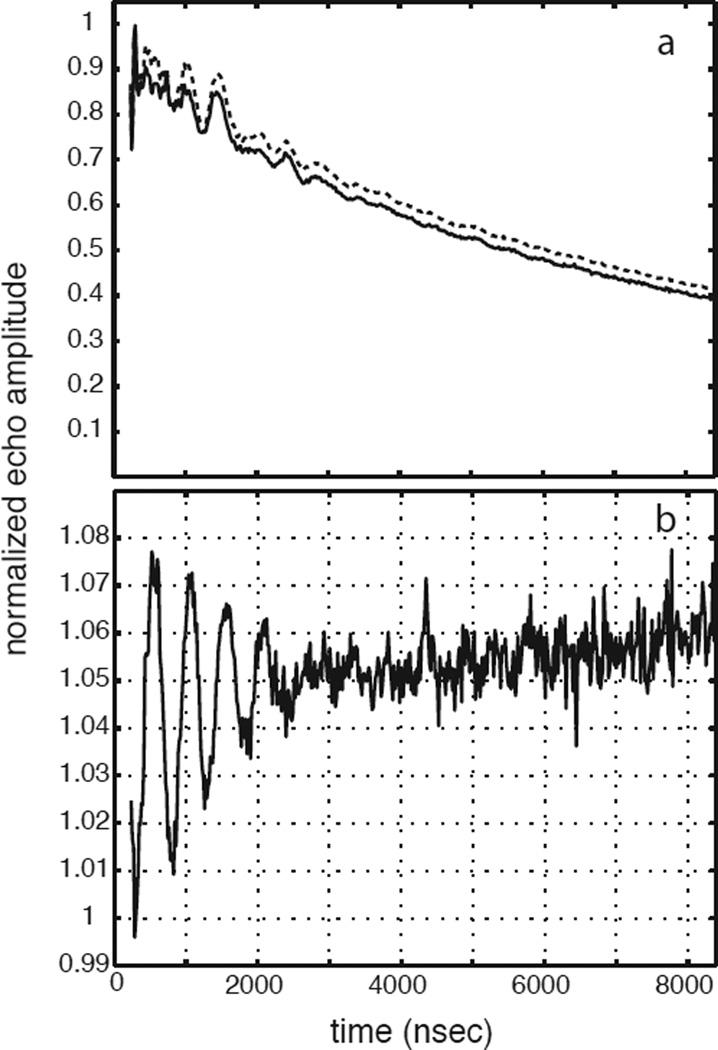
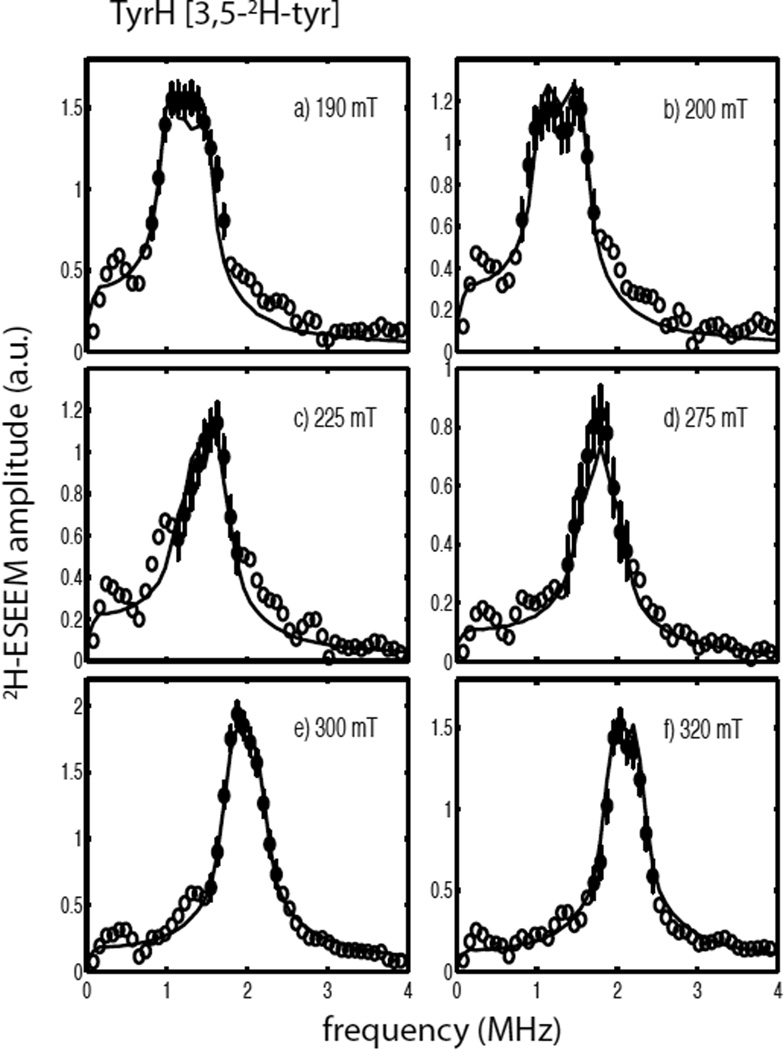
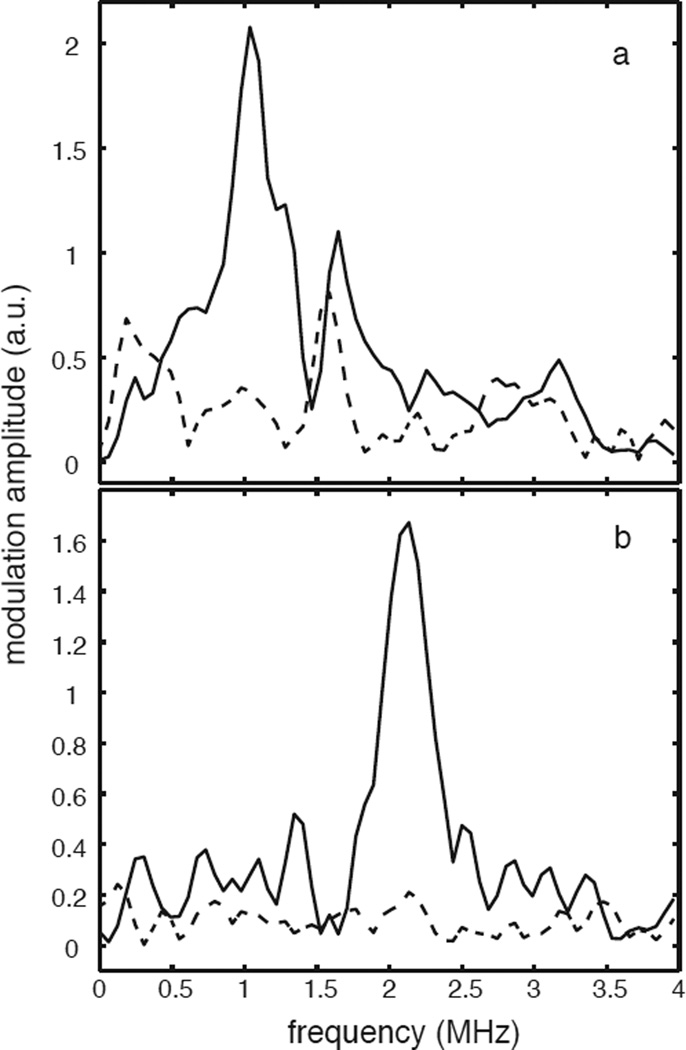
Figure 2a shows normalized 3-pulse ESEEM data sets for the ternary complex of TyrH/ NO/tyr (solid line) and the corresponding sample made with 3,5-²H- tyrosine (dashed line) collected at 300 mT (see Scheme 1 for the substrate numbering key). The time domain data sets were both normalized to one and are nearly identical. The quotient modulation function is shown in Figure 2b and reveals ²H ESEEM with a modulation depth of about 6% of the overall signal amplitude. The corresponding ²H-ESEEM frequency spectrum of these data is represented by the open and filled circles (with error bars) centered about the deuterium Larmor frequency of 2.0 MHz in Figure 3e. Figure 3 also shows the results of repeating the measurements described above at five other magnetic field positions spanning the EPR spectrum from g =4 to g=2. In the g=4 region, Figures 3a and 3b, broader lineshapes that are nearly flat at their maximum amplitude, were observed. Spectra obtained in the g = 2 region, Figures 3e and 3f, show larger amplitudes, but narrower lineshapes. For all six field positions, the data points displayed as filled circles with error bars were used for analysis. These data points are centered about the deuterium Larmor frequency and were chosen because they exceeded an amplitude threshold of 0.4 – 0.6 and are most likely free of spurious peaks that can result from data division. Evidence for these spurious peaks can be seen in all six of the ESEEM quotient spectra shown in Figure 3 by tracing through the points represented by the open circles on the low and high frequency sides of the ²H-ESEEM peaks.

Figure 2.

(a) 3-pulse ESEEM data collected for TyrH/NO/tyrosine (solid line) and TyrH/NO/ 3,5-²H- tyrosine (dashed line) under the following conditions: field strength, 300 mT; microwave frequency, 9.684 GHz; tau, 156 ns; sample temperature, 4.0 K. (b) The ratio of the two time domain data sets shown in (a).

Figure 3.

²H-ESEEM spectra (open and filled circles) obtained by Fourier transformation of ESEEM data from the ternary complexes of TyrH/NO/3,5-²H- tyrosine divided by TyrH/NO/tyr. Data were collected at 9.684 GHz using the following field positions and tau values a) 190 mT, 124 ns; b) 200 mT, 116 ns; c) 225 mT, 104 ns; d) 275 mT, 84 ns; e) 300 mT, 156 ns; and f) 320 mT, 148 ns. The solid lines in each frame are best fit ESEEM simulations to the data points represented by the filled circles with error bars using the following spin Hamiltonian parameters: g_n = 0.8574, T = 0.18 MHz, β_hf = 26°, γ_hf = 0°, e²qQ/h = 0.27 MHz, β_nqi = 62° and γ_nqi = 38°.

The solid lines shown in Figure 3 are simulated ²H-ESEEM spectra that represent the best fit of the spin Hamiltonian model provided in Eqn. 2 for a single, coupled deuteron to the data. The simulations took into account the complex nature of the cw-EPR spectrum of the TyrH/NO/ tyr sample as summarized in Table 1 by including contributions from both paramagnetic centers, |E|/D = 0.02 and 0.04, weighted by the scaling factors, 0.91 and 0.09, respectively. The results yield a ²H-dipolar coupling, T = 0.18 MHz, which corresponds to an effective dipole-dipole distance of 4.1Å as obtained from Eqn. 3. The orientation of the principal axis system (PAS) of the hyperfine coupling tensor with respect to the PAS of the ZFS tensor was described by the Euler angles, β_hf = 26° and γ_hf = 0°. These parameters and those obtained for the ²H-nuclear quadrupole interaction are provided in table 2. The overall quality of the non-linear least squares fit to the data was expressed as ${\chi }_{\nu }^2=1.2$ in Table 2 and was computed using Eqn. 5.

The errors reported for the best-fit spin Hamiltonian parameters determined for the coupled tyrosine deuteron were determined from plots of χ² as a function of changing individual parameter values while holding the other spin Hamiltonian parameters at their best-fit values. For the calculation at hand, on the TyrH/NO/3,5-²H-tyr sample, these “single-parameter χ² plots” are provided as Figure S2 of the supporting information. The standard deviations given in Table 2 are derived from measuring the width of each parameter distribution at ${\chi }_{\nu }^2+1,X^2=130$ for this case (marked with an arrow in Figure S2). For this sample, the single-parameter χ² plots for the dipolar coupling, T, β_hf and e²qQ/h were narrow and nearly parabolic in shape, while the plots obtained for γ_hf, β_nqi and γ_nqi were broader reflecting greater uncertainty.

A covariance analysis was also done using the best fit parameter set from Figure 3 and the results are tabulated as standard deviations, Table S3, and a full covariance matrix, Table S4, in the supplementary information. The standard deviations are the square roots of the diagonal elements of the covariance matrix and are all smaller than the values derived from the single-parameter χ² plots. However, the off-diagonal elements of the covariance matrix show a substantial degree of coupling between γ_hf and γ_nqi, and lesser interactions between the parameters that describe the deuterium nuclear quadrupole interaction, e²qQ/h, β_nqi, and γ_nqi. The effects of this covariance, or coupling, between γ_nqi and γ_hf were explored further by repeating the fitting procedure with the values for the hyperfine coupling parameters, T andβ_hf, fixed to their best fit values of 0.18 MHz and 26°, respectively. For each optimization,γ_hf was set to a fixed value between 0 and 90° and the three parameters that describe the nqi, e²qQ/h, β_nqi, and γ_nqi were varied to find a minimum in χ². While the best fits to the data were realized for values of γ_hf in the range from 0 – 20°, optimizations that gave χ² values below the ±1σ “threshold” defined by ${\chi }_{\nu }^2+1$, could be found for all values of γ_hf over the 0 – 90° range. Each of these calculations yielded values for e²qQ/h and β_nqi that varied little from those found for the best-fit solution, 0.27 MHz and 62°, respectively (Table 2), and fell within the standard deviations measured from the single-parameter χ² plots (Figure S2). In contrast, the optimized values of γ_nqi tracked the fixed value assigned to γ_hf so tha |γ_nqi − γ_hf| = 38 ± 7°. The modest dependence of the spectral fitting on γ_hf is not surprising given that the cw-EPR spectrum is nearly axial. The sensitivity of these simulations to β_nqi an |γ_nqi − γ_hf| is expected because these angles serve to define the relative orientation of the nqi with respect to the electron-nuclear hyperfine interaction.

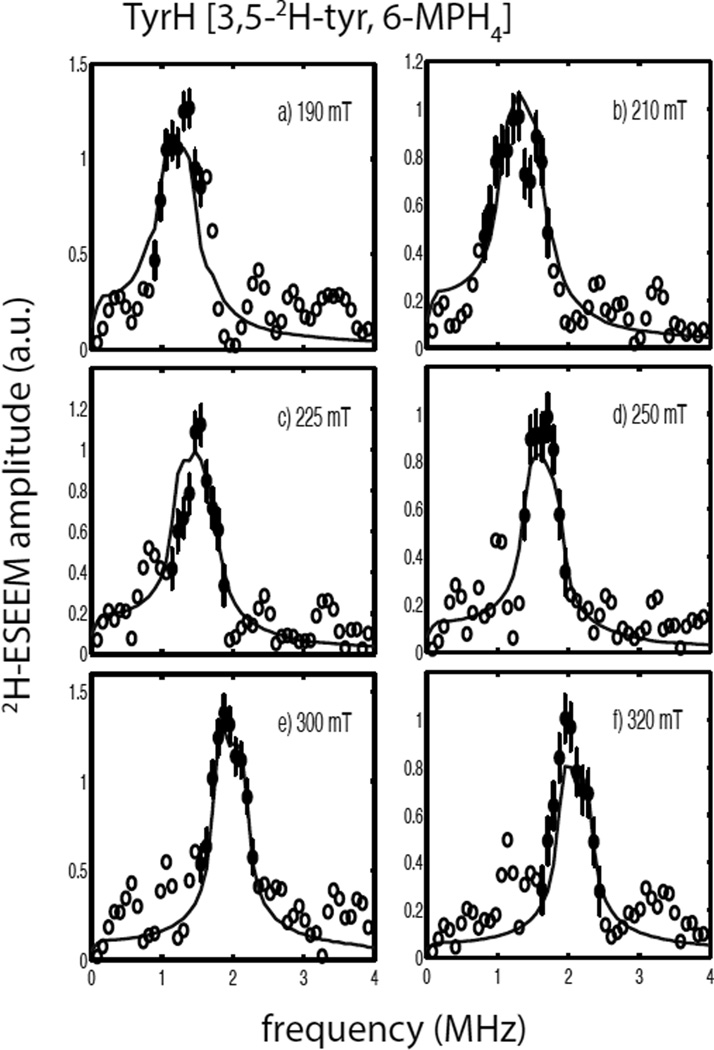
Figure 4 shows a composite drawing of the ²H-ESEEM spectra collected for the quaternary complex of TyrH/NO/3,5-²H-tyr/6-MPH₄ collected at six different field positions across EPR spectrum. Overall, these data show smaller ²H-peak amplitudes than those observed for the ternary complex with just 3,5-²H-tyr and NO (Figure 3). In the g = 4 region at 190 mT (Figure 4a) and 210 mT (Figure 4b), amplitudes were reduced by about 20%, while in the g = 2 region, amplitude reductions ranged from 20–50%. Unfortunately, as shown by the open circles in the spectra, these data were also plagued by distortions, or spurious peaks that stem from the division process used to reveal the deuterium ESEEM spectra. As a result, the lineshape data were less useful in guiding the analysis. The results of spectral simulations are shown with solid lines in Figure 4 and yield a dipolar coupling of T = 0.12 MHz, or an effective dipole-dipole distance of 4.7 Å, for a model that considered a single, coupled ²H. The Euler angles for orienting the hyperfine coupling tensor within the ZFS axis system were: β_hf, 94 ± 10°; and γ_hf, 20°. The value of ${\chi }_{\nu }^2=2.2$ obtained for these fits was substantially worse than for the ternary complex, TyrH/NO/3,5-²H-tyr. Single parameter χ² plots and the covariance matrix calculated from the best fit parameters are shown in Figure S5 and Tables S6 and S7, respectively. While this quaternary complex shows a higher percentage of more rhombic {FeNO}⁷ centers, 40% of the sites have |E|/D = 0.05, our spectral fits were also insensitive to γ_hf. As γ_hf was varied from 0 to 90° in the fitting procedure, optimized values of ${\chi }_{\nu }^2$ varied from a low of 2.2 at γ_hf values of 20 – 40° to a maximum of ${\chi }_{\nu }^2=2.6\text{at}{90}^{\circ }$. The best fit values of e²qQ/h = 0.34 MHz and β_nqi = 69° varied by just ± 0.02 MHz and ± 2° over this full range of γ_hf, while γ_nqi tracked the γ_hf values such tha |γ_nqi − γ_hf| = 20 ± 8°.

Figure 4.

²H-ESEEM spectra (open and filled circles) obtained by Fourier transformation of ESEEM data from the quaternary complexes of TyrH/NO/3,5-²H- tyr/6-MPH4 divided by TyrH/ NO/tyr/6-MPH4. Data were collected at 9.68 GHz using the following field positions and tau values a) 190 mT, 124 ns; b) 210 mT, 112 ns; c) 225 mT, 104 ns; d) 250 mT, 92 ns; e) 300 mT, 156 ns; and f) 320 mT, 148 ns. The solid lines in each frame are best fit ESEEM simulations to the data points represented by the filled circles with error bars using the following spin Hamiltonian parameters: gn = 0.8574, T = 0.12 MHz, β_hf = 94°, γ_hf = 20°, e²qQ/h = 0.34 MHz, β_nqi = 71° and γ_nqi = 40°.

Figure 5 shows ²H-ESEEM spectra collected for two different samples treated with 6,7-²H-6-MPH₄ at 178 mT (Figure 5a) and 320 mT (Figure 5b) (the pterin numbering scheme is provided in Scheme 1). The spectra represented with the solid lines are for a quaternary complex of TyrH/NO/tyr/6,7-²H-6-MPH₄ and show peaks centered at the deuterium Larmor frequency of 1.2 MHz at 178 mT and 2.1 MHz at 320 mT. The spectra represented by the dashed lines are from a ternary complex of TyrH/NO/6,7-²H-6-MPH₄ and are void of any ²H-ESEEM response. Figure 5a also shows a peak at 1.6 MHz that is present for both samples. This peak is typical of the distortions that we observed in the g = 4 region from data division and illustrates a complication that we avoided in our ²H-ESEEM analysis by not considering data collected at field positions below 190 mT (g=3.6).

Figure 5.

3-pulse ²H-ESEEM spectra obtained for the ternary complex TyrH/NO/6,7-²H-6-MPH₄ (dashed line) and the quaternary complex TyrH/NO/tyr/6,7-²H-6-MPH₄ (solid line) at (a) 178 mT, τ = 132 ns and (b) 320 mT, τ = 148 ns.

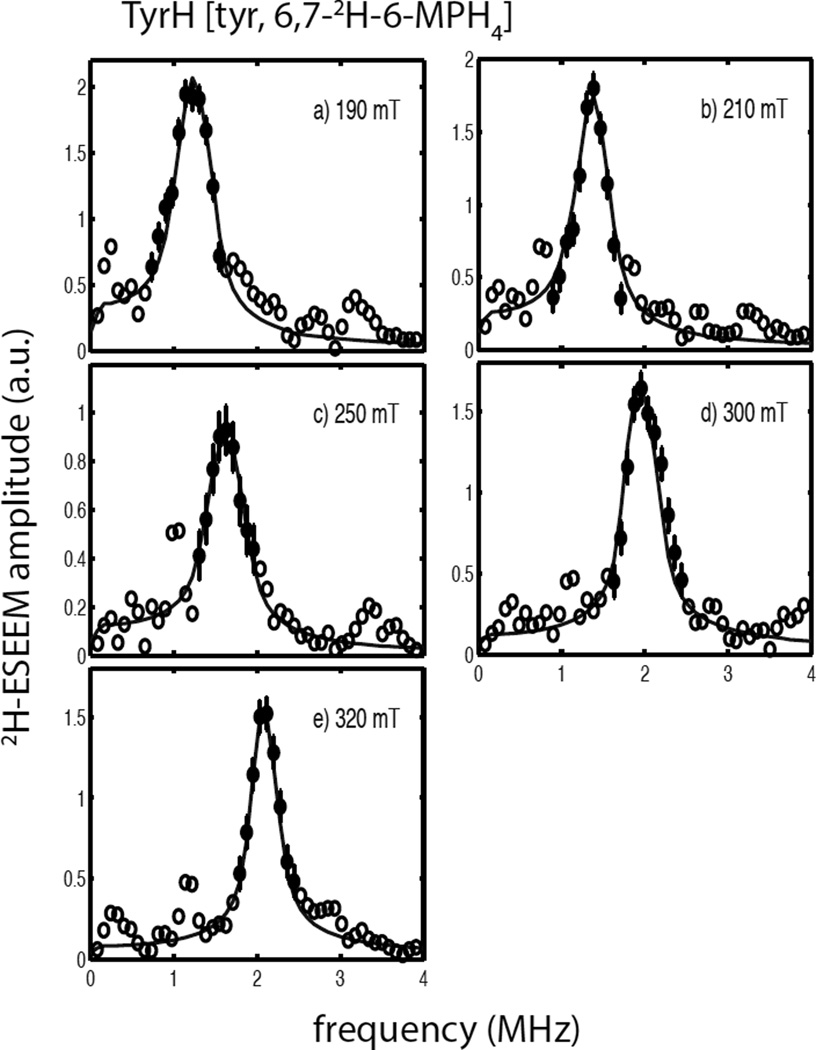
Figure 6 shows a composite drawing of ²H-ESEEM spectra observed for the quaternary complex of TyrH/NO/tyr/6,7-²H-6-MPH₄ at five magnetic field positions across the EPR spectrum. Overall, the ²H-ESEEM spectral amplitudes are greater for this sample and the lineshapes are narrowed and more symmetrical about the ²H-Larmor frequency as compared to those observed for the ²H-tyr samples shown above. The solid lines in Figure 6 are the best fit simulations to the data points showed as filled circles and yield a dipolar coupling of T = 0.14 MHz, or an effective dipolar distance of 4.4Å. The orientation of the hyperfine coupling tensor with respect to the ZFS PAS was given by β_hf = 66 ± 5° and a γ_hf value of 0° was used for the simulations shown. Single parameter χ² plots and the covariance matrix calculated from the best fit parameters are shown in Figure S8 and Tables S9 and S10, respectively. As with the previous analyses, fits of these data were not sensitive to γ_hf and optimizations done as a function γ_hf gave parameters for the nqi of e²qQ/h = 0.22 MHz, β_nqi = 70° an |γ_nqi − γ_hf| = 26°. The error estimates for these parameters (Table 2) come from the single parameter χ² plots of Figure S8. The errors for the Euler angles describing the orientation of the nqi principal axes with respect to the ZFS PAS are quite large for this sample as reflected in the unique edge-like shape of the single parameter χ² plot for β_nqi and the shallow nature of the global minima found for γ_nqi.

Figure 6.

²H-ESEEM spectra (open and filled circles) obtained by Fourier transformation of ESEEM data from the ternary complexes of TyrH/NO/tyrosine/6,7-²H-6-MPH₄ divided by TyrH/ NO/tyr/6-MPH₄. Data were collected at 9.68 GHz using the following field positions and tau values a) 190 mT, 124 ns; b) 210 mT, 112 ns; c) 250 mT, 92 ns; d) 300 mT, 156 ns; and e) 320 mT, 148 ns. The solid lines in each frame are best fit ESEEM simulations to the data points represented by the filled circles with error bars using the following spin Hamiltonian parameters: g_n = 0.8574, T = 0.14 MHz, β_hf = 66°, γ_hf = 0°, e²qQ/h = 0.22 MHz, β_nqi = 70° and γ_nqi = 26°.

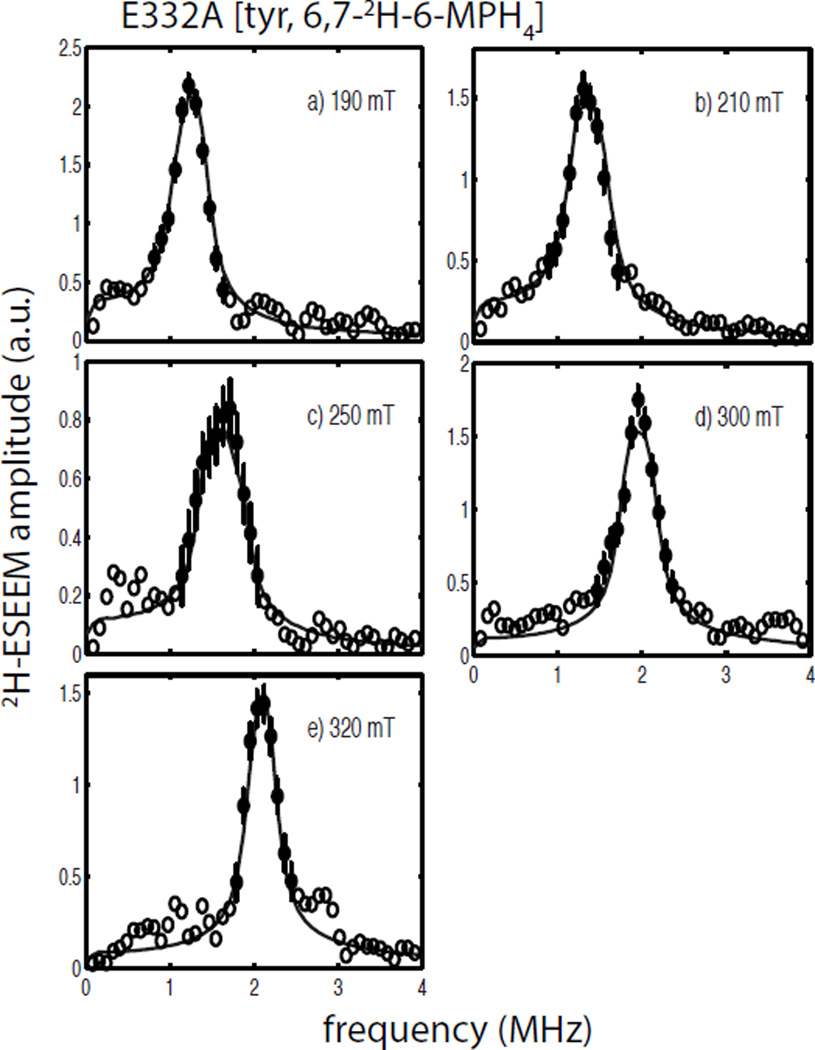
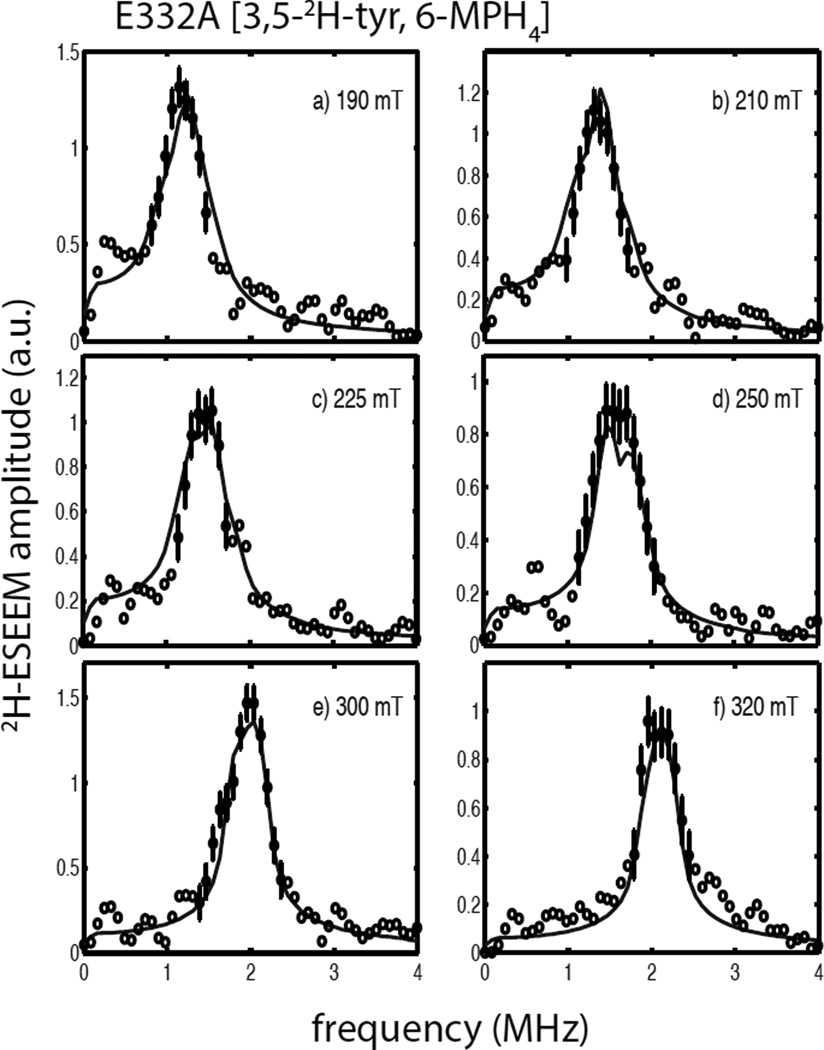
Composite figures of the ²H-ESEEM spectra collected for the quaternary complexes of the E332A variant of TyrH with 6,7-²H-6-MPH₄ and 3,5-²H-tyr are shown in Figures 7 and 8, respectively. A comparison of the spectra for E332A/NO/tyr/6,7-²H-6-MPH₄ (Figure 7) and wild type TyrH/NO/tyr/6,7-²H-6-MPH₄ (Figure 6) show only subtle differences in amplitude and lineshape across the EPR spectrum, with the most notable difference being a difference in lineshape at 250 mT (compare Figure 6c with 7c). The solid lines in Figure 7 are the best fit simulations to the spectral data and provide nearly identical values to those obtained above for the wild type enzyme (Table 2). A comparison of the field-dependent ESEEM spectra obtained for the quaternary complexes of E332A/NO/3,5-²H-tyr/6-MPH₄ (Figure 8) and wild type TyrH/ NO/3,5-²H-tyr/6-MPH₄ (Figure 4) appear to differ little except for the poorer signal-to-noise ratio observed for the wild-type protein samples. Analyses of these data led to simulations summarized by the solid lines drawn in Figure 8 and provide a dipolar coupling of T = 0.12 MHz and a hyperfine tensor orientation described by β_hf = 89 ± 9°. The ${\chi }_{\nu }^2$ value for the fit of these data was 1.2, supplying more confidence for the analysis of the wild-type TyrH/NO/3,5-²H-tyr/6-MPH₄ data presented above. Single parameter χ² plots to support the data analyses presented for the quaternary complexes of E332A/NO/tyr/6,7-2H-6-MPH4 and E332A/NO/3,5-2H-tyr/ 6MPH4 are provided as Figures S11 and S12 in the supplementary information.

Figure 7.

²H-ESEEM spectra (open and filled circles) obtained by Fourier transformation of ESEEM data from the ternary complexes of E332A/NO/tyrosine/6,7-²H-6-MPH₄ divided by E332A/NO/tyr/6-MPH₄. Data were collected at 9.68 GHz using the following field positions and tau values a) 190 mT, 124 ns; b) 210 mT, 112 ns; c) 250 mT, 92 ns; d) 300 mT, 156 ns; and e) 320 mT, 148 ns. The solid lines in each frame are best fit ESEEM simulations to the data points represented by the filled circles with error bars using the following spin Hamiltonian parameters: g_n = 0.8574, T = 0.14 MHz, β_hf = 65°, γ_hf = 0°, e²qQ/h = 0.20 MHz, γ_nqi = 66° and γ_nqi = 18°.

Figure 8.

²H-ESEEM spectra (open and filled circles) obtained by Fourier transformation of ESEEM data from the ternary complexes of E332A/NO/3,5-²H-tyr/6-MPH₄ divided by E332A/ NO/3,5-²H-tyr/6-MPH₄. Data were collected at 9.68 GHz using the following field positions and tau values a) 190 mT, 124 ns; b) 210 mT, 112 ns; c) 225 mT, 104 ns; d) 250 mT, 92 ns; e) 300 mT, 156 ns; and f) 320 mT, 148 ns. The solid lines in each frame are best fit ESEEM simulations to the data points represented by the filled circles with error bars using the following spin Hamiltonian parameters: g_n = 0.8574, T = 0.12 MHz, β_hf = 89°, γ_hf = 20°, e²qQ/h = 0.29 MHz, β_nqi = 44° and γ_nqi = 34°.

Discussion

The ²H-ESEEM spectra described here establish that substrate amino acid and tetrahydropterin cofactor bind to TyrH differently in the quaternary complex TyrH/NO/tyr/6-MPH₄ as compared to their positions in the respective ternary complexes, TyrH/NO/tyr and TyrH/NO/6-MPH₄. For the TyrH/NO/6,7-²H-6-MPH₄ ternary complex, no ²H-ESEEM could be detected above the noise floor of the experiment. The noise level can be estimated from these spectra as 0.3–0.4 at g = 4 and 0.1 – 0.2 at g = 2 (Figure 5). Spectral simulations done using the Euler angles determined for the TyrH/NO/tyr/6,7-²H-6-MPH₄ quaternary complex showed that a reff of 5.9 Å would provide ²H signal amplitudes just above the noise level. Therefore, for the ternary complex of TyrH/NO/6,7-²H-6-MPH₄, we conclude that the closest deuteron is greater than 5.9 Å from the {FeNO}⁷ center. ²H-ESEEM spectra obtained at multiple field positions from the cofactor 6,7-²H-6-MPH₄ when tyrosine is bound to the enzyme showed a dipolar coupling of T = 0.14 ± 0.01 MHz which translates into an effective dipole-dipole distance of 4.4 ± 0.2 Å (Eqn. 3). These findings provide a structural explanation for the observation that the initial reaction between Fe(II)-bound O₂ and BH₄ in TyrH requires the binding of tyrosine⁽⁴⁴⁾. Specifically, the binding of substrate tyrosine results in structural changes at the active site that bring the 6-MPH₄ cofactor into position for the first step of the catalytic mechanism. The effective cofactor distances determined in this study are similar to those determined for PheH by X-ray crystallography. Those studies showed that the addition of the substrate analog thienylalanine to PheH loaded with BH₄ resulted in the movement of the C₆ carbon of bound BH₄ from a distance of 7.3Å from the Fe to 5.0 Å^{(15, 16)}.

In addition to the structural information derived from the effective dipolar distance, the ²H-ESEEM analysis also provides Euler angles, β_hf and γ_hf, that define the position of the dipolar coupling vector in the ZFS axis system, and a set of nqi angles that define the orientation of the C-²H bond of the coupled deuteron within that same axis system. Overall, we found that our analyses were not sensitive to γ_hf. While specific values, or a range of values for this parameter were needed to obtain the best-fit values of ${\chi }_{\nu }^2$, it was possible to fit the data with modest adjustments of the nqi parameters so that any value of γ_hf could be used to obtain a fit that fell beneath the threshold defined by the best fit value of ${\chi }_{\nu }^2+1$. While there was some dependence of the best-fit values of e²qQ/h, β_nqi, an |γ_nqi − γ_hf| on the value of γ_hf chosen for an optimization, their variation easily fell within the uncertainty derived from single-parameter χ² plots. The errors provided for the analysis results in Table 2, show that the dipolar coupling strength, T, and orientation, β_hf can be determined with reasonable certainty for all of the enzyme forms studied. The angles describing the orientation of the nqi were only accurately determined for the ternary complex of TyrH/NO/3,5-²H-tyr.

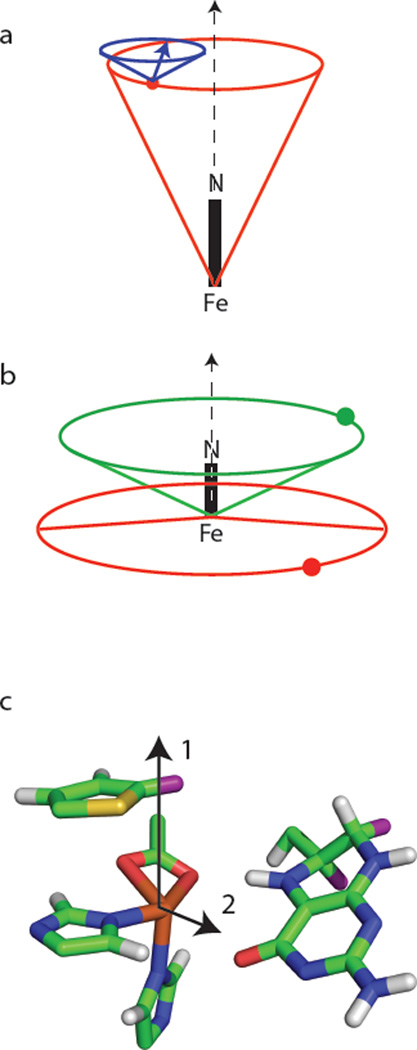
Figure 9a summarizes the deuterium coupling data for the ternary complex of TyrH/NO/ 3,5-²H-tyr. The near axial symmetry of the ZFS and the associated lack of sensitivity to γ_hf as summarized above, create a model where β_hf and reff describe a cone about the g = 2.00 axis, an axis that is nearly coincident with the Fe-NO bond⁽²⁵⁾, where the coupled deuteron is located. Our results show a single deuteron at an effective distance of 4.1Å from the paramagnetic center that lies on the base of a cone that makes a 26° angle with the Fe-NO bond axis. For this particular adduct, a second cone representing the information held in the nqi parameters can be constructed with its symmetry axis parallel to the Fe-NO bond direction and it’s apex centered on the coupled nucleus. This second cone makes an angle of β_nqi = 62° with its symmetry axis. A vector (figure 9a) that is colinear with the C-²H bond associated with this deuteron is then confined to the surface of this cone and positioned ± |γ_nqi − γ_hf| = 38° from where the cone surface intersects the plane defined by the Fe-NO bond and the coupled ²H.

Figure 9.

Cone diagrams for schematic representation of the ²H spin Hamiltonian parameters given in Table 2 and obtained for (a) the ternary complex of TyrH/NO/3,5-²H-tyr; (b) the quaternary complexes of TyrH/NO/3,5-²H-tyr/6-MPH₄ (red) and TyrH/NO/tyr/6,7-²H-6-MPH₄ (green). Figure (c) shows a stick diagram of the catalytic site of PheH crystalized with thienylalanine and BH₄ (taken from PDB file: 1MMK). The vectors show possible orientations for the Fe-NO bond axis.

When 6-MPH₄ is added to the protein to form the quaternary complex of TyrH/NO/3,5-²H-tyr/6-MPH₄, the effective dipolar distance for the coupled tyr deuteron lengthens to 4.7 Å and the angle that reff makes with the Fe-NO bond axis is increased to 94° (Figure 9b). While substantial structural changes in response to pterin binding to TyrH have been observed in fluorescence anisotropy studies of a flexible polypeptide loop associated with the metal binding site⁽⁴⁵⁾, X-ray crystallographic studies of TyrH have shown that no structural changes are associated with the binding of 7,8-dihydrobiopterin to the ferric enzyme⁽⁷⁾. Considering these previous findings, it is most likely that the large change in β_hf reflects a change in the coordination of NO with respect to bound tyrosine when 6-MPH₄ is bound. It is instructive to view these changes in terms of the X-ray crystal structure for the catalytic domain of PheH crystallized in the presence of BH₄ and soaked anaerobically with a slow-substrate, thienylalanine, PDB designation 1MMK. A stick drawing of the Fe site of this structure created with MacPyMol is shown in Figure 9c. The structure shows a four coordinate Fe(II) with the side-chain of the glutamate ligand coordinated to Fe(II) in a bidentate fashion. The two histidine ligands that make up the balance of the facial triad are bound so that one is nearly planar with the glutamate oxygens forming an “equatorial plane” and the other is bound axially, essentially trans to the closest proton of the substrate analog. The protons shown in this structure were added by the viewing program with the positions occupied by the closest substrate deuteron and the 6,7 deuterons of 6-MPH₄ colored in purple. This structure shows that the closest proton on thienylalanine is 4.1 Å from the Fe(II) center, while the distances to the deuterons on the 6 and 7 carbons of BH₄ are 5.6 and 7.1 Å from the Fe(II), respectively. Our ²H-ESEEM results for the ternary complex of TyrH/NO/3,5 - ²H-tyr fit well with this structure if the NO is coordinated at a position that is opposite the axial histidine ligand or “in-line” with the substrate, consistent with the vector labelled “1” in Figure 9c.

For the quaternary complexes of TyrH/NO/3,5-²H-tyr/6-MPH₄ and Tyr/NO/tyr/6,7-²H-6-MPH₄, the orientations of the ²H-dipolar coupling vectors can be explained if NO coordinates to Fe in an equatorial, or “off-line” fashion like that of the vector marked “2” in Figure 9c. However, the distance from the {FeNO}⁷ center to the closest coupled deuteron of the pterin as predicted from the dipolar coupling of 0.14 MHz is 4.4 Å, 1.2 Å shorter than the distance between Fe(II) and the C₆-proton of cofactor BH₄ in the the PheH structure of Figure 9c. Likewise, the dipolar coupling of 0.12 MHz measured for the closest deuteron of substrate tyrosine translates into a dipole-dipole distance of 4.7 Å, a 0.6 Å increase from the 4.1Å distance measured for the TyrH/NO/3,5-²H-tyr ternary complex by ESEEM and estimated from the X-ray crystal structure of PheH reproduced in Figure 9c. These discrepancies are consistent with a modest distribution of unpaired electron spin density onto the NO ligand with the coupling between the {FeNO}⁷ paramagnetic center and the closest deuteron of tyr providing a measure of the size of the effect. Specifically, if one assumes that both substrate tyr and Fe remain at the same physical distance from one another, and that the presence of bound 6-MPH₄ serves only to re-direct the coordination of NO, then the reorientation of the ligand results in a 0.06 MHz reduction in the dipolar coupling. A reduction of this size in the dipolar coupling measured for the C₆-²H of 6-MPH₄, T = 0.14 MHz, would increase the dipolar distance estimated from the point dipole-dipole approximation from 4.4 Å to 5.3 Å. While this estimate is in much better agreement with the pterin locale reported in the PheH crystal structure, it is a crude approximation that begs further theoretical and experimental study. It is possible that the short effective dipolar distance measured for the C₆-²H in this study indicates that the cofactor is bound closer to the Fe in the TyrH/NO/tyr/6-MPH4 complex than what is predicted from the corresponding PheH crystal structure.

The possibility that NO remains bound to the position where it is “in-line” with tyr, along the vector marked “1” in Figure 9c, for the quaternary complex containing 6-MPH₄ was examined by constraining fits of the ²H-ESEEM data from the TyrH/NO/3,5-²H-tyr/6-MPH₄ (Figure 4) and E332A/NO/3,5-²H-tyr/6-MPH₄ (Figure 8) samples so that β_hf was < 45°. For both enzyme samples, a minimum in χ² was found for β_hf = 17°, with the normalized value, ${\chi }_{\nu }^2$, being 3.1 for wild-type TyrH and 2.1 for the E332A variant. These values are 0.9 higher than the ${\chi }_{\nu }^2$ values reported for the β_hf ≅ 90° solutions discussed above (Table 2). Our reasons for favoring the β_hf ≅ 90° solutions were that they gave the best values of ${\chi }_{\nu }^2$ and that this orientation for the principle axis of the ZFS tensor provided a ready explanation for the combined lengthening of the effective dipolar distance observed for 3,5-²H-tyr in response to pterin binding and the shorter dipolar distance determined for coupled 6,7-²H-6-MPH₄ in the TyrH quaternary complex as discussed above.

Recently, Olsson and coworkers have used the results of DFT calculations and NMR relaxation measurements to propose a structure for the catalytic site of PheH in the presence of BH₄ and bound O₂. Their structure, shown in Figure 6a of their paper, is based on the 1MMK crystallographic structure for the catalytic domain of PheH in the presence of bound BH₄ and thienylalanine. This structure brings the C₄-carbonyl oxygen of BH₄ to within 1.9Å of the Fe(II), close enough to bind to the metal ion, but leaves the distance between the C₆-²H on the pterin and Fe(II) at 5.8 Å, 1.4Å longer than the distance measured in our study⁽⁴⁶⁾. Unfortunately, their structure shows the pterin binding to the metal at essentially the same position where we propose the NO to bind when both substrate tyr and 6-MPH₄ are present. At this point, the best fits to our data preclude pterin binding to Fe(II), but more measurements will be needed to evaluate this intriguing proposal.

Table 2 summarizes our ²H-ESEEM findings for quaternary complexes of the variant E332A. A comparison of these findings with those of the wild type enzyme shows that the structural relationship between the {FeNO}⁷ paramagnetic center and coupled deuterons of both substrate tyrosine and cofactor 6-MPH₄ are identical given experimental error. This is consistent with previous spectroscopic studies of the E332A TyrH/tyr/6-MPH₄ complex that showed that the mutant still exhibits the change from 6- to 5-coordinate upon binding both substrates and that the electronic properties of the mutant complex are very similar to that of the wild type enzyme ⁽⁸⁾. Both results are somewhat surprising because the side chain of this glutamate residue forms two hydrogen bonds with the pterin cofactor, and the E332A enzyme oxidizes tetrahydropterins without hydroxylating tyrosine ⁽¹⁹⁾. (While the mutant enzyme also exhibits a 10-fold increase in the K_M value for 6-MPH₄, the concentrations of substrates used here were sufficiently high to saturate the mutant protein.) One explanation for the uncoupling of the mutant enzyme despite formation of an apparently normal reactive complex, previously proposed by Chow et al., is that a critical role of Glu332 is to transfer a proton to the proper oxygen atom in the proposed peroxo intermediate, facilitating the heterolytic cleavage of the oxygen-oxygen bond required for formation of the Fe(IV)-oxo hydroxylating intermediate⁽⁸⁾. Alternatively, the lost hydrogen bonds due to the mutation may destabilize the peroxo intermediate sufficiently that it breaks down unproductively before the Fe(IV)-oxo is formed; spectroscopic analyses carried out at liquid helium temperatures would be unlikely to detect such kinetic effects. Because the present study has used only a single dipolar coupling to characterize the positions of the cofactor and substrate, it is not possible to form conclusions about their conformations with respect to the coordination sphere of Fe. An intriguing issue that may pertain to the coupling of the two hydroxylation reactions that comprise the TyrH catalytic mechanism involves the coordination of NO to Fe(II) and how well the behavior observed in our studies represents the actual chemistry of O₂. Previous biochemical studies have shown that the addition of both substrate and cofactor enhance the binding constant for O₂ by a factor of 100. The work presented here, shows that when both cofactor 6-MPH₄ and substrate tyrosine are bound to TyrH, the coordination of NO to Fe(II) is directed to an equatorial position which most likely poises the system for the first hydroxylation reaction with pterin, but also positions the Fe-NO bond so that it is perpendicular to the substrate protons. Presumably, this bond will have to reorient prior to commencement of substrate hydroxylation. The E332 mutation to alanine may lead to a structural change that impedes this reorientation of the Fe(IV)=O species.

Summary

The results presented in this paper provide three new pieces of structural information regarding TyrH. Specifically, that the binding of tyrosine results in a conformational change that brings 6-MPH₄ closer to {FeNO}⁷ in a fashion analogous to that observed in X-ray structures of PheH; that the coordination of NO to Fe(II) is directed by the presence of 6-MPH₄ at the active site, binding in a fashion that may be important for directing the first step of the catalytic cycle towards hydroxylation of the cofactor; and that the E332A mutation, known to lead to an uncoupling of tyrosine hydroxylation from pterin oxidation does not lead to a detectable reorientation of the cofactor.

Abbreviations

TyrH

tyrosine hydroxylase

PheH

phenylalanine hydroxylase

BH₄

tetrahydrobiopterin

6-MPH₄

6-methyltetrahydropterin

DOPA

dihydroxyphenylalanine

tyr

tyrosine

EPR

Electron Paramagnetic Resonance

ESEEM

Electron Spin Echo Envelope Modulation

hf

hyperfine

nqi

nuclear quadrupole interaction

PAS

principal axis system

MAHMA NONOATE

6-(2-hydroxy-1-methyl-2-nitrosohydrazino)-N-methyl-1-hexanamine

EDTA

ethylenediamine tetraacetic acid

TACN

1,4,7-triazacyclononane