VARIABLE SELECTION AND ESTIMATION IN HIGH-DIMENSIONAL VARYING-COEFFICIENT MODELS

Abstract

Nonparametric varying coefficient models are useful for studying the time-dependent effects of variables. Many procedures have been developed for estimation and variable selection in such models. However, existing work has focused on the case when the number of variables is fixed or smaller than the sample size. In this paper, we consider the problem of variable selection and estimation in varying coefficient models in sparse, high-dimensional settings when the number of variables can be larger than the sample size. We apply the group Lasso and basis function expansion to simultaneously select the important variables and estimate the nonzero varying coefficient functions. Under appropriate conditions, we show that the group Lasso selects a model of the right order of dimensionality, selects all variables with the norms of the corresponding coefficient functions greater than certain threshold level, and is estimation consistent. However, the group Lasso is in general not selection consistent and tends to select variables that are not important in the model. In order to improve the selection results, we apply the adaptive group Lasso. We show that, under suitable conditions, the adaptive group Lasso has the oracle selection property in the sense that it correctly selects important variables with probability converging to one. In contrast, the group Lasso does not possess such oracle property. Both approaches are evaluated using simulation and demonstrated on a data example.

1. Introduction

Consider a linear varying coefficient model with p_n variables

$$y_i\left(t_{ij}\right)=\sum _{k=1}^p{x}_{ik}\left(t_{ij}\right){\beta }_k\left(t_{ij}\right)+{∊}_i\left(t_{ij}\right),i=1,\dots ,n,j=1,\dots ,n_i,$$ (1.1)

where y_i(t) is the response variable for the ith subject at time point t ∈ T, T is the time interval on which the measurements are taken, ε_i(t) is the error term, x_ik(t) is the covariate variable with time-varying effects, β_k(t) is the corresponding smooth coefficient function. Such a model is useful in investigating the time-dependent effects of covariates on responses measured repeatedly. One well known example is longitudinal data analysis (Hoover et al. (1998)) where the response for the ith experimental subject in the study is observed on n_i occasions, and the observations at times t_ij : j = 1, . . . , n_i are correlated. Another important example is the functional response model (Rice (2004)), where the response y_i(t) is a smooth real function, although only y_i(t_ij), j = 1, . . . , n_i are observed in practice. In both examples, the response y_i(t) is a random process and the covariate x_i(t) = (x_i1(t), . . . , x_ip(t))′ is a p-dimensional vector of random processes. In this paper, we investigate the selection of the important covariates and the estimation of their relative coefficient functions in high-dimensional settings, in the particular case $p\gg n$, under the assumption that the number of important covariates is “small” relative to the sample size. We propose penalized methods for variable selection and estimation in (1.1) based on basis expansion of the coefficient functions, and show that under appropriate conditions, the proposed methods can select the important variables with high probability and estimate the coefficient functions effciently.

Many methods have been developed for variable selection and estimation in varying coefficient models (1.1). See, for example, Fan and Zhang (2000) and Wu and Chiang (2000), for the local polynomial smoothing method; Wang and Xia (2008) for the local polynomial method with Lasso penalty; Huang, Wu, and Zhou (2004) and Qu and Li (2006) for basis expansion and the spline method; Chiang, Rice, and Wu (2001) for the smoothing spline method; Wang, Li, and Huang (2008) for basis function approximation with SCAD penalty (Fan and Li (2001); Fan and Lv (2010)). In addition to these methods, much progress has been made in understanding such properties of the resulting estimators as selection consistency, convergence, and asymptotic distribution. However, in all these studies, the number of variables p is fixed or less than the sample size n. To the best of our knowledge, there has been no work on the problem of variable selection and estimation in varying coefficient models in sparse, $p\gg n$ situations.

There has been much work on the selection and estimation of groups of variables. For example, Yuan and Lin (2006) proposed the group Lasso, group Lars, and group nonnegative garrote methods. Kim, Kim, and Kim (2006) considered the group Lasso in the context of generalized linear models. Zhao, Rocha, and Yu (2008) proposed a composite absolute penalty for group selection that can be considered a generalization of the group Lasso. Huang et al. (2007) considered the group bridge approach which can be used for simultaneous group and within group variable selection. However, there has been no investigation of these methods in the context of high-dimensional varying coefficient models.

In this paper, we apply the group Lasso and basis expansion to simultaneously select the important variables and estimate the coefficient functions in (1.1). With basis expansion, each coefficient function is approximated by a linear combination of a set of basis functions. Thus the selection of important variables and estimation of the corresponding coefficient functions amounts to the selection and estimation of groups of coefficients in the linear expansions. It is natural to apply the group Lasso, since it takes into account the group structure in the approximation model. We show that, under appropriate conditions, the group Lasso selects a model of the right order of dimensionality, selects all variables with coefficient function ${\ell }_2$ norms greater than a certain threshold level, and is estimation consistent. In order to achieve selection consistency, we apply the adaptive group Lasso. We show that the adaptive group Lasso can correctly select important variables with probability converging to one based on an initial consistent estimator. In particular, we use the group Lasso to obtain the initial estimator for the adaptive group Lasso. This approach follows the idea of the adaptive Lasso (Zou (2006)). An important aspect of our results is that p can be much larger than n.

The rest of the paper is organized as follows. In Section 2, we describe the procedure for selection and estimation using the group Lasso and the adaptive group Lasso with basis expansion. In Section 3, we state the results on estimation consistency of the group Lasso and the selection consistency of the adaptive group Lasso in high-dimensional settings. Proofs are given in Section 6. In Section 4, simulations and data examples are used to illustrate the proposed methods. Summary and discussion are given in Section 5.

2. Basis Expansion and Penalized Estimation

Suppose that the coefficient function β_k can be approximated by a linear combination of basis functions,

$$g_k\left(t\right)=\sum _{l=1}^{d_k}{\gamma }_{kl}{B}_{kl}\left(t\right),t\in T,k=1,\dots ,p,$$ (2.1)

where B_kl(t), t ∈ T, l = 1, . . . , d_k, are basis functions and d_k is the number of basis functions, which is allowed to increase with the sample size n.

Let G_k denote all functions that have the form ${\sum }_{l=1}^{d_k}{\gamma }_{kl}{B}_{kl}\left(t\right)$ for a given basis system {B_kl, l = 1, . . . , d_k}. For g_k ∈ G_k, define the approximation error by

$${\rho }_k\left(t\right)={\beta }_k\left(t\right)-g_k\left(t\right)={\beta }_k\left(t\right)-\sum _{l=1}^{d_k}{\gamma }_{kl}{B}_{kl}\left(t\right),t\in T,k=1,\dots ,p.$$

Let $\text{dist}({\beta }_k,G_k)={\text{inf}}_{g_k\in G_k}{\text{sup}}_{t\in T}\mid {\rho }_k\left(t\right)\mid$ be the L_∞ distance between β_k and G_k, and take ρ = max_1≤k≤p dist(β_k, G_k).

By the definition of ρ_k and (2.1), model (1.1) can be written as

$$y_i\left(t_{ij}\right)=\sum _{k=1}^p\sum _{l=1}^{d_k}{x}_{ik}\left(t_{ij}\right){\gamma }_{kl}{B}_{kl}\left(t_{ij}\right)+\sum _{k=1}^p{x}_{ik}\left(t_{ij}\right){\rho }_k\left(t_{ij}\right)+{∊}_i\left(t_{ij}\right),$$ (2.2)

for i = 1, . . . , n and j = 1, . . . , n_i. In low-dimensional settings, we can minimize the least squares criterion

$$\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^{n_i}{\{y_i\left(t_{ij}\right)-\sum _{k=1}^p\sum _{l=1}^{d_k}{\gamma }_{kl}{x}_{ik}\left(t_{ij}\right)B_{kl}\left(t_{ij}\right)\}}^2$$ (2.3)

with respect to γ_kl's. The least squares estimator of β_k is ${\widehat{\beta }}_k\left(t\right)={\sum }_{l=1}^{d_k}{\widehat{\gamma }}_{kl}{B}_{kl}\left(t\right),t\in T$, where ${\widehat{\gamma }}_{kl}’\mathrm{s}$ are the minimizer of (2.3).

When the number of variables p or ${\sum }_{k=1}^p{d}_k$ is larger than the sample size n, however the least squares method is not applicable since there is no unique solution to (2.3). In such case, regularized methods are needed. We apply the group Lasso (Yuan and Lin (2006)),

$$\text{arg}\underset{\gamma }{\text{min}}\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^{n_i}{(y_i\left(t_{ij}\right)-\sum _{k=1}^p\sum _{l=1}^{d_k}{x}_{ik}\left(t_{ij}\right){\gamma }_{kl}{B}_{kl}\left(t_{ij}\right))}^2+\sum _{k=1}^p\lambda {\Vert {\gamma }_k\Vert }_k,$$ (2.4)

where λ is the penalty parameter, γ_k = (γ_k1, . . . , γ_kd)′ is a d_k-dimensional coefficient vector corresponding to the kth variable, and ${\Vert {\gamma }_k\Vert }_k^2={\gamma }_k^{\prime }{R}_k{\gamma }_k$. Here R_k = (r_ij)_dk×d_k is the kernel matrix whose (i, j)th element is

$$r_{ij}={\int }_T{B}_{ki}\left(t\right)B_{kj}\left(t\right)dt,\text{for}i=1,\dots ,d_k,j=1,\dots ,d_k,k=1,\dots ,p,$$ (2.5)

it is a symmetric positive definite matrix by Lemma A.1 in Huang, Wu, and Zhou (2004).

To express the criterion function (2.4), let

$$Y={(y_1\left(t_{11}\right),\dots ,y_1\left(t_{1n_1}\right),\dots ,y_n\left(t_{n1}\right),\dots ,y_n\left(t_{n{n}_n}\right))}^{\prime },X=(X_1,\dots ,X_p)$$

with X_k = (x_1k(t₁₁), . . . , x_1k(t_1n1), . . . , x_nk(t_n1), . . . , x_nk(t_nnn))′ and define

$$B\left(t\right)=\left(\begin{array}{cccccccc}\hfill B_{11}\left(t\right)\hfill & \hfill B_{12}\left(t\right)\hfill & \hfill \dots \hfill & \hfill B_{1d_1}\left(t\right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill B_{p1}\left(t\right)\hfill & \hfill B_{p2}\left(t\right)\hfill & \hfill \dots \hfill & \hfill B_{p{d}_p}\left(t\right)\hfill \end{array}\right),$$

and $\gamma ={({\gamma }_1^{\prime },\dots ,{\gamma }_p^{\prime })}^{\prime }$. Set U = (U₁₁, . . . , U_1n1, . . . , U_n1, . . . , U_nnn)′ with $U_{ij}^{\prime }=x_i{\left(t_{ij}\right)}^{\prime }B\left(t_{ij}\right)$ for i = 1, . . . , n, j = 1, . . . , n_i. Then the group Lasso penalized criterion (2.4) can be rewritten as

$$\widehat{\gamma }=\text{arg}\underset{\gamma }{\text{min}}\frac{1}{2}{(Y-U\gamma )}^{\prime }(Y-U\gamma )+\sum _{k=1}^p\lambda {\Vert {\gamma }_k\Vert }_k.$$ (2.6)

The group Lasso estimator is ${\widehat{\beta }}_k\left(t\right)={\sum }_{l=1}^{d_k}{\widehat{\gamma }}_{kl}{B}_{kl}\left(t\right),k=1,\dots ,p$.

Let w = (w₁, . . . , w_p′ be a given vector of weights, where 0 ≤ w_k ≤ ∞, 1 ≤ k ≤ p. Then a weighted group Lasso criterion is

$${\widehat{\gamma }}^{\ast }=\text{arg}\underset{\gamma }{\text{min}}\frac{1}{2}{(Y-U\gamma )}^{\prime }(Y-U\gamma )+\sum _{k=1}^p\tilde{\lambda }{\omega }_k{\Vert {\gamma }_k\Vert }_k.$$ (2.7)

The weighted group Lasso estimator ${\widehat{\beta }}_k^{\ast }\left(t\right)={\sum }_{l=1}^{d_k}{\widehat{\gamma }}_{kl}^{\ast }{B}_{kl}\left(t\right),k=1,\dots ,p$, where ${\widehat{\gamma }}^{\ast }$ is the minimizer of (2.7). When the weights are dependent on the data through an initial estimator, such as $\widehat{\beta }$, then we call the resulting ${\widehat{\beta }}_k^{\ast }$ an adaptive group Lasso estimator.

3. Theoretical Results

In this section, we describe the asymptotic properties of the group Lasso and the adaptive group Lasso estimators defined in (2.6) and (2.7) of Section 2 when p can be larger than n, but the number of important covariates is relatively small.

In (1.1), without loss of generality, suppose that the first q_n variables are important. Let A₀ = {q_n+1, . . . , p_n}. Here we write q_n, p_n to indicate that q and p are allowed to diverge with n. Thus all the variables in A₀ are not important. Let |A| denote the cardinality of any set $A\subset \{1,\dots ,p_n\}$ and $d_A={\sum }_{k\in A}{d}_k$. For any set $A\subset \{1,\dots ,p_n\}$, define

$$U_A=(u_{kj}:j=1,\dots ,d_k;k\in A)\text{and}{\Sigma }_{AA}=U_A^{\prime }\frac{U_A}{n}.$$

Here U_A is a n × d_A dimensional submatrix of the ‘designed’ matrix U. Take ${\Vert {\beta }_k\Vert }_2={\left[{\int }_T{\beta }_k^2\left(t\right)\right]}^{1∕2}dt$ whenever the integral exists.

We rely on the following conditions.

• (C1) There exist constants q* > 0, c_* > 0 and c* > 0 where 0 < c_* ≤ c* < ∞ such that

  $$c_{\ast }\le \frac{{\Vert U_A\nu \Vert }_2^2}{n{\Vert \nu \Vert }_2^2}\le c^{\ast },\forall A\text{with}\mid A\mid =q^{\ast }\text{and}\nu \in {\mathbb{R}}^{d_A}.$$

• (C2) There is a small constant η₁ ≥ 0 such that ${\sum }_{k\in A_0}{\Vert {\beta }_k\Vert }_2\le {\eta }_1$.

• (C3) The random errors ε_i(t), i = 1, . . . , n are independent and identically distributed as ε(t), where E[ε(t)] = 0 and E[ε(t)²] ≤ σ² < ∞ for t ∈ T ; moreover, the tail probabilities satisfy $P(\mid ∊\left(t\right)\mid >x)\le K\text{exp}(-C{x}^2)$ for t ∈ T , x > 0, and some constants C and K

• (C4) There exists a positive constant M such that $\mid x_{ik}\left(t\right)\mid \le M$ for all t ∈ T and i = , . . . , n, k = 1, . . . , p_n.

Condition (C1) is the sparse Riesz condition for varying coefficient models, which controls the range of eigenvalues of the matrix U. This condition was formulated for the linear regression model in Zhang and Huang (2008). If the covariate matrix X satisfies (C1), then the matrix U also satisfies (C1) and $c^{\ast },c_{\ast }\sim O\left(d_a^{-1}\right)$. See Lemma A.1 in Huang, Wu, and Zhou (2004). Condition (C2) assumes that the varying coefficients of the unimportant variables are small in the ${\ell }_2$ sense, but do not need to be exactly zero. If η₁ = 0, (C2) becomes β_k(t) ≡ 0 for all k ∈ A₀. This can be called the narrow-sense sparsity condition (NSC) (Wei and Huang (2008)). Under the NSC, the problem of variable selection is equivalent to distinguishing nonzero coefficient functions from zero coefficient functions. Under (C2), it is no longer sensible to select the set of all nonzero coefficient functions, the goal is to select the set of important variables with large coefficient functions. From the standpoint of statistical modeling and interpretation, (C2) is mathematically weaker and more realistic. Condition (C3) assumes that the error term is a mean zero stochastic process with uniformly bounded variance function and has a sub-Gaussian tail behavior. Condition (C4) assumes that all the covariates are uniformly bounded, which is satisfied in many practical situations.

3.1. Estimation consistency of group Lasso

For the matrix R_k at (2.5), by the Cholesky decomposition there exists a matrix Q_k such that R_k = d_kQ^′_kQ_k.

Let Q_kb be the smallest eigenvalue of matrix Q_k, Q_b = min_k Q_kb, d_a = max_k d_k, d_b = max_k d_k, d_b = d_a/d_b, $N={\sum }_{i=1}^n{n}_i\text{and}{m}_n={\sum }_{k=1}^{p_n}{d}_k$. Thus N is the number of total observations, m_n is the number of all approximation coefficients in the basis expansions. Note that for k = 1, . . . , p_n, d_k can increase as n increases to give a more accurate approximation. For example, as in non-parametric regression, we can choose d_k = O(n^τ) for some constant 0 < τ < 1/2. With $\stackrel{‒}{c}=c^{\ast }∕c_{\ast }$, (C1), let

$$M_1=2+4d\stackrel{‒}{c},M_2=\frac{2}{3}+\frac{4}{9}d\stackrel{‒}{c}(7+4\stackrel{‒}{c}),$$ (3.1)

and consider the constraint

$$\lambda \ge \text{max}\{{\lambda }_0,{\lambda }_{n,p_n}\},$$ (3.2)

where ${\lambda }_0=\text{inf}\{\lambda :M_1{q}_n+1\le q^{\ast }\},\text{inf}\varnothing =\infty ,\text{and}{\lambda }_{n,p_n}=2\sigma \rho \sqrt{8(1+c_0)d_a{d}^2{q}^{\ast }\stackrel{‒}{c}N{c}^{\ast }\text{log}{m}_n},c_0\ge 0$. Note that when q* is fixed, ${\lambda }_{n{p}_n}=O_p\left(\rho {\left(N\text{log}{m}_n\right)}^{1∕2}\right)$.

Let $\widehat{A}=\{k:{\Vert {\widehat{\beta }}_k\Vert }_2\ne 0,1\le k\le p_n\}$ represent the set of indices of the variables selected by the group Lasso. The cardinality of  is

$$\widehat{q}=\mid \widehat{A}\mid =\#\{k:{\Vert {\widehat{\beta }}_k\Vert }_2\ne 0,1\le k\le p_n\}.$$ (3.3)

This describes the dimension of the selected model; if q̂ = O(q_n), then the size of the selected model is of the same order as the underlying model. To measure the important variables missing in the selected model, take

$${\xi }_2^2=\sum _{k\notin A_0}{\Vert {\beta }_k\Vert }_2^{2}I\{{\Vert {\widehat{\beta }}_k\Vert }_2=0\}.$$ (3.4)

Theorem 1. Assume (C1)–(C4) and that η₁ ≤ ρ. Let q̂ and ξ₂ be defined as in (3.3) and (3.4), respectively, for the model selected by the group Lasso from (2.6). Let M₁ and M₂ be defined as in (3.1). If the constraint (3.2) is satisfied, then, with probability converging to 1 and $B_1^2\left(\lambda \right)={\lambda }^2{d}_b^2{q}_n∕c^{\ast }N$,

1. q̂ ≤ M₁q_n,

2. ${\xi }_2^2\le 2{\left(\frac{M^2\rho q_n^{3∕2}}{n{c}_{\ast }}+\rho \sqrt{q_n}\right)}^2+2\frac{M_2{B}_1^2\left(\lambda \right)}{c_{\ast }N}$.

Part (i) of Theorem 1 shows that the group Lasso selects a model whose dimension is comparable to the underlying model, regardless of the large number of unimportant variables. Part (ii) implies that all the variables with coefficient functions ${\Vert {\beta }_k\Vert }_2^2\ge 2{\left(M^2{q}_n^{3∕2}\rho ∕\left(n{c}_{\ast }\right)+q_n^{1∕2}\rho \right)}^2+2M_2{B}_1^2∕\left(c_{\ast }N\right)$ are selected in the model with high probability.

Let ${\tilde{\beta }}_k\left(t\right)=E\left({\widehat{\beta }}_k\left(t\right)\right)$ be the mean of ${\widehat{\beta }}_k\left(t\right)$ conditional on X. It is useful to consider the decomposition ${\widehat{\beta }}_k\left(t\right)-{\beta }_k\left(t\right)={\widehat{\beta }}_k\left(t\right)-{\tilde{\beta }}_k\left(t\right)+{\tilde{\beta }}_k\left(t\right)-{\beta }_k\left(t\right)$ where ${\widehat{\beta }}_k\left(t\right)-{\tilde{\beta }}_k\left(t\right)$ and ${\tilde{\beta }}_k\left(t\right)-{\beta }_k\left(t\right)$ contribute to the variance and bias terms, respectively. Let ${\Vert \beta \Vert }_2={\left({\sum }_{k=1}^{p_n}{\Vert {\beta }_k\Vert }_2^2\right)}^{1∕2}$, where β = β(t) = (β₁(t), . . . , β_pn(t))′.

Theorem 2 (Convergency of group Lasso). Let $\{\stackrel{‒}{c},c_0,\sigma ,d\}$ be fixed and 1 ≤ q_n ≤ n ≤ p_n → ∞. Suppose the conditions in Theorem 1 hold. Then, with probability converging to one,

$$\begin{array}{cc}\hfill & {\Vert \tilde{\beta }-\beta \Vert }_2\le \left(\frac{M^2{q}_n}{n{c}_{\ast }}+1\right)\sqrt{q_n}\rho +\rho ,\hfill \\ \hfill & {\Vert \widehat{\beta }-\tilde{\beta }\Vert }_2\le \frac{2\sigma {\left(M_1\text{log}{m}_n{q}_n\right)}^{1∕2}}{Q_b\sqrt{d_{a}N{c}_{\ast }}}+\frac{\lambda {\left(d_b{M}_1{q}_n\right)}^{1∕2}}{Q_{b}N{c}_{\ast }}.\hfill \end{array}$$

Consequently, with probability converging to one,

$${\Vert \widehat{\beta }-\beta \Vert }_2\equiv {\left[\sum _{k=1}^{p_n}\left({\Vert {\widehat{\beta }}_k-{\beta }_k\Vert }_2^2\right)\right]}^{1∕2}\le \frac{2\sigma \sqrt{M_1{q}_n\text{log}{m}_n}}{Q_b\sqrt{d_{a}N{c}_{\ast }}}+\frac{\lambda \sqrt{d_b{M}_1{q}_n}}{Q_{b}N{c}_{\ast }}+(\frac{M^2{q}_n}{n{c}_{\ast }}+1)\sqrt{q_n}\rho +\rho .$$

This theorem gives the rate of convergence of β(t) as determined by four terms: the stochastic error and bias due to penalization (the first and second terms, ${\Vert \widehat{\beta }-\tilde{\beta }\Vert }_2$), the basis approximation error (the third and fourth terms, ${\Vert \tilde{\beta }-\beta \Vert }_2$). Under the conditions of Theorem 1 and Theorem 2, the group Lasso is estimation consistent in model selection.

Immediately from Theorem 2, we have the following corollary.

Corollary 1. Let λ = O_p(ρ(N log m_n)^1/2). Suppose the conditions in Theorem 2 hold. Then Theorem 1 holds and, with probability converging to one, ${\Vert \tilde{\beta }-\beta \Vert }_2=O_p\left((q_n^{3∕2}{d}_a∕n+q_n^{1∕2}+1)\rho \right)$ and ${\Vert \widehat{\beta }-\tilde{\beta }\Vert }_2=O_p\left((d_a+\rho d_a^{5∕2}){(q_n\text{log}{m}_n∕N)}^{1∕2}\right)$. Consequently, with probability converging to one,

$${\Vert \widehat{\beta }-\beta \Vert }_2=O_p\left((d_a+\rho d_a^{5∕2})\sqrt{\frac{q_n\text{log}{m}_n}{N}}+(\frac{q_n^{3∕2}{d}_a}{n}+q_n^{1∕2}+1)\rho \right).$$

This corollary follows by substituting the given λ value into the expression in the results of Theorem 2 and using $Q_b=O\left(d_a^{-1}\right)$ by Lemma A.1 in Huang, Wu, and Zhou (2004). Note that ${\tilde{\beta }}_k\left(t\right)$ can be interpreted as the best approximation in the estimation space G_k(t) to β_k(t); under appropriate conditions, the bias term ${\Vert {\tilde{\beta }}_k\left(t\right)-\beta \left(t\right)\Vert }_2$ is asymptotically negligible to the variance ${\Vert \widehat{\beta }-\tilde{\beta }\Vert }_2$. For example, a special extreme case: for k = 1, . . . , p_n, if β_k(t) is a constant function independent of t, then (1.1) simplifies to a high-dimensional linear regression problem, ${\Vert \tilde{\beta }-\beta \Vert }_2\equiv 0$. Thus by choosing appropriate λ, ${\Vert \widehat{\beta }-\beta \Vert }_2=O_p\left(\sqrt{q_n\text{log}{p}_n∕n}\right)$ which is consistent with the result obtained in Zhang and Huang (2008). If we use B-spline basis functions to approximate β(t), by Theorem 6.27 in Schumaker (1981), for k = 1, . . . , p_n, if β_k(t) has bounded second derivatives and lim sup_n d_a/d_b < ∞, then $\rho =O\left(d_a^{-2}\right)$, thus ${\Vert \tilde{\beta }-\beta \Vert }_2=O_p\left((q_n^{3∕2}{d}_a∕n+q_n^{1∕2}+1)d_a^{-2}\right)$.

Collary 2. Suppose B-spline basis approximation, for k = 1, . . . , p_n, with coefficient functions β_k(t) having bounded second derivates, limsup_n d_a/d_b < ∞, and the conditions in Corollary 1. Then

$${\Vert \widehat{\beta }-\beta \Vert }_2=O_p\left(\frac{d_a\sqrt{q_n\text{log}{m}_n}}{\sqrt{N}}+(\frac{q_n^{3∕2}{d}_a}{n}+q_n^{1∕2}+1)d_a^{-2}\right).$$

For the conditions given in Corollary 2, the number of covariates p_n can be as large as $\text{exp}\left(o(N∕\left(d_a^2{q}_n\right))\right)$, which can be much larger than n.

4. Selection Consistency of Adaptive Group Lasso

As just shown, the group Lasso has nice selection and estimation properties. It selects a model that has the same order of dimension as that of the underlying model. However, there is still room for improvement. To achieve variable selection accuracy and reduce the estimation bias of the group Lasso, we consider the adaptive group Lasso given an initial consistent estimator $\stackrel{‒}{\beta }\left(t\right)$. Take weights

$${\omega }_k=\{\begin{array}{cc}{\left(\sqrt{d_k}{\Vert {\stackrel{‒}{\beta }}_k\Vert }_2\right)}^{-1},\hfill & \text{if}{\Vert {\stackrel{‒}{\beta }}_k\Vert }_2>0,\hfill \\ \infty ,\hfill & \text{if}{\Vert {\stackrel{‒}{\beta }}_k\Vert }_2=0,\hfill \end{array}\phantom{\}}$$ (4.1)

so w_k is proportional to the inverse of the norm of ${\stackrel{‒}{\beta }}_k\left(t\right)$. Here we define 0·∞ = 0. Thus the variables not included in the initial estimator are not included in the adaptive group Lasso. Given a zero-consistent initial estimator (Huang, Ma, and Zhang (2008)), the adaptive group Lasso penalty level λ_k goes to zero when ${\Vert {\gamma }_k\Vert }_2$ is large, which satisfies the conditions given in Lv and Fan (2009) for a penalty function having the oracle selection property.

Consider the following additional conditions.

• (C5) The initial estimator $\stackrel{‒}{\beta }\left(t\right)$ is zero-consistent with rate r_n if

  $$\underset{k\in A_0}{\text{max}}{\Vert {\stackrel{‒}{\beta }}_k\Vert }_2=o_p\left(1\right),r_n\underset{k\in A_0}{\text{max}}{\Vert {\stackrel{‒}{\beta }}_k\Vert }_2=O_p\left(1\right),r_n\to \infty$$

  and there exists a constant ξ_b > 0 such that $P({\text{min}}_{k\in A_0^c}{\Vert {\stackrel{‒}{\beta }}_k\Vert }_2>{\xi }_b{\theta }_b)\to 1$ as n → ∞, where ${\theta }_b={\text{min}}_{k\in A_0^c}{\Vert {\beta }_k\Vert }_2$.
• (C6) If s_n = p_n – q_n is the number of unimportant variables,

  $$\frac{\sqrt{d_a\left(\text{log}{q}_n\right)}}{\sqrt{N}{d}_b{\theta }_b}+\frac{\tilde{\lambda }{d}_a^{3∕2}{q}_n}{N{d}_b^2{\theta }_b^2}+\frac{\sqrt{Nd\text{log}{s}_n}}{\tilde{\lambda }{r}_n}+\frac{d_a{d}^{3∕2}{q}_n^2}{r_n{\theta }_b}\to 0.$$

• (C7) All the eigenvalues of ${\Sigma }_{A_0^c{A}_0^c}$ are bounded away from zero and infinity.

Theorem 3. Suppose that (C3), (C5)–(C7) are satisfied. Under NSC,

$$P({\Vert {\widehat{\beta }}_k^{\ast }\Vert }_2\ne 0,k\notin A_{0}and{\Vert {\widehat{\beta }}_k^{\ast }\Vert }_2=0,k\in A_0)\to 1.$$

Theorem 3 shows that the adaptive group Lasso is selection consistent if an initial consistent estimator is available. Condition (C5) is critical, and is very difficult to establish. It assumes that we can consistently differentiate between important and unimportant variables. For fixed p_n and d_k, the ordinary least squares estimator can be used as the initial estimator. However, when p_n > n, the least squares estimator is no longer feasible. Theorem 1 and Theorem 2 show that, under certain conditions, the group Lasso estimator is zero-consistent with rate

$$r_n={\left((d_a+\rho d_a^{5∕2}){\left(q_n\text{log}\frac{m_n}{N}\right)}^{1∕2}+(\frac{q_n^{3∕2}{d}_a}{n}+q_n^{1∕2}+1)\rho \right)}^{-1}.$$

Thus if we use the group Lasso estimator as the initial estimator for the adaptive group Lasso, we have the selection consistent property in Theorem 3. In addition, we reduce the dimensionality of the problem using this initial estimator. Condition (C6) restricts the numbers of important variables and basis functions, the penalty parameter, and the smallest important coefficient function (in the ${\ell }_2$ sense). When d and θ_b are fixed constants and the n_i, i = 1, . . . , n are bounded, (C6) can be simplified to

$$\text{log}\frac{q_n}{n}+\frac{\tilde{\lambda }{q}_n}{n}+\frac{\sqrt{n\text{log}{s}_n}}{\tilde{\lambda }{r}_n}+\frac{q_n^2}{r_n}\to 0,$$

which can be obtained by choosing appropriate $\tilde{\lambda }$ and initial estimator. Condition (C7) assumes that the eigenvalues of ${\Sigma }_{A_0^c{A}_0^c}$ are finite and bounded away from zero; this is reasonable since the number of important variables is small in a sparse model.

Using the group Lasso result as the initial estimator for the adaptive group Lasso, we then have the following theorem.

Theorem 4. Suppose the conditions of Theorem 1 hold, and θ_b > t_b for some constant t_b > 0. Let $\tilde{\gamma }=O\left(N^{\alpha }\right)$ for some 0 < α < 1/2. Then with probability converging to one,

$${\Vert {\widehat{\beta }}^{\ast }-\beta \Vert }_2=O_p\left({\left(\frac{q_n}{d_{a}N}\right)}^{1∕2}+{\left(\frac{1}{d_{a}N}\right)}^{1∕2}+(\frac{q_n^{3∕2}{d}_a}{n}+q_n^{1∕2}+1)\rho \right),$$

For k = 1, . . . , p_n, if all β_k(t) are constant functions, q_n and the number of observations n_i for the ith subject are fixed, then the result of Theorem 4 is consistent with the well-known result for low-dimensional linear regression problem, ${\Vert {\widehat{\beta }}^{\ast }-\beta \Vert }_2=O_p\left(n^{-1∕2}\right)$. Moreover, similar to Corollary 2, if B-spline basis functions are used to approximate the regression coefficient functions, then we have the following.

Corollary 3. Consider B-spline basis approximation and choose d_a = O(n^1/5). For k = 1, . . . , p_n, the coefficient function β_k(t) has a bounded second derivative, lim sup_n d_a/d_b < ∞, and the conditions in Theorem 4 hold. If q_n and n_i are fixed, then with probability converging to one, ${\Vert {\widehat{\beta }}^{\ast }-\beta \Vert }_2=O_p\left(n^{-2∕5}\right)$.

5. Numerical Studies

In this section, we derive a group coordinate descent algorithm to compute the group Lasso and adaptive group Lasso estimates in varying coefficient models. For the adaptive group Lasso, we use the group Lasso as the initial estimator. We compare the results from the group Lasso and the adaptive group Lasso with the results from the group SCAD (Antoniadis and Fan (2001); Wang, Li, and Huang (2008)).

5.1. The group coordinate descent algorithm

The group coordinate descent algorithm is a natural extension of standard coordinate descent, see for example, Fu (1998) and Friedman et al. (2007). Meier, Van de Geer and Bülmann (2008) also used a group coordinate descent for selecting groups of variables in high-dimensional logistic regression.

Let ${\tilde{\gamma }}_k=R_k^{1∕2}{\gamma }_k$ and ${\tilde{U}}_k=U_k{R}_k^{-1∕2}$ for k = 1, . . . , p_n, so (2.6) can be rewritten as

$${\tilde{\gamma }}^{\ast }=\text{arg}\underset{\tilde{\gamma }}{\text{min}}\frac{1}{2}{(Y-\tilde{U}\tilde{\gamma })}^{\prime }(Y-\tilde{U}\tilde{\gamma })+\sum _{k=1}^{p_n}\lambda {\Vert {\tilde{\gamma }}_k\Vert }_2.$$ (5.1)

The group Lasso estimates ${\widehat{\gamma }}_k$ of (2.6) can then be obtained as ${\widehat{\gamma }}_k=R_k^{-1∕2}{\tilde{\gamma }}_k^{\ast }$ for k = 1, . . . , p_n.

Denote by $L\left(\tilde{\gamma }\right)$ the objective function in (5.1). Suppose we have estimates ${\tilde{\gamma }}_l$ for $l\ne j$ and wish to partially optimize with respect to ${\tilde{\gamma }}_j$. The gradient at ${\tilde{\gamma }}_j$ only exists is ${\Vert {\tilde{\gamma }}_j\Vert }_2\ne 0$, and then

$$\frac{\partial L}{\partial {\tilde{\gamma }}_j}=-\frac{1}{N}{\tilde{U}}_j^{\prime }(Y-\tilde{U}\tilde{\gamma })+\lambda \frac{{\tilde{\gamma }}_j}{{\Vert {\tilde{\gamma }}_j\Vert }_2}=-\frac{1}{N}{\tilde{U}}_j^{\prime }(Y-Y^{(-j)})+\frac{1}{N}{\tilde{U}}_j^{\prime }{\tilde{U}}_j+\lambda \frac{{\tilde{\gamma }}_j}{{\Vert {\tilde{\gamma }}_j\Vert }_2},$$

where $Y^{(-j)}={\sum }_{l\ne j}{\tilde{U}}_l{\tilde{\gamma }}_l$ is the fitted value excluding the contribution from ${\tilde{U}}_j$. With ${\tilde{U}}_k^{\prime }{\tilde{U}}_k∕N=I_{d_k\times d_k}$ for k = 1, . . . , p_n, simple calculus shows that the group coordinate-wise update has the form

$${\tilde{\gamma }}_j=(1-\frac{\lambda }{{\Vert z_j\Vert }_2})+z_j,$$

where $z_j=N^{-1}{\tilde{U}}_j^{\prime }(Y-Y^{(-j)})$ and ${\left(x\right)}_{+}=x{I}_{\{x\ge 0\}}$. Then for fixed λ, the above estimator ${\tilde{\gamma }}^{\ast }$ can be computed with the following iterative algorithm.

1. Center and standardize Y and Ũ, such that ${\sum }_{i=1}^N{Y}_i=0,{\tilde{U}}_j^{\prime }{\tilde{U}}_j∕n=I_{d_j\times d_j}$ for j = 1, . . . , p_n.

2. Initialize ${\tilde{\gamma }}^{\left(0\right)}=0$ and let m = 0, r = Y.

3. Calculate $z_j=N^{-1}{\tilde{U}}_j^{\prime }r+{\tilde{\gamma }}_j^{\left(m\right)}$.

4. Update ${\tilde{\gamma }}_j^{(m+1)}={(1-\lambda ∕{\Vert z_j\Vert }_2)}_{+}{z}_j,\text{for}j=1,\dots ,p_n$.

5. Update $r=r-{\tilde{U}}_j({\tilde{\gamma }}_j^{(m+1)}-{\tilde{\gamma }}_j^{\left(m\right)})$ and m = m + 1.

6. Repeat Steps 3-5 until convergence or a fixed number of maximum iterations has been reached. The $\tilde{\gamma }$ at convergence is the group Lasso estimate ${\tilde{\gamma }}^{\ast }$ of (5.1).

7. Change ${\tilde{\gamma }}^{\ast }$ to the original scale corresponding to original Y and Ũ before centering and standardization, and ${\widehat{\gamma }}_k=R_k^{-1∕2}{\tilde{\gamma }}_k^{\ast }$.

It can be seen that the idea of the group coordinate descent algorithm is simple but effcient, every update cycle requires only O(N_pn) operations and the computational burden increases linearly with p_n. If the number of iterations is smaller than p_n, the solution is reached with even less computational burden than the $N{p}_n^2$ operations required to solve a linear regression problem by QR decomposition.

For the adaptive group Lasso, we can use the same coordinate descent algorithm by simple substitution, as in (2.6) and (5.1). We use the same set of cubic B-spline basis functions for each β_k. That is, d₁ = . . . = d_pn ≡ d₀ and $B_{kl}=B_{k^{\prime }l}\text{for}k\ne k^{\prime },1\le k,k^{\prime }\le p_n$. In our application, apply the BIC criterion (Schwarz (1978)) to select (λ, d₀) for the group Lasso and $(\tilde{\lambda },d_0)$ for the adaptive group Lasso. The BIC criterion is

$$BIC(\lambda ,d_0)=\text{log}\left(RS{S}_{\lambda ,d_0}\right)+\text{log}N\cdot \frac{d{f}_{\lambda ,d_0}}{N},$$

where RSS is the residual sum of squares, df is the number of selected variables for a given (λ, d₀). We choose d₀ from an increasing sequence of ten values, starting from 5 to 14; for any given value of d₀, we choose λ from a sequence of 100 values, starting from λ_max to 0.001λ_max with ${\lambda }_{max}={\text{max}}_{1\le k\le p_n}{\Vert {\tilde{U}}_k^{\prime }Y\Vert }_2∕\sqrt{d_0}$, where Ũ_k is the N × d₀ submatrix of the “designed” matrix Ũ corresponding to the covariate X_k. This λ_max is the smallest penalty value that forces all the estimated coefficients to be zero.

5.2. Monte Carlo simulation

We used simulation to assess the performance of the proposed procedures. Because our main interest is in the case when p_n is large, we focused on the case p_n > n. We consider the model

$$y_i\left(t_{ij}\right)=\sum _{k=1}^{p_n}{x}_{ik}\left(t_{ij}\right){\beta }_k\left(t_{ij}\right)+{∊}_i\left(t_{ij}\right).$$

The time points t_ij for each individual subject are scheduled to be {1, . . . , 30}, each scheduled time point has some probability to be skipped, then the number of actual observed time points n_i for diffierent subject is diffierent. This generating model is similar to the one in Wang, Li, and Huang (2008).

The first six variables x_i1, x_i2, x_i3, x_i4, x_i5 and x_i6, i = 1, . . . , 100, are the true relevant variables, and were simulated as follows: x_i1(t) was uniform [t/10, 2 + t/10] at any given time point t; x_ij(t), j = 2, . . . , 5, conditioned on x_i1(t), were i.i.d. from the normal distribution with mean zero and variance (1 + x_i1(t))/(2 + x_i1(t)); x_i6, independent of x_ij, j = 1, . . . , 5, was normal with mean 3 exp(t/30) and variance 1. For k = 7, . . . , 500, each x_ik(t), independent of others, was multivariate normal distribution with covariance structure cov(x_ik(t), x_ik(s)) = 4 exp(–|t – s|). The random error ε_i(t) was Z(t) + E(t), where Z(t) had the same distribution as x_ik, k = 7, . . . , 500, and E(t) were independent measurement errors from N(0, 2²) at each time point t. The coefficient functions were

$${\beta }_1\left(t\right)=15+20\text{sin}\left(\frac{\pi t}{15}\right),{\beta }_2\left(t\right)=15+20\text{cos}\left(\frac{\pi t}{15}\right),{\beta }_3\left(t\right)=2-3\text{sin}\left(\frac{\pi (t-25)}{15}\right),{\beta }_4\left(t\right)=2-3\text{cos}\left(\frac{\pi (t-25)}{15}\right),{\beta }_5\left(t\right)=6-0.2t^2,{\beta }_6\left(t\right)=-4+\frac{{(20-t)}^3}{2000},{\beta }_7\left(t\right)=\cdots ={\beta }_{500}\left(t\right)\equiv 0.$$

The observation time points t_ij for each individual were generated from scheduled time points {1, . . . , 30}, each scheduled time point had a probability of 60% being skipped, and the actual observation time t_ij was obtained by adding a random perturbation from uniform [–0.5, 0.5] to the non-skipped scheduled time.

We consider the cases n = 50, 100, 200 with p_n = 500, to see the performance of our proposed methods as sample size increases. The penalty parameters were selected using BIC. The results for the group Lasso, the adaptive group Lasso, and the group SCAD methods are given in Tables 1 and 2 based on 200 replications. The columns in Table 1 include the average number of variables (NV) selected, model error (ER), percentage of occasions on which correct variables were included in the selected model (%IN), and percentage of occasions on which the exactly correct variables were selected (%CS), with standard error in parentheses. Table 2 summarizes the mean square errors for the six important coefficient functions $N^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^{n_i}{({\widehat{\beta }}_j\left(t_{ij}\right)-{\beta }_j\left(t_{ij}\right))}^2$, with standard error in parentheses.

Table 1.

Simulation study.

Results for high dimension cases, p = 500
	adaptive group Lasso				group Lasso				group SCAD
	NG	ER	IN%	CS%	NG	ER	IN%	CS%	NG	ER	IN%	CS%
n = 200	6.13 (0.38)	15.18 (3.33)	99 (0.01)	93 (0.26)	6.20 (0.64)	21.07 (5.88)	99 (0.01)	82 (0.38)	6.12 (0.37)	14.29 (2.37)	100 (0.00)	95 (0.22)
n = 100	6.21 (0.72)	15.20 (3.58)	87 (0.34)	84 (0.36)	6.34 (1.25)	26.81 (4.44)	87 (0.34)	69 (0.51)	6.25 (0.78)	15.37 (2.52)	90 (0.10)	83 (0.37)
n = 50	7.04 (1.43)	15.98 (3.86)	72 (0.48)	68 (0.52)	10.29 (5.64)	27.09 (4.96)	72 (0.48)	53 (0.57)	6.99 (1.38)	15.74 (3.12)	78 (0.42)	70 (0.49)

NG, number of selected variables; ER, model error; IN%, percentage of occasions on which the correct variables were included in the selected model; CS%, percentage of occasions on which exactly correct variables were selected, averaged over 200 replications. Enclosed in parentheses are the corresponding standard errors.

Table 2.

Simulation study.

	β 1	β 2	β 3	β 4	β 5	β 6
	n = 200
adaptive group Lasso	6.49 (2.71)	4.46 (1.21)	2.28 (1.10)	1.36 (0.95)	1.49 (0.98)	7.72 (3.58)
group Lasso	16.41 (9.09)	9.72 (4.10)	8.31 (3.08)	4.98 (2.39)	5.14 (3.92)	10.81 (11.91)
group SCAD	6.46 (2.70)	4.44 (1.20)	2.27 (1.09)	1.34 (0.93)	1.45 (0.94)	7.59 (3.31)
	n = 100
adaptive group Lasso	8.19 (3.82)	7.65 (2.17)	3.97 (1.44)	2.02 (1.30)	2.14 (1.35)	9.10 (5.27)
group Lasso	29.99 (15.95)	18.04 (5.15)	11.12 (3.96)	8.51 (3.85)	9.69 (5.09)	22.03 (18.55)
group SCAD	8.20 (3.84)	7.65 (2.17)	3.95 (1.39)	2.01 (1.28)	2.12 (1.30)	9.70 (6.05)
	n = 50
adaptive group Lasso	9.08 (3.88)	8.20 (3.84)	4.49 (1.76)	3.41 (1.73)	3.86 (1.75)	9.72 (5.56)
group Lasso	34.39 (20.25)	26.05 (17.44)	14.15 (4.92)	12.98 (4.80)	12.64 (6.66)	33.49 (22.18)
group SCAD	9.05 (3.86)	8.22 (3.91)	4.51 (1.77)	3.38 (1.64)	3.82 (1.72)	9.73 (5.64)

Mean square errors for the important coefficient functions based on 200 replications. Enclosed in parentheses are the corresponding standard errors.

Several observations can be obtained from Tables 1 and 2. The model that was selected by the adaptive group Lasso was similar to the one selected by the group SCAD, and better than the one selected by the group Lasso in terms of model error, the percentage of occasions on which the true variables were selected and the mean square errors for the important coefficient functions. The group Lasso included the correct variables with high probability. For smaller sample sizes, the performance of both methods was worse. This is expected since variable selection in models with a small number of observations is more difficult. To examine the estimated time-varying coefficient functions from the adaptive group Lasso, we plot them along with the true function components in Figure 1. The estimated coefficient functions are from the adaptive group Lasso method in one run when n = 200. From the graph, the estimators of the time-varying coefficient functions β_k(t), k = 3, 4, 5, fit the true coefficient functions well, which is consistent with the mean square errors for the coefficient functions reported in Table 2.

Figure 1.

Adaptive group Lasso method. The estimated coefficient functions (dashed line) and true coefficient (solid line) functions in one run when n = 200

These simulation results have the adaptive group Lasso with good selection and estimation performance, even when p is larger than n. They also suggest that the adaptive group Lasso can better the selection and estimation results of the group Lasso.

5.3. Identification of yeast cell cycle transcription factors

We apply our procedures to investigate the transcription factors (TFs) involved in the yeast cell cycle, which is helpful for understanding the regulation of yeast cell cycle genes. The cell cycle is an ordered set of events, culminating in cell growth and division into two daughter cells. Stages of the cell cycle are commonly divided into G1-S-G2-M. The G1 stage stands for “GAP 1”. The S stage stands for “Synthesis”; is the stage when DNA replication occurs. The G2 stage stands for “GAP 2”. The M stage stands for “mitosis”, when nuclear (chromosomes separate) and cytoplasmic (cytokinesis) division occur. Coordinate expression of genes whose products contribute to stage-specific functions is a key feature of the cell cycle (Simon et al. (2001), Morgan (1997), Nasmyth (1996)). Transcription factors (TFs) have been identified that play critical roles in gene expression regulation. To understand how the cell cycle is regulated and how cell cycle regulates other biological processes, such as DNA replication and amino acids biosynthesis, it is useful to identify the cell cycle regulated transcription factors.

We apply the group Lasso and the adaptive group Lasso methods to identify the key transcription factors that play critical roles in the cell cycle regulations from a set of gene expression measurements which are captured at equally spaced sampling time points. The data set we use comes from Spellman et al. (1998). They measured the genome-wide mRNA levels for 6178 yeast ORFs simultaneously over approximately two cell cycle periods in a yeast culture synchronized by α factor relative to a reference mRNA from an asynchronous yeast culture. The yeast cells were measured at 7-min intervals for 119 mins, with a total of 18 time points after synchronization. Using a model-based approach, Luan and Li (2003) identified 297 cell-cycle-regulated genes based on the α factor synchronization experiments. In our study, we consider 240 genes without missing values out of these 297 cell-cycle-regulated genes. Let y_i(t_j) denote the log-expression level for gene i at time point t_j during the cell cycle process, for i = 1, . . . , 240 and j = 1, . . . , 18. We then use the chromatin immunoprecipitation (ChIP-chip) data of Lee et al. (2002) to derive the binding probabilities x_ik for these 240 cell-cycle-regulated genes for a total of 96 transcriptional factors with at least one nonzero binding probability in the 240 genes. We assume the following varying coefficient model to link the binding probabilities to the gene expression levels

$$y_i\left(t_j\right)={\beta }_0\left(t_j\right)+\sum _{k=1}^{96}{\beta }_k\left(t_j\right)x_{ik}+{∊}_{i{t}_j},$$

where β_k(t_j) represents the effect of the kth TF on gene expression at time t_j during the cell cycle process. Our goal is to identify the TFs that might be related to the cell cycle regulated gene expression.

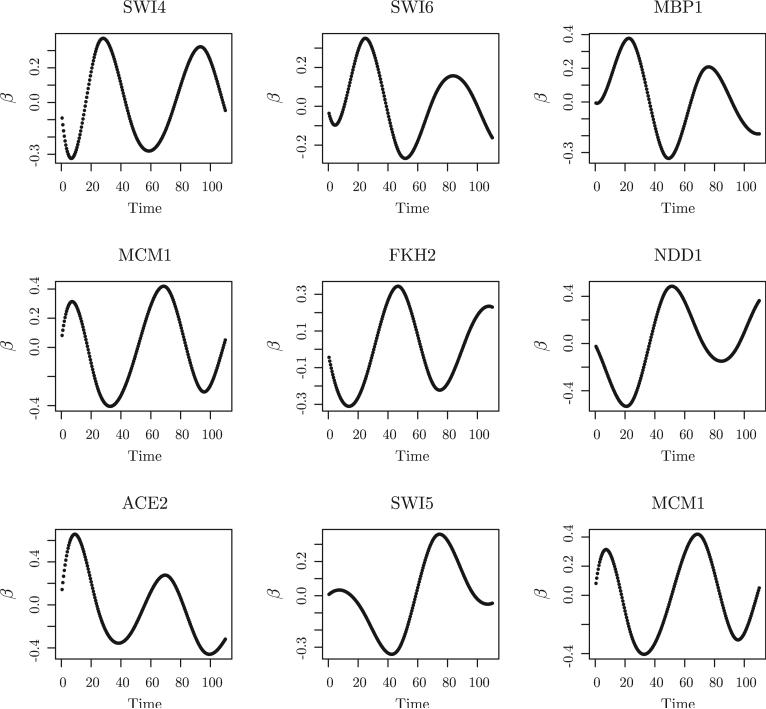
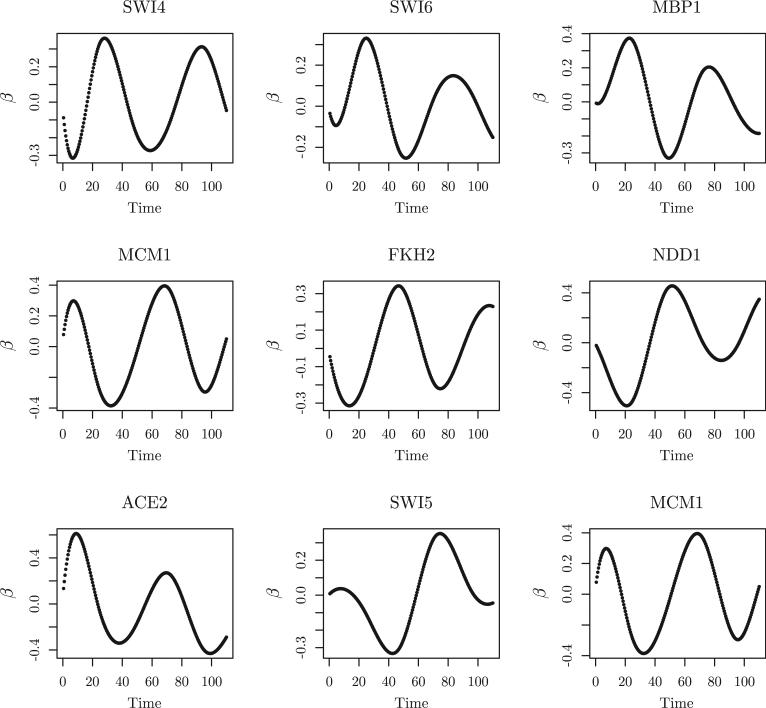
We used BIC to select the tuning parameters in the group Lasso and adaptive group Lasso. The selected tuning parameters were d₀ = 7, λ = 0.89 and λ = 1.07. The group Lasso identified a total of 67 TFs related to yeast cell-cycle processes, including 19 of the 21 known and experimentally verified cell-cycle related TFs. The other two TFs, LEU3 and MET31, were not selected by the group Lasso method. Using the result from the group Lasso as the initial estimator for the adaptive group Lasso, adaptive group Lasso identified a total of 54 TFs, including the same 19 of the 21 known and experimentally verified cell-cycle related TFs. In addition, all of the identified TFs showed certain estimated periodic transcriptional effects on the cell cycle regulated gene expression, for example, MBP1, SWI4, SWI6, MCM1, FKH1, FKH2, NDD1, SWI5, and ACE2 (Simon et al. (2001)). The transcriptional effects of these 9 TFs are shown in Figure 2 and Figure 3 estimated by the group Lasso and the adaptive group Lasso methods, respectively. MBP1, SWI4, and SWI6 control late G1 genes. MCM1, together with FKH1 or FKH2, recruits the NDD1 protein in late G2, and thus controls the transcription of G2/M genes. MCM1 is also involved in the transcription of some M/G1 genes. SWI5 and ACE2 regulate genes at the end of M and early G1 (Simon et al. (2001)).

Figure 2.

Application to yeast cell cycle gene expression data. The results are from the group Lasso.

Figure 3.

Application to yeast cell cycle gene expression data. The results are from the adaptive group Lasso.

Moreover, the identified key TFs from both the group Lasso and the adaptive group Lasso include many pairs of cooperative or synergistic pairs of TFs involved in the yeast cell cycle process reported in the literature (Banerjee and Zhang (2003), Tsai, Lu, and Li (2005)). Among the 67 TFs identified by the group Lasso, 27 of them belong to the cooperative pairs of the TFs identified by Banerjee and Zhang (2003), including 23 out of 31 significant cooperative TF pairs. For the 54 TFs identified by the adaptive group Lasso, 25 of them belong to the cooperative pairs of the TFs, including 21 out of 31 significant cooperative TF pairs. The results are summarized in Table 2.

For this data set, the binding data are only available for 96 TFs. The sample size is larger than the number of variables. In order to see the performance of our proposed method with p > n, we artificially added 200 more variables to this data set. We randomly chose 200 values from the whole binding data set without replacement to add those 200 additional variables to each gene. We repeated this process 100 times. We first looked at the results concerning the 21 known TFs, since this is the only ‘truth’ we know about this data set. The average number of the 21 known important TFs identified was: the group Lasso 17.0 (standard deviation 0.12), the adaptive group Lasso 14.2 (standard deviation 0.42). The group Lasso tended to have a much higher false positive rate. The selected TFs sets after we artificially added 200 variables had a large intersection with the ones selected using only the data set itself. This suggests our method works well with many noisy variables in the model.

Finally, to compare the group Lasso and the adaptive group Lasso with simple linear regression with lasso penalty, we performed simple linear regression with binding probability as the predictors and the gene expression at each time point as the response with lasso penalty. We found only 1 TF significant related to cell cycle regulation. The result is not surprising, since the effects of the TFs on gene expression levels are time-dependent. Overall, our procedures can effectively identify the important TFs that affect the gene expression over time.

6. Concluding Remarks

In this article, we studied the estimation and selection properties of the group Lasso and adaptive group Lasso in time varying coefficient models with high dimensional data. For the group Lasso method, we considered its properties in terms of the sparsity of the selected model, bias, and the convergence rate of the estimator, as given in Theorems 1 and 2. An interesting aspect in our study is that we can allow many small non-zero coefficient functions as long as the sum of their ${\ell }_2$ norm is below a certain level. Our simulation results indicate that the group Lasso tends to select some non-important variables. An effective remedy then is to use the adaptive group Lasso. Compared with the group Lasso, the advantage of the adaptive group Lasso is that it has the oracle selection property. Moreover, the convergence rate of the adaptive group Lasso estimator is better. In addition, the computational cost is the same as the group Lasso. The adaptive group Lasso that uses group Lasso as the initial estimator is an effective way to analyze varying coefficient problems in sparse, high-dimensional settings.

In this paper, we have focused on the group Lasso and the adaptive group Lasso in the context of linear varying coefficient models. These methods can be applied in a similar way to other nonlinear and nonparametric regression models, but more work is needed.

Table 3.

Yeast cell cycle study. Identified cooperative pairs of TFs involved in the cell cycle process.

	adaptive group Lasso	group Lasso
	MBP1-SWI6,	MBP1-SWI6,
	MCM1-NDD1,	MCM1-NDD1,
	FKH2-MCM1,	FKH2-MCM1,
	FKH2-NDD1,	FKH2-NDD1,
	SWI4-SWI6,	SWI4-SWI6,
	FHC1-GAT3,	FHL1-GAT3
	NRG1-YAP6,	NRG1-YAP6,
	GAT3-MSN4,	GAT3-MSN4,
	REB1-SKN7,	REB1-SKN7
	ACE2-REB1,	ACE2-REB1,
	GCN4-SUM1,	GAL4-RGM1,
	FKH1-FKH2,	GCN4-SUM1
	CIN5-NRG1,	FKH1-FKH2,
	SMP1-SWI5,	CIN5-NRG1,
	FKH1-NDD1,	SMP1-SWI5
	ACE2-SWI5,	FKH1-NDD1,
	CIN5-YAP6,	ACE2-SWI5,
	STB1-SWI4,	CIN5-YAP6
	ARG81-GCN4,	STB1-SWI4,
	NDD1-STB1,	ARG81-GCN4,
	NRG1-PHD1.	NDD1-STB1,
		DAL81-STP1,
		NRG1-PHD1.
No. of pairs	21	23

Appendix: Proofs

This section provides the proofs of the results in Sections 3 and 4. For simplicity, we often drop the subscript n from certain quantities, for example, we simply write p for p_n, q for q_n. Let ỹ = E(y) = X(t)β(t), $\tilde{\gamma }={\text{min}}_{\gamma ={({\gamma }_{A_0^c},0)}^{\prime }}{(\tilde{y}-U\gamma )}^{\prime }(\tilde{y}-U\gamma )$, then $\tilde{\beta }\left(t\right)=B\left(t\right)\tilde{\gamma }$. We write $\widehat{\beta }-\beta =(\widehat{\beta }-\tilde{\beta })+(\tilde{\beta }-\beta )$, and find the rates of convergence of ${\Vert \tilde{\beta }-\beta \Vert }_2\text{and}{\Vert \widehat{\beta }-\tilde{\beta }\Vert }_2$.

For any two sequences {a_n, b_n, n = 1, 2, . . .}, we write $a_n\asymp b_n$ if there are constants 0 < c₁ < c₁ < ∞ such that c₁ ≤ a_n/b_n ≤ c₂ for all n sufficiently large, and write $a_n{\asymp }_p{b}_n$ if this inequality holds with probability converging to one.

Lemma A.1. ${\Vert \tilde{\beta }-\beta \Vert }_2=O_p(\rho q^{3∕2}∕\left(n{c}_{\ast }\right)+\rho q^{1∕2}+\rho )$.

Proof of Lemma A.1. By the properties of basis functions and (C2), there exists $g^{\ast }\left(t\right)=(g_1^{\ast }\left(t\right),\dots ,g_q^{\ast }\left(t\right),0,\dots ,0)$ for $g_k^{\ast }\in G_k\left(t\right),k=1,\dots ,q$ such that ${\Vert g^{\ast }-\beta \Vert }_{\infty }=\rho$. Thus $\exists {\gamma }^{\ast }={({\gamma }_1^{{\ast }^{\prime }},\dots ,{\gamma }_p^{{\ast }^{\prime }})}^{\prime }={({{\gamma }_{A_0^c}^{\ast }}^{\prime },{{\gamma }_{A_0}^{\ast }}^{\prime })}^{\prime }$ with ${\gamma }_k^{\ast }={({\gamma }_{k1}^{\ast },\dots ,{\gamma }_{k{d}_k}^{\ast })}^{\prime }$ for $k\notin A_0$ and ${\gamma }_k^{\ast }={(0,\dots ,0)}^{\prime }$ for k ∈ A₀, such that g*(t = B(t)γ*

By the definition of ỹ, $\tilde{\gamma }$ and Lemma A.3 in Huang, Wu, and Zhou (2004), we have

$$\tilde{\gamma }=\left(\begin{array}{c}\hfill {\left(U_{A_0^c}^{\prime }{U}_{A_0^c}\right)}^{-1}{U}_{A_0^c}^{\prime }\tilde{y}\hfill \\ \hfill 0\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\tilde{\gamma }}_{A_0^c}\hfill \\ \hfill {\tilde{\gamma }}_{A_0}\hfill \end{array}\right).$$

Thus ${\tilde{\gamma }}_{A_0^c}-{\gamma }_{A_0^c}^{\ast }={\left(U_{A_0^c}^{\prime }{U}_{A_0^c}\right)}^{-1}{U}_{A_0^c}^{\prime }\tilde{y}-{\left(U_{A_0^c}^{\prime }{U}_{A_0^c}\right)}^{-1}{U}_{A_0^c}^{\prime }{U}_{A_0^c}{\gamma }_{A_0^c}^{\ast }={\left(U_{A_0^c}^{\prime }{U}_{A_0^c}\right)}^{-1}{U}_{A_0^c}^{\prime }(\tilde{y}-U_{A_0^c}{\gamma }_{A_0^c}^{\ast })$. By Lemma 1 in Zhang and Huang (2008),

$${\Vert {\tilde{\gamma }}_{A_0^c}-{\gamma }_{A_0^c}^{\ast }\Vert }_2^2\le \frac{{\Vert U_{A_0^c}^{\prime }(\tilde{y}-U_{A_0^c}{\gamma }_{\left(1\right)}^{\ast })\Vert }_2^2}{n^2{c}_{\ast }^2\left(\mid A_0^c\mid \right)}.$$

By (C4),

$$\mid {\tilde{y}}_i-U_{A_{0i}^c}{\gamma }_{A_0^c}^{\ast }\mid =\mid x_i^{\prime }\beta \left(t_i\right)-x_i^{\prime }{B}_{A_0^c}\left(t_i\right){\gamma }_{A_0^c}^{\ast }\mid =\mid x_i^{\prime }\beta \left(t_i\right)-x_i^{\prime }B\left(t_i\right){\gamma }^{\ast }\mid =\mid x_i^{\prime }(\beta \left(t_i\right)-g^{\ast }\left(t_i\right))\mid \le Mq\rho .$$

It follows that

$${\Vert {\tilde{\gamma }}_{A_0^c}-{\gamma }_{A_0^c}^{\ast }\Vert }_2^2\le \frac{1}{n^2{c}_{\ast }^2\left(\mid A_0^c\mid \right)}\left(\sum _{k=1}^q\sum _{l=1}^{d_k}{\left(\sum _{i=1}^n{x}_{ik}{B}_{kl}\left(t_i\right)({\tilde{y}}_i-U_{A_{0i}^c}{\gamma }_{A_0^c}^{\ast })\right)}^2\right)\le \frac{M^2{q}^2{\rho }^2}{n^2{c}_{\ast }^2\left(\mid A_0^c\mid \right)}\left(\sum _{k=1}^q\sum _{l=1}^{d_k}{\left(\sum _{i=1}^n{x}_{ik}{B}_{kl}\left(t_i\right)\right)}^2\right)\le \frac{{\left(M^{2}q\rho \right)}^2\left(\sum _{k=1}^q{d}_k\right)}{n^2{c}_{\ast }^2\left(\mid A_0^c\mid \right)}\le \frac{{\left(M^{2}q\rho \right)}^{2}q{d}_a}{n^2{c}_{\ast }^2\left(\mid A_0^c\mid \right)}.$$

By Lemma A.1 in Huang, Wu, and Zhou (2004),

$${\Vert \tilde{\beta }-g^{\ast }\Vert }_2={\Vert B\tilde{\gamma }-B{\gamma }^{\ast }\Vert }_2{\asymp }_p\frac{{\Vert \tilde{\gamma }-{\gamma }^{\ast }\Vert }_2}{\sqrt{d_a}}\le \frac{M^2\rho q^{3∕2}}{n{c}_{\ast }\left(\mid A_0^c\mid \right)}.$$

Since ${\Vert \tilde{\beta }-\beta \Vert }_2={\Vert \tilde{\beta }-g^{\ast }+g^{\ast }-\beta \Vert }_2\le {\Vert \tilde{\beta }-g^{\ast }\Vert }_2+{\Vert g^{\ast }-\beta \Vert }_2$ and η₁ ≤ ρ,

$${\Vert \tilde{\beta }-\beta \Vert }_2\le \frac{M^2{q}^{3∕2}\rho }{n{c}_{\ast }\left(\mid A_0^c\mid \right)}+\sqrt{q}\rho +\rho .$$

This completes the proof of Lemma A.1.

Proof of Theorem 1. The proof of Theorem 1 is similar to the proof of the rate consistency of the group Lasso in Wei and Huang (2008). The only diffierence is in Step 3 of their proof of Theorem 1, where we need to consider the approximation error of the regression coefficient functions by basis expansion. Thus we omit the other details of the proof here.

From (2.6) and the definition of $\tilde{\gamma }$, we know

$$\widehat{\gamma }=\text{arg}\underset{\tilde{\gamma }}{\text{min}}{(y-U\tilde{\gamma })}^{\prime }(y-U\tilde{\gamma })+\sum _{k=1}^p\lambda {\Vert {\tilde{\gamma }}_k\Vert }_k.$$ (A.1)

If ${\tilde{\gamma }}_k^{\ast }=Q_k{\tilde{\gamma }}_k,U_k^{\ast }=U_k{Q}_k^{-1}$, then (2.6) can be rewritten as

$${\widehat{\gamma }}^{\ast }=\text{arg}\underset{{\tilde{\gamma }}^{\ast }}{\text{min}}{(y-U^{\ast }{\tilde{\gamma }}^{\ast })}^{\prime }(y-U^{\ast }{\tilde{\gamma }}^{\ast })+\sum _{k=1}^p\lambda \sqrt{d_k}{\Vert {\tilde{\gamma }}_k^{\ast }\Vert }_2,$$ (A.2)

and the estimator of (A.1) can be approximated by ${\widehat{\gamma }}_k=Q_k^{-1}{\widehat{\gamma }}_k^{\ast }$ where ${\widehat{\gamma }}^{\ast }$ is the estimator of (A.2).

By the definition of $\tilde{\gamma }$, we have NSC on the regression coefficient $\tilde{\gamma }$, namely, ${\sum }_{k\in A_0}{\Vert {\tilde{\gamma }}_k\Vert }_2=0$. From Lemma A.3 in Huang, Wu, and Zhou (2004), the matrix U* satisfies (C1). Compared with the sufficient conditions for the group Lasso problem given in Wei and Huang (2008), the only change is in the error terms in our (A.2). From (2.2), we have

$$y_i\left(t_{ij}\right)=\sum _{k=1}^p\sum _{l=1}^{d_k}{x}_{ik}\left(t_{ij}\right){\gamma }_{kl}{B}_{kl}\left(t_{ij}\right)+\sum _{k=1}^p{x}_{ik}\left(t_{ij}\right){\rho }_k\left(t_{ij}\right)+{∊}_i\left(t_{ij}\right).$$

Define

$${\delta }_n\left(ij\right)=\sum _{k=1}^p{x}_{ik}\left(t_{ij}\right){\rho }_k\left(t_{ij}\right)+{∊}_i\left(t_{ij}\right)={\rho }_n\left(ij\right)+{∊}_n\left(ij\right),$$

for i = 1, . . . , n, j = 1, . . . , n_i. Let δ_n = (δ_n(11), . . . , δ_n(nn_n))′, ε_n = (ε_n(11), . . . , ε_n(nn_n)) and ρ_n = (ρ_n(11), . . . , ρ_n(nn_n))′. By (C4), we have ${\Vert {\rho }_n\Vert }_2\le C_1\sqrt{N{\rho }^2}$ for some constant C₁ > 0. Define

$$x_m=\underset{\mid A\mid =m}{\text{max}}\underset{{\Vert b_{A_k}\Vert }_2=1,k=1,\dots ,m}{\text{max}}\mid {\delta }_n^{\prime }\frac{V_A}{{\Vert V_A\Vert }_2}\mid \text{and}{x}_m^{\ast }=\underset{\mid A\mid =m}{\text{max}}\underset{{\Vert b_{A_k}\Vert }_2=1,k=1,\dots ,m}{\text{max}}\mid {∊}_n^{\prime }\frac{V_A}{{\Vert V_A\Vert }_2}\mid ,$$ (A.3)

where $V_A=U_A^{\ast }{\left(U_A^{{\ast }^{\prime }}{U}_A^{\ast }\right)}^{-1}{\stackrel{‒}{S}}_A-(I-P_A)U^{\ast }{\gamma }^{\ast },A_k\in A,{\stackrel{‒}{S}}_{A_k}=\lambda \sqrt{d_{A_k}}{b}_{A_k}$, and b_Ak is a d_Ak-dimensional unit vector. For a sufficiently large constant C₂ > 0, also define, as Borel sets in R^n×m_n × Rⁿ,

$$\begin{array}{cc}\hfill {\Omega }_{m_0}& =\{(U^{\ast },∊):x_m\le \sigma \rho C_2\sqrt{(m{d}_b\vee d_b)\text{log}{m}_n},\forall m\ge m_0\},\hfill \\ \hfill {\Omega }_{m_0}^{\ast }& =\{(U^{\ast },∊):x_m^{\ast }\le \sigma \rho C_2\sqrt{(m{d}_b\vee d_b)\text{log}{m}_n},\forall m\ge m_0\},\hfill \end{array}$$

where m₀ ≥ 0. As in the proof of Theorem 1 of Wei and Huang (2008), $(U^{\ast },∊))\in {\Omega }_q\Rightarrow \mid \widehat{A}\mid \le M_{1}q$. By the triangle and Cauchy-Schwarz inequalities,

$$\frac{\mid {\delta }_n^{\prime }{V}_A\mid }{{\Vert V_A\Vert }_2}=\frac{\mid {∊}_n^{\prime }{V}_A+{\rho }_n^{\prime }{V}_A\mid }{{\Vert V_A\Vert }_2}\le \frac{\mid {∊}_n^{\prime }{V}_A\mid }{{\Vert V_A\Vert }_2}+{\Vert {\rho }_n\Vert }_2.$$

In the proof of Theorem 1 of Wei and Huang (2008), it is shown that $P((U^{\ast },{∊}_n)\in {\Omega }_0^{\ast })\to 1$. Since $\mid {\rho }_n^{\prime }{V}_A\mid ∕{\Vert V_A\Vert }_2\le {\Vert {\rho }_n\Vert }_2\le C_1\sqrt{N{\rho }^2}$, we have for all m ≥ 0 and p sufficiently large that ${\Vert {\rho }_n\Vert }_2\le C_1\sqrt{N{\rho }^2}\le \sigma \rho C_2\sqrt{(m\vee 1)d_b\text{log}{m}_n}$. Then P((U*, ε_n) → 1. By the definition of λ_n,p, and $x_m^{\ast }$ we have

$$(U^{\ast },∊)\in {\Omega }_{m_0}\Rightarrow {\mid u^{\prime }∊\mid }^2\le {\left(x_m^{\ast }\right)}^2\le \left({\sigma }^2{\rho }^2{C}_2^2(m{d}_b\vee d_b)\text{log}{m}_n\right)\le \frac{(\mid A_1\mid \vee d_b){\lambda }_b^2{d}_b}{4d_{a}N{c}^{\ast }},\text{for}\mid A_1\mid \ge m_0\ge 0,$$ (A.4)

where u is defined as in the proof of Theorem 1 of Wei and Huang (2008). Since ε₁(t), . . . , ε_n(t) are iid with Eε_i(t_ij) = 0, by (C3) and the proof of Theorem 1 of Wei and Huang (2008), we have $\widehat{q}\le M_{1}q$ and

$$\sum _{k\notin A_0}{\Vert {\tilde{\gamma }}_k\Vert }_2^{2}I\{{\Vert {\widehat{\gamma }}_k\Vert }_2=0\}\le \frac{M_2{B}_1^2}{c_{\ast }N}.$$ (A.5)

From Lemma A.1 in Huang, Wu, and Zhou (2004) and (A.5), we have,

$$\sum _{k\notin A_0}{d}_k{\Vert {\tilde{\beta }}_k\Vert }_2^{2}I\{{\Vert {\widehat{\beta }}_k\Vert }_T=0\}\le \frac{M_2{B}_1^2}{c_{\ast }N}.$$ (A.6)

By the definition of ξ₂ and the triangle inequality,

$$\begin{array}{cc}\hfill {\xi }_2^2& =\sum _{k\notin A_0}{\Vert {\beta }_k\Vert }_2^{2}I\{{\Vert {\widehat{\beta }}_k\Vert }_2=0\}\hfill \\ \hfill & \le \sum _{k\notin A_0}{({\Vert {\tilde{\beta }}_k-{\beta }_k\Vert }_2+{\Vert {\tilde{\beta }}_k\Vert }_2)}^{2}I\{{\Vert {\widehat{\beta }}_k\Vert }_2=0\}\hfill \\ \hfill & \le 2\sum _{k\notin A_0}{\Vert {\tilde{\beta }}_k-{\beta }_k\Vert }_2^{2}I\{{\Vert {\widehat{\beta }}_k\Vert }_2=0\}+2\sum _{k\notin A_0}{\Vert {\tilde{\beta }}_k\Vert }_2^{2}I\{{\Vert {\widehat{\beta }}_k\Vert }_2=0\}.\hfill \end{array}$$

From Lemma A.1, (A.6) and d_k ≥ 1, we have

$${\xi }_2^2\le 2{\left(\frac{M^2\rho q^{3∕2}}{n{c}_{\ast }}+\rho \sqrt{q}\right)}^2+2\frac{M_2{B}_1^2}{c_{\ast }N}.$$

This completes the proof of Theorem 1.

Proof of Theorem 2. From the proof of Theorem 1 and Theorem 2 of Wei and Huang (2008),

$${\Vert \widehat{\gamma }-\tilde{\gamma }\Vert }_2={\left(\sum _{k=1}^p{\Vert Q_k^{-1}({\widehat{\gamma }}_k^{\ast }-{\tilde{\gamma }}_k^{\ast })\Vert }_2^2\right)}^{1∕2}\le \frac{2\sigma \sqrt{M_1\text{log}{m}_{n}q}}{Q_b\sqrt{N{c}_{\ast }}}+\frac{\lambda d_b\sqrt{d{M}_{1}q}}{Q_{b}N{c}_{\ast }}.$$

By Lemma A.1 in Huang, Wu, and Zhou (2004), we know that, ${\Vert \widehat{\beta }-\tilde{\beta }\Vert }_2={\Vert \widehat{\gamma }-\tilde{\gamma }\Vert }_k\asymp {\Vert \widehat{\gamma }-\tilde{\gamma }\Vert }_2∕\sqrt{d_a}$. Then

$${\Vert \widehat{\beta }-\tilde{\beta }\Vert }_2\le \frac{2\sigma \sqrt{M_1\text{log}{m}_{n}q}}{Q_b\sqrt{d_{a}N{c}_{\ast }}}+\frac{\lambda d_b\sqrt{d{M}_{1}q}}{Q_b\sqrt{d_a}N{c}_{\ast }}.$$

By Lemma A.1, we know that ${\Vert \tilde{\beta }-\beta \Vert }_2\le M^2\rho q^{3∕2}∕\left(n{c}_{\ast }\left(\mid A_0^c\mid \right)\right)+\sqrt{q}\rho +\rho$. Thus

$${\Vert \widehat{\beta }-\beta \Vert }_2\le {\Vert \widehat{\beta }-\tilde{\beta }\Vert }_2+{\Vert \tilde{\beta }-\beta \Vert }_2\le \frac{2\sigma \sqrt{M_1\text{log}{m}_{n}q}}{Q_b\sqrt{d_{a}N{c}_{\ast }}}+\frac{\lambda \sqrt{d_b{M}_{1}q}}{Q_{b}N{c}_{\ast }}+(\frac{M^{2}q}{n{c}_{\ast }}+1)\sqrt{q}\rho +\rho .$$

This completes the proof of Theorem 2.

Proof of Theorems 3 and 4. Theorems 3 and 4 can be obtained directly from Theorems 3 and 4 of Wei and Huang (2008) and Lemma A.1 in Huang, Wu, and Zhou (2004); we omit the proofs here.