Accelerating free breathing myocardial perfusion MRI using multi coil radial k-t SLR

Abstract

The clinical utility of myocardial perfusion MR imaging (MPI) is often restricted by the inability of current acquisition schemes to simultaneously achieve high spatio-temporal resolution, good volume coverage, and high signal to noise ratio. Moreover, many subjects often find it difficult to hold their breath for sufficiently long durations making it difficult to obtain reliable MPI data. Accelerated acquisition of free breathing MPI data can overcome some of these challenges. Recently, an algorithm termed as k − t SLR has been proposed to accelerate dynamic MRI by exploiting sparsity and low rank properties of dynamic MRI data. The main focus of this paper is to further improve k − t SLR and demonstrate its utility in considerably accelerating free breathing MPI. We extend its previous implementation to account for multi-coil radial MPI acquisitions. We perform k − t sampling experiments to compare different radial trajectories and determine the best sampling pattern. We also introduce a novel augmented Lagrangian framework to considerably improve the algorithm's convergence rate. The proposed algorithm is validated using free breathing rest and stress radial perfusion data sets from two normal subjects and one patient with ischemia. k − t SLR was observed to provide faithful reconstructions at high acceleration levels with minimal artifacts compared to existing MPI acceleration schemes such as spatio-temporal constrained reconstruction (STCR) and k − t SPARSE/SENSE.

1. Introduction

Myocardial perfusion MRI (MPI) is a promising tool to non invasively detect and evaluate ischemic disease. The slow nature of MRI acquisitions often makes it difficult to simultaneously achieve high spatio-temporal resolution, good volume coverage, and high signal to noise ratio in MPI. Moreover, the breath hold demands during MPI are often long. This can be challenging for patients with arrhythmias, and/or impaired respiratory function, pediatric subjects, especially during stress. Accelerating free breathing MPI acquisitions can improve the above trade offs. In addition, acceleration can also enable high resolution systolic imaging and ungated imaging which have shown some advantages (Shin et al., 2010; Radjenovic et al., 2010; DiBella et al., 2012). Classical schemes to accelerate dynamic MRI exploit the redundancy of the dynamic data in the Fourier domain (spatial-spectral or (x − ƒ) space). Several such schemes such as k − t BLAST (Gebker et al., 2007 Dec) have been applied to improve breath held myocardial perfusion MRI. Multi-coil variants (Kellman et al., 2004; Plein et al., 2007), and compressed sensing schemes (Otazo et al., 2010) have also been developed. However, the direct extension of these schemes to operate in a free breathing regime is not straightforward. Specifically, the modulation of the signal by breathing motion significantly increases the temporal bandwidth, which reduces the x − ƒ space sparsity. This often limits the maximum achievable acceleration. One approach to address this is to use principal component models that adapt to the free breathing MPI signal. This allows the signal to be represented by fewer coefficients when compared to the classical model based x − ƒ approaches, hence permitting signal reconstruction at higher accelerations. The early versions of these schemes relied on a two-step reconstruction strategy (eg:(Liang, 2007),(Pedersen et al., 2009)). These methods first estimate the temporal basis functions (or the principal components) from fully sampled low resolution “training data” using principal component analysis (PCA). In the second step, they estimate the coefficients of these temporal basis functions by fitting the model to the undersampled k-space measurements. The main challenge with these two-step schemes is that they are associated with trade-offs between the sampling density in central and higher k-space regions, which manifests as a compromise between accurate modeling of temporal dynamics and efficient suppression of spatial artifacts (Lingala et al., 2011).

The above mentioned two-step PCA-based methods have been recently reinterpreted as heuristic algorithms to recover a low rank matrix from its undersampled measurements. This reinterpretation has allowed the introduction of efficient single-step recovery schemes (eg. incremented rank power factorization (IRPF) algorithm (Haldar and Liang, 2010) and the spectral regularization framework (Lingala et al., 2011). Since these methods simultaneously estimate the temporal basis functions and their coefficients from undersampled data, they are capable of overcoming the trade-offs associated with earlier two step schemes. More importantly, these algorithms are readily applicable to flexible sampling schemes such as the use of radial or spiral trajectories, which are demonstrated to have several advantages. (Shin et al., 2012; Adluru et al., 2009). We have shown that the joint use of the total variation (TV) prior (as a sparsity penalty) along with the spectral prior (as a low rank penalty) further improves the reconstructions (Lingala et al., 2011); the resulting algorithm was termed as k − t SLR since it exploits the sparsity and low rank properties of dynamic data. Our studies in (Lingala et al., 2011) however were based on retrospective resampling of a single coil Cartesian MPI dataset. In this paper, we exploit the full power of the k−t SLR algorithm by (a) extending it to account for multi-coil acquisitions and to handle different weights for TV in space and time as done in (Adluru et al., 2009), (b) using radial k-space acquisitions, and (c) introducing a novel augmented Lagrangian optimization framework to significantly improve the convergence rate. To exploit the flexibility offered by radial sampling, we customize the sampling pattern to the proposed algorithm using k − t radial sampling experiments on multi-coil data. We use the improved k − t SLR algorithm to achieve quality reconstructions from undersampled radial free breathing MPI datasets. Such acceleration will enable the improvement of volume coverage. We design an experimental paradigm wherein accelerated reconstructions are performed with the multi-coil k − t SLR algorithm by considering subsets of the acquired radial data. The reconstructions are tested by comparisons against the reference fully sampled datasets. We base our studies on rest and adenosine stress datasets acquired from two normal subjects and one patient with myocardial ischemia. We compare the k − t SLR reconstructions with STCR (spatio-temporal constrained reconstruction) and k − t SPARSE with SENSE.

2. Theory

2.1. Low rank model representation

In first pass myocardial perfusion imaging, the temporal profiles of pixels corresponding to specific anatomic regions (eg. myocardium, blood pool) are highly correlated. Hence, the temporal profiles of the pixels in the dynamic dataset γ(x, t) can be expressed as a weighted linear combination of few temporal basis functions υ_i(t):

$$\gamma (\mathbf{x},t)=\sum _{i=0}^{r-1}{\rho }_i(\mathbf{x}){\upsilon }_i(t);r<<n,$$ (1)

where ρ_i(x) represents the model coefficients and n the number of time frames. r is the number of temporal basis functions and x = (x, y) is the spatial location. This model thus accounts for the similarity between the time profiles of pixels in specific anatomic regions. The above model implies that the temporal profiles of the pixels lie in a low-dimensional space, which is equivalent to imposing a low-rank constraint on the Casorati matrix Γ (Liang, 2007) (see Fig. 1 and Eq. 2). The columns of Γ corresponds to the images at different time instants, while each row of Γ is the temporal profile of the corresponding pixel:

Figure 1.

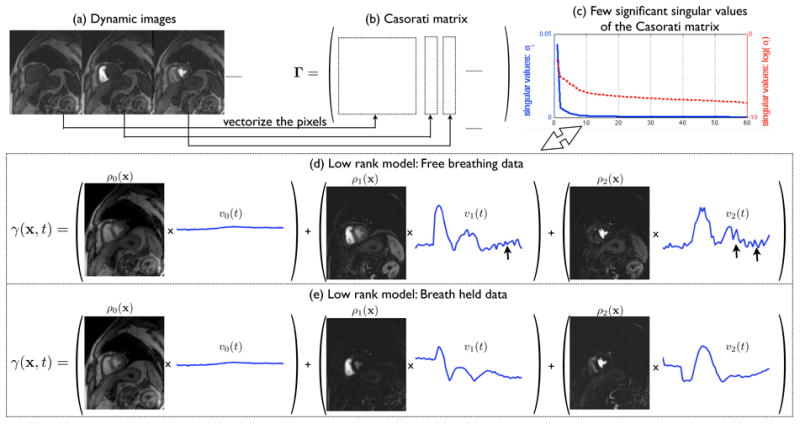
The low rank Casorati matrix representation of dynamic data: The pixels in each spatial frame of the dynamic data (a) are vectorized and represented column wise in the Casorati matrix (b). This matrix is low rank (c) which enables the decomposition of the dynamic data as a linear combination of few data derived orthogonal temporal bases (Eq. 1). Note from (d) and (e), how the bases adapt to model the respiratory motion in the free breathing data (see arrows in (d) that correspond to motion). Also note that the number of bases will increase with the motion induced temporal variations.

$${\mathbf{\Gamma }}_{m\times n}=\left(\begin{array}{ccccc}\gamma ({\mathbf{x}}_0,t_0)& \cdot & \cdot & \cdot & \gamma ({\mathbf{x}}_0,t_{n-1})\\ \gamma ({\mathbf{x}}_1,t_0)& \cdot & \cdot & \cdot & \gamma ({\mathbf{x}}_1,t_{n-1})\\ \cdot & \cdot & \cdot & \cdot & \cdot \\ \gamma ({\mathbf{x}}_{m-1},t_0)& \cdot & \cdot & \cdot & \gamma ({\mathbf{x}}_{m-1},t_{n-1})\end{array}\right);$$ (2)

where m denotes the number of voxels in each frame, and n is the total number of time frames. The correlations among the pixel time series result in linear dependencies between the rows of Γ thus resulting in the matrix having a low rank specified by r. Fig. 1 shows the low rank model representations of fully sampled free breathing and breath held MPI datasets. Note that the model is capable of adapting to motion induced intensity variations in the free breathing data. Furthermore, it is also important to note that the number of basis functions required to accurately represent the signal will increase with the motion-induced temporal variations. The proposed k − t SLR algorithm jointly estimates the temporal basis functions υ_i (t) and the spatial weights (ρ_i(x)) in Eq. 1 from the undersampled k − t measurements in an iterative framework by solving a spectrally regularized problem; this will be described in the next section.

2.2. Radial k − t SLR with parallel imaging

The undersampled radial acquisition of sensitivity weighted dynamic perfusion images can be modeled as: b = (Γ) + n, where b is a concatenated vector containing the measured non-Cartesian noisy k − t measurements for each coil. n is the additive white noise. Γ is the m × n Casorati matrix containing the dynamic data as defined in Eq. 2 (m is the total number of pixels in a frame and n is the number of time frames). The operator models the coil sensitivity encoding as well as Fourier encoding on the specified radial trajectory. We determine the radial sampling pattern that provides the best recovery with the k − t SLR algorithm based on k − t sampling experiments using multi-coil data (section 3.3); specifically, we employ a sampling scheme with golden ratio spacing between successive radial rays.

We formulate the recovery of Γ as a spectral and sparsity regularized optimization problem (Fig.2):

Figure 2.

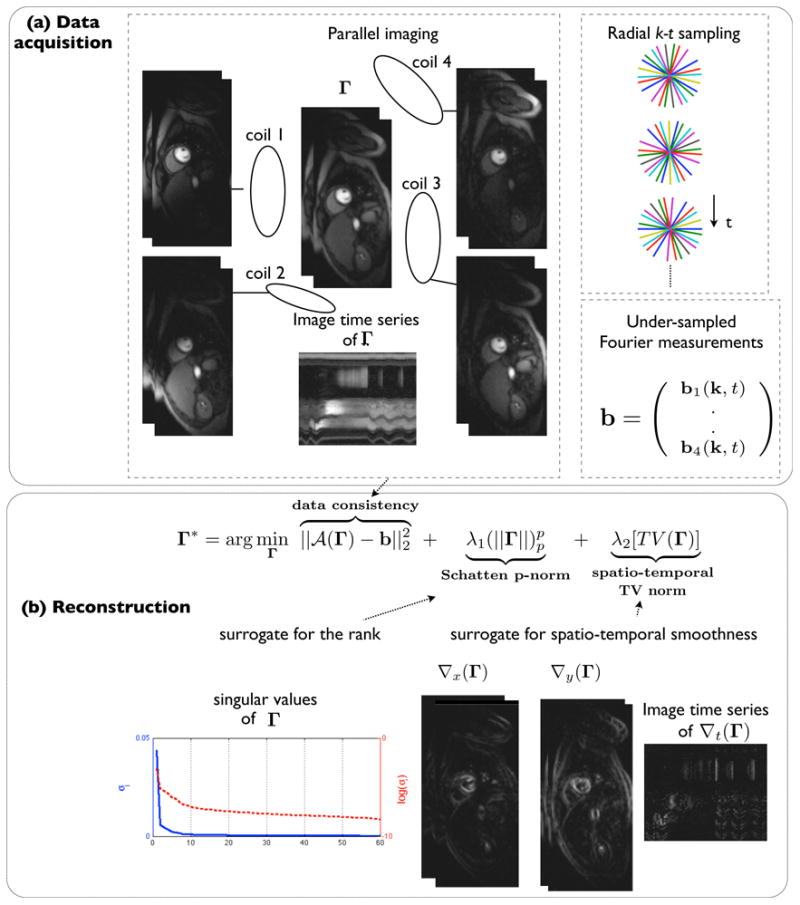
k−t SLR with parallel MRI for accelerated imaging: The perfusion images are acquired using multiple coils and radial sampling with golden angle ray spacing (a). k − t SLR exploits the low rank and smooth spatio-temporal properties of perfusion data by utilizing the non-convex Schatten p-norm (p<1) and the spatio-temporal total variation norm (b). The reconstruction in (b) is formulated as a spectral and sparsity penalized optimization problem; the coil sensitivity encoding in combination with radial sampling improves data consistency in the formulation.

$${\mathbf{\Gamma }}^{\ast }=arg\underset{\mathbf{\Gamma }}{min}\underset{\text{data consistency}}{\underbrace{\parallel \mathcal{A}(\mathbf{\Gamma })-\mathbf{b}{\parallel }_2^2}}+\underset{\text{Schatten p-norm}}{\underbrace{{\mathrm{\lambda }}_1\mathrm{\Phi }(\mathbf{\Gamma })}}+\underset{\text{spatiotemporal TV norm}}{\underbrace{{\mathrm{\lambda }}_2\mathrm{\Psi }(\mathbf{\Gamma })}}.$$ (3)

Here, the non-convex Schatten p-norm Φ(Γ) is the surrogate for the rank defined as:

$$\mathrm{\Phi }(\mathbf{\Gamma })={(\parallel \mathbf{\Gamma }{\parallel }_p)}^p=\sum _{j=0}^{n-1}{\sigma }_j^p;p<1;$$ (4)

where σ_j are the singular values of Γ (elements of the diagonal matrix Σ_n×n) in the singular value decomposition: $\mathbf{\Gamma }={\mathbf{U}}_{m\times n}{\sum }_{n\times n}{\mathbf{V}}_{n\times n}^H$. Ψ(Γ) is the spatio-temporal total variation norm and is the surrogate for spatio-temporal smoothness of Γ defined as :

$$\mathrm{\Psi }(\mathbf{\Gamma })={\Vert \sqrt{|{\nabla }_x(\mathbf{\Gamma }){|}^2+|{\nabla }_y(\mathbf{\Gamma }){|}^2+\alpha |{\nabla }_t(\mathbf{\Gamma }){|}^2}\Vert }_1;$$ (5)

where ∇_x, ∇_y, ∇_t are the difference operators along the x, y and t dimensions. The factor α ≥ 1 controls the relative weight of the temporal and spatial gradients, and ‖‖₁ denotes the ℓ₁ norm. λ₁ and λ₂ in Eq. 3 are the regularization parameters that control the balance between the two norms and the data fidelity.

2.3. Fast augmented Lagrangian (AL) algorithm

The penalty terms in Eq. 3 are non-differentiable. Hence, the use of gradient based schemes to solve Eq. 3 will result in prohibitively slow convergence. In addition, since a non-convex spectral penalty is used, this approach can result in the solution being trapped in the local minima of the criterion. To overcome these problems, we employ an augmented Lagrangian (AL) optimization algorithm with continuation (Ramani and Fessler, 2011).

A variable splitting technique is used to reformulate the unconstrained optimization problem in Eq. 3 to the constrained optimization problem in Eq. 6. This splitting enables us to decouple the non-quadratic penalties from the quadratic data term; the complex problem is decoupled into a sequence of simpler subproblems.

$$arg\underset{\mathbf{\Gamma },\mathbf{S},\mathbf{T}}{min}\parallel \mathcal{A}(\mathbf{\Gamma })-\mathbf{b}{\parallel }_2^2+{\mathrm{\lambda }}_1{(\parallel \mathbf{S}{\parallel }_p)}^p+{\mathrm{\lambda }}_2{\Vert \sqrt{{|{\mathbf{T}}_1|}^2+{|{\mathbf{T}}_2|}^2+\alpha {|{\mathbf{T}}_3|}^2}\Vert }_1;$$ (6)

$$\begin{array}{l}\text{subject to}.,\mathbf{\Gamma }=\mathbf{S};\underset{\mathbf{T}}{\underbrace{\left[\begin{array}{c}{\mathbf{T}}_1\\ {\mathbf{T}}_2\\ {\mathbf{T}}_3\end{array}\right]}}=\underset{\nabla .\mathbf{\Gamma }}{\underbrace{\left[\begin{array}{c}{\nabla }_x(\mathbf{\Gamma })\\ {\nabla }_y(\mathbf{\Gamma })\\ {\nabla }_t(\mathbf{\Gamma })\end{array}\right]}};\end{array}$$

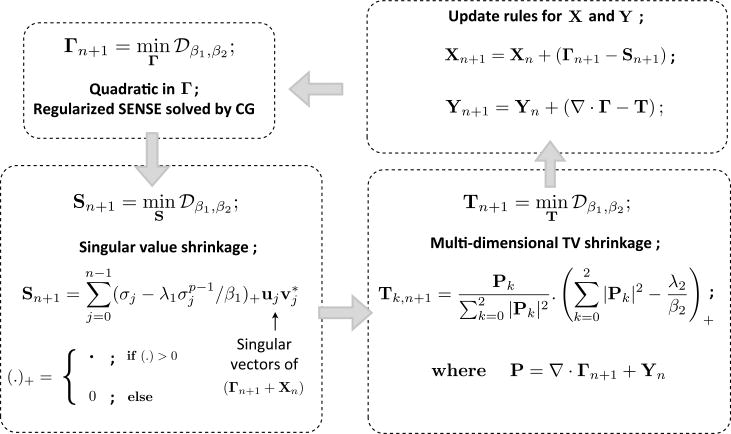
We now use the AL method to solve the above constrained optimization problem. Specifically, the constraints are enforced using quadratic penalty terms and Lagrange multiplier terms X and Y, as shown in the appendix. The strength of the quadratic penalty terms are specified by β₁ and β₂, respectively. The main benefit in using the AL scheme is that β₁ and β₂ does not have to be taken to ∞ to enforce the constraints; the algorithm converges slowly when β₁ and β₂ are high. We show in the appendix that the AL scheme simplifies to the algorithm shown below (also illustrated in Fig. 9). Note that the algorithm involves the alternation between simple steps, which are implemented efficiently. The pseudo code of the algorithm is given below:

Figure 9.

The augmented Lagrangian frame work with the different sub problems. The original problem in (3) is broken into a series of multiple simpler problems by using the augmented Lagrangian framework. Specifically, the algorithm iterates between the steps of regularized SENSE (that is solved by the method of conjugate gradient (CG)), singular value shrinkage, shrinkage and update rules for Lagrange multipliers. These steps are all solved by simple operations.

Initialization: ${\mathbf{\Gamma }}_0={\mathcal{A}}^T(\mathbf{b}),{\beta }_1=\frac{1}{max({\sum }_0)},{\beta }_2=\frac{1}{|max({\mathbf{\Gamma }}_0)|}$; Σ₀ is a matrix containing the singular values of Γ₀;

while (|costn − costn−1|/|costn| < 10−6) ; stopping rule (cost as defined in Eq. (3);

Γn ←(A.1); regularized SENSE problem solved by conjugate gradients;

Sn ←(A.2); singular value shrinkage;

Tn ←(A.3); total variation shrinkage;

Xn ←(A.4); linear update rule;

Yn ←(A.5); linear update rule;

if (|costn − costn−1|/|costn| < 10−1)

β1 = β1 * 1.2, β2 = β2 * 1.2; continuation

end

end

The algorithm employs a continuation strategy where the β₁, β₂ parameters are initialized to small values, and are gradually incremented when the cost in Eq. (3) stagnates to a threshold level of 10⁻¹. This strategy is similar to homotopic like continuation schemes employed to solve non convex problems (Trzasko and Manduca, 2009). We observed the continuation scheme to be a key aspect in avoiding convergence to local minima solutions. The proposed algorithm was implemented on a desktop system with 47 GB RAM, 24 core Intel Xenon E5645 2.4 GHz processors, an NVDIA Tesla C2075 (5 GB RAM) graphical processing unit, and Matlab R2012a 64 bit with Accelereyes Jacket v2.2. Jacket is a library that enables computations on the GPU within Matlab using NVIDIA CUDA. Thanks to the fast convergence of the AL scheme and the fast GPU computations, the reconstructions of large multi-coil data sets (of sizes: [N_x × N_y × N_t × L : 256 × 256 × 60 × 4]) with the k − t SLR algorithm takes about 1-2 minutes of run time. In this work we considered pre-interpolation of the radial data onto Cartesian grid points that were within 0.5 unit of a measured sample. This facilitated the use of Fast Fourier Transforms (FFTs) in the forward and backward models of the iterative algorithm. We did not observe any noticeable change in the quality of the reconstructions by using the preinterpolated data with FFTs when compared to using the nonuniform radial data with NUFFTs, INUFFTs in the iterative algorithm, as also noted in (Adluru et al., 2009) .

3. Materials and Methods

3.1. Multi-coil radial acquisition of free breathing myocardial perfusion data

Two normal subjects and one patient with cardiac disease were scanned at the University of Utah, in accordance with the institutional review board. Data was acquired with a perfusion radial FLASH saturation recovery sequence (TR/TE ≈ 2.6/1.2 ms, 3 slices per beat, flip angle of 14 degrees, 2.3 × 2.3 × 8 mm voxel size, FOV: 280 mm², Bandwidth 1002 Hz/pixel) on a Siemens 3T Trio scanner (DiBella et al., 2011). 72 radial rays equally spaced over π radians and with 256 samples per ray were acquired for a given time frame and a given slice. These rays were acquired in an interleaved manner in subsets of 6 rays each. The rays in successive frames were rotated by a uniform angle of π/288 radians, which corresponded to a period of 4 across time (see Fig. 4) . Data was acquired with the Siemens cardiac coil array and combined into four coils. For coil sensitivity estimation, the complex valued k space measurements from each coil were averaged along time. From the resultant time averaged image data, the complex valued sensitivity estimates were obtained by dividing each component coil image by the root of sum of absolute squared intensities from all the coils.

Figure 4.

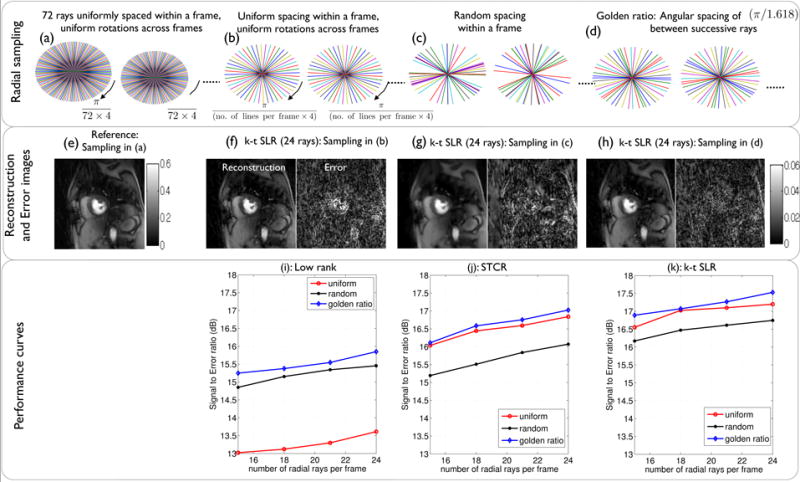
Performance of different radial sampling schemes: The different k − t radial sampling schemes along with the corresponding reconstructions are respectively shown in the first and second rows. The third row shows the signal to error ratio plots for the reconstruction algorithms at different acceleration rates. As seen from the third row, the golden ratio sampling gave the best performance with all the algorithms. From the second row, with k − t SLR, uniform sampling was suboptimal as the conditions of incoherent sampling were not met. Random sampling was suboptimal since some regions of k-space are under-sampled. The golden ratio sampling satisfied the requirements of incoherency and uniformity and was found to be optimal.

Rest data sets were acquired after a Gd bolus administration of 0.02 mmol/kg. Stress data sets were acquired with an adenosine infusion, where 0.03 mmol/kg of Gd contrast agent was injected after 3 minutes of infusion. A total of three rest and three stress data sets were used in this study. A SENSE based reconstruction with mild regularization based on spatio-temporal total variation (TV) constraints was used to resolve residual aliasing in the acquired data. The regularized SENSE reconstructions still contained background noise which was denoised by using a block matching 4-D (BM4D) denoising filter (Maggioni et al., 2011) - these denoised images formed the reference datasets.

3.2. Undersampled reconstruction with different algorithms

The acquisition described in the previous section had a compromise in the slice coverage (3 slices). In order to demonstrate that the slice coverage of such an acquisition could be further increased, retrospective accelerated experiments were performed. Undersampled reconstructions were performed by different reconstruction algorithms by considering subsets of the measured data. Specifically, the performance of the k − t SLR, STCR (Adluru et al., 2009), low rank, and k − t SPARSE/SENSE (Otazo et al., 2010) algorithms were compared. The comparisons were done at various acceleration levels by considering different numbers of subsets of the measured data that used 24 to 15 rays/frame. The quality of these reconstructions were evaluated against the above reference datasets. All the algorithms relied on the knowledge of coil sensitivities. STCR was implemented by considering λ₁ = 0 in k − t SLR. The low rank penalty based reconstruction was implemented by considering λ₂ = 0 in k − t SLR. k − t SPARSE/SENSE was implemented by minimizing the l₁ norm of the signal in the spatial-spectral (x − f) space. All the algorithms were optimized for the regularization parameters that gave the maximum signal to error ratio (SER) between the reconstructions and the reference data:

$${\text{SER}}_{\text{ROI}}=-10{log}_{10}\frac{{\displaystyle {\sum }_{i=1}^n\left(\frac{\parallel {\mathbf{\Gamma }}_{\mathbf{\text{recon}},i}-{\mathbf{\Gamma }}_{\mathbf{\text{ref}},i}{\parallel }_F^2}{\parallel {\mathbf{\Gamma }}_{\mathbf{\text{ref}},i}{\parallel }_F^2}\right)}}{n};$$ (7)

where n is the number of time frames. During this optimization, the SER_ROI metric was evaluated only in a field of view that contained regions of the heart. This was motivated by recent findings in (Bilen et al., 2010), and by our own experience in determining a quantitative metric that best describes the accuracy in reproducing the perfusion dynamics in different regions of the heart, and the visual quality in terms of preserving crispness of borders of heart, and minimizing visual artifacts due to reconstructions. The details of optimization of the regularization parameters in this work are described in the appendix section.

3.3. Simulations to determine an optimal radial sampling trajectory

The quality of the reconstructed data is dependent on the specific sampling strategy. With the objective of choosing a radial pattern that provides good recovery, the performance of different sampling trajectories were studied. As described in section 3.1, the reference 72 ray data sets were acquired using radial rays uniformly spaced within each frame, and uniform rotations across frames. To simulate undersampling, subsets of the acquired data were chosen based on the following three families of radial sampling trajectories (see Fig. 4):

1. uniform spacing of radial rays within a frame, with uniform rotations across frames.

2. completely random spacing of radial rays within a frame.

3. golden ratio spacing of (π/1.618) between successive rays⁺.

The performance of the low rank, STCR, k − t SLR reconstruction algorithms were compared with each of the above sampling scenarios. The performance was studied at different undersampling factors by considering 24, 21,18, 15 rays/frame.

3.4. Metrics used for quantitative comparison

The reconstructions of the different algorithms were quantitatively compared based on the following three metrics (also see Fig. 7)

Figure 7.

Quantitative comparison of reconstructions from undersampled radial data (21 rays/frame) using different algorithms.

• Signal to Error ratio in a region of interest containing the heart (SER_ROI): As described in Eq.(7), this metric gives a measure of overall accuracy in reproducing the spatio-temporal dynamics in the regions of the heart.

• Normalized high frequency error metric (HFEN): The HFEN metric gives a measure of the quality of fine features, edges, and spatial blurring in the images. We adapt this metric from (Ravishankar and Bresler, 2011) which is defined as:

  $${\text{HFEN}}_{\text{ROI}}=-10{log}_{10}\frac{{\displaystyle {\sum }_{i=1}^n\left(\frac{\parallel LoG({\mathbf{\Gamma }}_{\text{ref},\mathrm{i}})-LoG({\mathbf{\Gamma }}_{\text{recon},\mathrm{i}}){\parallel }_2^2}{\parallel LoG({\mathbf{\Gamma }}_{\text{ref},\mathrm{i}}){\parallel }_2^2}\right)}}{n},$$ (8)

  where LoG is a Laplacian of Gaussian filter that capture edges. We use the same filter specifications as in (Ravishankar and Bresler, 2011): kernel size of 15 × 15 pixels, with a standard deviation of 1.5 pixels. We evaluate this metric in a square region of interest containing the heart.

• Signal to error ratio of temporal curves in the left ventricle (SER_TC): This metric gives a measure of accuracy in reproducing the temporal dynamics in the left ventricular blood pool and myocardium. It also quantifies temporal blurring. To evaluate this metric consistently, the reference data sets were initially registered to estimate the deformation maps that correspond to breathing motion. For registration, we employed the non-rigid demons registration algorithm (Thirion, 1996) using the normalized cross correlation as the similarity metric. Starting from the second frame, the deformations were obtained by matching the n^th frame in the moving sequence to the (n − 1)^th frame of the deformed sequence. The deformation maps were used to warp the reconstructions, after which the time intensity profiles in the region of interest of left ventricular blood pool and myocardium region of interests were evaluated. The SER_TC metric is evaluated as:

  $${\text{SER}}_{\text{TC}}=-10{log}_{10}\frac{{\displaystyle {\sum }_{i=1}^k\left(\frac{\parallel \text{TC}(\mathcal{W}.{\mathbf{\Gamma }}_{\text{ref},\mathrm{i}})-\text{TC}(\mathcal{W}.{\mathbf{\Gamma }}_{\text{recon},\mathrm{i}}){\parallel }_2^2}{\parallel \text{TC}(\mathcal{W}.{\mathbf{\Gamma }}_{\text{ref},\mathrm{i}}){\parallel }_2^2}\right)}}{k},$$ (9)

  where TC is an operator that extracts the time curves for a specified pixel in the left ventricle; k is the total number of pixels in the left ventricle. 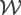is an image warping operator that applies the deformation maps corresponding to breathing motion to the reconstructions.

3.5. Qualitative evaluation: clinical scoring

In addition to the quantitative validation, we also performed a qualitative analysis by obtaining clinical scores from a cardiologist with 15 years of cardiac MRI experience. Image quality and artifact assessment was performed on the reference images reconstructed from the 72 ray acquisition, and on the k − t SLR images reconstructed from 24 ray subsampled data. The grading scale was (5-1, highest quality to lowest quality). All the images were presented as 4 image sets with each set containing time series of 3 slices for both stress and rest. Image sets from a patient with decreased perfusion and from two normal subjects were presented to the cardiologist in a blinded fashion in a random order.

4. Results

4.1. Convergence analysis

In Fig.3, the convergence behavior of the k − t SLR algorithm is shown. Here, undersampled reconstructions were performed with golden ratio sampling using 24 rays/frame. As seen in Fig.3, our previous implementation of k − t SLR (Lingala et al., 2011) that relied solely on the increments of (β₁, β₂ towards ∞) had a slow convergence. In contrast, the proposed AL method had a faster convergence, and did not require high values of β₁, β₂ for convergence. The initial values of the continuation parameters were {β₁, β₂ = 10³,10⁵}, while the final values (at convergence) with and without AL respectively were: {β₁, β₂ ≈ 10⁶,10⁸}, {β₁, β₂ ≈ 10⁹,10¹¹}. From Fig.3, it can also be seen that the streaking artifacts were fully resolved with the proposed k-t SLR algorithm.

Figure 3.

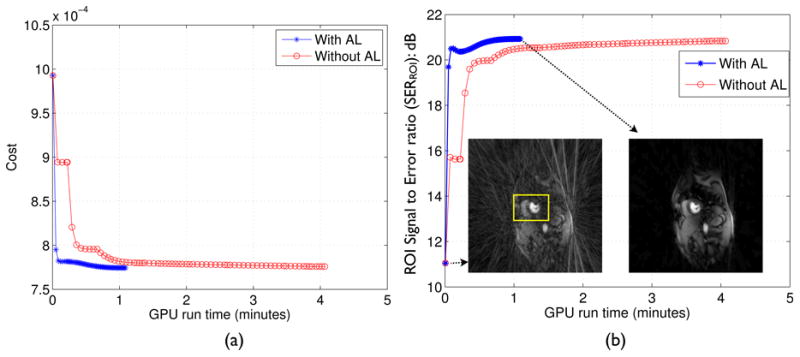
Convergence analysis: (a) Cost in Eq.3 v/s GPU run time, (b) Region of interest signal to Error ratio (SER_ROI) as defined in Eq.7 in (dB) v/s GPU run time. From (a), (b), it can be seen that k − t SLR has a faster convergence (by a factor of 4) with the augmented Lagrangian (AL) algorithm in comparison to the previous implementation without the Lagrange multiplier updates. The converged reconstruction in (b) show that the radial streaking artifacts are fully resolved. The SER_ROI is evaluated in a square region of interest containing the heart as depicted in (b).

4.2. Simulations to determine an optimal radial trajectory

The comparisons of different radial sampling methods are shown in Fig. 4. From the SER plots, it is observed that the low rank method does not perform as well with uniform sampling. This is expected since uniform sampling results in more repeated k-space measurements at the same locations in k-space and has less incoherency. In contrast, the STCR method is insensitive to the pattern, as long as the completely random pattern is not used. When the low rank and total variation penalties are merged into k − t SLR, the golden ratio patterns provide better results than the completely random sampling pattern or the uniform pattern. This observation is consistent with the findings reported in the context of standard compressed sensing (Chan et al., 2011),(Vasanawala et al., 2011). From these simulations, the golden ratio sampling pattern was found to be optimal, and therefore was used for undersampling in all the algorithms.

4.3. k − t SLR compared to other MPI acceleration schemes

In Fig. 5, the comparisons of MPI reconstructions using different algorithms from 21 ray undersampled data are shown. These comparisons are from a rest acquisition on a normal subject with breathing motion. The k − t SPARSE/SENSE method was observed to be sensitive to the breathing motion, and yielded motion related artifacts as depicted both in the temporal curves and the error images of Fig. 5 (b). The low rank reconstruction was more robust to breathing motion, when compared to k − t SPARSE/SENSE. However, it had poor temporal fidelity especially during the contrast uptake frames. This is depicted from temporal curve blurring during contrast uptake, and also in the error images of Fig. 5(c). STCR had better temporal fidelity, thus preserving contrast dynamics and motion. However edge blurring and patchy artifacts were evident. The k − t SLR algorithm preserved the temporal fidelity and had less smoothing of edges and less patchy artifacts as depicted in Fig. 5(e). From this figure, it is also observed that the performance of k − t SLR is comparable to that of STCR in the frames corresponding to contrast uptake. This is expected since the presence of contrast makes the images more or less piece wise constant and the SNR high. However, k − t SLR provides better suppression of artifacts in the pre and post contrast frames. Additionally, from Fig.5, it can be seen that the quantitative metrics correlate well with the visual comparisons. Specifically in comparison to k − t SLR, the SER_TC metric were low with the k − t SPARSE/SENSE and low rank methods due to temporal blurring, while the HFEN_ROI metric in STCR was low due to spatial smoothing. The SER_ROI metric was higher with k − t SLR than the other algorithms due to a better overall image quality.

Figure 5.

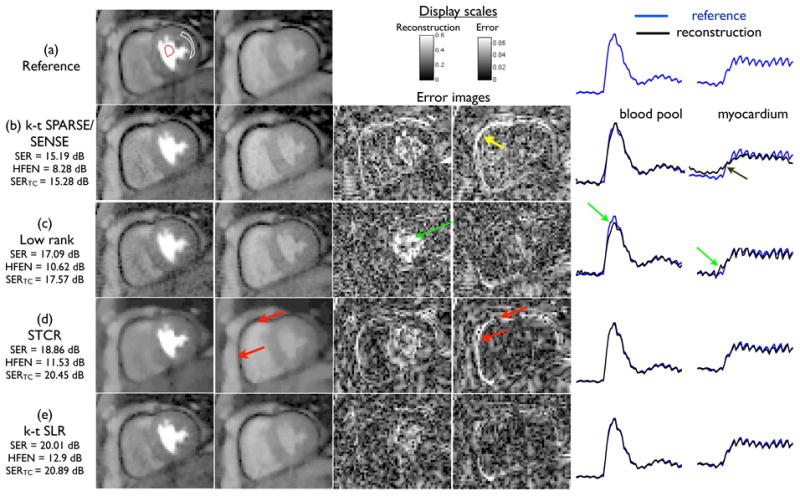
Comparisons of different MPI algorithms on a rest dataset with breathing motion. Each row shows the reconstructions, error images and time profile curves for the different algorithms. The image frames in the first and second columns respectively correspond to the peak left ventricular blood enhancement, and peak myocardial wall enhancement instants. The time curves are shown after averaging the signal intensity of the blood pool and myocardial regions (as denoted in (a)) for the registered reconstructions overlaid on the registered reference data. The k − t SPARSE/SENSE method was sensitive to motion and resulted in temporal blurring (see arrows in (b)). The low rank model yielded noise enhancement and temporal blur due to ill-conditionness (arrows in (c)). STCR was relatively robust to motion, however suffered from loss of resolution especially near the edges (see arrows in (d)). k − t SLR was found to maintain a good compromise between spatial and temporal blurs.

In Fig. 6, the comparisons of the algorithms on rest and stress data sets from a patient with ischemia are shown. Under stress conditions, this patient exhibited a reduction in the uptake of the contrast dynamics in the inferior wall of the myocardium. The patient was able to breath normally during rest, however breathed heavily during stress. The reconstructions are shown using 21 radial rays/frame. We observed similar trade offs amongst the methods. Specifically, k − t SPARSE was sensitive to breathing, and the low rank method yielded reduced temporal fidelity during contrast uptake. STCR showed patchy artifacts in some frames, but was robust to motion. k − t SLR was robust to motion and had less patchy artifacts. Similar to Fig. 5, all the quantitative metrics correlate well with the visual observations.

Figure 6.

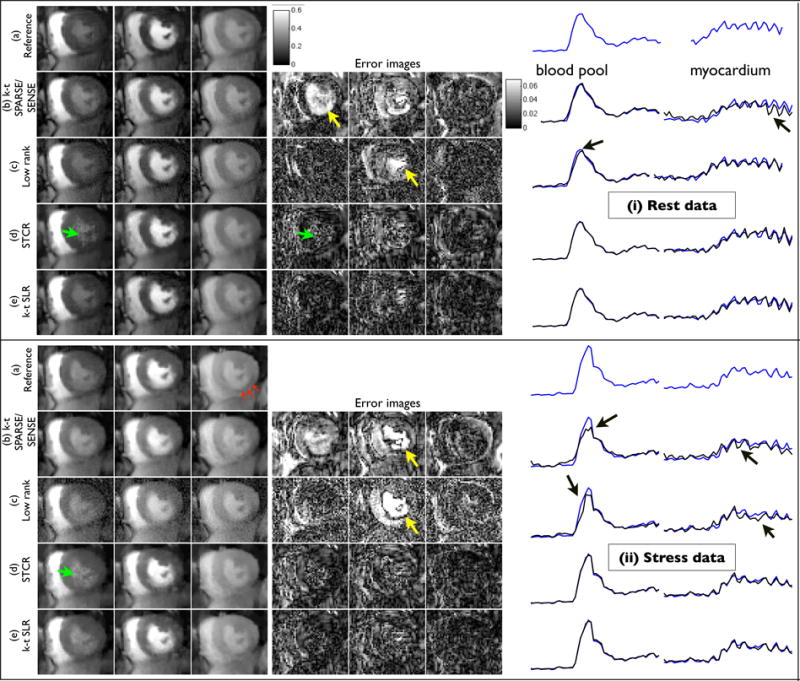
Example comparisons of different MPI acceleration algorithms using rest (i) and stress (ii) perfusion data from a patient with myocardial ischemia. The image frames in the first three columns respectively correspond to peak right ventricular blood enhancement, transition between right ventricle and left ventricle, and peak myocardial wall enhancement. During stress, the patient showed reduced contrast uptake in the inferior myocardium wall due to ischemia (see red arrows in (ii.a)). The time curves correspond to the regions depicted in i.a, ii.a). The k − t SLR reconstructions were observed to be less sensitive to artifacts observed with other methods. Specifically k-t SPARSE/SENSE yielded motion blur artifacts (see arrows in i.b, ii.b, and the time curves), low rank method had some temporal blur especially during peak contrast frames (see arrows in ii.c, ii.d, and the time curves). STCR exhibited patchy artifacts (see arrows in (i.d) and (ii.d)). k − t SLR had better quality across all frames in comparison to the other methods. We also observe that the regions of low contrast uptake to be well preserved in the k-t SLR reconstructions.

Figure.7 summarizes the quantitative comparisons of all the algorithms across all the datasets using 21 rays/frame. From this figure, it is observed that the performance of k − t SLR was consistently better than the other algorithms across all the datasets.

4.4. Qualitative evaluation by a cardiologist

The clinical scores are presented in table 1. With the patient, the clinician was able to identify the ischemia in the inferior myocardium wall in both the reference and k − t SLR reconstructions (see Fig. 8). More specifically, he confidently identified reduced blood flow in both the rest and stress scans of the reference data set. With the k − t SLR images, he found the ischemic defect to be evident in the stress reconstruction, and border line positive in the rest reconstruction. After looking at the delayed enhancement images, the clinician classified these ischemic regions as infarction. With the normal subjects, the quality scores of the k − t SLR reconstructions were in close agreement with the reference images. No dark rim artifacts were observed in all the images. Slight residual streaking artifacts were present with the k − t SLR method in one of the normal subjects. However, these artifacts were outside the field of view of the heart, which the cardiologist was not very concerned about.

Table 1. Quality scores from a cardiologist on three subjects.

Subject id	Reconstruction	Rest	Stress	Presence of disease
		Quality score	Quality score
Subject 1	Reference	4	4	positive
Subject 1	k−t SLR	4	4	positive
Subject 2	Reference	4	4	negative
Subject 2	k−t SLR	3.75	3.75	negative
Subject 3	Reference	4	4	negative
Subject 3	k−t SLR	4	4	negative

Figure 8.

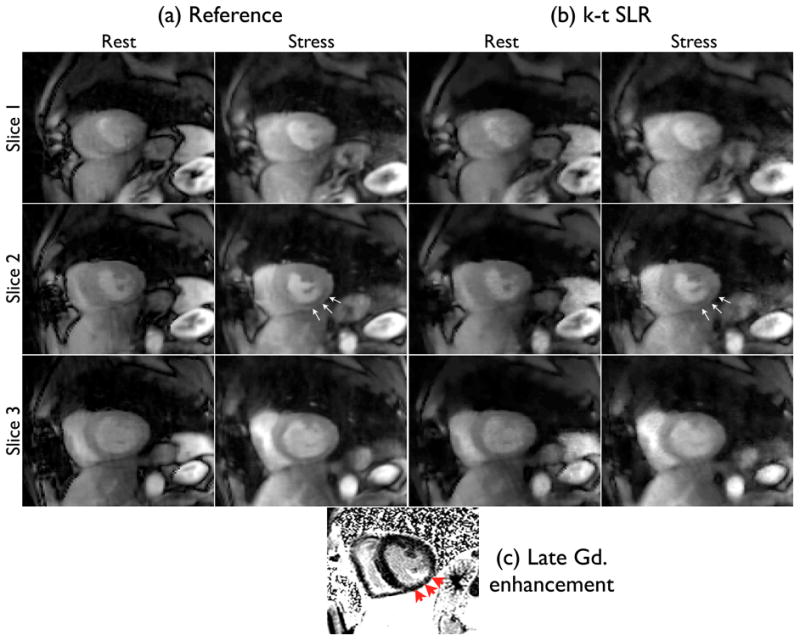
Peak myocardial wall enhancement images from (a) reference (72 rays/frame), and (b) k−t SLR (24 rays/frame) reconstructions. Subtle ischemic areas were identified by the cardiologist in the inferior myocardial wall on the second slice in both the reconstructions (see arrows in a,b). These regions were subsequently classified as infarcted regions from the gadolinium enhancement observed in the delayed enhancement image (c).

5. Discussion

In this study, the feasibility of k − t SLR in providing robust free breathing MPI reconstructions at high acceleration levels was evaluated. This study considered retrospectively accelerating free breathing MPI datasets that were acquired using 72 radial rays/frame at 2.3 mm² in plane resolution and 3 slices. The results of obtaining good fidelity k − t SLR reconstructions from highly undersampled data suggest that k − t SLR could be used to improve the slice coverage and the spatial resolution in a prospective acquisition. For a reliable quantification of perfusion parameters from free breathing MPI data, it should be noted that the breathing motion should be compensated. In this work, we used a basic non-rigid registration algorithm to correct for the breathing motion, and analyzed the temporal curves in the registered reconstructions. The results show that the temporal profiles from the undersampled k − t SLR reconstructions match well with the temporal profiles from the reference reconstructions. This suggests that the good temporal fidelity of the k − t SLR reconstructions may lead to reliable estimation of quantitative perfusion parameters.

All the reconstruction algorithms considered in this work were based on nonlinear reconstruction strategies. Unlike the classical linear k-t reconstruction strategies, the performance of these algorithms cannot be characterized by a single point spread function (Blaimer et al., 2011). To analyze the performance of the nonlinear algorithms, this study relied on quantitative metrics that gave a measure of overall spatio-temporal fidelity, image sharpness, and temporal accuracy. Our comparisons against MPI accelerated schemes show that the k − t SLR scheme is capable of reducing motion blurring and edge smoothing artifacts. In general, the k − t SLR algorithm benefited from total variation sparsity regularization in being robust to temporal and spatial smoothing. The STCR method performed well in regions where the signal was piece wise constant both spatially and temporally - or equivalently during peak contrast frames and datasets with less motion. However, it was observed during the pre and post contrast frames, STCR yielded patchy artifacts and edge blurring. In such scenarios, k − t SLR provided more robust and natural textures and less edge blurring. During the peak contrast frames, the use of the low rank regularizer alone yielded temporal blur, which was minimized with k − t SLR.

During this study, we observed that performance evaluation using the noisy SENSE based reconstructions as reference datasets were not conclusive since the noise in these reconstructions were higher than the subtle differences between the different reconstruction methods. To address this, we denoised the SENSE based reconstructions using the block matching 4D (BM4D) denoising algorithm. The BM4D algorithm is reported to give state of the art denoising performance. The algorithm performs denoising by exploiting nonlocal similarities of spatio- temporal patches. Since the BM4D algorithm is very different from all the reconstruction algorithms considered in this work, the performance comparisons are free from any bias. In addition, the BM4D algorithm has an automatic selection of parameters based on the estimation of the noise level, which minimizes the risk of subjectivity.

During the review of the paper, it was suggested that breath held data sets from a second injection could be used as reference ground truth images. The main challenge however would be to perform a good registration between the undersampled free breathing reconstructions and the breath held datasets for a head to head comparison; this is difficult due to out of plane motion, especially when only a few slices are imaged. In addition, any residual contrast from the first bolus may bias the comparisons. In this context, we believe that the usage of the free breathing datasets as reference sets would better fit to the goals of the current work.

In this study, optimization of λ₁, λ₂ in k − t SLR was performed with a fixed value of p = 0.1 and α = 4. The choices of p and α were motivated by empirical observations and worked well in practice for free breathing MPI data. A thorough search in a 4-dimensional space of p, α, λ₁, λ₂ could improve the k − t SLR reconstructions. The automatic tuning of regularization parameters for iterative nonlinear reconstruction algorithms is an actively researched area. There exists some strategies such as cross validation (Lukas, 2006), and Stein unbiased risk estimator (SURE) methods (Ramani et al., 2012). In the future, we plan to investigate the adaption of one of these methods to our setting.

The performance of all the nonlinear iterative reconstruction algorithms in this study were evaluated based on quantitative metrics that gave measures of image sharpness, temporal blurring, and overall mean square error. Recently, the resolution of reconstructed images from nonlinear algorithms were characterized by determining the local point spread functions at every image pixel (Wech et al., 2012). Such an analysis could be adapted to our setting to characterize the resolution of the images from the different algorithms.

The augmented Lagrangian optimization algorithm used in this study was found to provide fast convergence. Speed up factors of about four were observed when compared to the previous implementation of k − t SLR. In this study, we used a simple sum of squares approach (Roemer et al., 2005) to estimate the coil sensitivities from time averaged data. In the future, we plan to consider other extensions for better estimations such as moving window approaches for time varying sensitivities, and/or joint estimation of the sensitivities along with the reconstructions (Ying and Sheng, 2007).

The current study has limitations in that data from only three subjects were used for analysis. To fully evaluate the clinical feasibility of k − t SLR and draw statistical conclusions, a study with a cohort of patient datasets is needed with validation against gold standard coronary x-ray angiography.

6. Conclusion

In this study, the feasibility of the low rank and sparse reconstruction algorithm (k − t SLR) to accelerate free breathing myocardial perfusion MRI acquisition was demonstrated. The algorithm was extended to include actual radial sampling for better incoherent artifact distribution. Multi-coil sensitivity encoding data was used to improve data consistency. A fast augmented Lagrangian (AL) optimization algorithm was introduced to provide fast convergence. The AL scheme was observed to considerably reduce the computation time, compared with the previous reported implementation of k − t SLR on in-vivo radial data. Using k − t sampling experiments, it was shown that sampling patterns with golden ratio spacing between successive rays provided the best reconstructions with the k − t SLR algorithm. Comparisons on myocardial perfusion rest and stress data sets showed that k − t SLR was able to achieve feasible reconstructions using few rays while being robust to artifacts such as spatio-temporal and motion blurring.

8. Appendix

8.1. Augmented Lagrangian (AL) algorithm steps

In this section, the derivation of the AL subproblems is described. Referring to Eq. 6, the constraints are enforced using Lagrange multiplier terms and quadratic penalties. The resulting optimization objective (termed as the AL function) is specified by:

$${\mathcal{D}}_{{\beta }_1,{\beta }_2}(\mathbf{\Gamma },\mathbf{S},\mathbf{T};\mathbf{X},\mathbf{Y})=\parallel \mathcal{A}(\mathbf{\Gamma })-\mathbf{b}{\parallel }_2^2+{\lambda }_1{({\Vert \mathbf{S}\Vert }_p)}^p+{\mathrm{\lambda }}_2\Vert {\sqrt{{|{\mathbf{T}}_1|}^2+{|{\mathbf{T}}_2|}^2+\alpha {|{\mathbf{T}}_3|}^2}\Vert }_1+\frac{{\beta }_1}{2}\parallel \mathbf{\Gamma }-\mathbf{S}{\parallel }_2^2+\frac{{\beta }_2}{2}\parallel \nabla \cdot \mathbf{\Gamma }-\mathbf{T}{\parallel }_2^2+{\beta }_1<\mathbf{X},\mathbf{\Gamma }-\mathbf{S}>+{\beta }_2<\mathbf{Y},\nabla \cdot \mathbf{\Gamma }-\mathbf{T}>;$$ (10)

where X, Y are matrices of Lagrange multipliers. β₁ and β₂ are the penalty parameters that determine the equivalence of Eq. 10 to Eq. 6, and hence the original problem in Eq. 3. In our earlier implementation (Lingala et al., 2011), we only relied on the quadratic penalty terms in Eq. 10 (second line of Eq. 10) to enforce the constraints in Eq. 6 due to which β₁ and β₂ were tended to ∞ and resulted in slow convergence. The main advantage of using the Lagrange terms (last line of Eq. 10) rather than enforcing the constraints using penalties alone is that the parameters β₁, β₂ need not tend to ∞ for the constraints in Eq. 6 to hold, which allows for a faster convergence.

All the five variables in Eq. 10 are estimated using an alternating minimization algorithm. Specifically, we minimize the AL objective function in Eq. 10 alternately with respect to one variable at a time, assuming the other to be fixed. This approach simplifies the original problem to a sequence of well understood sub-problems. These subproblems are shown in Fig.9. In essence, the algorithm cycles through: (a) regularized SENSE problem solved by conjugate gradient algorithm, (b) singular value shrinkage, (c) total variation shrinkage, and (d,e) linear update rules of the Lagrange multipliers. Additionally, a continuation strategy is employed where the parameters β₁ and β₂ are initialized with small values and are gradually incremented. This continuation strategy was observed to be a key aspect in avoiding convergence to local minima (Hu et al., 2012).

8.2. Choosing the regularization parameters

The k − t SLR algorithm depends on four parameters: λ₁, λ₂, α, p. Since it is impractical to tune for these parameters in a four dimensional space, we restrict ourselves to a simpler approach. The values of p and α were fixed to p = 0.1 and α = 4 based on empirical observations on free breathing MPI data. With the fixed values of α, p, we tune for λ₁, λ₂ in a 2D space. We tuned for λ₁, λ₂ for the rest and stress datasets from a single subject. The parameter optimization is shown in Fig. 10, where a rest dataset is recovered using 21 radial rays/frame. The SER_ROI plot in Fig. 10 was evaluated for the values of λ₁, λ₂ in the window: $\underset{{256}^2\times {10}^{-5}}{\underbrace{0.6554}}\times [0,6\times {10}^{-2},9\times {10}^{-2},3\times {10}^{-1},6\times {10}^{-1},9\times {10}^{-1},3,6]$. The optimal values of λ₁, λ₂ were chosen such that the SER_ROI was the maximum. The values of λ₁, λ₂ varied slightly for the rest and stress datasets. Since all the subjects were scanned with the same protocol under shallow breathing, we used the same values of λ₁, λ₂ tuned for the first subject for reconstruction of all the other datasets. The total time spent for tuning the regularization parameters was approximately two hours.

Figure 10.

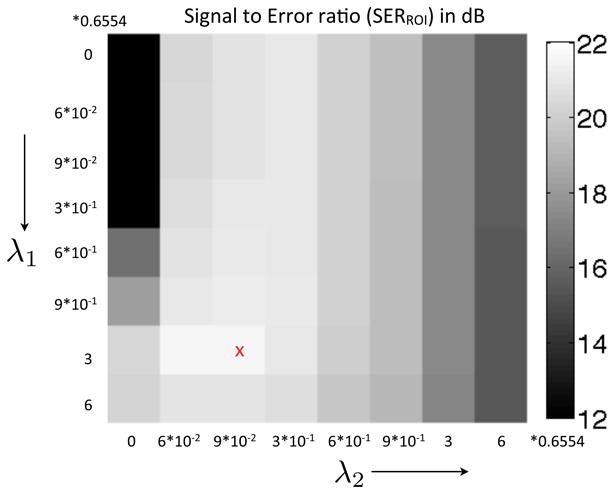
Tuning of the regularization parameters λ₁ and λ₂. The SER was evaluated in a field of view containing the regions of the heart. The optimal parameters were chosen corresponding to the region where the SER between the reconstruction and the reference data set was maximum.