Estimation with Cox models: cause-specific survival analysis with misclassified cause of failure

Abstract

While epidemiologic and clinical research often aims to analyze predictors of specific endpoints, time-to-the-specific-event analysis can be hampered by problems with cause ascertainment. Under typical assumptions of competing risks analysis (and missing-data settings), we correct the cause-specific proportional hazards analysis when information on the reliability of diagnosis is available. Our method avoids bias in effect estimates at low cost in variance, thus offering a perspective for better-informed decision-making. The ratio of different cause-specific hazards can be estimated flexibly for this purpose. It thus complements an all-cause analysis. In a sensitivity analysis, this approach can reveal the likely extent and direction of the bias of a standard cause-specific analysis when the diagnosis is suspect. These two uses are illustrated in a randomized vaccine trial and an epidemiologic cohort study respectively.

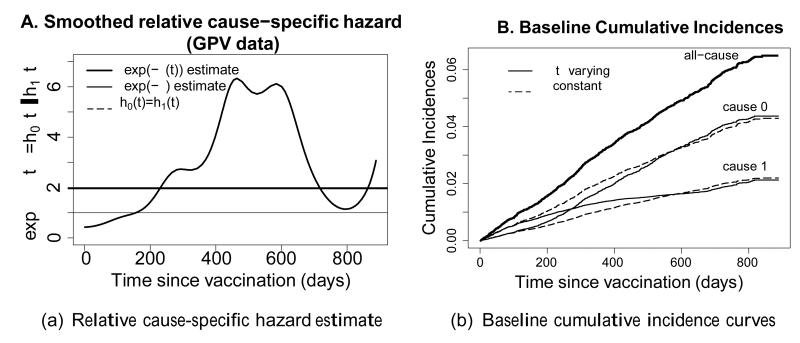
The study of life-threatening diseases typically relies on survival analyses to demonstrate the impact of prognostic factors and the effect of a given intervention. One may gain precision and acquire insight into the mechanism of action by conducting a more targeted competing risks analysis of cause-specific endpoints.^1;2 Traditional inference is then made through models for cause-specific hazards – the instantaneous rate at which events of a specific type occur – conditionally on surviving up to the observation time. We do not wish to interpret these cause-specific hazards in terms of latent failure times, referring to the unrealistic scenario where all other causes of death would have been removed, but instead view them as driving forces of mortality, acting on each individual locally in time and in constant competition with the other causes. As such, these hazards represent the internal mechanisms underlying the observed mortality, while intuition into their practical implications can best be obtained through derived cumulative incidence curves,³ as we have illustrated elsewhere (figures 3 and 4).

Figure 3. A. estimate of the relative cause-specific hazard $\frac{{\mathrm{h}}_0\left(\mathrm{t}\right)}{{\mathrm{h}}_1\left(\mathrm{t}\right)}=\exp (-\xi (\mathrm{t}\left)\right)$; B. resulting cumulative incidence curves.

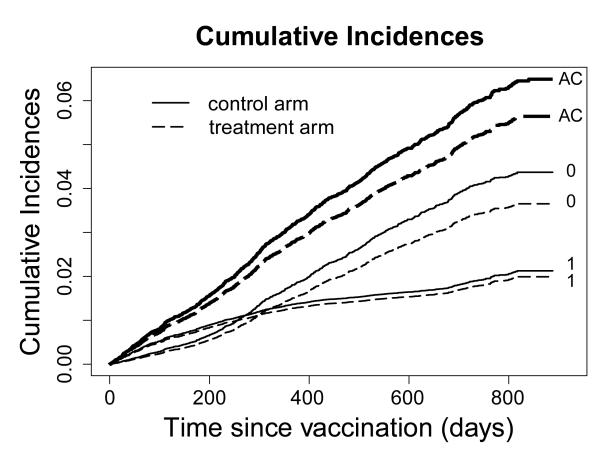
Figure 4. Cumulative incidence curves (AC=all-cause, 0=cause 0, 1=cause 1).

While much is to be gained by this approach, precise assessment of cause-specific information may be lacking due to practical, financial or ethical constraints. Epidemiologic studies in industrialized countries are often based on separately obtained mortality data, while cause-of-death errors on death certificates have been a longstanding issue.^4;5;6;7;8Also, studies in developing countries may not wish to invest in clinical autopsies.⁹ Imprecision in the assessment of cause of death results in misclassification, introduces bias in effect estimates, and undermines analytic power.^10;11 This happens through an attenuation of the exposure effect, which for a targeted intervention typically affects the event of interest much more strongly than it affects the competing risk. Sarfati, Blakely and Pearce¹² show that the type of misclassification typically drives the bias: non-differential misclassification has less impact than misclassification related to underlying factors (such as e.g. race).

We motivate our approach by illustrating the possible bias and power loss when misclassification is present. We propose a general method for time-to-event analysis that incorporates existing knowledge on the rate at which misclassified causes occur. The method uses standard proportionality assumptions to remove bias from effect estimates, allowing one to gain insight into the cause-specific structure of hazards. While estimators solve score equations, resampling strategies will yield variance estimators and hypothesis tests. We show how an additional proportionality assumption can be made, and illustrate bias removal. The method is used both for a primary analysis and as an additional sensitivity analysis of data from the Gambia Pneumococcal Vaccine Trial and the Belgian Interuniversity Research on Nutrition and Health-studies that suffer from known and suspected misclassification respectively. General issues in applying the method are discussed. The eAppendix provides supplementary materials addressing technical issues in more detail.

Bias and power loss due to misclassification

As a simple illustration of the problems of bias and power loss due to misclassification, consider a trial accruing 2543 patients uniformly over 2 years time, with an additional 4 years follow-up. Patients are randomized equally to treatment (X = 1) or control (X = 0). Two causes of death occur with constant cause-specific baseline hazard; for cause 1, h₁ equals 0.04 and for cause 0, h₀ equals 0.06. Treatment affects both the cause-1-specific hazard, lowering it by a factor exp( −0.3X), and the cause-0-specific hazard, increasing it by a factor exp(0.1X). Patients in the control arm have 16% chance of a type-1 event during the study, and 24% of a type-0 event. Under treatment this becomes 12% and 26%, respectively. The study was sized to yield a power of 80% for detecting this effect on the cause-1-specific hazard at the 5% significance level (a sample size calculation is provided in eAppendix).

Bias due to misclassification

The most important consequence of misclassification of cause-of-death is bias in cause-specific analyses. With proportional cause-specific hazards on both causes 0 and 1 (in a setting with and without misclassification of the death cause), we perform 10,000 simulations of the trial described above. If misclassification occurs, p₁ = 60% of all true cause-1 events are diagnosed as from cause 0, and p₀ = 10% of true cause-0 events as from cause 1. Such extreme rates were considered in a clinical trial by Jaffar et al. ¹⁰

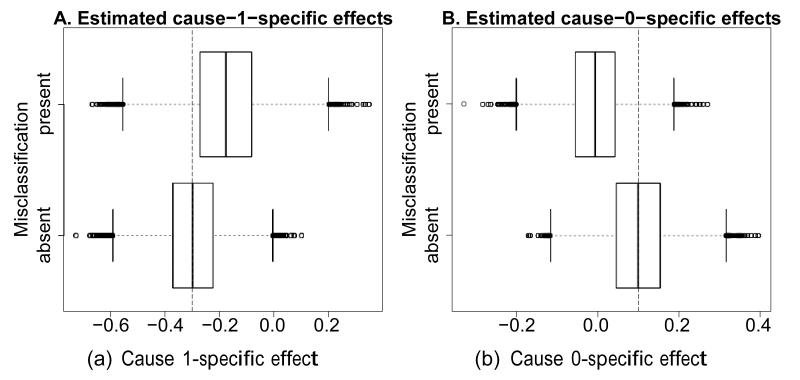
Figure 1 shows boxplots of the estimates for the treatment effect on cause 1 (Fig. 1A) and cause 0 (Fig. 1B). While unbiased estimation is confirmed in the absence of misclassification (bottom boxplots), the presence of misclassification results in bias (top boxplots): estimated effects on both causes are attenuated, contraindicating for example the use of naive Wald tests or confidence intervals. An all-cause analysis will avoid such effects, but its estimate has a possibly undesired marginal interpretation. The eAppendix presents a more elaborate simulation study of the bias for standard cause-specific analyses at various sample sizes and with various settings of misclassification rates, hazards and effect sizes.

Figure 1. Distribution of effect estimates (A. cause 1; B. cause 0) in the presence (top) and absence (bottom) of misclassification.

The true effects are indicated by vertical striped lines.

Power loss due to misclassification

In general, misclassification mixes cause-specific hazards within treatment groups leading to bias, and changes the number of observed specific events. Both effects influence the power and type I error rate of formal hypothesis tests. We compare the power of Wald tests from standard all-cause proportional hazards analysis (based on mixed treatment effects) to that from cause-specific proportional hazards analyses on either cause 0 or 1 (with estimates influenced by possible misclassification). Table 1 shows empirical powers based on 10,000 simulations: in the absence of misclassification (first row) the all-cause analysis has much lower power (10%) than the cause-1-specific assessment (79%) due to the extreme dilution of the effect, when the two cause-specific effects go in opposite directions. For the cause-0-specific analysis, the power is 24%. The second line of the table shows results when misclassification is introduced (again p₁ = 60% and p₀ = 10%). This confirms that the power of the all-cause analysis is unaffected by misclassification (10%), while the power of the cause-1-specific analysis drops to 23%, making it virtually useless. The power of the cause-0-specific analysis drops below that of the all-cause analysis to 5%. Further effects of misclassification are described in the eAppendix.

Table 1. Illustration of Power Loss Due to Misclassification With p₁ 0.6 and p₀ = 0.1 (Standard Error on Estimates Below 0.005).

Misclassification	All-cause	Cause Specific
		Cause 1	Cause 0
No	0.0984	0.7935	0.2412
Yes	0.0984	0.231	0.492

Baseline hazards are h₁ = 0.04 and h₀ = 0.06, treated vs. nontreated have cause 1-specific hazard ratio exp(−0.3) and cause 0-specific hazard ratio exp(0.1).

In this paper, we propose a correction for the misclassification probabilities p₀ and p₁ that avoids biased estimates and gains precision. It builds on a weighted logrank test by Van Rompaye, Jaffar and Goetghebeur¹³ to regain significant power under quite general assumptions, which becomes especially useful when events of interest are relatively rare and are often misclassified as competing risks. This is common in developing countries, where one cause appears against a high background mortality of diseases with overlapping signs and symptoms (see for example Jaffar et al. ¹⁰), but equally in studies of elderly populations¹⁴ or with rare, difficult-to-diagnose diseases.¹⁵ To allow correction for possible confounders,we extend previous work to develop a complete cause-specific Cox model incorporating known misclassification rates, with the goal of gaining precision and avoiding bias in targeted estimation.

Theoretical framework

As in Goetghebeur and Ryan,¹⁶ we rely on the framework of cause-specific proportional hazards to model possibly misclassified failure patterns. The corresponding partial likelihood weights the observed competing failure types relative to their relevance for the true cause-specific event rates. Without loss of generality, we restrict ourselves to two possible causes of failure, which are possibly misclassified or may even be completely unknown to yield missing causes of death (as in¹⁶).

Notation and model assumptions

We largely adopt notation from Van Rompaye, Jaffar and Goetghebeur,¹³ considering failure types 1 (cause of interest) and 0 (other causes), where δ_i = k ∈ {0,1} indicates the true (unobserved) type for individual i ∈ {1, …, n} and F_i the observed and possibly misclassified type. Misclassification is indicated by the binary covariate M_i. Time until failure D_i is possibly censored to yield observed time T_i until failure or censoring. Censoring is assumed to be non-informative¹⁷ and its occurence is indicated by C_i = 0, while observed events have C_i = 1.

The model assumptions follow Van Rompaye, Jaffar and Goetghebeur,¹³ but now allow for a multidimensional covariate space. We assume that a (possibly time-varying) covariate vector Z_i(t) acts proportionally on the type-1-specific hazard h₁(t; Z_i(t)), as does a second (possibly overlapping) covariate vector X_i(t) on the type-0-specific hazard h₀(t; X_i(t)):

Assumption 1

$$\begin{array}{cc}\hfill {\mathrm{h}}_1(\mathrm{t};{\mathrm{Z}}_{\mathrm{i}}(\mathrm{t}),{\mathrm{X}}_{\mathrm{i}}(\mathrm{t}\left)\right)& ={\mathrm{e}}^{{\phi }^{\mathrm{T}}{\mathrm{Z}}_{\mathrm{i}}\left(\mathrm{t}\right)}{\mathrm{h}}_1\left(\mathrm{t}\right)\hfill \\ \hfill {\mathrm{h}}_0(\mathrm{t};{\mathrm{X}}_{\mathrm{i}}(\mathrm{t}),{\mathrm{Z}}_{\mathrm{i}}(\mathrm{t}\left)\right)& ={\mathrm{e}}^{{\rho }^{\mathrm{T}}{\mathrm{X}}_{\mathrm{i}}\left(\mathrm{t}\right)}{\mathrm{h}}_0\left(\mathrm{t}\right)\hfill \end{array}$$ (1)

The effect of interest is thus represented by φ, while ρ represents the effect on the competing risk. To adjust effect estimates for misclassification, we introduce an arbitrary link function between the cause-specific baseline hazards h₀ and h₁:

$${\mathrm{h}}_0\left(\mathrm{t}\right)={\mathrm{e}}^{-\xi \left(\mathrm{t}\right)}{\mathrm{h}}_1\left(\mathrm{t}\right)$$ (2)

with e^−ξ(t) the relative cause-specific hazard, as opposed to exp(φ) and exp(ρ), the cause-specific relative hazards. This unconstrained link function allows one cause to appear more during one period of time, and be less important thereafter. However, when deemed appropriate, one can impose restrictions or make assumptions, such as proportional cause-specific hazards.

Finally, the misclassification probabilities are assumed known. To simplify matters (although extension is straightforward and sometimes needed^4;18), we consider non-differential misclassification rates, i.e. misclassification does not depend on covariates, but can depend on the time of death and the true cause of death k:

Assumption 2

$$\mathrm{P}({\mathrm{M}}_{\mathrm{i}}=1\mid {\mathrm{D}}_{\mathrm{i}}={\mathrm{t}}_{\mathrm{i}},{\mathrm{C}}_{\mathrm{i}}=1,{\delta }_{\mathrm{i}}=\mathrm{k},{\mathrm{Z}}_{\mathrm{i}}(\mathrm{t})={\mathrm{z}}_{\mathrm{i}}(\mathrm{t}),{\mathrm{X}}_{\mathrm{i}}(\mathrm{t})={\mathrm{x}}_{\mathrm{i}}(\mathrm{t}\left)\right)={\mathrm{p}}_{\mathrm{k}}\left({\mathrm{t}}_{\mathrm{i}}\right)$$ (3)

Typically 1 – p₁(t) is called the sensitivity of the cause-of-interest diagnosis at time t and 1 – p₀(t) the specificity.

Estimating equations and methodology

For mathematical expressions and details of this section, we refer to the eAppendix. Under assumptions 1 and 2 with time-varying e^−ξ(t) a log partial likelihood l is constructed from the conditional probabilities of an observed event of type f at time t_i, given that one such event was observed in the risk set R_i at that time. This likelihood deviates from the standard cause-specific partial likelihood¹⁷ by using contributions from both types of event, and by using weights reflecting the positive predictive value and one minus the negative predictive value of the observed event type, conditional on the covariate values and time.

With known exp( −ξ(t)), both φ and ρ can be estimated from the score equations $\frac{\partial \mathrm{l}}{\partial \phi }=0$ and $\frac{\partial \mathrm{l}}{\partial \rho }=0$. These equate the weighted covariate values for all failed individuals to the sum of model-based expected covariate values in the respective risk sets. Weights are constructed to conserve the balance between the various causes (imposed by e^−ξ(t)). Without misclassification (p₀ = p₁ = 0) the equations return to the standard solutions for the cause-specific effects of Z(t) and X(t).

When the relative cause-specific hazard exp( −ξ (t)) is not known in advance, it can be estimated. Partial likelihoods that condition on the event type (such as l) lose all information on the contrast between event types and hence ξ(t). This can be resolved by conditioning on just the occurrence of any type of event in the risk set at each observed failure time as Dewanji did,¹⁹ leading to a more informative log partial likelihood l*. This however no longer leads to the standard solutions in the absence of misclassification (p₀ = p₁ = 0), as both types continue to contribute to l*

Following the approach by Goetghebeur and Ryan,¹⁶ we use the partial likelihood l to jointly estimate φ and ρ in the standard manner, while adding an estimating equation for the nuisance parameter ξ(t) from the partial likelihood l*. To allow for different causes appearing with varying intensity over time, nonparametric estimation of ξ(t) using a kernel-weighted version of l* is possible as in Van Rompaye, Jaffar and Goetghebeur.¹³ In our analysis below of the Gambia Pneumococcal Vaccine Trial data, we rely on a localized version of the full log-likelihood l*, using a Gaussian kernel. Together with the (φ, ρ)-estimation this is iterated until convergence.

The complexity associated with the non-parametric $\widehat{\xi }\left(\mathrm{t}\right)$ prevents a closed-form estimator for the variance matrix of the estimates. We therefore work with resampling-based estimates, such as various types of jackknife estimates,^20;21 or a parametric bootstrap procedure for the covariance matrix.²² Below, we rely on the latter, fitting the model to the data and then repeatedly simulating from the fitted event and censoring distributions, applying the assumed misclassification rates.

An expression similar to the Breslow estimator for the baseline cumulative hazard is given in the eAppendix. This exploits the fact that exp( −ξ(t)) explicitly gives the ratio between the cause-specific baseline hazards to allow contributions from all observed event types. From the resulting estimates one could derive various residuals such as the martingale, Cox-Snell or Schoenfeld residuals.

In practice, simple parametric or piecewise constant models for ξ(t) will often combine interpretational ease with sufficient flexibility. The parameters of such models can be estimated by solving the corresponding score equations resulting from l*. In the following section, we single out the simplest of such models, a constant ξ model.

A proportional relative cause-specific hazard setting

In various settings the additional constraint of proportionality of the cause-specific baseline hazards is warranted, e.g. with stable diseases. We call this the time-constant ξ setting, and technically make

Assumption 3′>

$${\mathrm{h}}_0\left(\mathrm{t}\right)={\mathrm{e}}^{-\xi }{\mathrm{h}}_1\left(\mathrm{t}\right)$$ (4)

The solutions to the resulting joint estimating equations based on l and l* are consistent and asymptotically normal, with a covariance matrix estimator that is given in the eAppendix. In the remainder of this text, standard errors based on this expression will be called “model based”. Because the expression for the covariance matrix is complex, the parametric models could be misspecified and asymptotic properties may be hard to defend in finite samples; here too, one may prefer one of the resampling-based estimates mentioned before.

Illustration of bias removal and efficiency

Returning to the simple example described above, where the relative cause-specific hazard is constant at 3/2, we apply our method for time-constant ξ, using known misclassification probabilities p₀ = 0.1 and p₁ = 0.6 to obtain corrected estimates. With reasonable starting values, the iterative solution to the estimating equations typically converges in 2 or 3 steps. To avoid running parametric bootstrap steps within the simulation steps, Wald tests here use the model-based standard errors.

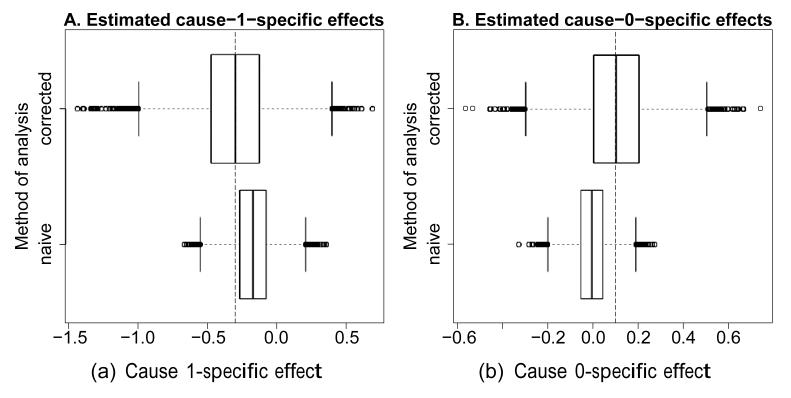
Figure 2 shows boxplots of the estimates, based on the same 10,000 simulated datasets used in the introductory example. One finds the bias of the naive cause-specific estimates removed by our method, at the cost of an increased variation. This reflects increased uncertainty inherent to the problem of misclassification: the missing information can be only partially recovered.

Figure 2. Simulated bias for the naive and corrected method (A. cause 1-specific; B. cause 0-specific).

At the top are the (unbiased) corrected estimates, at the bottom the (biased) uncorrected, naive estimates from Figure 1. The vertical striped lines indicate the true simulated effects.

Since the bias starts to dominate the variance with increasing sample size, large samples will favor our method because it has lower MSE than the naive approach, as was confirmed in simulations. The eAppendix presents a simulation-based examination of the exact balance of variance and bias in various hazard and misclassification settings.

With constant relative cause-specific hazard exp( −ξ), the treatment effect on the all-cause hazard h can be reconstructed as

$$\frac{\mathrm{h}(\mathrm{t};\mathrm{Z}=1,\mathrm{X}=1)}{\mathrm{h}(\mathrm{t};\mathrm{Z}=0,\mathrm{X}=0)}=\frac{{\mathrm{h}}_0(\mathrm{t};\mathrm{Z}=1,\mathrm{X}=1)+{\mathrm{h}}_1(\mathrm{t};\mathrm{Z}=1,\mathrm{X}=1)}{{\mathrm{h}}_0(\mathrm{t};\mathrm{Z}=0,\mathrm{X}=0)+{\mathrm{h}}_1(\mathrm{t};\mathrm{Z}=0,\mathrm{X}=0)}=\frac{{\mathrm{e}}^{\phi }+{\mathrm{e}}^{-\xi }{\mathrm{e}}^{\rho }}{1+{\mathrm{e}}^{-\xi }}$$ (5)

This expression is virtually indistinguishable from the standard all-cause effect, with minor differences arising from the constancy constraint on ξ(t). Hence the decomposition into cause-specific information and the modelling of ξ does not come at the expense of precision.

Two applications

Use of the proposed methodology as a primary analysis

We revisit the Gambia Pneumococcal Vaccine Trial,²³ also analyzed by Van Rompaye, Jaffar and Goetghebeur,¹³ which studied 17,433 children born between September 1999 and the beginning of 2003, to assess the impact of vaccination against pneumococcal infection on mortality from acute lower-respiratory-tract infections.²⁴ Vaccination usually took place between 40 and 400 days of age at a median of 75 days; 8,715 children were randomized to vaccine (for a total follow-up time of 16,390 person years) and 8,718 to placebo (total follow-up time 16,340 person years). Follow-up stopped in April 2004, with a median follow-up of 722 days and a maximum follow-up of 888 days. By that time, 491 deaths were observed in the control and 426 in the treatment arm. Of these 917 deaths, 186 were classified as due to acute infection of the respiratory tract (99 under control and 87 under treatment), and the rest as other causes. Verbal autopsy determined cause-of-death,⁹ with low expected sensitivity (40%) and specificity (90%).¹⁰ While the focus of the trial is the vaccine effect, Jaffar and colleagues²⁵ were interested in the cause-specific patterns of infant and childhood mortality by cause.

Van Rompaye, Jaffar and Goetghebeur¹³ compare a naive infection-specific test (with a p-value of 0.371) and an adapted logrank test (with p₀ = 10% and p₁ = 60%), assuming a constant ξ and a treatment effect on infection-specific but not on other cause mortality, with a p-value of 0.055. Still, an all-cause test yielded the lowest p-value (0.029), although the asymptotic efficiency of the adapted test was highest. It was then hypothesized this resulted from the treatment also affecting the competing risks. Jaffar et al.¹⁰ and Cutts et al.²³ also indicate this, hinting at a reduction in mortality when the lower-respiratory-tract infection is a secondary infection and at a reduction of pneumococcal meningitis. We investigate this using our corrected Cox model.

First, the treatment (a binary Z, no X) is assumed to influence only infection-specific mortality, under a time-constant ξ. This differs from the adapted logrank test in Van Rompaye, Jaffar and Goetghebeur,¹³ which estimates both ξ and the standard errors under the null. The asymptotically unbiased estimate for e^−ξ is 1.623, which is slightly lower than the possibly biased estimate from the null of 1.917. The estimate for φ is −0.327 (95% confidence interval [CI]=−0.699 to 0.045, p-value = 0.085), a slight increase in p-value that likely results from using no information from the null in the ξ-estimate, thereby slightly increasing its variance. Nevertheless, this analysis does not qualitatively differ from that in Van Rompaye, Jaffar and Goetghebeur.¹³

Next, a treatment effect on the competing risks is allowed (one binary Z, one binary X). Using standard proportional hazard models, we find an all-cause hazard ratio of 0.865 (95% CI 0.760 to 0.985), a naive infection-specific hazard ratio of 0.877 (CI 0.658 to 1.170) and a naive other-cause-specific hazard ratio of 0.862 (0.746 to 0.997). Using our method of analysis, we find an estimate for e^−ξ of 1.954 (1.570 to 2.338). The treatment lowers the hazard of infection-specific mortality by a factor 0.888 ($\widehat{\phi }=-0.118$, CI = −0.824 to 0.588), and the hazard for the competing risks by a factor 0.853 ($\widehat{\rho }=-0.159$, −0.545 to 0.227). Although some indication of vaccination effect on the infection-specific hazard is seen, the point estimate shows that the effect on the other-cause-hazard is stronger, even though the vaccine explicitly targets pneumococci responsible for these infections. The all-cause hazard ratio of 0.865 (0.763 to 0.981) in the third column of Table 2 is based on Equation 5, and is equal to the standard all-cause estimate. While these observations are scientifically interesting in guiding further research, none of these effects is deemed significant in this model, which reflects the persistent and strong uncertainty resulting from the misclassification.

Table 2. Effect Estimates (and Standard Errors) for the Various Analyses of the Gambian Pneumococcal Vaccine Trial Data.

Log (HR)	Naïve		Corrected
	Z, X, no ξ	Z, no X, ξ(t) = ξ	Z, X, ξ(t) = ξ	Z, X, ξ(t)
All-cause	−0.145 (0.066)	−0.112 (0.058)	−0.145 (0.064)	—
Infection-specific ϕ	−0.131 (0.147)	−0.327 (0.190)	−0.118 (0.360)	−0.069 (0.27)
Other cause-specific p	−0.148 (0.074)	0	−0.159 (0.197)	−0.184 (0.21)
ξ	—	−0.484 (0.186)	−0.670 (0.197)	—

Estimates of ξ are missing when allowed to vary over time; all-cause estimates are missing when incompatible with the model. No ξ indicates that separate standard cause-specific models were fit.

Another important aspect of the data is investigated through the nonparametric estimator of the relative cause-specific mortality pattern exp( −ξ(t)), shown in Figure 3A. This reveals that, under control, the airway infection is the most prevalent cause of death in young children, while at later ages other causes (such as malaria) become relatively more prevalent. This confirms and extends the observations made by Jaffar et al. ²⁵ concerning age dependence of causes of death (noting their estimates are based on older data, and are not corrected for possible misclassification). After 600 days into the study $\exp (-\widehat{\xi }(\mathrm{t}\left)\right)$ drops again, which results mainly from a decrease in other-cause mortality in older children. The rise of $\exp (-\widehat{\xi }(\mathrm{t}\left)\right)$ at the very end of the follow-up is presumably a boundary effect of the nonparametric estimator. To fully understand the mortality structure, one needs to take into account the baseline all-cause hazard itself, which is virtually constant here, with a slight increase after 1 year (not shown).

Using this nonparametric $\widehat{\xi }\left(\mathrm{t}\right)$ we obtain $\widehat{\phi }=-0.069$ and $\widehat{\rho }=-0.184$, or an estimated infection-specific hazard ratio of 0.933 and an estimated other cause-specific hazard ratio of 0.832. A parametric bootstrapping procedure yields estimated standard errors of 0.27 on $\widehat{\phi }$ (CI = −0.598 to 0.460) and 0.21 on $\widehat{\rho }$ (−0.596 to 0.228), making no substantive change in statistical significance. However, the point estimate indicates a much smaller effect on the cause of interest.

Intuitively appealing cumulative incidence curves are obtained from the Breslow-type estimator for the baseline cumulative cause-specific hazards (eAppendix) and estimates for φ, ρ and ξ(t). Figure 3B shows these for a time-varying and a time-constant ξ. The relatively large deviations between the two ξ estimates seen in Figure 3A, translate into substantial differences between the incidence curves in Figure 3B. As expected, all methods virtually coincide in their estimates of the cumulative all-cause incidences. Figure 4 illustrates the practical impact of the treatment on the various causes of death.

Use of the proposed methodology in sensitivity analyses

The Belgian Interuniversity Research on Nutrition and Health study is a survey on nutrition and health, where cause-specific mortality is of interest but is likely measured with error. Between 1981 and 1984, data on nutrition and medical parameters were collected from 10,577 Belgians between the age of 25 and 74, with sampling stratified by sex and age. They were subsequently followed for 10 years (for a total follow-up of 96,870 person years) with the goal of relating dietary habits to cause-specific mortality. Causes of death were ascertained from the person’s family doctor or the doctor who completed the death certificate, and supplemented if necessary with information from hospital or medical records. While this approach strongly improves the classification based solely on the death certificate itself, errors may still be expected. However, there is no precise indication of the expected frequency of cause misclassification. We removed data on 210 diabetic patients (because of their very specific risk character) and we removed all 324 remaining incomplete cases to avoid missing data issues. These issues are not relevant to our illustration, and no systematic missingness pattern was observed, making missingness completely at random plausible. Finally, of the observed 802 deaths, 258 were classified as being cardiovascular (CVD) deaths and 544 as deaths from other causes. More information on this study can be found in the paper by De Bacquer et al. ²⁶

As Sarfati, Blakely and Pearce¹² indicate, when there is doubt about the precise misclassification rates it is prudent to perform a sensitivity analysis by varying the misclassification probabilities used in the analysis. In the case of a corrected analysis using our method, this gives a sense of the stability of the estimates. In the case of a standard, uncorrected analysis, such a sensitivity analysis indicates the likely extent and direction of bias introduced by misclassification. This last principle is applied to the nutrition and health data.

Our main interest is the impact of baseline pulse rate on the rate of CVD. This is studied by means of proportional (cause-specific) hazard models, correcting for the possible effects of baseline risk factors smoking (Smoke = 1 if smoking, 0 else) and use of beta-blockers (BBl = 1 if using, 0 else), and including sex (Male=1 for men and =0 for women) and baseline age in years (Age), with age centered around its mean (48.42 years). Pulse rate is categorized following commonly used definitions of bradycardia and tachycardia (respectively, PR_<60=1 if rate < 60, 0 otherwise and PR_>100=1 if rate > 100, 0 otherwise). Main effect models are built in a backward fashion (referring to 5% significance), forcing the pulse rate effect to be included. Next, interactions of both age and sex with pulse rate are allowed if p<0.15, as these may be of interest to policy makers. We first consider the standard proportional hazard analyses which are available.

Standard analyses

Table 3 gives an overview of estimates and standard errors for three hazard notions. When information on cause-of-death is unreliable, typically a Cox model for the all-cause mortality is fitted, as given in the first column of Table 3. No interactions were retained at the 15% level, with the main effect of the categorical pulse rate being borderline significant at the 5% level (p=0.054). Extreme pulse rates in both directions (high or low) are associated with a higher overall mortality. Being older and male is significantly associated with a decreased survival, as are both smoking and beta-blocker use.

Table 3. Summary of Effect Estimates (Log Hazard Ratios With Standard Errors) for the Various Standard Analyses of the Belgian Interuniversity Research on Nutrition and Health Data (Models Built in a Backward Fashion).

	All-cause		Naive CVD-specific		Naive OC-specific
	Estimate (SE)	P	Estimate (SE)	P	Estimate (SE)	P
Male	0.59 (0.09)	<0.001	0.38 (0.16)	0.02	0.64 (0.11)	<0.001
Age (years)	0.100 (0.004)	<0.001	0.127 (0.007)	<0.001	0.089 (0.004)	<0.001
PR		0.05		0.22		0.28
PR<60	0.09 (0.15)		0.52 (0.46)		−0.19 (0.21)
PR>100	0.41 (0.17)		−1.30 (1.01)		0.28 (0.22)
BBI	0.32 (0.14)	0.03	0.71 (0.21)	<0.001	—	—
Smoke	0.48 (0.08)	<0.001	0.35 (0.14)	0.01	0.54 (0.10)	<0.001
Male × PR	—	—		<0.001	—	−
Male × PR<60	—	—	−0.006 (0.526)		—	—
Male × PR>100	—	—	2.535 (1.047)		—	—

In a next step, more detail is obtained from cause-specific models. The CVD-specific effects (second column of Table 3) include a significant pulse rate effect with sex-specific magnitude (p=0.053). Higher pulse rates are associated with higher CVD-specific mortality in men, but lower in women. Low pulse rates are associated with increased CVD-specific mortality in both groups.

For the other cause-specific hazard (third column) only sex, age and smoking show a significant additive effect on the log hazard. This shows how the pulse rate effect plays especially on cardiovascular mortality (where it is modulated by sex), while its effect on other causes is not significant. However, the suspected misclassification of some causes of death warrants a sensitivity analysis of these cause-specific results, showing how strongly the estimates can be affected by possible misclassification in the cause-of-death records.

Sensitivity analysis

In the sensitivity analysis, our model is repeatedly fit to the observed data, each time varying the assumed misclassification rates within a reasonable range of 0% and 20% for both death causes (see for instance Lloyd-Jones et al. ⁸ on coronary heart disease). We assume ξ is constant, and we use all combinations of p₀ and p₁ in 0.00001, 0.02, 0.04, 0.06, …, 0.2.

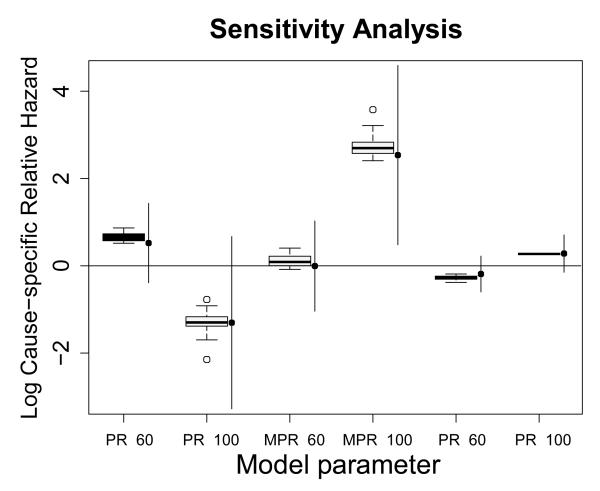
Figure 5 summarizes the sensitivity distributions of the estimates for the various pulse-rate effects. It shows the point estimates (dots) of the standard cause-specific models with their 95% confidence intervals (lines), alongside boxplots summarizing the distribution of the estimates marginal over the (p₀, p₁)-grid.

Figure 5. Standard cause-specific effect estimates (filled dots with 95% confidence intervals as vertical lines) with their sensitivity distributions (boxplots), using a uniform rectangular p₀, p₁ grid between 0 and 0.2.

MPR < 60 denotes the interaction between the indicators Male and PR_<60, MPR > 100 that between Male and PR_>100.

Figure 5 reveals that effect estimates most often change in one specific direction when misclassification is accounted for. This means that naive cause-specific analyses systematically over- or underestimate effects, which stresses the need for a thorough sensitivity analysis in settings prone to misclassification error.

Discussion

The present development fills a gap in methods currently available for cause-specific survival analysis when cause of death is uncertain. This problem is common in death registries, and most pressing in countries that lack both infrastructure and funds for precise registration of death causes.

Our method allows one to assess the relative role of various cause-specific dependencies on covariates, as long as misclassification rates are provided. When lacking precise information on misclassification rates, the method can be used to address sensitivity of conclusions from standard methods. It involves nonparametric estimation of the relative cause-specific hazard, which reveals how certain causes are relatively more prominent over time, and can thus help decide which subpopulations could be targeted when intervening.

The proposed method uses standard assumptions of proportional covariate effects on the cause-specific hazards, without constraining the relative cause-specific hazard exp( −ξ(t)). The necessary misclassification rates can sometimes be obtained from the literature, or may require a “gold standard” pilot study to estimate the rates. The main analysis may then include the data from the pilot study, as the score equations allow optimization of the weights to reflect the increased certainty for specific persons.

The general nature of the score equations even allows individualized misclassification rates, depending arbitrarily on time of death, on covariates in the model, or on covariates external to the death process (such as the diagnostic method used). Ebrahimi²⁷ instead starts from a fully parametric method with assumed error matrix, allowing the physician to specify the probability that each of a number of multiple possible diagnoses is the one causing the death. This can be translated to misclassification rates on an unambiguous diagnosis, and incorporated into our method using case-specific misclassification probabilities.

In the extreme case of missing causes of death, our method reduces to the one of Goetghebeur and Ryan^16;28 by adapting the likelihood as in the supplementary materials of Van Rompaye, Jaffar and Goetghebeur.¹³

Although our approach naturally incorporates common assumptions on misclassification and competing risks, other approaches could prove valuable. One option models the cumulative incidence function more directly,²⁹ an approach that has enjoyed increasing attention given the appealing interpretation of the cumulative incidence function. Key ingredient there would be a proportionality assumption on the two hazards of subdistribution, after which further developments are similar to ours, exploiting the resemblance between the likelihoods for proportional cause-specific hazards and proportional hazards of subdistribution. One additional difficulty may be the definition of the risk sets, which depends on the observed event type in the Fine and Gray model.²⁹ As no candidate model is obviously preferred for making the proportionality assumption, further development of the parallel method for the subdistribution hazard should allow researchers to use both methods in data analysis, as recommended in Grambauer, Schumacher and Beyersmann.³⁰

Any analysis of hazard ratios comes with the specific interpretation of hazards as conditional parameters characterizing unconditional (sub)distribution functions. As such, their causal interpretation becomes more intricate, as discussed by Hernán.³¹ Incidence curves are more straightforward to interpret, as the cause-specific counterpart of the unconditional survival curve they express the chance of experiencing the event of a specific type before a given time t. Should one have any interest in estimating the causal effect of particular treatment strategies, such curves can be adjusted. Furthermore, to allow for time-varying effects, one can explicitly include time-varying covariates in the model, or include a plot of average effect estimates over ever-increasing follow-up periods.

While our method involves exact prior knowledge of the misclassification rates, this prerequisite can be relaxed in a sensitivity analysis, as shown above. Such approach comes close to a Bayesian analysis, specifying a prior distribution on the misclassification rates. Explicitly developing a formal Bayesian framework could prove interesting, but lies outside the scope of this paper.

As different types of Cox models target different estimands, direct comparisons of efficiency may be secondary and hard to achieve. Under the standard assumptions in randomized clinical trials, substantial power for simple two-group comparisons can be regained,¹³ but in more complex models appropriate for observational epidemiology the standard errors in our model are inflated. The simulation above shows that our method removes bias but pays a price in terms of variance. In light of this bias/variance trade-off, one will need to make an informed decision on which method of analysis is preferable. Simulations illustrate how, with increasing sample sizes, our method becomes preferable to a naive cause-specific analysis in terms of MSE (work presented in the eAppendix). Also, no loss in MSE terms emerges for a standard all-cause analysis parameter.

The ambiguous view on efficiency complicates anticipation on the use of our method at the design stage. It therefore seems prudent to propose the all-cause mortality as the primary endpoint at the design of a study, and to use our method to complement the all-cause conclusions. This approach also appeals to common sense: researchers who are interested primarily in cause-specific results should, first and foremost, invest in reliable cause assessment.