Attosecond vacuum UV coherent control of molecular dynamics

Significance

We show that we can precisely control molecular dynamics on both nuclear (i.e., femtosecond) and electronic (i.e., attosecond) timescales. By using attosecond vacuum UV light pulse trains that are tunable in the frequency domain, we show that it is possible to switch population between electronically excited states of a neutral molecule on attosecond time scales, and use this ability to coherently control excitation and ionization through specific pathways. This paper represents a milestone advance because almost two decades after attosecond physics was demonstrated, attosecond chemistry has not yet been fully established because the wavelength and bandwidth of attosecond pulses did not well match molecular quantum states. The richness and complexity of the dynamics, even in a simple molecule, is remarkable and daunting.

Abstract

High harmonic light sources make it possible to access attosecond timescales, thus opening up the prospect of manipulating electronic wave packets for steering molecular dynamics. However, two decades after the birth of attosecond physics, the concept of attosecond chemistry has not yet been realized; this is because excitation and manipulation of molecular orbitals requires precisely controlled attosecond waveforms in the deep UV, which have not yet been synthesized. Here, we present a unique approach using attosecond vacuum UV pulse-trains to coherently excite and control the outcome of a simple chemical reaction in a deuterium molecule in a non-Born–Oppenheimer regime. By controlling the interfering pathways of electron wave packets in the excited neutral and singly ionized molecule, we unambiguously show that we can switch the excited electronic state on attosecond timescales, coherently guide the nuclear wave packets to dictate the way a neutral molecule vibrates, and steer and manipulate the ionization and dissociation channels. Furthermore, through advanced theory, we succeed in rigorously modeling multiscale electron and nuclear quantum control in a molecule. The observed richness and complexity of the dynamics, even in this very simplest of molecules, is both remarkable and daunting, and presents intriguing new possibilities for bridging the gap between attosecond physics and attochemistry.

The coherent manipulation of quantum systems on their natural timescales, as a means to control the evolution of a system, is an important goal for a broad range of science and technology, including chemical dynamics and quantum information science. In molecules, these timescales span from attosecond timescales characteristic of electronic dynamics, to femtosecond timescales characteristic of vibrations and dissociation, to picosecond timescales characteristic of rotations in molecules. With the advent of femtosecond lasers, observing the transition state in a chemical reaction (1), and controlling the reaction itself, became feasible. Precisely timed femtosecond pulse sequences can be used to selectively excite vibrations in a molecule, allow it to evolve, and finally excite or deexcite it into an electronic state not directly accessible from the ground state (2). Alternatively, interferences between different quantum pathways that end up in the same final state can be used to control the outcome of a chemical reaction (3–9).

In recent years, coherent high harmonic sources with bandwidths sufficient to generate either attosecond pulse trains or a single isolated attosecond pulses have been developed that are also perfectly synchronized to the driving femtosecond laser (10–12). This new capability provides intriguing possibilities for coherently and simultaneously controlling both the electronic and nuclear dynamics in a molecule in regimes where the Born–Oppenheimer approximation is no longer valid, to select specific reaction pathways or products. Here, we realize this possibility in a coordinated experimental–theoretical study of dynamics in the simplest neutral molecule: deuterated hydrogen (D₂).

The hydrogen molecule, as the simplest possible neutral molecule that can be fully described theoretically, has been the prototype molecule for understanding fundamental processes that lie at the heart of quantum mechanics (13–16). However, in such a small molecule, the coupled electron–nuclear dynamics are in the attosecond-to-few-femtosecond regime, whereas the electronically excited states lie in the vacuum UV (VUV) region of the spectrum. Because of the challenge of generating attosecond VUV waveforms using traditional laser frequency doubling or tripling in nonlinear crystals, it has not been possible to date to explore the dynamics of an electronically excited hydrogen molecule. Exploiting attosecond physics, however, only a handful of time-resolved experiments have been performed on H₂ (D₂), focusing mainly on controlling dissociation through electron localization in electronically excited ions (17–23). Recently it was realized that IR femtosecond laser pulses, in combination with a phased locked comb of attosecond VUV harmonics, can be used to control the excitation and ionization yields in He on attosecond timescales, by interfering electron wave packets (24, 25). These experiments extended the Brumer–Shapiro (3–9) two-pathway interference coherent control concept to the attosecond temporal and VUV frequency domain. More recently, it was shown that by manipulating the individual amplitude of VUV harmonics, it is possible to induce full electromagnetic transparency in He, by destructively interfering two electronic wave packets of the same amplitude and opposite phases (26). Other recent work used shaped intense femtosecond laser pulses to manipulate populations by controlling the oscillating charge distribution in a potassium dimer (27).

In this paper, we demonstrate that we can coherently and simultaneously manipulate multistate electronic and multipotential-well nuclear wave packet dynamics to control the excitation, nuclear wave packet tunneling, and dissociation and ionization channels of the only electronically excited neutral molecule where full modeling of the coupled quantum dynamics is possible—H₂ (for practical reasons, we used deuterated hydrogen in this experiment). By combining attosecond pulse trains of VUV with two near-IR fields, together with strong-field control that exploits a combination of the two-pathway interference Brumer–Shapiro (3–9) and pump-dump Tannor–Rice (2) approaches, we demonstrate that we can selectively steer the ionization, vibration, and dissociation of D₂ through different channels. Interferences between electronic wave packets (evolving on attosecond timescales) are used to control the population of different electronic states of the excited neutral molecule, which can be switched on attosecond timescales. Then, by optimally selecting the excitation wavelengths and time delays, we can control the vibrational motion, total excitation, ionization yield, and desired ionization and dissociation pathways. State-of-the-art quantum calculations, which have only recently become feasible, allowed us to interpret this very rich set of quantum dynamics, including both the nuclear motion and the coherently excited electronic state interferences. Thus, we succeed in both observing and rigorously modeling multiscale coherent quantum control in the time domain. The observed richness and complexity of the dynamics, even in this very simplest of molecules, is both remarkable and daunting.

We note that our approach for control, using a combination of phase-locked VUV and IR fields, where the VUV field consists of an attosecond pulse train with a 10-fs pulse envelope, is ideal for coherently exciting and manipulating electronic and vibrational states on attosecond time scales, while simultaneously retaining excellent spectral resolution necessary for state-selective attochemistry. Exciting electron dynamics in a molecule using a single, broad-bandwidth VUV attosecond pulse would simply excite many ionization/dissociation channels with little state selectivity, potentially masking the coherent electronic and nuclear quantum dynamics. For example, the bandwidth required to support an isolated 200-attosecond pulse around 15 eV is ∼5 eV. In contrast, the 10-fs VUV pulse train used here corresponds to a comb of VUV harmonics, each with a FWHM bandwidth of 183 meV, which can be tuned in the frequency domain (26) to coherently and selectively excite multiple electronic states.

Experiment

Fig. 1 illustrates our concept for attosecond coherent control of molecular dynamics. A neutral deuterium molecule is electronically excited and ionized by combined phase-locked VUV harmonics (7ω–13ω) and ultrafast IR (ω) pump fields at a center laser wavelength of 784 nm (see SI Text for further details). A second control IR pulse is time-delayed with respect to the combined VUV + IR fields. For simplicity, only the two most relevant electronically excited states of different parity in D₂ are shown in Fig. 1. As we will explain in more detail below, interferences between electron wave packets excited by the combined VUV harmonics (i.e., 7ω, 9ω, and 11ω) and the IR field (ω) are used to manipulate the ionization and excitation probabilities of different electronic states of the excited neutral molecule. To modulate the total electronic excitation in the neutral molecules on attosecond timescales, we use two-pathway quantum interference of electronic wave packets excited by 7ω + ω and 9ω − ω. Simultaneously, to modulate the total ionization yield on attosecond timescales, we use two-pathway quantum interference of electronic wave packets excited by 9ω + ω and 11ω − ω as the main mechanism. Finally, by tuning the VUV excitation wavelengths, we achieve other degrees of coherent control of coupled electron–nuclear wave packet dynamics, including vibration, ionization, and tunneling. First, we show how the population of two electronic states can be switched (i.e., between EF and B) on attosecond timescales (Fig. 1, Lower Left). Second, we show that by tuning the energy of the VUV harmonic comb, we can excite and control the population of different electronic and vibrational states, which in turn dictates how the neutral molecule vibrates and ionizes. Third, by exciting D₂ using tunable two-color VUV and IR fields, and then probing the dynamics using a second IR pulse, we can control tunneling of nuclear wavepackets in the EF potential of a neutrally excited D₂.

Fig. 1.

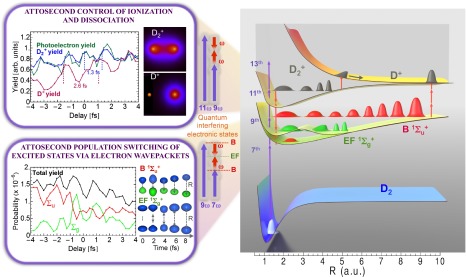
Attosecond control of the excitation and ionization pathways of D₂ on short timescales. (Right) Simplified potential energy surfaces of the D₂ and . The purple and red arrows represent the VUV harmonics and IR photons used to coherently control the populations of the excited neutral and ion states in the Franck–Condon region through two-pathway quantum interference of electronic wave packets in B, B* (single photon) and EF (two photon) states. (Lower Left) Calculated excitation probabilities into states of Σ_u and Σ_g symmetries of neutral H₂ (dominated, respectively, by the B and EF states) as a function of time delay. The blue lobes, plotted on the right of the panel, are sketches of the Σ_u and Σ_g orbitals representing the excited electron dynamics. Theoretical predictions show that the electronically excited populations can be switched between the even B and odd parity EF potentials on attosecond timescales, which can in turn control how the molecule vibrates. (Upper Left) The experimental photoelectron 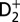and D⁺ yields modulate on full and half-cycle attosecond timescales, as the delay between the pump VUV + IR and control IR pulses is scanned.

In our experiment, the seventh and ninth harmonics coherently excite the molecule from its ground state, creating two nuclear wave packets in the same, odd-parity (i.e., 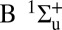) potential energy surface of D₂. When a small portion of the driving IR field (at an intensity of 3 × 10¹¹ W/cm²) copropagates with the VUV harmonics, we can also simultaneously populate the optically forbidden, even-parity (i.e., 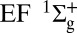) potential energy surface through two-photon (i.e., 7ω + ω, 9ω − ω) absorption processes. A second, time-delayed, and stronger IR (ω) pulse (at an intensity of 4 × 10¹² W/cm²) is then used in two different ways. First, on short attosecond timescales, the delayed IR field interferes with the IR field that copropagates with the VUV harmonics, and serves as a knob to control the excitation and ionization processes on attosecond timescales in the Franck–Condon region, by means of electron wave packet interferometry. Second, on long femtosecond timescales, the delayed IR field serves as a femtosecond knob to control the dissociation process by selectively ionizing the molecule at some optimal time after excitation. In this experiment, we used the Cold Target Recoil Ion Momentum Spectrometer (COLTRIMS) technique (28) to simultaneously collect the full 3D electron and ion momenta of all of the reaction products, which include 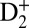and an electron, as well as the D⁺ dissociative ions (SI Text). All of the pulses (VUV attosecond pulse trains and two IR fields) were linearly polarized in the same direction. The VUV pulse duration was 5–10 fs, and the IR pulse durations were 30 fs. By changing the pressure in the gas-filled capillary, we can fine-tune the exact photon energies of the VUV harmonics while keeping the IR wavelength constant. This capability is key for uncovering the control mechanisms.

We first examine the attosecond control pathways at early times, before the onset of large-period vibrational wavepacket dynamics. Fig. 1, Upper Left plots the experimental photoelectron, 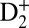, and D⁺ yields when the pump (VUV + IR) and the control (IR) pulses were overlapped in time, as a function of the time delay between them (see SI Text for additional data taken when the VUV harmonics were tuned to different photon energies). Very rapid, suboptical-cycle modulations in the photoelectron and 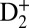yields result from the combination of optical interferences (two IR pulses) and quantum interferences of electronic wavepackets (i.e., 9ω + ω and 11ω − ω interfering pathways), as the phase of the control IR pulse changes relative to the pump VUV + IR pulse. Half-a-cycle periodicity suggests that the two-pathway quantum interferences play an important role in this particular case (29). The deep, full-cycle modulation of the dissociative D⁺ yield is simply a result of the optical interferences between the pump and control IR pulses (both 30 fs long) that lead to bond-softening of the ground state of 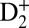and ionization of the 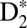excited states ∼10 fs after the pump pulse. Because the dissociation by bond-softening occurs after the VUV pulse is gone, this signal provides a reference point of the absolute phase in between the two IR pulses at each time delay, and allows us to precisely know the phase of the quantum interferences relative to the laser field.

Theoretical calculations (Fig. 1, Lower Left) show that the electronic population in the excited states also oscillates, with the same half-cycle periodicity. Moreover, theoretically, we can remove the parity degeneracy in the total excitation yield and see that the populations in the gerade and ungerade B and EF states are out of phase. Thus, a two-pathway quantum interference of the electron wave packets driven by the lower two harmonics and the delayed IR field (i.e., 7ω + ω vs. 9ω − ω, Fig. 1, Lower Left) can be used as an ultrafast population switch between even (EF) and odd parity (B) potentials; this demonstrates that the interference of electronic wavepackets can be used to switch and steer the electronically excited states on attosecond time scales, allowing simultaneous control of the electronic and vibrational excitation of an excited neutral 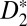molecule. Thus, we demonstrate how combined attosecond VUV and IR femtosecond fields can be used as a unique tool to coherently control chemical reactions on the fastest timescales.

It is worth noting that though there are other possible interfering pathways responsible for the excitation and the ionization yield modulations, they are significantly less likely because they require more photons. For example, the interference of electronic wave packets excited by 7ω3 + ω and 11ω − ω is possible. In this case, the total ionization probability is controlled by coupling the lower vibrational states of the B potential excited by the seventh harmonic, with the continuum electron wave packets created by the 11th harmonic. Though this channel competes with the state excited by the ninth harmonic, it requires absorption of four photons, and is thus much less probable compared with the pathway requiring absorption of two photons (one VUV and one IR).

Theory

Because we solve the full 3D time-dependent Schrödinger equation (TDSE) for H₂ exposed to a combined VUV and IR fields, we can theoretically examine the attosecond control mechanisms by fine-tuning the photon energy of the VUV pulse. The TDSE is numerically solved by expanding the time-dependent wave function in a large basis of Born–Oppenheimer molecular states, which are obtained by diagonalization of the electronic and nuclear Hamiltonians of H₂ (SI Text). The method includes all electronic and nuclear degrees of freedom and, therefore, accounts for electron correlation and the coupling between the electronic and nuclear motions. Time evolution starting from the ground state induces transitions between the Born–Oppenheimer states through laser-molecule and potential couplings. To make these complex calculations tractable, in the simulation we used IR and VUV pulses of 7.75 fs total duration. Although these pulses were shorter than the ones used experimentally (30 fs and 5–10 fs, respectively), a direct comparison between the theory and the experiment can still be made during the time-delay interval when the pump and probe pulses overlap. The theoretical results are shown in Fig. 2, and capture the main experimental observations—that the total yields modulate on attosecond timescales, and that the periodicity and the amplitudes of the oscillations strongly depend on the exact central energy of the VUV pulse. Here, we keep the IR laser wavelength constant while blue-shifting the VUV central wavelength as although the higher harmonics were generated by 784 nm, 770 nm, and 760 nm laser wavelengths shown, respectively, in Fig. 2. Not surprisingly, the modulation of the total ionization yield strongly depends on the exact energy of the VUV harmonics because the phases and the amplitudes of the interfering electron wave packets strongly depend on the laser-modified electronic structure of the molecule (28). In the case of H₂, as the central energy of the VUV beam blue-shifts from harmonics of 784 nm to harmonics of 740 nm, the ninth harmonic does not excite the B state in the Franck–Condon region, but accesses higher electronic states (SI Text). In this regime the Born–Oppenheimer approximation breaks down, because the evolution of the nuclear wavepackets in the B and EF potentials is on the same timescale as the duration of the attosecond VUV pulse train (Fig. 1, Lower Left) and can influence the electron wave packet interference process as well. These results thus demonstrate that we can precisely control which electronic states are excited by the tunable VUV harmonics, and show how these states can be switched on attosecond timescales.

Fig. 2.

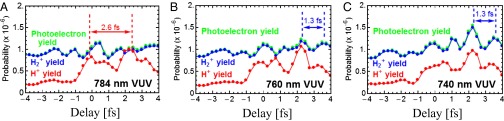
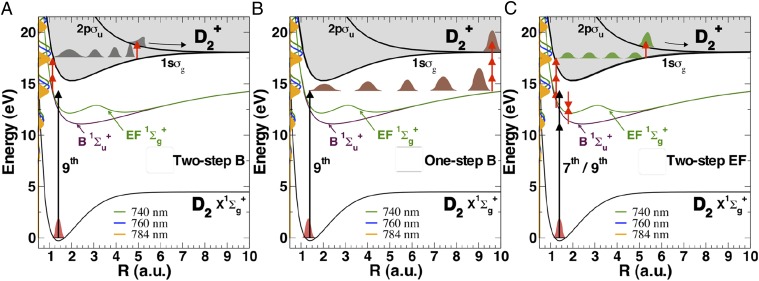
Theory of attosecond VUV coherent control of H₂ ionization/dissociation channels. (A–C) As the central photon energy of the VUV harmonics is blue-shifted from an effective driving laser wavelength of 784 nm to 740 nm, the total ionization yield switches to half-cycle periodicity due to different electronic wave packet interferences, thus demonstrating attosecond coherent control over the interfering electron wave packets and ionizing pathways in molecules.

Multiscale Quantum Control of Electronic and Nuclear Dynamics

To show experimentally how tunable attosecond VUV pulse trains can be used to precisely control the excitation probabilities of different electronic and vibrational states, and how to steer ionization and dissociation in 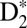, we delay the control IR field relative to the VUV + IR pump field on femtosecond timescales. Fig. 3 illustrates several possible ionization and dissociation pathways and plots the energies of the three different attosecond VUV harmonic combs we used to coherently and simultaneously control electronic and vibrational excitation, as well as nuclear wave packet tunneling in the EF potential. 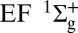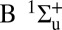The combined 7ω + ω, 9ω − ω, and 9ω fields coherently populate the and states, respectively. These nuclear wave packets oscillate with periods that depend on the exact energy of the VUV harmonics, and can couple the ground state to different vibronic bands of the B and EF potentials. The probe IR pulse can then ionize and dissociate 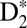through different channels as the electronically excited neutral molecule vibrates. Here we focus only on three channels that leave the most visible signature in the kinetic energy release (KER) spectrum of D⁺, which we label as two-step B, one-step B, and two-step EF (Fig. 3). In the two-step B case (Fig. 3A), the nuclear wave packet launched in the B state by the ninth harmonic is first probed in the inner classical turning point of the B potential energy curve by absorption of two IR photons, thus ionizing the Rydberg electron from the B potential and launching a second nuclear wave packet in the 1sσ_g state of 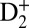. When the nuclear wave packet reaches the outer classical turning point of the 1sσ_g potential energy curve (after ∼ 10 fs), absorption of another IR photon, from the same probe IR pulse, leads to an efficient coupling of the bound 1sσ_g and the dissociative 2pσ_u states of the ion, thus leading to dissociation into D + D⁺ by a total absorption of 2 + 1 (i.e., three IR photons; Fig. 3A). Through this two-step channel, the molecule dissociates with a kinetic energy release of ∼0.7–0.9 eV, typical for a bond-softening process.

Fig. 3.

Combined coherent control of electronic and nuclear wave packet dynamics on longer timescales. (A) Two-step B mechanism (D⁺ high kinetic energy). (B) One-step B mechanism (D⁺ low kinetic energy). (C) Two-step EF mechanism (D⁺ high kinetic energy). We also show the tuning range of the VUV harmonics on the y axis (i.e., effective driving laser wavelengths of 784 nm, 760 nm, and 740 nm).

In the one-step B case (Fig. 3B), the neutral molecule first stretches to internuclear distances well beyond 9 a.u., which results in an increase of the effective ionization potential. At the instant the nuclear wave packet reaches the outer classical turning point of the B potential, the ionization of the molecule requires absorption of three IR photons. Through this channel, the nuclear wave packet is directly coupled to the 2pσ_u dissociative continuum and the molecule dissociates with lower KER compared with the two-step B case. Due to the absorption of an extra IR photon at the outer turning point, a modulation of the ionization probability is expected as the excited molecule vibrates in the B potential. Finally, in the two-step EF case (Fig. 3C), the nuclear wave packet launched by two-photon absorption (7ω + ω and 9ω − ω) is probed in the inner classical turning point of the EF potential energy curve by absorption of three IR photons, which generates a nuclear wave packet in the 1sσ_g potential, but with smaller probability compared with the two-step B case because the probability of observing this channel corresponds to a sequential absorption of 3 + 1 IR photons.

Fig. 4 validates the rich opportunities for state-selective, coherent excitation of multiple nuclear wave packet dynamics of neutrally excited D₂, as well as a possibility of controlling bond-breaking and dissociation through the pathways illustrated in Fig. 3. Fig. 4A plots the experimental D⁺ KER as a function of the pump-probe delay, whereas Fig. 4D plots the corresponding 2D Fourier transform (FT). One can clearly see oscillation periods of ∼83 fs and 58 fs at a D⁺ KER of 0.7–0.9 eV, corresponding to the vibrational wave packets in the B and EF states, respectively, that are obtained through the two-step B and two-step EF mechanisms. The larger probability of the one-step B channel vs. the two-step EF channel (Fig. 4D), confirms the three vs. four IR photon absorption mechanisms. Moreover, Fig. 4A shows that the two-step B channel (high KER) has a larger probability than the one-step B channel (low KER), due to a lower effective ionization potential of the excited molecule at shorter internuclear separation. Fig. 4A also shows that the two-step B and the one-step B channels are dephased, because the nuclear wave packet is probed at different times in those channels; this allows for steering of a desired dissociative route by precisely timing the second IR laser pulse as the neutral molecule vibrates.

Fig. 4.

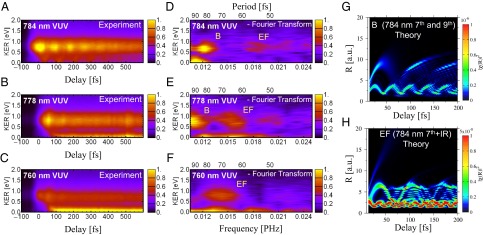
Controlling the dissociation channels by tuning the photon energy and through nuclear wave packet dynamics. (A–C) D⁺ kinetic energy release resulting from dissociation using three different VUV frequency combs that can be tuned to excite different 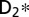electronic and vibrational states. (D–F) Corresponding 2D Fourier transforms of the D⁺ kinetic energy releases. (G) Calculated free evolution of the nuclear wave packets generated by the combined VUV + IR pulses in the B potential energy surface. (H) The same for the EF potential energy surface.

As seen in Fig. 1, to reach the outer turning point of the double-well EF potential and the vibrational period of ∼58 fs, the nuclear wave packet needs to tunnel through the potential barrier, which decreases the probability of observing the EF nuclear wave packet dynamics. The calculations nicely confirm the observed periodicities of these multiple nuclear wave packet dynamics in 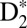(Fig. 4 G and H). To model the dynamics of D₂ on femtosecond timescales, we first solved the TDSE to calculate the excitation probabilities, and then propagated the corresponding nuclear wave packets in the given 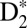potentials (see the SI Text for more detail on how the calculations were done). For example, Fig. 4G clearly shows how the EF nuclear wave packet starts reflecting and tunneling through the inner barrier at about R = 3 a.u. and 10 fs after the excitation. We also see that the nuclear wave packet tunnels with ∼20% probability compared with the main wave packet motion occurring in the inner well of the EF double-potential well. Moreover, the other striking feature of this calculation starts at ∼45 fs, when the nuclear wave packet in the inner well tunnels through the inner barrier for the second time and meets the outer-well nuclear wave packet on its way back from the outer classical turning point. The interference of the different nuclear wave packets is clearly visible from 45 fs onward. As the time evolves, multiple reflections/tunneling events from both sides of the inner barrier and the interferences of the nuclear wave packet in the EF potential are responsible for the fast decoherence of the EF nuclear wave packet. Movies, theoretical Fourier transforms, and further discussions illustrating dynamics in the 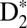are given in SI Text.

Finally, by blue-shifting the VUV harmonic wavelengths to effective driving wavelengths of 778 nm and 760 nm (while keeping the IR wavelength fixed at 784 nm), we can control the relative population of the different neutrally excited states of D₂. Fig. 4 B and C show the KER spectra as a function of pump-probe time delay, and Fig. 4 E and F plot the corresponding 2D Fourier transforms. Two striking features are apparent. First, by slightly increasing the energies of the seventh and ninth harmonics, the vibration periods in the B and EF potentials simultaneously increase due to excitation to higher vibrational levels in the Franck–Condon region. Second, the relative strength of the one-step EF channel increases compared with the two-step B channel. The latter feature can be explained as follows. As seen in Figs. 1 and 3C, simultaneous absorption of 7ω + ω and 9ω − ω creates a nuclear wave packet that can tunnel through the inner potential barrier (located at R = 3.5 a.u.) of the double-well EF potential. By slightly increasing the energy of the seventh harmonic, the tunneling process becomes more probable, thus increasing the nuclear wave packet density that vibrates with longer periods; this increases the relative visibility of the two-step EF channel with respect to the two-step B channel. For an effective driving wavelength of 760 nm, higher vibration levels of the EF potential are excited, allowing the nuclear wave packet to propagate freely above the inner barrier, moving along the EF potential energy curve with a vibrational period that is now close to that observed in the B state. Again, this interpretation is confirmed by TDSE calculations given in SI Text.

Finally, the two-step B channel also disappears when excited by 760 nm VUV harmonics, because the coupling of the ground and B states dramatically decreases in the Franck–Condon region. In this case, the ninth harmonic excites higher electronic states (i.e., B′ as shown in SI Text). Thus, we show how tunable attosecond VUV radiation can be used to precisely control excitation of different electronic and vibrational states.

Conclusions

In conclusion, we present a powerful approach for using tunable VUV and IR attosecond pulse trains to coherently excite and control an outcome of a simple chemical reaction in a D₂ molecule. The interference of electronic wave packets excited by multicolor VUV and IR fields can be used to control excitation and ionization on attosecond timescales while maintaining good energy resolution and state selectivity. Selective bond-breaking is achieved by controlling the excitation wavelength as well as the time delay between the pump and probe pulses. We also observe and control the nuclear wave packet tunneling in the double-well EF potential. This work thus demonstrates broad and unique capabilities for doing attosecond chemistry.