Significance
Animals can adapt the frequency and shape of their oscillatory body movements during locomotion in response to changes in the environment. Although central pattern generators (CPGs) are known to be the basic neuronal circuits responsible for generation of rhythmic movements, no conclusive evidence has so far been found to attribute adaptive behaviors solely to the function of CPGs. We have found a blueprint of a design by nature in terms of mathematical equations. Experimental and computational studies presented in this article demonstrate that CPGs are indeed capable of adapting oscillations to the environment through sensory feedback, but without detailed guidance from the brain.
Abstract
Owing to the complexity of neuronal circuits, precise mathematical descriptions of brain functions remain an elusive ambition. A more modest focus of many neuroscientists, central pattern generators, are more tractable neuronal circuits specialized to generate rhythmic movements, including locomotion. The relative simplicity and well-defined motor functions of these circuits provide an opportunity for uncovering fundamental principles of neuronal information processing. Here we present the culmination of mathematical analysis that captures the adaptive behaviors emerging from interactions between a central pattern generator, the body, and the physical environment during locomotion. The biologically realistic model describes the undulatory motions of swimming leeches with quantitative accuracy and, without further parameter tuning, predicts the sweeping changes in oscillation patterns of leeches undulating in air or swimming in high-viscosity fluid. The study demonstrates that central pattern generators are capable of adapting oscillations to the environment through sensory feedback, but without guidance from the brain.
A long-term ambition in neuroscience is to generate a detailed, complete model of the human brain (1). Still ambitious, and certainly more realistic, is the aim to model components of vertebrate nervous systems. Most advanced in this arena are models based on the circuits underlying motor functions, such as rhythmic body movements during locomotion. These movements are generated by spinal neural oscillator circuits called central pattern generators (CPGs) (2, 3). The enormous number of neurons in the vertebrate central nervous system currently prevents analysis at the level of defined circuits between individual neurons. However, the simpler, accessible CPGs underlying locomotion in the invertebrates provide dynamically rich platforms amenable to detailed analysis that can lead to deep understanding of how neuronal circuits generate extremely robust and adaptive oscillatory behaviors. The leech CPG for undulatory swimming provides such a platform. The isolated nerve cord, with most (4, 5), a few (6, 7), or even a single segmental ganglion (8, 9), displays “fictive swimming,” where the rhythmic motor pattern closely resembles that recorded in intact animals. Moreover, the leech continues to swim without the brain (10, 11), with the nerve cord severed in midbody (5), or with the body cut in half (7).
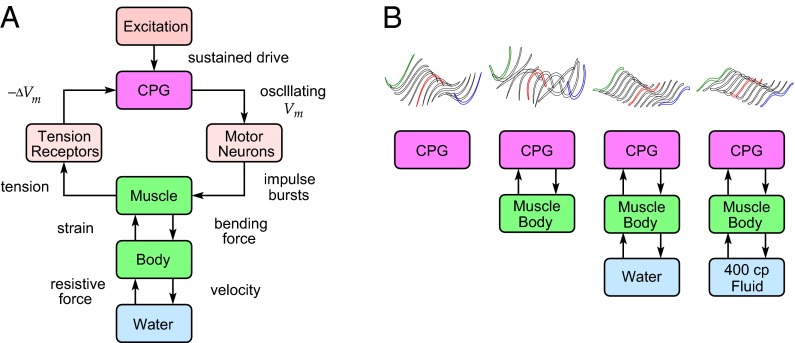
Our study addresses the following question: How does the leech swimming system achieve its astonishing robustness and adaptability? A detailed explanation of the mechanisms underlying such complex phenomena requires mathematical modeling and analysis because a unidirectional sequence of cause-and-effect relationships alone cannot explain dynamical properties arising from multiple feedback loops. An obstacle in exploring the emergence of the functional properties from highly interconnected neuronal circuits through model-based analysis is the lack of biological realism (1). We, therefore, have focused on the individual components of the leech swimming system and developed dedicated models, with full experimental validations, for capturing essential dynamics of the CPG (12), motoneuron (MN) impulse adaptation (13), passive and active muscle dynamics (14, 15), body–fluid interactions (16), and, finally, sensory feedback of body wall tension from peripheral receptors to the CPG (17). Here we put it all together (Fig. 1A) and show that the quantitative description of the comprehensive system can accurately reproduce nominal swimming behavior. Whereas we focus on closing the loop from motor output to sensory input at the CPG, higher-level excitation to the system (18) has been modeled simply as a constant input to the CPG. The integrated model, without further parameter tuning except for the excitatory input, predicts the results of biological experiments that place the leech far outside its normal environment. Namely, model simulations are found remarkably accurate in predicting adaptation of the undulatory body movements to perturbed environments: a shorter wavelength of traveling waves in a high-viscosity fluid (400 cp) and standing waves in air (Fig. 1B). Our results indicate that CPGs autonomously achieve adaptive pattern formation through sensory feedback, without descriptive signaling from the brain. This component-based analytical model provides an exemplar for those more ambitious projects to model the human brain. Our studies achieved an integrated, comprehensive description of an entire neuromechanical system that generates animal locomotion.
Fig. 1.
Neuronal control system for rhythmic movements of the leech. (A) Integrated view of feedback interactions between dynamical components. Body undulations during swimming result from interconnections of neuronal oscillator circuits, muscle-activated body, and fluid. (B) CPG adapts to environment through sensory feedback. Various body oscillation patterns (3D visualization in upper trace) are exhibited in different environments (lower trace).
Results
Integrated Model of Leech Swimming.
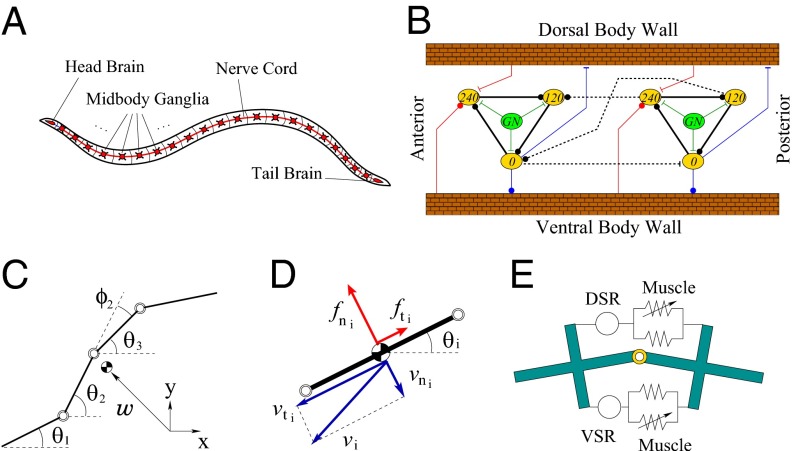
The leech is an elongated annelid that swims by vertically undulating its flattened, segmented body, sending traveling waves from head to tail, with the wavelength roughly equal to the body length (Fig. 2A). The undulation results from antiphasic local contractions of dorsal and ventral longitudinal muscles that propagate along the flexible body, interacting with fluid. The muscle contractions are controlled by bursts of efferent spikes from excitatory and inhibitory MNs, whose somata are found within all of the 21 midbody ganglia (M1–M21) of the ventral nerve cord. The bursting pattern in MNs is controlled by a group of 13 identified interneurons that are repeated serially in each ganglion of the nerve cord. Local, intrasegmental interactions between these interneurons form a segmental oscillator. These segmental oscillators are interconnected in a chain through the nerve cord, with intersegmental projections spanning about six segments. These complex interneuron circuits, comprising local, non-spike-mediated synaptic interactions and intersegmental, spike-mediated connections, form the CPG for leech swimming (19–22).
Fig. 2.
Leech swimming system. (A) Overview. (B) CPG circuit model; two segments are shown (repeated for 17 segments). Yellow ovals with inhibitory synapses (solid black lines) constitute a segmental oscillator; numbers indicate oscillation phase. Green ovals and lines indicate gating neuron excitation. Intersegmental connections (dashed lines) extend to five neighboring segments. Additional symbols: blue lines, muscle activation; red lines, stretch receptor feedback. (C) Leech body modeled by a chain of 18 rigid links (four shown). (D) Fluid force is determined from normal and tangential link velocities, with inertial and viscous drags. (E) Dorsal/ventral longitudinal muscles connect adjacent links. Springs represent passive and active tensions; the latter is driven by the CPG. Dorsal/ventral stretch receptors report tension.
We developed an integrated model of leech swimming by assembling the previously developed component models (Fig. 1A). Each component has complex dynamics; a major challenge of our analytical approach is to identify and retain only those elements that are essential for swimming. Our simplified component models are described in the following paragraphs and their mathematical details are given in Supporting Information.
CPG.
We modeled the CPG as a chain of 17 segmental oscillators embedded in midbody ganglia M2–M18 (12). During fictive swimming, 13 interneurons within each ganglion generate rhythmic bursting at three phases: 0°, 120°, and 240° (19). In our model (Fig. 2B, 2 of the 17 segments), each phase group is represented by a single neuron (yellow oval), three of which form a segmental oscillator through a simple recurrent cyclic inhibition loop (black solid lines). We use the simple three-neuron model because the details within each segment are not important for intersegmental phase coordination as long as the intrasegmental phases are captured correctly (23), and model complexity can then be significantly reduced. Dynamics for neurons and their synaptic interactions were modeled by a threshold function, time lag, and communication delay using experimentally derived input–output membrane potential data (21, 24–26). Topological structures in Fig. 2B were determined from detailed physiological data for neuronal interconnections between segments (dashed lines) (21, 27), for tension by MN activity (blue lines) (15, 28, 29) and for sensory feedback of muscle tension via stretch receptors (red lines) (5, 17, 30–32). Each segmental oscillator receives a constant excitatory input (assumed uniform over segments) from the gating neuron, which has the effect of controlling the cycle period (12).
Body–fluid interactions.
The leech body is supported by internal hydrostatic pressure, resulting from tonic activation of dorso-ventral muscles in conjunction with passive tonus and active contractions of the longitudinal muscles (19, 33). The mechanics of the leech body were modeled (16, 34) as a chain of 18 rigid links (Fig. 2C). We adopted this discrete model rather than a continuum beam model (35) because the leech body as well as the nerve cord (CPG) are indeed segmented. The essential hydrodynamic effects were captured by resistive force theory (36), with larger normal than tangential drag (Fig. 2D). The drag coefficients were determined from experimental kinematic data (16).
Muscle dynamics with MN activation.
We developed a model for leech longitudinal muscle and its neuronal activation through physiological experiments on semi-intact preparations (15). The tension developed in each segment is described as a dynamic function of the muscle strain and MN impulse frequency and can be viewed as a pair of parallel passive and active springs; the stiffness of the latter is controlled by MN activation. The muscle model is placed at each of the 17 joints (Fig. 2E) to generate tensions on the dorsal and ventral sides. The tension difference between the two sides gives rise to the muscle bending moment, which shapes body undulations. Each segmental CPG commands local muscle contraction through MN activation dynamics containing a time lag and impulse adaptation (13). CPG interneurons form a complex set of interactions with MNs to ensure that dorsal muscle is excited at 0° and inhibited at about 180°, and ventral muscle is driven in antiphase. Our model captures the net effect of experimentally identified excitatory/inhibitory MN connections (19), but for simplicity Fig. 2B schematically indicates the dorsal–ventral phase relationships and does not show the topologically correct interactions between CPG neurons and the longitudinal muscles through MNs (22, 29).
Stretch receptor.
In the leech, increased tension in longitudinal muscle hyperpolarizes the ventral stretch receptors (VSRs), which are strongly electrically coupled with an interneuron (cell 33) in the 240° phase group (17). Dorsal stretch receptors (DSRs) also have been identified, but their connections to the CPG are conjectural (19), and hence the model assumes that the effects of the two receptor types are antiphasic. The tension in longitudinal muscle is thus transduced by both dorsal and ventral stretch receptors (Fig. 2E) and fed back locally to segmental CPGs (Fig. 2B). In the model, the net effects of DSRs and VSRs are captured as sensory feedback of muscle bending moments, rather than the individual dorsal/ventral tensions. The effective strength of the sensory feedback is unknown, hence the 17 strength parameters for all of the segments were tuned to match the model-simulated body movement with experimental data under nominal swimming conditions.
The sensory gains are the only model parameters that were tuned; all other parameters were already fixed through experimental measurements when we developed the component models. Once tuned for the nominal condition, the sensory gains were fixed during model simulations under perturbed conditions. Overall, all simulations reported here were performed for a single set of parameter values, except that the control of frequency (excitatory neuron input to the CPG) was adjusted in the high-viscosity case.
Sensory Modification of Wave Number.
Body movements of midsize (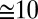 cm length) leeches were video recorded from the side while they swam nearly horizontally through a narrow tank of water. A representative sample of snapshots during one cycle of undulation is shown in Fig. 3 A1. The leech body forms roughly one full period of a quasi-sinusoidal traveling wave at each time instant, with crests passing from head to tail. The number of waves expressed by the body (body wave number) can be quantified as the time it takes for a wave to travel from head to tail, divided by the cycle period. The leech progresses about
cm length) leeches were video recorded from the side while they swam nearly horizontally through a narrow tank of water. A representative sample of snapshots during one cycle of undulation is shown in Fig. 3 A1. The leech body forms roughly one full period of a quasi-sinusoidal traveling wave at each time instant, with crests passing from head to tail. The number of waves expressed by the body (body wave number) can be quantified as the time it takes for a wave to travel from head to tail, divided by the cycle period. The leech progresses about 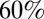 of the body length in one cycle. The cycle period, swim speed, and body wave number are summarized in Table 1, row B1.
of the body length in one cycle. The cycle period, swim speed, and body wave number are summarized in Table 1, row B1.
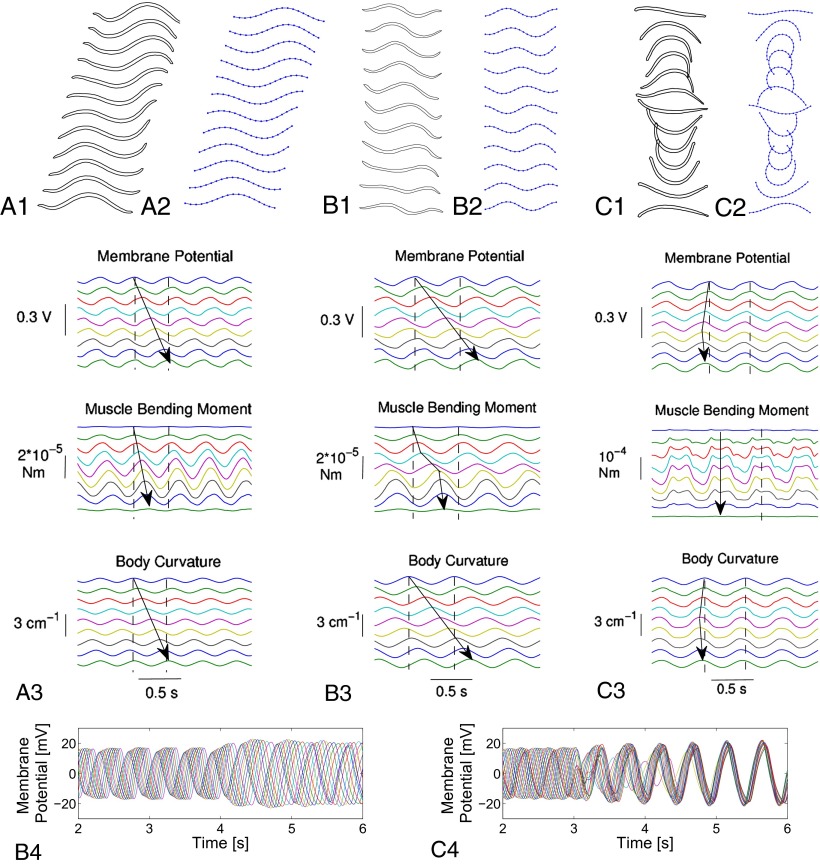
Fig. 3.
Undulatory movements of leech swimming. (A) In water. (A1) Intact animal (30 frames per second). The body expresses a full spatial period of a quasi-sinusoid wave traveling to the right (swim progression is to left). (A2) Simulated swimming (11 frames per cycle). (A3) Underlying traveling waves (arrows) at segments  . The time interval between the two vertical dashed lines is the cycle period. (B) In high-viscosity fluid (400 cp). (B1) Intact animal (15 frames per second). (B2) Simulated swimming (10 frames per cycle). (B3) Underlying traveling waves (arrows) at segments
. The time interval between the two vertical dashed lines is the cycle period. (B) In high-viscosity fluid (400 cp). (B1) Intact animal (15 frames per second). (B2) Simulated swimming (10 frames per cycle). (B3) Underlying traveling waves (arrows) at segments  . Dashed lines indicate cycle period. (B4) Adaptive behavior of the CPG. With model leech initially swimming in water, fluid viscosity was raised from 1 cp to 400 cp at time
. Dashed lines indicate cycle period. (B4) Adaptive behavior of the CPG. With model leech initially swimming in water, fluid viscosity was raised from 1 cp to 400 cp at time 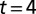 s; simultaneously the excitatory input to CPG was reduced at
s; simultaneously the excitatory input to CPG was reduced at 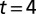 s to a quarter of the nominal level. The time courses of the membrane potentials of 0° phase group neurons in segments
s to a quarter of the nominal level. The time courses of the membrane potentials of 0° phase group neurons in segments  are shown. The phase lag and amplitude of traveling waves increase owing to higher viscosity. (C) In air. (C1) Debrained animal (30 frames per second). Without hydrodynamic forces, rostro-caudal wave progression is minimal; movements of body ends are in-phase, alternating between a “∪” and a “∩” shape every half cycle. (C2) Simulated movements (12 frames per cycle). (C3) Underlying traveling waves (arrows) at segments
are shown. The phase lag and amplitude of traveling waves increase owing to higher viscosity. (C) In air. (C1) Debrained animal (30 frames per second). Without hydrodynamic forces, rostro-caudal wave progression is minimal; movements of body ends are in-phase, alternating between a “∪” and a “∩” shape every half cycle. (C2) Simulated movements (12 frames per cycle). (C3) Underlying traveling waves (arrows) at segments  . The dashed lines show cycle period. (C4) Adaptive behavior of the CPG. With the model leech swimming in water, fluid is removed at
. The dashed lines show cycle period. (C4) Adaptive behavior of the CPG. With the model leech swimming in water, fluid is removed at 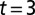 s. The time courses of the membrane potentials of 0° phase group neurons are shown for all segments. The traveling waves in water are modified to become standing waves in air.
s. The time courses of the membrane potentials of 0° phase group neurons are shown for all segments. The traveling waves in water are modified to become standing waves in air.
Table 1.
Characteristic parameters of leech data and model output
| Condition | Fluid | Viscosity, cp | Intrinsic period, ms | Period, ms | Swim speed, cm/s | Body wave no. | CPG wave no. |
| Leech data | |||||||
| A | — | — | 700–900 | — | — | — | 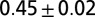 |
| B1 | Water | 1 | 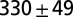 |
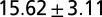 |
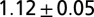 |
||
| B2 | Meth. cel. | 400 | 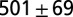 |
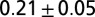 |
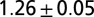 |
||
| C1 | Water | 1 | 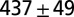 |
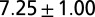 |
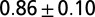 |
||
| C2 | Air | 0 | 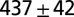 |
— | — | ||
| C2* | Air | 0 | 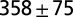 |
— | 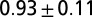 |
||
| Model output | |||||||
| a | — | — | 800 | — | — | — | 0.33 |
| a* | — | — | 423 | — | — | — | 0.48 |
| b1 | Water | 1 | 423 | 391 | 12.57 | 1.12 | 0.99 |
| b2 | Meth. cel. | 400 | 563 | 548 | 0.18 | 1.50 | 1.33 |
| c2 | Air | 0 | 423 | 490 | — | — | — |
| c2* | Air | 0 | 423 | 398 | — | 1.03 | 0.91 |
Leech swimming under four conditions (upper): A, isolated nerve cord; B1, freely swimming intact animals in water and B2, in 400 cp methyl cellulose (Meth. cel.) solution; C1, suspended leeches in water; and C2 and C2*, suspended leeches in air. Model dataset for leech swimming is matched to these conditions (lower): a and a*, CPG without sensory feedback at different excitatory input levels; b1, water; b2, 400 cp Meth. cel.; and c2 and c2*, air. Intrinsic period is the cycle period in the isolated nerve cord (leech data) or of the CPG without sensory feedback (model). Body wave number is defined as the time it takes for a body wave to travel from head to tail, divided by the cycle period. CPG wave number is the time it takes for a wave in the MN membrane potential to travel from M2 to M18, divided by the cycle period. Values are means and SDs. Data for A and B were derived from experiments on five leeches; those in A were published in ref. 5. Data for C were derived from air and water swimming in three animals, two of which provided the data for C2*. Model results were generated by simulations of analytical equations with the parameter set shown in Table S1.
The leech CPG in isolated nerve cords exhibits fictive swimming, where the pattern of oscillation in interneuron membrane potentials is similar to the body waves observed during intact swimming. That is, the membrane potentials oscillate at a common frequency, with the maximum occurring at each ganglion a fixed fraction of cycle later than the adjacent anterior ganglion, thereby exhibiting traveling waves. Thus, the wave number for the CPG can be defined as the time interval between two successive maxima of M2 and M18 membrane potentials, divided by the cycle period. This value would correspond to the body wave number if the membrane potentials were directly proportional to the body curvature at respective locations (Fig. 1B). Interestingly, the cycle frequency and wave number in fictive swimming do not closely match with, but are roughly half of, the values observed during intact swimming (Table 1, compare rows A and B1).
We initially thought that sensory feedback was solely responsible for the differences in the oscillation profiles. However, when the CPG model that closely captures the fictive swimming (Table 1, row a) was placed in the feedback loop in Fig. 1A, our attempts to tune the sensory feedback parameters failed to reproduce the nominal swimming behavior (Fig. 3 A1). Because excitatory inputs from gating neurons are known to increase the cycle frequency of fictive swimming (12), we increased the excitatory input to a level at which the intrinsic period of the CPG model was reduced by half (Table 1, row a*). With this modification, sensory parameters in the integrated model were retuned. Model simulations then indicated stable oscillations at a cycle frequency within the observed intact swimming range. Moreover, the sensory feedback increased the wave number to one; that is, a full wave (Table 1, row b1). The snapshots of simulated leech are shown in Fig. 3 A2. Thus, swimming movements in the model leech closely resemble those of live animals.
The model simulation predicts internal variables that are difficult to measure during swimming (Fig. 3 A3). It takes about one cycle for the crests of the body curvature to travel from head to tail (indicated by an arrow), resulting in one full wave in each snapshot. The speed of the traveling waves is roughly the same for the intersegmental progression of CPG membrane potentials but is much greater for the bending moment, consistent with the prediction previously derived from analysis of muscle, body, and fluid mechanics (37). The speed difference sets the timing of the moment and curvature in-phase near head, antiphase near tail, and 90° apart in the middle. The instantaneous muscle power is proportional to the product of the moment and the rate of change of curvature, and hence the average power is roughly equal to zero near head and tail and is positive in the midbody. Consequently, the energy for swimming is mainly supplied by midbody muscles, and the tail end oscillates almost passively (37).
More Waves in High-Viscosity Fluids.
Experiments on leeches swimming in high-viscosity fluid (methyl cellulose solutions) reveal that the frequency and pattern of body undulation are modified from that of nominal swimming in water. In particular, at 400 cp, the cycle period was increased by about 50%, the swim speed was reduced to about 1% of the nominal value, and the body wave number was increased by more than 10%. These parameters are summarized in Table 1, row B2; snapshots of the altered swimming behavior are shown in Fig. 3 B1. Two crests or troughs are clearly seen in the body wave simultaneously.
The observed behavior was not initially reproduced when the integrated model was simulated under 400 cp high-viscosity condition. However, if the excitatory input to the CPG was reduced to increase the intrinsic period from 423 ms to 563 ms, the simulation result was found close to the experimental observation and captured the tendency of reduced speed and increased wave number and period (Fig. 3 B2 and Table 1, row b2). The change in the pattern formation is clearly visible in the time courses shown in Fig. 3, B3. It takes more than one cycle for the waves of the membrane potential and body curvature to travel from head to tail, as indicated by arrows, meaning more than one wave was expressed in the body at every instant. Although the oscillation pattern was changed, the energetic mechanisms for swimming remained essentially the same: power supplied in the midbody, with passive tail oscillation.
The model thus predicts that the oscillation pattern can adapt to the environment. In laboratory experiments, leeches swam either in water or in the high-viscosity fluid, without transitioning from one to the other. In some simulations, we conducted virtual experiments in which the model leech moved from water into a higher-viscosity fluid during steady-state swimming (Fig. 3 B4). After the transition, the amplitudes of oscillations are slightly increased. More importantly, the phase lag between segments is increased so that the crests of the 12 segments shown are spaced equally over each cycle. Thus, the body segments 1 through 12 exhibit one full wave, and the whole body expresses more than one wave after the transition, consistent with Fig. 3 B2 and B3. The whole transition is smooth and occurs in about one cycle.
Standing Wave Oscillation in Air.
We have examined the oscillatory body movements in a radically perturbed condition in which the effect of the fluid force is essentially removed (38). In the laboratory, a debrained leech was suspended on its side by four long threads (Fig. S1). We observed and compared the body movements when swimming in water and when raised into the air. We found that suspended swimming in water was essentially normal (Table 1, row C1). When raised into air the period of oscillations remained nearly unchanged, but the oscillation pattern changed, with traveling body waves nearly lost; instead, undulations closely resembled a standing wave (Fig. 3 C1 and Table 1, row C2). In air, the CPG seems to detect the absence of water through feedback from the tension receptors and modify its oscillation pattern.
Simulated movements of the leech model support this idea. With the same parameter values as those for water swimming, the integrated model with fluid forces removed exhibited standing waves similar to the movements observed in leeches (Fig. 3 C2). The cycle period was slightly increased in comparison with the water swimming case (Table 1, compare rows b1 and c2). However, the time courses in Fig. 3 C3 indicate that the signals are almost in-phase along the body. Also, the muscle bending moments are several times larger in magnitude than those during water swimming and are roughly antiphase to the body curvatures, indicating passive oscillation of the whole body.
The transition from traveling waves to standing waves was observed in physical experiments when leeches swimming in water were raised into air. The integrated model reproduces this adaptive pattern formation behavior as well. Fig. 3 C4 shows how the membrane potentials are modified through sensory feedback after the hydrodynamic forces are turned off in the model to mimic the experimental procedure. Before the turn-off at 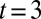 s, the membrane potentials have crests equally spaced over one cycle, resulting in one full wave expressed in the body as in Fig. 3 A2. A few cycles after the turn-off, all of the signals become roughly in-phase, resulting in standing waves as in Fig. 3 C2.
s, the membrane potentials have crests equally spaced over one cycle, resulting in one full wave expressed in the body as in Fig. 3 A2. A few cycles after the turn-off, all of the signals become roughly in-phase, resulting in standing waves as in Fig. 3 C2.
When simulating the integrated model, the disturbance caused by pulling the threads in physical experiments was effected by transiently doubling the muscle damping for 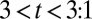 s. This disturbance actually triggered the transition of the body oscillation pattern. If the damping was kept constant throughout, traveling waves characteristic of water swimming continued in membrane potentials and body curvatures (Table 1, row c2*). Interestingly, traveling waves were lost in the muscle bending moments, which presumably compensate for the lack of fluid forces to maintain the similar body undulation pattern. Thus, the model predicts that smooth transition can result in traveling-wave undulations even in air. Indeed, we observed that during some transitions to air the leech continued to generate traveling, rather than standing, body waves (Table 1, row C2*). According to the model, the underlying mechanism is within the nonlinear dynamics that embed two stable limit cycle oscillations corresponding to the standing and traveling waves. The mechanical disturbance during the transition from water to air could push the state from one oscillation to the other.
s. This disturbance actually triggered the transition of the body oscillation pattern. If the damping was kept constant throughout, traveling waves characteristic of water swimming continued in membrane potentials and body curvatures (Table 1, row c2*). Interestingly, traveling waves were lost in the muscle bending moments, which presumably compensate for the lack of fluid forces to maintain the similar body undulation pattern. Thus, the model predicts that smooth transition can result in traveling-wave undulations even in air. Indeed, we observed that during some transitions to air the leech continued to generate traveling, rather than standing, body waves (Table 1, row C2*). According to the model, the underlying mechanism is within the nonlinear dynamics that embed two stable limit cycle oscillations corresponding to the standing and traveling waves. The mechanical disturbance during the transition from water to air could push the state from one oscillation to the other.
Discussion
The importance of sensory input in animal locomotion was recognized long ago by Gray et al. (39), who observed that leeches swim with a lower frequency in media of high viscosity. More recently, numerous studies (5, 30, 31, 40–42) have shown that the oscillation pattern of CPGs is modified by sensory feedback. However, it was largely unknown which sensory signals are responsible for the pattern adjustment, or whether the brain plays a crucial role by commanding the CPG during adaptive locomotion behaviors. Our study shows that feedback of muscle tension, directly to the CPG without passing through and processing by the brain, is sufficient to achieve the adaptive pattern formation observed in leeches undulating in air or high-viscosity fluid. The brain, which was removed for the “air-swimming” experiments, seems to play no role in these adaptations. Our results clearly indicate that sensory feedback from the environment is an essential component of the CPG controlled adaptive system, rather than a simple modulator of ongoing activity.
The leech swimming CPG achieves adaptive pattern formation through sensory feedback. Fundamental questions remain. Why does the body exhibit one full wave in water? Why does the wave number increase in a high-viscosity fluid? Why does the body oscillate with either traveling or standing waves in air? What are the common principles, if any, that can explain all these phenomena? An interesting observation pertinent to these questions is that the undulation with standing waves in air (Fig. 3 C1 and C2) resembles the first mode of natural oscillation of a flexible beam. Indeed, the displacement is antiphase with the force (Fig. 3 C3), suggesting that the CPG controls the body oscillation to exploit passive muscle stiffness and body inertia. Thus, the leech CPG seems to configure the entire system so that, given a particular environment, oscillations conform with a natural mode of the coupled body–environment dynamics. The ability of CPGs to entrain to a resonance was previously verified in an independent theoretical study (43). It may also be possible to explain the differing body wave numbers observed in water and high-viscosity fluids in terms of entrainment to natural oscillations.
A major objective of neuroscience is to uncover how the CNS works. Because of the high complexity, mathematical modeling is essential for understanding mechanisms underlying neuronal information processing in the CNS. Taking animal locomotion as a tractable focus of study, a number of models have previously been developed, ranging from neuronal circuit models for CPGs (44–47) and body–fluid interactions during swimming (35, 48) to integrated neuromechanical models for locomotion (49–51). An ultimate goal is to have dynamical models that are simple and amenable not only to numerical simulations but also to analytical studies, and which are fully validated by experimental data, with demonstrated predictability under perturbed conditions. Equipped with these properties, the integrated model of leech swimming presented here offers a solid step toward the goal of understanding and modeling the CNS.
Methods
Animals.
Experiments were carried out on adult leeches, Hirudo verbena, obtained from American suppliers. Where surgery was required, animals were anesthetized with cold (4 °C) saline.
Experimental Setup for Intact Swimming.
Intact, medium-sized animals (about 10 cm) swam in a narrow, transparent Plexiglas trough (75 cm long, 3 cm wide, water depth 10 cm), filled with water or methyl cellulose 400 cp solution. Swimming behavior was initiated by touch or electrical shock. Trough length ensured that leeches exhibit steady-state swimming in midtrough, the location of the camera capture window.
Experimental Setup for Air Swimming.
Nearly intact animals undulated in the horizontal plane, suspended from four 42-cm-long threads attached equispaced along the lateral midline to dennervated body wall. Both anterior and posterior brains were disconnected from the ventral nerve cord. Threads were sufficiently long to minimally impede body motion and reduce the gravity effect (Fig. S1).
Motion Capture and Data Processing.
Body movements were captured by a video camera (60 frames per second). In each video frame, numerical coordinates of body boundary points were obtained using ImageJ software. Discrete time courses of motion variables (link angles and location of the center of gravity) were calculated and fit by sinusoids to generate an oscillation profile for quantitative analysis and graphical depiction.
Integrated Model Analysis.
The model differential equations were simulated with Matlab. The initial conditions were at first set to zero except for the membrane potentials that were chosen near the expected oscillation orbit. Once a reasonable behavior was found, the steady-state values at a fixed time instant were used as the initial condition for other simulations to reduce the time for the initial transient. Simulated values were used to animate the body motion and obtain snapshots of model swimming.
Supplementary Material
Acknowledgments
We thank Andrew Ra, Greg Mattingly, and Ruey-Jane Fan for assistance in experiments on leeches swimming in high-viscosity fluid. This research was supported by National Institutes of Health Grant R01NS46057 (to T.I. and W.O.F.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1313933111/-/DCSupplemental.
References
- 1.Markram H. The blue brain project. Nat Rev Neurosci. 2006;7(2):153–160. doi: 10.1038/nrn1848. [DOI] [PubMed] [Google Scholar]
- 2.Duysens J. Van de Crommert HW Neural control of locomotion: The central pattern generator from cats to humans. Gait Posture. 1998;7(2):131–141. doi: 10.1016/s0966-6362(97)00042-8. [DOI] [PubMed] [Google Scholar]
- 3.Dimitrijevic MR, Gerasimenko Y, Pinter MM. Evidence for a spinal central pattern generator in humans. Ann N Y Acad Sci. 1998;860:360–376. doi: 10.1111/j.1749-6632.1998.tb09062.x. [DOI] [PubMed] [Google Scholar]
- 4.Pearce RA, Friesen WO. Intersegmental coordination of leech swimming: Comparison of in situ and isolated nerve cord activity with body wall movement. Brain Res. 1984;299(2):363–366. doi: 10.1016/0006-8993(84)90720-0. [DOI] [PubMed] [Google Scholar]
- 5.Yu X, Nguyen B, Friesen WO. Sensory feedback can coordinate the swimming activity of the leech. J Neurosci. 1999;19(11):4634–4643. doi: 10.1523/JNEUROSCI.19-11-04634.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pearce RA, Friesen WO. Intersegmental coordination of the leech swimming rhythm. II. Comparison of long and short chains of ganglia. J Neurophysiol. 1985;54(6):1460–1472. doi: 10.1152/jn.1985.54.6.1460. [DOI] [PubMed] [Google Scholar]
- 7.Hocker CG, Yu X, Friesen WO. Functionally heterogeneous segmental oscillators generate swimming in the medicinal leech. J Comp Physiol. 2000;186(9):871–883. doi: 10.1007/s003590000140. [DOI] [PubMed] [Google Scholar]
- 8.Weeks JC, Kristan WB., Jr Initiation, maintenance and modulation of swimming in the medicinal leech by the activity of a single neuron. J Exp Biol. 1978;77(1):71–88. [Google Scholar]
- 9.Hashemzadeh-Gargari H, Friesen WO. Modulation of swimming activity in the medicinal leech by serotonin and octopamine. Comp Biochem Physiol C. 1989;94(1):295–302. doi: 10.1016/0742-8413(89)90182-5. [DOI] [PubMed] [Google Scholar]
- 10.Schlüter E. Die bedeutung des centralnervensystems von hirudo medicinalis fur locomotion and raumorientierung. Z Wiss Zool. 1933;143:538–593. [Google Scholar]
- 11.Kristan WB, Jr, Stent GS, Ort CA. Neuronal control of swimming in the medicinal leech I. dynamics of the swimming rhythm. J Comp Physiol. 1974;94(2):97–119. [Google Scholar]
- 12.Zheng M, Friesen WO, Iwasaki T. Systems-level modeling of neuronal circuits for leech swimming. J Comput Neurosci. 2007;22(1):21–38. doi: 10.1007/s10827-006-9648-7. [DOI] [PubMed] [Google Scholar]
- 13.Tian J, Iwasaki T, Friesen WO. Analysis of impulse adaptation in motoneurons. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2010;196(2):123–136. doi: 10.1007/s00359-009-0499-3. [DOI] [PubMed] [Google Scholar]
- 14.Tian J, Iwasaki T, Friesen WO. Muscle function in animal movement: Passive mechanical properties of leech muscle. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2007;193(12):1205–1219. doi: 10.1007/s00359-007-0278-y. [DOI] [PubMed] [Google Scholar]
- 15.Chen J, Tian J, Iwasaki T, Friesen WO. Mechanisms underlying rhythmic locomotion: Dynamics of muscle activation. J Exp Biol. 2011;214(11):1955–1964. doi: 10.1242/jeb.052787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chen J, Friesen WO, Iwasaki T. Mechanisms underlying rhythmic locomotion: Body-fluid interaction in undulatory swimming. J Exp Biol. 2011;214(4):561–574. doi: 10.1242/jeb.048751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cang J, Yu X, Friesen WO. Sensory modification of leech swimming: Interactions between ventral stretch receptors and swim-related neurons. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2001;187(7):569–579. doi: 10.1007/s003590100229. [DOI] [PubMed] [Google Scholar]
- 18.Friesen WO, Mullins OJ, Xiao R, Hackett JT. Positive feedback loops sustain repeating bursts in neuronal circuits. J Biol Phys. 2011;37(3):317–345. doi: 10.1007/s10867-010-9210-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kristan WB, Jr, Calabrese RL, Friesen WO. Neuronal control of leech behavior. Prog Neurobiol. 2005;76(5):279–327. doi: 10.1016/j.pneurobio.2005.09.004. [DOI] [PubMed] [Google Scholar]
- 20.Friesen WO. Neuronal control of leech swimming movements: Interactions between cell 60 and previously described oscillator neurons. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1985;156(2):231–242. [Google Scholar]
- 21.Stent GS, et al. Neuronal generation of the leech swimming movement. Science. 1978;200(4348):1348–1357. doi: 10.1126/science.663615. [DOI] [PubMed] [Google Scholar]
- 22.Friesen WO. Neuronal control of leech swimming movements II. Motor neuron feedback to oscillator cells 115 and 28. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1989;166(2):205–215. [Google Scholar]
- 23.Chen Z, Zheng M, Friesen WO, Iwasaki T. Multivariable harmonic balance analysis of the neuronal oscillator for leech swimming. J Comput Neurosci. 2008;25(3):583–606. doi: 10.1007/s10827-008-0105-7. [DOI] [PubMed] [Google Scholar]
- 24.Granzow B, Friesen WO, Kristan WB., Jr Physiological and morphological analysis of synaptic transmission between leech motor neurons. J Neurosci. 1985;5(8):2035–2050. doi: 10.1523/JNEUROSCI.05-08-02035.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Angstadt JD, Friesen WO. Modulation of swimming behavior in the medicinal leech. I. Effects of serotonin on the electrical properties of swim-gating cell 204. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1993;172(2):223–234. doi: 10.1007/BF00189398. [DOI] [PubMed] [Google Scholar]
- 26.Mangan PS, Cometa AK, Friesen WO. Modulation of swimming behavior in the medicinal leech. IV. Serotonin-induced alterations of synaptic interactions between neurons of the swim circuit. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1994;175(6):723–736. doi: 10.1007/BF00191844. [DOI] [PubMed] [Google Scholar]
- 27.Nusbaum MP, Friesen WO, Kristan WB, Jr, Pearce RA. Neural mechanisms generating the leech swimming rhythm: swim-initiator neurons excite the network of swim oscillator neurons. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1987;161(3):355–366. doi: 10.1007/BF00603961. [DOI] [PubMed] [Google Scholar]
- 28.Stuart AE. Physiological and morphological properties of motoneurones in the central nervous system of the leech. J Physiol. 1970;209(3):627–646. doi: 10.1113/jphysiol.1970.sp009183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ort CA, Kristan WB, Jr, Stent GS. Neuronal control of swimming in the medicinal leech II. Identification and connections of motor neurones. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 1974;94(2):121–154. [Google Scholar]
- 30.Cang J, Friesen WO. Sensory modification of leech swimming: Rhythmic activity of ventral stretch receptors can change intersegmental phase relationships. J Neurosci. 2000;20(20):7822–7829. doi: 10.1523/JNEUROSCI.20-20-07822.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yu X, Friesen WO. Entrainment of leech swimming activity by the ventral stretch receptor. J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2004;190(11):939–949. doi: 10.1007/s00359-004-0549-9. [DOI] [PubMed] [Google Scholar]
- 32.Fan RJ, Friesen WO. Morphological and physiological characterization of stretch receptors in leeches. J Comp Neurol. 2006;494(2):290–302. doi: 10.1002/cne.20818. [DOI] [PubMed] [Google Scholar]
- 33.Skierczynski BA, Wilson RJ, Kristan WB, Jr, Skalak R, Skalak R. A model of the hydrostatic skeleton of the leech. J Theor Biol. 1996;181(4):329–342. doi: 10.1006/jtbi.1996.0135. [DOI] [PubMed] [Google Scholar]
- 34.Saito M, Fukaya M, Iwasaki T. Serpentine locomotion with robotic snake. IEEE Control Syst Mag N Y. 2002;22(1):64–81. [Google Scholar]
- 35.McMillen T, Holmes P. An elastic rod model for anguilliform swimming. J Math Biol. 2006;53(5):843–886. doi: 10.1007/s00285-006-0036-8. [DOI] [PubMed] [Google Scholar]
- 36.Taylor G. Analysis of the swimming of long and narrow animals. Proc R Soc Lond A Math Phys Sci. 1952;214(1117):158–183. [Google Scholar]
- 37.Chen J, Friesen WO, Iwasaki T. Mechanisms underlying rhythmic locomotion: interactions between activation, tension and body curvature waves. J Exp Biol. 2012;215(2):211–219. doi: 10.1242/jeb.058669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bowtell G, Williams T. Anguilliform body dynamics: Modeling the interaction between muscle activation and body curvature. Philos Trans R Soc Lond B Biol Sci. 1991;334(1271):385–390. [Google Scholar]
- 39.Gray J, Lissmann HW, Pumphrey RJ. The mechanism of locomotion in the leech (Hirudo Medicinalis Ray) J Exp Biol. 1938;15(3):408–430. [Google Scholar]
- 40.Wallén P. Spinal mechanisms controlling locomotion in dogfish and lamprey. Acta Physiol Scand Suppl. 1982;503:1–45. [PubMed] [Google Scholar]
- 41.McClellan AD, Jang W. Mechanosensory inputs to the central pattern generators for locomotion in the lamprey spinal cord: Resetting, entrainment, and computer modeling. J Neurophysiol. 1993;70(6):2442–2454. doi: 10.1152/jn.1993.70.6.2442. [DOI] [PubMed] [Google Scholar]
- 42.Tytell ED, Cohen AH. Rostral versus caudal differences in mechanical entrainment of the lamprey central pattern generator for locomotion. J Neurophysiol. 2008;99(5):2408–2419. doi: 10.1152/jn.01085.2007. [DOI] [PubMed] [Google Scholar]
- 43.Iwasaki T, Zheng M. Sensory feedback mechanism underlying entrainment of central pattern generator to mechanical resonance. Biol Cybern. 2006;94(4):245–261. doi: 10.1007/s00422-005-0047-3. [DOI] [PubMed] [Google Scholar]
- 44.Wallén P, et al. A computer-based model for realistic simulations of neural networks. II. The segmental network generating locomotor rhythmicity in the lamprey. J Neurophysiol. 1992;68(6):1939–1950. doi: 10.1152/jn.1992.68.6.1939. [DOI] [PubMed] [Google Scholar]
- 45.Wadden T, Hellgren J, Lansner A, Grillner S. Intersegmental coordination in the lamprey: Simulations using a network model without segmental boundaries. Biol Cybern. 1997;76(1):1–9. [Google Scholar]
- 46.Skinner FK, Mulloney B. Intersegmental coordination of limb movements during locomotion: Mathematical models predict circuits that drive swimmeret beating. J Neurosci. 1998;18(10):3831–3842. doi: 10.1523/JNEUROSCI.18-10-03831.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ijspeert AJ. A connectionist central pattern generator for the aquatic and terrestrial gaits of a simulated salamander. Biol Cybern. 2001;84(5):331–348. doi: 10.1007/s004220000211. [DOI] [PubMed] [Google Scholar]
- 48.Tytell ED, Hsu CY, Williams TL, Cohen AH, Fauci LJ. Interactions between internal forces, body stiffness, and fluid environment in a neuromechanical model of lamprey swimming. Proc Natl Acad Sci USA. 2010;107(46):19832–19837. doi: 10.1073/pnas.1011564107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ekeberg O, Grillner S. Simulations of neuromuscular control in lamprey swimming. Philos Trans R Soc Lond B Biol Sci. 1999;354(1385):895–902. doi: 10.1098/rstb.1999.0441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Cang J, Friesen WO. Model for intersegmental coordination of leech swimming: Central and sensory mechanisms. J Neurophysiol. 2002;87(6):2760–2769. doi: 10.1152/jn.2002.87.6.2760. [DOI] [PubMed] [Google Scholar]
- 51.Ijspeert AJ, Crespi A, Ryczko D, Cabelguen JM. From swimming to walking with a salamander robot driven by a spinal cord model. Science. 2007;315(5817):1416–1420. doi: 10.1126/science.1138353. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.