Delineating cooperative responses of processive motors in living cells

Significance

Although many vesicles and organelles are known to be transported by groups of interacting cytoskeletal motors, the precise impact of collective motor behaviors on intracellular transport and trafficking processes remains controversial. By engineering COS-7 cells to provide genetic control over the density of motors on, and the sizes of vesicles (peroxisomes), we performed systematic comparisons of the collective behaviors of kinesin and myosinVa motors. The responses of cargo velocities, run lengths, and position fluctuations to these parameters suggest that myosinVa motors can cooperate more productively than kinesins when transporting cargos as a team. This behavior is derived from the mechanochemical properties of these motors and suggests that the collective functions of motors like myosinV can be regulated more sensitively than those of kinesin.

Abstract

Characterizing the collective functions of cytoskeletal motors is critical to understanding mechanisms that regulate the internal organization of eukaryotic cells as well as the roles various transport defects play in human diseases. Though in vitro assays using synthetic motor complexes have generated important insights, dissecting collective motor functions within living cells still remains challenging. Here, we show that the protein heterodimerization switches FKBP-rapalog-FRB can be harnessed in engineered COS-7 cells to compare the collective responses of kinesin-1 and myosinVa motors to changes in motor number and cargo size. The dependence of cargo velocities, travel distances, and position noise on these parameters suggests that multiple myosinVa motors can cooperate more productively than collections of kinesins in COS-7 cells. In contrast to observations with kinesin-1 motors, the velocities and run lengths of peroxisomes driven by multiple myosinVa motors are found to increase with increasing motor density, but are relatively insensitive to the higher loads associated with transporting large peroxisomes in the viscoelastic environment of the COS-7 cell cytoplasm. Moreover, these distinctions appear to be derived from the different sensitivities of kinesin-1 and myosinVa velocities and detachment rates to forces at the single-motor level. The collective behaviors of certain processive motors, like myosinVa, may therefore be more readily tunable and have more substantial roles in intracellular transport regulatory mechanisms compared with those of other cytoskeletal motors.

The transport of vesicles and organelles along cytoskeletal filaments by processive motor proteins is essential to physiological processes in eukaryotic cells requiring the spatial regulation of signaling complexes and other important subcellular commodities. Aberrant motor functions have also been implicated in several human diseases (1). The mechanochemical properties of motors have been studied extensively using suites of single-molecule and bulk biochemical techniques. However, many cargos are propelled in cells by systems of motors containing multiple copies of the same and even of different types of microtubule and actin-dependent motors (2). Characterizing how these motors cooperate or compete with one another is therefore critical to understanding mechanisms that regulate the internal organization of cells and how disrupted motor functions lead to diseases.

Despite increased attention, current studies of collective motor behaviors are often limited by the challenges associated with analyzing or controlling the number and organization of motors on individual cargos. These issues have been addressed in part by synthetic approaches that use protein (3, 4) and DNA-based molecular scaffolds (5–8) to prepare organized multiple motor complexes of known composition. Subsequent theoretical studies of these systems have uncovered key differences in the way that classes of processive motors function in groups (9, 10). Relatively modest increases in cargo run lengths and detachment forces have been observed when multiple processive motors possessing high single-motor stalling forces, such as kinesin-1, are grouped together on a common cargo (5, 6, 8). These weak collective responses occur due to effects from motor interference as well as kinetic constraints that limit the abilities of multiple kinesin complexes to bind cytoskeletal filaments in configurations that allow motors to share applied loads equally (8, 9, 11–13). Similar studies have shown that motors whose velocities decrease more rapidly with increasing load, such as the nonprocessive, minus-end directed kinesin called NCD (kinesin-14), can cooperate much more productively via load sharing, yielding higher sensitivities of cargo transport parameters to variation in motor number (6). Along these lines, our group has demonstrated that the velocities of elastically coupled myosinVa motors are much more sensitive to changes in motor number than systems of coupled kinesins in the absence of an applied load (14). Under these conditions, coupled myosinVa motors were found to move with lower velocities than single myosinVa molecules, a response we attributed to the large step size and relatively small stalling force of myosinVa. Together, these properties lead to high sensitivity of collective motor stepping rates to strain produced when the motors step asynchronously. As with NCD, we also expect that this behavior will allow multiple myosinVa motors to cooperate more productively than kinesins in the presence of an applied load. Such distinctions are significant because they suggest cells may be able to modulate the collective functions of certain types of motors more sensitively than others, which could elevate the role of these motor systems in mechanisms that regulate cargo motion.

Various signatures of the collective behaviors observed in vitro appear to be reflected in recent particle-tracking and optical-trapping analyses of cargo transport in living cells (15, 16). However, resolving the responses of cargo transport to the number and organization of motors on endogenous cargos in living cells remains challenging. It is still not clear whether the collective responses found using synthetic motor complexes, where the motors are coupled elastically, translate directly to scenarios where motors are bound to vesicular cargos that are transported along the native cytoskeleton. Resolving this issue is critical to ultimately determining how sensitively regulatory factors that affect motor functions can modulate intracellular transport processes, and how severely mutations in motor proteins can perturb a cell’s transport machinery.

Here, we describe a method to configure live-cell particle (peroxisome)-tracking assays where the type of motor, motor surface density on vesicular cargos, and cargo size are controlled via the regulation of synthetic genes. Comparisons of the collective behaviors exhibited by kinesin-1 and myosinVa motors revealed several key distinctions in the way that these motors cooperate as a team. MyosinVa motors display much higher sensitivities to changes in motor density and appear to cooperate more productively when transporting vesicular cargos against cargo size-dependent viscoelastic loads imposed by the cytoplasm compared with kinesin motors. Implications of these different responses to mechanisms that regulate intracellular trafficking and transport processes are discussed.

Results

Controlling Motor Number and Cargo Size in Living Cells.

Building upon the experimental framework of the live-cell peroxisomal trafficking assays developed by Kapitein et al. (17, 18), clonal COS-7 cell lines were generated to gain genetic-level control over the number of motors attached to and the size of peroxisomes via the inducible regulation of two genes. The first gene encodes for a PEX3-mYFP-FKBP protein construct that functions as an engineered peroxisomal surface receptor for recombinant motors; it was prepared by fusing the FK506 binding protein (FKBP) portion of the FKBP-rapalog-FRB protein heterodimerization system (19) to a yellow fluorescent protein, mYFP, and a peroxisome membrane-targeting signal, the transmembrane domain segment of the peroxin PEX3 (Fig. 1A). This design allows overexpressed motor constructs containing FKBP-rapamycin binding domain (FRB) fusions (Kif5B770-FRB or MyoVa1098-FRB) to be coupled to peroxisome surfaces by adding a cell-permeable analog of the drug rapamycin (rapalog) to the cell media (Fig. 1B). The synthetic PEX3-mYFP-FKBP gene was placed under the control of a doxycycline-inducible (TET-ON) promoter and integrated into the COS-7 cell genome using lentiviral transduction techniques. The maximum number of FKBP receptor sites available for motor binding can therefore be tuned by modulating PEX3-mYFP-FKBP receptor expression with different doxycycline concentrations (Fig. S1). With this approach, motor densities on peroxisomes can be controlled while using saturating rapalog concentrations to enable efficient formation of the FKBP-rapalog-FRB complex, which triggers motor-dependent transport.

Fig. 1.

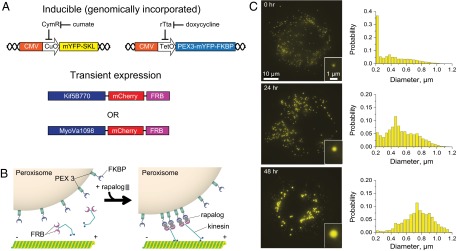
Expression regulation of motor densities and cargo sizes in COS-7 cells. (A and B) The TET-ON and cumate operons are used to regulate the expression levels of the PEX-mYFP-FKBP and mYFP-SKL genes, which are targeted to the surface and lumen of peroxisomes, respectively. Incubation with rapalog couples transiently expressed motors (kinesin-1 and myosinVa) incorporating mCherry and FRB fusion to peroxisome surfaces via the formation of a FKBP-rapalog-FRB complex. (C) Peroxisome diameters increase dramatically in time when mYFP-SKL expression is induced with 100 μg/mL of cumate. Each histogram displays size distributions of >7,000 peroxisomes measured in ∼100 cells.

PiggyBac transposase technologies were used to integrate a second gene into the COS-7 genome that encoded for a mYFP reporter fused to the tripeptide serine-lysine-leucine (SKL) that targets proteins to the peroxisomes lumen (Fig. 1A). While this synthetic gene was introduced to further enhance peroxisome fluorescence intensities, we discovered that the distribution of peroxisome sizes can be controlled by regulating mYFP-SKL protein expression. The diameters of nearly half of the peroxisomes are smaller than the diffraction limit of an optical microscope (<250 nm) in the absence of cumate (Fig. 1C). The sizes of the remaining peroxisomes are distributed across a broad range. However, the proportion of peroxisomes possessing larger diameters increased dramatically with time, after mYFP-SKL expression is induced, which makes it possible to examine the dynamics of a sufficient number of large peroxisomes to evaluate size-dependent trends. Confocal microscopy showed that the large diameter peroxisomes can be counterstained with a fluorescently tagged, peroxisomal membrane protein construct, PMP34-cerulean (Fig. S2A), indicating that peroxisomal membrane proteins are retained on their surfaces. Furthermore, mYFP signals do not colocalize with a fluorescent construct composed of a RFP fusion to the lysosome-associated membrane protein, LAMP1 (Fig. S2B). Hence, the increase in peroxisome size is not caused by lysosomal autophagy. Taken together, these results suggest that the engineered COS-7 cells can serve as an experimental platform to perform live-cell structure–function assays where the densities of different types of motors and cargo sizes are controllably tuned.

Size-Dependent Peroxisome Mobilities.

Peroxisome localization behaviors and mobilities were first characterized in the absence of expressed motors to evaluate whether the regulation of peroxisome size affects non–motor-dependent interactions between peroxisomes and the COS-7 cell cytoskeleton (Fig. 2). Single-particle tracking analyses have shown peroxisomes are rarely transported by endogenous motor proteins, and tend to diffuse locally within the perinuclear space in COS-7 cells (Fig. 3A, Left) (20). Neither of these behaviors changed appreciably when peroxisome sizes were modulated. Peroxisomes were much more uniformly dispersed throughout the cytoplasm when cells were exposed to the microtubule depolymerizing drug nocodazole (Fig. 2A), indicating that the microtubule meshwork plays a key role in their perinuclear confinement. Mean squared displacements (MSD) analyses of peroxisome trajectories also reflect particle confinement by the microtubule cytoskeleton (Fig. 2). Plots of average peroxisome MSD values as a function of time tend to exhibit concave downward curvature (Fig. 2B). This behavior is consistent with power-law dependencies describing subdiffusive particle motions (21, 22). Peroxisome mobilities decreased with increasing particle size and with nocodazole treatment. This effect indicates that peroxisomes can diffuse more freely within the native cytoskeleton compared with the denser actin networks alone.

Fig. 2.

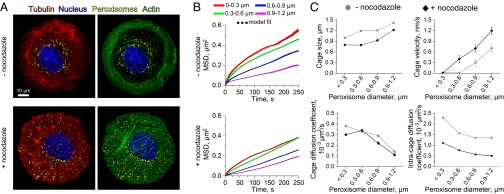
Size-dependent mobility of peroxisomes in COS-7 cells. (A) Confocal images show that peroxisomes (yellow) localize to the perinuclear region of COS-7 cells due to microtubule (red) confinement. Upon treatment with nocodazole, actin filaments (green) reorganize and peroxisomes become more uniformly distributed throughout the cell body. (B) MSD analyses of passively diffusing peroxisomes show peroxisome mobilities decrease with increasing particle size in both untreated and nocodazole-treated cells. More than 1,500 peroxisome trajectories were averaged in each MSD curve. Line widths indicate SEM. The black dashed lines indicate fits to a corralled diffusion model (Eq. 2; R² and adjusted R² > 0.99). (C) The model fits in B provide estimates of rheological parameters, including the average size of cytoskeletal cages, cage velocities due to activated filament motions, passive cage diffusion coefficients, and the intracage peroxisome diffusion coefficients. The observed trends generally reflect lower mobilities of the large peroxisomes. Error bars indicate SEM, but are only visible in plots of cage velocity because the errors in the remaining plots are smaller than the size of the symbols.

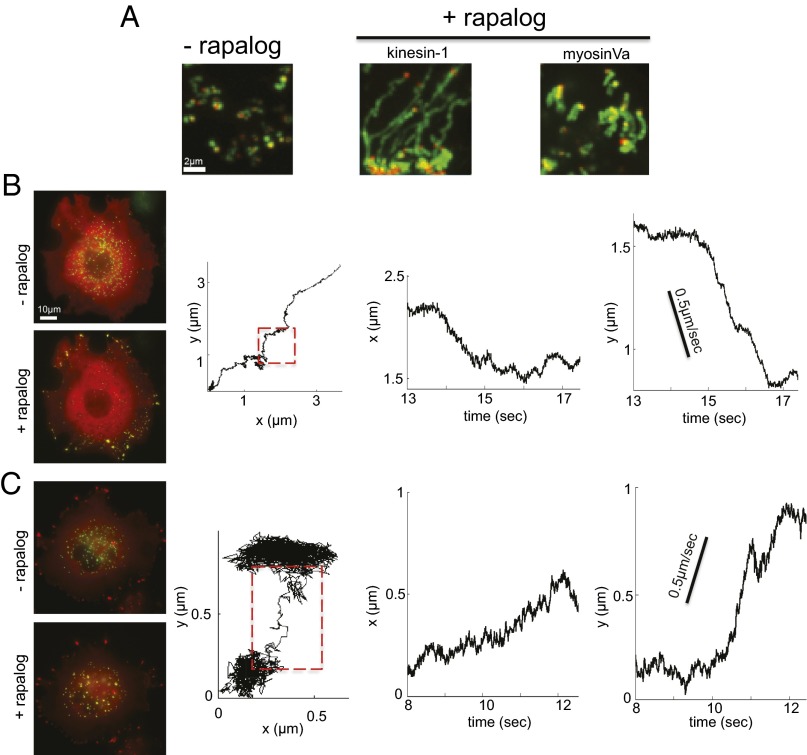
Fig. 3.

Rapalog-dependent induction of peroxisome transport. (A) SD maps of pixel intensities measured in movies displaying peroxisome trajectories in the presence and absence of rapalog. The red dot indicates the starting position of the peroxisome. (B and C) Fluorescence images showing rapalog-dependent redistribution of peroxisomes to the COS-7 cell periphery and local peroxisome aggregation when transport is driven by kinesin-1 (B) and myosinVa (C) motors, respectively. The yellow hue indicates peroxisome (green) and motor (red) colocalization. Representative trajectories recorded at 91 fps for each motor type are displayed.

To gain further insight into physical constraints imposed by the COS-7 cell cytoskeleton, MSD data were also analyzed using a rheological model of corralled diffusion that assumes particles diffuse within cages that also diffuse locally and move with some average velocity due to activated cytomechanical processes (21, 23) (Eq. 2 in Materials and Methods). Average MSD data for each peroxisome size group were fit to this model to estimate the sizes of peroxisome cages, cage velocities, and diffusion coefficients, as well as intracage diffusion coefficients (Fig. 2 B and C). Plots of these fit parameters as a function of peroxisome size display two key trends. First, cage sizes increase with increasing peroxisome size (Fig. 2C, Upper Left). Though this trend persisted both in the presence and absence of nocodazole, cage sizes were smaller when microtubules were depolymerized and the peroxisomes diffused in the actin meshwork. Importantly, calculated cage sizes were only slightly larger than the corresponding average peroxisome size determined from image analyses. The difference between peroxisome and cage sizes also decreases with increasing peroxisome size. These observations suggest that the peroxisomes can only move a small distance along or away from a filament before they encounter another cytoskeletal filament, particularly at large peroxisome sizes. The second trend is displayed in plots of the cage diffusion and intracage diffusion coefficients (Fig. 2C, Lower). Both of these parameters decreased with increasing size, consistent with expected size-dependent behaviors of particles within viscoelastic media. Of note, intracage diffusion coefficients are appreciably higher than cage diffusion coefficients, indicating that peroxisomes diffuse within cages more rapidly than their cages diffuse themselves, at least in the absence of rapalog-coupled motors.

Rapalog-Induced Motor Transport of Peroxisomes.

We next performed a series of live-cell peroxisome trafficking assays where rapalog was used to controllably induce kinesin-1– or myosinVa-dependent peroxisome transport. Both motors were introduced by transient transfection of the engineered COS-7 cells with constitutively active motor constructs possessing mCherry and FRB fusions (kinesin-1: Kif5B770-mCherry-FRB; or myosinVa: MyoVa1098-mCherry-FRB). The expression of PEX3-mYFP-FKBP and mYFP-SKL was also regulated with doxycycline and cumate, respectively. Both genes were induced before transfection with the motor constructs. The doxycycline concentration was varied between 2 and 10 μg/mL to tune PEX3-mYFP-FKBP receptor densities. Within this concentration range, a sufficient number of peroxisomes exhibited activated transport behaviors within observational windows that were amenable to fast particle tracking [91 frames per second (fps) for 2–3 min], particularly in the myosinVa assays. Cumate concentrations and incubation times were the same for all assays (100 μg/mL, and 76 h). These conditions produced broad distributions of peroxisome sizes. Consequently, trajectories of different size peroxisomes can be examined in the same cells to minimize effects stemming from potential cross-talk among PEX3-mYFP-FKBP receptor, mYFP-SKL, and motor expression. As found by Kapitein et al. (17), the coupling of kinesin-1 motors to peroxisome surfaces leads to greatly enhanced peroxisome mobility (Fig. 3A) and efficient transport from the perinuclear space to the cell periphery due to the plus end-directed movement of kinesin along microtubules (Fig. 3B, Left). Despite their rapid redistribution, individual peroxisome trajectories contained multiple segments, or runs. Unidirectional motion of peroxisomes was interspersed between events where they moved much more slowly, presumably due to a variety of behaviors where the particles diffused locally, stalled, and/or switched transport directions at filament intersections (Fig. 3B, Right). Overall, such behavior highlights the need to consider the roles of multiple types of transport modes as well as the potential impact of local environmental factors when characterizing structure–function relationships underlying collective motor responses.

Following transient transfection with MyoVa1098-mCherry-FRB, rapalog addition triggered myosinVa recruitment to the peroxisome surfaces, resulting in increased mobilities (Fig. 3A). In this case, particle trajectories also appeared to be composed of activated transport, diffusive, and pausing events. However, myosinVa-driven peroxisomes moved in more random directions and exhibited distinct localization behaviors compared with those found for kinesin-1 (Fig. 3 A and C). Instead of translocation to the cell periphery, a portion of the peroxisomes tended to cluster within local regions of the cell body. The triggering of myosinVa-dependent transport was also commonly accompanied by the slow contraction of the cells over long incubation periods (>20 min). These behaviors imply that myosins on the surfaces of individual peroxisomes readily form linkages between different actin filaments and apply appreciable forces to the actin networks.

Motor Density and Peroxisome Size–Velocity Relationships Differ for Kinesin and MyosinVa.

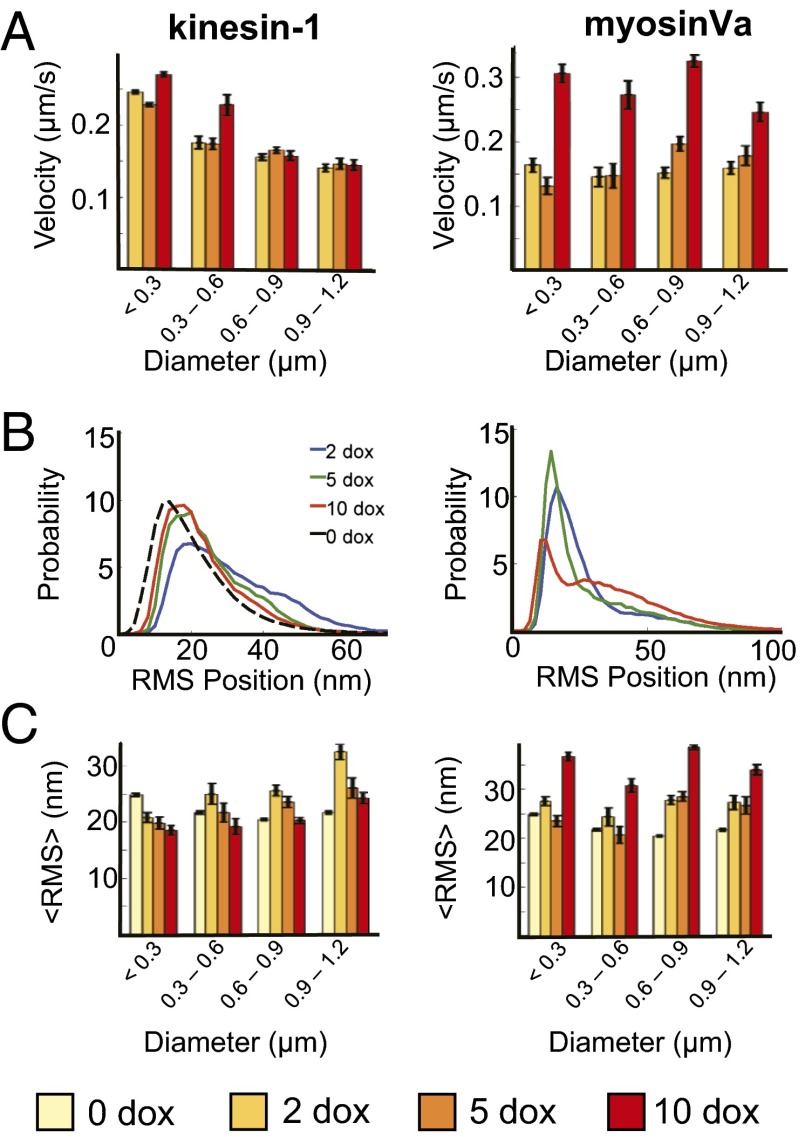
Analyses of the responses of peroxisome velocities to doxycycline concentration and peroxisome sizes revealed significant differences between kinesin and myosinVa transport behaviors (Fig. 4). For simplicity, we first compared peroxisome velocities that were averaged over entire trajectories. In this case, peroxisome velocities were much less sensitive to doxycycline concentration in the kinesin-1 assays compared with the myosinVa experiments. For example, the average velocities of peroxisomes whose diameters were larger than 600 nm changed by less than 2 ± 5% when the doxycycline concentration varied between 2 and 10 μg/mL (Fig. 4A). The average velocities of smaller peroxisomes increased by 30 ± 6% at most. In contrast, myosinVa-dependent velocities increased by a minimum of 51 ± 6% and as much as 112 ± 4% over the same doxycycline concentration range. This result indicates that the regulation of PEX3-mYFP-FKBP receptor expression provides systematic control over relative motor surface densities, at least within a size group. Kinesin-driven peroxisomes velocities also decreased by as much as 48 ± 4% with increasing peroxisome size between the smallest (<300 nm diameter) and largest (0.9–1.2 nm diameter) size groups. MyosinVa-powered peroxisome velocities exhibited different and more complicated dependencies of cargo size. Nevertheless, the trends in Fig. 4C appeared to reflect an overall weaker sensitivity of transport velocities to cargo size, and suggest the size-dependent factors affecting peroxisome velocities in kinesin assays may be less influential to myosinVa-dependent transport modes. Of note, average peroxisome velocities were considerably lower (∼200 nm/s for each motor type) than in vitro measurements of single, unloaded kinesin or myosinVa motors. The low speed is reflected by distributions of kinesin-dependent velocities, which possessed a dominant low velocity peak (∼50 nm/s), and a long tail extending toward much higher velocities (Fig. 5A). Myosin velocities were distributed similarly (Fig. 5D). Consistent with the properties of individual trajectories, such behavior indicates that despite their rapid redistribution in the cytoplasm upon addition of rapalog, peroxisomes spend an appreciable amount of time either diffusing or paused. Doxycycline and peroxisome size-dependent modulation of this behavior is therefore likely influencing velocity trends shown Fig. 4.

Fig. 4.

Collections of kinesin-1 and myosinVa motors exhibit distinct motile behaviors. (A) Average peroxisome velocities are largely insensitive to doxycycline concentration/motor density, but decrease with peroxisome size when transport is driven by kinesin-1 (Left). MyosinVa-dependent velocities (Right) display characteristically different size dependencies and generally increase with increasing motor density. (B and C) Distributions of rms position fluctuations and mean rms position fluctuation amplitudes exhibit unique dependencies on doxycycline concentration and cargo size in kinesin-1 (Left) and myosinVa (Right) assays. The rms positional distributions in B correspond to large peroxisomes (diameter = 0.9–1.2 μm). The black line in B displays rms position distributions measured in the absence of rapalog. More than 100 trajectories in a minimum of 10 cells were measured for each bin in A and C. Doxycycline (Dox) concentrations are reported in milligrams per milliliter. Error bars represent SEM.

Fig. 5.

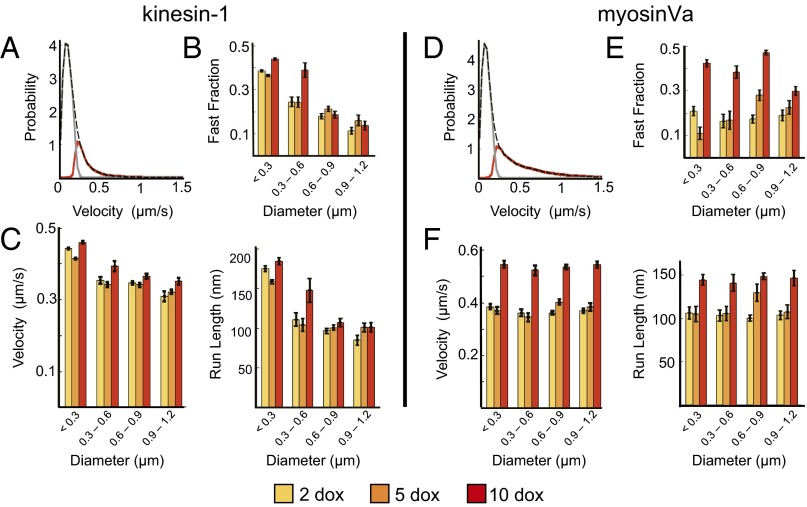
Structure–function analyses of fast components of peroxisome trajectories. (A) An example of fast (red) and slow (gray) components of peroxisome velocity distributions were identified within kinesin trajectories using an HMM approach. The total distribution is indicated by the black dashed line. (B) The fraction of kinesin-dependent trajectory components attributed to fast directional motion is largely insensitive to motor density, but decreases with increasing size. (C) Similar trends are found for the average velocities (Left) and the lengths of the fast runs (Right). (D) Hidden Markov modeling analyses of Myosin-dependent velocity distributions. (E) In contrast to kinesin, the fraction of fast transport events increased as much as 171 ± 12% with increasing motor density. (F) Average peroxisome velocities and transport distances exhibit a similar positive dependence on motor density. Analyses were performed on the same trajectories evaluated in Fig 4. Error bars represent SEM. Statistical analyses are presented in Table 1.

Positional Fluctuation Analysis of Kinesin vs. MyosinVa.

Expecting that peroxisome position fluctuations should change as motors are recruited to their surfaces and engaged in transport, we next explored whether kinesin-dependent responses to doxycycline would be reflected in measurements of peroxisome position noise. To do so, rms position fluctuations within x,y trajectories were calculated by measuring average position deviations relative to traces that were smoothed using a 15-frame boxcar average. Rms position fluctuation amplitudes indicate the extent to which peroxisomes move in a constant direction and with a uniform velocity when they are transported actively by motors, as well as the amplitude positional noise when they diffuse passively within their cytoskeletal cages or pause along filaments.

Somewhat surprisingly, rms position fluctuations were more broadly distributed when rapalog was used to induce kinesin transport compared with distributions measured in the absence of rapalog-coupled motors (Fig. 4B, Left). These trends were most pronounced with distributions for the large peroxisomes (900–1,200 nm diameter), which developed a shoulder at large rms values (>30 nm) in the presence of rapalog. This response suggests that the kinesin motors are responsible for generating the high rms noise. Subsequent analyses of rms position fluctuations within fast, activated transport components of trajectories (identified using the procedures described below) confirmed this behavior (Fig. S3). Nonetheless, average rms values decreased as a function of increasing doxycycline by as much as 25 ± 7% (Fig. 4C, Left). This response is accompanied by the loss of amplitude in the shoulder of the distribution at large rms values and provides evidence that the doxycycline-dependent modulation of FKBP receptor expression provides systematic control over kinesin density. Furthermore, the dependence of positional fluctuations on doxycycline at all particle sizes suggests that though the kinesin motors behave as noise source, the noise generated by individual motors is reduced as motor density increases.

Distributions of rms position fluctuations displayed characteristically different dependencies on doxycycline concentration and cargo size when rapalog was used to trigger myosinVa motions instead of kinesin (Fig. 4 B and C, Right). In this case, the amplitude of the shoulder at high rms values (>20 nm) increased with increasing doxycycline and even emerged as a distinct peak at 10 μg/mL doxycycline for all peroxisome size groups (Fig. S3). Rms distributions also contained a prominent peak at ∼10 nm. This peak shifts toward lower rms values with increasing doxycycline concentration. The opposing shifts of the high and low rms components yielded more complicated dependencies of average rms position fluctuations on peroxisome size and doxycycline concentration (Fig. 4C, Right). Nevertheless, average positional fluctuations increased significantly (a minimum of 23 ± 6%) at high doxycycline concentration (10 μg/mL), indicating that, in contrast to the trends found for kinesin, position noise is increased by the binding of multiple motors to actin filaments.

Collections of Kinesins and MyosinVa Motors Exhibit Distinct Load-Dependent Responses.

Considering that motors experience viscoelastic loads when transporting cargos in the cytoplasm, the dependence of average peroxisome velocities on cargo size described above suggests that collections of kinesins and myosinVa motors possess different collective force production capabilities. However, in each case, peroxisomes also exhibit multiple types of transport behaviors: fast activated transport modes, and slower modes that are likely associated with peroxisome diffusion or pausing during transport. Thus, factors other than the load imposed on a cargo may also play a role in governing collective motor responses. To address this complexity, we developed approaches to delineate these components within trajectories. The goal was to examine whether changes in the velocity and/or prevalence of certain transport modes, particularly those where peroxisomes moved directionally with large velocities, dominate the responses to doxycycline concentration and cargo size shown in Fig. 4. To avoid methods requiring potentially biased manual selection of trajectory components, we analyzed peroxisome velocity distributions using a simple, two-state hidden Markov model (HMM). This objective approach can be used to evaluate the potential presence of subpopulations within velocity distributions without prior knowledge of their properties. The derived subdistributions can then be used to identify trajectory components possessing properties underlying their associated velocity distributions.

Again, kinesin and myosinVa velocity distributions both possessed prominent low velocity peaks and a long tail extending toward much higher velocities (Fig. 5 A and D). The HMM identified two distinct components within these distributions: a high-velocity subpopulation peaked at ∼200 nm/s and a low-velocity component peaked at 50 nm/s that we attribute to combinations of peroxisome diffusion and pausing behaviors convolved with drift due to the slow motions of the cytoskeletal filaments. Inspection of individual peroxisome trajectories show that the components contributing to the high-velocity subdistribution are primarily associated with relatively persistent runs where the peroxisomes moved continuously with high velocities (Fig. S4). The remaining low-velocity components stemmed from much slower and less deterministic motions.

Further analysis of the fast components within kinesin trajectories showed that the probability that a peroxisome moved in a fast transport mode, the average velocities, and the distances traveled during these transport events are all largely insensitive to variation in doxycycline concentration (Fig. 5 B and C; Table 1). As with analyses of entire trajectories in Fig. 4, all three of these parameters decrease with increasing peroxisome size. The size dependence of kinesin velocities in both Figs. 4 and 5 implies that the directional transport of the large peroxisomes may require the production of larger forces in comparison with the small peroxisomes. Estimates of drag forces imposed on peroxisomes obtained using the microrheological formalism developed by Mason (24) supports this interpretation (Materials and Methods). Using this approach, the drag force on a peroxisome moving with a constant velocity of 500 nm/s is predicted to increase from 2 to 15 pN, approximately twice the stalling force of a single kinesin, when peroxisome diameters increase from across the full range of peroxisomes sizes (Fig. S5). Of note, this formalism treats the cytoskeletal environment as a homogeneous viscoelastic medium. Factors affecting the loads on the peroxisomes could vary considerably depending on their local environment and the presence of specific obstructions presented by other organelles and subcellular structures. We believe these estimates should be considered as an upper bound for the average forces imposed on the peroxisomes. Nevertheless, the decrease in the proportion of fast transport events, as well as peroxisome velocities and distances traveled, suggest the loads introduced by these factors increase with increasing peroxisome size. Moreover, the weak response of these parameters to doxycycline concentrations/kinesin density implies that the presence of additional kinesins does not fully compensate for the increased loads presented when multiple kinesins transport large peroxisomes in the cytoplasm.

Table 1.

Summary of maximum and minimum responses of kinesin-1 and myosinVa behaviors to changes in motor density and peroxisome size

	Kinesin		Myosin
	Motor density (Dox)*	Peroxisome size*	Motor density (Dox)*	Peroxisome size*
Active fraction
Max change ± SEM (P value)	↑ 60 ± 16% (0.001)	↓ −71 ± 4% (<0.001)	↑ 171 ± 12% (<0.001)	38 ± 6 (0.006)
Min change ± SEM (P value)	(0.7)†	↓ −56 ± 7% (<0.001)	↑ 57 ± 17% (<0.001)	(0.57)†
Velocity
Max change ± SEM (P value)	↑ 11 ± 5% (0.05)	↓ −30 ± 3% (<0.001)	↑ 48 ± 3% (<0.001)	(0.25)†
Min change ± SEM (P value)	↑ 3 ± 1% (<0.001)	↓ −22 ± 2% (<0.001)	↑ 42 ± 4% (<0.001)	(0.94)†
Run length
Max change ± SEM (P value)	↑ 33 ± 15% (0.03)	↓ −51 ± 4% (<0.001)	↑ 48 ± 5% (<0.001)	(0.75)†
Min change ± SEM (P value)	(0.1)†	↓ −36 ± 4% (<0.001)	↑ 36 ± 9% (<0.001)	(0.84)†

^*Values were compared across the full range of doxycycline concentrations and peroxisome sizes examined in Fig. 5 (2–10 μg/mL doxycycline; <300–900 to 1,200-nm size bins, respectively).

^†Denotes differences were not statistically significant at α = 0.05.

The high-velocity components found within the myosin-dependent trajectories exhibited characteristically different responses to modulation in doxycycline concentration/myosin density and peroxisome size compared with the kinesin trends described above (Fig. 5 D–F). In this case, the proportion of trajectories corresponding to fast-transport events increased significantly with increasing doxycycline (e.g., by a minimum of 57 ± 17%, and as much as 171 ± 12% between 2 and 10 μg/mL doxycycline). Thus, motor surface densities influence the probability that a myosinVa team will transport peroxisomes actively in the COS-7 cytoplasm to a much greater degree compared with multiple kinesins. Average velocities and lengths of the fast trajectory components also increased by as much as 48 ± 3% with increasing doxycycline. Finally, in contrast to kinesin, all of these transport parameters were largely insensitive to particle size (Table 1), indicating multiple myosinVa motors can readily produce large forces and cooperate more productively under loads than collections of kinesins.

Discussion

Recent studies of collective motor functions suggest that the abilities of processive cytoskeletal motor proteins to cooperate productively may depend strongly on motor type. Such behavior can result in differential sensitivities to changes in motor number and cargo size, and implies that the collective functions of certain cytoskeletal motors could have particularly significant roles in mechanisms that regulate intracellular transport. However, various confounding factors have limited live-cell analyses of these effects. To address these issues, we developed engineered COS-7 cell lines that can facilitate structure–function analyses of collective motor behaviors in living cells. These assays harness FKBP-rapalog-FRB protein heterodimerization switches to control the coupling of either kinesin-1 or myosinVa motors to the surfaces of vesicular cargos (peroxisomes). Genetic regulation of the FKBP component of the switch, which is targeted to the peroxisome membrane via a PEX3 gene fusion, provides control over the density of motor-binding sites on peroxisome surfaces. The simultaneous regulation of the expression of a second peroxisome-targeting protein (mYFP-SKL) protein provides control over peroxisome size.

MyosinVa Motors Work Better as a Team than Kinesin Motors.

Live-cell assays using these handles revealed key distinctions between the collective behaviors of kinesin-1 and myosinVa motors (summarized in Table 1). Consistent with expectations that multiple kinesins have difficulties cooperating productively, collections of kinesin-1 motors transported large peroxisomes more slowly than smaller peroxisomes, presumably due to the increased viscoelastic load imposed by the COS-7 cell cytoplasm. Moreover, this trend was largely unaffected by doxycycline-dependent regulation of motor surface densities, indicating that the number of kinesin motors engaged in transport does not change appreciably as the total number of kinesins on a cargo is modulated. In contrast, the velocities of myosinVa-driven cargos were generally much more responsive to doxycycline-controlled motor density and less responsive to peroxisome size. Overall, these responses are suggestive of much more productive collective behaviors where the addition of motors increases the net force production capabilities of the motor system.

Variations in Fast vs. Slow Transport for the Two Motors.

Analyses of fast and slow transport components of trajectories using the hidden Markov model also highlighted key distinctions between the collective behaviors of kinesin-1 and myosinVa motors. The ratio of these events was largely insensitive to kinesin density. However, the proportion of fast, directional transport events decreased significantly with increasing peroxisome size, indicating that cargo size influences the probability that a peroxisome switches between these two general transport modes. It is difficult to distinguish whether the slow transport events should be attributed to diffusive or pausing behaviors without additional information. Nevertheless, the observation that the length of the fast runs also decreases with increasing peroxisome size may provide insights. The average distances traveled during fast kinesin runs is much smaller than the run length of a single kinesin (∼1 μm) at all particle sizes. This behavior implies that fast runs are often terminated when peroxisomes reach a cage boundary. Assuming the microtubule network plays a role in defining the effective cage sizes, this dependence suggests that many of the slow transport events can be attributed to peroxisome interactions at microtubule intersections. In turn, because the number of these events is insensitive to doxycycline, the probability that a peroxisome will pause, or remain paused, at filament intersections does not appear to depend strongly on motor density, at least in the motor number regime explored here.

In contrast to kinesin-1 behaviors, the ratio of fast-to-slow transport components of trajectories is much more sensitive to myosinVa density. Assuming the slow transport events correspond to peroxisome diffusion, this response suggests that the collective binding of multiple myosinVa motors to the actin filaments has an appreciable influence over their ability to engage in activated transport in cells. Alternatively, if these events primarily reflect pausing behaviors, the sensitivity to doxycycline concentration suggests that increasing motor number affects the ability of a peroxisome to transition into and out of a pause state. Furthermore, the distances traveled during the fast transport events were insensitive to peroxisome size, implying that cytoplasmic/cytoskeletal cage sizes are not the only factor affecting the lengths of myosinVa runs. Considering the multiple lines of evidence that collection of myosinVa motors can produce large forces, the sensitivity of these behaviors to myosin density may stem from the ability of myosinVa motors to cooperate with one another to reposition their surrounding actin filaments as they move through the filament meshwork.

Predictions of Cellular Behavior from in Vitro-Derived Parameters.

The distinctive collective behaviors of kinesin-1 and myosinVa motors in COS-7 cells appears to be consistent with theoretical models that have been used successfully to describe the cooperative behaviors of synthetic multiple motor complexes in vitro (9, 11). These models suggest that the sensitivity (susceptibility) of motor velocities and detachment rates to force at the single-motor level play key roles in determining whether a team of motors can cooperate productively by sharing the applied load imposed on a cargo. The unloaded velocities of kinesin-1 and myosinVa are similar; however, myosinVa stalls at a much lower force (∼1 pN) compared with kinesin-1 (∼7 pN) (8, 25–27). Consequently, myosinVa stepping rates/velocities will decrease more rapidly with increasing force [i.e., the derivative of motor velocity with respect to force (dv/dF) is large at most forces]. The resultant high susceptibility of myosinVa velocity to force also dictates that motors within a complex will move with different velocities when they bear different portions of the applied load on a cargo. This behavior increases the probability that a group of myosinVa motors will transition into filament-bound configurations where the motors share their applied load. In contrast, the differences between individual kinesin-1 velocities will be much smaller in circumstances where one or a few motors bear the applied load. As a result, these relatively unproductive states will persist for longer periods of time, yielding less productive collective force production and transport behaviors.

The force-dependent susceptibility of motor detachment rates is also an important determinant of collective motor behaviors. This property dictates whether a team of motors can remain associated with a filament for a sufficient amount of time to allow it to transition from states where loads are distributed unequally to those where motors share their applied load. This sensitivity can be approximated by a parameter called the critical detachment force (F_d). It is important to note that F_d is not an actual force, but rather a parameter that characterizes the free energy profile of the detachment reaction coordinate (i.e., F_d = k_BT/d, where d approximates the distance between the filament-bound state and the transition state along the coordinate). Single-motor analyses suggest that F_d for myosinVa is appreciably higher than its stalling force (F_d ∼ 4pN) (28), whereas F_d for kinesin is much lower than its stalling force (F_d ∼ 3pN) (9, 29). Consequently, motors within a multiple kinesin system will be more prone to detachment as they attempt to generate load sharing configurations.

Finally, this picture of collective motor dynamics was developed through detailed analyses of synthetic complexes where motors were coupled elastically using polymer linkers. The differences between kinesin-1 and myosinVa behaviors in the engineered COS-7 cell suggest the factors outlined above also influence collective motor behaviors when motors are connected to vesicular cargos, and could potentially diffuse much more freely on the surface of a cargo.

Implications for Cellular Trafficking.

The sensitivity of multiple myosinVa behaviors may have important implications for mechanisms that regulate cargo motion in cells. Multiple copies of kinesins, myosins, and other types of processive motors, including dynein, are often bound to the same cargo (2, 15, 16). The maximum force that a system of processive kinesin or myosinVa motors is capable of producing is predictive of which motor team will win a competition between these motors at filament intersections (30). The present responses suggest that the balance between kinesin and myosin can be tilted more sensitively via control over myosinVa number/activity level during these competitions. Insensitivities to the density of other motors like kinesin-1 could also increase how robustly regulation of myosinV number and activity level impacts cargo trafficking between cytoskeletal networks. This expectation is consistent with results from live-cell motility assays showing that the addition of myosinVb motors to cargos can arrest kinesin-2–dependent vesicle motions (31). Such responses are also consistent with observations that myosinV motors play key roles in neuronal trafficking processes while interacting with kinesins (32). Fully confirming such behavior will require further investigations and assays using additional cell types. Nevertheless, the synthetic biology approach provided by this cellular platform will likely provide important avenues to resolve these mechanisms.

Materials and Methods

DNA Constructs and Cell Lines.

All genes were generated using standard cloning procedures and were verified by sequencing. Genes encoding the FKBP and FRB proteins were obtained from ARIAD Pharmaceuticals. The PEX3-mYFP-FKBP gene was generated using overlap PCR and cloned into a TET-ON Lentiviral vector (Clontech). The mYFP-SKL gene was prepared similarly and cloned into a cumate-inducible vector (pCumate; System Biosciences). Both vectors were used to generate clonal COS-7 cell lines as described below. The kinesin-1 and myosinVa constructs (KIF5B-mCherry-FRB and MyoVa-mCherry-FRB) were cloned into separate pEGFP-N1 vectors (Clontech). Each construct incorporated a CMV promoter and was expressed in the engineered COS-7 cells via transient transfection. The PMP34-cerulean and Lamp1-RFP vectors were kind gifts from James McNew (Rice University, Houston).

Stable cell lines expressing PEX3-mYFP-FKBP under the control of the TET-ON regulator was created using lentiviral vectors (Clontech) according to the manufacturer’s protocol. Briefly, cells were first transduced with the TET-ON regulator vector daily for five consecutive days, selected with G418, and then further transduced with lentivirus containing the PEX3-mYFP-FKBP gene. After a final round of selection with G418 and puromycin, clonal cell populations were prepared from the resulting cell population via the limited dilution method. PiggyBac transposase technologies were then used to incorporate the cumate-inducible mYFP-SKL gene into the COS-7 cell genome. In this step, the cells were cotransfected transiently with pCumate-mYFP-SKL (10 μg) and pCMV-PiggyBac (33) (1 μg; a gift from Matthew H. Wilson, Baylor College of Medicine, Houston) vectors using Xfect transfection reagents (Clontech). Clonal cells were then generated via a second round of limited dilution. Clonal COS-7 cells incorporating pCumate-mYFP-SKL gene alone were also prepared similarly. In each case, inducible PEX3-mYFP-FKBP and mYFP-SKL expression control was confirmed by fluorescence microscopy.

Live Cell Imaging.

The engineered COS-7 cells were prepared for live cell motility assays as follows. mYFP-SKL and PEX3-mYFP-FKBP expression was induced for 76 and 48 h, respectively. The doxycycline concentration was varied between 2 and 10 μg/mL depending on the experiment. mYFP-SKL expression was induced using 100 μg/mL cumate for all peroxisome motility assays. Under these conditions, peroxisome size distributions contained significant amplitudes at all particles sizes, which allowed the motile behaviors of different sized particles to be assayed while maintaining the same FKBP induction period. The cells were transfected with motor constructs for 24 h before seeding them into custom-fabricated, glass-bottom incubation chambers. The cell line that incorporated only the pCumate-mYFP-SKL gene was found to express mYFP-SKL more rapidly than the PEX3-mYFP-FKBP expressing cells and required shorter incubation times to generate larger peroxisomes, presumably due to increased pCumate-mYFP-SKL gene copy number in these cells.

Motility assays were performed using microscope cell incubator (Okolab) to maintain 5% CO₂ and a humidified atmosphere at 37°. The mCherry signals from the motor constructs were imaged to locate cells exhibiting the transient motor expression. Motor-driven peroxisome transport was then initiated by adding rapalog (AP21967) at a final concentration of 1 μM. All rapalog-triggered motility assays were performed within 6 h after cells were seeded into their chambers. Peroxisomes were imaged using a 100× 1.4 N.A. oil immersion objective and an Eclipse TiE epi-fluorescent microscope, except for the images from Fig. 2 and Fig. S2, which were collected using a hyperspectral confocal laser scanning microscope (Nikon A1). Long-range peroxisome motions were monitored using a 14-bit depth EMCCD (Luca; Andor) at 1–2 frames per second (fps) over a period of 20–30 min. Particle-tracking analyses were performed with a 16-bit depth EMCCD (PhotonMAX 512; Princeton Instruments) at a 90-fps rate. Trajectories were analyzed using a centroid tracking algorithm written in MatLab as described in ref. 34 with some minor modifications.

Peroxisome Size Determination.

Peroxisome sizes were determined by comparing their intensity profiles to a standard curve that was generated computationally as follows. The point spread function (PSF) of the microscope was measured in three dimensions using 50-nm radius fluorescent microspheres (FluoSpheres; Invitrogen), which allowed the PSF of single mYFP molecules to be estimated and used to approximate the size-dependent PSFs of computer-generated spherical particles that were homogeneously filled with mYFP (Fig. S6). Here, the intensity profile for each sphere corresponds to the convolved signal from each internal fluorescent protein. The apparent mean squared radii, 〈r²〉, of computationally generated particles in the microscopes image plane were then plotted over a range if particle sizes using the following formula:

where 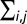is the sum over all (i, j) pixels in the tracked particle neighborhood; r_ij is the distance of the (i, j) pixel from the particles center; and I_i,j is the intensity of the (i, j) pixel. Finally, the resultant plot of simulated vs. real radius was fit with a polynomial function to generate a final calibration curve for peroxisome size estimates.

Analyses of peroxisome sizes were performed by subtracting mean background signals in each image. The centroid position of peroxisomes in each frame of a movie was determined by fitting their intensity profiles to a Gaussian function. Values for r_ij and I_ij were then measured to calculate . Only the top 80% of the peroxisome intensity profiles were used to estimate to reduce the influence of local intensity fluctuations. Identical treatment was applied to the calculated PSFs used to generate the calibration curve for consistency. Peroxisome radii were measured at each time point in a trajectory and averaged. The SE of these measurements was less than 60 nm. We note peroxisome motions are largely restricted to a 2D plane in COS-7 cells due to the highly spread and flat geometry of these cells. Thus, effects from motions in the z-direction are minimized in these cells.

Rheological Analyses.

The size-dependent diffusive properties of peroxisomes were examined by analyzing their MSD vs. time in the absence of rapalog. Under these conditions, peroxisomes primarily diffused randomly in the cytoplasm. Trajectories containing rare active transport events were identified by examining the trajectory aspect ratios in the x,y plane as described by Huet et al. (35) and were excluded from MSD analyses. The viscoelastic properties of the COS-7 cells were then analyzed by fitting measured MSD curves with an equation describing corralled particle diffusion:

where t is time; R_cage is the effective radius of cytoskeletal cage; D_a is the peroxisome diffusion coefficient inside the cage; D_b is the cage diffusion coefficient; and V is the cage drift velocity. It should be noted that R_cage corresponds the dimension of the space effectively explored by a particle. When the particle size is much smaller than the cage size, this radius will be equal to the R_cage cage. However, for a particle whose radius is comparable to cytoskeletal cage sizes, a particles-excluded volume must also be considered. In this case, R_cage is assumed to be equivalent to R + r, where r is the peroxisome radius. To estimate the average drag force acting on a peroxisome moving in viscoelastic cell cytoplasm we used the same method as described in ref. 36. Briefly, the frequency (ω)-dependent complex shear modulus, G*(ω), of the cytoplasm was found using the formula derived in ref. 24:

where k_B is Boltzmann constant; T is temperature; r is the peroxisome radius for which MSD was measured; Γ is gamma function; and α(ω)) is the slope of a log-log MSD plot vs. time at the point t = 1/ω. Then the real part, Re(η(ω)), of the cytoplasm viscosity, η, was calculated as

Finally, the average drag force, F_drag, acting on peroxisome moving with velocity v can be estimated as

HMM Analyses and Estimation of Transport Parameters.

Peroxisome velocities distributions and trajectory components were analyzed using a two-state HMM procedure similar to methods described in ref. 37. The velocity distributions used for these analyses were constructed by examining the distance peroxisomes were displaced in a 77-ms time window. Using this approach, the HMM also examines subdistributions of distances peroxisomes are transported within a 77-ms window.

Instantaneous peroxisome velocities were measured using 15-frame sliding linear regression procedure. Average peroxisome velocities were determined from these values. The length of the fast and directional “runs” were calculated as the total distance the peroxisome were displaced in the x,y plane during HMM-identified fast-transport events. Rms position fluctuations were measured by calculating the difference between peroxisome positions in the x,y plane to their corresponding position in a trajectory that was smoothed using a 15-frame boxcar averaging procedure.