Resonant secondary light emission from plasmonic Au nanostructures at high electron temperatures created by pulsed-laser excitation

Significance

Light emission from plasmonic nanostructures at wavelengths shorter than the wavelength of pulsed-laser excitation is typically described as two-photon absorption followed by fluorescence. In this work, we present an alternate description of the secondary light emission as a resonant electronic Raman scattering process. Experiments on aqueous suspensions of Au nanorods are quantitatively described by a two-temperature model. The results will facilitate the design of imaging experiments and understanding of background in surface-enhanced Raman scattering.

Abstract

Plasmonic nanostructures are of great current interest as chemical sensors, in vivo imaging agents, and for photothermal therapeutics. We study continuous-wave (cw) and pulsed-laser excitation of aqueous suspensions of Au nanorods as a model system for secondary light emission from plasmonic nanostructures. Resonant secondary emission contributes significantly to the background commonly observed in surface-enhanced Raman scattering and to the light emission generated by pulsed-laser excitation of metallic nanostructures that is often attributed to two-photon luminescence. Spectra collected using cw laser excitation at 488 nm show an enhancement of the broad spectrum of emission at the electromagnetic plasmon resonance of the nanorods. The intensity of anti-Stokes emission collected using cw laser excitation at 785 nm is described by a 300 K thermal distribution of excitations. Excitation by subpicosecond laser pulses at 785 nm broadens and increases the intensity of the anti-Stokes emission in a manner that is consistent with electronic Raman scattering by a high-temperature distribution of electronic excitations predicted by a two-temperature model. Broadening of the pulse duration using an etalon reduces the intensity of anti-Stokes emission in quantitative agreement with the model. Experiments using a pair of subpicosecond optical pulses separated by a variable delay show that the timescale of resonant secondary emission is comparable to the timescale for equilibration of electrons and phonons.

The unique optical properties of Au and Ag nanostructures have enabled a wide variety of innovations in optical detection, sensing, and imaging (1). Two of the most important and widely studied of these applications involve the emission of light at a different wavelength than the excitation, i.e., secondary light emission: (i) sensing of molecular layers by surface-enhanced Raman scattering (SERS) (2, 3); and (ii) imaging of biological microstructures using light emission generated by ultrafast laser pulses, a process often referred to as two-photon luminescence (TPL) (4, 5).

A common limitation of SERS for sensing adsorbed species is the background (6) that appears as a broad continuum of light emission underlying the desired signal generated by the vibrational modes of the adsorbed molecules. This background is often attributed to unintentional fluorescence by impurities, although processes involving photoluminescence of the substrate (7, 8) and electronic Raman scattering by localized surface electronic states associated with the molecule/metal chemical bond (9, 10) have also been invoked.

The quantum efficiency of TPL from metal nanoparticles is small compared with a molecular dye, but TPL from metal nanoparticles generally has a much higher stability, i.e., does not show bleaching or blinking (5). The benefit of two-photon excitation is an improvement of the spatial resolution over what can typically be achieved by confocal fluorescence imaging. Proposed mechanisms for luminescence from Au or Ag nanostructures include fluorescence by interband transitions (7, 11–16), intraband transitions (17), and radiative decay of surface plasmons (18–21).

The electromagnetic resonance of Au or Ag nanostructures are thought to play a critical role in both the background in SERS and the emission typically described as TPL. In the language of quantum mechanics, the optical process for the annihilation of an incident photon and the creation of an emitted photon involves a resonance with a plasmon; therefore, light emission by plasmonic nanostructures is a type of resonant secondary emission. The interpretation of resonant secondary light emission in terms of fundamental processes has been controversial for 40 y. Klein (22) and Solin and Merkelo (23, 24) argued that resonant Raman scattering and hot luminescence are formally equivalent. Shen (25, 26) countered that emission can be broken down into a Raman scattering component and a luminescence component (27, 28) based on the longitudinal and transverse relaxation times. In a 1991 review, Kono and coworkers found a similar division into “Raman-like” and “fluorescence-like” components of the secondary emission (29).

We do not attempt to address this controversy directly but instead point out that resonant electronic Raman scattering and resonant fluorescence may both be useful descriptions of the secondary emission. An important conclusion of our work is, however, that blue-shifted secondary emission generated by pulsed-laser excitation at a plasmon resonance in the near-infrared is not the result of a two-photon absorption followed by radiative decay of a plasmon and is instead better described by electronic Raman scattering from single-particle electron-hole pair excitations (30, 31) of the Au or Ag metal that are resonantly enhanced by the plasmon. [In a classic study published nearly 50 y ago, Kawabata and Kubo (32) described the mechanisms by which a plasmon decays by transferring energy to electron-hole pairs.] In particular, the changes in the anti-Stokes spectra with the energy and duration of the ultrafast laser pulse are quantitatively predicted by a two-temperature model; and the timescale of the nonlinearity is consistent with the cooling time of hot electrons.

Results and Discussion

Fig. 1 compares the optical absorption spectra and the spectra of light emission using 488-nm continuous-wave (cw) laser excitations for aqueous suspensions of Au nanorods (AuNRs) with three aspect ratios. To facilitate this comparison, we use a common x axis for both plots; because we will argue that the light emission by the AuNRs can be described by a resonant Raman scattering process, we label the x axis of both plots “Raman shift.” The corresponding wavelength for absorption or emission is given on the top axis. Raman scattering by the band of OH stretching vibrations of water is the dominant feature near a shift of 3,300 cm⁻¹. The spectra of light emission from all three AuNR suspensions show a broad peak near 525 nm. For aspect ratios of 2.3 and 3.8, the spectra also show a broad peak at longer wavelengths that corresponds to the position of the peak absorption created by the longitudinal plasmon resonance. The ratio of scattering cross-section and absorption cross-section of the AuNRs of our dimensions is smaller than 0.05 (33); thus, the y axis in Fig. 1A can be approximately set as absorbance instead of extinction.

Fig. 1.

(A) Absorption spectra of AuNRs of different abstract ratios (ARs): green (AR = 1.2), blue (AR = 2.3), and cyan (AR = 3.8). The unit of the lower axis is given as a frequency shift relative to the 488-nm laser excitation for the convenience of comparison with B. The upper axis provides the corresponding wavelengths. The y axis is the absorbance (abs), i.e., the negative of the base-10 logarithm of the optical transmission. (B) Spectra of water and AuNRs of different absorption peaks excited by 488-nm cw laser with 1-mW power. S is the spectral density of the intensity of scattered light, and P is the average excitation laser power. Thus, the y axis is the output of the CCD camera of the spectrometer normalized by the data acquisition time and the power of the excitation laser.

The similarity of the optical absorption and light emission spectra of AuNR has been noted before (12, 17, 19, 20) and is typically attributed to light emission associated with the plasmon resonance of the AuNR (19, 20). The proposed mechanisms of the luminescence involve (i) the creation of energetic electron-hole pairs by the 488-nm photon; (ii) the relaxation of these electron-hole pairs by excitation of the collective longitudinal plasmon; (iii) radiative decay of the longitudinal plasmon by emission of near infrared photons.

Inspired by Klein’s assertion of the equivalence of hot luminescence and resonant Raman scattering (22), we assert that the secondary light emission under 488-nm excitation is equally well described by Raman scattering by a broad spectrum of single-particle electron-hole excitations and that the peak observed in the spectra is the result of the enhancements of the electric fields of the scattered radiation by the plasmon resonance of the AuNR. In the usual situation where the spectrum of excitations is sharp and the resonance effects are weakly dependent on wavelength, the wavelength of the Raman scattered light will shift with the excitation wavelength. The system we are studying is the opposite: the spectrum of excitations is broad and the resonance effects have a strong dependence on wavelength. Because the plasmon resonance is fixed by the geometry of the AuNR, a change in the excitation wavelength will not change the peak position. Further support for this description comes from prior studies (12, 17, 19, 20) which used varying excitation wavelengths and found that the emission peak of AuNRs overlapped with the optical absorption or dark-field scattering peak.

We next focus our attention on the largest-aspect ratio AuNRs that have a resonance that was intentionally tuned to be close to the wavelength of operation of the Ti:sapphire laser oscillator. Fig. 2A compares the Raman scattering spectra from AuNRs excited by cw and pulsed-laser excitation at 785 nm. The y axis of these plots has been normalized by the average power of the excitation laser and the data acquisition time, i.e., the y axis shows the intensity of scattered light normalized by the incident photon flux. The cw mode excitation produces a narrow anti-Stokes spectrum and a broad Stokes spectrum that does not change with the average power of the excitation laser. This indicates that the emission process is linear when the excitation laser is operated in cw mode. The anti-Stokes data are well described by a thermal population of excitations with a characteristic temperature of 300 K.

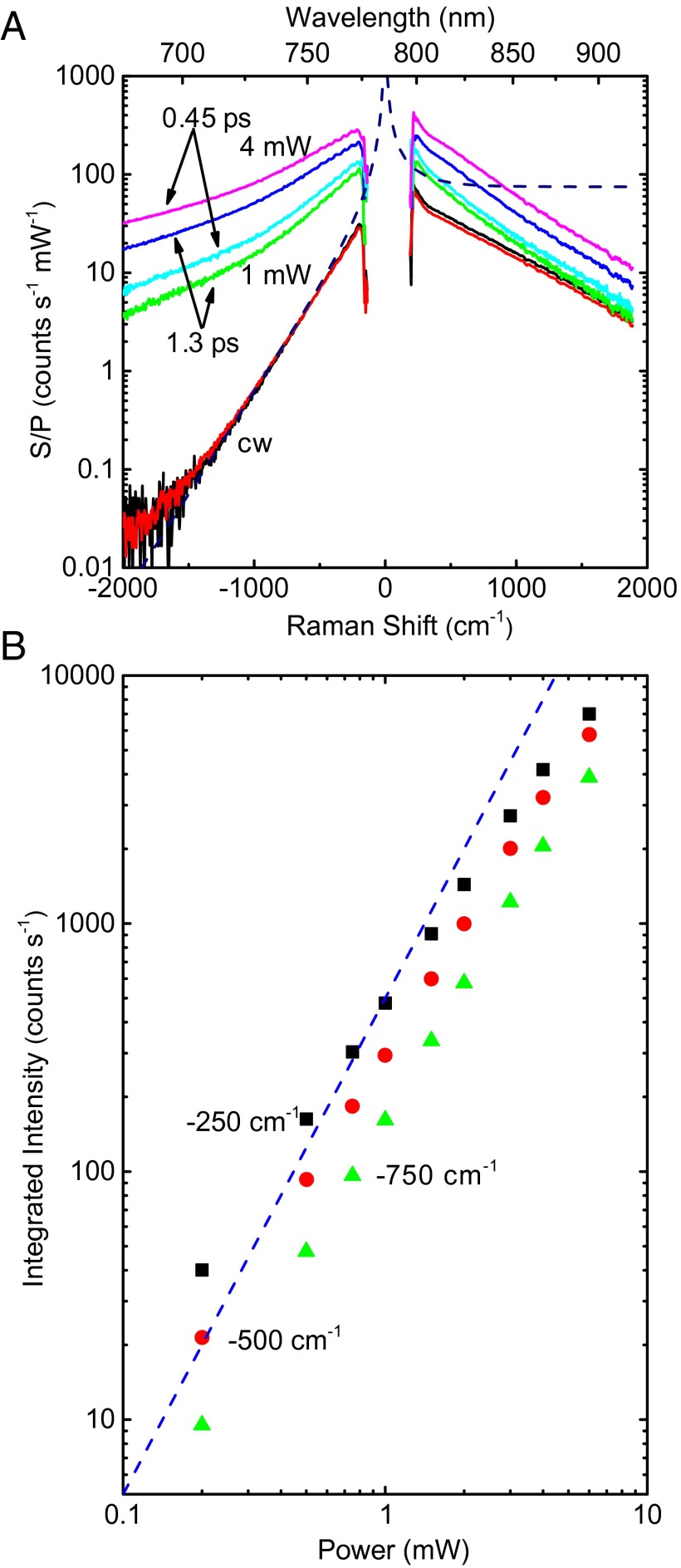
Fig. 2.

(A) Raman scattering spectra for AuNRs with the absorption peak at 787 nm excited by cw laser light at 785 nm at incident powers of 1 mW (black), 4 mW (red); by mode-locked laser pulses of 0.45-ps width with average incident powers of 1 mW (cyan) and 4 mW (magenta); and by mode-locked laser pulses of 1.3-ps width with average incident powers of 1 mW (green) and 4 mW (blue). The y axis is the same as in Fig. 1B: S is the scattered intensity, and P is the average power of the excitation laser. Data for 1 and 4 mW using the cw laser overlap. The dashed line is the calculated intensity for a characteristic temperature of 300 K assuming constant Raman cross-section and enhancement factors at all Raman shifts; the vertical scale of the dashed line is adjusted to match the experimental anti-Stokes intensity. (B) Raman scattering intensity vs. average incident power for AuNRs with absorption peak at 787 nm excited by pulsed 785-nm laser pulses of 0.45-ps width integrated over a Raman shift range of −240 to −260 cm⁻¹ (black squares), −490 to −510 cm⁻¹ (red circles), and −740 to −760 cm⁻¹ (green triangles). The blue dashed line with a slope of 2 indicates a quadratic relation between the spectral intensity and average incident power.

With pulsed-laser excitation, however, the spectra become significantly more intense, broaden dramatically on the anti-Stokes side of the spectra, and depend on the laser pulse duration and average power. The emission is thus a nonlinear function of the incident photon flux. For spectra obtained with pulses of 0.45-ps duration, and a change in laser power of a factor of 4, the normalized anti-Stokes intensity increases by a factor of ∼3 at small energy shifts (−250 cm⁻¹) and by a factor of ∼4 at large energy shifts (−1,000 cm⁻¹).

The nonlinear relationship between the spectral intensity S and the average power P of the pulsed-laser excitation on the anti-Stokes side is emphasized further in Fig. 2B and Fig. S1A. We believe that this nonlinearity, which is approximately quadratic, has been often misinterpreted as signature of nonlinear optical absorption via two-photon excitation of interband transitions (16) followed by fluorescence. We argue that this nonlinear optical response is explained by a high-temperature distribution of electron-hole excitations created by the short laser pulses and is not the signature of a direct optical nonlinearity. In the language of Raman scattering, the strength of the scattering is high because both the incident and scattered fields are enhanced by the electromagnetic resonance of the AuNR.

Furthermore, the intensity does not scale quadratically with the average laser intensity. At constant energy per pulse, we calculate that changing the pulse duration from 0.45 to 1.3 ps, decreases the integral of the square of the intensity by a factor of ∼3.5. An emission process that was initiated by two-photon absorption should therefore decrease in intensity by a factor of 3.5 when the pulse duration is broadened. In our experiments, broadening the pulse duration reduces the emission intensity by a factor of only ∼1.5.

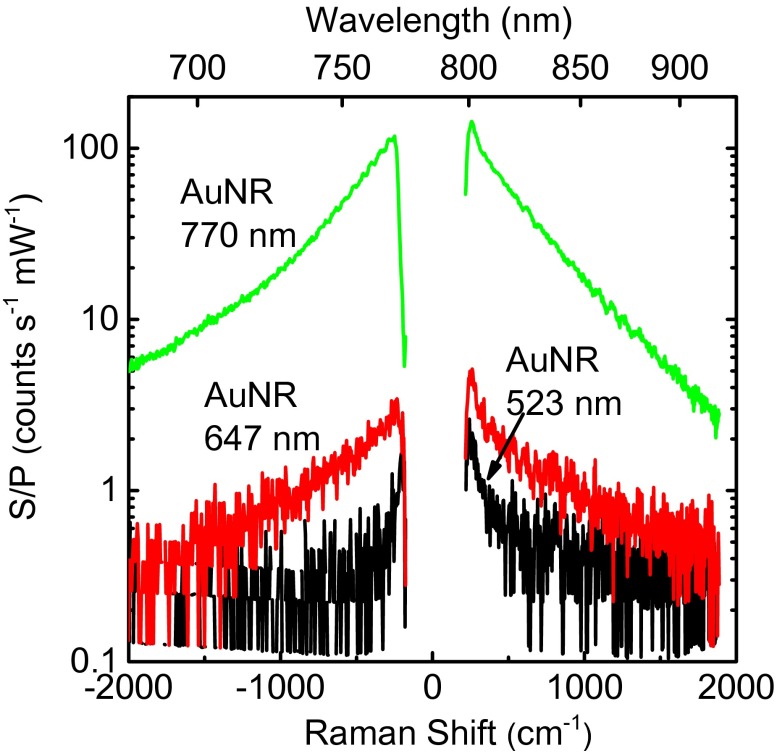
To further test the role of the plasmon resonance, we also collected emission spectra of AuNRs with smaller aspect ratios excited by 785-nm laser pulses with an average power of 1 mW (Fig. 3). Spectra for AuNRs with longitudinal plasmon resonances at 523 and 647 nm have much lower intensities because of the low enhancement factors, and the low optical cross-section that results in low electronic temperatures. (We could not measure emission spectra for these nonresonant AuNRs using cw excitation at 785 nm because the signals are too weak for our apparatus to detect reliably.)

Fig. 3.

Raman scattering spectra for AuNRs with the absorption peaks at 523 nm (black), 647 nm (red), and 770 nm (green) excited by 785-nm laser pulses of 0.45-ps duration with an average incident power of 1 mW.

We approximately describe the intensity S(Δω) of anti-Stokes electronic Raman scattering by the electron-hole excitations of the AuNR by the following equation (34, 35):

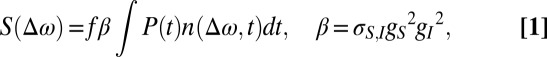where P(t) is the laser intensity of an individual laser pulse as a function of time t; f = 80 MHz is repetition rate of laser pulse; n(Δω,t) is the time-dependent electron-hole occupation number; σ_S,I is the Raman cross-section of AuNR at the incident and scattering light frequencies; g_S is the Raman enhancement factor for the scattered light; and g_I is the Raman enhancement factor for the incident light. We define the sign of the Raman frequency shift Δω as a negative value on the anti-Stokes side of the spectra and positive on the Stokes side.

The time-dependent electron-hole occupation number is as follows:

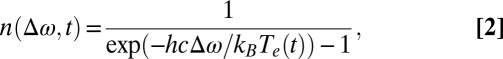where T_e(t) is the time-dependent electronic temperature of AuNRs; h is the Planck constant; and c is the speed of light. In cw mode, T_e(t) = T₀ = 300 K. In pulsed mode, T_e(t) greatly exceeds T₀ during the optical pulse.

We cannot determine T_e(t) experimentally and instead focus our attention on an effective temperature T_eff for the scattering process that we can derive from the data. We define T_eff (36) by equating the integral of the time-dependent scattering intensity to the scattering intensity that would be created by a constant electronic temperature. T_eff can be thought of as a time average of T_e(t) that is weighted by the emission intensity:

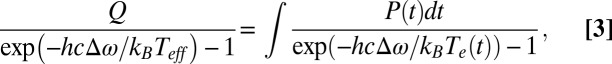where 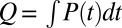is the total energy in one laser pulse.

Eq. 3 describes how we derive a prediction for T_eff from a model for T_e(t). We extract an experimental value for T_eff from the data by dividing the intensity generated by pulsed-laser excitation by the intensity generated by cw laser excitation:

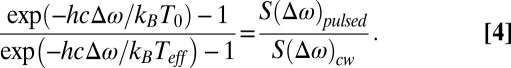This approach has the advantage of eliminating the Raman enhancement factors, Raman cross-sections, and the calibration of the spectrometer from the analysis at the same Raman shift; but has the disadvantage of giving a different value of T_eff for every value of the Raman shift. Data for the change in the effective temperature ΔT_eff = T_eff − T₀ as a function of average laser power of the pulsed laser are summarized in Fig. 4A and Fig. S1B.

Fig. 4.

(A) Change in the effective temperature relative to room temperature ΔT_eff = T_eff − 300 K of Raman scattering by AuNRs with absorption peak at 787 nm excited by laser pulses of 0.45-ps width. ΔT_eff calculated from the data using Eq. 4 are shown as lines that show some noise. ΔT_eff calculated using Eqs. 4 and 6 with the optical cross-section σ_abs as a fitting parameter are shown as smooth lines. The best fit to the data for −1,500 cm⁻¹ < Δω < 1,500 cm⁻¹ gives σ_abs = 2,700 nm². (B and C) ΔT_eff of the measurement at a Raman shift of (B) −500 cm⁻¹ and (C) 500 cm⁻¹ with laser pulse duration of 0.45 ps (black squares) and 1.3 ps (red circles). The solid lines show the predicted values of ΔT_eff from Eqs. 4 and 6 as a function of laser power using σ_abs = 2,700 nm².

The effective temperature on the Stokes side is defined in the same way and can also be calculated using Eq. 4. (For Stokes scattering, n is replaced by n+1 in Eq. 1; Eqs. 3 and 4 are valid for Stokes scattering where Δω > 0, and Eq. S3 provides more details.) ΔT_eff derived from the data deviates from the prediction at average laser power >1 mW with 0.45-ps pulses and at average laser power >2 mW with 1.3-ps pulses.

To make this analysis more quantitative, we use a conventional two-temperature model to predict how the electron temperature varies as a function of time during the laser pulse. In the two-temperature model, the electron-hole excitations of the metal are assumed to have a thermal distribution characterized by a temperature T_e(t). Because we are only interested in the electronic temperature, and the heat capacity of the phonons is large compared with the heat capacity of the electronic system, we do not consider time variations of the phonon temperatures and set T₀ = 300 K, independent of time:

In Eq. 5, C_e is the volumetric heat capacity of electrons; γ = 66 J⋅m⁻³⋅K⁻² is a constant (37); σ_abs is the AuNR optical absorption cross-section of the AuNR; r₀ = 4.7 μm is the 1/e² intensity radius of the focused laser spot radius; V is the AuNR volume; and g = 3.0 × 10¹⁶ W⋅m⁻³⋅K⁻¹ is the electron–phonon coupling parameter for Au (37). In our experiments, we use two forms of P(t), with and without an etalon. Without the etalon, we approximate P(t) by a Gaussian as a function of time with full width at half maximum (FWHM) of 0.45 ps. With the etalon, we approximate P(t) by an exponential decay with a time-broadened onset. Further details about how we determined and modeled P(t) in the two cases are given by Eqs. S1 and S2 in The Laser Pulse Shape and Duration.

T_e(t) is calculated numerically by integrating Eq. 5. Examples of calculated values of T_e(t) are included as Fig. S2B. The ratio of scattered light produced by pulsed and cw excitation in each pulse cycle of 12.5 ns is then the following:

We treat σ_abs as an adjustable parameter in Eq. 5 and find that σ_abs = 2,700 nm² produces the best fit for the pulsed vs. cw ratio between the anti-Stokes data and the model at low average laser power at 0.45-ps pulse excitations. The calculated ratio using the same σ_abs value also agrees well with the anti-Stokes data at 1.3-ps pulse excitations. We use the anti-Stokes side of the spectra in this fit because the anti-Stokes data provide greater sensitivity to T_eff than the Stokes data. The results of the calculation using σ_abs = 2,700 nm² to calculate T_e(t) from Eq. 5, and therefore the ratio of pulsed vs. cw spectra intensity as a function of frequency shift and laser power using Eq. 6, are shown in Fig. S3.

Once σ_abs is fixed, and therefore T_e(t) can be calculated from the two-temperature model, we calculate ΔT_eff using Eq. 4. These predictions for ΔT_eff are compared with ΔT_eff derived from the experiment in Fig. 4 A and B. At low laser powers, the predictions agree closely with experiment for both pulse durations and both the anti-Stokes and Stokes side of the spectra. At high laser power, the experimental value for ΔT_eff exceeds the predictions. The deviation of the data from the prediction is larger for short pulse duration and larger on the Stokes side of the spectra than the anti-Stokes side of the spectra. We speculate on the origin of these discrepancies at high electron temperature below.

Predicted values of σ_abs using the discrete dipole approximation method are σ_abs = 3,800 nm² for 44 × 10.7 nm² AuNRs (38) and σ_abs = 4,700 nm² for 48 × 12.2 nm² AuNRs (33) for linearly polarized light oriented with the electric field vector along the long axis of the AuNR. For circularly polarized light, the maximum optical absorption cross-section is reduced by a factor of 2. Thus, the expected values of the maximum possible cross-sections and the value of σ_abs = 2,700 nm² we used to fit the anti-Stokes data agree to within a factor of 2, and we conclude that both the intensity of the scattering and the changes in the scattering with laser power are adequately described by a two-temperature model.

We do not expect better agreement between the predicted and fitted cross-sections because of the nonlinearity of the light emission and the multiple inhomogeneities in the experiment: (i) polydispersity of the aspect ratio of the AuNR; (ii) the Gaussian spatial profile of the excitation laser; and (iii) the 3D random orientations of the AuNRs. The polydispersity and 3D orientations of AuNRs will tend to decrease the apparent cross-section; the Gaussian profile of the excitation laser will tend to increase the apparent cross-section because of the factor of 2 larger intensity (and therefore higher electronic temperatures) at the center of the beam compared with the average intensity calculated using an effective beam area of πr₀².

In Fig. 4 B and C, we make a more detailed comparison between measured and calculated ΔT_eff at the Raman shifts of −500 and 500 cm⁻¹. We do not yet understand the origin of the discrepancy at high average laser power and speculate that the cross-section for secondary emission increases for some reason at higher electronic temperatures. The strong enhancement of emission on the Stokes side of the spectra relative to the prediction of Raman scattering by single electron-hole pairs suggests to us that higher-order processes are involved. These higher-order processes may be analogous to multiphonon resonant Raman scattering that is often observed when the excitation photon energy exceeds the band gap of a semiconductor (22, 39).

We directly determined the timescale for the nonlinearity of the light emission using a pair of ultrafast excitation pulses at 785 nm separated by a variable time delay. In this experiment, the laser pulse is in Gaussian shape with 0.45-ps duration, and the total average power is 1 mW, i.e., the average power carried by each of the excitation pulses is 0.5 mW. Typical emission spectra are shown in Fig. S4. The relative values of the intensity integrated over a 200 cm⁻¹ range centered at −500 and 900 cm⁻¹ are plotted in Fig. 5 as a function of the delay time τ. The y axis of Fig. 5 is the intensity of the light emission as a function of the delay time, normalized by the intensity when the pulse separation is −10 ps. The ratio of the intensity with overlapping pulses (τ = 0) to the intensity with well-separated pulses (τ = −10 ps) is ∼1.6 for intermediate Raman shifts (−400 to −600 cm⁻¹) and ∼1.8 for large Raman shifts (−800 to −1,000 cm⁻¹).

Fig. 5.

Ratios of integrated intensity at various delay times I(τ) with data at −400 to −600 cm⁻¹ (black square), −800 to −1,000 cm⁻¹ (red circle), and the model calculation at −500 cm⁻¹ (black line) and −900 cm⁻¹ (red line).

We model the scattered intensity by a two-pulse excitation using extensions of the models presented above. The time-dependent electronic temperature calculation of Eq. 5 is modified by including two laser pulses separated by delay time of τ. The relative electronic Raman scattering intensity at the Raman shift Δω and delay time τ is then the following:

The calculated intensity ratio at various delay times τ vs. τ = −10 ps is plotted in Fig. 5 as solid lines. The model closely resembles the experimental results but there are discrepancies: in particular, although the decay rates of the signal as a function τ are similar for experiment and theory, the experimental data are more sharply peaked than the model.

In this modeling, we are making the standard assumption within the two-temperature model that the occupation of the electronic excitations is well described by an equilibrium distribution of temperature T_e. However, both the generation of electron-hole pairs and the coupling of electronic excitations to the lattice will cause the distribution to deviate from equilibrium. Because the electron–electron scattering time is short compared with the electron thermalization time (tens of femtoseconds vs. picoseconds), this deviation from equilibrium is usually assumed to be small (40), but we point out that the equilibration time of electronic excitations becomes significantly longer than the electron–electron scattering time as the excess energy decreases (41). It is possible that deviations from a thermal distribution are revealed in this type of two-pulse experiment but a quantitative treatment of these effects is beyond the scope of the present work.

In conclusion, we propose that resonant electronic Raman scattering from the continuum electron-hole pairs provides a useful description of secondary light emission from a model Au nanostructure. The peak of emission that is usually attributed to radiative decay of plasmons is described by the enhancement of the Raman scattered light by the electromagnetic resonance. The nonlinear light emission usually attributed to two-photon absorption followed by fluorescence is quantitatively described by a broad spectrum of anti-Stokes electronic Raman scattering created by high electronic temperatures. The timescale of the nonlinearity is consistent with the timescale for the exchange of thermal energy between the electronic system and the lattice.

Materials and Methods

We synthesized AuNRs with average aspect ratios of 1.2 ± 0.2, 2.3 ± 0.3, and 3.8 ± 0.4 using the methods described previously (42). The AuNRs are subsequently coated with poly(acrylic acid) (43) to increase their thermal stability in aqueous solution during laser heating (44). A quartz cuvette with optical path length of 200 μm is used as the sample holder for the optical measurements.

All three aspect ratios of AuNRs were studied using a conventional Raman spectrometer with 488-nm cw excitation. (For all of the data reported below, the AuNR suspensions are at room temperature.) The microscope objective that focuses the incident light and collects the scattered light has a numerical aperture of 0.17. AuNRs with an average aspect ratio of 3.8, dimension of 47 × 12.5 nm², and longitudinal surface plasmon resonance peak at 787 nm were studied more extensively with a second custom-built Raman spectrometer that uses a Ti:sapphire laser as the excitation source (45). A 10× microscope objective lens with a numerical aperture of 0.25 is used to focus the laser on the sample with a 1/e² intensity radius of ∼4.7 μm. The laser can be operated in either cw or pulsed mode with a repetition frequency of 80 MHz. The spectrum of the excitation pulses is limited to 785 ± 1.5 nm by a bandpass optical filter. Due to dispersion of optical elements, the FWHM duration of the laser pulses is ∼0.45 ps. In a second set of experiments, we placed a Fabry–Pérot etalon after the bandpass optical filter to broaden the pulse to produce a FWHM of ∼1.3 ps. We include details about the pulse durations and shapes in The Laser Pulse Shape and Duration.

We illuminate the sample using circularly polarized light to improve the homogeneity of the energy absorbed by AuNRs with different orientations. Scattered light collected by the microscope objective passes through a quarter-wave plate, polarizing beam splitter, a beam block for specularly reflected light, and two holographic notch filters before reaching the spectrometer (45). Data acquisition time is typically 100 s for the cw mode and 10 s for the pulsed mode. A quartz lamp source was used correct the data for variations in the wavelength dependence of the quantum efficiency of the CCD detector, the reflectivity of the spectrometer grating, and the transmission coefficients of the optical elements.

We checked for extrinsic contributions to the light emission by testing all of the reagents used in synthesizing the AuNRs at concentrations of ∼10⁵ times of that in the final AuNRs samples and could not detect any background fluorescence with excitation by pulsed 785-nm excitation. AuNRs with different surface modification were also tested to exclude the possibility of surface-enhanced fluorescence from impurities or ligands on the surfaces of AuNR. We also provided the emission spectra of aspect ratio-3.8 AuNRs at short wavelength ranges in Fig. S5.

The characteristic timescale of the nonlinear light emission was measured using two-pulse excitation. The time delay between the two pulses is adjusted using a mechanical delay stage (45). The two pulses have the same spectrum of 785 ± 1.5 nm and orthogonal circular polarization. The two beams are colinear; a transient absorption measurement is used to optimize the spatial overlap of the two pulses within the sample cell (46). We set the zero of delay time at the position of the maximum of the signal.