Robust Non-Local Multi-Atlas Segmentation of the Optic Nerve

Abstract

Labeling or segmentation of structures of interest on medical images plays an essential role in both clinical and scientific understanding of the biological etiology, progression, and recurrence of pathological disorders. Here, we focus on the optic nerve, a structure that plays a critical role in many devastating pathological conditions – including glaucoma, ischemic neuropathy, optic neuritis and multiple-sclerosis. Ideally, existing fully automated procedures would result in accurate and robust segmentation of the optic nerve anatomy. However, current segmentation procedures often require manual intervention due to anatomical and imaging variability. Herein, we propose a framework for robust and fully-automated segmentation of the optic nerve anatomy. First, we provide a robust registration procedure that results in consistent registrations, despite highly varying data in terms of voxel resolution and image field-of-view. Additionally, we demonstrate the efficacy of a recently proposed non-local label fusion algorithm that accounts for small scale errors in registration correspondence. On a dataset consisting of 31 highly varying computed tomography (CT) images of the human brain, we demonstrate that the proposed framework consistently results in accurate segmentations. In particular, we show (1) that the proposed registration procedure results in robust registrations of the optic nerve anatomy, and (2) that the non-local statistical fusion algorithm significantly outperforms several of the state-of-the-art label fusion algorithms.

1. INTRODUCTION

The optic nerve (ON) plays a critical role in many devastating pathological conditions (e.g., glaucoma, ischemic neuropathy, and optic neuritis). As a result, accurate and robust segmentation of the ON plays an essential role in developing an understanding of the biophysical etiology, progression, and recurrence of these diseases. The long-held “gold standard” for highly robust segmentation has been through expert manual delineation. Yet, manual delineation is extremely resource consuming and plagued by both inter- and intra-rater variability. Alternatively, fully-automated approaches, while very accurate for specific classes of problems, often require manual intervention in order to prevent catastrophic failure on images that are hindered by noise and artifacts [1].

Atlas-based segmentation models form a middle-ground between fully-manual and fully-automatic segmentation approaches [2]. Recently, the use of multiple atlases (i.e., multi-atlas segmentation) has gained traction due to its robustness and accuracy for a wide range of applications [3, 4]. In multi-atlas segmentation, multiple atlases are separately registered to the target image and the voxelwise label conflicts between the registered atlases are resolved using label fusion [5–7]. Previously, atlas-based techniques have been proposed for segmentation of the optic nerves [8, 9]. However, these methods have had limited success in terms of overall robustness and accuracy – resulting in Dice Similarity Coefficients (DSC) between 0.39 and 0.78.

Herein, we are particularly interested in the development of a highly reliable technique for the segmentation of the ON using multi-atlas segmentation on clinically acquired computed tomography (CT) images. As a result, the dataset that we use contains a wildly varying range of fields-of-view (ranging from whole head to more localized images of the orbit) and slice thicknesses (ranging from 0.4 to 5.0 mm) (Table 1). We present our method in two subsequent steps. First, we propose a straightforward registration framework in which the boney structure (achieved through thresholding) of the atlases and the target are rigidly registered. The centroids of the ON are then estimated using the majority vote estimate of the rigidly registered atlases. Using these centroids, a reasonable region-of-interest is localized for both the target and the atlas images before performing a final non-rigid registration. Secondly, we utilize a recently proposed non-local label fusion algorithm (Non-Local STAPLE [10]), in which the local errors in registration are accounted for using a non-local correspondence model between the atlases and the target intensities within the well-known Simultaneous Truth and Performance Level Estimation (STAPLE) [6] framework. In the end, we show that this technique results in highly robust and highly accurate segmentations of the ON despite the wildly varying dataset.

Table 1.

Gamut of slice thicknesses (mm) for the considered dataset.

Slice Thickness (mm)	0.4	0.5	1.0	2.0	2.5	3.0	5.0
Number of Images	2	8	1	5	12	2	1

This manuscript is organized in the following manner. First, the theory for Non-Local STAPLE (NLS) is briefly derived. Second, the registration framework is described, and the results for the proposed framework are presented. Finally, we conclude with a brief discussion on the optimality of the approach and the potential for improvement.

2. THEORY

NLS provides a novel approach for accounting for consistent registration errors and bias within the traditional STAPLE estimation framework. In order to accomplish this, NLS incorporates the theory of non-local means [11]. This approach deconstructs image volumes into a collection of small volumetric patches and the similarity (or correspondence) is quantified in order to learn information about the underlying image structure.

2.1 Problem Definition

Consider a target gray-level image represented as a vector, I ∈ ℝ^N×1. Let T ∈ L^N×1 be the latent representation of the true target segmentation, where L = {0, …, L − 1} is the set of possible labels that can be assigned to a given voxel. Consider a collection of R registered atlases with associated intensity values, A ∈ ℝ^N×R, and label decisions, D ∈ L^N×R. Let θ ∈ ℝ^R×L×L parameterize the performance level of raters (registered atlases). Each element of θ, θ_js′s, represents the probability that rater j observes label s′ given that the true label s is at a given target voxel and the corresponding voxel on the associated atlas — i.e., θ_js′s ≡ f(D_i*j = s′, A_j|T_i = s, I_i, θ_js′s), where i* is the voxel on atlas j that corresponds to target voxel i. Throughout, the index variables i, i* and i′ will be used to iterate over the voxels, s and s′ over the labels, and j over the registered atlases.

2.2 Non-Local Correspondence Model

The goal of the NLS estimation model is to reformulate the STAPLE model of rater behavior from a non-local means perspective. Thus, we need to define an appropriate non-local correspondence model. Given a voxel on the target image, i, this correspondence model provides a technique for determining the corresponding voxel on a given atlas, i*. In our model, there are two components that are required to define the non-local correspondence: (1) the intensity similarity model between a given atlas voxel and the target voxel of interest, and (2) the spatial compatibility between two voxel locations in the common target image coordinate system. Together, we define the probability of correspondence between an atlas voxel and the given target voxel (i.e., f(A_i′j|I_i)) to be the product of two Gaussian distributions.

$$f(A_{i\prime j}|I_i)\equiv {\alpha }_{\mathit{\text{ji}}\prime i}=\frac{1}{Z_{\alpha }}\text{exp }(-\frac{{\Vert \wp (A_{i\prime j})-\wp (I_i)\Vert }_2^2}{2{\sigma }_i^2}\left)\text{ exp }\right(-\frac{{ℰ}_{\mathit{\text{ii}}\prime }^2}{2{\sigma }_d^2})$$ (1)

where the first distribution is the intensity similarity model, the second distribution is the spatial compatibility model, and Z_α is a partition function. In the intensity similarity model, ℘(·) is the set of intensities in the patch neighborhood of a given intensity location and σ_i is the standard deviation of the assumed distribution. In the spatial compatibility model, ℰ_ii′ is the Euclidean distance between voxels i and i′ in image space and σ_d is the corresponding standard deviation. Lastly, the partition function, Z_α enforces the constraint that

$${\displaystyle \sum _{i\prime \in 𝒩(i)}}{\alpha }_{\mathit{\text{ji}}\prime i}=1.$$ (2)

where 𝒩(i) is the set of voxels in the search neighborhood of a target voxel. Through this constraint, α_ji′i can be directly interpreted as the probability that voxel i′ on atlas j is the corresponding voxel, i*, to a given target voxel i.

2.3 Estimation Framework

As with the original STAPLE algorithm, NLS simultaneously estimates both (1) the voxelwise label probabilities, and (2) the rater performance parameters, within an Expectation-Maximization (EM) framework. Within this framework, the estimation process can be broken up into two iterated steps, the E-step and the M-step. In the E-step, the voxelwise label probabilities are estimated using the current estimate of the rater performance level parameters. In the M-step, the rater performance parameters, θ, are maximized with respect to the conditional log-likelihood of the current estimated voxelwise label probabilities.

First, we derive the E-step of the algorithm. Let W ∈ ℝ^L×N, where $W_{\mathit{\text{si}}}^{(k)}$ represents the probability that the true label associated with voxel i is label s at iteration k of the algorithm given the provided information and model parameters. Using a Bayesian expansion and the assumed conditional independence between the registered atlas observations, $W_{\mathit{\text{si}}}^{(k)}$ can be written as

$$W_{\mathit{\text{si}}}^{(k)}=\frac{f(T_i=s){\displaystyle {\prod }_j}f(D_{i^{*}j}=s\prime ,{\mathit{A}}_j|T_i=s,I_i,{\theta }_{\mathit{\text{js}}\prime s}^{(k)})}{{\sum }_{n}f(T_i=n){\displaystyle {\prod }_j}f(D_{i^{*}j}=s\prime ,{\mathit{A}}_j|T_i=n,I_i,{\theta }_{\mathit{\text{js}}\prime n}^{(k)})}$$ (3)

where f(T_i = s) is a voxelwise a priori distribution of the underlying segmentation, and D_i*j is the label decision by atlas j at the atlas image voxel i* that corresponds to voxel i on the target image. Note that the denominator of Eq. 3 is simply the solution for the partition function that enables W to be a valid probability mass function (i.e., ∑_s W_si = 1).

Using the non-local correspondence model in Eq. 1, we can then define the final value for the E-step as

$$W_{\mathit{\text{si}}}^{(k)}=\frac{f(T_i=s){\displaystyle {\prod }_j}{\sum }_{i\prime \in 𝒩(i)}{\theta }_{\mathit{\text{js}}\prime s}^{(k)}{\alpha }_{\mathit{\text{ji}}\prime i}}{{\sum }_{n}f(T_i=n){\displaystyle {\prod }_j}{\sum }_{i\prime \in 𝒩(i)}{\theta }_{\mathit{\text{js}}\prime n}^{(k)}{\alpha }_{\mathit{\text{ji}}\prime i}}.$$ (4)

The estimate of the performance level parameters (M-step) is obtained by finding the parameters that maximize the expected value of the conditional log-likelihood function (i.e., using the result in Eq. 4)

$${\mathit{\theta }}_j^{(k+1)}=\underset{{\mathit{\theta }}_j}{\text{arg max}}{\displaystyle \sum _i}E[\text{ln }f(D_{i^{*}j}=s\prime ,{\mathit{A}}_j|T_i=s,I_i,{\theta }_{\mathit{\text{js}}\prime s}^{(k)})|\mathit{D},\mathit{A},\mathit{I},{\mathit{\theta }}^{(k)}].$$ (5)

In order to solve for each element of θ_j, we need to take the derivative of this density function with respect to the current element of the performance level parameters and introduce a Lagrange multiplier to enforce the constraint that sum of each column of the performance level parameters is equal to unity. After taking this derivation and using the non-local correspondence model present in Eq. 1, the final value for each element of the performance level parameters is

$${\theta }_{\mathit{\text{js}}\prime s}^{(k+1)}=\frac{{\sum }_i\left({\sum }_{i\prime \in {𝒩}_s(i):D_{i\prime j}=s\prime }{\alpha }_{\mathit{\text{ji}}\prime i}\right)W_{\mathit{\text{si}}}^{(k)}}{{\sum }_i{W}_{\mathit{\text{si}}}^{(k)}}.$$ (6)

2.4 Initialization, Model Parameters, and Detection of Convergence

As is typical [6], NLS was initialized with performance parameters equal to 0.95 along the diagonal and randomly setting the off-diagonal elements to fulfill the required constraints. For all presented experiments, the voxelwise label prior, f(T_i = s), was initialized using the probabilities from a “weak” log-odds majority vote (i.e., decay coefficient set to 0.5) [7]. Note that a decay coefficient of 0.5 voxels (i.e., less than the standard 1.0 voxels) was used in order to achieve a smoother and less restrictive prior for the non-local estimation process. Voxels where all raters agree were ignored in the estimation process (i.e., “consensus” voxels were ignored). The search neighborhood, 𝒩_s(i), was initialized to an 3 × 3 × 3 mm window centered at the target voxel of interest, and the patch neighborhood, 𝒩_p(·), was initialized to an 1 × 1 × 1 mm window centered at the voxels of interest. The values of the standard deviation parameters, σ_i and σ_d, were set to 0.1 and 2 mm, respectively. Lastly, convergence of the algorithm was detected when the average change in the on-diagonal elements of the performance level parameters fell below 10⁻⁵.

3. METHODS AND RESULTS

3.1 Registration Framework

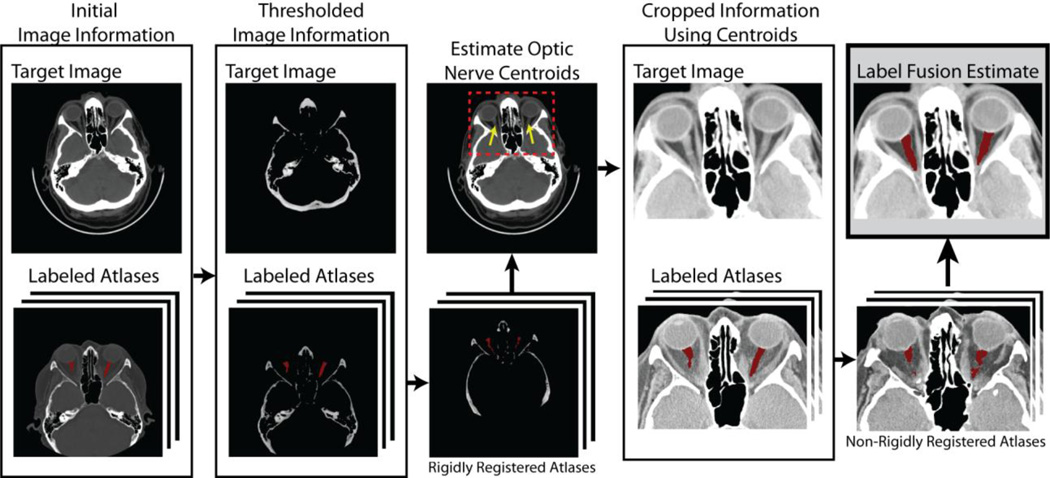
Due to the wildly varying data used in this manuscript, traditional registration techniques consistently fail to detect reasonable correspondence between the target and the various atlases. As a result, we introduce a straightforward registration framework that consistently (1) localizes the optic nerve centroids and (2) detects reasonable correspondence within smaller region-of-interests determined by the estimated optic nerve centroids. A flowchart demonstrating this registration procedure can be seen in Figure 1. Within this framework, we begin by performing a rigid registration (FSL’s FLIRT [12]) between the boney structures of the target and the atlases (achieved through thresholding at an intensity value of 1500). After rigidly registering the atlases, the centroids of both optic nerves are estimated by computing the centroid of voxels by which 90% of raters agree on the location of the optic nerve. A smaller region-of-interest is then computed by extending these centroids by 40 mm in all directions. The final registrations are then computed by performing a non-rigid registration (ART [13]) between the cropped target and atlases. Using this registration procedure, all atlases were able to achieve a non-zero DSC value when compared to the target labels. To contrast, if the images are rigidly registered together using a standard intensity-based procedure (e.g., normalized mutual information), less than 10% of the registered atlases resulted in non-zero DSC values when compared to the expert labels.

Figure 1.

Flowchart demonstrating the proposed registration procedure. As the volumes used in this dataset are wildly varying in terms of field-of-view and voxel resolution, a robust registration procedure is needed. Our model begins by rigidly registering the bone structure of the target and the atlas images (achieved through thresholding). Using these rigid registrations the optic nerve centroids are estimated on the target image in order to estimate an appropriate region-of-interest. Using this consistent region-of-interest, consistent non-rigid registration can then be performed in order to achieve the highest possible correspondence between the targets and the atlases.

3.2 Benchmarks

As benchmarks, we compare the results of NLS against several of the state-of-the-art label fusion algorithms using the previously described registration framework. First, we compare to log-odds majority vote [7], with a decay coefficient set to 1.0 voxels. Additionally, we compare to the original STAPLE algorithm [6] and a recent advancement to the STAPLE framework, Spatial STAPLE [5], in which STAPLE is extended to allow for spatially varying performance level estimations. Lastly, we compare to a Locally Weighted Vote (LWV) [7], with a decay coefficient set to 1.0 voxels, and the intensity difference standard deviation set to 0.1. For comparison, we compare the algorithms using the mean DSC across both optic nerve labels per target and the mean surface distance error across the estimated labels from the fusion algorithms.

3.3 Data and Experimental Setup

The empirical data consisted of 31 clinically acquired CT images of the brain which were retrieved in anonymous form under IRB supervision. The voxel size of the various images varied wildly, with in-plane resolution approximately 0.5 mm and slice thickness ranging from 0.4 mm to 5 mm for the various targets (Table 1). The “ground truth” optic nerve labels were obtained from an experienced rater and were verified by multiple additional raters.

Using a leave-one-out cross-validation (LOOCV) we compared the accuracy of the various algorithms for the segmentation of both optic nerves on all 31 of the CT images available in the dataset. To summarize the results, we present both quantitative and qualitative results. For the quantitative results, we compare NLS and the various benchmarks in terms of the mean DSC value and the mean surface distance error for all 31 target images. For the qualitative results, we present representative target results that emphasize both the slice-wise and volumetric accuracy of the various algorithms.

3.4 Quantitative Results

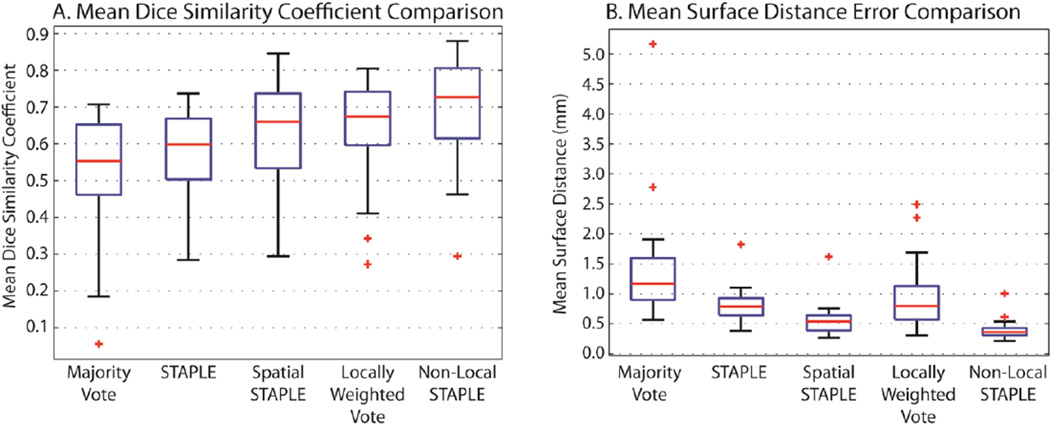
The quantitative results for the 31 target images can be seen in Figure 2. For all considered algorithms, the mean DSC and mean surface distance error are presented across all considered target images are presented. Using both metrics, NLS provides significant improvement (p < 0.05, paired t-test) over each of the considered benchmarks. For NLS, all but one of the datasets provided mean DSC values between 0.48 and 0.88, which is a significant improvement over previously reported results. The remaining dataset was the target image with a 5.0 mm slice thickness in which the optic nerve only appears on one slice of the image and, thus, the registrations were considerably poorer than the other targets. In terms of the mean surface distance error, NLS was the only algorithm that obtained a mean value of less than 0.5 mm. Interestingly, LWV, which is a rather popular algorithm in the label fusion literature, performed poorly in terms of the mean surface distance error, due to the fact that “speckle noise” is much more likely to be apparent in this estimation model. Thus, despite slightly worse mean DSC values, the dramatic improvement of Spatial STAPLE over a LWV in terms of the mean surface distance error seems to indicate that it exhibits more consistent overall performance.

Figure 2.

The quantitative results in a comparison between various state-of-the-art label fusion algorithms for multi-atlas segmentation. Using the previously described registration procedure, the accuracy of majority vote, STAPLE, Spatial STAPLE, Locally Weighted Vote, and Non-Local STAPLE are presented in terms of the mean DSC across the two optic nerves, and the mean surface distance error for each of the considered 31 target volumes.

3.5 Qualitative Results

The qualitative results are presented in both Figure 3 and Figure 4. In Figure 3, representative slices for three of the target volumes are presented for each of the considered benchmarks. First, it is important to note that all of the presented qualitative results represent reasonable segmentations of the ON, which highlights the importance of the proposed registration framework. With that said, it is evident that the two voting algorithms consistently underestimate the size of the ON, with LWV consistently outperforming a majority vote across the target volumes. Alternatively, both STAPLE and Spatial STAPLE seem to consistently overestimate the size of the optic nerves. On the other hand, NLS provides the most consistent segmentations as it simultaneously includes the intensity information and the overall rater performance across the volumes. The mean DSC values presented for each algorithm support these observations where NLS consistently provides the best performance.

Figure 3.

Qualitative comparison of the considered algorithms in terms of their mean DSC between the two estimated optic nerve volumes per target. The target image and expert labels can be seen in (A) and (B), respectively. A representative slice from each of the estimated segmentations for majority vote, STAPLE, Spatial STAPLE, locally weighted vote, and Non-Local STAPLE can be seen in (C), (D), (E), (F), and (G), respectively.

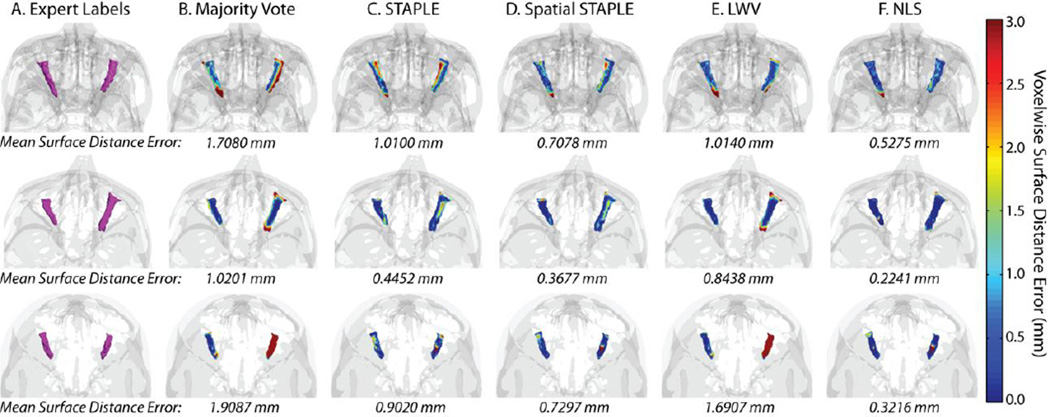
Figure 4.

Qualitative comparison of the considered algorithms in terms of their voxelwise surface distance between the estimated labels and the expert labels. The expert labels can be seen in (A). A 3D rendering of the voxelwise surface distance errors for majority vote, STAPLE, Spatial STAPLE, locally weighted vote, and Non-Local STAPLE can be seen in (B), (C), (D), (E), and (F), respectively.

In Figure 4, three representative target volumes are examined and the accuracy of each algorithm, in terms of the voxelwise surface distance error is presented via a 3D rendering of the estimated volumes. Using this representation, the benefits in terms of accurate boundary representation are particularly visible as it provides a mechanism for quantifying the voxelwise surface error. As in Figure 3, NLS provides consistent improvement in terms of overall accuracy for the various target volumes with the mean surface distance error well below 1 mm for all presented target images. Unlike Figure 3, however, the STAPLE based algorithms both consistently outperform the two voting algorithms in terms of the voxelwise surface distance error. This benefit highlights the need for quantifying rater performance in order to achieve accurate and consistent estimations in terms of underlying shape and appearance. To contrast, the voting algorithms treat each voxel independently, and, thus, are able to converge to estimates that are not necessarily representative or consistent with the shape/appearance of the observed atlas volumes. Note that for the third volume, both majority vote and LWV dramatically underestimate the right ON volume resulting in very high surface distance error.

4. DISCUSSION

The proposed, fully-automated framework uses multi-atlas segmentation in order to provide consistent and robust segmentation of the ON that significantly outperforms previous atlas-based approaches. Our approach to the multi-atlas segmentation procedure is two-fold: (1) we present a robust registration framework that is able to consistently handle data with very high variability in terms of field-of-view and voxel resolution (Figure 1), and (2) we use a recently proposed non-local statistical label fusion algorithm, NLS, that is able to account for the inherent lack of correspondence between the registered target and atlases. We demonstrate that NLS is able to significantly outperform several of the state-of-the-art label fusion algorithms for multi-atlas segmentation. In particular, we show that NLS is able to provide significant improvement in terms of both mean DSC and mean surface distance error over all of the considered benchmarks (Figure 2). Additionally, we show that, in addition to this quantitative improvement, consistent qualitative improvement is also visible in terms of both a 2D slice-wise representation of the data and a 3D rendering of the voxelwise surface distance between the expert and estimated labels (Figures 3 and 4).

Despite the promise of the proposed framework, there are several potential advancements that could potentially provide significant improvement in terms of overall accuracy, shape, and robustness. First, a large-scale evaluation of available non-rigid registration techniques should be compared in order to provide the most consistent results. We used the ART non-rigid registration algorithm described in [13] due to its robustness and speed of computation. However, other registration algorithms may be able to provide significant improvement in terms of registration quality, and, thus, segmentation accuracy. Second, there have been several recent advancements in terms of post-processing steps that refine multi-atlas segmentation estimates (e.g., Markov Random Fields [6], intensity-based refinement [14], and the modeling of consistent segmentation errors [15]). Incorporations of theses refinement techniques into the estimation framework could provide significant improvement in overall accuracy. Alternatively, using these estimated segmentations as a pre-processing step to some form of shape/appearance model could provide significantly more consistent results [1].

To provide a methodological note, there have been a large number of recent advancements to the STAPLE estimation model. For example, the presented model, NLS, provides a mechanism for incorporating inherent registration error and bias into the estimation framework. Alternatively, Spatial STAPLE, provides a mechanism for incorporating spatially varying performance models into the estimation framework. While these models are seemingly competitors of one another, their advancements are not mutually exclusive. As a result, the incorporation of both of these advancements into a single, coherent estimation model presents a fascinating area of continuing research.

In conclusion, the proposed approach provides a fully automated mechanism to segment the optic nerve on CT data which is robust to the extreme degree of variation present in clinical data. The estimated segmentations could be used to provide analysis context (i.e., navigation), volumetric assessment, or enable regional nerve characterization (i.e., localize changes). Refinement of baseline segmentations with purpose constructed methods would appear to be a very promising area of investigation [1].