RNA conformational classes

Abstract

RNA exhibits a large diversity of conformations. Three thousand nucleotides of 23S and 5S ribosomal RNA from a structure of the large ribosomal subunit were analyzed in order to classify their conformations. Fourier averaging of the six 3D distributions of torsion angles and analyses of the resulting pseudo electron maps, followed by clustering of the preferred combinations of torsion angles were performed on this dataset. Eighteen non-A-type conformations and 14 A-RNA related conformations were discovered and their torsion angles were determined; their Cartesian coordinates are available.

INTRODUCTION

The ribosomal subunit structures provide the best examples of the diversity and complexity of RNA folding. The many folds exhibited by the RNA contained in the recently determined crystal structures of the large ribosomal subunit (1), the small subunit (2,3) and the complete ribosome (4) are a consequence of the high flexibility of the polynucleotide backbone.

A nucleotide has seven torsional degrees of freedom, including the torsion angle χ around the glycosidic bond; this multidimensionality of the nucleotide conformational space represents a major obstacle to its systematic analysis. Early work indicated that a key part of the conformational behavior of the RNA backbone lies in the two torsion angles involved in the phosphodiester link. Empirical analyses of a very limited set of crystal data revealed that the behavior of the phosphodiester link leads to seven major conformational classes (5). The dimensionality of the problem can be reduced by introducing virtual bonds (6) as was done on an analysis of ribosomal RNA from 30S and 50S crystal structures (7). Another approach to tackling RNA multidimensional conformational space is to divide the six-dimensional nucleotide space into two 3D subspaces without considering potential correlations of the torsions at the phosphodiester bond. This recent study of two 3D distributions, as well as an analysis of potential errors in the experimental crystal structures, led to the identification of 42 conformational families (8).

In the work presented here, the multidimensional RNA conformational space and the very large number of possible correlations among the individual torsion angles were simplified by focusing on the interrelationships of the conformation angles that define the phosphodiester linkage (torsion angles ζ_i and α_i+1) and the other backbone torsion angles. A single near-atomic resolution structure with over 2800 nucleotides from the 23S and 5S rRNA molecules of the large ribosome subunit (1,9) (NDB code RR0033, PDB code 1JJ2) serves as a database for the analysis. Using a Fourier averaging method developed earlier for analyzing hydration patterns (10) coupled with a clustering technique led to identification of 18 distinct non-A-type dinucleotide conformations as well as 14 A conformations. These dinucleotide conformations are fully described by torsion angles and their Cartesian coordinates are available.

MATERIALS AND METHODS

Summary of the protocol

The 14 dinucleotide torsion angles (Fig. 1) of both 23S and 5S rRNA molecules from the 50S ribosomal subunit (1,9) were organized into a data matrix (Table 1). Its 2841 rows are the dinucleotides; the columns contain the 14 torsion angles for each dinucleotide. The conformations of the 830 non-A-RNA dinucleotides were analyzed for six 3D distributions of torsion angles by using Fourier techniques to transform the point distributions into pseudo electron densities. The peaks in these maps represent preferred conformations. Each peak was named by a letter and the data points were assigned to peaks if they were in a limiting distance to that peak. Because six maps were analyzed, the conformation of each data point is represented by six letters forming a six-letter word. The data points were clustered by sorting their representative words alphabetically. Further molecular analyses of the resultant conformations of the dinucleotides were done. The dinucleotides with A-like conformation (ζ_i ≈ 290° and α_i+1 ≈ 300°) were analyzed separately.

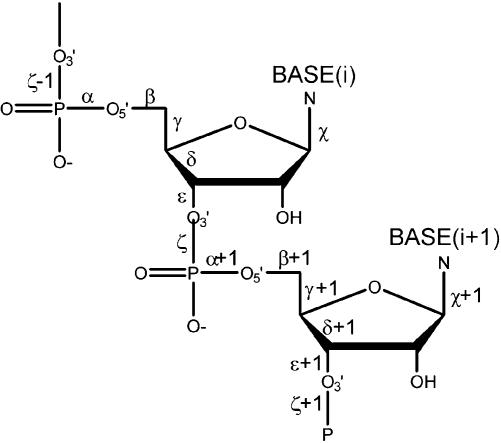
Figure 1.

A chemical diagram of a dinucleotide fragment shows definitions of the backbone torsions.

Table 1. The data matrix.

Residue			Peak assignment in maps						Torsion angle (deg)
i		i + 1	ζi–αi+1–δi	ζi–αi+1–γi+1	αi–γi–δi	ζi–αi+1–χi	ζi–αi+1–εi	ζi–δi–χi	δi	εi	ζi	χi	αi+1	γi+1
246	G	A	C	C	B	D	G	–	143	236	165	250	291	46
247	A	A	D1	G	B	E	E	D	150	263	85	227	67	165
175	G	A	C	C	–	D	L	F	148	196	143	261	287	41
213	G	A	C	C	–	D	L	F	148	185	154	264	293	42
381	G	A	C	C	–	D	L	–	156	190	140	275	290	46
795	G	U	C	C	B	D	G	F	147	211	157	246	280	43

Selected items of a few data points of the data matrix. Residue 246 is guanosine-5′-phosphate and residue 247 is adenosine-5′-phosphate. The 246th row of the data matrix consists of data for residues G246 and A247. For that row, torsion angles labeled i (shown are torsions δ_i, ε_i, ζ_i and χ_i) shown in the rightmost columns of table belong to G246 and those labeled i + 1 (α_i+1, γ_i+1) belong to A247. The columns headed ‘Peak assignment in maps’ list peak names which were assigned to each data point for the six analyzed maps. Peaks were labeled by one- or two-letter symbols in order of their intensity starting with A. The actual names, such as C, B, D1 or E, bear no meaning and serve only as labels used in the clustering process. Labels ‘-’ mean that no peak could be assigned for the map.

The table also demonstrates lexicographical clustering. Data points 175 and 213 are represented by the same word ‘CC–DLF’, and point 381 is represented by a similar word ‘CC–DL–’. Because all three dinucleotides overlap well they can be grouped into one conformation, 7. Dinucleotides of data points 246 and 795 belong to a related but distinct family 5, and point 247 belongs to conformation 4.

Data selection and data matrix

Both 23S and 5S rRNA molecules from the 2.4 Å crystal structure of the 50S ribosomal subunit (1,9) (NDB code RR0033, PDB code 1JJ2) were used for the analysis. A nucleotide has six backbone torsion angles α, β, γ, δ, ε and ζ, and a glycosidic angle χ (Fig. 1). Thus there are 14 conformational variables for a dinucleotide. Backbone torsion angles of the 2841 dinucleotide units of the rRNA molecules from the structure RR0033 form rows of the data matrix; each row is labeled by the number of its first nucleotide i. A brief excerpt from the matrix is shown in Table 1; the entire matrix is deposited as Supplementary Material.

The majority (∼70%) of all nucleotides of RR0033 are located within a narrow range of torsion angle values at the phosphodiester link (ζ_i ≈ 290° and α_i+1 ≈ 300°). These dinucleotides have A-type conformations and were excluded from the original data matrix before Fourier averaging; a heavy concentration of points in a narrow area of the map deforms the pseudo electron densities in other regions. Thus data points with torsion values within ±3.5 ESD (estimated standard deviation) from the ζ and α average values in the average A-RNA were excluded (Table 2). By this procedure, 2011 data points were labeled as A-type RNA; the remaining 830 points were Fourier averaged as described below.

Table 2. The average values of the backbone torsion angles in A-form double-helical oligonucleotides in high resolution crystals.

		Canonical A-type							Minor A-type population
		α	β	γ	δ	ε	ζ	χ	α	γ	δ	χ
A-RNA	Average (deg)	295	173	54	80	210	287	199	130	182	133	226
	ESD	10	11	9	4	9	7	19	26	13	13	46
	N	595	620	676	662	611	599	662	18	17	16	16
A-DNA	Average (deg)	293	176	55	83	204	287	199	150	181	131	232
	ESD	13	12	11	7	12	9	9	15	13	15	18
	N	552	638	631	646	626	622	650	73	81	27	27

The averages of torsion angles α, β, γ, δ, ε, ζ and χ were calculated for structures with crystallographic resolution better than 1.9 Å without mismatched bases and complexed drugs. In total, over 650 nucleotides found in 27 A-RNA structures and about the same number of nucleotides from 47 A-DNAs were analyzed. The RNA and DNA torsion averages (rows ‘Average’) agree well within one estimated standard deviation (ESD); N is the number of torsion angles in the analyzed sample. A large majority of the data (∼600 nt) have canonical A-RNA conformations; ∼3% of torsions α, γ, δ and χ occur in a minor population.

Preliminary conformational analysis

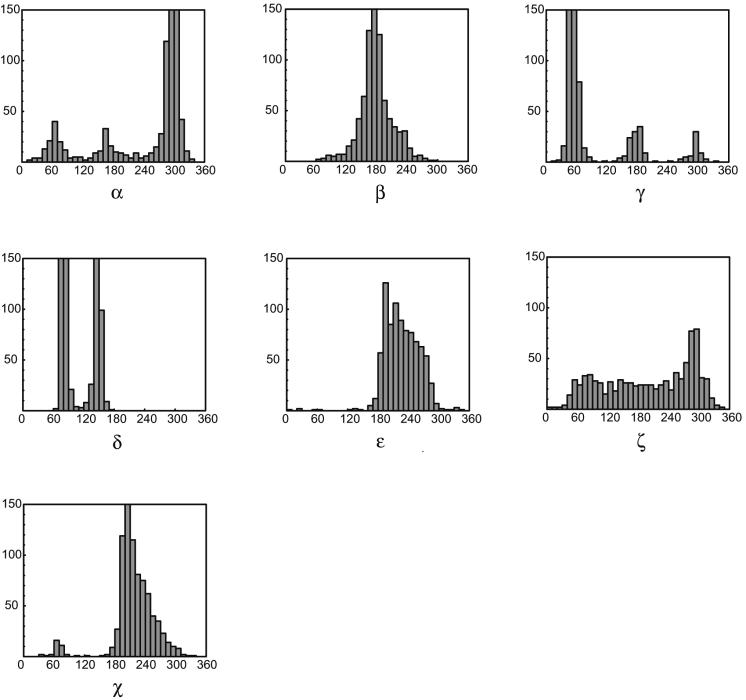
The torsion angles were examined using 1D distributions as illustrated by the histograms in Figure 2 and 2D distributions as shown by the scattergrams in Figure 3. These analyses serve to exclude torsional variables and their combinations that do not carry useful information. Detailed analysis of the RNA backbone torsions was performed in 3D projections of the torsional multidimensional space. Of the many possible combinations of three torsion angles in a dinucleotide [14!/(11! × 3!) = 364], six 3D maps were selected for analysis based on the previous knowledge of the nucleotide conformational space and the analysis of 1D and 2D torsion distributions.

Figure 2.

Histograms for the six backbone torsion angles α, β, γ, δ, ε and ζ and the torsion χ at the glycosidic bond in 23S and 5S rRNA of the crystal structure of the 50S ribosomal subunit (NDB code RR0033, PDB code 1JJ2) (1,9).

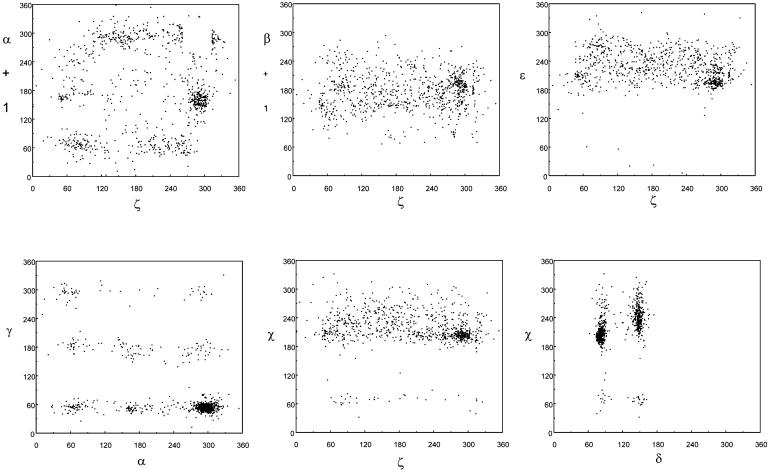
Figure 3.

Scattergrams (ζ_i, α_i+1), (ζ_i, β_i+1), (ζ_i, ε_i), (α_i, γ_i), (ζ_i, χ_i) and (δ_i, χ_i) of 23S and 5S rRNA torsion angles from the crystal structure of the 50S ribosomal subunit (NDB code RR0033, PDB code 1JJ2) (1,9). Only 830 data points are shown; 2011 data points with torsion angle values ζ_i and α_i+1 at the phosphodiester link labeled as A-RNA with values of ζ_i ≈ 290° and α_i+1 ≈ 300° were excluded. See text for further details.

Fourier averaging

The 3D torsional maps for the 830 non-A conformations were further analyzed using Fourier averaging. Each map consists of a distribution of points (τ1, τ2, τ3)_i. The averaging technique described previously (10) transforms these data points into pseudo electron densities by using standard crystallographic procedures as implemented in the program XtalView (11). The data points (τ1, τ2, τ3)_i, were first Fourier transformed into reciprocal space; a second Fourier transformation was then used to calculate pseudo electron densities. These maps were visually inspected to localize and fit peak positions.

In order to use a standard crystallographic program for this study, it was necessary to set certain parameters. For this application the data points in torsion maps were treated as equivalent to atoms in a crystal structure. All data points were treated as the same ‘atom type’, oxygen, with full occupancy and temperature factor B = 15. Cell dimensions were set to 36 × 36 × 36 Å. The space group was set as P1. Of all the parameters used in Fourier averaging, only the crystallographic resolution is critical for extracting useful information from extremely noisy data. By trial and error, resolution between 2.8 and 3.2 Å was found to be most useful for map interpretation. At this resolution range, each map has ∼8–12 well-shaped peaks.

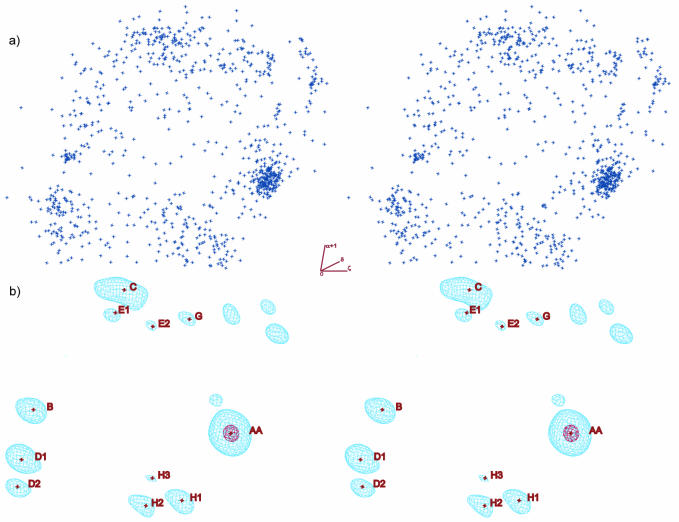
Figure 4 shows the 3D distribution (ζ_i, α_i+1, δ_i). The distribution of points (Fig. 4a) would be difficult to interpret, but its pseudo electron representation (Fig. 4b) is quite clear and allows identification of positions of preferred conformations.

Figure 4.

Two representations of a 3D distribution. (a) The distribution of torsion angles (ζ_i, α_i+1, δ_i) from rRNA of the 50S ribosome structure (NDB code RR0033, PDB code 1JJ2) (1,9). The 830 individual conformations (data points) are shown as blue crosses. (b) Fourier transform of point distribution (a) is rendered as pseudo electron density isocurves in light blue for ∼5% of the maximum density and red for 85% of the maximum density. In both (a) and (b), torsion ζ_i is approximately horizontal, α_i+1 is vertical and δ_i is perpendicular to the plane of the paper. Peak positions AA, B, C, D1, D2 etc. refer to sites of preferred values of torsions ζ_i, α_i+1, δ_i and were used to cluster residues of similar conformations. Both figures are in stereo.

Density map analysis

As is shown in Figure 4, pseudo electron densities have a small number of peak maxima. In each of the six analyzed maps, ∼10 peak maxima were identified; their positions were fitted and named by letters as AA, B, H1, H2 etc. approximately in order of their intensities. In the cases where two or more peaks were found close to each other or inside a wider cloud of common pseudo electron density, their one-letter names were supplemented by a numeric index. For instance, H1, H2 and H3 have a common envelope and are close, and E1 and E2 are close to each other. The peak names bear no structural meaning.

Each peak was approximated by a sphere based on its intensity in the pseudo electron map. Once peak positions as centers of probable conformations were identified and named, their distances to the 830 individual data points (τ1, τ2, τ3)_i were measured. If the data point was inside the peak radius it was labeled by the peak’s name. In the case when a data point was inside two or more peaks, it was assigned to the peak with the highest intensity. Data points which fell outside the radii of all peaks were not assigned to any peak.

All data points (Table 1; see Supplementary Material for full matrix) were labeled by names of the neighboring peaks in all six maps. As a result, each data point (dinucleotide) was characterized by a six-letter ‘word’. For instance, data point 246 (Table 1) is labeled by C in the first map (ζ_i, α_i+1, δ_i) because it is close to the peak C in that map. After all six maps were considered, data point 246 was labeled by peak names C, C, B, D, G and –, respectively, for each map. The last label ‘-’ means that point 246 was found to be too far from any of the peaks of the last map (ζ_i, δ_i, χ_i). Thus the word ‘CCBDG–’ characterizes the dinucleotide conformation of data point 246. In this way it can be easily compared with words assigned to all other data points.

Clustering

Words assigned to the data points were clustered by a technique called ‘lexicographical clustering’ (12). Lexicographical clustering alphabetically sorts words, or classification sequences, for the six maps in the same way as one would order words in a dictionary, i.e. by their lexicographical value. An identical (or close to identical) imprint for a group of data points defines a cluster. Because each imprint represents a conformation near peak positions, each cluster can represent a dinucleotide conformational family.

In addition to using lexicographical clustering of the imprints we also tested another clustering algorithm, clique-searching clustering (12). The results obtained by this algorithm do not differ significantly from those obtained by the lexicographical clustering method. Only the results of lexicographical clustering are discussed in the following sections.

Molecular analyses of clusters

The ultimate test as to whether the Fourier averaging and clustering worked or not was to evaluate the overlap of the dinucleotides in the real 3D space of atoms. The atomic geometries of the dinucleotides in each cluster were therefore compared using least-squares overlap of dinucleotide atoms. Based on the values of the root mean square deviations (RMSDs) and visual inspection of the overlapping dinucleotides, outliers were removed. After the outliers were removed, RMSD values for the tightest clusters were around 0.2 Å; looser clusters had RMSD values of 0.5–0.7 Å. The data matrix in the Supplementary Material lists RMSD values for all overlapping dinucleotides.

Results

One- and two-dimensional distributions of torsion angles

Histograms of the seven backbone torsion angles (Fig. 2) show broad distributions in cases where high variability of the backbone and statistical noise overlap. Torsions α and γ have trimodal distributions that are well known from analyses of DNA structures. Torsion β has a broad Gaussian-like peak centered at 180°. The clearly non-Gaussian single peak of ε suggests some internal features such as correlations with other torsions; however, the range of its values is limited to values >180° by the condition of the ribose ring closure. Values of δ are also limited by the constraints of the ribose ring closure; it has a sharply bimodal distribution reflecting the C3′-endo and C2′-endo ribose puckers. Bimodal distribution of χ reflects the major anti and minor syn conformations of bases. Torsion ζ has an extremely broad distribution without any sharp preferences; its preference to values of 270°–300° is much weaker than in double-helical DNA structures. Clearly, a significant portion of RNA conformational variability comes from this torsion angle.

Examples of 2D distributions of torsion angles displayed as scattergrams are shown in Figure 3. The most distinctive features are seen in the scattergram of the torsions at the phosphodiester bonds, (ζ_i, α_i+1); clustering is also clearly visible in the scattergrams of (α_i, γ_i) and (χ_i, δ_i). With the exception of these scattergrams, the others do not show clear clustering or correlations. Analysis of the RNA backbone conformations therefore needs to be approached at a higher dimensionality to reveal relationships among different parts of the RNA backbone.

A weak but significant correlation was observed between two torsion angles with relatively few features, χ and ε, and torsion δ. In the major C3′-endo conformation (δ ≈ 80°), both ε and χ have slightly but systematically lower values than in the minor C2′-endo conformations (δ ≈ 140°). This subtle observation is in agreement with early RNA conformational studies (13) and independently confirms the validity of the statistical analysis of the 50S rRNA structures.

Analysis of 3D distributions of torsion angles

The concept of the ‘rigid nucleotide’ (14) as well the 1D (Fig. 2) and 2D (Fig. 3) distributions suggest which torsion angles and their combinations are needed for a description of the RNA conformational space. A 3D analysis should include the three distributions with the most distinct features: (ζ_i, α_i+1), (α, γ) and (χ, δ). Torsion δ with its sharp bimodal distribution, perhaps overemphasized by the refinement constraints, is needed for understanding the relationship between the ribose pucker and the backbone conformation. Torsion angle χ is the only torsion associating the backbone conformation with the base orientation. Since χ is crucial for understanding potential relations between base-pairing patterns and backbone conformations, χ was included in two 3D maps, (ζ_i, α_i+1, χ_i) and (ζ_i, δ_i, χ_i). The limited use of torsion ε is due to the restricted range of its values; only one map, (ζ_i, α_i+1, ε_i), includes ε. Torsion β shows unimodal distribution and has few features in 2D scattergrams; this torsion was not included in the maps. In summary, the Fourier averaging analysis was performed on the following six maps: (ζ_i, α_i+1, δ_i), (ζ_i, α_i+1, γ_i+1), (α_i, γ_i, δ_i), (ζ_i, α_i+1, χ_i), (ζ_i, α_i+1, ε_i) and (ζ_i, δ_i, χ_i).

Labeling and clustering

About a quarter (201) of the 830 Fourier-transformed data points were assigned to peaks in all six analyzed maps; no or only one peak was assigned to another quarter (211) of the points. To obtain clusters of reasonable number of dinucleotide fragments, the lexicographical clustering was initially performed on only two maps. Based on their quality, maps (ζ_i, α_i+1, δ_i) and (ζ_i, α_i+1, γ_i+1) were used for the initial clustering. Of the 830 Fourier-averaged data points, 362 points (44%) were simultaneously assigned in both maps and these form the core of the conformational analysis presented here. About 90% (320) of these data points were grouped into the 19 clusters described below.

The protocol used here was not able to classify 510 dinucleotides. Some of them are located ‘close’ to peak(s) in 3D map(s) and could perhaps be included in existing clusters if they were defined using more tolerant criteria. Conformations of most of the unclassified dinucleotides are, however, simply too unique to be considered a part of any cluster or an intermediate between two or more clusters.

RNA conformational families (Table 3)

Table 3. Characterization of the RNA conformations.

(A) Non-A-type conformations
Conformation	Torsions (deg)														Characterization	C1′i–	Pi–
	αi	βi	γi	χi	δi	εi	ζi	αi+1	βi+1	γi+1	δi+1	εi+1	ζi+1	χi+1		C1′i+1	O3′i+1
1	295	168	53	208	82	208	53	165	149	50	148	263	139	218	Stack	5.9	4.8
2	295	171	53	203	81	194	292	161	162	53	84	228	276	203	Bases parallel, no stack	7.0	9.5
3	295	178	53	206	86	226	206	296	154	49	81	226	276	(212)	Bases parallel, no stack	7.4	10.4
4	(301)	190	(54)	232	148	270	84	66	190	177	85	227	280	(201)	χ scattered, stacking possible	5.9	10.1
5	(301)	178	54	256	149	222	152	292	164	46	83	218	290	188	Bases parallel, low rise	7.1	11.2
6	301	178	54	256	149	222	152	292	164	46	146	252	(106)	226	Bases parallel, low rise	6.8	11.8
7	275	96	156	257	149	195	150	292	147	46	84	220	286	185	Platform, zero rise	6.8	10.3
8	(301)	181	51	232	148	270	83	68	175	58	149	243	(266)	227	No stack, bases perpendicular	8.0	7.8
9	(301)	181	294	56	148	237	83	68	175	58	149	269	312	240	No stack, bases perpendicular	8.4	5.3
10	295	186	53	198	81	237	65	66	119	177	82	237	281	212	No stack, χ scattered	9.0	6.2
11	(295)	167	53	212	84	221	137	293	167	46	82	216	268	(210)	No stack, first base unwound	8.7	7.9
12	95	170	53	214	81	222	160	287	166	46	83	224	294	190	No stack, bases parallel, unwound	8.6	8.8
13	(95)	170	53	214	81	222	160	287	166	46	147	258	(190)	243	No stacking, bases parallel	8.4	9.5
14	(295)	171	53	207	85	256	253	66	168	54	84	220	(250)	198	Open, no stacking, χ scattered	9.0	9.7
15	295	181	53	198	81	225	211	60	201	49	81	207	202	196	Open, no stacking	9.2	9.1
16	295	181	53	198	81	225	211	60	201	49	142	259	(184)	238	Open, no stacking	9.1	10.2
17	(301)	192	54	243	148	256	245	63	171	54	87	239	278	211	Open, no stacking	8.7	9.9
18	295	178	53	202	85	256	261	59	182	305	136	234	(165)	(209)	Stacking	7.8	9.5
(B) A-RNA-type conformations
Conformation	Torsions (deg)														Characterization	C1′i–	Pi–
	αi	βi	γi	χi	δi	εi	ζi	αi+1	βi+1	γi+1	δi+1	εi+1	ζi+1	χi+1		C1′i+1	O3′i+1
19	295	175	53	203	81	194	292	156	194	180	83	175	185	298	Stacking, ‘AII-RNA’	5.4	11.1
20	295	174	54	198	81	211	291	296	175	54	84	212	273	202	Canonical A-RNA	5.9	10.6
21	295	175	54	200	85	220	267	300	175	53	93	218	245	213	Shift in ζ value	6.1	10.8
22	74	185	59	225	150	265	295	290	196	55	110	235	204	212	First ribose C2′-endo	7.9	10.1
23	295	190	60	240	148	255	285	290	200	60	110	236	205	194	First ribose C2′-endo	7.6	10.5
24	155	196	177	184	83	223	288	300	173	50	83	211	284	201	α–γ of the first nt shifted	5.7	10.4
25	56	181	292	191	92	206	297	286	179	55	81	213	289	198	α–γ of the first nt shifted	5.5	10.3
26	169	168	54	195	83	219	291	296	171	55	87	218	277	208	α–γ of the first nt shifted	5.6	10.2
27	67	163	52	189	84	217	290	294	178	53	89	219	269	204	α–γ of the first nt shifted	5.8	10.3
28	297	225	286	208	90	206	299	288	183	57	83	218	252	201	α–γ of the first nt shifted	5.6	10.6
29	69	176	185	190	83	224	289	183	176	56	92	212	284	205	α–γ of the first nt shifted	6.0	11.3
30	289	153	182	197	81	223	285	176	175	54	90	217	260	213	α–γ of f the first nt shifted	5.9	11.4
31	289	175	51	210	80	218	282	278	113	175	104	221	229	202	γ–β compensated at second nt	6.2	9.7
32	301	167	50	224	84	212	280	297	221	295	138	240	236	233	γ–β compensated at second nt	7.7	10.3

The column ‘Conformation’ labels families by their sequential number as used in the text. Torsion angles of the first and second nucleotide are labeled i and i + 1, respectively. Estimated standard deviations of all torsion values in all clusters can be found in the Supplementary Material. The column ‘Characterization’ gives the most typical features of the conformations. The last two columns list the distances between the respective atoms in angstroms. Torsional values used for the initial clustering, δ_i, ζ_i, α_i+1 and γ_i+1 are in bold type. Values in parentheses for α_i, γ_i, ε_i+1, ζ_i+1 and χ_i+1 have higher deviations from the mean than the other values.

Torsions in the two primarily analyzed maps (δ_i, ζ_i, α_i+1, γ_i+1) are defined by the sequence of atoms: C5′_i–C4′_i–C3′_i–O3′_i–P_i+1–O5′_i+1–C5′_i+1–C4′_i+1–C3′_i+1 (Fig. 1). The positions of these atoms are fixed or ‘locked’ for any given set of values of these four torsions; two dinucleotides with identical values of these four torsions have identical conformations between C5′_i and C3′_i+1. Because dinucleotides in the identified clusters do not have identical but similar values of torsion angles, the initially clustered dinucleotides were compared by the standard least-squares fit and outliers were excluded. Final overlaps for three conformations are shown in Figure 5. The remaining torsions analyzed in the torsional maps α_i, γ_i, ε_i and χ_i were determined from peak coordinates (conformations 1–9 in Table 3) or by arithmetic averaging of torsion values from the data matrix (conformations 10–19). Torsions δ_i+1, χ_i+1 and β_i, β_i+1 were not analyzed by any of the six maps and their values were always determined after the clustering procedure by arithmetic averaging of their respective values. The torsion angles of dinucleotides in the identified conformational families were used to determine their Cartesian coordinates; values of bond distances and angles were taken from the compilation of geometric parameters in nucleotides (15).

Figure 5.

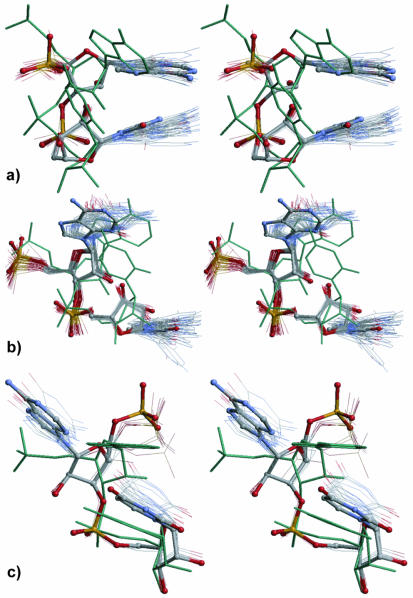
Stereo views of three selected conformational RNA families identified in the 23S and 5S rRNA of the crystal structure of the 50S ribosomal subunit (NDB code RR0033, PDB code 1JJ2) (1,9): (a) conformation 1 with Z-DNA-like backbone but both bases in the anti orientation; (b) conformation 2 which is seen in the tetraloops with sequences RNRN; (c) conformation 7 with parallel bases as in the adenine platform. For further description of the conformations see Table 3 and text. Overlaps of individual dinucleotides are shown by thin lines. The representative averaged conformation is shown as ball-and-stick model using the chemical convention for coloring. The canonical A-RNA (pale green) is superimposed on the average conformation.

The quality of the conformational families can be quantitatively judged by RMSDs of overlaps of dinucleotides and by ESDs of individual torsion angles. RMSD values for different conformational families were <1 Å. Larger clusters, such as 1, 2 or 19 (Table 3), show tight overlap; the dinucleotides are conformationally very similar and the RMSD values are <0.5 Å. Some smaller clusters, such as 11, overlap less well with RMSDs >0.5 Å. Assignment of all individual residues to clusters and RMSD of their overlaps can be found in the Supplementary Material which also contains ESD values of the dinucleotide torsions for all identified clusters in Table 3. Torsion angles determined by Fourier transform averaging, primarily δ_i, ζ_i, α_i+1, γ_i+1 and χ_i, have very low ESD values, in most cases <10°, which is comparable to the ESD of torsions in a very well defined statistical sample of A-RNA double-helical structures (Table 2). The other dinucleotide torsions have variable ESD values. Torsion angles close to both 5′- and 3′-ends of a dinucleotide have larger ESDs.

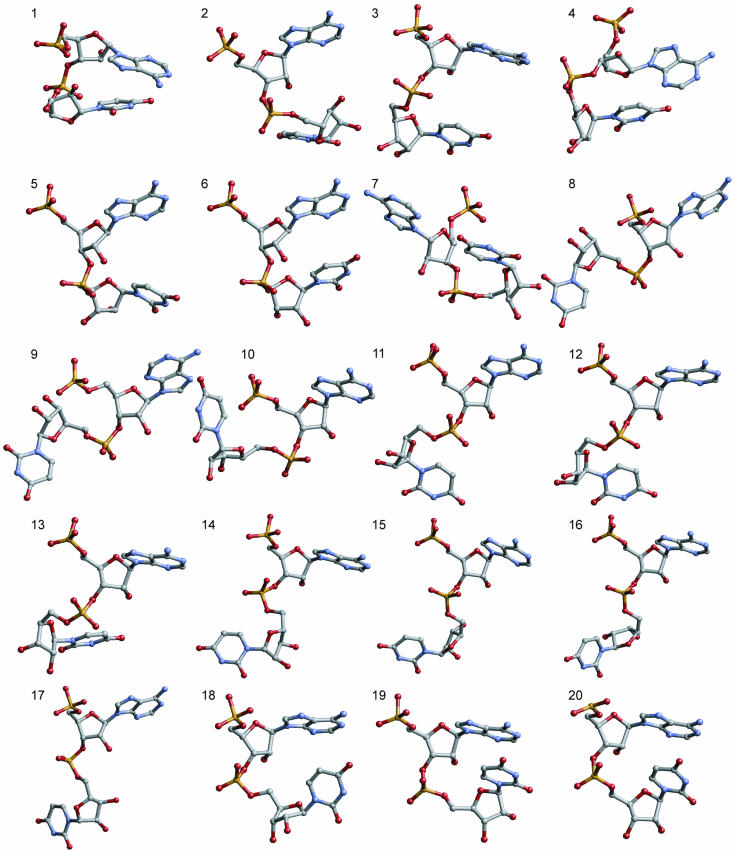
The characteristics of the 18 non-A conformations as well as the A-type conformations shown in Table 3 are presented here. Figure 5 shows three examples of the overlap within each family. A gallery of each of the 19 conformations is shown in Figure 6.

Figure 6.

Gallery of the 19 RNA conformational families (conformations 1–19) in their averaged geometries and the canonical A-RNA (conformation 20). Dinucleotides were drawn with the 5′-end on top. All have sequence 5′-AU-3′ and are numbered as in Table 3 and the text.

Non-A conformations with stacked or parallel bases, ‘normal’ rise (Table 3A). The backbone conformation 1 (Fig. 5a) is close to that of the purine–pyrimidine (RY) steps of Z-DNA (16). However, unlike Z-DNA both bases have anti orientation, similar to what was seen in the structure of an RNA dinucleotide with sequence UA (17). In this sample, the conformation does not show any sequence preference. Dinucleotides in this conformation are found most often in double-helical regions rich in non-canonical base pairs and bulges. The first or second residue is either unpaired or involved in non-WC base pair with the opposite strand. The conformation can also stand at the beginning of a single-strand link or a short loop. The family was observed >30 times; overlap of the contributing dinucleotides is tight.

Conformation 2 (Fig. 5b) has a preference for short, mostly tetra-, loops with prevailing sequence RNRN. This sequence preference, observed in the 23S and 5S rRNA, is slightly broader than the known tetraloop sequence pattern GNRA. This conformation is most often located at the stem–loop interface and one nucleotide of the motif forms a non-canonical pair, typically G·A, of a tetraloop. It can also be found in single-strand links between two double-helical regions. An unusual combination of torsions ζ_i–α_i+1–β_i+1–γ_i+1 reverses the direction of the backbone at the beginning of the second nucleotide so that the second ribose is flipped upside down from its A-type position and the second base is rotated anticlockwise from its A-type position by ∼180° and the bases do not stack. The second ribose positions the following phosphate, P_i+2, at the site of A-RNA base. The cluster is tight and contains 42 dinucleotides.

Conformation 3, which is defined by ∼20 dinucleotides, has a well-defined geometry. The conformation is characterized by a clockwise rotation of the first nucleotide by ∼30° with respect to the A-RNA so that the twist angle is larger than in the A-type. Bases are in parallel orientation but are too far to effectively stack. Dinucleotides of the family are involved in several types of secondary structure types, mainly in non-canonical base pairs and short single-strand links between double-helical regions.

In conformation 4, the first phosphate is very far from its A-type position so that the backbone direction is radically altered when it assumes this conformation. The backbone conformation allows bases to stack but base positions are scattered. The dinucleotides of the family slightly prefer RR sequences, are observed in short loops, junctions and single-strand links, and are not involved in base pairing. The family is a smaller and is found in ∼10 cases.

Non-A conformations with parallel bases and low-to-zero rise (Table 3A). In all three conformations 5, 6 and 7, bases have low rise, are in edge-to-edge orientation and can form non-canonical hydrogen bonds directly or via a water molecule.

In conformations 5 and 6, both bases are often involved in non-canonical base pairs of double-helical regions but can also occur in single-strand links. A significant feature is that the dinucleotides can occur at the opposite strands of double helices with non-canonical base pairs forming a specific motif as in the following fragment:

5′-1316 G A A 1318-3′

···

3′-1339 G G A 1341-5′

The dinucleotides in the motif are shown in bold type, non-canonical base pairs are indicated by full dots (·) and numbers are sequence numbers taken from Ban et al. (1). Both conformations 5 and 6 prefer purine-rich regions, and the motif itself shows a preference for the RR sequence.

Conformation 7 (Fig. 5c) is very similar to the motif known as the ‘adenine platform’ (18). In contrast with the adenine platform, this conformation shows no sequence preference among the 23S and 5S dinucleotides; the sequence GU occurs six times, GA occurs three times and UA occurs once. The sequence AA was found only twice in conformations 5–7. The most striking feature of the conformation is the relative position of both bases which lie in one plane and can form direct hydrogen bonds; its first phosphate group is positioned far above the base plane owing to distinct values of torsions β and γ; The high values of χ_i cause a flat orientation of the bases.

Open conformations: non-A, non-stacked bases, short-to-normal P_i–P_i+2 and large C1_i–C1_i+1 distances (Table 3A). In conformations 8 and 9 the backbone forms a U-shaped turn in the RNA direction with short P_i–P_i+2 distances (O2P_i and O2′_i+1 can form a hydrogen bond). The second base is rotated 180° away from its position in the A-type but lies in the same plane. Differences between conformations 8 and 9 are localized at the first nucleotide: conformation 9 has a value of γ_i of ∼300° so that the base and phosphate positions as observed in the A-type are swapped. This unusual γ_i rotation also allows a minor syn orientation of the base, observed only in this conformation, and an extremely short P_i–P_i+2 distance. Conformation 8, with a longer P_i–P_i+2 distance, has a normal value of γ_i (∼60°) and less radically altered base and phosphate positions.

Conformation 9 was found in the kink–turn motif described by Klein et al. (9). This conformation is adopted by a dinucleotide in the internal loop of the motif while the kink in the opposite strand is realized by conformation 4, 5 or 6. The example below shows the kink–turn motif number 7 from Klein et al. (9); the dinucleotide A80–G81 (bold type) adopts conformation 4 and A95–A96 (bold type) adopts conformation 9:

5′-G79 A80 G81 C82-3′

··||

3′-A98 G97 A96 A95 G94 C93 G92-5′

Dinucleotides of both families participate mostly in single-strand links or bulges between double-helical regions as in the kink–turn motif and form base pairs only rarely; they are never involved in the canonical base pairs. Each was observed ∼10 times.

Conformation 10 is a small family similar to conformation 4, with a short P_i–P_i+2 distance and the first phosphate at the position of a base in the A-type. Residues of this conformation are found in links between two double helices or in longer loops and do not form base pairs.

Conformations 11, 12 and 13 occur at the ends or beginnings of double helices linked by short single-strand regions and one base is usually involved in the canonical base pair at the end or beginning of the double helix. The first unwound phosphate serves as a hinge between the double helix and the single strand. The first base acquires the site of phosphate in the A-type; both bases are approximately in the same planes as in the A-RNA and have the same vertical separation but do not stack owing to their relative rotation. Most differences between these three conformations are located in the second, less A-like, nucleotide. Each conformation is represented by ∼10 dinucleotides.

The crystal structure of the dinucleotide with sequence UA has two molecules in the asymmetric unit (17). One has conformation 12 (RMSD 0.27 Å). The other has a conformation between 1 (RMSD 0.79 Å) and 9 (RMSD 0.86 Å)

Similar to conformations 11–13, conformations 14–17 form hinges between a short single-strand link and a double helix. Conformations 15 and 16 also occur in loops, typically 7 or 8 nt long. The positions of the base and phosphate attached to the second ribose are swapped and the backbone of these dinucleotides has an extended S-shape form with C1′_i–C1′_i+1 distances longer than in the other ‘open’ conformations and much larger than in A-RNA (∼9 Å). The bases are rotated away from each other; the first base is ‘above’ the P_i and the second is ‘below’ the P_i+2, and they border the dinucleotide at both ends. These four conformations have common characteristics and about seven representatives each.

Conformation 18 is a small family which is A-like because atypical values of some torsion angles (α_i+1 and γ_i+1) cancel out. The major difference between conformation 18 and the canonical A-RNA is an anticlockwise rotation of both bases.

A-RNA conformations (Table 3B). Conformation 19 is a minor but distinct A-form conformation AII-RNA (Table 3B, conformation 19) and is well represented by ∼100 examples. The main characteristic of this conformation is a combination of torsions ζ_i ≈ 300°, α_i+1 ≈ 180° and γ_i+1 ≈ 180° with a ‘crankshaft motion’ compensation of the atypical values of α_i+1 and γ_i+1. The value of γ ≈ 180° is highly characteristic for this A-RNA form; over 40% of all γ values between 160° and 200° contribute to AII-RNA.

Nucleotides in the A-type conformations with typical values of ζ_i and α_i+1 of ∼300° were not studied by the Fourier averaging technique. Because they form ∼70% of the 23S and 5S rRNA molecules in the structure RR0033 (9), they were investigated further. A large majority of these ‘A-like’ dinucleotides (1513) are classified as canonical A-RNA (Table 3B, conformation 20). Torsion values for canonical A-RNA shown in Table 3 were calculated from the analyzed rRNA molecules and closely correspond to the respective values determined from the high resolution structures of A-RNA oligonucleotides as shown in Table 2.

There are, however, several other well defined conformational families with small but pronounced deviations from the canonical A-RNA (Table 3B, conformations 21–32). These deviations are localized in one or two torsion angles of the first or second nucleotide. For instance, conformation 21, represented by ∼100 cases, is characterized by a small but quantitative change of the angle ζ_i from its ‘canonical’ value to 265° so that the twist angle of the dinucleotide is slightly lowered.

Several A-type conformational families, labeled as 24–30 in Table 3B, deviate from the canonical A-RNA in values of α and γ of the first nucleotide. In most of these conformations, a simultaneous change of α_i and γ_i from their typical values compensate for each other; conformations 24 (100 cases) and 25 (25 cases) are examples. Conformations 26 (70 cases) and 27 (30 cases) can be described as A-RNA dinucleotides with the preceding nucleotide rotated around the P_i–O5′_i bond by –120° and +120°, respectively.

Two minor A-like conformational families, 31 and 32, have significantly different torsion γ_i+1 of the second nucleotide. In both these families atypical rotations around the C5′_i+1–C4′_i+1 bond are compensated for by a rotation around the bond O5′_i+1–C5′_i+1 in the opposite direction. This results in unusual values of the torsion β_i+1 (110° and 220°).

RNA conformations found in the 16S rRNA of 30S ribosomal subunit

A preliminary analysis of overlaps of all dinucleotides from the 16S rRNA from a ribosomal structure (PDB code 1J5E) by Wimberly et al. (3) over the 32 identified conformational families unequivocally identified families 1 (≥10 cases of tight overlap), 2 (≥10 cases), 12 (∼10 cases), 5 (≥8 cases), 18 (≥8 cases) and both 8 and 9 (∼5 cases each). The canonical A-RNA was observed for many 16S dinucleotides. Minor A-RNA conformations were also observed including 30 cases of AII-RNA (conformation 19), 20 cases of conformations 23, 24, 25, 26 and 27, and 10 cases of conformation 29. Even though this analysis is preliminary, it suggests that the conformations identified here are not artifacts of the protocol used to analyze the 23S and 5S rRNA structures (1,9).

DISCUSSION

The conformational space of RNA consists primarily of the A-type building block and a minority of diverse other conformations. This work shows that there are distinct classes of these minority conformations. The identified RNA conformations and their idealized coordinates can facilitate analysis of RNA structures and their computer simulations. We also believe that a knowledge of preferred conformations will lead to further specification of torsional parameters in force fields of programs for molecular simulations as well as for refinement of experimental X-ray and NMR structures. Understanding nucleic acid conformations is difficult for several reasons: (i) the conformational space of nucleic acids has many variables, (ii) RNA molecules lack well classified secondary motifs other than A-RNA and (iii) until recently there were very few RNA structures.

The volume of available structural data of nucleic acids, especially of ribosomal RNA, has changed so dramatically in the last few years that a phenomenological assignment of allowed conformational regions and their characterization is now possible. Murray et al. (8) performed an analysis of RNA conformations with goals similar to this work. Although their methods differ from ours, the results are similar in many respects. They studied the ribose-to-ribose unit by analyzing two 3D torsional subspaces of ‘heminucleotides’, δ–ε–ζ and α–β–γ; the base orientation at the torsion χ at the glycosidic bond was not considered. They described 47 conformations of heminucleotides. Comparison of the torsion angle values of some conformational families in the paper by Murray et al. (8) and in this work shows similar conformations. For instance, the highly populated conformation 1 in this work corresponds to the conformation ‘3′epttp2′’ of Murray et al. (8); conformation 2 corresponds to their ‘3′emttp3′’. Recent work by Hershkowitz et al. (18) also analyzed the torsional space of rRNA from the structure RR0033 (1,9). An automated pattern recognition approach concentrated on analysis of torsions α, γ, δ and ζ with the highest variability. They characterized regions of tetraloops and A-RNA helices; however, the 37 declared conformations are not described sufficiently to be compared with the conformations reported here.

We attempted to correlate the sequence and secondary structure diagram of the 23S rRNA (1) with the occurrence of the dinucleotide conformational motifs found in this study. Sequence preferences of the conformations were observed in very few cases, often in purine-rich regions. Conformations 4, 5 and 6 prefer RR, and conformation 2 occurs in tetraloops with sequences RNRN. In contrast, conformation 7, resembling the ‘adenine platform’ motif (19), showed no clear sequence preference.

The predominant conformation in rRNA structures is A-RNA in both double-helical and single-strand regions. Non-A conformational families (conformations 1–18) rarely link to one another and in most cases occur between A-RNA conformations. Conformations 1–18 often occur in non-double-helical regions at single-strand links, loops and bulges. Many open conformations (numbers 8–17) occur in single-strand regions linking two or more double helices. Conformations 11–17 often form ‘hinges’ at short single-strand sequences between two double helices; one of the nucleotides is the first or last residue of a double helix, and the other residue is part of the hinge. Conformations with stacked or parallel bases (conformations 2–4, but not 1) can be a part of (mostly short) links between double helices. Conformation 4 is also involved in topologically more complicated links which occur at junctions. Conformation 1, with well-stacked bases, as well as conformations 3 and 5–7, locally disrupt the helices by forming a bulge or non-canonical base pair(s).

The present work suggests that the multidimensionality of the RNA conformational space can be approached by analysis of conformations at the phosphodiester link O3′_i–P_i+1–O5′_i+1, defined by torsion angles ζ_i–α_i+1. We deduce the central role of torsions ζ_i–α_i+1 from the fact that they exhibit the highest variability yet are limited into well defined regions, noise notwithstanding. We suggest that the character and importance of the ζ_i–α_i+1 scattergram can be compared with the cornerstone of protein structural science, the Ramachandran plot of the protein backbone torsion angles Φ and Ψ (20). To become a useful tool for the routine analysis of the quality of newly determined structure, our knowledge of the ζ_i–α_i+1 scattergram and its correlations with the remaining backbone torsions has to be refined. In addition, the regions of preferred, allowed and disallowed conformations need to be determined and validated. This work is a step in reaching this goal.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.