Abstract
Abstract The inferior olivary nucleus (IO) in in vitro slices from postnatal mice (P5.5–P15.5) spontaneously generates clusters of neurons with synchronous calcium transients, and intracellular recordings from IO neurons suggest that electrical coupling between neighbouring IO neurons may serve as a synchronizing mechanism. Here, we studied the cluster-forming mechanism and find that clusters overlap extensively with an overlap distribution that resembles the distribution for a random overlap model. The average somatodendritic field size of single curly IO neurons was ∼6400 μm2, which is slightly smaller than the average IO cluster size. Eighty-seven neurons with overlapping dendrites were estimated to be contained in the principal olive mean cluster size, and about six non-overlapping curly IO neurons could be contained within the largest clusters. Clusters could also be induced by iontophoresis with glutamate. Induced clusters were inhibited by tetrodotoxin, carbenoxelone and 18β-glycyrrhetinic acid, suggesting that sodium action potentials and electrical coupling are involved in glutamate-induced cluster formation, which could also be induced by activation of N-methyl-d-aspartate and α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid receptors. Spikelets and a small transient depolarizing response were observed during glutamate-induced cluster formation. Calcium transients spread with decreasing velocity during cluster formation, and somatic action potentials and cluster formation are accompanied by large dendritic calcium transients. In conclusion, cluster formation depends on gap junctions, sodium action potentials and spontaneous clusters occur randomly throughout the IO. The relative slow signal spread during cluster formation, combined with a strong dendritic influx of calcium, may signify that active dendritic properties contribute to cluster formation.
Key points.
One of the two main inputs to the cerebellum consists of climbing fibres from neurons in the inferior olivary nucleus (IO).
The IO spontaneously forms clusters of co-active neurons in transverse brainstem slices from 1- to 2-week-old animals, coinciding with a critical time period in cerebellar development.
Here, we studied the cluster-forming mechanisms, and find that randomly occurring spontaneous clusters overlap extensively, and contain 10 to hundreds of IO neurons with an average somatodendritic field size that is slightly smaller than the average IO cluster size.
Cluster formation is dependent on sodium action potentials and electrical coupling between IO neurons, and may spread with decreasing velocity and may involve active dendritic properties.
The results help us better understand the basic mechanism underlying cluster formation in the IO, which is an important feature in the generation of patterned input to the cerebellum.
Introduction
The inferior olivary nucleus (IO) spontaneously forms clusters of co-active neurons in transverse slices from postnatal day (P)5.5–P15.5 animals under in vitro conditions (Rekling et al. 2012). This activity coincides with a critical postnatal period in olivocerebellar development, and the clusters may be forerunners of the ensembles of IO neurons shown to be co-active in adult animals spontaneously and during motor acts (Smith, 1998). Stimulus-evoked ensembles of subthreshold neuronal oscillations and time-coherent activation in IO neurons have been demonstrated in postnatal rats (Leznik et al. 2002; Leznik & Llinas, 2005; Urbano et al. 2006), which may be another manifestation of synchronous activity in neighbouring IO neurons. Patches of spontaneous oscillatory activity were also noted in an in vitro voltage imaging study with low spatial resolution (Devor & Yarom, 2002). Thus, the IO appears to be able to generate both subthreshold and firing synchronicity in clusters of neighbouring neurons starting in a critical postnatal period.
The physiological significance of cluster formation in the IO is still unknown. Ensembles of closely positioned (within ∼200 μm) dorsal accessory olive neurons in rats show synchronized and rhythmic discharges during locomotion, but not during rest and, interestingly, continue the rhythmicity during missed steps in phase with the ongoing step cycle rhythm (Smith, 1998). Rhythmic licking in rats is associated with groups of Purkinje cells showing synchronous complex spikes, indicating rhythmic co-activity in IO neurons in this motor paradigm (Welsh et al. 1995). Thus, in rhythmic motor acts cluster formation may be part of the underlying timing mechanisms, but the precise function remains obscure. A better understanding of cluster-forming mechanisms, when clusters occur in relation to the execution of motor commands and the effect of afferent sensory input on cluster formation may be crucial in understanding olivocerebellar function at the systems level.
Here, we studied the cluster-forming mechanisms, and begin to address the important question of whether spontaneous cluster formation has an underlying spatial structure, i.e. do clusters form in random positions, or are they constrained in some way? The afferent input from somatosensory nuclei to the IO shows a somatotopic organization (Gellman et al. 1983; Molinari et al. 1996), but the forelimb input to the dorsal accessory olive (DAO) in cats via preolivary nuclei has an imprecise overlapping topography (McCurdy et al. 1998). Supramedullary afferent input to the IO may occupy the same areas as spinally derived input (McCurdy et al. 1992), observations which together raise the intriguing possibility that cluster formation in the IO might be very dynamic, with changing afferent input determining the position and size of clusters of co-active IO neurons. Thus, clusters may not be static structures determined by developmental and activity-dependent mechanisms, but emergent and constantly changing structures with overlapping territories at different times during execution of motor programmes. Support for this idea awaits experimental paradigms that permit identifying cluster activity during normal motor acts.
In the mechanistic studies we take advantage of the fact that the IO receives glutamatergic afferent input (Zhang et al. 1990; Onodera & Hicks, 1995), and expresses glutamate receptors (Watanabe et al. 1994; Paarmann et al. 2000; Chen et al. 2006), to induce repetitive cluster formation using glutamate iontophoresis. We also present the first optical recordings of dendritic calcium transients in IO neurons, induced by somatic action potentials, and cluster formation.
Methods
Ethical approval
All experiments and procedures were approved by the Department of Experimental Medicine, were undertaken according to procedures laid out by the Danish Ministry of Justice and the Danish National Committee for Ethics in Animal Research, and conform to the principles of UK regulations, as described in Drummond ()2009.
In vitro preparation, Fluo-8, AM loading and calcium imaging
Thick brainstem slices from postnatal (P6.5–P15.5) US Naval Medical Research Institute (NMRI) mice containing the IO were prepared as previously described (Rekling et al. 2012). In brief, mice were anaesthetized with isoflurane and killed with a cut across the thorax, and the heart and lungs were removed. The neuraxis was removed by dissection in an ice cold, oxygenated (95% O2, 5% CO2) solution containing (in mm) 250 glycerol, 3 KCl, 5 KH2PO4, 36 NaHCO3, 10 d-(+)-glucose, 2 MgSO4 and 0.7 CaCl2. A 950 μm-thick brainstem slice was cut using a Vibratome (Microm HM 650 V, Walldorf, Germany), with a rostral cut placed at the level of the rostral third of the IO containing the dorsomedial cell column (DMCC). The preparation was glued to a piece of filter paper using cyanoacrylate, and loaded with the calcium-sensitive dye Fluo-8, AM (AAT Bioquest, Sunnyvale, CA, USA) by placing it in a loading solution, which was prepared by dissolving 50 μg Fluo-8, AM in 50 μl DMSO, and then combining 20 μl of the Fluo-8, AM solution with 5 μl cremophore EL (Fluka, St Louis, MO, USA) and 5 μl of 20% Pluronic F-127 in DMSO (AAT Bioquest). We added the 30 μl Fluo-8, AM solution to 1 ml artificial cerebrospinal fluid with 100 mm d-mannitol (Sigma-Aldrich, St Louis, MO, USA) and 100 μm MK-571 (Enzo Life Sciences, Farmingdale, NY, USA). The final Fluo-8, AM concentration was 20 μm, and the preparation was loaded for 1–1.5 h at room temperature under bubbling with 95% O2, 5% CO2. Following loading with Fluo-8, AM the preparation was transferred to a recording chamber, mounted with the rostral surface up and stabilized by placing a silver frame on the filter paper.
Optical recordings commenced 20–30 min after the preparation was placed in the recording chamber. The recording chamber had a volume of 2 ml, a temperature of 29.0°C and was constantly superfused at a rate of 2 ml min−1 with preheated oxygenated (95% O2, 5% CO2) artificial cerebrospinal fluid, which contained (in mm) 129 NaCl, 3 KCl, 5 KH2PO4, 22 NaHCO3, 30 d-(+)-glucose, 0.4 MgSO4 and 0.7 CaCl2. For detection of Fluo-8 fluorescence, a metal halide light source (Leica EL6000, Wetzlar, Germany; or PhotoFluor II, 89North, Burlington, VT, USA) was coupled to a stereo microscope (Leica MZ16 FA, Wetzlar, Germany) via a liquid light guide, and appropriate optical filters (Leica GFP3: excitation 470/40 nm; barrier: 525/50) were used. Image stacks were captured by an EMCCD camera (Andor LucaEM S DL-658M, 658 × 496 pixels, Andor Technology, Belfast, UK), controlled by SOLIS software (Andor Technology). Imaging was done at a magnification of 40–115×, at 10 frames s−1, in image sessions lasting 20–90 s. An Olympus BX51 (Olympus, Tokyo, Japan) was also used for calcium imaging, visualizing clusters or individual IO neurons using x20 or x63 water immersion objectives (imaging: 10–217 frames s−1, 10 frames s−1 un-binned, 128,217 frames s−1 4 × 4 binning), a standard BX51 mercury fluorescent lamp, optical filters (Olympus U-MWIB: excitation 460–490 nm; dichroic: 505, emission: 515 nm long pass), and a similar EMCCD camera.
Golgi–Cox and toluidine labelling
A modified Golgi–Cox method was used to label IO neurons and reconstruct the dendritic arborization (Ranjan & Mallick, 2010). In short, freshly prepared un-fixed slices were placed in a modified Golgi–Cox solution, containing 5:5:4:10 volume parts of 5% potassium dichromate solution, 5% mercuric chloride solution, 5% potassium chromate solution and distilled water, for 48 h at 37.0°C. Sections of 150 μm were then cut on a vibratome, rinsed in distilled water, dehydrated in 50% ethanol for 5 min, kept in ammonia solution (3:1, ammonia/distilled water) for 10 min, rinsed twice (5 min each) in distilled water, kept in 5% sodium thiosulphate for 10 min in the dark, rinsed twice (5 min each) in distilled water, dehydrated twice (5–10 min each) in 70, 80, 95 and 99% ethanol, cleared in toluene and mounted in Eukitt on gelatinized slides (all compounds from Sigma-Aldrich). Labelled IO neurons were reconstructed by hand using a camera lucida system. Paraformaldehyde-fixed (4% in PBS) slices were embedded in Technovit (Heraus Kulzer, Wehrheim, Germany), cut in 2–3 μm sections on a microtome, counterstained with 0.1% Toluidine blue (Sigma-Aldrich), mounted in Eukitt, and examined under a microscope to determine cells density and diameter in the medial accessory olive (MAO), dorsal accessory olive (DAO) and principal olive (PO).
Whole cell recordings, glutamate iontophoresis and compounds
For whole cell recordings neurons located in the IO were visualized using an Olympus BX51 (upright, modified to be fixed stage, mounted on an XY platform) with a 2.5× and a 63× objective. The 2.5× objective was used to visualize the entire cut surface of the preparation identifying the PO or the DMCC. The 63× water immersion objective was used in conjunction with oblique illumination optics to visualize the soma of individual neurons and the recording pipette tip. The preparation was illuminated from below using a 100 W halogen lamp, and the image was acquired by the EMCCD camera, software contrast enhanced and displayed on a PC monitor. Glass micropipettes were pulled from filamented glass tubes (outer diameter 1.5 mm, inner diameter 0.86 mm; Harvard Apparatus, Holliston, MA, USA) using a PUL-100 micropipette puller (World Precision Instruments, Sarasota, FL, USA) and filled with a solution containing (in mm): 165 potassium d-gluconate, 10 NaCl, 0.5 MgCl2, 0.5 EGTA, 10 Hepes, 4 ATP (Mg2+) and 0.4 GTP (Na+), pH = 7.3. Recording pipettes were mounted in a HS-2 headstage (Gain 0.01) and current clamp recordings performed with an AxoClamp2B amplifier (Molecular Devices, Sunnyvale, CA, USA). Pipette resistance before seal formation was typically 1–3 MΩ and after the whole cell configuration was achieved series resistance was 3–10 MΩ. Membrane potentials were calculated as the difference between the intracellular potential and the potential measured at the end of the recording session when the electrode was retracted to the extracellular space.
Iontophoresis pipettes were pulled on a PUL-100 micropipette puller from filamented glass tubes (outer diameter 1.5 mm, inner diameter 0.86 mm), broken down to a tip size of 1–2 μm and filled with 500 mm glutamate (monosodium salt, pH = 8.0). Following placement of the iontophoresis pipette in the IO, 50–100 μm below the cut surface, repetitive iontophoresis current pulses (500 ms duration, ejection current: –50–500 nA, holding current: 10–50 nA) was applied every 10 s using an iontophoresis device (IP-X5; Neurodata Instruments Corp., New York, USA). R/S-α-Amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (R/S-AMPA; 10 mm, pH = 8.0, Sigma-Aldrich) and N-methyl-d-aspartate (NMDA; 100 mm, pH = 8.0, Sigma-Aldrich) were iontophoresed using a similar current pulse protocol.
Tetrodotoxin (TTX; 2 μm, Sigma-Aldrich) was applied in some experiments to block sodium-dependent action potentials, and in other experiments carbenoxelone (100 μm, Sigma-Aldrich) or 18β-glycyrrhetinic acid (150 μm, Sigma-Aldrich) was added to block gap junctions.
Image and whole cell recording analysis
Analysis of optical and whole cell recordings was done offline using Igor Pro v. 6.31 (WaveMetrics, Lake Oswego, OR, USA), Clampex v. 10.3 (Molecular Devices) and ImageJ v. 1.47 (Open Source, National Institutes of Health, Bethesda, MD, USA, http://rsbweb.nih.gov/ij/). Substantial bleaching of the Fluo-8 fluorescence was noted throughout the imaging sessions, which was partially corrected for during the analysis by (1) normalizing the images of a stack to the same mean intensity (used in the cluster-detection algorithm), or (2) a running background removal subtracting the image 1 s before each frame in the stack (used for identifying glutamate-induced clusters).
Spontaneous cluster events were identified and quantified using a novel automated cluster-detection algorithm, as follows. (1) Bleach correction of the entire image stack. (2) ΔF/F calculation by determining the minimum intensity of every pixel throughout the entire stack. This minimum value was then subtracted from the pixel at any given frame. Finally, the new pixel value at each frame was divided by the original pixel value at that frame. (3) One frame subtraction. For each pixel at each frame the value of the same pixel in the frame before was subtracted. Negative values were given the value 0. (4) The entire IO and an area that was located outside the IO, referred to as the noise sample, were selected manually. (5) Determining the mean intensity and standard deviation for all pixels within the noise sample throughout the entire stack. (6) Applying a threshold, set at the mean plus two standard deviations in the noise sample. Every pixel at any frame that had a higher value than the threshold was given the value of 255, while the other pixels were discarded. (7) Finding pixels with a value of 255. If one pixel had at least one neighbour that also had a value of 255 the entire continuous collection of pixels was referred to as a particle. If there were at least 40 directly neighbouring pixels, which made up the particle then the particle was preserved; otherwise the pixels that made up the particle were given a value of 0. The edges of all of these particles were increased by 1 pixel. (8) Re-analysis of all the particles keeping only particles with a continuous area of at least 5600 μm2. (9) The precise pixels that make up the particle along with the frame number at which the particle was observed was stored as a region of interest (ROI), and these ROIs were then referred to as cluster events. Individual areas and the size of overlapping areas between all cluster events were then calculated for a given image stack.
A custom-made ImageJ script was used to create three different surrogate datasets, simulating spontaneous cluster events constrained by three position models, by shuffling 458 cluster events previously found in a typical experiment (P10.5 animal). The models were based on measurements of the length and distance between layers of the three-layer tubular structure of the IO comprising the DAO and PO in five preparations from P10.5–P13.5 animals. For the three position models the shape and orientation of the cluster events was kept constant, while the spatial position was varied. In all three models the placement on the y axis was similar, mimicking the three-layer tubular structure, and the relative overlap of cluster events in these subnuclei. Thus, there was a 50% probability of an event being placed in the dorsal lamella of the PO, while the DAO and ventral lamella of the PO had a probability of 25% each. All cluster events were placed at least 135 μm away from the edge of the frame on both axis. The models were as follows. (1) In the random model, cluster events were placed 157 μm apart on the y axis, plus a further y-axis random displacement of 0–81 μm, and were displaced at random 0–1388 μm along the x axis. (2) In the close hub model, cluster events were placed 157 μm apart on the y axis, plus a further y-axis random displacement of 0–81 μm. The events were then placed on one of nine hub positions, defined as sites where clustered activity emerges at increased probability, distributed evenly along the x axis at a distance of 157 μm, plus a further x-axis random displacement of 0–81 μm. The seven positions in the middle had a probability of 12.5% while the right and left position had a probability of only 6.25%. (3) In the remote hub model, cluster events were placed 298 μm apart on the y axis, plus a further y-axis random displacement of 0–81 μm. The events were then placed on one of six hub positions distributed evenly along the x axis at a distance of 298 μm, plus a further x-axis random displacement of 0–81 μm. The four positions in the middle had a probability of 20% while the right and left position had a probability of only 10%. The hub positions thus created a spatial structure around which events occurred with some variation. An additional 18 models spanning an inter-cluster distance of 0–298 μm in steps of 15 μm on the x axis were also evaluated to explore the space between the three models. For data analysis the procedure was repeated three times creating three unique simulated image stacks. For each of the three surrogate datasets and the original dataset a histogram for the distribution of the cluster overlap was created. The bins had a width of 0.01, containing all values between 0 and 1, i.e. a total of 100 bins for each dataset. The count at any given bin for each of the three surrogate datasets was then plotted against the count in the same bin in the original dataset. The Pearson correlation between the three surrogate datasets against the original dataset was then determined.
Glutamate-induced clusters were visualized and quantified in image stacks that were bleach corrected by a running background subtraction, Kalman filtered, colour coded (rainbow RGB, black: small ΔF, red to white: large ΔF), 2–10-point mean-filtered (mean of adjacent 2 × 2–10 × 10 points), and brightness and contrast enhanced using ImageJ. Note that the fluorescence output from Fluo-8, AM-labelled tissue is dependent on loading time, age of the animal, light exposure time and bleaching, all variables that changed substantially from experiment to experiment. For these reasons amplitude calibration bars on ΔF images have been omitted, but the relative changes in the data within one experiment can be distinguished as changes in colour code in single images. Blue to red indicated low to high calcium concentration. Contrast and colour range was kept constant when showing several images from the same experiment. In some experiments ROIs were defined and average ΔF/F values within the ROI were plotted versus time.
Imaging at high frame rates (128,217 frames s−1, 4 × 4 binning) was used to follow the temporal development of cluster formation in IO neurons comprising a glutamate-induced or spontaneous cluster. ΔF waveforms from ROIs placed over individual neurons were smoothed (sliding average), and the time of the rising phase of calcium transients was determined by thresholding (0.65 of maximum amplitude). Contour plots of the signal spread were generated based on transient differences in time between the first IO neuron above threshold in a cluster and successive IO neurons above threshold, and relationships between Euclidean distances, signal velocities and transient differences were calculated.
Statistical values are given as mean ± SD, and Student’s t test was used for statistical comparisons unless otherwise stated.
Results
Overlapping clusters in the PO, and dendritic territory compared to cluster size
In our original report of spontaneous cluster formation in the IO in postnatal mice we used a human observer-based demarcation of clusters, and noted that clusters appeared to overlap in both the PO and the DMCC (Rekling et al. 2012). Here, we analysed spontaneous cluster formation in the IO using a fully automated cluster-detection algorithm, and quantified the size and amount of overlap between neighbouring clusters (Fig. 1). The mean combined DAO, MAO, PO and DMCC cluster size was 9269 ± 4012 μm2 (with a lower arbitrarily set cut-off value of 5600 μm2, n= 1407) with a left-skewed distribution, i.e. many small clusters and only few large clusters (Fig. 1A and B, n= 5 P10.5–P13.5 animals). The relative overlap between any two clusters (Fig. 1A, top panel insert) was calculated (expressed as 0–1 overlap), discarding completely non-overlapping clusters. Thus, in this analysis a high or total overlap can be the result of either a repeating cluster or a smaller cluster that is contained within a larger cluster. Cluster activity was found to be heterogeneous throughout the IO, with a surprisingly high cluster activity in the dorsal lamella of the PO and the DMCC (Fig. 1A). Excluding the DMCC data, quantification of the combined DAO, PO and MAO data gave a mean overlap of 0.28 ± 0.26, a median of 0.21 and a highly left-skewed distribution (Fig. 1C, skewness: 0.82, n= 58,180 cluster events in five P10.5–P13.5 animals). This high degree of overlap raises the question of whether spontaneous cluster activity is occurring at randomly spaced positions in the IO, or is constrained spatially in some way. To begin to answer this question we compared the observed overlap distribution for the combined DAO and PO data with distributions drawn from three surrogate data models. The models were based on measurements of the total length (3712 ± 410 μm) and distance (157 ± 8) μm between layers of the three-layer tubular structure of the IO comprising the DAO, the dorsal lamella of the PO and the ventral lamella of the PO (Fig. 1D–F, n= 5 P10.5–P13.5 animals). The random model placed cluster events at randomly spaced positions in this tubular structure, the close hub model placed events around hubs, defined as sites where clustered activity emerges at increased probability, spaced 157 μm apart, and the remote hub model placed events around hubs spaced 298 μm apart. The random model gave a mean overlap of 0.26 ± 0.24 (n= 65,535 cluster events, Fig. 1D), the close hub model had a mean overlap of 0.31 ± 0.26 (n= 63,331, Fig. 1E) and the remote hub model had a much higher mean overlap of 0.46 ± 0.22 (n= 12,952, Fig. 1F). Importantly, the overlap distribution in the random model was closer in shape to the original dataset with a median of 0.20 and a skewness of 0.87, while the close hub model was more centre heavy with a median of 0.27 and a skewness of 0.57. Again the remote hub model was very dissimilar with a median of 0.44 and a skewness of 0.46. Thus, the shape of the overlap distribution of the original dataset is best reproduced by the random model. There was a highly significant (P < 0.001, Kolmogorov–Smirnov test) difference between all of the models and the original dataset, indicating that no model was a perfect fit for the original dataset, but a Kolmogorov–Smirnov test shows a D value of 0.046 for the random model, 0.0727 for the close hub model and 0.382 for the remote hub model. The relative distributions of the overlap were also compared using a Pearson correlation, performed on a 100 bin histogram of each of the distributions. The correlation coefficient between the original dataset and the random model was 0.993, for the close hub model 0.982 and for the remote hub model –0.153. An additional 18 models spanning the space between the three models were also evaluated, showing that the Pearson correlation coefficient increased linearly with closer spaced events, and flattened out at >0.98 at the close hub distance of 157 μm. Thus, the random and close hub models showed the closest fit to the experimental data.
Figure 1.
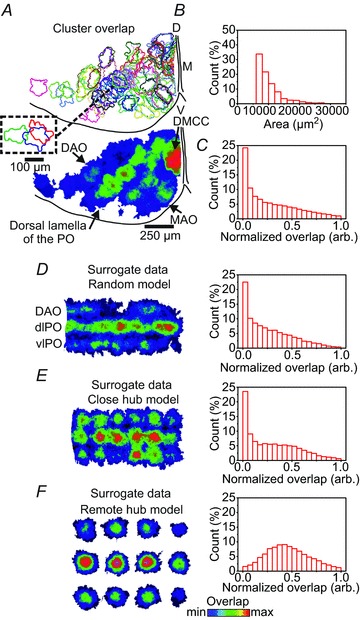
Spontaneous clusters in the IO overlap extensively A, upper panel: random colour-coded outlines of spontaneous cluster events cumulated over 10 s in a hallf IO slice from a P10.5 mouse. D, dorsal; V, ventral; M, midline. Inset: outlines of three overlapping clusters in the dorsal lamella of the PO. Lower panel: cumulative (50 s) heat map indicating the amount (min: blue, max: red) of overlap of cluster events in the same half IO slice. DAO, dorsal accessory olive; MAO, medial accessory olive; PO, principal olive; DMCC, dorsomedial cell column. Note the high degree of overlap in the DMCC and the dorsal lamella of the PO. B, cluster area histogram based on cumulative data from five P10.5–P13.5 mice. C, normalized overlap histogram from five P10.5–P13.5 mice. D, left panel: cumulative heat map of cluster overlap based on surrogate data random model; DAO and dorsal and ventral lamella of the PO (dlPO, vlPO) are indicated. Right panel: normalized overlap histogram based on the random model. E, left panel, cumulative heat map of cluster overlap based on surrogate data close hub model. Right panel: normalized overlap histogram based on the close hub model. F, left panel: cumulative heat map of cluster overlap based on surrogate data remote hub model. Right panel: normalized overlap histogram based on the remote hub model. Note the similar-shaped distributions in C and D, right panel.
Next, we sought to determine how much of the dendritic territory of a given IO neuron may be encompassed by a cluster by labelling IO neurons using a modified Golgi–Cox method and reconstructing the somatodendritic morphology using a camera lucida system (Fig. 2). Reconstruction of PO neurons in six P10.5–P11.5 animals showed dendritic morphologies with straight (n= 3) or curly (n= 23) appearances (Fig. 2A). In curly PO neurons the average somatodendritic field size, defined as the convex hull of the trace, was 6357 ± 2152 μm2 (Fig. 2A, bottom), the ferret diameter, defined as the longest chord of the projection of the object at a specific angle, was 117 ± 23 μm, and the largest radius from soma was 72 ± 17 μm (n= 23). This compares to an average PO cluster size in a similarly aged animal (P10.5) of 9984 ± 4632 μm2 (range 5600–38,892 μm2, Fig. 2B, bottom), and a ferret diameter of 159 ± 36 μm (n= 458 clusters). Thus, the average somatodendritic field size of single curly PO neurons is slightly smaller than the average PO cluster size, and about six non-overlapping curly PO neurons could be contained within the largest PO clusters. In histological sections counterstained with Toluidin blue (not shown) the combined DAO, PO and MAO cell density was 1376 ± 145 cell mm−2, and the cell diameter was 13.1 ± 0.7 μm (n= 16 sections and n= 50 cells from four P6.5–P7.5 animals).
Figure 2.
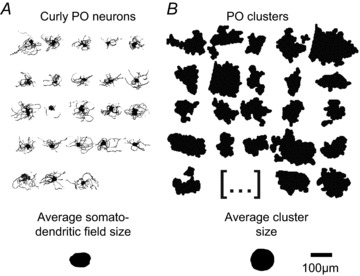
Somatodendritic field size of PO neurons is slightly smaller than mean PO cluster size A, camera lucida drawings of curly PO neurons. Lower panel: average somatodendritic field size of PO neurons (n= 23). B, representative cluster profiles from a P10.5 animal. Lower panel: average PO cluster size (n= 458). Note that the somatodendritic field size of curly neurons is slightly smaller than the average PO cluster size.
Glutamate-induced cluster formation is inhibited by TTX and gap junction blockers
To determine if sodium action potentials and electrical coupling between IO neurons are necessary for cluster formation we used glutamate iontophoresis to repeatedly induce cluster formation. Thus, repetitive (10 s intervals) 500 ms duration glutamate iontophoresis, performed with a glass pipette containing 0.5 m glutamate placed just below the surface of the slice, induced cluster formation in both the DMCC and the PO (Fig. 3, n= 8 P10.5–P12.5 animals). Increasing ejection current amplitudes resulted in an increase in cluster size to either a plateau (Fig. 3A, lower panel, coefficient of variation (CV) at plateau: 10 ± 4%)) with an average cluster size of 28,174 ± 6957 μm2, or a plateau with further size increases at higher injection currents (Fig. 3B, lower panel, n= 3 DMCC, n= 5 PO). Repeated glutamate iontophoresis resulted in induction of equal sized clusters. In one example a repeating spontaneous neighbouring cluster shared two cells with the outer rim of an expanding glutamate-induced cluster, suggesting that the expanding glutamate bolus might recruit neurons in neighbouring clusters (Fig. 3C). Indeed, dual clusters could be induced by glutamate iontophoresis (Fig. 3D, n= 3). Iontophoresis of either NMDA (100 mm in pipette) or AMPA (10 mm in pipette) induced cluster formation with an average cluster size of 26,896 ± 8512 μm2 (NMDA, n= 5) and 31,312 ± 10,600 μm2 (AMPA, n= 5).
Figure 3.
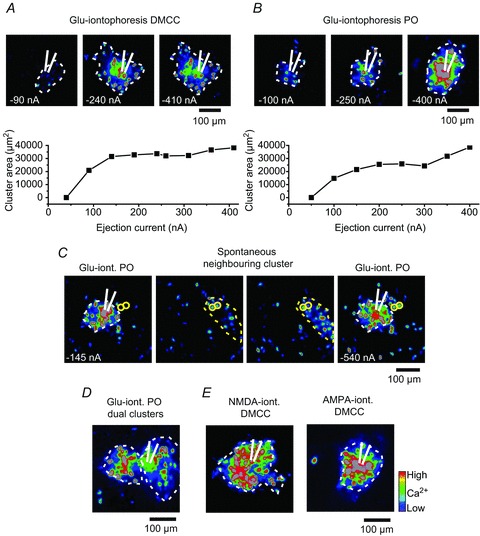
Glutamate-induced cluster formation in the DMCC and PO A, upper panels: Z-projection ΔF images (maximum values over 10 frames) at the time of glutamate iontophoresis (net ejection current is noted in the lower left corner) with a glass pipette positioned in the DMCC (white lined tip). Lower panel: plot of injection current versus DMCC cluster area. B, Z-projection ΔF images at the time of glutamate iontophoresis with a glass pipette positioned in the PO. Lower panel: plot of injection current versus PO cluster area. Note that the cluster area reaches a plateau in the DMCC and PO. C, Z-projection images of glutamate-induced PO cluster (white dotted line; iont., iontophoresis), and a repeating spontaneous neighbouring cluster (yellow dotted line). Note that two neurons in the spontaneous cluster (yellow circles) are also activated at the outer rim of the glutamate-induced cluster at the strongest glutamate iontophoresis (rightmost panel). D, Z-projection ΔF images of glutamate-induced dual PO clusters. E, Z-projection ΔF images of NMDA- and AMPA-induced cluster formation in the DMCC. Blue, low calcium; red, high calcium (applies to all images).
Blocking sodium channels with TTX (2 μm) reduced the size of glutamate-induced clusters to 23 ± 9% of the control (Fig. 4A, n= 7), and the remaining glutamate-induced calcium transient was abolished by adding Cd2+ (200 μm). Application of the gap junction blocker carbenoxelone (100 μm) reduced the size of glutamate-induced clusters to 35 ± 15% of the control (Fig. 4B, 60 min application, n= 5), and 18β-glycyrrhetinic acid (150 μm) reduced the size to 41 ± 28% of the control (Fig. 4C, 30 min application, n= 5). Thus, sodium action potentials and electrical coupling are involved in glutamate-induced cluster formation.
Figure 4.

TTX and gap junction blockers inhibit glutamate-induced cluster formation A, Z-projection ΔF images of glutamate-induced cluster in the PO before and after adding TTX (2 μm), or TTX + Cd2+ (200 μm). Net ejection current is noted in the lower left corner. Right panel is a bar plot of group data (error bar: SEM, **P < 0.01, ***P < 0.001). B, Z-projection ΔF images of glutamate-induced cluster in the PO before and after adding carbenoxelone (Carb., 100 μm). C, Z-projection ΔF images of glutamate-induced cluster in the PO before and after adding 18β-glycyrrhetinic acid (18-beta., 150 μm). Note that TTX and both gap junction blockers reduce glutamate-induced cluster formation.
Glutamate iontophoresis induces spikelets and transient depolarizing responses
To further investigate the mechanism underlying cluster formation we performed whole-cell recordings from IO neurons during glutamate iontophoresis, resulting in cluster formation in the DMCC or PO (Fig. 5). At iontophoresis-pipette to recording-pipette distances ranging from 30 to 100 μm, a 500 ms glutamate iontophoresis induced a slowly rising depolarizing response with one or several action potentials riding at the peak (Fig. 5A, n= 18 DMCC, 7 PO neurons). However, two other types of responses were noted in some IO neurons with longer inter-pipette distances (75–115 μm): (1) spikelets with an amplitude of 6.4 ± 1.7 mV and a duration of 6.5 ± 1.8 ms (at half max amplitude, n= 5 neurons) – multiple amplitude spikelets could be observed in the same neuron (Fig. 5B, 3, n= 3 neurons); and (2) a small (4.4 ± 1.7 mV) transient depolarizing response (Fig. 5B, 2) lasting 171 ± 84 ms measured from slightly hyperpolarized levels subthreshold to spike initiation (n= 7 neurons). The transient depolarization was followed by an afterhyperpolarization (AP) in some cells (1.4 ± 0.7 mV, 50 ms to 1.4 s in duration, Fig. 5C, n= 3 neurons). IO neurons showing spikelets had full action potentials which could depart almost directly from baseline during the glutamate iontophoresis (Fig. 5B, top trace), and an amplitude of 75.8 ± 17.8 mV and a duration of 22.4 ± 7.4 ms (n= 5). The iontophoresis-pipette to recording-pipette distance in IO neurons showing glutamate-induced depolarizing response was 66 ± 23 μm, shorter than that for IO neurons showing glutamate-induced spiking directly from baseline (91 ± 23 μm, n= 30 and 7, P < 0.05, Mann–Whitney test).
Figure 5.
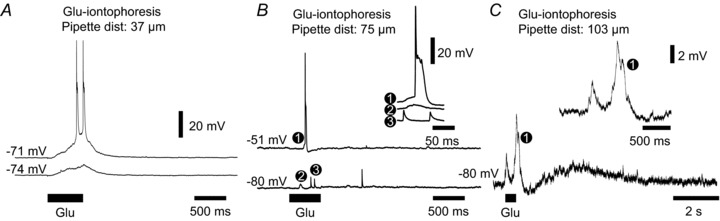
Glutamate iontophoresis induces spikelets and transient depolarizing responses A, whole-cell recording from a DMCC neuron during cluster-inducing glutamate iontophoresis. The neuron was held at rest and at a slightly hyperpolarized level using bias current (lower trace). Note the slowly developing glutamate-induced membrane depolarization during the 500 ms iontophoresis. B, recording from a DMCC neuron during glutamate iontophoresis with a 75 μm inter-pipette distance. Inset: traces at increased resolution corresponding to the full spike at rest (1), the transient depolarization (2) and spikelets (3) recorded at a hyperpolarized level. Note the different spikelet amplitudes during the glutamate iontophoresis. C, recording from a DMCC neuron during glutamate iontophoresis with a 103 μm inter-pipette distance. The neuron was held at subthreshold for spiking during the glutamate iontophoresis. Inset: trace at increased resolution corresponding to the double transient depolarization at (1). Note that the second transient depolarization is followed by a small AP merging into a longer glutamate-induced depolarization.
Somatic APs and cluster formation are accompanied by dendritic calcium transients
The presence of a small transient depolarizing response followed by an AP, resembling electrotonically attenuated dendritic spikes in other neuron types, prompted us to look for possible active properties of dendrites in IO neurons. When Fluo-8, Na+ salt (400 μm) was present in the recording solution during whole-cell recording of IO neurons, large amplitude calcium transients were observed in IO dendrites when APs were elicited by 50 ms depolarizing pulses (Fig. 6). The amplitude of the dendritic calcium transient was strongly dependent on whether the AP was elicited by pulses (reaching the same final current level) from resting Vm or from a hyperpolarized potential (Fig. 6A, B). Thus, APs elicited from resting Vm by a 50 ms depolarizing pulse had a duration of 22.5 ± 3.6 ms versus APs induced from a hyperpolarized Vm (20–30 mV below resting Vm using pre-pulse bias current), which had a duration of 8.1 ± 3.7 ms (P < 0.05, n= 4 IO neurons). These APs gave rise to large amplitude calcium transients in dendritic segments (length: 26 ± 9 μm) at a distance of 33 ± 6 μm from soma, and the calcium transient amplitude was smaller during APs elicited from a hyperpolarized Vm relative to calcium transients during AP elicited from resting Vm (46 ± 20%, P < 0.05, one-tailed t test, n= 4). Calcium transients, captured at 69 frames s−1, during APs showed a good fit to a bi-exponential function (Fig. 6A, blue trace) with decay constants of τ1 52 ± 7 ms, τ2 1362 ± 304 ms for transients associated with APs elicited from resting Vm, and τ1 57 ± 18 ms, τ2 3583 ± 2505 ms for transients associated with APs elicited from a hyperpolarized Vm (n.s., n= 4).
Figure 6.

IO dendrites show large amplitude calcium transients during AP and cluster formation A, cycle-triggered averages (eight bouts) of dendritic calcium transients (top red trace), membrane potential (Vm, middle trace, spike height is truncated – dotted line), and current injection (I, bottom trace) during a two-pulse paradigm eliciting APs in a PO neuron from resting Vm (left insert, single spike), or from a hyperpolarized Vm (right insert, single spike). The blue trace overlaid on the top red trace is a bi-exponential fit to the data. B, two cycle-triggered ΔF images of the soma, and dendrite (white outline) used in the analysis in A. Note that APs have a longer duration when elicited from resting Vm, and that the associated dendritic calcium transient is larger. C, cumulative fluorescence images of two neighbouring PO neurons, where proximal dendritic profiles are visible, and associated fluorescence traces taken from ROIs at the soma (1,3), and dendritic regions (2,4). Note that dendrites of both neurons show calcium transients concurrent with spontaneous simultaneous somatic calcium transients (black arrows on trace 2,4).
In some experiments proximal IO dendrite profiles were readily observed in Fluo-8, AM-loaded preparations (Fig. 6C). Calcium transients in dendritic segments (length: 5 ± 2 μm) were observed coinciding with cluster formation (2–4 neighbouring IO neurons coactive in the same field of view) and somatic calcium transients at somatodendritic distances of 31 ± 9 μm (n= 9). A lower frame rate of 10 frames s−1 was used to capture these weaker dendritic calcium signals, which showed half amplitude duration of 534 ± 233 ms versus accompanying somatic calcium transients lasting 1409 ± 554 ms (P < 0.001,n= 9).
Calcium transients spread with decreasing velocity during cluster formation
The involvement of electrical coupling and the prolonged transient depolarizing responses during cluster formation (see Fig. 5B, 2, and Fig. 5C, 1) prompted us to investigate the temporal development of calcium transients in individual IO neurons during cluster formation (Fig. 7). The relative temporal occurrence of calcium transients in IO neurons was determined in glutamate-induced and spontaneous clusters in the DMCC and PO using high frame rates and binning (128,217 frames s−1 4 × 4 binning). Cluster formation was initiated close to the glutamate-containing pipette and spread with a mean signal velocity (SV: Euclidean distance divided by the transient delay (TD) between the first and next IO neuron) of 3.7 ± 1.6 μm ms−1 in the DMCC (Fig. 7A, n= 6 clusters in two P7.5–P8.5 animals, average number of neurons per cluster: 12) and 6.6 ± 32.0 μm ms−1 in the PO (n= 7 clusters in three P7.5–P9.5 animals, average number of neurons per cluster: 7). Signal velocity decreased with increasing Euclidian distance from the initiation point, which could be visualized in contour plots of the signal spread (expressed in milliseconds relative to the initiation point) throughout a cluster (Fig. 7A, lower panel). A log–log plot showing the combined (DMCC plus PO, n= 3 P7.5–9.5 animals) transient delay versus signal velocity showed a near linear relationship (Fig. 7D), i.e. the longer time between calcium transients in the initiating and successive IO neurons within a glutamate-induced cluster the lower the signal velocity between those neurons. Spontaneous clusters showed a similar temporal spread, starting at some point, and then spreading linearly (Fig. 7B) or concentrically (Fig. 7C) with a mean signal velocity of 1.3 ± 1.5 μm ms−1 in the DMCC (Fig. 7B, n= 10 clusters in four P8.5–P11.5 animals, average number of neurons per cluster: 14) and 7.4 ± 24.1 μm ms−1 in the PO (n= 8 clusters in eight P7.5–P10.5 animals, average number of neurons per cluster: 6). The signal velocity also decreased with increasing Euclidian distance, and a log–log plot showing the transient delay versus signal velocity revealed a near linear relationship (Fig. 7E). One possible model that captures this form of signal spread is a power law of the form logf(x) =–ax log(x) +k (Fig. 7F, f(x): signal velocity, x: transient difference, a: constant, k: constant), which produce a linear relationship between the transient delay and the signal velocity in a log-log plot (Fig. 7F, lower graph). Using the original PO data constrained by the power law equation (log(SV) =–0.61 * log(TD)+1.33) on a set of model IO neurons spaced on average 60 μm apart produced a contour map that simulates how the signal spread with decreasing velocity the further out it gets from the starting point of the cluster.
Figure 7.
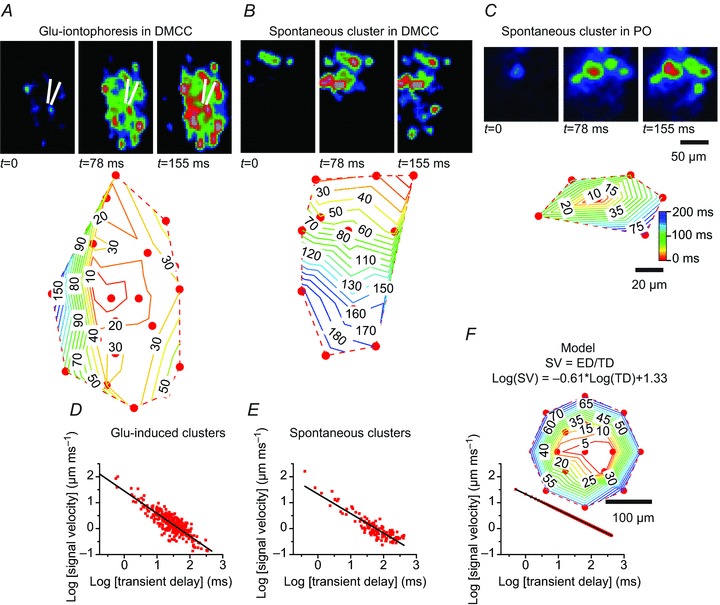
Glutamate-induced or spontaneous clusters form with decreasing signal velocity with increasing Euclidian distance from the initiation point A, upper panel: ΔF images of the temporal development (relative time (in ms) is indicated below the image) of a glutamate-induced cluster in the DMCC. Lower panel: contour plot of the signal spread within the cluster expressed as relative time (in ms) to the initiation point. B, upper panel: ΔF images of the temporal development of a spontaneous cluster in the DMCC. Lower panel: contour plots of the signal spread. C, upper panel: ΔF images of the temporal development of a spontaneous cluster in the PO. Lower panel: contour plots of the signal spread. D, group data (DMCC and PO) of glutamate-induced clusters in a log–log plot of transient delay versus signal velocity (n= 299 pairs of initiating and successive IO neurons in 13 clusters). E, group data (DMCC and PO) of spontaneous clusters in a log–log plot of transient delay versus signal velocity (n= 130 pairs of initiating and successive IO neurons in 18 clusters). F, power-law model of the signal spread. Log–log plot of transient difference versus signal delay using simulated data, drawn from the experimental PO data constrained by the model (n= 833 pairs of initiating and successive IO neurons in a 17-neuron cluster with 60 μm between cells). Inset: contour plot of the signal spread. SV, signal velocity; ED, Euclidean distance; TD, transient delay. Note that the signal in both glutamate-induced and spontaneous clusters spreads from an initiation point at high velocity, but then slows down the further out in the cluster it gets.
Discussion
Spontaneous cluster formation in the IO was found to be dependent on sodium action potentials, and on electrical coupling between IO neurons. It spreads with decreasing velocity, and may involve active dendritic properties. Activation of AMPA and NMDA receptors induces cluster formation, and randomly occurring spontaneous clusters overlap extensively, suggesting that excitatory afferent input may be inducing cluster formation in spatio-temporal overlapping configurations. The physiological significance of cluster formation in the IO during execution of motor programmes is still unknown.
Extensively overlapping clusters
Spontaneous clusters in the IO overlap extensively. The DMCC appears to be a specialized region, as spontaneous cluster activity occurs repetitively, and clusters can cover the entire subnucleus (Rekling et al. 2012). We hypothesized that the DMCC, which contains vestibular-related IO neurons, may be on a fast developmental track because a functional vestibular system early in postnatal life is of critical importance to the animal. Here our automated cluster detection algorithm also detected particularly high cluster activity in the dorsal lamella of PO, an IO region that has also been implicated in vestibulo-ocular integration via midbrain nuclei (Swenson & Castro, 1983a; Onodera, 1984). The cluster detection algorithm did not distinguish between repeating and overlapping clusters, and the temporal development of individual clusters may also result in detection of the same cluster more than once. Thus, the current method of quantification of the overlap overestimates the true overlap within the image acquisition times used here. One important question then is whether the spontaneous cluster formation has an underlying spatial structure, i.e. do clusters form in random positions, thereby producing randomly overlapping regions, or are they constrained in some way. The current data offer no definite answer to this question, but a comparison between the original PO data and three surrogate data models suggest that the spontaneous cluster formation may indeed be random, or constrained by positions closer than the 157 μm set in the close hub model. The overestimation error due to multiple detection of repeating and temporally developing clusters will tend to skew the overlap distribution towards a hub-like distribution, yet the analysis still showed that the best fit to the experimental data was a random model. However, glutamate iontophoresis resulted in dual neighbouring clusters in a few instances, suggesting that the threshold for cluster formation may not be uniform in the IO. Thus, the question needs to be readdressed using in vivo experiments that more directly investigate whether cluster formation in fact is spatially constrained or random during normal motor acts. If the indication presented here holds true, i.e. that cluster formation is random throughout the PO, it has the important implication that clusters may not be static, but emergent and constantly changing structures with varying spatio-temporal configurations during execution of motor programmes (Fig. 8A).
Figure 8.
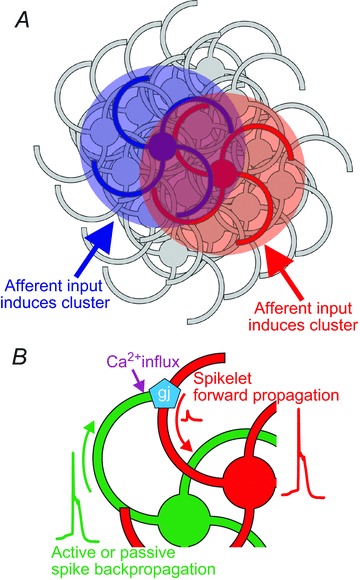
Model of cluster formation in the IO A, clusters may possibly be emergent and constantly changing structures with overlapping territories at different times during execution of motor programmes. Time-varying afferent input may be the primary pattern-forming mechanism. B, cellular mechanisms contributing to cluster formation. Active or passive spike backpropagation into the dendritic compartment of curly IO neurons induces forward propagating spikelets in gap junction-coupled neighbouring IO neurons, which may reach threshold for spike initiation in the somatic region or axon. Backpropagating action potentials may also induce calcium influx through dendritic HVA calcium channels, which could have a modulatory effect on connexins in the gap junctions.
The ΔF signal from a detected cluster comes from both somatic and dendritic calcium transients as Fluo-8, AM also loaded into dendritic compartments. Consequently, it was of interest to compare the cluster size in P10.5–P11.5 animals to the somatodendritic territory covered by IO neurons in animals of this age. Thus, the modified Golgi–Cox labelling of curly IO neurons showed that the average somatodendritic field size of single curly PO neurons is slightly smaller than the average PO cluster size, and about six non-overlapping curly PO neurons could be contained within the largest PO clusters. Using the soma density in the combined DAO, PO and MAO we show that the somas of an estimated 87 IO neurons can be contained in the PO mean cluster size of 9984 μm2 if clusters are nearly spherical, and the largest clusters (38,892 μm2) in the DMCC could contain the somas of 692 neurons. Not all neighbouring IO neurons within a cluster volume may be activated during cluster formation, but clusters clearly contain tens to hundreds of IO neurons with overlapping dendritic territories (Fig. 8A). For comparison, data from the cat suggest that the number of neurons positioned with the dendritic territory of a single IO is ∼115 (Ruigrok et al. 1990). Spontaneous clusters take spherical but also elongated forms (e.g. Fig. 3C), but whether there is a preferential involvement of straight and curly PO neurons in these different forms is unknown.
Glutamate-induced cluster formation
The IO receives afferent input from numerous regions in the CNS ranging from the lumbar spinal cord to the cerebral cortex (Brown et al. 1977; Swenson & Castro, 1983a, 1983b). Some of these connections are probably glutamatergic (Zhang et al. 1990; Onodera & Hicks, 1995), and both NMDA and AMPA receptors are expressed in IO neurons (Watanabe et al. 1994; Paarmann et al. 2000; Chen et al. 2006). These observations prompted us to see if application of glutamate might induce cluster formation. Indeed, 500 ms iontophoresis of glutamate, AMPA, or NMDA all induce cluster formation in both the PO and DMCC. The fact that the region of neurons showing glutamate-induced transients increased to a plateau suggests that clusters are indeed being elicited, and glutamate is not just activating an expanding region of neurons. This interpretation is also supported by the observation that glutamate iontophoresis with longer distances (50–100 μm) between the iontophoresis and recording pipette induced spike activity (or spikelets) without any noticeable pre-depolarization (Fig. 5B). Thus, these observations suggest that glutamate-induced cluster formation is carried by a neuron–neuron signal which outruns the expanding effect of the glutamate bolus. The number of cells recruited by glutamate, AMPA or NMDA iontophoresis may have been larger than the number of cells recruited by equally sized spontaneous clusters, which may involve not all neighbouring IO neurons.
Cellular mechanism underlying cluster formation
Repeated glutamate-induced cluster formation allowed a more direct investigation of the cellular mechanism involved in cluster formation. Thus, blocking sodium channels with TTX and gap junctions with carbenoxelone or 18β-glycyrrhetinic acid all reduced glutamate-induced cluster formation, demonstrating that sodium action potentials and electrical coupling is necessary for cluster formation. A residual calcium signal close to the iontophoresis pipette in the TTX experiments was abolished by the non-specific calcium channel blocker Cd2+, suggesting that the remaining signal might have been due to voltage-gated calcium channels recruited by the glutamate depolarization. Glutamate-induced cluster formation was accompanied by spikelets with different amplitudes, and a transient depolarizing response. We interpret the spikelets as sodium action potentials that actively or passively backpropagate in the dendrites of IO, cross into nearby cluster members through dendro-dendritic gap junctions (De Zeeuw et al. 1995) and forward propagate to the soma (Fig. 8B). The different spikelet amplitudes may be the result of different electrotonic distances from the dendro-dendritic coupling from several IO neurons. The transient depolarizing response remains unexplained, but we hypothesize that it may be the result of a dendritic calcium conductance that is being activated by the depolarization of the dendritic compartment. Two observations support this: first, action potentials induced by somatic current injection or spontaneous cluster-related action potentials were accompanied by large amplitude dendritic calcium transients (Fig. 7 and Fig. 8B). Secondly, the transient depolarization was followed by an AP in some cells, which possibly could be the result of a calcium-activated potassium conductance. Dendrites of IO neurons are endowed with high-voltage activated (HVA) calcium, and calcium-activated potassium conductances (Llinas & Yarom, 1981a, 1981b; Schweighofer et al. 1999), and the present study is the first to demonstrate dendritic calcium influx in IO neurons using calcium imaging. Interestingly, the amplitude of the dendritic calcium transient was strongly dependent on the shape of the action potential, i.e. long-duration action potentials elicited from resting Vm was accompanied by large dendritic calcium transients. This has the consequence that there will probably be a large difference in the dendritic calcium influx depending on whether actions potentials are elicited on the top or on the bottom of subthreshold oscillations, which have important consequences for the olivo-cerebellar interaction (Mathy et al. 2009; de Gruijl et al. 2012). HVA calcium conductances are probably supported by P/Q-type calcium channels, and the phase-resetting of subthreshold oscillations in IO clusters is lost in the absence of the pore-forming α1A subunit, coded by the CaV2.1 gene (Choi et al. 2010), demonstrating the importance of HVA channels in IO synchronicity. It is tempting to speculate whether the large dendritic calcium influx driven by spike activity may influence the gap junction coupling between IO neurons (Fig. 8B). Connexin36, which is present in IO dendro-dendritic gap junctions (De Zeeuw et al. 2003), is coupled to calcium signalling via interaction with calcium/calmodulin-dependent kinase II (Alev et al. 2008), but an effect on gap junctional conductances remains to be demonstrated. The particularly strong expression of calcium binding proteins, such as parvalbumin and calbindin, in the developing and adult IO (Wassef et al. 1992; Allen Mouse Brain Atlas, http//mouse.brain-map.org) suggests that calcium signalling is under strict temporal control in IO neurons. The strong dendritic calcium transients observed in this study had fast (∼50 ms) and slow (∼1.5 s) decaying profiles, some of which obviously can be attributed to the binding characteristics of the Fluo-8, but the bi-exponential profile might also be a sign of the effect of intracellular buffering of the calcium signal with consequences for calcium-dependent processes in the dendrites.
The calcium transient signal spread with decreasing velocity from the starting point of the glutamate-induced or spontaneous clusters with a mean velocity of 1–7 μm ms−1. Interestingly, the signal spread was well fitted with a power law-type equation, i.e. initially a high velocity followed by a progressively decreasing velocity as the cluster developed. The underlying cellular mechanism for this type of spread is unknown, but we hypothesize that the decrease in velocity and final ending of the cluster may result from temporal dispersion of the signal in a massively interconnected network of gap junction coupled IO neurons. Thus, electrically coupled IO neurons close to the initiation point will tend to have tightly synchronized spikes, whereas IO neurons further out in the cluster will have progressively more and more variation in the timing of the spike, and hence at some point fall below threshold for spike initiation altogether. This scenario fits well with the observation that calcium transient coherence decrease with increasing Euclidean distance between cluster-forming IO neurons (Rekling et al. 2012). The temporal dispersion of the signal could be the result of the properties of the dendrites, gap junctional conductances and the somatic membrane capacitance, which together will act as a low-pass like filter on the current transfer between cluster members. Possible calcium-dependent modulation of gap junctions could conceivably also contribute to the time-dependent modulation of signal transfer between cluster members.
In conclusion, the experiments presented here suggest that cluster formation depends on gap junctions and sodium action potentials, and may occur randomly through the IO. The relatively slow signal spread during cluster formation, combined with a strong dendritic influx of calcium, may signify that active dendritic properties contribute to cluster formation.
Acknowledgments
We thank Lis Hansen for technical assistance.
Glossary
- AMPA
α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid
- AP
afterhyperpolarization
- DAO
dorsal accessory olive
- DMCC
dorsomedial cell column
- HVA
high-voltage activated
- IO
inferior olivary nucleus
- NMDA
N-methyl-d-aspartate
- PO
principal olive
- ROI
region of interest
- SV
signal velocity
- TD
transient delay
- TTX
tetrodotoxin
Additional information
Competing interests
None declared.
Author contributions
M.K., F.C.M., H.J. and J.C.R. all contributed to the conception and design of the experiments and contributed to the collection, analysis and interpretation of the data. J.C.R. drafted the article, M.K., F.C.M. and H.J. contributed to revising it critically for important intellectual content, and all authors approved the final version of the manuscript.
Funding
This work was supported by The Lundbeck Foundation, Den Owensenke Fond, Lægeforeningens forskningsfond, Agnes og Pouls Friis Fond, Fonden til Lægevidenskabens Fremme, Brødrene Hartmans fond, and Mindefonden for Alice Brenaa.
References
- Alev C, Urschel S, Sonntag S, Zoidl G, Fort AG, Hoher T, Matsubara M, Willecke K, Spray DC, Dermietzel R. The neuronal connexin36 interacts with and is phosphorylated by CaMKII in a way similar to CaMKII interaction with glutamate receptors. Proc Natl Acad Sci U S A. 2008;105:20964–20969. doi: 10.1073/pnas.0805408105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown JT, Chan-Palay V, Palay SL. A study of afferent input to the inferior olivary complex in the rat by retrograde axonal transport of horseradish peroxidase. J Comp Neurol. 1977;176:1–22. doi: 10.1002/cne.901760102. [DOI] [PubMed] [Google Scholar]
- Chen LW, Tse YC, Li C, Guan ZL, Lai CH, Yung KK, Shum DK, Chan YS. Differential expression of NMDA and AMPA/KA receptor subunits in the inferior olive of postnatal rats. Brain Res. 2006;1067:103–114. doi: 10.1016/j.brainres.2005.10.054. [DOI] [PubMed] [Google Scholar]
- Choi S, Yu E, Kim D, Urbano FJ, Makarenko V, Shin HS, Llinas RR. Subthreshold membrane potential oscillations in inferior olive neurons are dynamically regulated by P/Q- and T-type calcium channels: a study in mutant mice. J Physiol. 2010;588:3031–3043. doi: 10.1113/jphysiol.2009.184705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Gruijl JR, Bazzigaluppi P, de Jeu MT, De Zeeuw CI. Climbing fiber burst size and olivary sub-threshold oscillations in a network setting. PLoS Comput Biol. 2012;8:e1002814. doi: 10.1371/journal.pcbi.1002814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Zeeuw CI, Chorev E, Devor A, Manor Y, van der Giessen RS, de Jeu MT, Hoogenraad CC, Bijman J, Ruigrok TJ, French P, Jaarsma D, Kistler WM, Meier C, Petrasch-Parwez E, Dermietzel R, Sohl G, Gueldenagel M, Willecke K, Yarom Y. Deformation of network connectivity in the inferior olive of connexin 36-deficient mice is compensated by morphological and electrophysiological changes at the single neuron level. J Neurosci. 2003;23:4700–4711. doi: 10.1523/JNEUROSCI.23-11-04700.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Zeeuw CI, Hertzberg EL, Mugnaini E. The dendritic lamellar body: a new neuronal organelle putatively associated with dendrodendritic gap junctions. J Neurosci. 1995;15:1587–1604. doi: 10.1523/JNEUROSCI.15-02-01587.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devor A, Yarom Y. Generation and propagation of subthreshold waves in a network of inferior olivary neurons. J Neurophysiol. 2002;87:3059–3069. doi: 10.1152/jn.2002.87.6.3059. [DOI] [PubMed] [Google Scholar]
- Drummond GB. Reporting ethical matters in the Journal of Physiology: standards and advice. J Physiol. 2009;587:713–719. doi: 10.1113/jphysiol.2008.167387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gellman R, Houk JC, Gibson AR. Somatosensory properties of the inferior olive of the cat. J Comp Neurol. 1983;215:228–243. doi: 10.1002/cne.902150210. [DOI] [PubMed] [Google Scholar]
- Leznik E, Llinas R. Role of gap junctions in synchronized neuronal oscillations in the inferior olive. J Neurophysiol. 2005;94:2447–2456. doi: 10.1152/jn.00353.2005. [DOI] [PubMed] [Google Scholar]
- Leznik E, Makarenko V, Llinas R. Electrotonically mediated oscillatory patterns in neuronal ensembles: an in vitro voltage-dependent dye-imaging study in the inferior olive. J Neurosci. 2002;22:2804–2815. doi: 10.1523/JNEUROSCI.22-07-02804.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llinas R, Yarom Y. Electrophysiology of mammalian inferior olivary neurones in vitro: different types of voltage-dependent ionic conductances. J Physiol. 1981a;315:549–567. doi: 10.1113/jphysiol.1981.sp013763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llinas R, Yarom Y. Properties and distribution of ionic conductances generating electroresponsiveness of mammalian inferior olivary neurones in vitro. J Physiol. 1981b;315:569–584. doi: 10.1113/jphysiol.1981.sp013764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathy A, Ho SS, Davie JT, Duguid IC, Clark BA, Hausser M. Encoding of oscillations by axonal bursts in inferior olive neurons. Neuron. 2009;62:388–399. doi: 10.1016/j.neuron.2009.03.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCurdy ML, Gibson AR, Houk JC. Spatial overlap of rubrospinal and corticospinal terminals with input to the inferior olive. Neuroimage. 1992;1:23–41. doi: 10.1016/1053-8119(92)90005-8. [DOI] [PubMed] [Google Scholar]
- McCurdy ML, Houk JC, Gibson AR. Organization of ascending pathways to the forelimb area of the dorsal accessory olive in the cat. J Comp Neurol. 1998;392:115–133. [PubMed] [Google Scholar]
- Molinari HH, Schultze KE, Strominger NL. Gracile, cuneate, and spinal trigeminal projections to inferior olive in rat and monkey. J Comp Neurol. 1996;375:467–480. doi: 10.1002/(SICI)1096-9861(19961118)375:3<467::AID-CNE9>3.0.CO;2-0. [DOI] [PubMed] [Google Scholar]
- Onodera S. Olivary projections from the mesodiencephalic structures in the cat studied by means of axonal transport of horseradish peroxidase and tritiated amino acids. J Comp Neurol. 1984;227:37–49. doi: 10.1002/cne.902270106. [DOI] [PubMed] [Google Scholar]
- Onodera S, Hicks TP. Patterns of transmitter labelling and connectivity of the cat’s nucleus of Darkschewitsch: a wheat germ agglutinin-horseradish peroxidase and immunocytochemical study at light and electron microscopical levels. J Comp Neurol. 1995;361:553–573. doi: 10.1002/cne.903610402. [DOI] [PubMed] [Google Scholar]
- Paarmann I, Frermann D, Keller BU, Hollmann M. Expression of 15 glutamate receptor subunits and various splice variants in tissue slices and single neurons of brainstem nuclei and potential functional implications. J Neurochem. 2000;74:1335–1345. doi: 10.1046/j.1471-4159.2000.0741335.x. [DOI] [PubMed] [Google Scholar]
- Ranjan A, Mallick BN. A modified method for consistent and reliable Golgi–Cox staining in significantly reduced time. Front Neurol. 2010;1:157. doi: 10.3389/fneur.2010.00157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rekling JC, Jensen KH, Jahnsen H. Spontaneous cluster activity in the inferior olivary nucleus in brainstem slices from postnatal mice. J Physiol. 2012;590:1547–1562. doi: 10.1113/jphysiol.2011.222570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruigrok TJ, De Zeeuw CI, van der Burg J, Voogd J. Intracellular labeling of neurons in the medial accessory olive of the cat: I. Physiology and light microscopy. J Comp Neurol. 1990;300:462–477. doi: 10.1002/cne.903000403. [DOI] [PubMed] [Google Scholar]
- Schweighofer N, Doya K, Kawato M. Electrophysiological properties of inferior olive neurons: a compartmental model. J Neurophysiol. 1999;82:804–817. doi: 10.1152/jn.1999.82.2.804. [DOI] [PubMed] [Google Scholar]
- Smith SS. Step cycle-related oscillatory properties of inferior olivary neurons recorded in ensembles. Neuroscience. 1998;82:69–81. doi: 10.1016/s0306-4522(97)00213-3. [DOI] [PubMed] [Google Scholar]
- Swenson RS, Castro AJ. The afferent connections of the inferior olivary complex in rats: an anterograde study using autoradiographic and axonal degeneration techniques. Neuroscience. 1983a;8:259–275. doi: 10.1016/0306-4522(83)90064-7. [DOI] [PubMed] [Google Scholar]
- Swenson RS, Castro AJ. The afferent connections of the inferior olivary complex in rats: a study using the retrograde transport of horseradish peroxidase. Am J Anat. 1983b;166:329–341. doi: 10.1002/aja.1001660307. [DOI] [PubMed] [Google Scholar]
- Urbano FJ, Simpson JI, Llinas RR. Somatomotor and oculomotor inferior olivary neurons have distinct electrophysiological phenotypes. Proc Natl Acad Sci U S A. 2006;103:16550–16555. doi: 10.1073/pnas.0607888103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wassef M, Chedotal A, Cholley B, Thomasset M, Heizmann CW, Sotelo C. Development of the olivocerebellar projection in the rat: I. Transient biochemical compartmentation of the inferior olive. J Comp Neurol. 1992;323:519–536. doi: 10.1002/cne.903230405. [DOI] [PubMed] [Google Scholar]
- Watanabe M, Mishina M, Inoue Y. Distinct distributions of five NMDA receptor channel subunit mRNAs in the brainstem. J Comp Neurol. 1994;343:520–531. doi: 10.1002/cne.903430403. [DOI] [PubMed] [Google Scholar]
- Welsh JP, Lang EJ, Suglhara I, Llinas R. Dynamic organization of motor control within the olivocerebellar system. Nature. 1995;374:453–457. doi: 10.1038/374453a0. [DOI] [PubMed] [Google Scholar]
- Zhang N, Walberg F, Laake JH, Meldrum BS, Ottersen OP. Aspartate-like and glutamate-like immunoreactivities in the inferior olive and climbing fibre system: a light microscopic and semiquantitative electron microscopic study in rat and baboon (Papio anubis. Neuroscience. 1990;38:61–80. doi: 10.1016/0306-4522(90)90374-d. [DOI] [PubMed] [Google Scholar]


