Abstract
We describe MUSCLE, a new computer program for creating multiple alignments of protein sequences. Elements of the algorithm include fast distance estimation using kmer counting, progressive alignment using a new profile function we call the log-expectation score, and refinement using tree-dependent restricted partitioning. The speed and accuracy of MUSCLE are compared with T-Coffee, MAFFT and CLUSTALW on four test sets of reference alignments: BAliBASE, SABmark, SMART and a new benchmark, PREFAB. MUSCLE achieves the highest, or joint highest, rank in accuracy on each of these sets. Without refinement, MUSCLE achieves average accuracy statistically indistinguishable from T-Coffee and MAFFT, and is the fastest of the tested methods for large numbers of sequences, aligning 5000 sequences of average length 350 in 7 min on a current desktop computer. The MUSCLE program, source code and PREFAB test data are freely available at http://www.drive5.com/muscle.
INTRODUCTION
Multiple alignments of protein sequences are important in many applications, including phylogenetic tree estimation, structure prediction and critical residue identification. The most natural formulation of the computational problem is to define a model of sequence evolution that assigns probabilities to elementary sequence edits and seeks a most probable directed graph in which edges represent edits and terminal nodes are the observed sequences. No tractable method for finding such a graph is known. A heuristic alternative is to seek a multiple alignment that optimizes the sum of pairs (SP) score, i.e. the sum of pairwise alignment scores. Optimizing the SP score is NP complete (1) and can be achieved by dynamic programming with time and space complexity O(LN) in the sequence length L and number of sequences N (2). A more popular strategy is the progressive method (3,4), which first estimates a tree and then constructs a pairwise alignment of the subtrees found at each internal node. A subtree is represented by its profile, a multiple alignment treated as a sequence by regarding each column as an alignable symbol. A variant on this strategy is used by T-Coffee (5), which aligns profiles by optimizing a score derived from local and global alignments of all pairs of input sequences. Misalignments by progressive methods are sometimes readily apparent (Fig. 1), motivating further processing (refinement). For a recent review of multiple alignment methods, see Notredame (6). Here we describe MUSCLE (multiple sequence comparison by log-expectation), a new computer program for multiple protein sequence alignment.
Figure 1.
Motifs misaligned by a progressive method. A set of 41 sequences containing SH2 domains (44) were aligned by the progressive method T-Coffee (above), and by MUSCLE (below). The N-terminal region of a subset of five sequences is shown. The highlighted columns (upper case) are conserved within this family but are misaligned by T-Coffee. It should be noted that T-Coffee aligns these motifs correctly when given these five sequences alone; the problem arises in the context of the other sequences. Complete alignments are available at http://www.drive5.com/muscle.
MUSCLE algorithm
Here we give an overview of the algorithm; a more detailed discussion is given in Edgar (submitted). Following guide tree construction, the fundamental step is pairwise profile alignment, which is used first for progressive alignment and then for refinement. This is similar to the strategies used by PRRP (7) and MAFFT (8).
Distance measures and guide tree estimation
MUSCLE uses two distance measures for a pair of sequences: a kmer distance (for an unaligned pair) and the Kimura distance (for an aligned pair). A kmer is a contiguous subsequence of length k, also known as a word or k-tuple. Related sequences tend to have more kmers in common than expected by chance. The kmer distance is derived from the fraction of kmers in common in a compressed alphabet, which we have previously shown to correlate well with fractional identity (9). This measure does not require an alignment, giving a significant speed advantage. Given an aligned pair of sequences, we compute the pairwise identity and convert to an additive distance estimate, applying the Kimura correction for multiple substitutions at a single site (10). Distance matrices are clustered using UPGMA (11), which we find to give slightly improved results over neighbor-joining (12), despite the expectation that neighbor-joining will give a more reliable estimate of the evolutionary tree. This can be explained by assuming that in progressive alignment, the best accuracy is obtained at each node by aligning the two profiles that have fewest differences, even if they are not evolutionary neighbors.
Profile alignment
In order to apply pairwise alignment to profiles, a scoring function must be defined on an aligned pair of profile positions, i.e. a pair of multiple alignment columns [see, for example Edgar and Sjolander (13)]. Let i and j be amino acid types, pi the background probability of i, pij the joint probability of i and j being aligned to each other, fxi the observed frequency of i in column x of the first profile, and f xG the observed frequency of gaps in that column at position x in the family (similarly for position y in the second profile). The estimated probability αxi of observing amino acid i in position x can be derived from fx, typically by adding heuristic pseudo-counts or by using Bayesian methods such as Dirichlet mixture priors (14). MUSCLE uses a new profile function we call the log-expectation (LE) score:
LExy = (1 – f xG) (1 – f yG) log Σ i Σ j f xi f yj pij/pi pj 1
This is a modified version of the log-average function (15):
LAxy = log Σ i Σ j αxi αyj pij/pi pj 2
MUSCLE uses probabilities pi and pij derived from the 240 PAM VTML matrix (16). Frequencies fi are normalized to sum to 1 when indels are present (otherwise the logarithm becomes increasingly negative with increasing numbers of gaps even when aligning conserved or similar residues). The factor (1 – fG) is the occupancy of a column, introduced to encourage more highly occupied columns to align. Position-specific gap penalties are used, employing heuristics similar to those found in MAFFT and LAGAN (17).
Algorithm
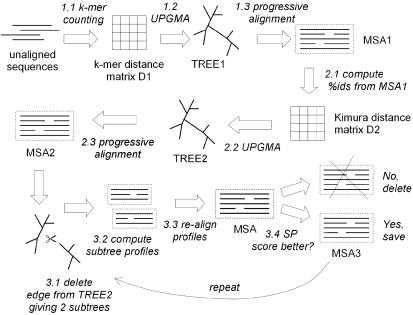
The high-level flow is depicted in Figure 2.
Figure 2.
This diagram summarizes the flow of the MUSCLE algorithm. There are three main stages: Stage 1 (draft progressive), Stage 2 (improved progressive) and Stage 3 (refinement). A multiple alignment is available at the completion of each stage, at which point the algorithm may terminate.
Stage 1, Draft progressive. The goal of the first stage is to produce a multiple alignment, emphasizing speed over accuracy.
1.1 The kmer distance is computed for each pair of input sequences, giving distance matrix D1.
1.2 Matrix D1 is clustered by UPGMA, producing binary tree TREE1.
1.3 A progressive alignment is constructed by following the branching order of TREE1. At each leaf, a profile is constructed from an input sequence. Nodes in the tree are visited in prefix order (children before their parent). At each internal node, a pairwise alignment is constructed of the two child profiles, giving a new profile which is assigned to that node. This produces a multiple alignment of all input sequences, MSA1, at the root.
Stage 2, Improved progressive. The main source of error in the draft progressive stage is the approximate kmer distance measure, which results in a suboptimal tree. MUSCLE therefore re-estimates the tree using the Kimura distance, which is more accurate but requires an alignment.
2.1 The Kimura distance for each pair of input sequences is computed from MSA1, giving distance matrix D2.
2.2 Matrix D2 is clustered by UPGMA, producing binary tree TREE2.
2.3 A progressive alignment is produced following TREE2 (similar to 1.3), producing multiple alignment MSA2. This is optimized by computing alignments only for subtrees whose branching orders changed relative to TREE1.
Stage 3, Refinement.
3.1 An edge is chosen from TREE2 (edges are visited in order of decreasing distance from the root).
3.2 TREE2 is divided into two subtrees by deleting the edge. The profile of the multiple alignment in each subtree is computed.
3.3 A new multiple alignment is produced by re-aligning the two profiles.
3.4 If the SP score is improved, the new alignment is kept, otherwise it is discarded.
Steps 3.1–3.4 are repeated until convergence or until a user-defined limit is reached. This is a variant of tree-dependent restricted partitioning (18).
Complete multiple alignments are available at steps 1.3, 2.3 and 3.4, at which points the algorithm may be terminated. We refer to the first two stages alone as MUSCLE-p, which produces MSA2. MUSCLE-p has time complexity O(N2L + NL2) and space complexity O(N2 + NL + L2). Refinement adds an O(N3L) term to the time complexity.
ASSESSMENT
We assessed the performance of MUSCLE on four sets of reference alignments: BAliBASE (19,20), SABmark (21), SMART (22–24) and a new benchmark, PREFAB. We compared these with four other methods: CLUSTALW (25), probably the most widely used program at the time of writing; T-Coffee, which has the best BAliBASE score reported to date; and two MAFFT scripts: FFTNS1, the fastest previously published method known to the author (in which diagonal finding by fast Fourier transform is enabled and a progressive alignment constructed), and NWNSI, the slowest but most accurate of the MAFFT methods (in which fast Fourier transform is disabled and refinement is enabled). Tested versions were MUSCLE 3.2, CLUSTALW 1.82, T-Coffee 1.37 and MAFFT 3.82. We also evaluated MUSCLE-p, in which the refinement stage is omitted. We also tried Align-m 1.0 (21), but found in many cases that the program either aborted or was impractically slow on the larger alignments found in SMART and PREFAB.
BAliBASE. We used version 2 of the BAliBASE benchmark, reference sets Ref 1–Ref 5. Other reference sets contain repeats, inversions and transmembrane helices, for which none of the tested algorithms is designed.
SABmark. We used version 1.63 of the SABmark reference alignments, which consists of two subsets: Superfamily and Twilight. All sequences have known structure. The Twilight set contains 1994 domains from the Astral database (26) with pairwise sequence similarity e-values ≤1, divided into 236 folds according to the SCOP classification (27). The Superfamily set contains sequences of pairwise identity ≤50%, divided into 462 SCOP superfamilies. Each pair of structures was aligned with two structural aligners: SOFI (28) and CE (29), producing a sequence alignment from the consensus in which only high-confidence regions are retained. Input sets range from three to 25 sequences, with an average of eight and an average sequence length of 179.
SMART. SMART contains multiple alignments refined by experts, focusing primarily on signaling domains. While structures were considered where known, sequence methods were also used to aid construction of the database, so SMART is not suitable as a definitive benchmark. However, conventional wisdom [e.g. Fischer et al. (30)] holds that machine-assisted experts can produce superior alignments to automated methods, so performance on this set is of interest for comparison. We used a version of SMART downloaded in July 2000, before the first version of MUSCLE was made available; eliminating the possibility that MUSCLE was used to aid construction. We discarded alignments of more than 100 sequences in order to make the test tractable for T-Coffee, leaving 267 alignments averaging 31 sequences of length 175.
PREFAB. The methods used to create databases such as BAliBASE and SMART are time-consuming and demand significant expertise, making a fully automated protocol desirable. Perhaps the most obvious approach is to generate sequence alignments from automated alignments of multiple structures, but this is fraught with difficulties; see for example Eidhammer et al. (31). With this in mind, we constructed a new test set, PREFAB (protein reference alignment benchmark) which exploits methodology (21,32,33), test data (13,34,35) and statistical methods (19) that have previously been applied to alignment accuracy assessment. The protocol is as follows. Two proteins are aligned by a structural method that does not incorporate sequence similarity. Each sequence is used to query a database, from which high-scoring hits are collected. The queries and their hits are combined and aligned by a multiple sequence method. Accuracy is assessed on the original pair alone, by comparison with their structural alignment. Three test sets selected from the FSSP database (36) were used as described in Sadreyev and Grishin (34) (data kindly provided by Ruslan Sadreyev), and Edgar and Sjolander (13,35), which we call SG, PP1 and PP2, respectively. These three sets vary mainly in their selection criteria. PP1 and PP2 contain pairs with sequence identity ≤30%. PP1 was designed to select pairs that have high structural similarity, requiring a z-score of ≥15 and a root mean square deviation (r.m.s.d.) of ≤2.5 Å. PP2 selected more diverged pairs with a z-score of ≥8 and ≤12, and an r.m.s.d. of ≤3.5 Å. SG contains pairs sampled from three ranges of sequence identity: 0–15, 15–30 and 30–97%, with no z-score or r.m.s.d. limits. We re-aligned each pair of structures using the CE aligner (29), and retained only those pairs for which FSSP and CE agreed on 50 or more positions. This was designed to minimize questionable and ambiguous structural alignments as done in SABmark and MaxBench (33). We used the full-chain sequence of each structure to make a PSI-BLAST (37,38) search of the NCBI non-redundant protein sequence database (39), keeping locally aligned regions of hits with e-values below 0.01. Hits were filtered to 80% maximum identity (including the query), and 24 selected at random. Finally, each pair of structures and their remaining hits were combined to make sets of ≤50 sequences. The limit of 50 was arbitrarily chosen to make the test tractable on a desktop computer for some of the more resource-intensive methods, in particular T-Coffee (which needed 10 CPU days, as noted in Table 4). The final set, PREFAB version 3.0, has 1932 alignments averaging 49 sequences of length 240, of which 178 positions in the structure pair are found in the consensus of FSSP and CE.
Table 4. Q scores and times on PREFAB.
| Method | All | 0–20% | 20–40% | 40–70% | 70–100% | CPU |
|---|---|---|---|---|---|---|
| MUSCLE | 0.645 | 0.473 | 0.813 | 0.937 | 0.980 | 1.7 × 104 |
| MUSCLE-p | 0.634 | 0.460 | 0.802 | 0.942 | 0.985 | 2.0 × 103 |
| T-Coffee | 0.615 | 0.464 | 0.795 | 0.935 | 0.976 | 1.0 × 106 |
| NWNSI | 0.615 | 0.448 | 0.772 | 0.930 | 0.939 | 1.4 × 104 |
| FFTNS1 | 0.591 | 0.423 | 0.756 | 0.931 | 0.938 | 1.0 × 103 |
| CLUSTALW | 0.563 | 0.382 | 0.732 | 0.916 | 0.930 | 3.3 × 104 |
The average Q score for each method over all PREFAB alignments (All), and the total CPU time in seconds are given. The remaining columns show average Q scores on subsets in which the structure pairs fall within the given pairwise identity ranges. Note that T-Coffee required 10 CPU days to complete the test, compared with <5 h for MUSCLE and ∼30 min for MUSCLE-p.
Accuracy measurement
We used three accuracy measures: Q, TC and APDB. Q (quality) is the number of correctly aligned residue pairs divided by the number of residue pairs in the reference alignment. This has previously been termed the developer score (32) and SPS (40). TC (total column score) is the number of correctly aligned columns divided by the number of columns in the reference alignment; this is Thompson et al.’s CS and is equivalent to Q in the case of two sequences (as in PREFAB). APDB (41) is derived from structures alone; no reference alignment of the sequences or structures is needed. For BAliBASE, we use Q and TC, measured only on core blocks as annotated in the database. For PREFAB, we use Q, including only those positions on which CE and FSSP agree, and also APDB. For SMART, we use Q and TC computed for all columns. For SABmark, we average the Q score over each pair of sequences. TC score is not applicable to SABmark as the reference alignments are pairwise.
Statistical analysis
Following Thompson et al. (19), statistical significance is measured by a Friedman rank test (42), which is more conservative than the Wilcoxon test that has also been used for alignment accuracy discrimination (5,7,8) as fewer assumptions are made about the population distribution. In particular, the Wilcoxon test assumes a symmetrical difference between two methods, but in practice we sometimes observe a significant skew. PREFAB and SABmark use automated structure alignment methods, which sometimes produce questionable results. Many low-quality regions are eliminated by taking the consensus between two independent aligners, but some may remain. In PREFAB, assessment of a multiple alignment is made on a single pair of sequences, which may be more or less accurately aligned than the average over all pairs. In SABmark, the upper bound on Q is less than 1 to a varying degree because the pairwise reference alignments may not be mutually consistent. These effects can be viewed as introducing noise into the experiment, and a single accuracy measurement may be subject to error. However, as the structural aligners do not use primary sequence, these errors are unbiased with respect to sequence methods. A difference in accuracy between two sequence alignment methods can therefore be established by the Friedman test, and the measured difference in average accuracy will be approximately correct when measured over a sufficient number of samples.
RESULTS
Quality scores and CPU times are summarized in Tables 1–234567; rankings and statistical significance on PREFAB and BAliBASE for all pairs of methods are given in Table 8. On all test sets and quality measures, MUSCLE achieves the highest ranking (in some cases jointly with other methods due to lack of statistical significance), and MUSCLE-p is statistically indistinguishable from T-Coffee and NWNSI. MUSCLE achieves the highest BAliBASE score reported to date, but the improvement of 1.6% in Q and 2.2% in TC over T-Coffee has low significance (P = 0.15). A similar result is found on SABmark, where MUSCLE achieves a 1.5% improvement over T-Coffee in Q with P = 0.14. The Q score on PREFAB is best able to distinguish between methods, giving statistically significant rankings to MUSCLE > MUSCLE-p, MUSCLE > T-Coffee, MUSCLE > NWNSI and MUSCLE-p > NWNSI. SMART also ranks MUSCLE highest. SMART cannot be considered definitive due to the use of sequence methods in construction of the database, although any bias from this source is likely to favor methods that were available to the SMART developers (i.e. to be against MUSCLE). The SMART results could be interpreted as suggesting that MUSCLE alignments are more consistent with refinements made by human experts. The APDB score appears to be relatively insensitive, showing no significant improvement due to the refinement stage of MUSCLE (similarly for MAFFT; not shown), and is not able to distinguish between the four highest scoring methods. We speculate that the scatter observed in the correlation between APDB and more conventional measures such as TC (40) injects sufficient noise to obscure meaningful differences in accuracy that can be resolved using Q. The low rank of Align-m on SABmark differs from results quoted by Van Walle et al. (21), who assessed pairwise alignments produced by an intermediate step in the algorithm, whereas we used the final multiple alignment.
Table 1. BAliBASE scores and times.
| Method | Q | TC | CPU |
|---|---|---|---|
| MUSCLE | 0.896 | 0.747 | 97 |
| MUSCLE-p | 0.883 | 0.727 | 52 |
| T-Coffee | 0.882 | 0.731 | 1500 |
| NWNSI | 0.881 | 0.722 | 170 |
| CLUSTALW | 0.860 | 0.690 | 170 |
| FFTNS1 | 0.844 | 0.646 | 16 |
Average Q and TC scores for each method on BAliBASE are shown, together with the total CPU time in seconds. Align-m aborted on two alignments; average scores on the remainder were Q = 0.852 and TC = 0.670, requiring 2202 s.
Table 2. BAliBASE Q scores on subsets.
| Method | Ref1 | Ref2 | Ref3 | Ref4 | Ref5 |
|---|---|---|---|---|---|
| MUSCLE | 0.887 | 0.935 | 0.823 | 0.876 | 0.968 |
| MUSCLE-p | 0.871 | 0.928 | 0.813 | 0.857 | 0.974 |
| T-Coffee | 0.866 | 0.934 | 0.787 | 0.917 | 0.957 |
| NWNSI | 0.867 | 0.923 | 0.787 | 0.904 | 0.963 |
| CLUSTALW | 0.861 | 0.932 | 0.751 | 0.823 | 0.859 |
| FFTNS1 | 0.838 | 0.908 | 0.708 | 0.793 | 0.947 |
The average Q score for each method on each BAliBASE subset is shown. Ref1 is the largest subset with 81 test sets, comprising almost 60% of the database. Other subsets are smaller. For example, Ref4 and Ref5 have 12 alignments each, and there are large variances in the individual scores from which the averages are computed. In our opinion, it is not possible to draw meaningful conclusions about the relative performance of different methods on these subsets.
Table 3. BAliBASE TC scores on subsets.
| Method | Ref1 | Ref2 | Ref3 | Ref4 | Ref5 |
|---|---|---|---|---|---|
| MUSCLE | 0.815 | 0.574 | 0.577 | 0.627 | 0.902 |
| MUSCLE-p | 0.795 | 0.558 | 0.550 | 0.598 | 0.891 |
| T-Coffee | 0.780 | 0.573 | 0.510 | 0.751 | 0.903 |
| NWNSI | 0.788 | 0.514 | 0.514 | 0.742 | 0.859 |
| CLUSTALW | 0.782 | 0.579 | 0.470 | 0.542 | 0.638 |
| FFTNS1 | 0.732 | 0.496 | 0.350 | 0.451 | 0.831 |
The average TC score for each method on each BAliBASE subset is shown.
Table 5. APDB scores on PREFAB.
| Method | APDB |
|---|---|
| NWNSI | 62.0 |
| MUSCLE | 61.9 |
| T-Coffee | 61.9 |
| MUSCLE-p | 61.4 |
| FFTNS1 | 60.8 |
| CLUSTALW | 59.1 |
The average APDB score of each method on the PREFAB reference alignments is given. There is no statistically significant difference between the four best methods. The top four are significantly better than FFTNS1 (MUSCLE-p > FFTNS1 with P = 0.009), and FFTNS1 is significantly better than CLUSTALW (P = 3 × 10–5).
Table 6. Q scores and CPU times on SABmark.
| Method | All | Superfamily | Twilight | CPU |
|---|---|---|---|---|
| MUSCLE | 0.430 | 0.523 | 0.249 | 1886 |
| T-Coffee | 0.424 | 0.519 | 0.237 | 5615 |
| MUSCLE-p | 0.416 | 0.511 | 0.230 | 304 |
| NWNSI | 0.410 | 0.506 | 0.223 | 629 |
| CLUSTALW | 0.404 | 0.498 | 0.220 | 206 |
| FFSNT1 | 0.373 | 0.467 | 0.190 | 75 |
| Align-m | 0.348 | 0.445 | 0.172 | 8902 |
All gives the average Q score over all SABmark alignments, Superfamily and Twilight are average Q scores on the two subsets. These are computed first by averaging Q for each pair in a single multiple alignment, then averaging over multiple alignments. This corrects for the lack of independence between pairs in a given multiple alignment. Align-m aborted in nine cases; quoted averages for this program are for completed alignments. Selected P-values are: MUSCLE > T-Coffee P = 0.14, MUSCLE > MUSCLE-p P = 4×10–5, MUSCLE > NWNSI P = 6 × 10–6, MUSCLE-p > NWNSI P = 0.03, T-Coffee > MUSCLE-p P = 0.1, T-Coffee > Align-m P < 10–10.
Table 7. Q and TC scores on SMART.
| Method | Q | TC | Significance |
|---|---|---|---|
| MUSCLE | 0.855 | 0.537 | 0.07 |
| NWNSI | 0.848 | 0.546 | 0.03 |
| MUSCLE-p | 0.836 | 0.505 | 0.54 |
| T-Coffee | 0.835 | 0.503 | 0.16 |
| CLUSTALW | 0.823 | 0.504 | 0.07 |
| FFTNS1 | 0.817 |
The average Q and TC accuracy scores over the 267 reference alignments in SMART that have no more than 100 sequences are given. The last column is the P-value of the difference between the method in a row and the method in the next row, measured on the Q score. The P-value for MUSCLE > T-Coffee is 0.0004 on Q and 0.01 on TC; the P-value for NSI > T-Coffee is 0.19 on Q and 0.0002 on TC. The difference between MUSCLE and NWNSI is only weakly significant on the Q score (P = 0.07) and is not significant on the TC score (P = 0.3).
Table 8. Ranks and statistical significance on BAliBASE and PREFAB.
| MUSCLE | MUSCLE-p | T-Coffee | NWNSI | FFTNS1 | CLUSTALW | |
|---|---|---|---|---|---|---|
| MUSCLE | +0.001 | (0.15) | + 0.005 | +2 × 10–6 | +0.0002 | |
| MUSCLE-p | –6 × 10–6 | (0.3) | (0.7) | +0.0002 | +0.02 | |
| T-Coffee | –0.0002 | (0.4) | (0.55) | +7 × 10–5 | +0.01 | |
| NWNSI | –<10–10 | –<10–10 | –10–7 | +0.0001 | (0.06) | |
| FFTNS1 | –<10–10 | –<10–10 | –<10–10 | –<10–10 | –0.04 | |
| CLUSTALW | –<10–10 | –<10–10 | –<10–10 | –<10–10 | –0.008 |
Each entry in the table contains the P-value assigned by a Friedman rank test to the difference between a pair of methods. The upper-right corner of the matrix is obtained from Q scores on BAliBASE, the lower-left corner from Q scores on PREFAB. If the method to the left is ranked higher than the method above, the P-value is preceded by +. If the method to the left is ranked lower, the P-value is preceded by –. If the P-value is >0.05, the difference is not considered significant and is shown in parentheses. So, for example, MUSCLE ranks higher than T-Coffee on PREFAB with P = 0.0002 and MUSCLE-p higher than CLUSTALW on BAliBASE with P = 0.02.
Resource requirements for large numbers of sequences
To investigate resource requirements for increasing number of sequences N, we used the Rose sequence generator (43) (complete results not shown). In agreement with other studies, [e.g. Katoh et al. (8)], we found that T-Coffee was unable to align more than approximately 102 sequences of typical length on a current desktop computer. CLUSTALW was able to align a few hundred sequences, with a practical limit around N = 103 where CPU time begins to scale approximately as N4. The largest set had 5000 sequences of average length 350. MUSCLE-p completed this test in 7 min, compared with 10 min for FFTNS1; we estimate that CLUSTALW would need approximately 1 year.
DISCUSSION
We have described a new multiple sequence alignment algorithm, MUSCLE, and presented evidence that it creates alignments with average accuracy comparable with or superior to the best current methods. It should be emphasized that performance differences between the better methods emerge only when averaged over a large number of test cases, even when alignments are considered trustworthy. For example, on BAliBASE, the lowest scoring of the tested methods (FFTNS1) achieved a higher Q than the highest scoring (MUSCLE) in 21 out of 141 alignments and tied in 19 more; compared with T-Coffee, MUSCLE scored higher or tied in 95 cases, but lower in 24. This suggests the use of multiple algorithms and careful inspection of the results. MUSCLE is comparable in speed with CLUSTALW, completing a test set (PREFAB) averaging 49 sequences of length 240 in about half the time. The progressive method MUSCLE-p, which has average accuracy statistically indistinguishable from T-Coffee and the most accurate MAFFT script, is the fastest algorithm known to the author for large numbers of sequences, able to align 5000 sequences of average length 350 in 7 min on a current desktop computer. The MUSCLE software, source code and test data are freely available at: http://www.drive5.com/muscle.
REFERENCES
- 1.Wang L. and Jiang,T. (1994) On the complexity of multiple sequence alignment. J. Comput. Biol., 1, 337–348. [DOI] [PubMed] [Google Scholar]
- 2.Waterman M.S., Smith,T.F. and Beyer,W.A. (1976) Some biological sequence metrics. Adv. Math., 20, 367–387. [Google Scholar]
- 3.Hogeweg P. and Hesper,B. (1984) The alignment of sets of sequences and the construction of phyletic trees: an integrated method. J. Mol. Evol., 20, 175–186. [DOI] [PubMed] [Google Scholar]
- 4.Feng D.F. and Doolittle,R.F. (1987) Progressive sequence alignment as a prerequisite to correct phylogenetic trees. J. Mol. Evol., 25, 351–360. [DOI] [PubMed] [Google Scholar]
- 5.Notredame C., Higgins,D.G. and Heringa,J. (2000) T-Coffee: a novel method for fast and accurate multiple sequence alignment. J. Mol. Biol., 302, 205–217. [DOI] [PubMed] [Google Scholar]
- 6.Notredame C. (2002) Recent progress in multiple sequence alignment: a survey. Pharmacogenomics, 3, 131–144. [DOI] [PubMed] [Google Scholar]
- 7.Gotoh O. (1996) Significant improvement in accuracy of multiple protein sequence alignments by iterative refinement as assessed by reference to structural alignments. J. Mol. Biol., 264, 823–838. [DOI] [PubMed] [Google Scholar]
- 8.Katoh K., Misawa,K., Kuma,K. and Miyata,T. (2002) MAFFT: a novel method for rapid multiple sequence alignment based on fast Fourier transform. Nucleic Acids Res., 30, 3059–3066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Edgar R.C. (2004) Local homology recognition and distance measures in linear time using compressed amino acid alphabets. Nucleic Acids Res., 32, 380–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kimura M. (1983) The Neutral Theory of Molecular Evolution. Cambridge University Press. [Google Scholar]
- 11.Sneath P.H.A. and Sokal,R.R. (1973) Numerical Taxonomy. Freeman, San Francisco. [Google Scholar]
- 12.Saitou N. and Nei,M. (1987) The neighbor-joining method: a new method for reconstructing phylogenetic trees. Mol. Biol. Evol., 4, 406–425. [DOI] [PubMed] [Google Scholar]
- 13.Edgar R.C. and Sjolander,K. (2004) A comparison of scoring functions for protein sequence profile alignment. Bioinformatics, DOI: 10.1093/bioinformatics/bth090. [DOI] [PubMed] [Google Scholar]
- 14.Sjolander K., Karplus,K., Brown,M., Hughey,R., Krogh,A., Mian,I.S. and Haussler,D. (1996) Dirichlet mixtures: a method for improved detection of weak but significant protein sequence homology. CABIOS, 12, 327–345. [DOI] [PubMed] [Google Scholar]
- 15.von Ohsen N. and Zimmer,R. (2001) Improving profile–profile alignment via log average scoring. In Gascuel,O. and Moret,B.M.E. (eds), Algorithms in Bioinformatics, First International Workshop, WABI 2001. Springer-Verlag, Berlin, Germany, pp. 11–26. [Google Scholar]
- 16.Muller T., Spang,R. and Vingron,M. (2002) Estimating amino acid substitution models: a comparison of Dayhoff’s estimator, the resolvent approach and a maximum likelihood method. Mol. Biol. Evol., 19, 8–13. [DOI] [PubMed] [Google Scholar]
- 17.Brudno M., Do,C.B., Cooper,G.M., Kim,M.F., Davydov,E., Green,E.D., Sidow,A. and Batzoglou,S. (2003) LAGAN and Multi-LAGAN: efficient tools for large-scale multiple alignment of genomic DNA. Genome Res., 13, 721–731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hirosawa M., Totoki,Y., Hoshida,M. and Ishikawa,M. (1995) Comprehensive study on iterative algorithms of multiple sequence alignment. CABIOS, 11, 13–18. [DOI] [PubMed] [Google Scholar]
- 19.Thompson J.D., Plewniak,F. and Poch,O. (1999a) BAliBASE: a benchmark alignment database for the evaluation of multiple alignment programs. Bioinformatics, 15, 87–88. [DOI] [PubMed] [Google Scholar]
- 20.Bahr A., Thompson,J.D., Thierry,J.C. and Poch,O. (2001) BAliBASE (Benchmark Alignment dataBASE): enhancements for repeats, transmembrane sequences and circular permutations. Nucleic Acids Res., 29, 323–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Van Walle I., Lasters,I. and Wyns,L. (2004) Align-m—a new algorithm for multiple alignment of highly divergent sequences. Bioinformatics, DOI: 10.1093/bioinformatics/bth116. [DOI] [PubMed] [Google Scholar]
- 22.Schultz J., Milpetz,F., Bork,P. and Ponting,C.P. (1998) SMART, a simple modular architecture research tool: identification of signaling domains. Proc. Natl Acad. Sci. USA, 95, 5857–5864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Schultz J., Copley,R.R., Doerks,T., Ponting,C.P. and Bork,P. (2000) SMART: a web-based tool for the study of genetically mobile domains. Nucleic Acids Res., 28, 231–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ponting C.P., Schultz,J., Milpetz,F. and Bork,P. (1999) SMART: identification and annotation of domains from signalling and extracellular protein sequences. Nucleic Acids Res., 27, 229–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Thompson J.D., Higgins,D.G. and Gibson,T.J. (1994) CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res., 22, 4673–4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Brenner S.E., Koehl,P. and Levitt,M. (2000) The ASTRAL compendium for protein structure and sequence analysis. Nucleic Acids Res., 28, 254–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Murzin A.G., Brenner,S.E., Hubbard,T. and Chothia,C. (1995) SCOP: a structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol., 247, 536–540. [DOI] [PubMed] [Google Scholar]
- 28.Boutonnet N.S., Rooman,M.J., Ochagavia,M.E., Richelle,J. and Wodak,S.J. (1995) Optimal protein structure alignments by multiple linkage clustering: application to distantly related proteins. Protein Eng., 8, 647–662. [DOI] [PubMed] [Google Scholar]
- 29.Shindyalov I.N. and Bourne,P.E. (1998) Protein structure alignment by incremental combinatorial extension (CE) of the optimal path. Protein Eng., 11, 739–747. [DOI] [PubMed] [Google Scholar]
- 30.Fischer D., Barret,C., Bryson,K., Elofsson,A., Godzik,A., Jones,D., Karplus,K.J., Kelley,L.A., MacCallum,R.M., Pawowski,K., Rost,B., Rychlewski,L. and Sternberg,M. (1999) CAFASP-1: critical assessment of fully automated structure prediction methods. Proteins, Suppl. 3, 209–217. [DOI] [PubMed] [Google Scholar]
- 31.Eidhammer I., Jonassen,I. and Taylor,W.R. (2000) Structure comparison and structure patterns. J. Comput. Biol., 7, 685–716. [DOI] [PubMed] [Google Scholar]
- 32.Sauder J.M., Arthur,J.W. and Dunbrack,R.L.,Jr (2000) Large-scale comparison of protein sequence alignment algorithms with structure alignments. Proteins, 40, 6–22. [DOI] [PubMed] [Google Scholar]
- 33.Leplae R. and Hubbard,T.J. (2002) MaxBench: evaluation of sequence and structure comparison methods. Bioinformatics, 18, 494–495. [DOI] [PubMed] [Google Scholar]
- 34.Sadreyev R. and Grishin,N. (2003) COMPASS: a tool for comparison of multiple protein alignments with assessment of statistical significance. J. Mol. Biol., 326, 317–336. [DOI] [PubMed] [Google Scholar]
- 35.Edgar R.C. and Sjolander,K. (2004) COACH: profile-profile alignment of protein families using hidden Markov models. Bioinformatics, DOI: 10.1093/bioinformatics/bth091. [DOI] [PubMed] [Google Scholar]
- 36.Holm L. and Sander,C. (1998) Touring protein fold space with Dali/FSSP. Nucleic Acids Res., 26, 316–319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Altschul S.F., Madden,T.L., Schaffer,A.A., Zhang,J., Zhang,Z., Miller,W. and Lipman,D.J. (1997) Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res., 25, 3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Schaffer A.A., Aravind,L., Madden,T.L., Shavirin,S., Spouge,J.L., Wolf,Y.I., Koonin,E.V. and Altschul,S.F. (2001) Improving the accuracy of PSI-BLAST protein database searches with composition-based statistics and other refinements. Nucleic Acids Res., 29, 2994–3005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pruitt K.D., Tatusova,T. and Maglott,D.R. (2003) NCBI Reference Sequence project: update and current status. Nucleic Acids Res., 31, 34–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Thompson J.D., Plewniak,F. and Poch,O. (1999b) A comprehensive comparison of multiple sequence alignment programs. Nucleic Acids Res., 27, 2682–2690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.O’Sullivan O., Zehnder,M., Higgins,D., Bucher,P., Grosdidier,A. and Notredame,C. (2003) APDB: a novel measure for benchmarking sequence alignment methods without reference alignments. Bioinformatics, 19 Suppl. 1, I215–I221. [DOI] [PubMed] [Google Scholar]
- 42.Friedman M. (1937) The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc., 32, 675–701. [Google Scholar]
- 43.Stoye J., Evers,D. and Meyer,F. (1998) Rose: generating sequence families. Bioinformatics, 14, 157–163. [DOI] [PubMed] [Google Scholar]
- 44.Sjolander K. (1998) Phylogenetic inference in protein superfamilies: analysis of SH2 domains. Proc. Int. Conf. Intell. Syst. Mol. Biol., 6, 165–174. [PubMed] [Google Scholar]