Functional Linear Model with Zero-value Coefficient Function at Sub-regions

Abstract

We propose a shrinkage method to estimate the coefficient function in a functional linear regression model when the value of the coefficient function is zero within certain sub-regions. Besides identifying the null region in which the coefficient function is zero, we also aim to perform estimation and inferences for the nonparametrically estimated coefficient function without over-shrinking the values. Our proposal consists of two stages. In stage one, the Dantzig selector is employed to provide initial location of the null region. In stage two, we propose a group SCAD approach to refine the estimated location of the null region and to provide the estimation and inference procedures for the coefficient function. Our considerations have certain advantages in this functional setup. One goal is to reduce the number of parameters employed in the model. With a one-stage procedure, it is needed to use a large number of knots in order to precisely identify the zero-coefficient region; however, the variation and estimation difficulties increase with the number of parameters. Owing to the additional refinement stage, we avoid this necessity and our estimator achieves superior numerical performance in practice. We show that our estimator enjoys the Oracle property; it identifies the null region with probability tending to 1, and it achieves the same asymptotic normality for the estimated coefficient function on the non-null region as the functional linear model estimator when the non-null region is known. Numerically, our refined estimator overcomes the shortcomings of the initial Dantzig estimator which tends to under-estimate the absolute scale of non-zero coefficients. The performance of the proposed method is illustrated in simulation studies. We apply the method in an analysis of data collected by the Johns Hopkins Precursors Study, where the primary interests are in estimating the strength of association between body mass index in midlife and the quality of life in physical functioning at old age, and in identifying the effective age ranges where such associations exist.

1. Introduction

We study the functional linear regression (FLR) model

$$Y_i=\mu +\sum _{d=1}^D{\int }_0^T{X}_{id}(t){\beta }_d(t)dt+e_i,$$ (1.1)

where Y_i denotes the ith response, X_id(t) are realizations of random processes X_d(t), β_d(t) are the corresponding smooth coefficient functions on [0, T], and e_i ~ N(0, σ²) are random errors independent of X_id(t), i = 1, 2, …, n. The response Y reflects the weighted cumulative effects of functional predictors X_d(t), and the coefficient functions β_d(t) represent the corresponding weights. In practice, it is often of interest to know which areas of X_d(t) contribute to the value of Y and in what magnitude. That is, we are interested in learning the null region in which β_d(t) = 0, and in estimating the values of β_d(t) when they are non-zero.

Regression models with functional predictors have application in functional data analysis (FDA), and lately in longitudinal data analysis (LDA) when the longitudinal covariate measurements are collected intensively. Ramsay and Silverman (2005) and Ferraty and Vieu (2006) reviewed theoretical and methodological developments and gave many examples. A non-exhaustive list of recent works includes the followings. Estimation of β_d(t) with a spline approach was proposed by Cardot, Ferraty, and Sarda (2003). Crambes, Kneip, and Sarda (2009) proposed a smoothing spline estimator of β_d(t) with a new penalty term to ensure existence of the estimator, and studied its asymptotic behavior. Fan and Zhang (2000) studied the FLR problem with a functional response. Cai and Hall (2006) investigated prediction issues in FLR. With an additional link function in model (1.1), Müller and Stadtmüller (2005) studied the generalized functional linear model. Yao, Müller, and Wang (2005) extended the scope of the problem to cover longitudinal data. James, Wang, and Zhu (2009) emphasized the importance of the interpretability of β_d(t) and proposed to use a version of the Dantzig selector (Candes and Tao (2007)) for this purpose. They equated the problem of identifying zero-value regions of the corresponding order derivative of β_d(t) to that of variable selection in a multiple linear regression setting; however, to precisely identify the null region of β_d(t), the Dantzig selector needs to use a large number of knots, and the quality of the estimated β_d(t) deteriorates on the non-null region with the increasing number of knots. It is known that with the number of parameters increasing and increasing with sample size, the variation of estimation increases. We illustrate this phenomenon in our specific setting in Section 4. Further, the asymptotic distribution, a property tends to be desired by a functional data analysis approach, is not reported for their estimator. We derived the asymptotic distribution for our proposed estimator in Section 3.

In this paper, we propose a two-stage estimator to simultaneously identify the null region of β_d(t) and estimate β_d(t) on the non-null region. The goal behind this approach is to avoid having a large number of parameters in either stage and still maintain a high quality of estimation performance. We roughly identify the null region at stage one, and adaptively regularize the estimate of β_d(t) on the null and non-null regions at stage two, applying different group penalties. At stage one, an initial estimator identifies and preferably over-estimates the null region; the desired precision is reached at the second stage. When the number of parameters is large, a direct implementation of the Dantzig selector gives poor estimation of the coefficient function in the non-null region. Our two-stage procedure simplifies the problem, naturally reduces over-shrinking of the coefficient functions in the non-null region, and achieves superior numerical performance.

We structure the paper as follows. In Section 2, we present our proposed method as a B-spline approximation coupled with shrinkage, which takes the advantage of the local property of B-spline basis functions. In Section 3, we show that the proposed estimator enjoys the Oracle property and we give its asymptotic distribution. Simulation studies are reported in Section 4. In Section 5, we apply the proposed method to data from the Johns Hopkins Precursors Study to investigate the effect of body mass index at midlife on a quality of life index for physical functioning at old age. Concluding remarks are given in Section 6. Assumptions for the theoretical properties and sketch of the proofs are provided in the Appendix. The exact algorithms to implement the proposed method, detailed proofs, and additional numerical results are reported in a supplementary document.

2. Estimation of Coefficient Functions and Their Null Regions

To simplify the notation and presentation, we take D = 1, suppress the subscript d in model (1.1), and write

$$Y_i=\mu +{\int }_0^T{X}_i(t)\beta (t)dt+e_i.$$ (2.1)

We assume e_i ~ N (0, σ²) and μ = 0. Without loss of generality, we let σ = 1. Generalization of the method to the cases D > 1 is discussed in Section 2.3. The asymptotic properties under (2.1) can be extended to model (1.1).

As in James, Wang, and Zhu (2009), we assume that the processes X_i(t) are known while, in practice, X_i(t) are usually not completely observable. Instead, the observations (Y_i, t_ij, X_ij) are available for i = 1, …, n and j = 1, …, m_i, where X_ij = X_i(t_ij). In practice, X_i(t) are measured at discrete and perhaps irregular time points and it is common to include a pre-smoothing step. See Ramsay and Silverman (2005) for insight and illustrations, and Hall and Van Keilegom (2008) for theoretical considerations. We report the effects of pre-smoothing in the numerical studies.

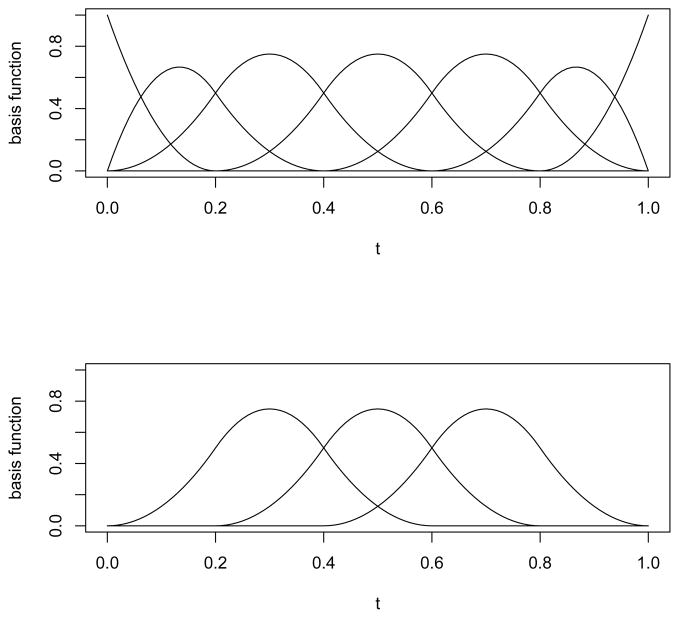
For estimating the coefficient function, β(t), as well as identifying its null region, denoted by , we use B-splines. Given k_0,n + 1 evenly-spaced knots, 0 = τ₀ < τ₁ < τ₂ < … < τ_k0,n−1< τ_k0,n = T, let I_j = [τ_j−1, τ_j] for j = 1, …, k_0,n. Associated with this set of knots, there are (k_0,n + h) B-spline basis functions, B₀(t) = (B_0,1(t), …, B_0,k0,n+h(t))T, each of which is a piecewise polynomial of degree h with support on at most h+1 subintervals I_j. The upper panel of Figure 1 shows the seven basis functions with h = 2 and knots {0.0, 0.2, 0.4, 0.6, 0.8, 1.0}. Given the sample size n and the k_0,n + 1 knots, the coefficient function can be expressed as

Figure 1.

Local support of B-spline basis function.

$$\beta (t)={\mathit{B}}_0^T(t){\mathit{b}}_0+e_0(t),$$ (2.2)

where b₀ = (b_0,1, …, b_0,k0,n+h)^T is the B-spline approximation coefficient, e₀(t) is an approximation error that is uniformly bounded on [0, T] with the bound going to 0 as k_0,n goes to infinity. For details on B-spline approximation, see Schumaker (1981). Using the B-spline approximation for β(t) in (2.2), (2.1) can be re-written as

$$Y_i={\mathit{z}}_{0,i}^T{\mathit{b}}_0+{\epsilon }_{0,i},\text{or}\mathit{Y}={\mathit{Z}}_0{\mathit{b}}_0+{\mathit{\epsilon }}_0,$$ (2.3)

where z_0,i is a (k_0,n + h) × 1 vector with the jth element ${\int }_0^T{X}_i(t)B_{0,j}(t)dt,{\epsilon }_{0,i}=e_i+{\int }_0^T{X}_i(t)e_0(t)dt$, and Y and Z₀ are, respectively, the n × 1 vector and n × (k_0,n + h) matrix that contain Y_i and z_0,i as entries.

Note that the choices of B₀(t), I_j, and consequently, the values of b₀, e₀(t), ε_0,i and z_0,i, vary with the sample size n. To simplify notation, the subscript n is suppressed; we use the subscript 0 to indicate the association with the initial stage.

2.1. Initial estimate of the null region

It is convenient to let the end points of fall on the end points of certain subintervals I_j. With the initial knots ${\{{\tau }_j\}}_{j=0}^{k_{0,n}}$, assume each I_j is entirely contained either in or in 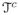, the complement of . Having no prior information on the location of , we use a moderate number of evenly-spaced internal knots on [0, T]. The initial location of can be roughly established through I_j and an estimate of b₀ in (2.3).

We use the Dantzig selector to estimate b₀ at this stage, argmin_b||b||_l1 subject to $\mid {\mathit{Z}}_{0,k}^T(\mathit{Y}-{\mathit{Z}}_0\mathit{b})\mid \le {\lambda }_D$, with ${\mathit{Z}}_{0,k}^T$ being the kth column of Z₀, ${\lambda }_D=\sqrt{2\mathit{log}(k_{0,n}+h)}$, and ||b||_l1 denoting the L₁ norm of b. We denote this initial estimate of b₀ by b̃₀. The conditions of equivalence between the Dantzig selector and LASSO have been reported in James, Radchenko, and Lv (2009), Bickel, Ritov, and Tsybakov (2009), and references therein. It is not essential to have high precision during this stage, so other regularization estimators such as LASSO or SCAD can be used here, even though the simulation outcomes from James, Wang, and Zhu (2009) imply numerical advantages of the Dantzig selector over LASSO. For further details on the Dantzig selector, see Candes and Tao (2007).

With the B-spline basis supported on at most h + 1 subintervals, the value of ${\mathit{B}}_0^T(t){\mathit{b}}_0$ on a single subinterval I_j is determined by h +1 coefficients in b₀. For example, in Figure 1, the estimated β(t) for any t ∈ [0.4, 0.6] depends only on the coefficients of the three basis functions in the lower panel. When the h + 1 coefficients associated with I_j are all 0, the subinterval I_j is contained in the null region of ${\mathit{B}}_0^T(t){\mathit{b}}_0$; otherwise, it is in the non-null region. In practice, even if I_j ⊂ , its associated h + 1 coefficients in b₀ might not all be 0, but we only need a rough estimate of null region at this stage. We simply use a small threshold value at the initial stage to identify the subintervals within the null region of β(t). Thus, if the absolute values of all h + 1 coefficients are smaller than d_n, we classify the corresponding I_j as part of . The union of all identified subintervals is taken as the initial estimate of , denoted by . 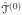We let the threshold value d_n go to 0 as n goes to infinity. The rates of d_n and k_0,n are given and discussed in Section 3, and their numerical determination is in Section 4.

2.2. Null region refinement and function estimation

The second stage of our estimator refines the estimated location of and the estimate of β(t) on 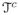. We develop a grouped smoothly-clipped absolute deviation (SCAD) method and a boundary grid-search algorithm at the second stage to refine the null region and to achieve the estimate of β(t) on 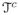. The asymptotic distribution of the estimated β(t) can be naturally established. Our estimator overcomes the concerns of large numbers of parameters, maintains the sparse property, readily adopts the existing efficient computation algorithm, and achieves desired numerical and theoretical qualities.

In Stage 1, k_0,n+1 evenly-spaced internal knots are placed in [0, T] to identify the initial estimate of ; in Stage 2, we use a grid-search based algorithm to find the refined null region within 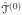by examining a sequence of working null regions 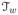⊆ 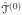. We let the search algorithm and the penalty determination in grouped SCAD share the same objective function so that we can conduct the evaluation jointly. A practical algorithm of specifying a sequence of 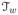’s is given in the supplementary document.

Having 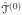, we remove all initial knots within 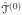, and place k_1,n +1 evenly-spaced knots on 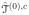, with k_1,n < k_0,n in general. With the grid size in the boundary search procedure not related to k_1,n, the determination of grid size is a numerical decision. The smaller grid size gives more precise boundary but can lead to a computationally more demanding task. In our simulation studies, we used a grid size of 0.02T, where T is the range of t.

Using the new set of knots corresponding to each 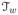, we generate a new set of B-spline basis functions ${\mathit{B}}_1^w(t)$ and the corresponding new variables, ${\mathit{z}}_{1,i}^w$ following the same procedure described below (2.3). Moreover, (2.1) can be rewritten as

$$Y_i={\mathit{z}}_{1,i}^{wT}{\mathit{b}}_1^w+{\epsilon }_{1,i}^w,\text{or}\mathit{Y}={\mathit{Z}}_1^w{\mathit{b}}_1^w+{\mathit{\epsilon }}_1^w,$$ (2.4)

where ${\mathit{b}}_1^w,{\mathit{z}}_{1,i}^w$ and ${\mathit{Z}}_1^w$ are equivalently defined as b₀, z_0,i and Z₀, respectively, in (2.3), and the ith entry of ${\mathit{\epsilon }}_1^w$ is ${\epsilon }_{1,i}^w=e_i+{\int }_0^T{X}_i(t)e_1^w(t)dt$, with the approximation error $e_1^w(t)=\beta (t)-{\mathit{B}}_1^{wT}(t){\mathit{b}}_1^w$. As in (2.3), ${\mathit{Z}}_1^w,{\mathit{b}}_1^w,{\mathit{B}}_1^w(t)$, and ${\mathit{\epsilon }}_1^w$ vary with the sample size n. The subscript n is suppressed to simplify the notation, and the subscript 1 indicates the association with the refinement stage.

To estimate ${\mathit{b}}_1^w$, we propose a group penalized least squares method. According to 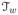, the coefficients in b are divided into groups b_N,w (null) and b_S,w (signal). Specifically, if a subinterval is part of 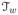, then all coefficients b_i that are associated with this subinterval are put into b_N,w; the group b_S,w contains the remainder.

Different penalty functions are available in the literature, including the L₂ penalty of ridge regression, the L₁ penalty of LASSO regression (Tibshirani (1996)), and the SCAD penalty function (Fan and Li (2001)). We use the SCAD penalty function with coefficients in the two groups b_N,w and b_S,w penalized separately. Using the L₂ penalty does not help us to identify , and Zou (2006) pointed out that the LASSO estimator is not consistent, which prevented us from considering the group LASSO (Yuan and Lin (2006)). That SCAD penalizes less on coefficients with large absolute values allows the non-zero coefficient functions to be better estimated. With the division of b into b_N,w and b_S,w, ${\mathit{b}}_1^w$ is estimated as the minimizer of the objective function

$$\sum _{i=1}^n{(Y_i-{\mathit{z}}_{1,i}^w\mathit{b})}^2+n\{p_{\lambda }({\left|\right|{\mathit{b}}_{N,w}\left|\right|}_{l_1})+p_{\lambda }({\left|\right|{\mathit{b}}_{S,w}\left|\right|}_{l_1})\},$$

where p_λ(·) is the SCAD penalty of Fan and Li (2001), defined through its derivative $p_{\lambda }^{\prime }(\mid \theta \mid )=\lambda \{I(\mid \theta \mid \le \lambda )+\frac{(a\lambda -\mid \theta \mid )+}{(a-1)\lambda }I(\mid \theta \mid >\lambda )\}$; a is usually taken as 3.7, and λ is a tuning parameter selected by the criterion C( 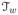, λ), which can be the generalized cross validation criterion (GCV), Akaike’s information criterion (AIC), the Bayesian information criterion (BIC; Schwarz), or the residual information criterion (RIC), as specified in the supplementary document. By calculating a criterion for each working 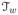, we simultaneously select the 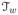and λ, that minimize it. Penalizing the coefficients, b, in groups helps to shrink the coefficients in b_N,w to zero, simultaneously.

Given an initial value of ${\mathit{b}}_1^w$, the local quadratic approximation (LQA) is used in the algorithm of Fan and Li (2001) to approximate the penalty function. However, as pointed out in Zou and Li (2008), the LQA estimator does not provide a sparse representation. Instead, Zou and Li (2008) proposed a one-step local linear approximation (LLA) and converted the SCAD problem to a LASSO regression that utilized the LARS algorithm of Efron et al. (2004) to get the sparse estimate. We use the LLA for the group penalty in our method for the same reason.

Let b̃₁ be the initial estimate, which can be the ordinary least squares estimator, and b̃_1N,w and b̃_1S,w be the coefficients inside and outside the working null region 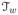, respectively. We approximate the group penalty p_λ(||b_N,w||_l1) by

$$p_{\lambda }({\left|\right|{\mathit{b}}_{N,w}\left|\right|}_{l_1})\approx p_{\lambda }({\left|\right|{\stackrel{\sim }{\mathit{b}}}_{1N,w}\left|\right|}_{l_1})+p_{\lambda }^{\prime }({\left|\right|{\stackrel{\sim }{\mathit{b}}}_{1N,w}\left|\right|}_{l_1})\{{\left|\right|{\mathit{b}}_{N,w}\left|\right|}_{l_1}-{\left|\right|{\stackrel{\sim }{\mathit{b}}}_{1N,w}\left|\right|}_{l_1}\}.$$

The penalty p_λ(||b_S,w||l1) is approximated equivalently. Using these approximations, we estimate ${\mathit{b}}_1^w$ by minimizing the objective function

$$Q_n({\mathcal{J}}_w,\lambda ,\mathit{b})=\sum _{i=1}^n{(Y_i-{\mathit{z}}_{1,i}^w\mathit{b})}^2+n\left\{p_{\lambda }^{\prime }({{\left|\right|{\stackrel{\sim }{\mathit{b}}}_{1N,w}\left|\right|}_l}_1){\left|\right|{\mathit{b}}_{N,w}\left|\right|}_{l_1}+p_{\lambda }^{\prime }({{\left|\right|{\stackrel{\sim }{\mathit{b}}}_{1S,w}\left|\right|}_l}_1){\left|\right|{\mathit{b}}_{S,w}\left|\right|}_{l_1}\right\}.$$ (2.5)

With ||b_N,l||lwand ||b_S,l||_lw as the L₁ norms of b_N,w and b_S,w and $p_{\lambda }^{\prime }({\left|\right|{\stackrel{\sim }{\mathit{b}}}_{1N,w}\left|\right|}_{l_1})$ and $p_{\lambda }^{\prime }({\left|\right|{\stackrel{\sim }{\mathit{b}}}_{1S,w}\left|\right|}_{l_1})$ as weights, the task of minimizing Qn(b) can be carried out using the adaptive LASSO of Zou (2006) and the efficient LARS algorithm of Efron et al. (2004). By the LLA, the coefficients within the same group are penalized with the weights according to their group memberships. When $p_{\lambda }^{\prime }({\left|\right|{\stackrel{\sim }{\mathit{b}}}_{1S,w}\left|\right|}_{l_1})\to 0$ as λ → 0, the coefficients in b_S,w are barely penalized. As a result, the estimation bias of β(t) on ${\mathcal{J}}_w^c$, induced by the shrinkage penalty, can be greatly reduced.

For a fixed dimension of the regression parameters, we note that Wang, Chen, and Li (2007) developed an alternative group SCAD estimator using the L₂-norm and the local quadratic approximation. Their estimator does not have a sparse representation, so our procedure is more suitable here.

To summarize, we take the refined estimate of the null region, 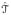, as

$$\widehat{\mathcal{J}}=arg\underset{{\mathcal{J}}_w\subseteq {\widehat{\mathcal{J}}}^{(0)}}{min}C({\mathcal{J}}_w,arg\underset{\lambda >0}{min}C({\mathcal{J}}_w,\lambda )).$$ (2.6)

With

$${\widehat{\mathit{b}}}_1=arg\underset{\mathit{b}}{min}{Q}_n(\widehat{\mathcal{J}},arg\underset{\lambda >0}{min}C(\widehat{\mathcal{J}},\lambda ),\mathit{b}),$$ (2.7)

the refined estimate of β(t) is

$$\widehat{\beta }(t)={\mathit{B}}_1^T(t){\widehat{\mathit{b}}}_1,$$

where B₁(t) are the B-spline basis functions associated with .

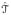2.3. Generalization to D > 1

We have taken D = 1 in (1.1). When D > 1, all steps can be carried out without much modification, as follows. After obtaining variables z_0,i for each β_d(t), the Dantzig selector can be applied to obtain initial estimates simultaneously for each β_d(t) by including the variables z_0,i of all β_d(t) in (2.3). The adaptive knots and the variables z_1,i in (2.4) can then be obtained one by one for each d. Finally, after having the variables ${\mathit{z}}_{1,i}^w$ of all β_d(t) in (2.4), the refinement procedure with group SCAD is performed with the coefficient b in Q_n( 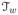, λ, b) partitioned into 2D groups, two groups being associated with each β_d(t).

3. Oracle Property

In this section, we show that, under certain conditions, our estimator enjoys the Oracle property for identifying and for estimating β(t) on 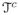. The conditions and the proofs of the theorems are deferred to the Appendix or to the supplementary document.

Recall that the parameters b₀ and b₁ in (2.3) and (2.4) vary with the sample size n. In the asymptotic studies, we denote them as b₀(n) and b₁(n), respectively. Similarly, B₁(t) is denoted as B₁(n, t), the initial estimator of b₀(n) as b̃₀(n), and the refined estimator of b₁(n) as b̂₁(n). The tuning parameter λ is denoted as λ_n.

For the estimator in the initial stage, we have an asymptotic result.

Theorem 1

Let b̃₀(n) = (b̃_0,1(n), …, b̃_0,k0,n+h(n))^T be the Dantzig estimate of b₀(n), with e_i ~ N (0, 1) and μ = 0. For the tuning parameter ${\lambda }_D(n)=\sqrt{2\mathit{log}(k_{0,n}+h)}$ in the Dantzig selector, and under the conditions A₁–A₆ in the Appendix, we have

1. ||b̃₀(n)− b₀(n)||_l2 = Op{n^−1/2k_0,n(logk_0,n)^1/2};

2. sup|b̃_0,j(n)| = O_p{n^−1/2k_0,n(logk_0,n)^1/2}for b_0,j(n) associated with ;

3. With probability tending to 1,

   $$\mathcal{J}\subseteq {\widehat{\mathcal{J}}}^{(0)}\mathit{and}{\widehat{\mathcal{J}}}^{(0)}\cap {\mathcal{J}}^c\subseteq \mathrm{\Omega }(k_{0,n}),$$

where, with r ≥ 3 as in the condition A₁, $\mathrm{\Omega }(k_{0,n})=\{t\in [0,T]:0<\mid \beta (t)\mid <k_{0,n}^{-r+2}\}$is a sub-region of [0, T], converging to the empty set as n → ∞.

Theorem 1 shows that the Dantzig selector estimate of b₀(n) is consistent. The L₂ convergence rate follows from Bickel, Ritov, and Tsybakov (2009); see also Raskutti, Wainwright, and Yu (2010); The sup-norm convergence rate can be derived following Lounici (2008); proof of part (iii) is given in the supplementary document.

Let the n × (k_1,n + h) matrix Z₁(n) = (z_1,1, z_1,2, …, z_1,n)^T, where z_1,i is defined in (2.4). Recall that the estimate of the coefficient function is $\widehat{\beta }(t)={\mathit{B}}_1^T(n,t){\widehat{\mathit{b}}}_1(n)$, where B₁(n, t) contains the B-spline basis functions at the refinement stage. Further, divide the basis functions B₁(n, t) into B_1N (n, t) and B_1S(n, t) and the matrix Z₁(n) into Z_1N (n) and Z_1S(n), according to the membership of their corresponding coefficients b_1N (n), related to the null region 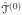, and b_1S(n).

For the estimator in the refinement stage, we have an asymptotic result.

Theorem 2

Assume the conditions A₁–A₈ in the Appendix and an initial estimator with the rate ||b̃₁(n) − b₁(n)||_l2= O_p(n^−1/2k_1,n), with e_i ~ N(0, 1) and μ = 0.

1. for t ∈ 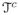, we have β̂(t) = 0, with probability tending to 1.

2. for t ∈ , we have

   $${(n/k_{1,n})}^{1/2}[\widehat{\beta }(t)-\beta (t)-{\mathcal{B}}_n(t)-{\mathcal{W}}_n(t)]\stackrel{\mathcal{D}}{\to }N[0,{\sigma }^2(t)],$$
   where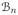 (t) denotes the estimation bias, ${\mathcal{W}}_n(t)=\beta (t)-{\mathit{B}}_1^T(n,t){\mathit{b}}_1(n)$is the B-spline approximation error, and

   $$\begin{array}{c}{\sigma }^2(t)=\underset{n\to \infty }{lim}{\mathit{B}}_{1S}^T(n,t){[(k_{1,n}/n){\mathit{Z}}_{1S}^T(n){\mathit{Z}}_{1S}(n)]}^{-1}{\mathit{B}}_{1S}(n,t),\\ {(n/k_{1,n})}^{1/2}\mid {\mathcal{B}}_n(t)\mid =O_p(n^{1/2}{k}_{1,n}^{-r}),\\ {(n/k_{1,n})}^{1/2}\mid {\mathcal{W}}_n(t)\mid =O_p(n^{1/2}{k}_{1,n}^{-r-1/2}).\end{array}$$
3. With $n^{-1}{k}_{1,n}^{2r}\to \infty$ in A₅, we have

   $${(n/k_{1,n})}^{1/2}[\widehat{\beta }(t)-\beta (t)]\stackrel{\mathcal{D}}{\to }N[0,{\sigma }^2(t)].$$

The assumed rate for the initial estimator b̃₁(n) is verified for the ordinal least squares estimator in the supplementary document.

Properties in Theorems 1 and 2 correspond to the Oracle properties reported in Zou (2006). Precisely, with a large n, we are able to identify the correct subregions in which the coefficient functions are non-zero; furthermore, we are able to estimate the values of the coefficient functions on the non-null regions as if we knew their exact locations.

4. Finite Sample Numerical Performances

We conducted simulation studies to evaluate the finite sample performance of our estimators.

Study 1

In this simulation study, we considered two covariate functions and the model

$$Y_i=2+{\int }_0^{10}{X}_{i1}(t){\beta }_1(t)dt+{\int }_0^{10}{X}_{i2}(t){\beta }_2(t)dt+e_i,$$

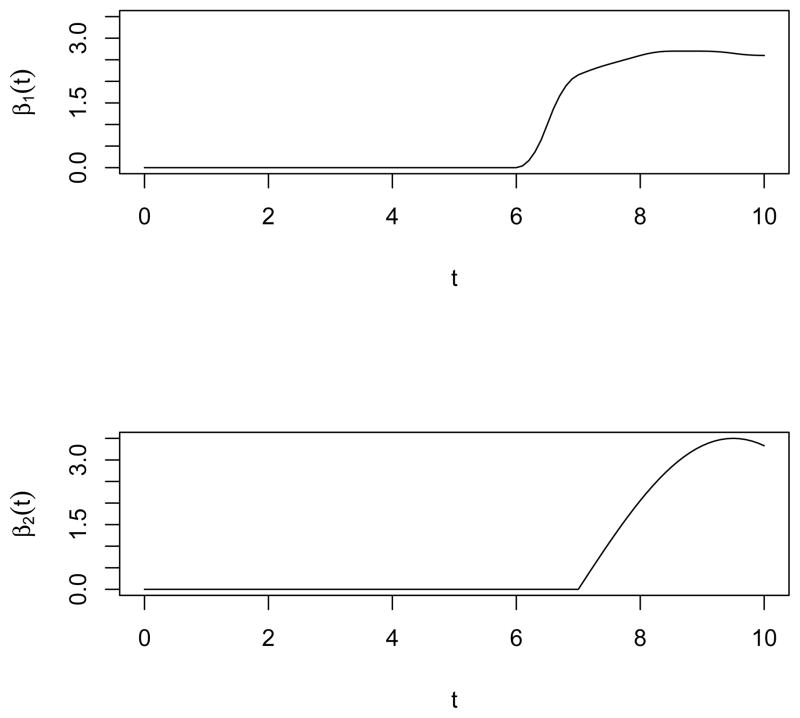
for i = 1, 2, …, n, with random errors e_i ~ N(0, 1). The covariate functions X_i1(t) and X_i2(t) were quadratic spline functions on [0, 10] with 50 equally-spaced knots and the corresponding coefficients were generated uniformly from [−5, 5]. We took m = 50 observations within [0, 10] from the true functions as the observed data and re-constructed X_i1(t) and X_i2(t) by B-spline approximations. We used coefficient functions β₁(t) and β₂(t) as follows.

1. β₁(t) was a piecewise quadratic function generated from quadratic B-spline functions with evenly-spaced knots at {0.0, 0.5, …, 9.5, 10.0}, while its coefficients were from a 22×1 vector with the last eight entries (2.0, 2.3, 2.5, 2.7, 2.7, 2.7, 2.6, 2.6)^T, and the rest of the entries zero.

2. The non-zero part of β₂(t) was a Trigonometric function:

   $${\beta }_2(t)=\{\begin{array}{ll}3.5sin\{\pi (t+3)/5\},\hfill & \text{if}t>7;\hfill \\ 0\hfill & \text{if}t\le 7.\hfill \end{array}$$

These coefficient functions are plotted in Figure 2. The shape of the function β₁(t) is commonly observed in biological studies; it indicates the pattern of growing into a stable state. As shown in the figure, β₁(t) = 0 on [0, 6] and β₂(t) = 0 on [0, 7].

Figure 2.

Plots of β₁(t) and β₂(t) for Study 1.

In each study, we generated 250 data sets with sample size n = 150. To evaluate the performance of the estimator, the estimated functions β̂₁(t) and β̂₂(t) were compared to the corresponding true functions. For the comparison, we report two quantities,

$$A_0=\frac{1}{l_0}{\int }_{\mathcal{J}}\mid {\widehat{\beta }}_d(t)-{\beta }_d(t)\mid dt{A}_1=\frac{1}{l_1}{\int }_{{\mathcal{J}}^c}\mid {\widehat{\beta }}_d(t)-{\beta }_d(t)\mid dt.$$

For β₁(t), = [0, 6], 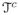= (6, 10], and l₀ = 6, l₁ = 4. For β₂(t), = [0, 7], 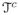= (7, 10], and l₀ = 7, l₁ = 3. The quantity A₀ measures the integrated absolute differences between the estimated coefficient functions and the true functions on the null regions, while A₁ measures it on the non-null regions.

We first evaluate the performance of the Dantzig estimates of β_d(t) (d = 1, 2) with different numbers of knots. Ideally, in order to reach high precision in determining the null region with a direct application of the Dantzig selector, one would need a very large number of knots. However, performance also deteriorates when the number of parameters is very large. Here, we can decide the number of variables in our problem, and design the procedure to improve numerical performance. Below, we show the effect of the total number of knots, k_0,n + 1, on the performance of the Dantzig estimator of β_d(t), varying the number of knots among k_0,n = 50, 100, 200, and 300.

The performances of the estimated coefficient functions by least squares with k_0,n = 50, and the Dantzig selector with k_0,n = 50, 100, 200, and 300, are summarized in Table 1. The entries of the table give the Monte Carlo averages of A₀ and A₁ over the 250 generated data sets, while the corresponding standard deviation is reported in parentheses. Since the same X_i1(t) and X_i2(t) were generated for each value of k_0,n, the results of the Dantzig estimator in Table 1 differ only by k_0,n. Table 1 shows that the least square estimator performed poorly on both regions, even with 50 knots. The Dantzig estimator performed well on the null region throughout, which is indicated by the small values of A₀. However, its estimation of β_d(t) on the non-null regions was increasingly worse with growth in the number of knots. The poor performance of the Dantzig estimator on the non-null regions in Table 1 indicates the necessity of a refining stage.

Table 1.

Integrated absolute biases of the least squares and the Dantzig estimates for Study 1. Each entry is the Monte Carlo average of A_j, j = 0 or 1; the corresponding standard deviation is reported in parentheses.

		β1(t)		β2(t)
Estimator	k0;n	A0	A1	A0	A1
Least Squares	50	2.220 (1.414)	3.272 (2.150)	1.905 (1.253)	3.982 (2.783)
Dantzig Selector	50	0.005 (0.010)	0.695 (0.090)	0.004 (0.007)	0.792 (0.114)
Dantzig Selector	100	0.010 (0.019)	1.416 (0.100)	0.009 (0.014)	1.687 (0.136)
Dantzig Selector	200	0.008 (0.021)	2.318 (0.102)	0.006 (0.013)	2.661 (0.141)
Dantzig Selector	300	0.007 (0.020)	2.724 (0.104)	0.004 (0.011)	3.120 (0.133)

We next evaluate the performance of the proposed one-step group SCAD estimator. The method, as described in Sections 2.1 to 2.3 with D = 2, refined the initial null region estimates and estimated β_d(t) on the non-null regions simultaneously, using the proposed algorithm. Based on the theoretical rates in Section 3, we let k_0,n = c_k0n^0.23, k_1,n = c_k1n^0.20, and d_n = c_dn^−0.25. We used a 10-fold cross validation on five data sets to choose the c’s, and then fixed them throughout the simulation. With the grid-search algorithm to determine the boundary of null regions, we do not expect outcomes to be sensitive to the choices of c_k0 and c_d, and a bad choice could simply lead to more computation in locating the boundaries at the second stage. This is indeed the case. The 10-fold CV results are indifferent over the range of c_d we tried, c_d varying from 0.05 to 0.5 (d_n varying between 0.014 and 0.143). The CV values varied near their minimums for k_0,n between 35 and 55 for all five data sets. We used k_0,n = 50 ≈ 13n^0.23, k_1,n = 12 ≈ 4.5n^0.20, and d_n = 0.2n^−0.25. For comparison, we calculated the adaptive LASSO estimates of β_d(t) by estimating the B-spline coefficients associated with the same adaptive knots, with the adaptive weights (Zou (2006)) being the inverse of absolute values of initial estimates by least squares. The criterion C( 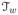, λ) was specified as GCV, AIC, BIC, or RIC, defined in the supplementary document. The same set of criteria were also used to select the tuning parameter in adaptive LASSO. The performances of estimated coefficient functions with AIC and BIC criteria, as well as the Oracle estimates that used the known null regions, are summarized in Table 2. The results with GCV and RIC, which are comparable to those with AIC and BIC, are reported in the supplementary document. The outcomes show that the criteria work about equally well. We tried different k_0,n values but, as expected, they do not play much of a role in our procedure.

Table 2.

Integrated absolute biases of the least squares, the Dantzig selector, the adaptive LASSO (adpLASSO), and the one-step group SCAD (gSCAD) estimates for Study 1. Each entry is the Monte Carlo average of A_j, j = 0 or 1; the corresponding standard deviation is reported in parentheses.

	β1(t)		β2(t)
Estimator	A0	A1	A0	A1
Oracle Estimator	-	0.157 (0.041)	-	0.166 (0.046)
Least Squares	2.205 (1.432)	3.283 (2.549)	1.963 (1.256)	4.088 (2.716)
Dantizig Selector	0.006 (0.013)	0.692 (0.094)	0.006 (0.010)	0.821 (0.132)
adpLASSO AIC	0.041 (0.030)	0.193 (0.059)	0.036 (0.028)	0.214 (0.069)
adpLASSO BIC	0.031 (0.031)	0.212 (0.059)	0.025 (0.029)	0.240 (0.074)
gSCAD AIC	0.024 (0.033)	0.143 (0.038)	0.024 (0.030)	0.155 (0.048)
gSCAD BIC	0.004 (0.013)	0.140 (0.037)	0.003 (0.009)	0.154 (0.049)

It may seem surprising that the Oracle estimator gives slightly larger A₁ values than the proposed estimators. This is due to the fact that the proposed estimators shrink the small non-zero values on the boundary toward zero, and consequently achieve less varied and better estimated outcomes near the null boundary.

The initial null regions of β₁(t) and β₂(t) identified by the Dantzig selector and the refined null regions of the one-step group SCAD method are shown in Table 3, where the averages of the lower and upper limits of the estimated null regions over the 250 generated data sets, as well as the corresponding standard deviations in parentheses, are summarized. The true null regions are [0, 6] for β₁(t) and [0, 7] forβ₂(t), respectively.

Table 3.

Null region estimates for Study 1. Each entry is the Monte Carlo average of estimated boundary of the null region; the corresponding standard deviation is reported in parentheses.

	β1(t)		β2(t)
Estimator	lower	upper	lower	upper
Dantzig Selector	0.008 (0.064)	6.230 (0.175)	0.002 (0.038)	7.123 (0.202)
gSCAD AIC	0.011 (0.091)	5.773 (0.479)	0.004 (0.063)	6.666 (0.528)
gSCAD BIC	0.010 (0.082)	6.058 (0.171)	0.003 (0.051)	6.951 (0.181)

As shown in Tables 2 and 3, the least squares estimates of β_d(t) are poor on both null and non-null regions of β_d(t). The Dantzig selector tends to have less favorable performance on the non-null regions of β_d(t). Moreover, the initial null region identified by it tends to be larger than the true region. The one-step group SCAD method seems to satisfactorily estimate the coefficient functions on both null and non-null regions. Furthermore, by refining the null region initial estimates, our method, particularly using the BIC or RIC criterion, tends to identify the null regions of β_d(t) with a greater accuracy than the Dantzig selector. The one-step group SCAD method also outperforms adaptive LASSO on both null and non-null regions.

The full simulation results with GCV, AIC, BIC, and RIC criteria, reported in the supplementary document, show that the performances of the criteria in the method are, in general, satisfactory; see Wang, Li, and Tsai (2007) for another report of using these four criteria in comparison of performances of SCAD methods. The results show that BIC and RIC are less conservative in identifying the null regions. This is expected because the BIC and RIC criteria put heavier penalty on the effective number of parameters than the AIC criterion (Shi and Tsai (2002)).

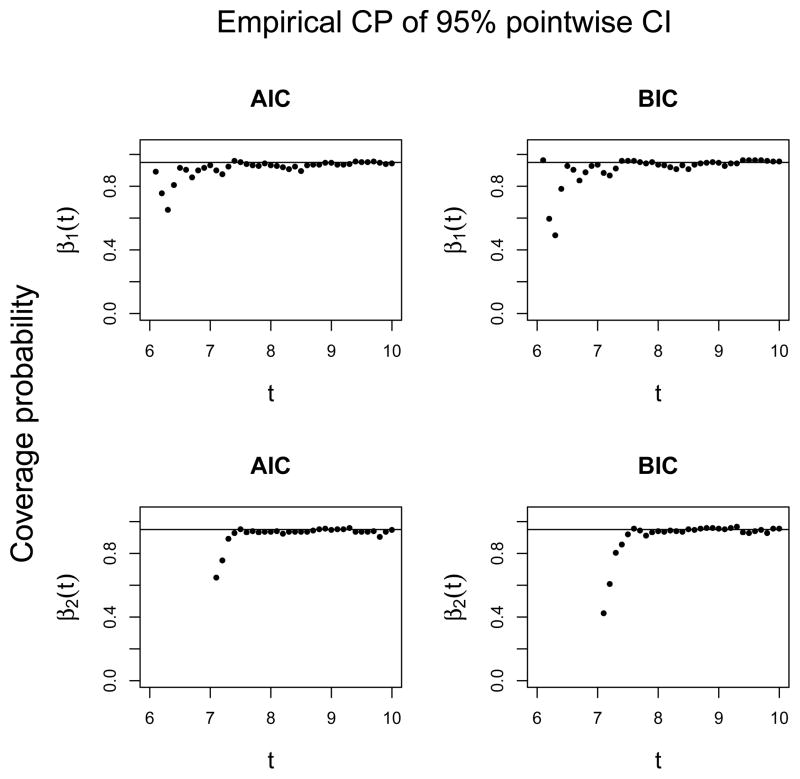
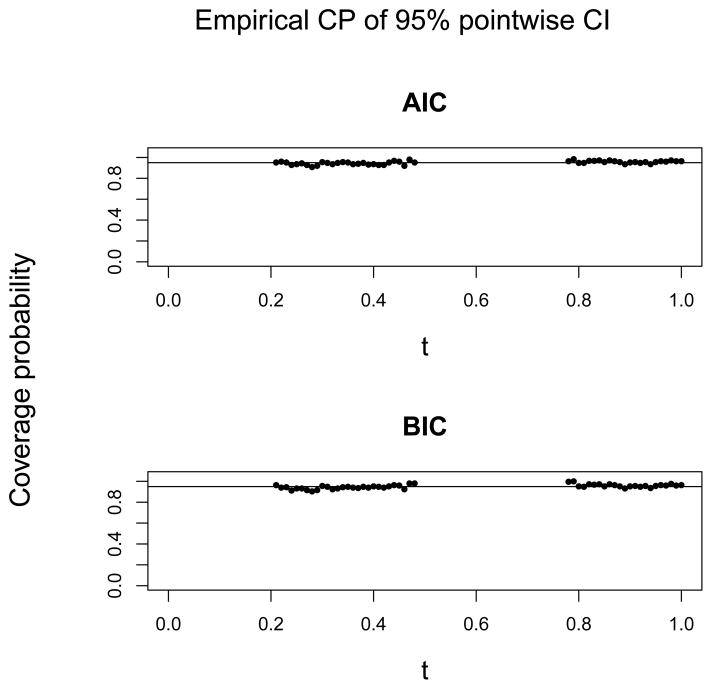
One advantage of the proposed estimators is that they readily provide inferences for non-zero coefficient functions. Here, we computed the variance of the point estimator given in Theorem 2 and constructed the pointwise 95% confidence interval according to the asymptotic normality results in Theorem 2 for t in the non-null regions. At each point, the true value of coefficient function β₁(t) or β₂(t) was compared with the computed pointwise 95% confidence interval, and the coverage probabilities (CP) of the confidence intervals were computed over the 250 generated data sets. Besides CP, we also calculated the Monte Carlo biases, standard deviations (SD), and mean square errors (MSE) for points in the non-null regions. For β₁(t), we took t = 6.1, 6.2, ···, 10.0, and for β₂(t), t = 7.1, 7.2, ···, 10.0. Using AIC and BIC, the entries of Table 4 give the averages of Monte Carlo biases, SDs, MSEs, and CP over these points, while the corresponding standard deviation is reported in parentheses. The coverage probabilities of the confidence intervals, computed over the 250 generated data sets at these points in the non-null regions of β₁(t) and β₂(t), are plotted in Figure 3, for AIC and BIC. Table 4 shows that the estimators based on AIC and BIC perform similarly on the non-null regions and all yield coverage probabilities of the pointwise confidence intervals close to the nominal level 0.95. The slightly lower coverage probabilities than the nominal level is due to the shrinkage of the estimates for t close to the boundary of the null regions, as shown in Figure 3. The GCV and RIC criteria have similar performances to AIC and BIC; their results are reported in the supplementary document.

Table 4.

Monte Carlo bias, standard deviation (SD), mean squared error (MSE), and empirical coverage probability (CP) of 95% pointwise confidence intervals of group SCAD (gSCAD) estimates for Study 1. Each entry is the average over the selected points in the non-null region of β₁(t) or β₂(t); the corresponding standard deviation is reported in parentheses.

	β1(t)
Estimator	Ave. MC Bias	Ave. MC SD	Ave. MC MSE	CP
gSCAD AIC	0.004 (0.013)	0.201 (0.213)	0.085 (0.331)	0.932 (0.047)
gSCAD BIC	−0.001 (0.019)	0.195 (0.218)	0.084 (0.339)	0.928 (0.094)
	β2(t)
Estimator	Ave. MC Bias	Ave. MC SD	Ave. MC MSE	CP
gSCAD AIC	−0.006 (0.031)	0.224 (0.247)	0.110 (0.394)	0.924 (0.053)
gSCAD BIC	−0.012 (0.043)	0.221 (0.242)	0.107 (0.378)	0.915 (0.098)

Figure 3.

Empirical coverage probabilities (CP) of 95% pointwise confidence intervals for coefficient estimate over non-null region of β₁(t) and β₂(t) for Study 1, by AIC and BIC. For β₁(t), the points are taken at t = 6.1, 6.2, ···, 10.0, for β₂(t), the points are taken at t = 7.1, 7.2, ···, 10.0.

We also briefly investigated the effects of having irregularly spaced time points by dropping 10% and 20% of the observations on X_i1(t) and X_i2(t) at random from the simulated data, followed by a pre-smoothing step. Our procedure was then applied to the pre-smoothed data. The relative performance of least squares, the Dantzig selector, the adaptive LASSO, and the one-step group SCAD, were similar to what is seen in Tables 1–4. We noted a slight decrease in the average coverage probabilities. For example, for group SCAD with the AIC criterion, the coverage probabilities for β₁(t) and β₂(t) were 90.6% and 88.7% for 10% dropped, and 87.7% and 85.6% for 20% dropped. A further investigation indicated that the decrease in average coverage probabilities mainly occurred near the boundary of null regions. This observation implies that the performance of our estimators near the boundary of null regions tends to be subject to the influence of the locations and numbers of observations on the covariate functions X_i1(t) and X_i2(t).

Study 2

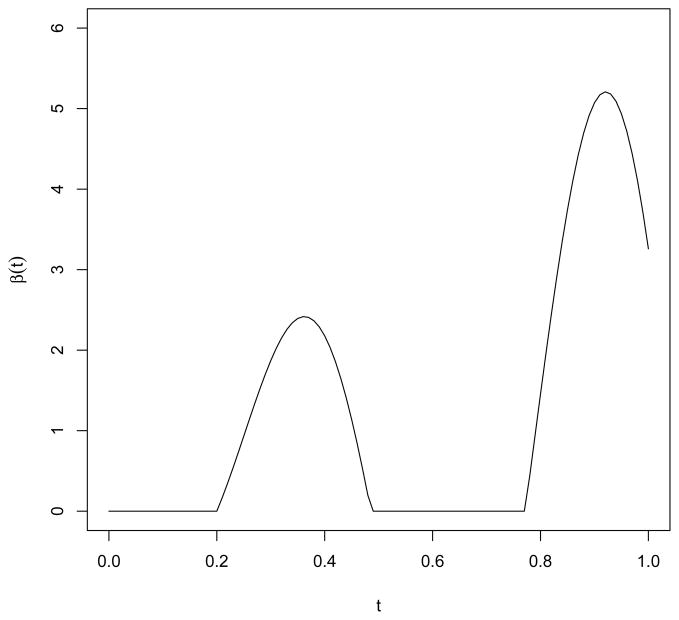
We conducted a second simulation study with

$$Y_i=2+{\int }_0^1{X}_i(t)\beta (t)dt+e_i,$$

and e_i ~ N(0, 0.25). The covariate functions X_i(t) were generated and reconstructed on [0, 1] by the same methods as in Study 1. The coefficient function was β(t) = max[0, 8log(t + 1) sin{3.5π(t − 0.2)}], shown in Figure 4. Its null region is = [0.0, 0.2]∪[0.486, 0.771].

Figure 4.

Plot of β(t) for Study 2.

We generated 250 data sets with sample size n = 500. The 10-fold CV results suggested the use of a much smaller k_0,n; we took k_0,n = 20, k_1,n = 10, and d_n = n^−0.25. The equivalent results to those in Study 1 are reported in Tables 5 to 7. The 95% CI overage probabilities (CP) are reported over t = 0.21, 0.22, …, 0.48, 0.78, 0.79, …, 1.00 within 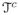. Tables 5 and 6 show that the method has better performance overall in estimating β(t) and identifying the null region of β(t) than the other methods, and behaves similarly as the oracle estimator. The Dantzig estimator tends to yield larger A₁, as usual. We repeated the simulation with k_0,n = 50 while keeping the rest of the setup unchanged. The Monte Carlo averages of A₀ for least-squares, Dantzig, adaptive LASSO (AIC), and grouped SCAD (AIC) were 3.755, 0.001, 0.198, and 0.043, respectively, while the corresponding values for A₁ were 3.840, 0.849, 0.268, and 0.246. Similar performances were obtained using other criteria. We note that the outcomes for adaptive LASSO and our method change little, mainly due to the slight changes of boundaries and the knot locations at the second stage. The least-squares and Dantzig estimators again suffered from the large number of parameters.

Table 5.

Integrated absolute biases of the least squares, the Dantzig selector, the adaptive LASSO (adpLASSO), and the one-step group SCAD (gSCAD) estimates for Study 2. Each entry is the Monte Carlo average of A_j, j = 0 or 1; the corresponding standard deviation is reported in parentheses.

Estimator	A0	A1
Oracle Estimator	-	0.257 (0.054)
Least Squares	0.246 (0.060)	0.240 (0.054)
Dantzig Selector	0.006 (0.007)	0.485 (0.069)
adpLASSO AIC	0.066 (0.063)	0.246 (0.063)
adpLASSO BIC	0.023 (0.041)	0.278 (0.079)
gSCAD AIC	0.038 (0.076)	0.230 (0.054)
gSCAD BIC	0.009 (0.020)	0.226 (0.056)

Table 7.

Monte Carlo bias, standard deviation (SD), mean squared error (MSE), and empirical coverage probability (CP) of 95% pointwise confidence intervals of group SCAD (gSCAD) estimates for Study 2. Each entry is the average over the selected points in the non-null region of β₁(t) or β₂(t); the corresponding standard deviation is reported in parentheses.

	β1(t)
Estimator	Ave. MC Bias	Ave. MC SD	Ave. MC MSE	CP
gSCAD AIC	−0.012 (0.055)	0.296 (0.173)	0.120 (0.265)	0.950 (0.016)
gSCAD BIC	−0.020 (0.072)	0.286 (0.183)	0.120 (0.272)	0.951 (0.020)

Table 6.

Null region estimates for Study 2. Each entry is the Monte Carlo average of estimated boundary of the null region; the corresponding standard deviation is reported in parentheses.

	[0.000, 0.200]		[0.486, 0.771]
Estimator	lower	upper	lower	upper
Dantzig Selector	0.001 (0.009)	0.199 (0.016)	0.502 (0.014)	0.749 (0.008)
gSCAD AIC	0.001 (0.009)	0.194 (0.021)	0.507 (0.019)	0.744 (0.016)
gSCAD BIC	0.001 (0.009)	0.199 (0.016)	0.502 (0.014)	0.749 (0.008)

5. The Johns Hopkins Precursors Study

The impact of cumulative lifelong risk exposure on quality of life (QoL) in old age is of great interest to researchers. We applied our method to data from the Johns Hopkins Precursors Study to investigate the effect of body mass index (BMI) at midlife on the quality of life at older ages. In this, we focused on the outcome of physical functioning (PF), an important QoL measure among the elderly, collected through the SF-36 health survey questionnaires (Ware and Sherbourne (1992)), with a score that ranged from 0 to 100. We restricted our analysis to data from 107 participants who had their PF scores assessed between 70 and 76 years of age. The age range of interest for the BMI was 40 to 70 years. The transformed PF score, $y=10\ast \mathit{asin}\sqrt{PF/100}$ was used as the response in model (2.1).

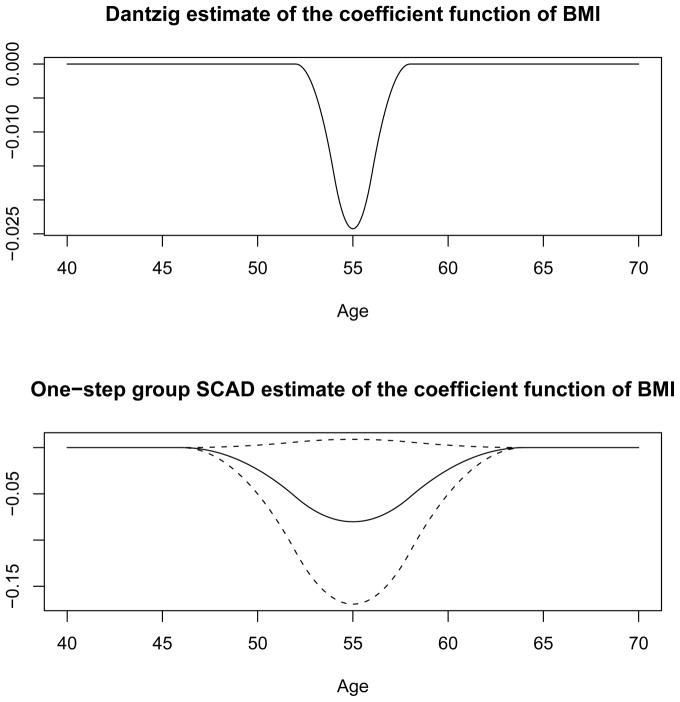
To obtain each participant’s trajectory of BMI on [40, 70], we first pre-smoothed the available BMI records for each subject (Ramsay and Silverman (2005)). The pre-smoothed and centered BMI trajectories on [38, 72] were then fitted by quadratic B-splines with evenly-spaced knots of {38, 40, ···, 70, 72}. In the initial stage of the method, the functional coefficient on [40, 70] was approximated by quadratic splines with evenly-spaced knots of {40, 42, ···, 68, 70}. The Dantzig selector, with the tuning parameter selected by leave-one-out cross validation, yielded the initial null region [40, 52] ∪ [58, 70]. The initial estimate of β(t) by the Dantzig selector is plotted in Figure 6.

Figure 6.

The estimated coefficient function for BMI in the Johns Hopkins Precursors Study. The upper panel shows the initial estimate by Dantzig selector. The lower panel shows the refined estimate by the proposed one-step group SCAD estimator with the dotted lines being the 95% pointwise CI for it in the refined non-null region [46, 64]. The AIC and RIC criteria yield the same refined estimates.

During the refining stage, we specified the working null regions as [40, 52 − l] ∪ [58 + l, 70] and let l = 0, 1, 2,···, 10. Using the method proposed in Section 2.2, the refined null region selected by both AIC and RIC was [40, 46] ∪ [64, 70]. The two criteria also led to identical refined estimates of β(t) on [40, 70], as well as the same pointwise 95% confidence intervals; they are plotted in Figure 6.

Figure 6 shows that greater values of BMI between ages 46 and 64 seem to be associated with greater decrease in the PF scores in early to mid 70 years of age. The 95% pointwise confidence intervals of β(t) on [46, 64], albeit not significant, are almost all in the negative range. In contrast to our approach, the Dantzig selector identified a larger null region and shrunk the estimated coefficient function on the non-null region toward zero. This is consistent with what we observed in the simulation study. The zero coefficient function in the mid-forties and younger implies that a greater BMI at this age range does not contribute much to additional risk of decreasing PF scores, after factoring in body weight patterns in the subsequent two decades. On the other hand, the zero coefficient function after the mid-sixties could be due to a mixture of two forces; high BMI is harmful in general, but being too thin may not be a good sign among the elderly either.

The non-significant finding could be due to the relatively small number of participants in our sample and the modest association between BMI and the PF scores, not uncommon in this kind of study. To better understand whether we had sufficient power to confirm a modest association, we conducted a small power analysis. In the analysis, we specified the true coefficient function as the curve estimated by the proposed method. Then, conditional on the available BMI records, we generated new PF scores according to the fitted model and applied the method to calculate 95% confidence intervals. The proportions of pointwise 95% confidence intervals that were completely negative at ages 50, 55, and 60, with the λ in SCAD penalty being fixed at the value selected in the data analysis, were 0.496, 0.256, and 0.522, respectively. The finding from the Precursors Study data nevertheless suggests the potential for added benefit of slower decline in physical functioning at old age in keeping a healthy body weight in midlife.

6. Concluding Remarks

With the development in variable selection when the number of predictors is large, we advance a method to estimate coefficient functions in functional linear model when the values of the functions are zero in certain sub-regions. Our aim is a functional data analysis (FDA) tool in which the final estimator on the non-null region behaves just like a regular FDA solution. Our estimator successfully attains the properties we desire: it maintains the sparsity and Oracle properties in the estimated coefficient functions, asymptotic normality applies, and it achieves superior numerical performances compared to existing alternatives in both identification of and the estimation of β(t). The proposed procedure borrows strength from existing efficient algorithms and can be easily carried out.

An additional point is that in functional data analysis, we select the number of basis functions and determine the number of parameters needed. When the number is unavoidably large, as in the variable selection problems in genomic studies, even the best estimator can be poor. When we reduce the number of parameters, we simplify the nature of the problem and consequently obtain improved results. There are alternatives to what we have proposed. In our method, as indicated in the supplementary document, we shrank the limits of each null interval in a symmetric way with a grid size of 0.02T. More effective search ideas, such as a combination of shrinking and expanding around the limits, could be conducted and should lead to some improvement. The performance of the estimates on the non-null region can be further improved by an adaptive selection of knots, as in the regular B-spline smoothing estimation. We have not pursued these directions here.

Figure 5.

Empirical coverage probabilities (CP) of 95% pointwise confidence intervals for coefficient estimate over non-null region of β(t) for Study 2, by AIC and BIC. The points are taken at t = 0.21, 0.22, ···, 0.48, 0.78, 0.79, ···, 0.99, 1.00.

Appendix: Assumptions and Technical Details

We provide the assumptions behind the theoretical properties and sketch their proofs in the Appendix; refer to the supplementary document for further details.

A.1. Notation and assumptions

Recall that k_0,n + 1, k_1,n + 1 are the numbers of knots, and Z₀(n) and Z₁(n) are the design matrices in models (2.3) and (2.4) for the two stages, respectively.

Let ${\mathit{Z}}_0^{\ast }(n)$ be a standardized version of Z₀(n) such that ${\mathrm{\Psi }}_{z0\ast }=n^{-1}{\mathit{Z}}_0^{\ast T}(n){\mathit{Z}}_0^{\ast }(n)$ has its diagonal elements, Ψ_z0*(j, j) ≡ 1, for all j. Take δ_b0(n) = b̃₀(n) − b₀(n), and let δ_b0, 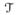(n) and δ_b0, 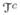(n) be δ_b0(n), corresponding to null and signal regions, respectively, with s(n) the number of non-zero coefficients in b₀(n). Recall the definitions of Z_1N (n) and Z_1S(n) in Section 3. To show the Oracle properties of the proposed estimator, consider the following conditions.

• A₁: β (t) has rth (r ≥ 3) bounded derivative on [0, T].

• A₂: ${\int }_0^T\mid X_i(t)\mid dt\le M^{\prime }{k}_{1,n}^{r-1}$, for i = 1, 2, …, n and some constant M′ < ∞.

• A₃: For some integers less than k_0,n + h and non-zero δ_bo(n),

  $$\underset{\mid s(n)\mid \le s}{min}\underset{{\mid {\delta }_{b_0,\mathcal{J}}(n)\mid }_{l_1}\le {\mid {\delta }_{b_0,{\mathcal{J}}^c}(n)\mid }_{l_1}}{min}\frac{{\mid {\mathit{Z}}_0^{\ast T}(n){\delta }_{b_0}(n)\mid }_{l_2}}{\mid \sqrt{n}{\mid {\delta }_{b_0,{\mathcal{J}}^c}(n)\mid }_{l_2}}>0.$$
• A₄: For a constant γ > 1 and s ≥ s(n),

  $${max}_{i\ne j}{\mathrm{\Psi }}_{z0\ast }(i,j)\le \frac{1}{3\gamma s}.$$

• A₅: For k_0,n, $n^{-1}{k}_{0,n}^{2r-2}{\mathit{logk}}_{0,n}\to 0$ and $n^{-1}{k}_{0,n}^{2r}{\mathit{logk}}_{0,n}\to \infty$. For k_1,n, $n^{-1}{k}_{0,n}^{2r-4}{k}_{1,n}^3\to \infty$.

• A₆: For the threshold value d_n, $d_n{n}^{1/2}{k}_{0,n}^{-1}{({\mathit{logk}}_{0,n})}^{-1/2}\to \infty$ and $d_n{k}_{0,n}^{r-2}\to 0$.

• A₇: For the tuning parameter λ_n, λ_n → 0 and ${\lambda }_n{k}_{0,n}^{r-2}\to \infty$.

• A₈: There are constants $0<c_1^{\prime }<c_2^{\prime }$ such that

  $$c_1^{\prime }{k}_{1,n}^{-1}\le {\lambda }_{\mathit{min}}\{n^{-1}{\mathit{Z}}_1^T(n){\mathit{Z}}_1(n)\}\le {\lambda }_{\mathit{max}}\{n^{-1}{\mathit{Z}}_1^T(n){\mathit{Z}}_1(n)\}\le c_2^{\prime }{k}_{1,n}^{-1},$$
  where λ_min(A) and λ_max(A) denote the smallest and largest eigenvalues of the matrix A. The same eigenvalue condition as for $n^{-1}{\mathit{Z}}_1^T(n){\mathit{Z}}_1(n)$ holds for the matrices $n^{-1}{\mathit{Z}}_{1N}^T(n){\mathit{Z}}_{1N}(n)$ and $n^{-1}{\mathit{Z}}_{1S}^T(n){\mathit{Z}}_{1S}(n)$. In addition,

  $${\lambda }_{\mathit{max}}\{n^{-1}{\mathit{Z}}_{1N}^T(n){\mathit{Z}}_{1S}(n){\mathit{Z}}_{1S}^T(n){\mathit{Z}}_{1N}(n)\}<c_3{k}_{1,n}^{-1},$$

  for a constant c₃ > 0.

Condition A₂ is weaker than one assumed in James, Wang, and Zhu (2009). The restricted eigenvalue condition A₃ from Bickel, Ritov, and Tsybakov (2009) controls the singularity of the first stage design matrix to ensure the L₂ rate, while A₄ is required to warrant the sup-norm rate in Theorem 1. The rate of the threshold value d_n given in condition A₆ guarantees that, with probability tending to 1 as n → ∞, is correctly identified by 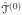. Condition A₈ is analogous to one in Fan and Peng (2004) when the number of predictors increases with n. It appears as lemmas in Zhou, Shen and Wolfe (1998) and Zhu, Fung and He (2008); to avoid redundancy, we simply use it as a condition.

A.2. Sketch Proof of Theorem 2

We use a_n > O_p(b_n) and a_n ≥ O_p(b_n) to denote that, as n → ∞ with probability tending to 1, b_n/a_n → 0 and b_n/a_n is bounded from above, respectively. Here we sketch the key steps in the proof of Theorem 2. Recall that b_1N (n) and b_1S(n) are the division of b₁(n) according to 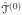. Since b_1N (n) contains the coefficients associated with 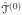, by Theorem 1 (iii), these coefficients are either associated with or with Ω(k_0,n). Consequently, by A₅, ${\left|\right|{\mathit{b}}_{1N}(n)\left|\right|}_{l_1}=O_p(k_{0,n}^{-r+2})$. Following the proof of Part (iii) of Theorem 1 in the supplementary document, it is easy to see that ||b_1S(n)||_l1 ≥ Op(1).

We assume the initial value b̃₁(n) satisfies ||b̃₁(n) − b₁(n)||_l2 = Op(n^−1/2 k_1,n). Note that b̃_1N (n) and b̃_1S(n) are the division of b̃₁(n) according to 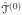. Given ||b̃_1N (n) − b_1N (n)||_l1 ≤ C||b̃_1N (n) − b_1N (n)||_l2= O_p(n^−1/2k_1,n), ${\left|\right|{\mathit{b}}_{1N}(n)\left|\right|}_{l_1}=O_p(k_{0,n}^{-r+2})$, and A₅, we have that ${\left|\right|{\stackrel{\sim }{\mathit{b}}}_{1N}(n)\left|\right|}_{l_1}=O_p(k_{0,n}^{-r+2})$ and ||b̃_1S (n)||_l2 ≥ O_p(1). Given A₇, with probability tending to 1, we have that $p_{{\lambda }_n}^{\prime }({\left|\right|{\stackrel{\sim }{\mathit{b}}}_{1N}(n)\left|\right|}_{l_1})={\lambda }_n$ and $p_{{\lambda }_n}^{\prime }({\left|\right|{\stackrel{\sim }{\mathit{b}}}_{1S}(n)\left|\right|}_{l_1})=0$.

Let Q_n be Q_n( 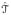, λ, b) in (2.5), and focus on the expansion of Q_n{b̂₁(n)} − Q_n{b₁(n)}as

$$\begin{array}{l}{[{\widehat{\mathit{b}}}_1(n)-{\mathit{b}}_1(n)]}^T{\mathit{Z}}_1^T(n){\mathit{Z}}_1(n)[{\widehat{\mathit{b}}}_1(n)-{\mathit{b}}_1(n)]-2{({\mathit{Z}}_1^T(n){\mathit{\epsilon }}_1(n))}^T[{\widehat{\mathit{b}}}_1(n)-{\mathit{b}}_1(n)]+n{\lambda }_n({\left|\right|{\widehat{\mathit{b}}}_{1N}(n)\left|\right|}_{l_1}-{\left|\right|{\mathit{b}}_{1N}(n)\left|\right|}_{l_1})\\ \ge {[{\widehat{\mathit{b}}}_1(n)-{\mathit{b}}_1(n)]}^T{\mathit{Z}}_1^T(n){\mathit{Z}}_1(n)[{\widehat{\mathit{b}}}_1(n)-{\mathit{b}}_1(n)]-2{({\mathit{Z}}_1^T(n){\mathit{\epsilon }}_1(n))}^T[{\widehat{\mathit{b}}}_1(n)-{\mathit{b}}_1(n)]+n{\lambda }_n({\left|\right|{\widehat{\mathit{b}}}_{1N}(n)-{\mathit{b}}_{1N}(n)\left|\right|}_{l_1}-2{\left|\right|{\mathit{b}}_{1N}(n)\left|\right|}_{l_1}),\end{array}$$

where b̂_1N (n), b̂_1S(n) and b_1N (n),b b_1S(n) are the divisions of b̂₁(n) and b₁(n), respectively, according to their association with 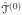. Handling the null and non-null coefficients separately, we show, with some detailed derivation, that a non-optimal bound for the convergence rate of b̂₁(n) holds as ${\left|\right|{\widehat{\mathit{b}}}_1(n)-{\mathit{b}}_1(n)\left|\right|}_{l_2}\le O_p(n^{-1/2}{k}_{1,n}^{3/2})$; this rate is sufficient for us to use in the proof of Theorem 2. The proof of b̂_1,j(n) = 0, with probability tending to 1, for any b̂_1,j(n) associated with 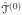, is a direct consequence of this convergence. Part (i) is proved.

We have $p_{{\lambda }_n}^{\prime }({\left|\right|{\stackrel{\sim }{\mathit{b}}}_{1N}(n)\left|\right|}_{l_1})={\lambda }_n$ and $p_{{\lambda }_n}^{\prime }({\left|\right|{\stackrel{\sim }{\mathit{b}}}_{1S}(n)\left|\right|}_{l_1})=0$ with probability tending to 1. We now give the key steps that lead to the asymptotic distribution of β̂(t) for t ∈ 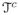. For large n, we have

$$\begin{array}{l}{(n/k_{1,n})}^{1/2}(\widehat{\beta }(t)-\beta (t))={(n/k_{1,n})}^{1/2}{\mathit{B}}_{1S}^T(n,t)\{{\widehat{\mathit{b}}}_{1S}(n)-{\mathit{b}}_{1S}(n)\}+{(n/k_{1,n})}^{1/2}\{{\mathit{B}}_1^T(n,t){\mathit{b}}_1(n)-\beta (t)\}\\ ={\mathit{B}}_{1S}^T(n,t){\{(k_{1,n}/n){\mathit{Z}}_{1S}^T(n){\mathit{Z}}_{1S}(n)\}}^{-1}\{{(n/k_{1,n})}^{-1/2}{\mathit{Z}}_{1S}^T(n)\mathit{e}(n)\}\\ +{\mathit{B}}_{1S}^T(n,t){\{(k_{1,n}/n){\mathit{Z}}_{1S}^T(n){\mathit{Z}}_{1S}(n)\}}^{-1}[{(n/k_{1,n})}^{-1/2}{\mathit{Z}}_{1S}^T(n)\{{\mathit{\epsilon }}_1(n)-\mathit{e}(n)\}]\\ +{\mathit{B}}_{1S}^T(n,t){\{(k_{1,n}/n){\mathit{Z}}_{1S}^T(n){\mathit{Z}}_{1S}(n)\}}^{-1}\{{(n/k_{1,n})}^{-1/2}{\mathit{Z}}_{1S}^T(n){\mathit{Z}}_{1N}(n){\mathit{b}}_{1N}(n)\}\\ +{(n/k_{1,n})}^{1/2}\{{\mathit{B}}_1^T(n,t){\mathit{b}}_1(n)-\beta (t)\}\\ =U_n(t)+{(n/k_{1,n})}^{1/2}{{\mathcal{B}}^{\prime }}_n(t)+{(n,k_{1,n})}^{1/2}{\mathcal{B}}_n^{″}(t)+{(n/k_{1,n})}^{1/2}{\mathcal{W}}_n(t).\end{array}$$

By Huang (1998), U_n(t) is the asymptotic normal component, ${\mathcal{B}}_n(t)={\mathcal{B}}_n^{\prime }(t)+{\mathcal{B}}_n^{″}(t)$ is the estimation bias, and W_n(t) contains the spline approximation error.

Given that e(n)~ N(0, I_n), we have that, for t ∈ ,

$$U_n(t)\stackrel{\mathcal{D}}{\to }N[0,{\sigma }^2(t)],$$

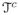where ${\sigma }^2(t)={lim}_{n\to \infty }{\mathit{B}}_{1S}^T(n,t){\{(k_{1,n}/n){\mathit{Z}}_{1S}^T(n){\mathit{Z}}_{1S}(n)\}}^{-1}{\mathit{B}}_{1S}(n,t)$.

By A₈, ${\lambda }_{\mathit{max}}((k_{1,n}/n){\mathit{Z}}_{1S}(n){\mathit{Z}}_{1S}^T(n))\le c_2^{\prime }$. Thus, we have $sup\mid {\epsilon }_{1,i}-e_i\mid \le M^{\prime }{Ck}_{1,n}^{-r}$ for some constant C, and ${\left|\right|{(n/k_{1,n})}^{-1/2}{\mathit{Z}}_{1S}^T(n)({\mathit{\epsilon }}_1(n)-\mathit{e}(n))\left|\right|}_{l_2}\le C^{\prime }{n}^{1/2}{k}_{1,n}^{-r}$ for some constant C′. Then

$${(n/k_{1,n})}^{1/2}\mid {\mathcal{B}}_n^{\prime }(t)\mid =O_p(n^{1/2}{k}_{1,n}^{-r}).$$

Also by A₈, we have

$${(n/k_{1,n})}^{-1}{\mathit{b}}_{1N}^T(n){\mathit{Z}}_{1N}^T(n){\mathit{Z}}_{1S}(n){\mathit{Z}}_{1S}^T(n){\mathit{Z}}_{1N}(n){\mathit{b}}_{1N}(n)\le c_2^{\prime 2}{\left|\right|{\mathit{b}}_{1N}(n)\left|\right|}_{l_2}^2.$$

By A₅, each coefficient in b_1N (n) is bounded by $C^{\prime }{k}_{0,n}^{-r+2}$ for some constant C′. Combined with the fact that $k_{0,n}^{-r+2}=o_p(1)$ by A₇, we can show that

$${(n/k_{1,n})}^{1/2}\mid {\mathcal{B}}_n^{″}(t)\mid =o_p(1).$$

Therefore, we have

$${(n/k_{1,n})}^{1/2}\mid {\mathcal{B}}_n(t)\mid =O_p(n^{1/2}{k}_{1,n}^{-r}).$$

The term 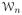(t) is the B-spline approximation error at β(t). Given A₁ and the B-spline approximation property, we have

$${(n/k_{1,n})}^{1/2}\mid {\mathcal{W}}_n(t)\mid =O_p(n^{1/2}{k}_{1,n}^{-r-1/2}).$$

Therefore we have, for t ∈ ,

$${(n/k_{1,n})}^{1/2}[\widehat{\beta }(t)-\beta (t)-{\mathcal{B}}_n(t)-{\mathcal{W}}_n(t)]\stackrel{\mathcal{D}}{\to }N[0,{\sigma }^2(t)].$$

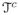Part (ii) is proved.

Assuming the additional stronger condition $n^{-1}{k}_{1,n}^{2r}\to \infty$ in A₅, it follows that (n/k_1,n)^1/2| 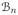(t)| = o_p(1) and (n/k_1,n)^1/2| 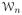(t)| = o_p(1). Therefore we have, for t ∈ ,

$${(n/k_{1,n})}^{1/2}[\widehat{\beta }(t)-\beta (t)]\stackrel{\mathcal{D}}{\to }N[0,{\sigma }^2(t)].$$

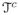Part (iii) is proved.