GENERALIZED DOUBLE PARETO SHRINKAGE

Abstract

We propose a generalized double Pareto prior for Bayesian shrinkage estimation and inferences in linear models. The prior can be obtained via a scale mixture of Laplace or normal distributions, forming a bridge between the Laplace and Normal-Jeffreys’ priors. While it has a spike at zero like the Laplace density, it also has a Student’s t-like tail behavior. Bayesian computation is straightforward via a simple Gibbs sampling algorithm. We investigate the properties of the maximum a posteriori estimator, as sparse estimation plays an important role in many problems, reveal connections with some well-established regularization procedures, and show some asymptotic results. The performance of the prior is tested through simulations and an application.

1. Introduction

There has been a great deal of work in shrinkage estimation and simultaneous variable selection in the frequentist framework. The LASSO of Tibshirani (1996) has drawn much attention to the area, particularly after the introduction of LARS (Efron et al. (2004)) due to its superb computational performance. There is a rich literature analyzing the LASSO and related approaches (Fu (1998), Knight and Fu (2000), Fan and Li (2001), Yuan and Lin (2005), Zhao and Yu (2006), Zou (2006), Zou and Li (2008)), with a number of articles considering asymptotic properties.

Bayesian approaches to the same problem became popular with the works of Tipping (2001) and Figueiredo (2003). By expressing Student’s t priors for basis coefficients as scale mixtures of normals (West (1987)), and relying on type II maximum likelihood estimation (Berger (1985)), Tipping (2001) developed the relevance vector machine for sparse estimation in kernel regression. In this setting, however, exact sparsity comes with the price of forfeiting propriety of the posterior by driving the scale parameter of the Student’s t distribution toward zero. In fact, driving both the scale parameter and the degrees of freedom to zero yields the so-called Normal-Jeffreys’ prior, π(θ) ∝ 1|θ|. The name emerges due to the fact that the hierarchy follows as θ ~ N(0, τ), π(τ) ∝ 1/τ, where the latter is the Jeffreys’ prior on the prior variance of θ. Figueiredo (2003) proposed an expectation-maximization algorithm for maximum a posteriori estimation under Laplace and Normal-Jeffreys’ priors, with estimates under the Laplace corresponding to the LASSO. The Normal-Jeffreys’ prior leads to substantially improved performance with finite samples due to the property of strongly shrinking small coefficients to zero while minimally shrinking large coefficients due to the heavy tails; however, it has no meaning from an inferential aspect as it leads to an improper posterior.

A Bayesian LASSO was proposed by Park and Casella (2008) and Hans (2009). However, these procedures inherit the problem of over-shrinking large coefficients due to the relatively light tails of the Laplace prior. Strawderman-Berger priors (Strawderman (1971), Berger (1980)) have some desirable properties yet lack a simple analytic form. Recently proposed priors have been designed to have high density near zero and heavy tails without the impropriety problem of Normal-Jeffreys. The horseshoe prior of Carvalho, Polson, and Scott (2009, 2010) is induced through a carefully-specified mixture of normals, leading to such desirable properties as an infinite spike at zero and very heavy tails. They studied sparse shrinkage estimation properties of the horseshoe in a normal means problem. Griffin and Brown (2007, 2010) proposed an alternative class of hierarchical priors for shrinkage with some similarities to the prior we propose, but it lacks a simple analytic form that facilitates the study of some properties.

There is a need for alternative shrinkage priors that lead to sparse point estimates if desired, do not over-shrink coefficients that are not close to zero, facilitate straight-forward computation even in large p cases, and result in a joint posterior distribution that does a good job of quantifying uncertainty. We propose the generalized double Pareto prior which independently finds mention in Cevher (2009). It has a simple analytic form, yields a proper posterior, and possesses such appealing properties as a spike at zero, Student’s t-like tails, and a simple characterization as a scale mixture of normals that leads to a straightforward Gibbs sampler for posterior inferences. We consider both fully Bayesian and frequentist penalized likelihood approaches based on this prior. We show that the induced penalty in the regularization framework yields a consistent thresholding rule having the continuity property in the orthogonal case, with a simple expectation-maximization algorithm described for sparse estimation in non-orthogonal cases. In another independent work motivated by applications to genome wide associations studies, Lee et al. (2011) consider a generalized t prior (McDonald and Newey (1988)) that includes the generalized double Pareto as a special case. Similarities to previous work are limited and our contributions beyond them are (i) the formal introduction of a generalized Pareto density, thresholded and folded at zero, as a shrinkage prior in Bayesian analysis, (ii) the scale mixture representation of the generalized double Pareto in Proposition 1 which is central to our work, (iii) its connection to the Laplace and Normal-Jeffreys’ priors as limiting cases in Proposition 2, (iv) the resulting fully conditional posteriors in a linear regression setting along with a simple Gibbs sampling procedure, (v) a detailed discussion on the hyper-parameters α and η and their treatment, along with the incorporation of a griddy sampling scheme into the Gibbs sampler, (vi) a detailed analysis of the induced penalty by the generalized double Pareto prior and the properties of the resulting thresholding rule, (vii) an explicit analytic form for the maximum a posteriori estimator in orthogonal cases, (viii) an expectation-maximization procedure to obtain the maximum a posteriori estimate in non-orthogonal cases using the normal mixture representation, (ix) the one-step estimator (Zou and Li (2008)) resulting from the Laplace mixture representation, revealing the connection of the resulting procedure to the adaptive LASSO of Zou (2006), and (x) the oracle properties of the resulting estimators.

2. Generalized Double Pareto Prior

The generalized double Pareto density is

$$f(\theta \mid \xi ,\alpha )=\frac{1}{2\xi }{\left(1+\frac{\mid \theta \mid }{\alpha \xi }\right)}^{-(\alpha +1)},$$ (2.1)

where ξ > 0 is a scale parameter and θ > 0 is a shape parameter. In contrast to (2.1), the generalized Pareto density of Pickands (1975) is parametrized in terms of a location parameter $\mu \in \mathbb{R}$, a scale parameter ξ > 0, and a shape parameter $\alpha \in \mathbb{R}$ as

$$f(\theta \mid \xi ,\alpha ,\mu )=\frac{1}{\xi }{\left(1+\frac{\theta -\mu }{\alpha \xi }\right)}^{-(\alpha +1)},$$ (2.2)

with θ ≥ μ for α > 0 and μ ≤ θ ≤ μ − ξα for α < 0. The mean and variance for the generalized Pareto distribution are $\mathbb{E}\left(\theta \right)=\mu +\xi ∕(1-1∕\alpha )$ for α ∉ [0, 1] and $\mathbb{V}\left(\theta \right)={\xi }^2{(1-1∕\alpha )}^{-2}{(1-2∕\alpha )}^{-1}$ for α ∉ [0, 2]. If we let μ = 0, (2.2) becomes an exponential density as α → ∞ with mean ξ and variance ξ².

To modify the generalized Pareto density to be a shrinkage prior, we let μ = 0 and reflect the positive part about the origin, assuming α > 0, for a density that is symmetric about zero. The mean and variance for the generalized double Pareto distribution are $\mathbb{E}\left(\theta \right)=0$ for α > 1 and $\mathbb{V}\left(\theta \right)=2{\xi }^2{\alpha }^2{(\alpha -1)}^{-1}{(\alpha -2)}^{-1}$ for α > 2. The dispersion is controlled by ξ and α, with α controlling the tail heaviness and α = 1 corresponding to Cauchy-like tails and no finite moments.

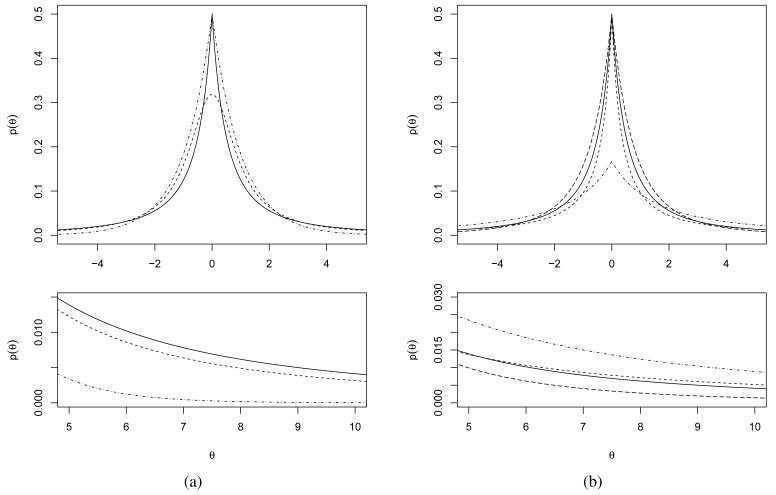
Figure 2.1 compares the density in (2.1) to Cauchy and Laplace densities for the special case ξ = α = 1, so that f(θ) = 1/{2(1 + |θ|)²}. We refer to this form as the standard double Pareto. Near zero, the standard double Pareto resembles the Laplace density, suggesting similar sparse shrinkage properties of small coefficients in maximum a posteriori estimation. It also has Cauchy-like tails, which is appealing in avoiding over-shrinkage away from the origin. This is illustrated in Figure 2.1(a). Figure 2.1(b) illustrates how the density in (2.1) changes for different values of ξ and α.

Figure 2.1.

(a) Probability density functions for standard double Pareto (solid line), standard Cauchy (dashed line) and Laplace (dot-dash line) (λ = 1) distributions. (b) Probability density functions for the generalized double Pareto with (ξ, α) values of (1, 1) (solid line), (0.5, 1) (dashed line), (1, 3) (long-dashed line), and (3, 1) (dot-dash line).

Prior (2.1) can be represented as a scale mixture of normal distributions leading to computational simplifications. As shorthand notation, let θ ~ GDP(ξ, α) denote that θ has density (2.1).

Proposition 1. Let θ ~ N(0, τ), τ ~ Exp(λ²/2), and λ ~ Ga(α, η), where α > 0 and η > 0. The resulting marginal density for θ is GDP(ξ = η/α, α).

Proposition 1 reveals a relationship between the prior in (2.1) and the prior of Griffin and Brown (2007), with the difference being that Griffin and Brown (2007) place a mixing distribution on λ² leading to a marginal density on θ with no simple analytic form.

In Proposition 2 we show that the prior in (2.1) forms a bridge between two limiting cases – Laplace and Normal-Jeffreys’ priors.

Proposition 2. Given the representation in Proposition 1, θ GDP(ξ = η/α, α) implies

1. f(θ) ∝ 1/|θ| for α = 0 and η = 0,

2. f(θ|λ′) = (λ′/2) exp (−λ′|θ|) for α → ∞, α/η = λ′ and 0 < λ′ < ∞

Proof. For the first item, setting α = η = 0 implies placing a Jeffreys’ prior on λ, π(λ) ∝ 1/λ. Integration over λ yields π(τ) ∝ 1/τ, which implies the Normal-Jeffreys’ prior on θ. For the second item, notice that π(λ) = δ(λ − λ′), where δ(.) denotes the Dirac delta function, since ${\lim }_{\alpha \to \infty }{\lim }_{\alpha ∕\eta \to {\lambda }^{\prime }}\mathbb{E}\left(\lambda \right)={\lambda }^{\prime }$ and ${\lim }_{\alpha \to \infty }{\lim }_{\alpha ∕\eta \to {\lambda }^{\prime }}\mathbb{V}\left(\lambda \right)=0$. Thus, ${\int }_0^{\infty }(\lambda ∕2)\exp (-\lambda \mid \theta \mid )\delta \left(d\lambda \right)=({\lambda }^{\prime }∕2)\exp (-{\lambda }^{\prime }\mid \theta \mid )$.

As noted in Polson and Scott (2010), if π(τ) has exponential or lighter tails, observations are shrunk towards zero by some non-diminishing amount, regardless of size. This phenomenon is well-understood and commonly observed in estimation under the Laplace prior, where an exponential density mixes a normal density. The higher-level mixing (over λ) in Proposition 1 allows π(τ) to have heavier tails, remedying the unwanted bias.

As α grows, the density becomes lighter tailed, more peaked and the variance becomes smaller, while as η grows, the density becomes flatter and the variance increases. Hence if we increase α, we may cause unwanted bias for large signals, though causing stronger shrinkage for noise-like signals; if we increase η we may lose the ability to shrink noise-like signals, as the density is not as pronounced around zero; and finally, if we increase α and η at the same rate, the variance remains constant but the tails become lighter, converging to a Laplace density in the limit. This leads to over-shrinking of coefficients that are away from zero. As a typical default specification for the hyperparameters, one can take α = η = 1. This choice leads to Cauchy-like tail behavior, which is well-known to have desirable Bayesian robustness properties.

To motivate this default choice, we assess the behavior of the prior shrinkage factor κ = 1/(1 + τ) ∈ (0, 1), where θ ~ N(0, τ) is the parameter of interest (Carvalho et al. (2010)). As κ → 0, the prior imposes no shrinkage, while as κ → 1 it has a strong pull towards zero. The generalized double Pareto distribution implies a prior π(κ) on κ upon integration over λ in Proposition 1. For the standard double Pareto, this is

$$\pi \left(\kappa \right)=\frac{1}{2{(1-\kappa )}^2}\left[\frac{\sqrt{\pi }\exp \left\{\frac{\kappa }{2(1-\kappa )}\right\}\text{Erfc}\left\{\sqrt{\frac{\kappa }{2(1-\kappa )}}\right\}}{\sqrt{2\kappa (1-\kappa )}}-1\right],$$

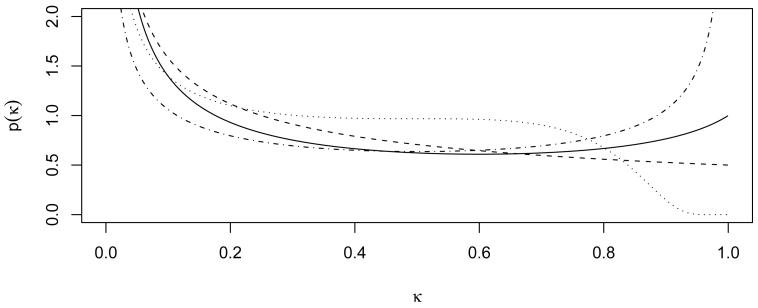
where Erfc(.) denotes the complementary error function. In Figure 2.2, we compare π(κ) under the standard double Pareto, Strawderman-Berger, horseshoe, and Cauchy priors, which may all be considered default choices. The priors behave similarly for κ ≈ 0, implying similar tail behavior. The behavior of π(κ) for κ ≈ 1 governs the strength of shrinkage of small signals. As κ → 1, π(κ) tends towards zero for the Cauchy, implying weak shrinkage, while π(κ) is unbounded for the horseshoe, suggesting a strong pull towards zero for small signals. The Strawderman-Berger and standard double Pareto priors are a compromise between these extremes, with π(κ) bounded for κ → 1 in both cases. The standard double Pareto assigns higher density close to one than the Strawderman-Berger prior, and has the advantage of a simple analytic form over the Strawderman-Berger and horseshoe priors.

Figure 2.2.

Prior density of κ implied by the standard double Pareto prior (solid line), Strawderman–Berger prior (dashed line), horseshoe prior (dot-dash line) and standard Cauchy prior (dotted line).

Of course it is best to adjust α and η according to any available prior information pertaining to the sparsity structure of the estimated vector. For general α > 0 and η > 0 values, the prior on κ is

$$\pi (\kappa \mid \alpha ,\eta )=\frac{2^{\alpha ∕2-1}{\eta }^{\alpha }{\kappa }^{(\alpha -1)∕2}{(1-\kappa )}^{-(\alpha +3)∕2}}{\Gamma \left(\alpha \right)}\times \left\{{\left(\frac{1}{\kappa }-1\right)}^{1∕2}\Gamma (\frac{\alpha }{2}+1){}_1\text{F}_1\left(\frac{\alpha }{2}+1,\frac{1}{2},\frac{{\eta }^2\kappa }{2(1-\kappa )}\right)-\sqrt{2}\eta \Gamma \left(\frac{\alpha +3}{2}\right){}_1\text{F}_1\left(\frac{\alpha +3}{2},\frac{3}{2},\frac{{\eta }^2\kappa }{2(1-\kappa )}\right)\right\},$$ (2.3)

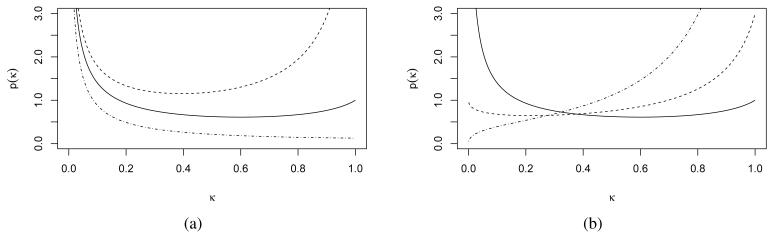
where ${}_1\text{F}_1$ denotes the confluent hypergeometric function. Note that π(κ|α, η) takes a “horseshoe” shape when α = η = 0. Carvalho, Polson, and Scott (2010) show that π(κ) ∝ κ⁻¹(1−κ)⁻¹ implies a Normal-Jeffreys’ prior on θ, which can also be observed by setting α = η = 0 in (2.3) in conjunction with Proposition 1. Hence π(κ|α, η) is unbounded at κ = 1 forcing π(θ|α, η) to be unbounded at 0 only if η = 0. The effects of α and η are now observed with better clarity from Figure 2.3. As η increases, less and less density is assigned to the neighborhood of κ ≈ 1, repressing shrinkage. On the other hand, increasing α values place more and more density in the neighborhood of κ ≈ 1 promoting further shrinkage. This notion is later reinforced by Proposition 3, such that the prior induces a thresholding rule under maximum a posteriori estimation if $\eta <2\sqrt{\alpha +1}$. Hence, we need to carefully pick these hyper-parameters, in particular α, as there is a trade-off between the magnitude of shrinkage and tail robustness.

Figure 2.3.

Prior density of κ (a) when α = 1 and η = 0.5 (dashed), η = 1 (solid), η = 2 (dot-dash) (b) when η = 1 and α = 1 (solid), α = 2 (dashed), α = 3 (dot-dash).

3. Bayesian Inference in Linear Models

Consider the linear regression model y = Xβ + ∊, where y is an n-dimensional vector of responses, X is the n × p design matrix and ∊ ~ N (0, σ²I_n). Letting β_j|σ ~ GDP(ξ = ση/α, α) independently for j = 1, …, p,

$$\pi (\beta \mid \sigma )=\underset{j=1}{\overset{p}{\Pi }}\frac{1}{2\sigma \eta ∕\alpha }{\left(1+\frac{1}{\alpha }\frac{\mid {\beta }_j\mid }{\sigma \eta ∕\alpha }\right)}^{-(\alpha +1)}.$$ (3.1)

From Proposition 1, this prior is equivalent to β_j|σ ~ N(0, σ²τ_j), with ${\tau }_j~\mathrm{Exp}({\lambda }_j^2∕2)$ and λ_j ~ Ga(α, η). We place the Jeffreys’ prior on the error variance, π(σ) ∝ 1/σ.

Using the scale mixture of normals representation, we obtain a simple data augmentation Gibbs sampler having the conditional posteriors (β|σ², T, y) ~ N (X′X + T⁻¹)⁻¹X′y, σ² (X′X + T⁻¹)⁻¹, (σ²|β, T, y) ~ IG{(n + p)/2, (y − Xβ)′(y − Xβ)/2}, (λ_j|β_j, σ²) ~ Ga(α + 1, |β_j|/σ + η), $({\tau }_j^{-1}\mid {\beta }_j,{\lambda }_j,{\sigma }^2)~\mathrm{Inv}-\mathrm{Gauss}\{\mu ={({\lambda }_j^2{\sigma }^2∕{\beta }_j^2)}^{1∕2},\rho ={\lambda }^2\}$, where T = diag(τ₁, …, τ_p) and Inv-Gauss denotes the inverse Gaussian distribution with location and scale parameters μ and ρ. In our experience, this Gibbs sampler is efficient with fast rates of convergence and mixing.

In the absence of any prior information on α and η, one may either set them to their default values or, as an alternative, choose hyper-priors to allow the data to inform about the values of α and η. We use π(α) = 1/(1+α)² and π(η) = 1/(1+η)² to correspond to generalized Pareto hyper-priors with location parameter 0, scale parameter 1 and shape parameter 1. The median value of the resulting distribution for α and η is 1, centered at the default choices suggested earlier, while the mean and variance do not exist.

For sampling purposes, let a = 1/(1+α) and e = 1/(1+η). These transformations suggest a uniform prior on a and e in (0, 1) given the generalized Pareto priors on α and η. Consequently, the conditional posteriors for a and e are

$$\pi (a\mid \beta ,\eta )\propto {\left(\frac{1-a}{a}\right)}^p\underset{j=1}{\overset{p}{\Pi }}{\left(1+\frac{\mid {\beta }_j\mid }{\sigma \eta }\right)}^{-1∕a},$$

$$\pi (e\mid \beta ,\alpha )\propto {\left(\frac{e}{1-e}\right)}^p\underset{j=1}{\overset{p}{\Pi }}{\left\{1+e\frac{\mid {\beta }_j\mid }{\sigma (1-e)}\right\}}^{-(\alpha +1)}.$$

We propose the embedded griddy Gibbs (Ritter and Tanner (1992)) sampling scheme:

1. Form a grid of m points a⁽¹⁾, …, a^(m) in the interval (0, 1).

2. Calculate w^(k) = π(a^(k)|β, η).

3. Normalize the weights, $w_N^{\left(k\right)}=w^{\left(k\right)}∕{\sum }_{k=1}^m{w}^{\left(k\right)}$.

4. Draw a sample from the set {a⁽¹⁾, …, a^(m)} with probabilities {$w_N^{\left(1\right)},\dots ,w_N^{\left(m\right)}$}, and set α = 1/a − 1 to be used at the current iteration of the Gibbs sampler.

Repeat the same procedure for e and obtain a random draw for η. We also experiment with fixing η as 1 while treating α as unknown. In this case, the prior variance of β|σ² is determined by α.

In what follows we establish the ties between the Bayesian approach we have taken and some frequentist regularization approaches. The simple analytic structure of the generalized double Pareto prior facilitates analyses while its hierarchical formulation leads to straight-forward computation.

4. Sparse Maximum a Posteriori Estimation

The generalized double Pareto distribution can be used not only as a prior in a Bayesian analysis, but also to induce a sparsity-favoring penalty in regularized least squares:

$$\tilde{\beta }=\text{arg}\underset{\beta }{\min }\left\{\frac{1}{2{\sigma }^2}{\parallel \mathrm{y}-\mathrm{X}\beta \parallel }^2+\sum _{j=1}^{p}p(\mid {\beta }_j\mid )\right\},$$ (4.1)

where X is initially assumed to have orthonormal columns and p(.) denotes the penalty function implied by the prior on the regression coefficients. Following Fan and Li (2001), let $\widehat{\beta }={\text{X}}^{\prime }\text{y}$, and denote the minimization problem in (4.1) for a component of β as

$${\tilde{\beta }}_j=\arg \underset{{\beta }_j}{\min }\left\{\frac{1}{2}{({\widehat{\beta }}_j-{\beta }_j)}^2+{\sigma }^{2}p(\mid {\beta }_j\mid )\right\},$$ (4.2)

with the penalty function p(|β_j|) = (α + 1) log (ση + |β_j|) that simply retains the term in −log π(β_j|α, η) that depends on β_j.

From Fan and Li (2001), a good penalty function should result in an estimator that is (i) nearly unbiased when the true unknown parameter is large, (ii) a thresholding rule that automatically sets small estimated coefficients to zero to reduce model complexity, and (iii) continuous in data (${\widehat{\beta }}_j$) to avoid instability in model prediction. In the following, we show that the penalty function induced by prior (3.1) may achieve these properties.

4.1. Near-unbiasedness

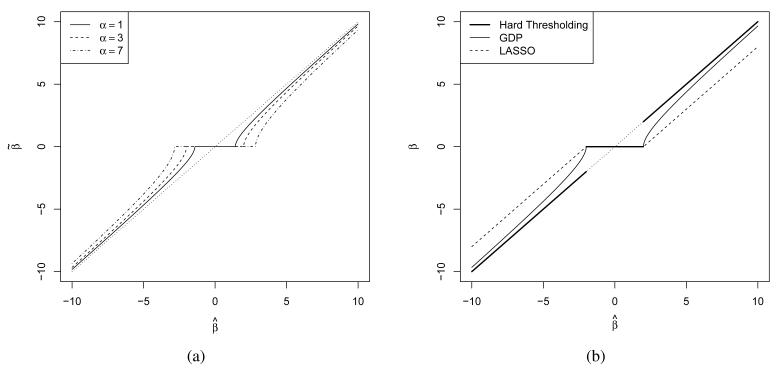
The first order derivative of (4.2) with respect to β_j is $\mathrm{sgn}\left({\beta }_j\right)\{\mid {\beta }_j\mid +{\sigma }^2{p}^{\prime }(\mid {\beta }_j\mid \left)\right\}-{\widehat{\beta }}_j=\mathrm{sgn}\left({\beta }_j\right)\{\mid {\beta }_j\mid +{\sigma }^2(\alpha +1)∕(\sigma \eta +\mid {\beta }_j\mid \left)\right\}-{\widehat{\beta }}_j$, where p′(|β_j|) = ∂p(|β_j|)/∂|β_j| is the term causing bias in estimation. Although it is appealing to introduce bias in small coefficients to reduce the mean squared error and model complexity, it is also desirable to limit the shrinkage of large coefficients with p′(|β_j|) → 0 as |β_j| → ∞. In addition, it is desirable for p′(|β_j|) to approach zero rapidly, implying shrinkage, and the associated introduction of bias rapidly decreases as coefficients get further away from zero. In fact, the rate of convergence of p′(|β_j|) to zero is of the same order under the generalized double Pareto and Normal-Jeffreys’ priors, with ${\lim }_{\mid {\beta }_j\mid \to \infty }\left\{\right(\alpha +1)∕(\sigma \eta +\mid {\beta }_j\mid \left)\right\}∕\{1∕\mid {\beta }_j\mid \}=\alpha +1$. As α controls the tail heaviness in the generalized double Pareto prior, with lighter tails for larger values of α, convergence of the ratio to (α + 1) is intuitive. In the case of LASSO, the bias, p′(|β_j|), remains constant regardless of |β_j|, which can also be observed in Figure 4.4(b).

Figure 4.4.

Thresholding functions for (a) generalized double Pareto prior with $\eta =\sqrt{\alpha +1}$, α = {1, 3, 7}, (b) Hard thresholding, generalized double Pareto prior with η = 2, α = 3 and LASSO with σ = 1.

4.2. Sparsity

As noted in Fan and Li (2001), a sufficient condition for the resulting estimator to be a thresholding rule is that the minimum of the function |β_j| + σ²p′(|β_j|) is positive.

Proposition 3. Under the formulation in Proposition 1, prior (3.1) implies a penalty yielding an estimator that is a thresholding rule if $\eta <2\sqrt{\alpha +1}$.

This result is obtained by finding the minimum of |β_j| + σ²p′(|β_j|) and taking it greater than zero. The thresholding is a direct consequence of the fact that when $\mid {\widehat{\beta }}_j\mid <{\min }_{{\beta }_j}\{\mid {\beta }_j\mid +{\sigma }^2(\alpha +1)∕(\sigma \eta +\mid {\beta }_j\mid \left)\right\}$, which requires that ${\min }_{{\beta }_j}\{\mid {\beta }_j\mid +{\sigma }^2{p}^{\prime }(\mid {\beta }_j\mid \left)\right\}>0$, the derivative of (4.2) is positive for all positive β_j and negative for all negative β_j. In this case, the penalized least squares estimator is zero. When $\mid {\widehat{\beta }}_j\mid >{\min }_{{\beta }_j}\{\mid {\beta }_j\mid +{\sigma }^2(\alpha +1)∕(\sigma \eta +\mid {\beta }_j\mid \left)\right\}$, two roots may exist. The larger one (in absolute value) or zero is the penalized least squares estimator. To elaborate more on this, the root(s) may exist for $\mathrm{sgn}\left({\beta }_j\right)\{\mid {\beta }_j\mid +{\sigma }^2{p}^{\prime }(\mid {\beta }_j\mid \left)\right\}-{\widehat{\beta }}_j=0$ only when $\mid {\widehat{\beta }}_j\mid >{\min }_{{\beta }_j}\{\mid {\beta }_j\mid +{\sigma }^2{p}^{\prime }(\mid {\beta }_j\mid \left)\right\}$. A helpful illustration is Figure 3 of Fan and Li (2001).

4.3. Continuity

Continuity in data is important if an estimator is to avoid instabilities in prediction. As in Breiman (1996), “a regularization procedure is unstable if a small change in data can make large changes in the regularized estimator”. Discontinuities in the thresholding rule may result in inclusion or dismissal of a signal with minor changes in the data used (see Figure 4.4(b)). Hard-thresholding, the “usual” variable selection, is an unstable procedure, while ridge and LASSO estimates are considered stable.

A necessary and sufficient condition for continuity is that the minimum of the function |β_j| + σ²p′(|β_j|) is at zero (Fan and Li (2001)). For our prior, the minimum of this function is obtained at $\mid {\beta }_j\mid =\sigma (\sqrt{\alpha +1}-\eta )$. Therefore $\eta =\sqrt{\alpha +1}$ yields an estimator with this property.

Proposition 4. Under the formulation in Proposition 1, a subfamily of prior (2.1) with $\eta =\sqrt{\alpha +1}$ yields an estimator with the continuity property.

In this particular case, the penalized likelihood estimator is set to zero if $\mid {\widehat{\beta }}_j\mid \le \sigma \sqrt{\alpha +1}$. When $\mid {\widehat{\beta }}_j\mid >\sigma \sqrt{\alpha +1}$

$${\tilde{\beta }}_j=\{\begin{array}{cc}\frac{{\widehat{\beta }}_j-\sigma \sqrt{\alpha +1}+{\{{\widehat{\beta }}_j^2+2{\widehat{\beta }}_j\sigma \sqrt{\alpha +1}-3{\sigma }^2(\alpha +1\left)\right\}}^{1∕2}}{2}\hfill & {\widehat{\beta }}_j>0,\hfill \\ \frac{{\widehat{\beta }}_j+\sigma \sqrt{\alpha +1}-{\{{\widehat{\beta }}_j^2-2{\widehat{\beta }}_j\sigma \sqrt{\alpha +1}-3{\sigma }^2(\alpha +1\left)\right\}}^{1∕2}}{2}\hfill & {\widehat{\beta }}_j<0.\hfill \end{array}\phantom{\}}$$ (4.3)

As can be observed in Figure 4.4(a), ensuring continuity by letting $\eta =\sqrt{\alpha +1}$ creates a trade-off between sparsity and tail-robustness. As the thresholding region becomes wider, the larger values are penalized further, yet not nearly at the level of LASSO.

4.4. Maximum a Posteriori Estimation via Expectation-Maximization

We assume a normal likelihood to formulate the procedure for non-orthogonal linear regression. Estimation is carried out via the expectation-maximization (EM) algorithm.

4.4.1. Exploiting the Normal Mixture Representation

We take the expectation of the log-posterior with respect to the conditional posterior distributions of (${\tau }_j^{-1}\mid {\beta }_j^{\left(k\right)}$, ${\lambda }_j,{\sigma }^{2\left(k\right)}$) and (${\lambda }_j\mid {\beta }_j^{\left(k\right)}$, σ^2(k)) at the kth step, then maximize with respect to β_j and σ² to get the values for the (k + 1)th step.

• E-step:

  
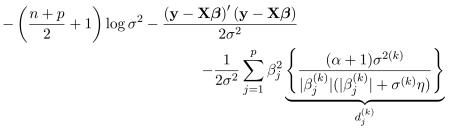
• M-step: Letting ${\text{D}}^{\left(k\right)}=\mathrm{diag}(d_1^{\left(k\right)},\dots ,d_p^{\left(k\right)})$, we have

  $${\beta }^{(k+1)}={({\text{X}}^{\prime }\text{X}+{\text{D}}^{\left(k\right)})}^{-1}{\text{X}}^{\prime }\text{y},$$

  $${\sigma }^{2(k+1)}=\frac{{(\text{y}-\text{X}{\beta }^{(k+1)})}^{\prime }(\text{y}-\text{X}{\beta }^{(k+1)})+{\beta }^{{(k+1)}^{\prime }}{\text{D}}^{\left(k\right)}{\beta }^{(k+1)}}{n+p+2}$$

We refer to this estimator as GDP(MAP).

4.4.2. Exploiting the Laplace Mixture Representation and the One-step Estimator

In the proof of Proposition 1, the integration over τ leads to a Laplace mixture representation of the prior. Since the mixing distribution of the Laplace is a known distribution the required expectation is obtained with ease, resulting in the maximization step,

$$\begin{array}{cc}\hfill {\beta }^{(k+1)}& =\arg \underset{\beta }{\max }\left\{-\frac{1}{2{\sigma }^{2\left(k\right)}}{(\text{y}-\text{X}\beta )}^{\prime }(\text{y}-\text{X}\beta )-\frac{1}{{\sigma }^{\left(k\right)}}\sum _{j=1}^p\mid {\beta }_j\mid \left(\frac{\alpha +1}{\mid {\beta }_j^{\left(k\right)}\mid ∕{\sigma }^{\left(k\right)}+\eta }\right)\right\},\hfill \\ \hfill {\sigma }^{2(k+1)}& =\frac{b^2-2ac-\sqrt{b^2-4ac{b}^2}}{2a^2},\hfill \end{array}$$ (4.4)

Where a = −(n + p +2), $b=(\alpha +1){\sum }_j\mid {\beta }_j^{(k+1)}\mid ∕(\mid {\beta }_j^{\left(k\right)}\mid ∕{\sigma }^{\left(k\right)}+\eta )$, and $c={(\text{y}-\text{X}{\beta }^{(k+1)})}^{\prime }(\text{y}-\text{X}{\beta }^{(k+1)})$. The component-specific multiplier on |β_j| is obtained from the expectation of λ_j with respect to its conditional posterior distribution, π(λ_j|β_j, σ²). Similar results to (4.4) are in Candes, Wakin and Boyd (2008), Cevher (2009), and Garrigues (2009).

An intuitive relationship to the adaptive LASSO of Zou (2006) and the one-step sparse estimator of Zou and Li (2008) can be seen via the Laplace mixture representation. As a computationally fast alternative to estimating the exact mode via the above EM algorithm, we can obtain a “one-step estimator” and exploit the LARS algorithm as in Zou and Li (2008). The one-step estimator is

$${\beta }^{\left(1\right)}=\arg \underset{\beta }{\min }\left\{{(\text{y}-\text{X}\beta )}^{\prime }(\text{y}-\text{X}\beta )+a^{†}\sum _{j=1}^p\frac{\mid {\beta }_j\mid }{\mid {\beta }_j^{\left(0\right)}\mid +{\eta }^{†}}\right\},$$ (4.5)

with α^† = 2σ²⁽⁰⁾(α + 1) and η^† = σ⁽⁰⁾η. This estimator resembles the adaptive LASSO. The LARS algorithm can be used to obtain β⁽¹⁾ very quickly. We refer to this estimator as GDP(OS).

Remark 1. For η^† = 0, the GDP(OS) solution path for varying α^† is identical to the adaptive LASSO solution path with γ = 1 (see (4) in Zou (2006)) using identical β⁽⁰⁾.

Remark 2. GDP(OS) forms a bridge between the LASSO and the adaptive LASSO: as η^† → ∞ and α^†/η^† → λ^† < ∞, GDP(OS) gives the LASSO solution with penalty parameter λ^†.

We derive the GDP(OS) estimator only to reveal a close connection with the adaptive LASSO of Zou (2006) and do not use it in our experiments.

4.4.3. Normal vs. Laplace Representations in Computation

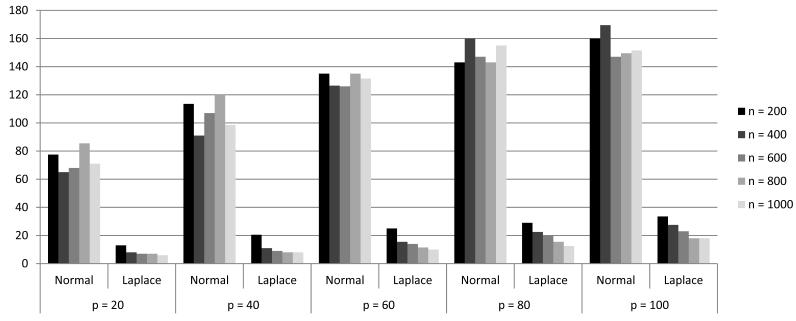
As pointed out by an anonymous referee, it is appropriate to compare the convergence behavior of the EM algorithms that exploit different mixture representations. We generated n = {200, 400, 600, 800, 1000} observations from $y_i={\text{x}}_i^{\prime }{\beta }^{\ast }+{∊}_i$, where the x_ij were independent standard normals for p = {20, 40, 60, 80, 100}, ∊ ~ N(0, σ²), and σ = 3. We set the first p/4 components of β* to be 1 and the rest to 0. For each (n, p) combination we simulated 100 data sets and ran the EM algorithms obtained from normal and Laplace scale mixture representations. Figure 4.5 illustrates the number of iterations taken by the two algorithms until ∥β^(k+1) − β^(k)∥₂ < 10⁻⁶. As expected, the convergence under the Laplace mixture representation was much faster with the intermediary mixing parameter τ_j integrated out rather than using the expectation step in the EM algorithm.

Figure 4.5.

Number of iterations until convergence of the EM algorithms under normal and Laplace representations.

4.5. Oracle Properties

Following Zou (2006) and Zou and Li (2008), we show that the GDP(MAP) and GDP(OS) estimators possess oracle properties. Relaxing the normality assumption on the error term leads to two conditions for Theorem 2 and Theorem 3.

• (A1)y_i = x_iβ* + ∊_i where ∊₁, …, ∊_n are independent and identically distributed with mean 0 and variance σ².
• (A2)$\frac{1}{n}{\text{X}}^{\prime }\text{X}\to \text{C}$, where C is a positive definite matrix.

In what follows, $\mathcal{A}=\{j:{\beta }_j^{\ast }\ne 0,j=1,\dots ,p\}$, ${\beta }_{\mathcal{A}}$ retains the entries of β indexed by $\mathcal{A}$, and ${\text{C}}_{\mathcal{A}}$ retains the rows and columns of C indexed by $\mathcal{A}$.

Theorem 1. Let

$${\beta }_n^{\left(\infty \right)}=\arg \underset{\beta }{\min }\left\{{(\text{y}-\text{X}\beta )}^{\prime }(\text{y}-\text{X}\beta )+{\alpha }_n^{\prime }\sum _{j=1}^p\log (\mid {\beta }_j\mid +{\eta }_n^{\prime })\right\}$$

denote the GDP(MAP) estimator, where ${\alpha }_n^{\prime }=2{\sigma }^2({\alpha }_n+1)$ and ${\eta }_n^{\prime }=\sigma {\eta }_n$. Let ${\mathcal{A}}_n=\{j:{\beta }_{nj}^{\left(\infty \right)}\ne 0,j=1,\dots ,p\}$. Suppose that ${\alpha }_n^{\prime }\to \infty$, ${\alpha }_n^{\prime }∕\sqrt{n}\to 0$ and, ${\eta }_n^{\prime }\sqrt{n}\to c<\infty$. Then ${\beta }_n^{\left(\infty \right)}$ is

1. consistent in variable selection in that ${\lim }_{n\to \infty }\mathbb{P}({\mathcal{A}}_n=\mathcal{A})=1$;

2. asymptotically normal with $\sqrt{n}({\beta }_{n,\mathcal{A}}^{\left(\infty \right)}-{\beta }_{\mathcal{A}}^{\ast })\stackrel{d}{\to }N(0,{\sigma }^2{\text{C}}_{\mathcal{A}}^{-1})$.

Remark 3. More generally, the above results hold if ${\alpha }_n^{\prime }∕\left(\sqrt{n}{\eta }_n^{\prime }\right)\to \infty$ and ${\alpha }_n^{\prime }∕\sqrt{n}\to 0$.

Theorem 2. Let ${\beta }_n^{\left(1\right)}$ denote the GDP(OS) estimator in (4.5) and ${\mathcal{A}}_n=\{j:{\beta }_{nj}^{\left(1\right)}\ne 0,j=1,\dots ,p\}$. Suppose that ${\alpha }_n^{†}\to \infty$, ${\alpha }_n^{†}∕\sqrt{n}\to 0$, and ${\eta }_n^{†}\sqrt{n}\to c<\infty$. Then ${\beta }_n^{\left(1\right)}$ is

1. consistent in variable selection in that ${\lim }_{n\to \infty }\mathbb{P}({\mathcal{A}}_n=\mathcal{A})=1$;

2. asymptotically normal with $\sqrt{n}({\beta }_{n,\mathcal{A}}^{\left(1\right)}-{\beta }_{\mathcal{A}}^{\ast })\stackrel{d}{\to }N(0,{\sigma }^2{\text{C}}_{\mathcal{A}}^{-1})$.

The proofs are deferred to Section 8.

5. Experiments

5.1. Simulation

In this section, we compare the proposed estimators to the posterior means obtained under the normal, Laplace, and horseshoe priors, to the Bayesian model averaged (BMA) estimator, as well as to the sparse estimates resulting from LASSO (Tibshirani (1996)) and SCAD (Fan and Li (2001)). GDP(PM) and GDP(MAP) denote the posterior mean and the MAP estimates, respectively, under the generalized double Pareto prior. Hyper-parameter values are provided in footnotes of Tables 5.1 and 5.2 when fixed in advance and are otherwise treated as random with the priors specified in Section 3. When not fixed, we first obtain the posterior means of the hyper-parameters from an initial Bayesian analysis, then use them in the calculation of the MAP estimates.

Table 5.1.

Model error comparisons.

	n = 50
Method	Model 1	Model 2	Model 3	Model 4	Model 5
Normal	2.2990.085	4.8790.263	2.5850.134	4.9720.385	2.8860.150
Laplace	2.6340.137	3.6620.233	2.8370.126	4.3260.211	3.4580.120
Horseshoe	2.2640.086	2.3160.167	3.2050.140	3.9290.218	4.4090.130
BMA	2.4510.123	1.6470.126	4.0430.233	3.0620.194	6.0150.301
GDP(PM)1	2.3060.114	2.4050.192	3.1930.215	4.1230.304	4.2830.142
GDP(PM)2	2.3030.095	2.3090.195	3.1240.153	3.9100.237	4.4510.109
GDP(PM)	2.2710.085	2.6060.167	3.0470.147	4.3480.171	3.6400.134
GDP(MAP)1	3.4140.148	1.6190.150	5.6050.298	2.9700.168	8.7690.403
GDP(MAP)2	4.2500.354	1.6180.153	6.3310.300	3.0400.163	9.3080.377
GDP(MAP)	4.8760.355	2.0910.182	4.2990.222	3.7400.284	5.7240.177
LASSO	2.1830.124	2.6180.152	3.2580.194	3.5310.172	5.6460.229
SCAD	3.7320.214	2.1320.229	5.2490.239	3.1790.193	8.5050.387
	n = 400
Normal	0.3950.014	0.4550.019	0.4260.016	0.4550.024	0.4120.013
Laplace	0.3150.016	0.3740.014	0.3880.016	0.4220.015	0.4570.014
Horseshoe	0.2190.016	0.2050.010	0.3410.014	0.3460.009	0.5140.023
BMA	0.1510.011	0.1250.005	0.2400.016	0.2110.009	0.6460.037
GDP(PM)1	0.2330.016	0.2060.009	0.3260.015	0.2840.014	0.6250.031
GDP(PM)2	0.2280.017	0.2150.009	0.3320.013	0.3030.010	0.5790.027
GDP(PM)	0.2480.017	0.1820.007	0.3770.016	0.3620.012	0.4660.016
GDP(MAP)1	0.1540.014	0.1110.011	0.2860.016	0.2100.011	0.7390.043
GDP(MAP)2	0.1610.013	0.1110.010	0.2840.016	0.2100.009	0.6520.035
GDP(MAP)	0.1850.017	0.1190.010	0.3260.016	0.3360.010	0.4780.020
LASSO	0.2510.014	0.2760.014	0.3390.020	0.3480.011	0.4850.021
SCAD	0.1210.010	0.1180.008	0.2330.011	0.2060.017	0.4690.019

¹α = 1, η = 1

²η = 1

Table 5.2.

Posterior means of the hyper-parameters and the resulting model error.

		n = 50		n = 400
		GDP(PM)	GDP(PM)2	GDP(PM)	GDP(PM)2
Model 2	α	2.464	1.165	0.688	0.870
	η	4.181	–	0.614
	ME	2.443	2.219	0.149	0.181
Model 5	α	5.262	1.200	9.400	0.560
	η	9.476	–	51.735	–
	ME	6.290	7.019	0.518	0.614

²η = 1

We generated n = {50, 400} observations from $y_i={\text{x}}_i^{\prime }{\beta }^{\ast }+{∊}_i$, where the x_ij were standard normals with Cov(x_j, x_j′) = 0.5^|j−j′|, ∊_i ~ N(0, σ²), and σ = 3. We used the following β* configurations:

• Model 1: 5 randomly chosen components of β* set to 1 and the rest to 0.

• Model 2: 5 randomly chosen components of β* set to 3 and the rest to 0.

• Model 3: 10 randomly chosen components of β* set to 1 and the rest to 0.

• Model 4: 10 randomly chosen components of β* set to 3 and the rest to 0.

• Model 5: β* = (0.85, …, 0.85)′.

In our experiments y and the columns of X were centered and the columns of X scaled to have unit length. For the calculation of competing estimators we used lars (Hastie and Efron (2011)), SIS (Fan et al. (2010)), monomvn (Gramacy (2010)) and BAS (Clyde and Littman (2005), Clyde, Ghosh, and Littman (2010)) packages in R. We mainly followed the default settings provided by the packages. Under the normal prior, the so-called “ridge” parameter was given an inverse gamma prior with shape and scale parameters 10⁻³. Under the Laplace prior, as a default choice, a gamma prior was placed on the “LASSO parameter” λ², as given in (6) of Park and Casella (2008), with shape and rate parameters 2 and 0.1, respectively. Under the horseshoe prior, the monomvn package uses the hierarchy given in Section 1.1 of Carvalho, Polson, and Scott (2010). For BMA, we used the default settings of the BAS package that employs the Zellner-Siow prior given in Section 3.1 of Liang et al. (2008). The tuning for LASSO and SCAD were carried out by the criteria given in Yuan and Lin (2005) and Wang, Li, and Tsai (2007), respectively, avoiding cross-validation.

100 data sets were generated for each case. In Table 5.1, we report the median model error. Model error was calculated as ${({\beta }^{\ast }-\widehat{\beta })}^{\prime }\text{C}({\beta }^{\ast }-\widehat{\beta })$, where C is the variance-covariance matrix that generated X and $\widehat{\beta }$ denotes the estimator in use. The values in the subscripts give the bootstrap standard error of the median model error values obtained. The bootstrap standard error was calculated by generating 500 bootstrap samples from 100 model error values, finding the median model error for each case, and then calculating the standard error for it. Under each model, the best three performances are boldfaced in the tables.

GDP(PM) estimates showed a similar performance to that of horseshoe under sparse setups. GDP(PM) (with α and η unknown) also showed great flexibility in adapting to dense models with small signals. GDP(MAP) estimates performed similarly to SCAD and much better than LASSO, particularly so with increasing sparsity, signal and/or sample size. The GDP(PM) and GDP(MAP) calculations are straightforward and computationally inexpensive due to the normal (and Laplace) scale mixture representation used. Being able to use a simple Gibbs sampler (especially when α = η = 1) makes the procedure attractive for the average user.

Letting α = η = 1 may be somewhat restrictive if the underlying model is very dense or very sparse, but in the cases we considered, it performed comparably to others and we believe that it constitutes a good default prior similar to standard Cauchy with the added advantage of thresholding ability. Although we do not take up p ⪢ n cases in this paper, in such situations much larger values of would need to be chosen to adjust for multiplicity.

5.2. Inferences on Hyper-parameters

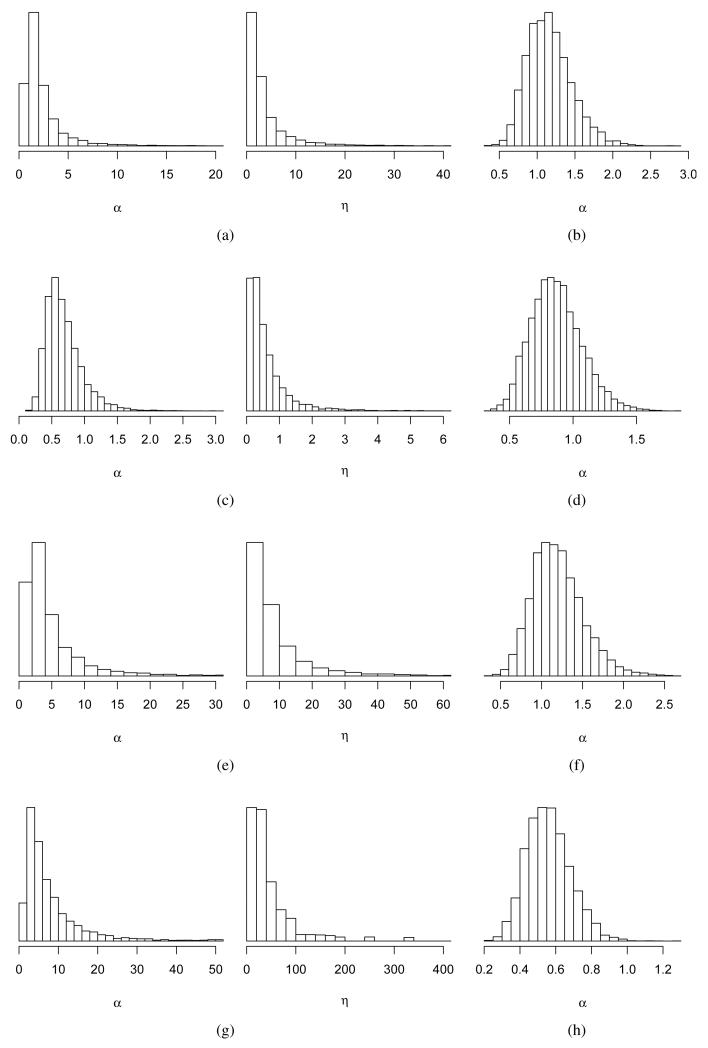
Here we take a closer look at the inferences on the hyper-parameters obtained from an individual data set for Models 2 and 5 from Section 5.1. This gives us some insight into how α and η are inferred with changing sample size and sparsity structure. Note that GDP(PM)² is more restrictive than GDP(PM) as η is fixed, treating only α as unknown. Figure 5.6 gives the marginal posteriors of α and η in cases of GDP(PM)² and GDP(PM) as described in Section 5.1, while Table 5.2 reports the posterior means for α and η, as well as model error (ME) performance (as calculated in Section 5.1) on the particular data set used. We clearly observe the adaptive nature and higher flexibility of GDP(PM) moving from a sparse to a dense model with a big increase, particularly in η, flattening the prior on β. There is not quite as much wiggle room in the case of GDP(PM)². All it can do is to drive α smaller to allow heavier tails to accommodate a dense structure. As observed in Table 5.1, however, GDP(PM)² performs comparably in sparse cases.

Figure 5.6.

Inferences for (a) GDP(PM) for n = 50 under Model 2, (b) GDP(PM)² for n = 50 under Model 2, (c) GDP(PM) for n = 400 under Model 2, (b) GDP(PM)² for n = 400 under Model 2, (e) GDP(PM) for n = 50 under Model 5, (f) GDP(PM)² for n = 50 under Model 5, (g) GDP(PM) for n = 400 under Model 5, (h) GDP(PM)² for n = 400 under Model 2.

6. Data Example

We consider the ozone data analyzed by Breiman and Friedman (1985) and by Casella and Moreno (2006). The original data set contains 13 variables and 366 observations. The modeled response is the daily maximum one-hour averaged ozone reading in Los Angeles over 330 days in 1976. There are p = 12 predictors considered and deleting incomplete observations leaves n = 203 observations. For validation, the data were split into a training set containing 180 observations and a test set containing 23 observations. We considered models including main effects, quadratic, and two-way interaction terms resulting in 2⁹⁰ possible subsets. The complex correlation structure of the data is illustrated in Figure 6.7.

Figure 6.7.

The correlation structure of the Ozone data.

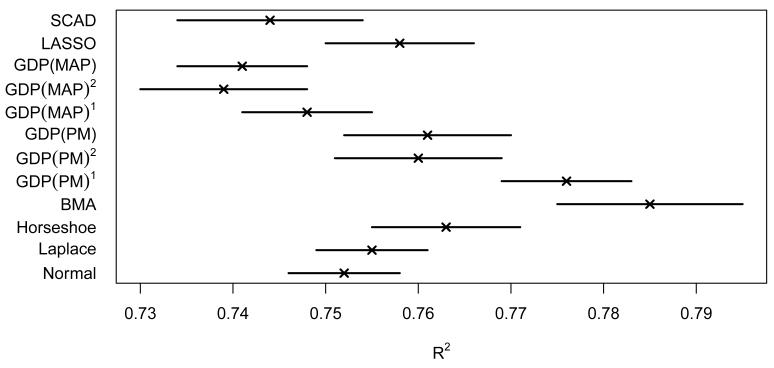
Figure 6.8 summarizes the performance of the proposed estimators and their competitors. Median values for ${\text{R}}_{\text{test}}^2$ and the ±2 standard error intervals were obtained by running the methods on 100 different random training-test splits. Standard errors were computed via bootstrapping the medians 500 times.

Figure 6.8.

Out-of-sample performance comparisons for Ozone data. (×) denotes the median value for ${\text{R}}_{\text{test}}^2$ while the lines represent the ±2 standard error regions. ¹α = 1, η = 1; ²η = 1.

The median number of predictors retained in the model by all three GDP(MAP) estimates was only 4 while it was 14 and 9 for LASSO and SCAD. Hence GDP(MAP) promoted much sparser models. In terms of prediction, GDP(PM)¹ yielded the second best results after BMA, with GDP(PM)², GDP(PM), and the horseshoe estimator all having somewhat worse performance. These shrinkage priors are designed to mimic model averaging behavior, so we expected to obtain results that were competitive with, but not better than, BMA. The improved performance for GDP(PM)¹ may be attributed to the use of default hyper-parameter values that were fixed in advance at values thought to produce good performance in sparse settings. Treating the hyper-parameters as unknown is appealing from the standpoint of flexibility, but in practice the data may not inform sufficiently about their values to outperform a good default choice. GDP(MAP)¹ and SCAD both performed within the standard error range of LASSO, while retaining a smaller number of variables in the model. As it is important to account for model uncertainty in prediction, the posterior mean estimator under the GDP prior is appealing in mimicking BMA. In addition, obtaining a simple model containing a relatively small number of predictors is often important, since such models are more likely to be used in fields in which predictive black boxes are not acceptable and practitioners desire interpretable predictive models.

7. Discussion

We have proposed a hierarchical prior obtained through a particular scale mixture of normals where the resulting marginal prior has a folded generalized Pareto density thresholded at zero. This prior combines the best of both worlds in that fully Bayes inferences are feasible through its hierarchical representation, providing a measure of uncertainty in estimation, while the resulting marginal prior on the regression coefficients induces a penalty function that allows for the analysis of frequentist properties under maximum a posteriori estimation. The resulting posterior mean estimator can be argued to be mimicking a Bayesian model averaging behavior through mixing over higher level hyper-parameters. Although Bayesian model averaging is appealing, it can be argued that allowing parameters to be arbitrarily close to zero instead of exactly equal to zero may be more natural in some problems. Hence we have a procedure that not only bridges two paradigms – Bayesian shrinkage estimation and regularization – but also yields three useful tools: a sparse estimator with good frequentist properties through maximum a posteriori estimation, a posterior mean estimator that mimics a model averaging behavior, and a useful measure of uncertainty around the observed estimates. In addition, the proposed methods have substantial computational advantages in relying on simple block-updated Gibbs sampling, while BMA requires sampling from a model space with 2^p models. Given the simple and fast computation and the excellent performance in small sample simulation studies, the generalized double Pareto should be useful as a shrinkage prior in a broad variety of Bayesian hierarchical models, while also suggesting close relationships with frequentist penalized likelihood approaches. The proposed prior can be used in generalized linear models, shrinkage of basis coefficients in non-parametric regression, and in such settings as factor analysis and nonparametric Bayes modeling.

8. Technical Details

Proof of Theorem 1. The proof follows along similar lines as does the proof of Theorem 2 in Zou (2006). We first prove asymptotic normality. Let $\beta ={\beta }^{\ast }+\text{u}∕\sqrt{n}$ and

$$V_n\left(\text{u}\right)={\left\{\text{y}-\sum _{j=1}^p{\text{x}}_j({\beta }_j^{\ast }+\frac{u_i}{\sqrt{n}}\right\}}^2+{\alpha }_n^{\prime }\sum _{j=1}^p\log \left\{\mid {\beta }_j^{\ast }+\frac{u_i}{\sqrt{n}}\mid +{\eta }_n^{\prime }\right\}.$$

Let ${\widehat{\mathrm{u}}}_n=\text{arg min}{V}_n\left(\text{u}\right)$, suggesting ${\widehat{\mathrm{u}}}_n=\sqrt{n}({\beta }_n^{\left(\infty \right)}-{\beta }^{\ast })$. Now

$$V_n\left(\text{u}\right)-V_n\left(0\right)={\text{u}}^{\prime }\left(\frac{1}{n}{\text{X}}^{\prime }\text{X}\right)\text{u}-2\frac{{∊}^{\prime }\text{X}}{\sqrt{n}}\text{u}+{\alpha }_n^{\prime }\sum _{j=1}^p\log \frac{\mid {\beta }_j^{\ast }+u_j∕\sqrt{n}\mid +{\eta }_n^{\prime }}{\mid {\beta }_j^{\ast }\mid +{\eta }_n^{\prime }}$$

and we know that X′X/n → C and ${∊}^{\prime }\text{X}∕\sqrt{n}\stackrel{d}{\to }\text{W}\stackrel{d}{=}N(0,{\sigma }^2\text{C})$. Consider the limiting behavior of the third term, noting that ${\lim }_{a\to \infty }{(1+b∕a)}^a=e^b$. If ${\beta }_j^{\ast }\ne 0$, then ${\alpha }_n^{\prime }\log \frac{\mid {\beta }_j^{\ast }+u_j∕\sqrt{n}\mid +{\eta }_n^{\prime }}{\mid {\beta }_j^{\ast }\mid +{\eta }_n^{\prime }}\le {\alpha }_n^{\prime }\log \frac{\mid {\beta }_j^{\ast }\mid +\mid u_j∕\sqrt{n}\mid +{\eta }_n^{\prime }}{\mid {\beta }_j^{\ast }\mid +{\eta }_n^{\prime }}={\alpha }_n^{\prime }\log (1+\frac{\mid u_j∕\sqrt{n}\mid }{\mid {\beta }_j^{\ast }\mid +{\eta }_n^{\prime }})\to 0$. If ${\beta }_j^{\ast }=0$, then ${\alpha }_n^{\prime }\log \frac{\mid u_j∕\sqrt{n}\mid +{\eta }_n^{\prime }}{{\eta }_n^{\prime }}={\alpha }_n^{\prime }\log (1+\frac{\mid u_j∕\sqrt{n}\mid }{{\eta }_n^{\prime }})$ which is 0 if u_j = 0, and diverges otherwise. By Slutsky’s Theorem

$$V_n\left(\text{u}\right)-V_n\left(0\right)\stackrel{d}{\to }\{\begin{array}{cc}{{\text{u}}^{\prime }}_{\mathcal{A}}{\text{C}}_{\mathcal{A}}{\text{u}}_{\mathcal{A}}-2{\text{u}}_{\mathcal{A}}^{\prime }{\text{W}}_{\mathcal{A}}\hfill & \text{if}{u}_j=0\forall j\notin \mathcal{A}\hfill \\ \infty \hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

V_n(u)−V_n(0) is convex and the unique minimum of the right hand side is ${({\text{C}}_{\mathcal{A}}^{-1}{\text{W}}_{\mathcal{A}},0)}^{\prime }$. By epiconvergence (Geyer (1994), Knight and Fu (2000)),

$${\widehat{\mathrm{u}}}_{n,\mathcal{A}}\stackrel{d}{\to }{\text{C}}_{\mathcal{A}}^{-1}{\text{W}}_{\mathcal{A}},{\widehat{\mathrm{u}}}_{n,{\mathcal{A}}^c}\stackrel{d}{\to }0.$$ (8.1)

Since ${\text{W}}_{\mathcal{A}}\stackrel{d}{=}N(0,{\sigma }^2{\text{C}}_{\mathcal{A}})$, this proves asymptotic normality.

Now $\forall j\in \mathcal{A},{\beta }_{nj}^{\left(\infty \right)}\stackrel{p}{\to }{\beta }_j^{\ast }$; thus $\mathbb{P}(j\in {\mathcal{A}}_n)\to 1$. Hence for consistency, it is sufficient to show that $\forall j^{\prime }\notin \mathcal{A},\mathbb{P}(j^{\prime }\in {\mathcal{A}}_n)\to 0$. Consider the event $j^{\prime }\in {\mathcal{A}}_n$. By the KKT optimality conditions, $2{\text{x}}_{j^{\prime }}^{\prime }(\text{y}-\text{X}{\beta }_n^{\left(\infty \right)})=\frac{{\alpha }_n^{\prime }}{{\eta }_n^{\prime }+\mid {\beta }_{n{j}^{\prime }}^{\left(\infty \right)}\mid }$. Noting that $\sqrt{n}{\beta }_{n{j}^{\prime }}^{\left(\infty \right)}\stackrel{p}{\to }0$ by (8.1), $\frac{{\alpha }_n^{\prime }}{\sqrt{n}{\eta }_n^{\prime }+\sqrt{n}\mid {\beta }_{n{j}^{prime}}^{\left(\infty \right)}\mid }\to \infty$, while

$$\frac{2{\text{x}}_{j^{\prime }}^{\prime }(\text{y}-\text{X}{\beta }_n^{\left(\infty \right)})}{\sqrt{n}}=2\left\{\frac{{\text{x}}_{j^{\prime }}^{\prime }\text{X}\sqrt{n}({\beta }^{\ast }-{\beta }_n^{\left(\infty \right)})}{n}+\frac{{\text{x}}_{j^{\prime }}^{\prime }∊}{\sqrt{n}}\right\}.$$

By (8.1) and Slutsky’s Theorem, we know that both terms in the brackets converge in distribution to some normal, so

$$\mathbb{P}(j^{\prime }\in {\mathcal{A}}_n)\le \mathbb{P}\left\{2{\text{x}}_{j^{\prime }}^{\prime }(\text{y}-\text{X}{\beta }_n^{\left(\infty \right)})=\frac{{\alpha }_n^{\prime }}{\mid {\beta }_{n{j}^{\prime }}^{\left(\infty \right)}\mid +{\eta }_n^{\prime }}\right\}\to 0.$$

This concludes the proof.

Proof of Theorem 2. We modify the proof of Theorem 2 in Zou (2006). Here ${\beta }_n^{\left(0\right)}$ denotes the least squares estimator. We first prove asymptotic normality. Let $\beta ={\beta }_n^{\ast }+\text{u}∕\sqrt{n}$ and

$$V_n\left(\text{u}\right)={\left\{y-\sum _{j=1}^p{x}_j({\beta }_{nj}^{\ast }+\frac{u_j}{\sqrt{n}}\right\}}^2+{\alpha }_n^{†}\sum _{j=1}^p\mid {\beta }_{nj}^{\ast }+\frac{u_j}{\sqrt{n}}\mid {(\mid {\beta }_{nj}^{\left(0\right)}\mid +{\eta }_n^{†})}^{-1}.$$

Let ${\widehat{\mathrm{u}}}_n=\text{arg min}{V}_n\left(\text{u}\right)$, suggesting ${\widehat{\mathrm{u}}}_n=\sqrt{n}({\beta }_n^{\left(1\right)}-{\beta }_n^{\ast })$. Now

$$V_n\left(\text{u}\right)-V_n\left(0\right)={\text{u}}^{\prime }\left(\frac{1}{n}{\text{X}}^{\prime }\text{X}\right)\text{u}-2\frac{{∊}^{\prime }\text{X}}{\sqrt{n}}\text{u}+\frac{{\alpha }_n^{†}}{\sqrt{n}}\sum _{j=1}^p{(\mid {\beta }_{nj}^{\left(0\right)}\mid +{\eta }_n^{†})}^{-1}\sqrt{n}(\mid {\beta }_{nj}^{\ast }+\frac{u_j}{\sqrt{n}}\mid -\mid {\beta }_{nj}^{\ast }\mid ),$$

and we know that X′X/n → C and ${∊}^{\prime }\text{X}∕\sqrt{n}\stackrel{d}{\to }\text{W}\stackrel{d}{=}N(0,{\sigma }^2\text{C})$. Consider the limiting behavior of the third term. If ${\beta }_{nj}^{\ast }\ne 0$ then, by the Continuous Mapping Theorem, ${\{\mid {\beta }_{nj}^{\left(0\right)}\mid +{\eta }_n^{†}\}}^{-1}\stackrel{p}{\to }{\{\mid {\beta }_{nj}^{\ast }\mid +{\eta }_n^{†}\}}^{-1}$ and $\sqrt{n}(\mid {\beta }_{nj}^{\ast }+u_j∕\sqrt{n}\mid -\mid {\beta }_{nj}^{\ast }\mid )\to u_j\mathrm{sgn}\left({\beta }_{nj}^{\ast }\right)$. By Slutsky’s Theorem, $({\alpha }_n^{†}∕\sqrt{n}){\{\mid {\beta }_{nj}^{\left(0\right)}\mid +{\eta }_n^{†}\}}^{-1}\sqrt{n}(\mid {\beta }_{nj}^{\ast }+u_j∕\sqrt{n}\mid -\mid {\beta }_{nj}^{\ast }\mid )\stackrel{p}{\to }0$. If ${\beta }_{nj}^{\ast }=0$, then $\sqrt{n}(\mid {\beta }_{nj}^{\ast }+u_j∕\sqrt{n}\mid -\mid {\beta }_{nj}^{\ast }\mid )=\mid u_j\mid$ and ${\alpha }_n^{†}{\{\mid {\beta }_{nj}^{\left(0\right)}\mid +{\eta }_n^{†}\}}^{-1}∕\sqrt{n}={\alpha }_n^{†}∕(\sqrt{n}\mid {\beta }_{nj}^{\left(0\right)}\mid +\sqrt{n}{\eta }_n^{†})$, where $\sqrt{n}{\beta }_{nj}^{\left(0\right)}=O_p\left(1\right)$. Again by Slutsky’s Theorem,

$$V_n\left(\text{u}\right)-V_n\left(0\right)\stackrel{d}{\to }\{\begin{array}{cc}{\text{u}}_{\mathcal{A}}^{\prime }{\text{C}}_{\mathcal{A}}{\text{u}}_{\mathcal{A}}-2{\text{u}}_{\mathcal{A}}^{\prime }{\text{W}}_{\mathcal{A}}\hfill & \text{if}{u}_j=0\text{for all}j\notin \mathcal{A}\hfill \\ \infty \hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

V_n(u)−V_n(0) is convex and the unique minimum of the right hand side is ${({\text{C}}_{\mathcal{A}}^{-1}{\text{W}}_{\mathcal{A}},0)}^{\prime }$. By epiconvergence (Geyer (1994), Knight and Fu (2000)),

$${\widehat{\mathrm{u}}}_{n,\mathcal{A}}\stackrel{d}{\to }{\text{C}}_{\mathcal{A}}^{-1}{\text{W}}_{\mathcal{A}},{\widehat{\mathrm{u}}}_{n,{\mathcal{A}}^c}\stackrel{d}{\to }0.$$ (8.2)

Since ${\text{W}}_{\mathcal{A}}\stackrel{d}{=}N(0,{\sigma }^2{\text{C}}_{\mathcal{A}})$, this proves the asymptotic normality.

Now $\forall j\in \mathcal{A},{\beta }_{nj}^{\left(1\right)}\stackrel{p}{\to }{\beta }_{nj}^{\ast }$; thus $\mathbb{P}(j\in {\mathcal{A}}_n)\to 1$. We show that for all $j^{\prime }\notin \mathcal{A}$, $\mathbb{P}(j^{\prime }\in {\mathcal{A}}_n)\to 0$. Consider the event $j^{\prime }\in {\mathcal{A}}_n$. By the KKT optimality conditions, $2{\text{x}}_{j^{\prime }}^{\prime }(\text{y}-\text{X}{\beta }_n^{\left(1\right)})={\alpha }_n^{†}{(\mid {\beta }_{n{j}^{\prime }}^{\left(0\right)}\mid +{\eta }_n^{†})}^{-1}$. We know that ${\alpha }_n^{†}{(\mid {\beta }_{n{j}^{\prime }}^{\left(0\right)}\mid +{\eta }_n^{†})}^{-1}∕\sqrt{n}\stackrel{p}{\to }\infty$, while

$$\frac{2{\text{x}}_{j^{\prime }}^{\prime }(\text{y}-\text{X}{\beta }_n^{\left(1\right)})}{\sqrt{n}}=2\left\{\frac{{\text{x}}_{j^{\prime }}^{\prime }\text{X}\sqrt{n}({\beta }_n^{\ast }-{\beta }_n^{\left(1\right)})}{n}+\frac{{\text{x}}_{j^{\prime }}^{\prime }∊}{\sqrt{n}}\right\}.$$

By (8.2) and Slutsky’s Theorem, we know that both terms in the brackets converge in distribution to some normal, so

$$\mathbb{P}(j^{\prime }\in {\mathcal{A}}_n)\le \mathbb{P}\left\{2{\text{x}}_{j^{\prime }}^{\prime }(\text{y}-\text{X}{\beta }_n^{\left(1\right)})=\frac{{\alpha }_n^{†}}{\mid {\beta }_{n{j}^{\prime }}^{\left(0\right)}\mid +{\eta }_n^{†}}\right\}\to 0,$$

which proves consistency.