Pronouced instability of tandem IU base pairs in RNA

Abstract

Optical melting was used to determine the stabilities of three series of RNA oligomers containing tandem XU base pairs, GGCXUGCC (5′XU3′), GGCUXGCC (5′UX3′) and GGCXXGGC/CCGUUCCG (5′XX3′), where X is either A, G or I (inosine). The helices containing tandem AU base pairs were the most stable in the first two series (5′XU3′ and 5′UX3′), with an average melting temperature ∼11°C higher than the helices with tandem 5′GU3′ base pairs and 25°C higher than the helices with tandem 5′IU3′ base pairs. For the third series (5′XX3′), the helix containing tandem GG is the most stable, with an average melting temperature ∼2°C higher than the helix with tandem AA base pairs and ∼24°C higher than the helix with tandem II base pairs. The thermodynamic stability of the oligomers with tandem IU base pairs was also investigated as a function of magnesium ion concentration. As with normal A–U or G–U tandem duplexes, the data could best be interpreted as non-specific binding of magnesium ions to the inosine-containing RNA oligonucleotides.

INTRODUCTION

Inosine occurs naturally in the wobble position of tRNA where it can hydrogen-bond with either adenosine, cytosine or uracil. In fact, deoxyinosine has been used as a universal base in sequencing reactions where it pairs with all four of the naturally occurring bases. Inosine is one of the most common mutations and occurs as the result of oxidative deamination of adenosine, converting AU base pairs into IU base pairs. RNA editing is an important mechanism to increase the diversity of mRNAs and therefore proteins. Metazoan organisms have evolved a system (ADAR, adenosine deaminase acting on RNA) to efficiently catalyze the conversion of A to I (1). For example, in mammalian brain, one out of every 17 000 nucleotides in mRNA is converted to inosine (2). These A to I conversions occur in coding sequences, thus altering translation, as well as in the 5′- or 3′-untranslated regions (UTRs). The role of inosines in the UTRs is unclear. Recent results suggest that, in RNA molecules, A to I editing prevents dsRNAs from entering the RNA interference (RNAi) pathway (3,4). Extended double-stranded RNA (dsRNA) duplexes can be hyper-edited by enzymes of the ADAR family (5) and, recently, Scadden and Smith (6) have described a cytoplasmic endonuclease that specifically cleaves IU and UI base pairs in hyper-edited dsRNAs. The IU base pair can form a structure isosteric with a GU base pair and maintain two hydrogen bonds between the bases (7). While IA base pairs form one of the more stable base pairs (8,9), the effect of IU base pairs on the stability of RNA has not been investigated. Here, we examine the effect of tandem IU base pairs on the stability of RNA oligomers and examine the interaction of magnesium ions with these oligomers.

MATERIALS AND METHODS

RNA synthesis and purification

Oligomers were synthesized on a solid support using the phosphoramidite approach with the 2′-hydroxyl protected as the tert-butyl dimethylsilyl ether. After ammonia and fluoride deprotection, the crude oligomer was purified by preparative TLC (n-propanol:ammonium hydroxide:water, 55:35:10) and Sep-Pak C18 (Waters) chromatography. Purities were checked by analytical TLC and were >95%.

Melting curves and data analysis

The buffer for the melting studies was either 1.0 M NaCl, 10 mM cadodylic acid, 0.1 mM EDTA pH 7, or 0.1 M NaCl, 10 mM cacodylic acid pH 7 with varying concentrations of magnesium ion. Single-stranded extinction coefficients were calculated from the extinction coefficients for dinucleotide monophosphate and nucleosides (10,11). Strand concentrations were determined from high-temperature absorbance at 280 nm. Absorbance versus temperature curves were measured at 280 nm with a heating or cooling rate of 1.0°C min^–1 on a Beckman DU 640 spectrophotometer as described previously (12). Absorbance versus temperature profiles were fit to a two-state model with sloping baselines using a non-linear least squares program (13). Each data point represents the average of 10–15 melts of the oligomer. The oligomer concentrations were varied over at least a 50-fold range between 1 mM and 10 µM. Thermodynamic parameters for the oligomers were determined from both the average of the individual melt curves and plots of the reciprocal melting temperature (T_m^–1) versus ln(C_t) for self-complementary or ln(C_t/4) for non-self-complementary sequences.

RESULTS

The three series of tandem XU oligomers, where XU is either AU, GU or IU, were melted in standard 1 M NaCl melt buffer. Table 1 shows the thermodynamic parameters derived from the optical melts. The oligomers with Watson–Crick base pairs are the most stable for the 5′XU/3′UX and 5′UX/3′XU series and only slightly less stable than the 5′GG/3′UU oligomer in the 5′XX/3′UU series. Substitution of a tandem wobble GU pair for the Watson–Crick AU pair decreases the stability of the duplex, as noted previously (13,14), and is dependent upon the orientation of the GU pairs. The 5′GG/3′UU oligomer is slightly more stable than the corresponding 5′AA/3′UU helix. The stability of all of the oligomers not containing inosine is predicted well by the nearest-neighbor model (15).

Table 1. Thermodynamic parameters of duplex formation^a.

Oligomers	Average of curve fits				Tm–1 versus log Ct plots
	–ΔH° (kcal/mol)	–ΔS° (eu)	–ΔG°37 (kcal/mol)	Tmb (°C)	–ΔH° (kcal/mol)	–ΔS° (eu)	–ΔG°37 (kcal/mol)	Tmb (°C)
XU
(GGCAUGCC)2	84.6	227.5	14.0	71.0	90.2	244.1	14.5	70.8
	83.2	222.6	14.2	72.2
(GGCGUGCC)2c	73.4	206.9	9.7	55.0	74.2	208.0	9.75	55.0
	78.7	220.3	10.4	56.9
(GGCIUGCC)2	59.1	168.9	6.7	42.4	59.9	171.2	6.8	43.0
UX
(GGCUAGCC)2	81.4	218.0	13.8	71.6	76.2	203.0	13.3	71.4
	81.6	216.8	14.3	73.8
(GGCUGGCC)2d	90.3	248.4	13.3	65.4	87.2	238.8	13.1	65.9
	86.4	237.3	12.8	64.9
(GGCUIGCC)2	73.8	211.4	8.2	47.9	68.6	193.6	8.6	50.7
XX
GGCAAGGC	79.2	211.5	13.6	67.3	72.8	192.6	13.0	67.5
CCGUUCCG	80.67	213.7	14.39	70.5
GGCGGGGC	77.4	204.4	14.0	70.1	76.5	202.2	13.8	69.5
CCGUUCCG	84.42	231.3	12.32	61.3
GGC II GGC	79.4	227.7	8.8	46.1	72.9	207.4	8.6	45.9
CCGUUCCG

^aSolutions are 1.0 M NaCl, 10 mM sodium cacodylate, 0.5 mM EDTA pH 7.

^bCalculated at 10^–4 M oligomer concentration. Values in italics are predicted (15).

^cHe et al. (14).

^dMcDowell and Turner (13).

Initially we attempted to melt IU oligomers with flanking sequences identical [i.e. (GCAIUUUGC)₂] to those used for the GU oligomers in a previous study (16); however, we were unable to obtain useful melt data as these duplexes had very low melt temperatures and no reliable lower baseline could be obtained. To investigate the effect of IU tandem base pairs on the stability of duplex formation, oligomers with more stable flanking sequences, shown in Table 1, were analyzed. Substituting tandem IU pairs produces a further decrease in stability relative to the GU oligomers, with the helices being on average 18°C less stable than tandem GU helices and 24°C less stable than the helices with Watson–Crick (AU) base pairs, and an average ΔG°₃₇, 4.3 and 6.0 kcal/mol, less stable than the GU and AU oligomers, respectively. Again, the orientation of the IU tandem pair influences the extent of the change in stability. Compared with the G-containing tandems, the tandem 5′II/3′UU oligomer had the largest decrease in stability, followed by the 5′UI/3′IU, with the 5′IU/3′UI oligomer having the smallest change in stability relative to the GU oligomers. Interestingly, those differences are not the same as those observed between A- and G-containing tandems and where there is a small increase in stability for the 5′GG/3′UU tandems relative to the 5′AA/3′UU oligomer.

Thermodynamic parameters for internal loop formation are listed in Table 2 and were calculated as described (17,18). For example, ΔG°₃₇ for the tandem internal loop IU/UI in duplex (GGCIUGCC)₂ is calculated as

Table 2. Thermodynamic parameters of loop formation.

RNA sequence	ΔG°37 (kcal/mol)	ΔH° (kcal/mol)	ΔS° (eu)
XU
CAUG
GUAC	–5.1	–31.3	–83.7
CGUG
GUGC	–0.9	–17.7	–55.4
CIUG
GUIC	+2.1	–3.3	–18.0
UX
CUAG
GAUC	–4.7	–22.7	–42.0
CUGG
GGUC	–4.3	–32.7	–91.5
CUIG
GIUC	+0.5	–15.2	–50.4
XX
CAAG
GUUC	–4.0	–23.1	–61.3
CGGG
GUUC	–4.6	–24.1	–62.6
CI IG
GUUC	+0.6	–23.3	–76.9

Calculated as described in the text.

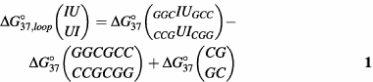
In this equation,

are the free energy change for duplex formation of (GGCIUGCC)₂ and (GGCGCC)₂, respectively. ΔG°₃₇(^CG_GC) is the free energy increment for the nearest-neighbor (^CG_GC) interaction that is interrupted by the tandem internal loop. All of the tandem IU base pairs are destabilizing. The 5′IU/3′UI tandem base pair is the most destabilizing of the group, while the 5′UI/3′IU and 5′II/3′UU tandem base pairs are slightly destabilizing.

We have previously investigated the effect of magnesium ion on the stability of RNA oligomers with Watson–Crick and wobble base pairs (16). To investigate the role of magnesium ions in the stability of RNA oligomers, the concentration of monovalent ions in the optical melting experiments was set to a more physiological concentration of 0.1 M NaCl. In all cases, there is good agreement between the thermodynamic values derived from the T_m^–1 versus log C_t plots and the melt curves (see Supplementary Material available at NAR Online). All of the oligomers are more stable in 1.0 M NaCl than in 0.1 M NaCl. The results are summarized in Table 3. The changes in melting temperature for the IU tandem base pairs (5.8°C on average) are less than those observed for oligomers of Watson–Crick (10.6°C) or GU base pairs (9.6°C on average) of comparable length (Table 3). The corresponding changes in free energy for duplex formation are slightly less for the IU (average of 1.2 kcal/mol) duplexes relative to either the fully Watson–Crick (2.2 kcal/mol) or GU (average of 1.9 kcal/mol) base-paired oligomers.

Table 3. Summary of changes in melting temperature and free energy upon addition of Na⁺ or Mg²⁺.

Oligomer	0.1–1.0 M NaCl		0.0–50 mM Mg2+ in 0.1 M NaCl
	ΔTm (°C)	ΔΔG°37 (kcal/mol)	ΔTm (°C)	ΔΔG°37 (kcal/mol)
CCAUAUGCa
GGUAUACG	10.6	2.2	11.3	3.0
CCAGUUGCa
GGUUGACG	9.3	1.4	11.5	1.8
GGCIUGCC
CCGUICGG	6.1	1.1	7.2	1.6
CCAUGUGCa
GGUGUACG	10.6	2.4	10.0	1.8
GGCUIGCC
CCGIUCGG	4.9	1.1	9.2	2.3
GCUGGUGCa
CCAUUACG	8.8	1.8	9.6	2.0
GGCI IGGC
CCGUUCCG	6.4	1.5	9.4	2.3

^aSerra et al. (16)

The three IU oligomers were then melted in 0.1 M NaCl melt buffer with a series of magnesium ion concentrations up to 50 mM. The thermodynamic parameters for the tandem IU oligomers as a function of Mg²⁺ concentration are available as Supplementary Material. These results are again summarized in Table 3. As expected, all of the IU oligomers are more stable in buffer containing Mg²⁺. The average melting temperature of the IU oligomers increases by 8.6°C. Again, these increases are slightly less than were observed for oligomers of Watson–Crick (11.2°C) or GU base pairs (10.4°C on average) of comparable length (Table 3). Interestingly, the change in free energy for duplex formation upon the addition of 50 mM Mg²⁺ to the melt buffer is slightly higher for the IU (on average 2.1 kcal/mol) oligomers than for the GU (on average 1.9 kcal/mol) oligomers, although not as large as for the fully Watson–Crick base-paired oligomer. As observed previously (16), the changes in both T_m and ΔΔG°₃₇ observed upon the addition of 50 mM Mg²⁺ are larger than those observed upon the addition of 900 mM Na⁺.

Figure 1A and B displays the changes in melting temperature with increasing magnesium ion concentration. The results seen here for the IU oligomers are similar to those observed previously for Watson–Crick RNA oligomers, indicating that similar interactions occur with magnesium ions and Watson–Crick and IU tandem base pairs. The effect of magnesium ions on the thermal stability of the oligomers can be interpreted using either of two simple models (19). The first one assumes that the larger stability can be viewed as an increase in the number of metal ions bound to the duplex relative to the single-stranded form. The graph of 1/T_m versus ln[Mg²⁺] should be a straight line with the slope related to Δn, the change in number of ions bound (see equation 1). Here, 1/T_m is the reciprocal melting temperature in °K, R is the gas constant and ΔH is the enthalpy for the formation of duplex.

Figure 1.

Stabilization of RNA oligomers with Watson–Crick base pairs by Mg²⁺. (A and B) Change in melting temperature (at 1 × 10^–4 M oligomer) as a function of [Mg²⁺]; (A) high and (B) low magnesium concentrations. (C) Reciprocal T_m plotted as a function of added Mg²⁺. The lines are the least squares fit of the data to equation 2. (D) Reciprocal T_m plotted as a function of added Mg²⁺. The curves are the least squares fit of the data to equation 3. (GGCIUGCC)₂, triangles; (GCCUIGGC)₂, squares; GGCIIGCC/CCGUUCCG, upside-down triangles.

Figure 1C displays the graph of 1/T_m versus ln[Mg²⁺] for the three IU oligomers. The results are summarized in Table 4 and, although approximate, indicate that on average less than one additional magnesium ion binds to the duplexes relative to the single strands. Δn is often expressed as the change in metal ions bound per base pair, in which case Δn would be less than 0.1 per base pair. The Δn values observed for the IU oligomers are identical or slightly less than those previously determined for Watson–Crick base-paired oligomers of equal length (Table 4).

Table 4. Summary of values as derived from model 1 (Δn) and from model 2 (K_f, K_u) for Mg²⁺ binding.

Oligomer	Δn	Δn/base pair	Kf	Ku	Kf/Ku
CCAUAUGGa
GGUAUACC	0.67	0.08	370	92	4.0
GGCIUGCC	0.35	0.04	40	14	2.9
CCGUICGG	(0.54)	(0.07)	(91)	(25)	(3.6)
GGCUIGCC	0.60	0.08	210	60	3.5
CCGIUCGG	(0.44)	(0.06)	(170)	(56)	(3.0)
GGCI IGGC	0.60	0.08	200	56	3.6
CCGUUCCG	(0.56)	(0.07)	(310)	(110)	(2.8)

^aSerra et al. (16). Values in parentheses are for duplexes with corresponding GU base pairs.

The second model assumes that the same number of ions is bound to the duplex and single-stranded forms (where the number of magnesium ions is assumed to be equal to half the number of phosphates in the RNA) but that the affinity of the metal ion for the duplex is greater (19). Here, R is the gas constant, m is the number of phosphates in the duplex, ΔH is the enthalpy for duplex formation, K_f and K_u are the binding constants for magnesium ion to the duplex and single-stranded forms of the oligomer, and 1/T_mo is the reciprocal melting temperature (in °K) in the absence of magnesium ion.

This analysis produces a graph of 1/T_m versus ln[Mg²⁺] which is sigmoidal. Figure 1D shows the 1/T_m versus ln[Mg²⁺] data fitted to the second model. As observed for Watson–Crick base-paired oligomers (16), the data fit the sigmoidal curve better than the linear fit above. Therefore, it appears that magnesium ions bind to the three IU duplexes in a non-specific manner. The values for the Mg²⁺ binding constants to the IU oligomers and a Watson–Crick oligomer of equal length are presented in Table 4. The values for the binding of magnesium ions to the IU oligomers are slightly less than those observed for the binding of magnesium to the Watson–Crick base-paired oligomers, indicating that there is no unusual attraction between the tandem IU base pairs and magnesium ions.

DISCUSSION

The stabilities of the oligomers with AU Watson–Crick pairs or GU tandem wobble pairs are predicted correctly by the current model for predicting the stability of RNA secondary structure (15). The ΔG°₃₇ for the GG oligomer is within 1.5 kcal/mol of the predicted value, but the melting temperature is 8°C higher than predicted. All of the other oligomers have stability within 1.5 kcal/mol of the predicted values and melting temperatures within 3°C of the predicted values.

For the three series of oligomers, alternating the center tandem base pairs from AU to GU and to IU has a dramatic effect upon the stability of the corresponding duplex. As observed previously (14,18), the stability of the tandem mismatches depends upon the mismatch sequence. The 5′UG/3′GU and 5′GG/3′UU tandem mismatches are among the most stable tandem mismatches known, and even the less stable 5′GU/3′UG tandem mismatch stabilizes duplex formation. Substitution with inosine dramatically reduces the stability of the corresponding oligomers. The average decrease in free energy (ΔG°₃₇) of the oligomers in changing from G to I is 4.7 kcal/mol. This is a larger change than expected for the substitution of an I for a G. For example, the substitution of I for G at position 1 of a tetraloop hairpin, where the amino group of the guanine residue forms two hydrogen bonds to the residue at position four of the tetraloop, only decreases the stability of the hairpin by 0.7 kcal/mol (20). Interestingly, the tandem IAs (either 5′AI/3′IA or 5′IA/3′AI) are significantly more stable than any of the IU tandem base pairs (8) and are in fact more stable than 5′AG/3′GA or 5′GA/3′AG, respectively.

The drop in melting temperature between the AU- and the IU-containing oligomers varies between 24 and 29°C, which is a surprisingly large change considering the minor chemical variation. Because of this chemical change, the IU base pair forms a wobble-like pair. However, the variation between the tandem GU and IU wobble pairs is comprised between 13 and 24°C, which is still a surprisingly large difference. In comparison, the stabilization effects brought about by 2′-O-methylation are much smaller [8°C between a fully methylated and a non-methylated hexamer (21)]. Often a loss of stability in an RNA molecule, following for example a base mutation, can be compensated by an increase in magnesium concentration. The measured effect of the magnesium ions on the stability of these RNA oligomers is relatively modest and non-specific and, thus, the influence of other factors must be considered. In molecular dynamics simulations, it was found that the presence of 2′-O-methyls increase the lifetimes and, consequently, the persistence of water networks around the oligonucleotides (22). Conversely, the absence of the 2-amino group in the minor groove of the wobble IU base pairs might lead to a severe decrease in the stability of water networks around such base pairs with an expected concomitant increase in the IU base pair opening dynamics.

SUPPLEMENTARY MATERIAL

Tables with the thermodynamics for each IU oligomer at the various magnesium ion concentrations investigated are available at NAR Online and at http://webpub.allegheny.edu/employee/m/mserra/professional/publications.shtml.

Tables with the thermodynamics for each IU oligomer at the various magnesium ion concentrations investigated are available at NAR Online and at http://webpub.allegheny.edu/employee/m/mserra/professional/publications.shtml.