A Vector Machine Formulation with Application to the Computer-Aided Diagnosis of Breast Cancer from DCE-MRI Screening Examinations

Abstract

This study investigates the use of a proposed vector machine formulation with application to dynamic contrast-enhanced magnetic resonance imaging examinations in the context of the computer-aided diagnosis of breast cancer. This paper describes a method for generating feature measurements that characterize a lesion’s vascular heterogeneity as well as a supervised learning formulation that represents an improvement over the conventional support vector machine in this application. Spatially varying signal-intensity measures were extracted from the examinations using principal components analysis and the machine learning technique known as the support vector machine (SVM) was used to classify the results. An alternative vector machine formulation was found to improve on the results produced by the established SVM in randomized bootstrap validation trials, yielding a receiver-operating characteristic curve area of 0.82 which represents a statistically significant improvement over the SVM technique in this application.

Introduction

Regular screening has been identified as key to improving breast cancer survival rates [1]. Genetic mutations on the BRCA1/2 genes confer up to an 85 % lifetime risk of developing breast cancer [2]. Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) has been shown to be the most sensitive screening methodology for detecting breast cancer when compared with x-ray mammography, ultrasound, and clinical breast examination among high-risk women [3]. Women with an inherited BRCA mutation who decline prophylactic mastectomy require regular breast screening starting at age 25–30 with the goal of detecting breast cancer at the earliest possible stage. DCE-MRI has been shown to be the most sensitive screening methodology for detecting breast cancer in high-risk women [4]. Accordingly, the American Cancer Society has recommended that women with a lifetime breast cancer risk of 20–25 % or greater based on a known mutation or a strong family history of breast cancer should receive annual MRI screening in addition to mammography [5].

In order to further improve the DCE-MRI-based breast cancer screening process, research has been conducted towards developing computer-aided diagnosis (CAD) systems to assist radiologists in image analysis. This paper is focused on evaluating a new vector machine formulation as a potential classifier combining spatially varying voxel information reflective of tumor vascular heterogeneity. A key component of such a CAD system is the selection of an appropriate classification algorithm responsible for the differential diagnosis between malignant and benign lesions. Support vector machines (SVMs) have been shown to outperform many alternative pattern-recognition techniques for breast cancer detection from MRI [6, 7]. We also present an alternative classification formulation utilizing spatially distributed information from breast MRI lesions. The technique has been shown to outperform the support vector machine on a lesion’s basic MRI based dynamic information [8]; however, this is the first study trying to apply the technique to lesion heterogeneity information. We compare the presented classification techniques as applied to a tissue’s vascular heterogeneity data using Efron et al.’s bootstrap validation method [9] with each randomized trial’s CAD system evaluated for robustness with receiver-operating characteristic (ROC) curve analysis [10].

Supervised learning techniques have been applied to breast MRI data in multiple studies [6, 11–13]. Previous work in the scientific literature on assessing the vascular heterogeneity of breast cancer from MRI examinations has involved the use of co-occurrence matrix texture analysis [14, 15]. Vascular heterogeneity has also been assessed using a voxel merging approach [16], pharmacokinetic modeling [17], and parallel thinning [18]. It is common for studies on breast MRI CAD to not indicate what type of dataset is involved in the study (screening, diagnostic, pre-biopsy, etc.). Diagnostic and pre-biopsy breast MRI datasets have the potential to be artificially easy ones on which to correctly identify malignancies. Screening datasets have the most potential to include challenging early stage malignancies that wouldn’t have been caught by mammography, ultrasound, palpation, or other methods. This study differs from those outlined above by taking a unique approach to the assessment of vascular heterogeneity of breast malignancies from MRI examinations using principal components analysis and vector machine formulations. This study’s analysis is also performed on a large breast MRI screening data set containing many small lesions.

Materials and Methods

Image Acquisition

Ethics approval was obtained from the clinical institution in which this research was conducted (Sunnybrook Health Sciences Centre). Between 1997 and 2009, 550 women at high risk for breast cancer were recruited from familial cancer clinics in southern Ontario and Montreal, Canada. Participation in screening was offered in the context of genetic counseling. Informed consent was obtained from all participants.

The screening protocol used was as follows. Simultaneous bilateral MRI was performed using a 1.5T magnet (GE Signa, v. 11.4). The same imaging device was used throughout the screening trial. Sagittal images were obtained with a phased-array coil arrangement using dual slab interleaved bilateral imaging [19]. This provided three dimension (3D)-volume data obtained with an RF spoiled gradient recalled sequence (SPGR, TR/TE/angle = 18.4/4.3/30°, 256 × 256 × 32 voxels, FOV: 18 × 18 × 6–8 cm). Imaging is performed before and after a bolus injection of 0.1 mmol/kg of contrast agent (Gd-DTPA). Each bilateral acquisition was obtained in 2 min and 48 s. Slice thickness was 2 to 3 mm and spatial resolution was 0.7 × 0.7 mm.

A total of 259 DCE-MRI breast lesions from high-risk patients were obtained, including 51 malignant cases and 208 benign cases. Ground truth was based on the diagnosis of the pathologist, who analyzed the tissue biopsies. Surgical biopsy of lesions was performed under MR guidance [20]. A benign diagnosis was accepted when a patient with a suspicious lesion did not receive a biopsy but returned to screening (> 1 year) without observed changes to the lesion.

Data Preprocessing

Image registration is the process of aligning images that vary in position over time. This is performed to compensate for any patient motion during the examination. Patient motion can obscure the analysis of suspicious lesions and in extreme cases, can completely hide a small tumor. For this study, we have used a three dimensional non-rigid registration technique for magnetic resonance breast images [21]. Registration was performed to align volumes acquired after contrast agent injection to the pre-contrast volume. The lesions that are included in this analysis are aligned as part of that overall process.

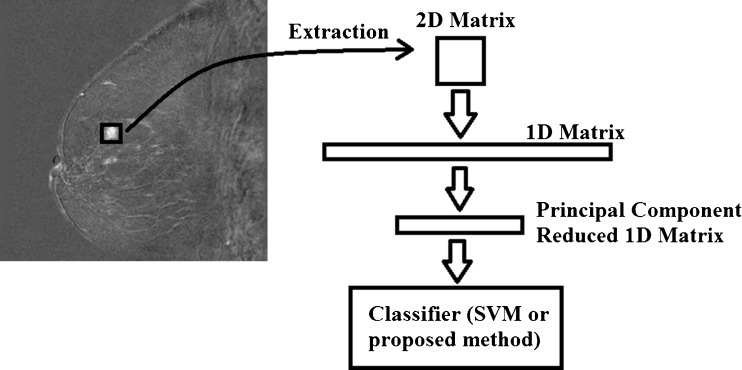
For each of the 259 lesions addressed in this study, a patch of relative signal intensities was extracted centered on the hyper-intense area of the lesion by a physicist with years of experience in breast MRI research and, guided by the original radiological reports, identifying suspicious lesions (see Fig. 1). Patch size was varied between 3 × 3, 5 × 5, 7 × 7, and 9 × 9 voxels. Each lesion was evaluated with the same set of features.

Fig. 1.

Flow diagram illustrating feature extraction and pre-processing steps

This process yields a set of either 9 (3 × 3), 25 (5 × 5), 49 (7 × 7), or 81 (9 × 9) feature measurements per lesion which are related to vascular heterogeneity. These two-dimensional patches were decomposed into a single one-dimensional array of features (see Fig. 1). This feature space is then down-sampled using principal components analysis, reducing the number of features extracted from the initial patch to four principal component features (see Fig. 1). This process was repeated for the spatial gradient data of the relative signal-intensity patch which yields more feature measurements (40 spatial gradient features for a 5 × 5 patch) which were also reduced to four principal component features. The spatial gradient was computed as the sum of the difference between neighboring relative signal intensities. This yielded an eight-dimensional feature measurement set on which tissue vascular heterogeneity in the context of the computer-aided diagnosis of breast cancer is assessed with the two classification techniques presented below. The effect of changing the number of principal component features is addressed in the discussion. Analysis was performed at each time point post contrast agent injection, so as to perform a comparison between taking vascular measures at different points during the examination.

Support Vector Machine-Based Classification

A classification technique inputs a set of training data with known labels/classes and then uses the criteria which distinguished the classes (benign and malignant) in the training set to classify an unknown test sample. In order to evaluate our proposed classification method, we elected to compare it to the SVM. The SVM has been shown to outperform k–nn, signal enhancement ratio, and other techniques for the diagnosis of breast cancer from MRI examinations [6, 7].

SVMs [22] operate by locating a hypersurface (or manifold) that attempts to split the training data into two categories. The hypersurface is selected such that its distance to the nearest training data on either side of the surface is maximized. If no hypersurface is capable of linearly separating the data, a kernel transformation function is used to map the data into a feature space so that it can be linearly separated using standard SVM techniques. Multiple kernels have been developed for this purpose. For this study, we are using a radial basis function (RBF) kernel which has been previously shown to be the best performing kernel function in many applications including CAD for breast MRI [6, 7].

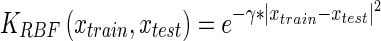1

where x_train are the training vectors and x_test is the test vector and γ is a kernel parameter. SVMs also incorporate a bias term parameter which acts as a threshold on the regression results of the classifier (see Eq. 2). The following formulation (Eq. 2) defines the support vector machine’s method for predicting the class of new test samples.

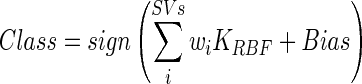2

Where w_i is the weight for any of the given support vectors (SVs) (assigned in the SVM training phase) and i cycles through all the training vectors. Non-linear kernel functions (like the RBF used here) provide flexibility to the SVM hyperplane. The RBF function also allows the classification space to be well-behaved as the learning technique’s test biasing is changed in order to vary points along the receiver-operating characteristic curve in a reliable manner. This equation allows the classification function to be non-linear in the input space. If the kernel function does not fully separate our data, a slack error variable is used to create a soft margin hyperplane for data separation. SVM-based classification has been implemented using the LIBSVM open source library [23].

Alternative Vector Machine Classification

The vector machine classification technique presented here has been previously demonstrated to outperform the SVM in separating malignant and benign lesions based on the dynamic information from a DCE-MRI examination [8]. This classification technique also uses the radial basis function from Eq. 1 to predict the class of a sample and is defined as follows:

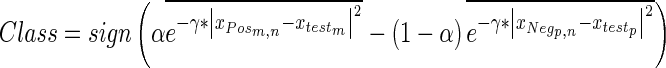3

Where, 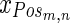is the positive training data with m samples and n measurements

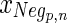is the negative training data with p samples and n measurements

γ is a kernel parameter

sign(x) = 1, x > = 0; sign(x) = −1, x < 0

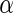is the input bias parameter ranging from 0 to 1

is a single test vector of n measurements replicated in m rows

is a single test vector of n measurements replicated in p rows

This formulation, while being a stand-alone-classification equation is also analogous to an SVM with every training sample used as a support vector and with a weight for each sample equal to the bias term (α and −(1-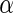) for the two classes, respectively) as well as averaging the kernel values together by class. This approach performs classification by assigning negative-valued results as negative predictions and positive-valued results as positive predictions as performed by the sign function. The approach supports regression by removing the sign term from Eq. 3, yielding an equation that produces floating point values that are analogous to making a vascular heterogeneity measurement, provided that the training samples extracted from the examinations are reflective of tissue vascularization. The technique is first optimized in classification mode and after the γ parameter is optimized via randomized trials (see below) the technique can provide vascular heterogeneity measurements (a one-dimensional index) by operating in regression mode (without the sign term).

Validation and Statistical Analysis

For both classification techniques, we perform validation by training and testing using the 0.638+ bootstrap method by Efron et al. [9] using 200 randomized trials per γ parameter setting. This technique was selected as it provides an established method for dividing data into testing and training groups, respectively, based on a relatively small amount of training data to assist in avoiding overfitting (alternatives such as leave-one-out validation and cross validation train on a larger percentage of samples). The radial basis function (for both the support vector machine and for the proposed method) has its input γ parameter varied across a wide range according to the following equation: γ = e^{Gamma Exponent Setting}, where the Gamma Exponent Setting = {−8.0 to 8.0} in steps of 0.1. For each setting of the unbounded input parameter γ, the area under the ROC curve [10] is computed for each of the two methods. ROC analysis was selected for evaluation as it is a robust technique that allows us to evaluate the tradeoff between the test’s sensitivity and specificity.

For the proposed classification technique, a single ROC curve is computed by varying the input parameter α (0 to 1 in steps of 0.001). ROC-based optimization for the proposed technique is accomplished in classification mode (not in regression mode) with each resultant sensitivity and specificity explicitly computed for each setting of the input parameter α. For the SVM method, the Bias term was varied in 3,000 equal-sized steps across the range of regression values (i.e., the sign term is dropped from Eq. 2) to yield a single receiver-operating characteristic curve. Although test biasing is performed differently between the two techniques, at each bias setting, each test has its sensitivity and specificity evaluated and the resultant area under the ROC curve is computed with the same absolute trapezoidal fit for both techniques.

Either the support vector machine or the alternative vector machine formulation can be used to provide an assessment of vascular heterogeneity by operating in regression mode (without the sign terms in Eqns. 2 and 3). The approaches presented test a given unknown sample and would provide a floating point result corresponding to an assessment of the tumor’s vascular heterogeneity when operating without the sign term.

The best performing results for the proposed technique and for the SVM were compared using the Wilcoxon sign rank statistical test.

Results

The lesions in this study include both mass type lesions as well as suspicious heterogeneously enhancing breast parenchyma. The dataset contains many small 2 to 5 mm lesions. The separation obtained between malignant and benign lesions based on the vascular heterogeneity data was measured by the ROC curve area. Changes in the average ROC curve area for the bootstrap validation trials were tracked with variations in the input parameter for the SVM RBF technique and for the presented alternative vector machine formulation and are provided in Fig. 2. These results were generated by extracting a 5 × 5 relative signal-intensity patch of voxels from each lesion. Patch sizes of 3 × 3, 7 × 7, and 9 × 9 voxels yielded suboptimal solutions.

Fig. 2.

Mean-bootstrapped ROC area results for the two classifiers as run on heterogeneity data from the first post contrast time point

The best performing setting for the SVM method (Gamma Exponent Setting: −1.2) yielded an average bootstrap validated ROC area of 0.79 (standard deviation: 0.05). The best performing setting for the alternative vector machine formulation (Gamma Exponent Setting: −2.3) yielded an averaged bootstrap validated ROC area of 0.81 (standard deviation: 0.046). These two bootstrapped distributions of ROC curve areas were compared with the Wilcoxon sign rank test which yielded a statistically significant p value (p < 0.0001). A plot demonstrating the effect of varying the time point at which the vascular heterogeneity measurements are made on the mean-bootstrapped ROC area is provided in Fig. 3.

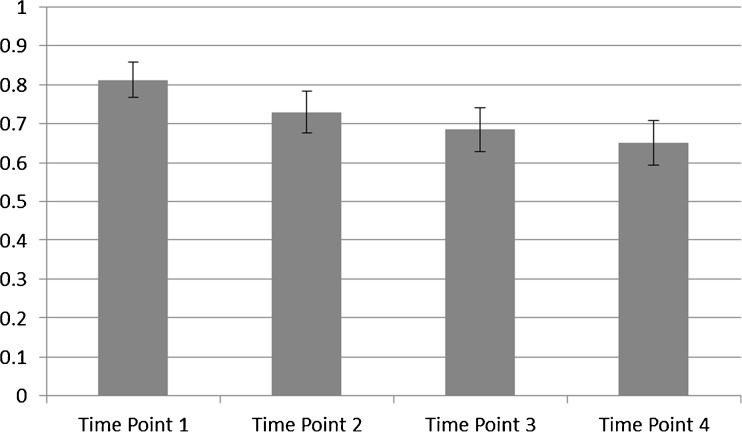
Fig. 3.

Effect of varying the time point from which heterogeneity features are extracted (temporal resolution: 2 min 48 s) on the best mean-bootstrapped ROC area

A CAD system based on the mean values of the dynamic curves yielded a mean-bootstrapped ROC area of 0.80 indicating that the heterogeneity measurements presented (mean-bootstrapped ROC area: 0.81) slightly outperform standard tissue dynamics. When we combined tissue dynamics with heterogeneity measurements, the best mean-bootstrapped ROC area improved to 0.82. This represents a statistically significant improvement in the distribution of ROC areas based on the Wilcoxon sign rank test (p ≤ 0.00032) when compared with the CAD system trained on vascular heterogeneity measurements and no dynamic information.

Discussion

This study is based on a challenging dataset containing many small 2–5 mm lesions; as such, it is thought that computer-aided diagnosis systems have the potential to assist in the screening process. The best CAD system presented in this study based purely on the heterogeneity information yielded a mean-bootstrapped ROC area of 0.81. Repeating the bootstrap validation trials on only the lesions’ dynamic information (how the brightness of the lesion changes over the course of the examination) yielded a mean-bootstrapped ROC area of 0.80. When we combined both the dynamic information which is commonly used in breast MRI CAD systems, with the heterogeneity measurements presented in this study, the resultant mean-bootstrapped ROC area climbed to 0.82. This indicates that most of the separation information available in the dynamic information is also available from the heterogeneity information obtained at the first time point before a voxel’s washout has been measured.

This study’s best heterogeneity results were obtained on the first time point after gadolinium injection. This was demonstrated in Fig. 3 which shows a degradation in the separation obtained between malignant and benign lesions from the heterogeneity information as the time point is increased. Over the course of the examination, more contrast agent diffuses from higher concentration voxels to neighboring lower concentration voxels and this process of intervoxel exchange causes a blurring of local vascular heterogeneity information. By analyzing the first time point, we minimize this effect. It is possible that increased separation between benign and malignant lesions would be available at earlier time points; however, our clinical acquisition protocol did not provide any earlier images.

Vascular heterogeneity was assessed with the use of a 5 × 5 pixel patch. A 5 × 5 patch was selected as varying the patch size to 3 × 3, 7 × 7, or 9 × 9 pixels degrades classifier results. These patch-based analyses were performed in two dimensions on the slice which best presented the given malignant lesion. Extension of the analysis to three dimensions was not performed for a number of reasons. Many of the hardest lesions to diagnose in this dataset were very small cancers (2–5 mm across) which typically present on only a single slice. Extending the analysis to 3D would not have been likely to help accurately diagnose these challenging cases. Adding 3D analyses to this type of data would also have added substantial noise to the measurements used by the CAD system. For example, for the spatial gradient data used in this analysis, adjacent voxels in the same plane share a border of size 0.7 by 2–3 mm, whereas adjacent through-plane voxels only share a border of size 0.7 by 0.7 mm, or about one fourth of the relevant surface area from the measurements used in this study. The smaller area dividing adjacent through-plane voxels would likely have resulted in more noise in the measured spatial gradient data as compared with adjacent in-plane voxels. Finally, extending the analysis to 3D would have increased the potential for instability in a system based on multidimensional statistics due to the known effect that the number of measurements should remain much lower than the number of samples [24].

Varying the number of principal components kept in the analysis provided relatively small changes to the best mean-bootstrapped ROC area results. However, when many principal components are kept, noise is added to the system. Raising the number of principal components kept can also yield unstable solutions due to the inherent stability problems that occur when multidimensional classifiers use large numbers of features [24].

This study’s limitations include training and testing on a single dataset using randomized validation techniques. Testing with additional independent high-quality screening datasets that contain many small lesions would be ideal for future work. This study is also limited by not including additional measures of possible malignancy such as margin assessment [25]. Acquisition of margin information requires lesion segmentation which is a challenging problem and an area of active research.

Future work will involve comparison of the results of computer-aided diagnosis with the performance of a trained radiologist in the context of multiple independently acquired breast MRI screening datasets. Future work will also involve experimentation to determine if the technique can be used in conjunction with standard radiological analysis in order to improve the overall screening process. Future work can also investigate the effects of varying the region-of-interest size with the size of the lesion being analyzed. Future work will look at enhancing the presented approach by adding additional measurements of potential malignancy such as the sharpness of a lesion’s margin and the irregularity of the shape of the lesion.

Conclusions

This paper presented an analysis of the vascular heterogeneity of breast disease from dynamic contrast-enhanced magnetic resonance imaging. The study compared two methods for performing multidimensional statistical classification and showed that vascular heterogeneity measurements can help separate malignant and benign breast MR lesions within the context of a computer-aided diagnosis system. It was demonstrated that this system outperforms a more traditional lesion dynamics based system and combining the two further improves the results, although most of the separation obtained by the dynamic information appears to be largely embedded in the separation obtainable from the heterogeneity data from the early phase of the exam. The results presented need to be followed by extensive clinical validation against known pathology across a broad range of disease entities in order to draw firm conclusions about the significance of these techniques. However, the results based on this study suggest that heterogeneity measurements, as well as the presented vector machine classification approach, may be useful in the computer-aided diagnosis of breast cancer from dynamic contrast-enhanced magnetic resonance imaging examinations.