Robust multicellular computing using genetically encoded NOR gates and chemical ‘wires’

Abstract

Computation underlies the organization of cells into higher-order structures, for example during development or the spatial association of bacteria in a biofilm^1–3. Each cell performs a simple computational operation, but when combined with cell–cell communication, intricate patterns emerge. Here we study this process by combining a simple genetic circuit with quorum sensing to produce more complex computations in space. We construct a simple NOR logic gate in Escherichia coli by arranging two tandem promoters that function as inputs to drive the transcription of a repressor. The repressor inactivates a promoter that serves as the output. Individual colonies of E. coli carry the same NOR gate, but the inputs and outputs are wired to different orthogonal quorum-sensing ‘sender’ and ‘receiver’ devices^4,5. The quorum molecules form the wires between gates. By arranging the colonies in different spatial configurations, all possible two-input gates are produced, including the difficult XOR and EQUALS functions. The response is strong and robust, with 5- to >300-fold changes between the ‘on’ and ‘off’ states. This work helps elucidate the design rules by which simple logic can be harnessed to produce diverse and complex calculations by rewiring communication between cells.

Boolean logic gates integrate multiple digital inputs into a digital output. Electronic integrated circuits consist of many layered gates. In cells, regulatory networks encode logic operations that integrate environmental and cellular signals^6–8. Synthetic genetic logic gates have been constructed, including those that perform AND, OR and NOT functions^9–12, and have been used in pharmaceutical and biotechnological applications^13,14. Multiple gates can be layered to build more complex programs^15–17, but it remains difficult to predict how a combination of circuits will behave on the basis of the functions of the individuals^11,18. Here we have compartmentalized a simple logic gate into separate E. coli strains and use quorum signalling to allow communication between the strains⁵. Compartmentalizing the circuit produces more reliable computation by population-averaging the response. In addition, a program can be built from a smaller number of orthogonal parts (for example transcription factors) by re-using them in multiple cells.

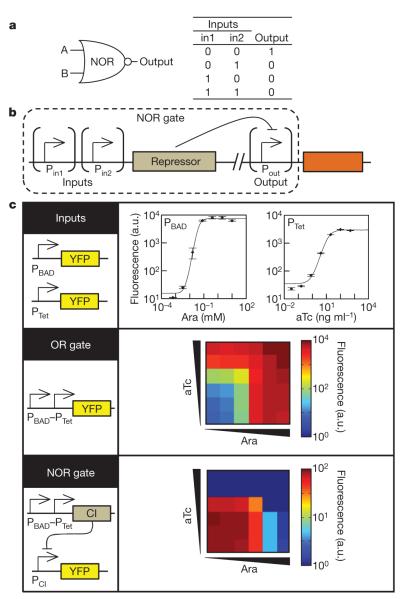
NOR and NAND gates are unique because they are functionally complete. That is, any computational operation can be implemented by layering either of these gates alone¹⁹. Of these, the NOR gate is the simplest to implement using existing genetic parts. A NOR gate is ‘on’ only when both inputs are ‘off’ (Fig. 1a). We designed a simple NOR gate by adding a second input promoter to a NOT gate²⁰. Tandem promoters with the same orientation drive the expression of a transcriptional repressor (Fig. 1b). Tandem promoters are common in prokaryotic genomes²¹. This is expected to produce an OR function; however, interference between the promoters can occur (Supplementary Figure 3). The repressor turns off a downstream promoter, which serves as the output of the gate. Both the inputs and the output of this gate are promoters; thus, multiple gates could be layered to produce more complex operations.

Figure 1. The genetic NOR gate.

a, b, Symbol, truth table (a) and genetic diagram (b) of the NOR gate. c, The transfer function is defined as the output as a function of input at steady state. The transfer functions of P_BAD and P_Tet (top), the P_BAD–P_Tet tandem promoter (middle), and the NOR gate (bottom) are shown. The inducer concentrations for the tandem promoter and NOR gate characterizations are 0, 0.0005, 0.005, 0.05, 0.5 and 5 mM Ara (squares from left to right) and 0, 0.025, 0.25, 2.5, 25 and 250 ng ml⁻¹ aTc (squares from bottom to top). Fluorescence values and their error bars are calculated as mean ± s.d. from three experiments. a.u., arbitrary units.

Each logic gate is encoded in separate strains of E. coli. Acyl homoserine lactone (AHL) cell–cell communication devices are used as signal-carrying ‘wires’ to connect the logic gates encoded in different strains^4,5,22. Gates are connected in series where the output of the first gate is the expression of the AHL synthase (Pseudomonas aeruginosa PAO1 LasI or RhlI). AHL diffuses through the cell membrane and binds to its cognate transcription factor (P. aeruginosa PAO1 LasR or RhlR). The promoter that is turned on by the transcription factor is used as the input to the next logic gate. These systems have been used previously to program cell–cell communication and have been shown to have little cross-talk⁴. Analogous to a series of electrical gates arrayed on a circuit board, compartmentalization of genetic gates in individual cells allows them to be added, removed or replaced simply by changing the spatial arrangement of the E. coli strains.

The stepwise construction of a NOR gate with P_BAD and P_Tet as the input promoters and yellow fluorescent protein (YFP) as the output gene is shown in Fig. 1c. P_BAD and P_Tet are activated in the presence of arabinose (Ara) and anhydrotetracycline (aTc), respectively. The individual transfer functions of P_BAD and P_Tet are measured using flow cytometry (Fig. 1c). An OR gate is constructed by placing the P_BAD and P_Tet promoters in tandem. P_BAD–P_Tet demonstrates OR logic with 7,000-fold induction between the ‘off’ state (−Ara, −aTc) and the ‘on’ state (+Ara, +aTc). Finally, to convert the OR gate into a NOR gate, the CI-repressor gene is placed under the control of P_BAD–P_Tet and YFP is expressed from a second plasmid under the control of the CI-repressible P_R promoter. Whereas the OR gates have some characteristics of fuzzy logic, the NOR gates are nearly digital (Fig. 1c).

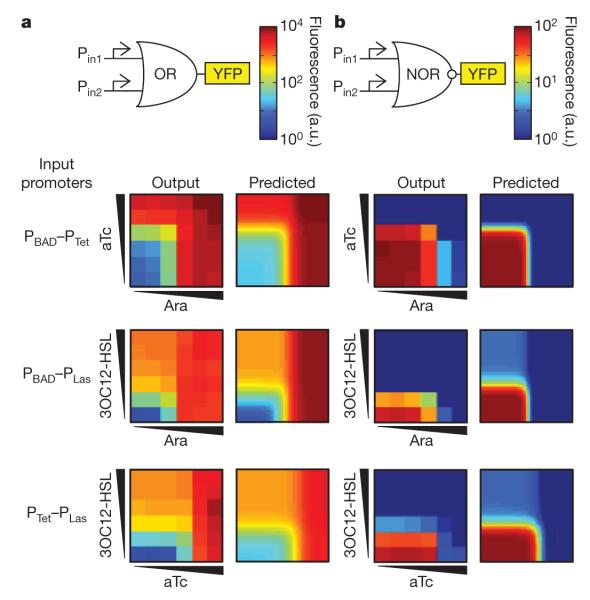
These OR and NOR gates use promoters as inputs. This feature imparts modularity to the gates; in other words, they can be engineered to respond to different inputs by replacing the promoters. To investigate this, we swapped the input promoters of the logic gates. Figure 2 shows the characterization data for three different tandem promoters: P_BAD–P_Tet, P_BAD–P_Las and P_Tet–P_Las. The promoter P_Las is activated by the quorum signal 3OC12-HSL²² (N-3-oxo-dodecanoyl-homoserine lactone). These gates perform as the additive combination of the individual transfer functions of the two input promoters and the CI-repressor NOT gate. The predicted transfer function for the six logic gates shown in Fig. 2 matched the experimental results. One tandem promoter, P_Tet–P_BAD, did not function as predicted (Supplementary Figure 3). The failure observed for P_Tet–P_BAD probably arises from some position-dependent interference. This could be the result of the effects of DNA looping, the occlusion of transcription-factor-binding sites or changes in the ratio or stability of output messenger RNAs, among other effects.

Figure 2. Input modularity of the gates.

a, Transfer functions for three OR gates (left) are compared with the predicted transfer function (right). The predicted transfer function is the simple sum of the transfer functions measured for the individual promoters (Supplementary Information). The Ara and aTc concentrations used are the same as in Fig. 1 and those for 3OC12-HSL are 0, 0.001, 0.01, 0.1, 1 and 10 μM (squares from bottom to top). b, Transfer functions for three NOR gates (left) are compared with the predicted transfer functions (right). The data represent means calculated from three experiments.

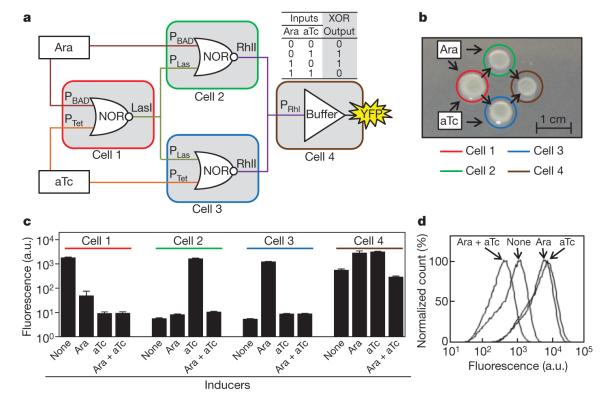
Complex logic can be designed using layers of simpler gates. An XOR gate is built with three NOR gates and a buffer gate (Fig. 3a). The output of an XOR gate is ‘on’ only when either (but not both) inputs are ‘on’. Four strains, each carrying a different logic gate, are used to construct an XOR circuit. The strains are spotted onto an agar plate in the spatial arrangement required to perform this function (Fig. 3b). Cell 1 carries a NOR gate that uses Ara and aTc as inputs and expresses LasI as the output. This allows cell 1 to be wired to the NOR gates in cells 2 and 3 by means of 3OC12-HSL. Cells 2 and 3 use Ara and aTc as their second inputs, respectively. Similarly, the output of the NOR gates in cells 2 and 3 is RhlI, which produces C4-HSL²² (N-butyryl-homoserine lactone). Cell 4 acts as a buffer gate and integrates the outputs from cells 2 and 3 by responding to C4-HSL. The output of a buffer gate is ‘on’ only when the input is ‘on’. The complete circuit consisting of all four strains behaves as a digital XOR gate with respect to the two inputs (Ara and aTc; Fig. 3c, d). Each intermediate colony performs its digital logical operations appropriately, as tested by replacing each output gene with YFP (Fig. 3c).

Figure 3. Construction of an XOR gate by programming communication between colonies on a plate.

a, Four colonies—each composed of a strain containing a single gate—are arranged such that the computation progresses from left to right, with the result of each layer communicated by means of quorum signals. The inputs (Ara and aTc) are added uniformly to the plate. b, Spatial arrangement of the colonies. c, Each colony responds appropriately to the combinations of input signals. Fluorescence values and their error bars are calculated as mean ± s.d. from three experiments. d, Cytometry data for the XOR gate (cell 4).

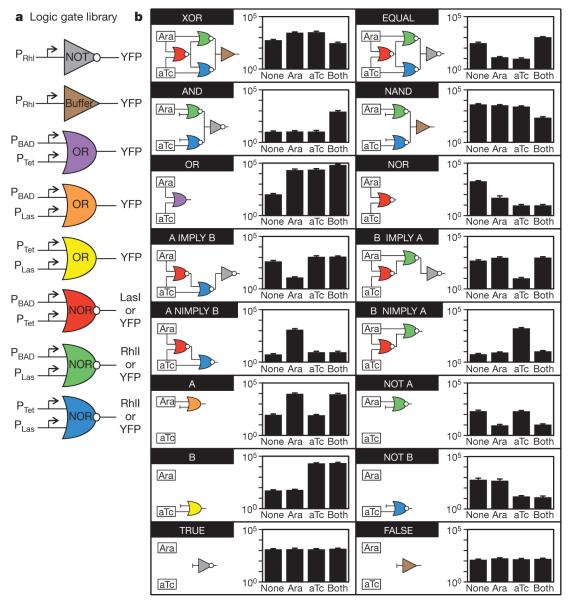
We constructed a small library of strains that act as simple logic gates, most of which are components of the XOR gate (Fig. 4a). Circuit diagrams showing how all of the sixteen possible two-input logic gates can be constructed using the library are shown in Fig. 4b. Each circuit diagram is reproduced by the spatial arrangement of the component strains. None of these circuits required additional genetic manipulation. The range of induction varies from 5-fold (XOR) to 335-fold (B gate). The dominant contribution to the dynamic range of the complete circuit is due to the intrinsic range of the final circuit (Supplementary Figure 7). For example, the XOR and NAND gates are limited by the output of P_Rhl. The addition of a NOT gate to this promoter increases the dynamic ranges of the EQUAL, AND, A IMPLY B and B IMPLY A gates, which is an effect described previously²³. No degradation in the signal is observed as a function of the number of layers.

Figure 4. Construction of all 16 two-input Boolean logic gates.

a, Library of simple logic gates carried by different strains (corresponding to plasmids in Supplementary Table 5). b, Colonies containing different gates were spotted to mimic the spatial arrangement of each logic circuit (Fig. 3b). For each circuit, the final colony was assayed by flow cytometry for all combinations of inducers added to the plate. The data correspond to the cytometry distributions in Supplementary Figure 6. Fluorescence values and their error bars are calculated as mean ± s.d. from three experiments. NIMPLY, NOT IMPLY.

The calculations are robust with respect to the distance between colonies and the time and density at which they are spotted (Supplementary Figure 10). This robustness is partially due to the population averaging that occurs, which reduces the effect of cell–cell variation. Despite the variability in the circuit response within a colony, this variability is effectively averaged and thus is not propagated to the next layer of the circuit. The use of chemical signals and population averaging could represent a common design rule for achieving computational operations robust enough to overcome the stochastic limitations of layered circuits in individual cells^24,25. Another source of robustness is the external clock that is implemented by delaying the spotting of colonies for each layer. Genetic computing is asynchronous and this may result in hazards, that is, transient incorrect outputs that occur as a result of mismatched delays in the circuit²⁶. This is apparent when circuits are measured in liquid culture, where the calculation is less robust with respect to timing and cell density (Supplementary Figure 12). To perform the calculation properly, all of the cells need to start in the ‘off’ state. As layered computation becomes more critical to the design of genetic programs, this will either require the implementation of a genetic clock²⁷ or the design of programs that are robust to asynchronous computation²⁸.

Cellular automata have been used to show how simple logic yields complex patterns in the organization of cells¹. These have been used to model biological pattern formation, development and complex collective behaviour^3,29. Here we demonstrate that a library of simple gates can be used to form more complex computational operations by linking the gates using diffusible chemical signals. The motif of multiple promoters in tandem driving the expression of a repressor is common in genomes²¹, and the resulting NOR gates may represent a ubiquitous fundamental unit of biological computation. Although our current ability to create logic gates within a single cell is limited, it may ultimately be possible to encode more complex circuits in individual cells that are then linked by cell–cell communication, akin to logic blocks in field-programmable gate arrays³⁰. Together, these principles can be used in the engineering of biological systems to create increasingly complex functions.

METHODS SUMMARY

Strains, plasmids and media

All studies were performed using E. coli strain DH10B. Luria–Bertani (LB)-Miller medium (Difco 244610) was used for the assays. The antibiotics used were 50 μg ml⁻¹ chloramphenicol (Acros 227920250) and/or 50 μg ml⁻¹ kanamycin (Fisher BP906-5). The inducers used were arabinose (Sigma A3256), anhydrotetracycline (Fluka 37919) and 3OC12-HSL (Sigma O9139).

Transfer function characterization

Cells harbouring the appropriate plasmids were incubated in 3 ml of LB broth medium (37 °C, 250 r.p.m. shaking) in culture tubes without the presence of inducers for 18 h. The cultures were then diluted 200-fold into 200 μl fresh LB broth medium (supplemented with appropriate inducers) in a 96-well plate format and incubated for additional 14 h before finally being diluted 100-fold into PBS solution for cytometry analysis.

Plate assay of circuit function

The plate medium was prepared by pouring 12 ml of LB broth agar medium (1.5% agar (Difco 214030), 2.5% LB-Miller) supplemented with inducers (2 mM Ara and/or 500 ng ml⁻¹ aTc) into a 100-mm Petri dish (Fisher 08-757-13). Bacterial logic gates were ‘fabricated’ on the plate by spotting 1 μl overnight culture of appropriate bacterial strains (Supplementary Table 5) to mimic the spatial arrangement of each logic circuit. The distance between each two colonies was set at 7 mm in square grids. Spotting was done with 12-h delay from the previous layer’s spotting to ensure communication signals had propagated sufficiently. After 12 h from the last layer’s spotting, the whole output colony of the circuit was scraped using inoculating loops and diluted into 10 ml PBS solution for cytometry analysis.

Flow cytometry

All data contained at least 50,000 events, obtained using BDFACS LSR2. Events were gated by forward and side scatter using MATLAB software. The geometric means of the fluorescence distributions were calculated. The autofluorescence value of E. coli DH10B cells harbouring no plasmid was subtracted from these values to give the fluorescence values reported in this study.