Taking the long view: how to design a series of Phase III trials to maximize cumulative therapeutic benefit

Abstract

Background

Traditional clinical trial designs strive to definitively establish the superiority of an experimental treatment, which results in risk-adverse criteria and large sample sizes. Increasingly, common cancers are recognized as consisting of small subsets with specific aberrations for targeted therapy, making large trials infeasible.

Purpose

To compare the performance of different trial design strategies over a long-term research horizon.

Methods

We simulated a series of two-treatment superiority trials over 15 years using different design parameters. Trial parameters examined included the number of positive trials to establish superiority (one-trial vs. two-trial rule), α level (2.5%–50%), and the number of trials in the 15-year period, K (thus, trial sample size). The design parameters were evaluated for different disease scenarios, accrual rates, and distributions of treatment effect. Metrics used included the overall survival gain at a 15-year horizon measured by the hazard ratio (HR), year 15 versus year 0. We also computed the expected total survival benefit and the risk of selecting as new standard of care at year 15 a treatment inferior to the initial control treatment, P(detrimental effect).

Results

Expected survival benefits over the 15-year horizon were maximized when more (smaller) trials were conducted than recommended under traditional criteria, using the criterion of one positive trial (vs. two), and relaxing the α value from 2.5% to 20%. Reducing the sample size and relaxing the α value also increased the likelihood of selecting an inferior treatment at the end. The impact of α and K on the survival benefit depended on the specific disease scenario and accrual rate: greater gains for relaxing α in diseases with good outcome and/or low accrual rates and greater gains for increasing K for diseases with poor outcomes. Trials with smaller sample size did not perform well when using stringent (standard) level of evidence. For each disease scenario and accrual rate studied, the optimal design, defined as the design that the maximized expected total survival benefit while constraining P(detrimental effect) < 2.5%, specified α = 20% or 10%, and a sample size considerably smaller than that recommended by the traditional designs. The results were consistent under different assumed distributions for treatment effect.

Limitations

The simulations assumed no toxicity issues and did not consider interim analyses.

Conclusions

It is worthwhile to consider a design paradigm that seeks to maximize the expected survival benefit across a series of trials, over a longer research horizon. In today’s environment of constrained, biomarker-selected populations, our results indicate that smaller sample sizes and larger α values lead to greater long-term survival gains compared to traditional large trials designed to meet stringent criteria with a low efficacy bar.

Introduction

Smaller sample size clinical trials are usually considered doomed, or even unethical, because they are underpowered [1]. In 1999, Sposto and Stram [2] proposed to evaluate the efficiency of small clinical trial design considering a series of successive trials. Focused on the context of childhood cancers, their conclusions did not receive a wide audience. With the advent of personalized medicine, time has come to reconsider this approach.

The standard approach to the design of randomized clinical trials is based on statistical hypothesis testing, where one rejects a null hypothesis of no difference at a given significance level, corresponding to the desired false-positive rate (FPR), α. The α level is usually set at 5% for a two-sided test, equivalent to 2.5% for a one-sided test. Quoting from the Consort Statement, ‘Ideally, a study should be large enough to have a high probability (power) of detecting as statistically significant a clinically important difference of a given size if such a difference exists’ [3]. In the context of oncology trials, with survival as the endpoint, even a small survival gain may be deemed clinically relevant. These stringent criteria inevitably yield sample sizes of many hundreds to a few thousands patients. As an example, for a disease associated with a baseline median survival of 12 months, 900 patients or more would be required to ensure a 90% power for an expected median survival benefit of 3 months, assuming 100 patients can be recruited annually. However, the value of a trial that accrues for more than 9 years is questionable. In addition, the standard level of evidence required by the Food and Drug Administration (FDA) for approval of a new drug is either efficacy demonstrated in two independent trials, each with a one-sided level of significance of 2.5%, or much stronger evidence of efficacy in a single trial [4].

The current stringent criteria for establishing efficacy evolved in a period when there were relatively few new treatments to test, thus it made sense to ensure that small treatment effects were not missed. It was also essential to minimize the chance of incorrectly concluding a treatment is effective when it is not, since this treatment might become a standard treatment of care for many patients and for many years. Another factor driving large clinical trials was that the treatment regimen was applied to an unselected patient population in which modest gains were expected. As large populations were mostly available, the large number of patients required did not represent a major issue for most cancers.

Recent breakthroughs in the understanding of tumor biology have led to the emergence of many new therapies available for testing, mostly targeted agents tailored to specific tumor aberrations. As a first consequence, major gains can be expected if the population is correctly selected. The downside of this personalized medicine approach is that only a small subset of patients may be available to confirm the efficacy of a new targeted agent. For example, the ALK (anaplastic lymphoma kinase) tyrosine kinase inhibitor, crizotinib, has shown remarkable antitumor activity in patients presenting a nonsmall cell lung cancer (NSCLC) with EML4–ALK fusion aberration [5,6]. These cases represent about 4% of all NSCLC cases [7]. The number of such rare cancers is likely to grow in coming years as we recognize that each common cancer is in fact an array of rare subentities. Additionally, the resources for performing large clinical trials are decreasing due to reduced funding. In this context, our ability to pursue the many promising agents available for clinical testing is directly compromised by investing large human and financial resources in a single direction.

In the context of rare disease, it is fairly common to perform a ‘sample size samba’ that involves retrofitting of the parameters to the number of available participants [8]. It is noticeable that only two of the three possible dancers are usually on stage: the difference worthy of detection and its associated power; the α parameter is notably absent, as if conventionally untouchable.

Trials of smaller sample sizes perform poorly when viewed in the context of a single trial with stringent evidence for establishing the efficacy of a new treatment: they are underpowered. In the context of pediatric cancer trials, Sposto and Stram [2] suggested evaluating the benefits and risks associated with trial designs using smaller sample sizes and relaxed α levels by considering a series of trials over a longer research horizon. Here we reconsider this approach in the current context of adult cancers, extending the work of Sposto and Stram by performing an extensive simulation study to assess the impact of conducting more (smaller) trials with different evidence criteria over a 15-year horizon.

Methods

The trial design parameters we evaluated were (1) criteria used to conclude efficacy, that is, different values for the level of significance, α, and two decision rules and (2) different number of trials, K, conducted over a 15-year research period and consequently different trial sample sizes. The study was performed for several disease scenarios, accrual rates, and distributions of treatment effect. The framework of the simulation study is described briefly below; the details are available in the online appendix.

We assumed that trials are performed in a series, each with two treatment arms: a control arm consisting of the current standard of care and an experimental arm. There is a fixed follow-up time (FU) after the last patient has been enrolled for the data to mature before the analysis of the current trial and the start of the next trial. The primary endpoint is overall survival, but the results would generalize to any other time-to-event endpoint. For a given trial, the treatment effect is characterized by the hazard ratio (HR) of death and is tested by a logrank test.

Simulation parameters

Level of statistical significance, α

Each simulated trial is a two-arm trial with a one-sided level of significance, α, for determining the superiority of the experimental arm to the control arm. We considered the following α values: 2.5%, 5%, 10%, 20%, 30%, 40%, and 50%. A one-sided α value equal to 2.5% corresponds to the standard approach. At the opposite, considering a one-sided α value equal to 50% means that we ignore the significance test and choose the treatment with the better observed outcome regardless of the p-value, as suggested by Schwartz and Lellouch [9] for the pragmatic approach.

Decision rule for adopting a new treatment

Two different decision rules were employed for determining whether an experimental treatment would be adopted as the new standard-of-care therapy (i.e., control arm for the next trial). For the one-trial rule, the experimental arm was selected if it was statistically superior to the control arm at the level of significance, α. In the two-trial rule, either (1) an experimental treatment would have to be statistically superior at the a level for two consecutive trials comparing the same treatments or (2) the experimental arm would have to be found superior in one trial at the α² level of significance.

Number of trials and sample size

In a given simulated series of successive trials, the sample size of each trial, n, was fixed, with no interim analysis, and n was identical through the series of trials. The sample size was derived from the number of trials K performed over the 15-year research period, the expected annual accrual rate, and FU (formula given in the online appendix). For a given disease scenario and accrual rate, the sample size of each trial decreases as the number of trials performed over 15 years increases.

We only considered numbers of trials yielding sample sizes of at least 50 patients. As an example, if 100 patients can be accrued per year and the FU is 1 year, we can perform from 2 successive trials recruiting 650 patients each up to 10 successive trials of 50 patients each.

Disease scenario and follow-up

A disease scenario was characterized by the survival distribution for the control arm at the start of the 15-year research period, representing the initial survival distribution for the standard of care. Four different baseline survival distributions were considered: 0.5-year median survival, 1-year median survival, 2-year median survival, and 2-year survival rate of 75%. The length of FU depending upon the disease scenario was 0.5, 1, 2, and 2 years, respectively.

Accrual rate

Three different accrual rates were considered: 100, 200, and 500 patients/year.

Treatment effect distribution

In our simulation study, we aimed to mimic a series of randomized trials evaluating a succession of new treatments, with the true treatment effect for a given trial randomly drawn from a specified distribution for the HR.

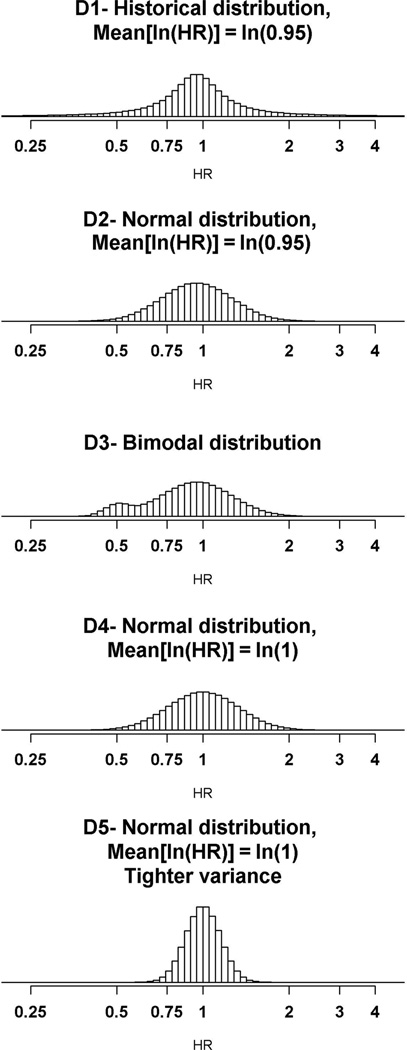
Four different hypotheses concerning the true treatment effect (HR) of the evaluated treatments were considered (Figure 1). The first distribution, D1, was used for the primary analysis and corresponds to a historical distribution, based on data from all Phase III randomized clinical trials conducted by the National Cancer Institute’s cooperative groups between 1955 and 2000 [10]. A fifth distribution, more pessimistic, was used for a sensitivity analysis.

Figure 1.

Hypothetical distributions of the true treatment effect of the experimental treatment compared with the standard treatment in the simulated trials, expressed in terms of ln(HR). HR: hazard ratio.

Simulation model

The patients’ data were simulated assuming an exponential distribution of survival times and proportional hazards. For each new experimental treatment, the treatment effect, HR, is randomly selected from the distribution under consideration. The disease scenario determines the event rate of the control arm of the first trial in the series of successive trials.

In each trial of the series of K trials, we generated data for n patients, assuming uniform accrual and1:1 randomization to the experimental and control arms. The total length of the trial is the time necessary to accrue n patients plus the minimum FU assuming that the next trial can start as soon as the previous one is completed and analyzed.

At the end of each trial, the analysis was performed when the last patient enrolled had been followed up for the defined follow-up duration. Patients who did not die prior to the date of analysis were right censored. We assumed there were no patient dropouts. A logrank test with one-sided a level of significance was used to compare the survival distribution between arms. When the experimental arm was considered superior to the control arm at the completion of a given trial (under either a one-trial or two-trial rule), it then became the control arm in the next trial; otherwise, the control arm remained the same.

We generated 5000 repetitions of a 15-year research period for each of the 6020 different sets of parameters: α values × decision rules × number of trials K × disease scenarios × accrual rates × distributions for the treatment effect. The study was performed using R version 2.11.1 [11].

Performance metrics evaluated from the simulations

A set of metrics was used to gauge the effect of the design parameters of interest. At the completion of a series of K trials, the overall survival improvement was measured by the overall hazard ratio (HR_O) comparing the event rate of patients who would receive the treatment recommended at the end of the 15 years to the baseline event rate (control arm of the first trial).

Using the results of the 5000 repetitions, we estimated the expected value of the overall hazard ratio (E(HR_O)) by computing the mean of the observed distribution. This was then expressed in terms of the expected total survival benefit, $E\left(\text{benefit}\right)=(\frac{1}{E({\text{HR}}_{\mathrm{o}})}-1)$. for example, the baseline median survival time was 1 year, and we observed an HR_O equal to 0.465, this means that the median survival times at year 15 becomes 2.15 years (=1/0.465), representing a 1.15-year absolute increase and a 115% relative increase, E(benefit) = 115%. We have also computed (1) the median value of the HR_O and its translation in terms of median total survival benefit, Med(benefit); (2) the probability of achieving a major improvement, defined as P(HR_O < 0.7); and (3) the probability that the event rate for the treatment selected at the end of the 15 years is worse than the event rate for the initial control arm, P(HR_O > 1), hereafter referred to as probability of a detrimental effect at 15 years.

Another measure used was the proportion of lives saved (PLS) over the entire 15-year period comparing the observed number of deaths in both treatment groups of the K successive trials to the expected number of deaths if the patients had been treated with the control treatment of the first trial.

This measure was used in two additional metrics: the expected proportion of lives saved (E(PLS)) and the probability of any mortality benefit, that is, the probability that there were less deaths among patients enrolled under this research design strategy than there would have been by chance if all patients had been treated with the initial control treatment over the 15 years, P(PLS > 0).

A final metric of interest was the expected number of false-positive trials (E(NFP)) over the 15-year period. A false-positive trial was defined as an instance when the experimental treatment was found to be statistically significantly superior to the control arm when it actually was not (HR ≥ 1). The false positive rate (FPR) is computed as

$$\text{FPR}=\frac{\mathrm{E}(\text{NFP})}{\mathrm{K}}$$

β and γ errors

Considering each trial in isolation, designed with a given sample size and a defined α error, we computed the β and γ errors associated with specific hypotheses. The β error, which is the chance of not concluding the experimental treatment efficacy when it is actually superior to the control treatment, was computed for a HR = 0.7. The γ error, which is the chance of concluding that the experimental treatment is superior to the control when the reverse is true [9], was computed for a HR = 1.25.

Results

For illustrative purposes, we first present the results of one specific scenario. We then follow with an expanded presentation of the results.

An example under the historical distribution D1 of the true treatment effect

The results that follow concern the second disease scenario (median survival = 1 year) with an accrual rate of 100 patients/year, under the historical distribution of treatment effect, D1.

Expected total survival benefit as a function of the number of trials and for different α values

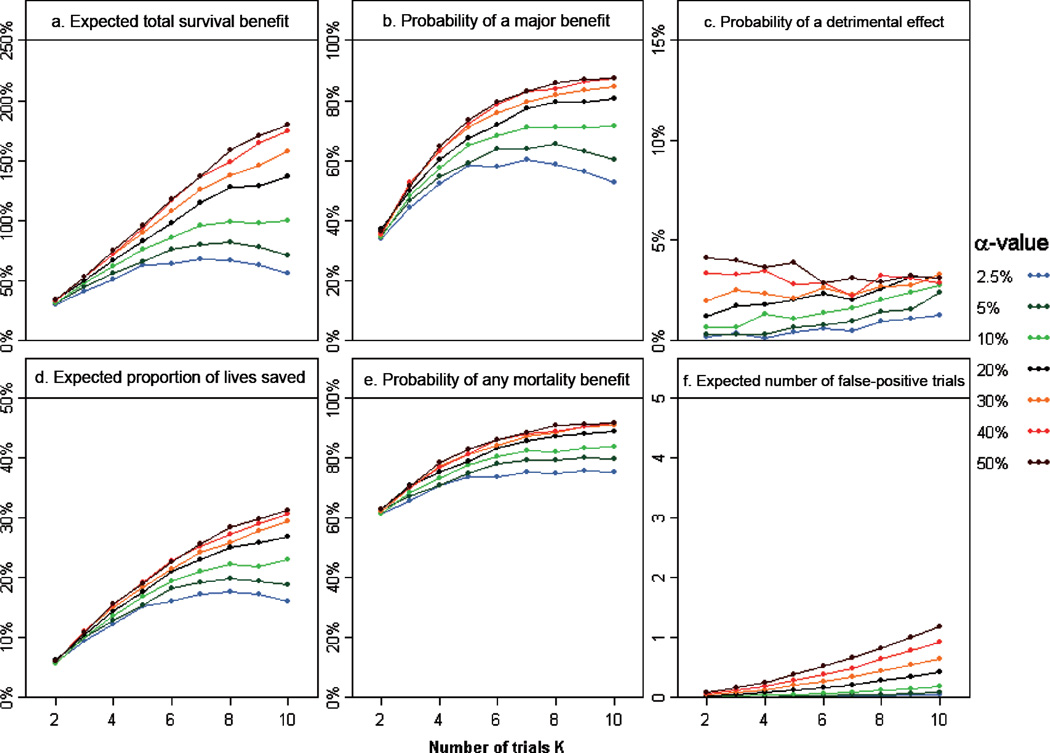
Figure 2 (a) illustrates the expected total survival benefit as a function of the number of trials and for different a values, using the one-trial decision rule. We make three key observations.

Figure 2.

Variation of the different metrics as functions of the number of trials K and for different α values, using a one-trial decision rule, for the second disease scenario (median survival = 1 year, FU = 1 year), accrual rate =100 patients/year, and under the historical distribution of treatment effect, D1: (a) expected total survival benefit, E(benefit); (b) probability of a major improvement at 15 years, P(HR_O < 0.7); (c) probability of a detrimental effect at 15 years, P(HR_O > 1); (d) expected proportion of lives saved, E(PLS); (e) probability of any mortality benefit, P(PLS > 0); and (f) expected number of false-positive trials, E(NFP). FU: follow-up time; HR: hazard ratio.

First, the expected total survival benefit monotonically increases with increasing α. Most of the survival gain occurs as α increases from 2.5% to 20%, whereas there is little additional gain for α values greater than 20%: for example, for 10 trials of 50 patients each, E(benefit) = 56%, 137%, and 180% for α = 2.5%, 20%, and 50%, respectively.

Second, the impact of relaxing the α level on the total survival benefit is rather small when the number of trials is small, that is, for trials with large sample sizes: for two trials of 650 patients each, E(benefit) = 29% and 34% for α = 2.5% and 50%, respectively. In contrast, as illustrated above, we observed a wide variation of the expected total survival benefit according to α when the number of trials increases.

Third, with large α levels, the expected total survival benefit monotonically increases with the number of trials, the strategy based on the smallest trials being associated with the greater expected gain. In contrast, with smaller α values, the expected total survival benefit is maximal for a number of trials equal to 7 when α = 2.5% and to 8 when α = 5%; reducing the sample size further (e.g., 10 trials of 50 patients each) yields smaller survival improvement when using traditional α levels.

Values of the other metrics as functions of the number of trials and for different α levels

The effect of the number of trials and the α value on the expected total survival benefit is similar to that on the probability of a major improvement at 15 years (Figure 2(b)), the expected proportion of lives saved (Figure 2(d)), and the probability of any mortality benefit (Figure 2(e)). In particular, for each α value, approximately the same number of trials K maximizes these four metrics. The results are also very similar when considering the median total survival benefit. Consequently, in what follows we focus on the expected total survival benefit as the metric used to assess the benefit of each design strategy and to define the optimal design parameters.

As anticipated, E(NFP) over the 15-year period is approximately a linear function of the number of performed trials for a given α level and is strongly related to the α value (Figure 2(f)). The probability that the new standard of care at the end of the 15-year period is less effective than the initial control arm is also intrinsically related to the α value (Figure 2(c)). Assuming that a strategy for which the probability of a detrimental effect at 15 years greater than 2.5% is unacceptable, α should not be increased above 20%. For α ≤ 20%, the chance of an inferior treatment being selected at the end of the 15 years increases as the sample size decreases (or K increases). As an example, this would rule out performing 10 trials using an α = 20%, since this strategy yields a probability of a detrimental effect at 15 years equal to 3.1%.

Definition of the optimal design parameters in this example

There is substantial interplay between the α level, the number of trials K to perform in the 15-year time frame, which directly relates to the trials’ sample sizes, and the overall survival gain that can be realized. We defined as the optimal design parameters the combination of α value and K that yields the highest expected total survival benefit provided that the probability of a detrimental effect at 15 years remains below 2.5%. In the given setting of a disease associated with a 1-year baseline median survival, with an accrual rate of 100 patients/year, the optimal design defined under the historical distribution combines α = 20% and seven trials, each trial recruiting 114 patients. Under the assumption D1, this design is associated with an expected total survival benefit E(benefit) = 115%, a median total survival benefit Med(benefit) = 134%, a probability of a major improvement P(HR_O < 0.7) = 77%, E(PLS) = 23%, and a probability of any mortality benefit P(PLS > 0) = 86%. These metrics compare favorably with the performance of a traditional design with α = 2.5% and two trials, each trial recruiting 650 patients: E(benefit) = 29%, Med(benefit) = 20%, P(HR_O < 0.7) = 34%, E(PLS) = 6%, and P(PLS > 0) = 61%. With the optimal design, The expected number of false positive trails (E(NFP)) and the probability of a detrimental effect remain low, although increased relative to the traditional design: 0.21 and 2.0% versus 0.004 and 0.2 respectively. The FPR is 3.0% (= 0.21/7) in the optimal design.

Another important observation is that this optimal design performs much better than one with reduced trial sample sizes (seven trials recruiting 114 patients each) but stringent evidential criteria (α= 2.5%): E(benefit) = 68%, indicating that adjustment to both the trial sample size and α value is necessary for best results.

Comparison of the two-trial decision rule to the one-trial decision rule

For all combinations of distributions for treatment effect, disease scenarios, accrual rates, α values, and numbers of trials, the one-trial rule (requiring only a single trial with a statistically significant result) outperforms the two-trial rule, as measured by E(HR_O) (Supplemental Figure 4). In particular, a two-trial rule with an α = 10% yields very similar results as a one-trial rule with an α = 2.5%.

Generalization to the other disease scenarios and accrual rates, under the historical distribution D1 of the true treatment effect

For each disease scenario, there is substantial improvement in survival as the accrual rate increases (Supplemental Figure 5). In addition, as the accrual rate increases, the probability of a detrimental effect decreases (Supplemental Figure 6). For each accrual rate, there is smaller improvement in survival as the baseline outcome improves.

The impact of increasing the number of trials, that is, reducing the sample size, or relaxing the α value differs greatly according to the situation. One extreme situation is represented by Scenario 1 (median survival = 0.5 years) combined with a high accrual rate (500 patients/year). In this situation, increasing the number of trials and consequently reducing the sample size has a major impact on the overall benefit, whereas relaxing the α value has little impact. The opposite situation occurs with a disease with a relatively good baseline outcome (Scenario 4: 2-year survival = 0.75) and low accrual (100 patients/year). In this case, there is little variation of the expected gain with the number of trials, but large variation according to the α level: the performance of designs with stringent α value is very poor compared to that of designs with relaxed significance levels. However, as the chance of selecting an inferior treatment at the end is much higher in this case, the optimization criterion rules out designs with α ≥ 20%. The optimal design parameters must thus be defined for each disease setting and each accrual rate.

Optimal design parameters for the different treatment effect distributions

Because of the uncertainty concerning the true treatment effect of the agents that will be evaluated in the next 15 years, simulations were performed under other specifications for the distribution of HR. For the second disease scenario (median survival = 1 year) and an accrual rate of 100 patients/ year, the recommendations would be to run seven trials with α = 20% under the historical distribution D1, whereas the optimal design would combine six trials and α = 20% under the distribution D2, eight trials and α = 20% under the distribution D3, and six trials and α = 10% under the distribution D4. The results for other disease scenarios and accrual rates are detailed in the online appendix (Table 3).

We observed that the optimal design parameters defined under the historical distribution D1 are very close to the parameters defined under the second and third distributions, D2 and D3, although D2 is slightly less optimistic and D3 is slightly more optimistic than D1. The fourth distribution leads to slightly more conservative recommendations (smaller a value or smaller number of trials).

The performance of the optimal design parameters defined under D1 were evaluated under the other hypotheses, in particular under the most pessimistic distribution D5 (sensitivity analysis). The probability of selecting an inferior treatment, P(HR_O > 1), is greater than 10% in several situations, but the chance of a clinically meaningful detriment to survival after the series of trials, P(HR_O > 1.1), remains under 1% in all cases.

Comparison of the optimal designs with the traditional designs

Table 1 summarizes the optimal design parameters, that is, a value and K, defined under the historical distribution, along with the corresponding sample sizes and trial accrual periods, as compared with the traditional trial sample sizes computed for a one-sided α = 2.5% and power = 90% for a minimum detectable difference of HR = 0.80.

Table 1.

Comparison of sample sizes between the proposed strategy (with the optimal number of trials K and α value defined under the historical distribution D1) and a traditional design with α = 2.5%, power = 90% for a minimal detectable difference of HR = 0.80

Situation			Optimal design						Traditional design
Accrual rate (patients/year)	Baseline survival	FU (years)	α (%)	K	Sample size	Accrual period (years)	Power for HR = 0.7 (%)	γ Error for HR = 1.25 (%)	Sample size	Accrual period (years)
100	Med(OS) = 0.5 year	0.5	20	10	100	1	73	3.5	889	8.9
100	Med(OS) = 1 year	1	20	7	114	1.1	73	3.3	932	9.3
100	Med(OS) = 2 years	2	10	4	176	1.8	69	0.6	1014	10.1
100	2-year OS = 0.75	2	10	4	176	1.8	50	1.5	1342	13.4
200	Med(OS) = 0.5 year	0.5	20	10	200	1	89	1.3	932	4.7
200	Med(OS) = 1 year	1	20	10	100	0.5	67	4.3	1013	5.1
200	Med(OS) = 2 years	2	20	5	200	1	83	1.9	1136	5.7
200	2-year OS = 0.75	2	10	4	350	1.8	69	0.5	1628	8.1
500	Med(OS) = 0.5 year	0.5	20	10	500	1	99	0.1	1050	2.1
500	Med(OS) = 1 year	1	20	10	250	0.5	88	1.3	1185	2.4
500	Med(OS) = 2 years	2	20	6	250	0.5	86	1.4	1340	2.7
500	2-year OS = 0.75	2	20	5	500	1	88	1.2	2105	4.2

The baseline survival defines the disease scenario (Scenarios 1–4).

Med(OS): median overall survival; 2-year OS: overall survival rate at 2 years.

The sample sizes under the proposed strategy are considerably smaller than the traditional designs. When trials are designed to detect an HR of 0.80 with a 90% power, the sample sizes of the traditional design are often 4–5 times greater than that for the proposed strategy. The largest differences in sample sizes between the proposed strategy and a traditional design occur in situations when the accrual rate is lowest, 100 patients/year.

By relaxing the a level in the proposed strategy at the single-trial level, we increase the chance of concluding the superiority of the experimental treatment when it is actually inferior. However, the γ error for HR = 1.25 remains below 5% in all cases (below 2.5% in 9 of the 12 studied situations), meaning that the chance of selecting a treatment associated with a 25% increase of the risk of death is reasonably controlled. The γ error remains below 2.5% when the a error is equal or less than 10% and is negligible in all the traditional designs.

Discussion

Our simulation results indicate that when few patients can be recruited per year, the designs using smaller sample sizes and relaxed α values yield greater expected survival benefits over a 15-year research horizon than the traditional design strategies aimed at detecting small differences with a high power and high level of evidence. Our results are consistent with previous findings of Sposto and Stram in the setting of one disease scenario and one assumption for the treatment effect [2]. Though our approach is similar to theirs in considering the survival benefits over a longer research horizon, it differs in that we identified the optimal pairing of number of trials and a level that produces the largest gains, for a variety of disease settings and distributions of treatment effect. Another difference is that they modeled the patient outcome through a cure model mimicking pediatric cancers, whereas we considered an exponential survival modeling more appropriate to adult cancers. Finally, we focused our long-term horizon to a 15-year period (compared to 25 years in Sposto and Stram) to measure the benefit on a realistic timeline. This reduction of scale may impact the magnitude of the total benefit, but the conclusions are similar.

The proposed strategy discussed herein is particularly appealing in the present context of many targeted agents available for testing on selected patient populations. With the increased interest in better tailoring oncology treatments, many common cancers are recognized as consisting of multiple rarer subtypes. Consequently, the proportion of rare cancers is very likely to increase as the biology of cancers is better known.

There are several limitations to our study. The most important limitations are that a new trial was assumed to start immediately after the previous trial is completed, we have not incorporated interim analyses, and we assumed that the treatments being compared are similar in all respects except for the efficacy as measured by the survival distribution, ignoring in particular the safety profiles of the treatment regimens. We performed a sensitivity analysis of adding a 6-month period between two trials; the main impact was to recommend slightly more conservative design parameters and to decrease the expected survival benefits at 15 years, but other conclusions remain valid. Many of the trials under the proposed strategy have extremely short accrual periods and so an interim analysis would have little impact in terms of reducing the trials’ sample size. However, interim analyses would benefit trials designed in the traditional manner. We acknowledge that interim analyses with futility rules or adaptive designs with sample size reestimation when the results are promising [12] are appealing in the current context; the study of such designs in our simulation framework is outside the scope of this article. Finally, many new targeted agents have fewer safety issues than cytotoxic treatments. The impact of this consideration would likely be small.

We acknowledge our simulation framework assumes that many new drugs are available for testing, since wrong decisions can be quickly corrected by subsequent trials. In cases where these assumptions are inaccurate, the traditional designs remain appropriate. As we randomly draw the treatment effect associated with the experimental treatment in terms of relative gain compared with the control arm, we also assume that the survival benefits can be cumulated trial after trial; this is arguable. In our simulation study, we assumed that the approval of a new drug only relied on a statistical test. However, we recognize that in real life, the treatment success is not based only on clinical significance but also in terms of investigators’ judgment on multiple endpoints [2,10].

An originality of our approach is to assess the performance of design parameters from a new viewpoint. In the traditional approach, the anticipated treatment effect is reduced to only two points, no difference (the null hypothesis) to determine the FPR, and a specified alternate hypothesis for the power definition. The reality is much richer, embracing a wide range of treatment effects. Considering a longer research horizon allows us to assess the performance of design parameters under realistic assumptions for the treatment effect and not only simple theoretical hypotheses. The downside of this approach is that the expected benefit we calculate depends upon the underlying assumption of expected treatment effect, which is uncertain. As this limitation cannot be avoided, we considered different distributions of the true treatment effect. Even though the design parameters we defined under the historical distribution might not be optimal under the other distributions, they performed rather well as compared to the traditional designs. Only very pessimistic assumptions of the true HR distribution meaningfully altered our proposed optimal strategy. We find it difficult to imagine that with increased biological knowledge, the next 15 years will result in poorer treatment options than the past 50 years (the base for our ‘historical’ distribution), thus we do not feel this should be an impediment to implementing this strategy.

Our investigations confirm that in rare diseases, the traditional clinical trial design criteria may be counterproductive. As already advocated by Stewart and Kurzrock [13], we recommend raising the efficacy bar, suggesting that trials be designed to identify larger clinical improvements, leading to smaller sample sizes. However, trials with smaller sample size do not perform well when using stringent level of evidence. Simply ‘increasing the bar’ by powering for larger effect sizes with no α adjustment did not optimize survival outcomes over a 15-year horizon, as in effect that strategy results in a high probability of discarding all but major advances. Our findings indicate that we must consider the interplay of the α level with the two other parameters. Our proposal stands between the traditional design of explanatory trials and the pragmatic attitude [9,14]. As suggested by several authors, the sample size dogma deserves reexamination [15,16].

Under all scenarios we considered, for a given number of trials performed over the 15-year period, the survival benefit increases substantially as accrual rate increases. Thus, our recommendation to relax the α level and decrease sample sizes must be accompanied by vigorous efforts to increase the accrual rate. That is, our proposal should not be taken as an encouragement to abandon collaborative projects with potential for broad participation.

We also recognize that reducing the sample size also reduces the available information on secondary outcomes such as toxicity. Further monitoring is recommended after drug approval.

In conclusion, in today’s environment of a multitude of targeted treatments and increasingly small patient populations, we suggest that a strategy of smaller sample sizes and larger α values (10%–20%) will lead to greater benefits in survival over an extended time period compared to traditional large trials designed to meet stringent criteria with a low efficacy bar and support more general consideration of such an approach.