Practical modifications to the Time-to-Event Continual Reassessment Method for phase I cancer trials with fast patient accrual and late-onset toxicities

Abstract

The goal of phase I cancer trials is to determine the highest dose of a treatment regimen with an acceptable toxicity rate. Traditional designs for phase I trials, such as the Continual Reassessment Method (CRM) and the 3+3 design, require each patient or a cohort of patients to be fully evaluated for the dose-limiting toxicity (DLT) before new patients can be enrolled. As such, the trial duration may be prohibitively long. The Time-to-Event Continual Reassessment Method (TITE-CRM, Cheung and Chappell, 2000) circumvents this limitation by allowing staggered patient accrual without the need for complete DLT follow-up of previously treated patients. However, in the setting of fast patient accrual and late-onset toxicities, the TITE-CRM results in overly aggressive dose escalation and exposes a considerable number of patients to toxic doses. We examine a modification to the TITE-CRM proposed by the original TITE-CRM creator and propose an alternative approach useful in this setting by incorporating an accrual suspension rule. A simulation study designed based on a neuro-oncology trial indicates that the modified methods provide a much improved degree of safety than the TITE-CRM while maintaining desirable design accuracy. The practical aspects of the proposed designs are discussed. The modifications presented are useful when planning phase I trials involving chemoradiation therapy.

1. Introduction

Cancer clinical trials involve several distinctive phases. Phase I trials are typically the first test of new agents in human subjects. A main objective of phase I cancer trials is to determine the highest dose of a new therapy associated with an acceptable level of toxicity to be used for subsequent phase II trials. More specifically, the purpose is to estimate the maximum tolerated dose (MTD) such that the percentage of patients experiencing the dose limiting toxicity (DLT) at the MTD is kept below a pre-specified target level. A common ethical dilemma clinical investigators face in the conduct of phase I cancer trials is to balance between increasing the dose slowly to avoid untoward toxicities and avoiding treating patients at low doses that may have no therapeutic effect. Ideally, phase I cancer trials should be designed to maximize the proportion of patients assigned to the optimal dose and minimize the number of patients treated on the trial.

In practice, the most widely used method for phase I dose-finding trials is perhaps the 3+3 design, also known as the cohort-of-three design. This is a rule-based scheme in which the dose levels are fixed in advance and the dose escalation decision depends on the number of patients at a dose that experience DLT [1, 2]. Initially, 3 patients are treated at the lowest dose. If 0 out of 3 patients experience DLT, dose is escalated to the next higher level where a cohort of 3 new patients are treated. If 1 out of 3 patients experiences DLT, an additional 3 patients are treated at the current dose. If 2 or more patients (out of 3 or 6 patients) experience DLT, the current dose is declared unsafe and de-escalate. Six patients must be treated at the dose declared as the MTD. If the lowest dose is deemed toxic or the highest dose is deemed safe, then no MTD is estimated. Historically, the popularity of the 3+3 design stems from its simplicity and ease of implementation; clinical investigators often feel comfortable using this design assuming that it is safe and its design properties are well-understood.

Although rarely emphasized in the literature, phase I dose-finding studies are inherently associated with a fixed time period. Specifically, a toxicity observation window is decided by the investigators at the design stage of the trial and subsequent dose assignment decisions are made based on DLT’s observed during this time-frame. In order for the estimated MTD to be relevant to the experimental therapy, this observation window should reflect a realistic time-frame during which the DLT’s induced by the study drug are expected to occur. In this article we are primarily concerned with a clinical setting in which the study drug is likely to cause late-onset (LO) toxicities. The MTD should thus be defined with respect to a longer period of time. This is a common scenario in phase I radio-chemotherapy trials in which radiation-induced adverse events may occur up to several months after the initiation of treatment. In this setting, the 3+3 design may be undesirable since it requires the trial to be closed to accrual during the DLT follow-up period for the previous cohort of patients. As such, the trial duration may be prohibitively long, especially when the lowest dose is far below the MTD. Another well-known deficiency of the 3+3 design is that it tends to treat many patients at doses below the biologically active level, hence diminishing the chance for therapeutic benefit.

In recent years, many alternative designs have been proposed to the standard 3+3 design that promise to improve the trial efficiency and statistical accuracy for phase I dose-finding trials [3]. The most prominent work among these is the Continual Reassessment Method (CRM) [4, 5, 6, 7] and its various extensions and modifications [8, 9, 10, 11, 12, 13]. Briefly, the CRM is a sequential sampling procedure that utilizes a mathematical model relating dose levels to the probability of DLT. Therefore, the CRM and its variations are often referred to as model-based approaches. In contrast to the 3+3 design for which dose escalation decision is based merely on patients treated at the current dose, the CRM utilizes information from all previously treated patients, updates the estimates of the DLT probability at each dose at each stage of the trial, and assigns a future patient adaptively to the dose estimated to be closest to the MTD. The design properties of the CRM have been studied extensively in the literature [14, 15, 16, 17, 18, 19, 20, 21]. The general consensus is that the CRM tends to treat a higher proportion of patients at the optimal dose and yields higher accuracy of the MTD estimate than the 3+3 design. However, in the context of LO toxicities, the CRM shares a common drawback with the 3+3 design in terms of prolonged trial duration. This is because the CRM involves treating one patient at a time and the dose assignment decision cannot be made for the next patient until DLT information is completely observed from previous patients. Although Goodman et al. [8] proposed refinements of the CRM by treating a cohort of ≥ 2 patients at a time, their approach may only offer marginal improvement in trial length in the setting of LO toxicities due to the lengthy toxicity follow-up required for each cohort of patients.

A method that specifically addresses the LO toxicity issue is the Time-to-Event Continual Reassessment Method (TITE-CRM) [22, 23]. While the estimation procedure and dose allocation scheme of the TITE-CRM follows closely the classic CRM paradigm, a TITE-CRM trial permits enrollment of a new patient when previous patients are still under observation (i.e. trial is always open to accrual), hence reducing the trial duration compared to the CRM. Since its inception, the TITE-CRM has slowly gained popularity and has been successfully implemented in several major academic cancer centers such as Columbia University and the University of Michigan [24, 25, 26, 27]. Nevertheless, there are some practical challenges associated with the TITE-CRM [28, 29]. For example, Bekele et al. [30] indicated that in the setting of LO toxicities and fast patient accrual, the TITE-CRM may be associated with a higher risk of treating patients at unsafe doses. This is because the TITE-CRM does not require suspension of patient accrual while waiting for toxicity information on previously treated patients to mature. As a result, new patients may be assigned to doses deemed safe but later found to be otherwise. They proposed a Bayesian dose-finding method to address this particular issue. However, their approach is mathematically complex and will require a specialized computer program and a sophisticated data collection infrastructure to facilitate the actual trial implementation. These added burdens will likely deter clinical investigators from adopting their method in practice.

This work was motivated by a phase I trial to be conducted jointly by the University of California-San Francisco (UCSF) and Memorial Sloan-Kettering Cancer Center (MSKCC). The intent of this work is to share our modification to the TITE-CRM, specifically to address the design challenge facing the TITE-CRM in the setting of LO toxicities and fast patient accrual. The performance of our method is compared with some existing approaches in the literature. This article is organized as follows: In Section 2, we briefly outline the TITE-CRM and introduce our modification to the TITE-CRM as well as other competing designs. Section 3 details the set-up for simulation studies in the context of a motivating example. Section 4 presents the results of the simulation studies to illustrate the operating characteristics of the designs under consideration. Section 5 provides practical guidelines on how the design parameters in our modification may be calibrated in practice. Section 6 concludes with discussions on the practical aspects of these methods.

2. Methods

2.1. Time-to-Event Continual Reassessment Method (TITE-CRM): a Review

We start with a brief review of the CRM since it shares many common theoretical elements with the TITE-CRM. Suppose in a typical phase I trial setting that k distinct doses, d₁ ≤ d₂ ≤ ⋯ ≤ d_k, are chosen for testing. The goal is to estimate the dose level d_θ associated with a target DLT probability θ that is determined at the beginning of the trial. The entire experiment can be summarized by the data {(d_[i]; y_i), i = 1, …, n}, where d_[i] is the dose administered to patient i and y_i is the binary indicator of a toxic response.

The CRM models the probability of DLT via a parametric model φ(x(d), β) that is strictly increasing in x for all β. Note that here the doses $x_i^{\prime }s$ are mapped from the actual doses $d_i^{\prime }s$ administered during the trial. They are transformed dose units that are obtained by backward substitution of the set of initial guesses of the DLT probability p₁, …, p_k into the dose-toxicity model. More specifically, x_i is redefined from the original units by solving p_i = φ(x_i, β̂₀) for x_i, where β̂₀ denotes the prior mean of β. Thus, the CRM requires the specification of $p_i^{\prime }s$, which are typically determined by the investigators based on information from experience. Many forms of the dose-toxicity model φ(x, β) are possible. A common choice is the one-parameter logistic model:

$$\phi (x_i,\beta )=\frac{\text{exp}(\alpha +\beta x_i)}{1+\text{exp}(\alpha +\beta x_i)},$$ (1)

where α is a fixed constant. In the originally proposed Bayesian CRM, the unknown model parameter β is considered a random variable and a prior distribution g(β) for β is assumed. The prior distribution represents our uncertainty about the initial guess of the true dose-toxicity relationship.

The CRM starts by assigning the first patient to the dose for which the DLT probability is deemed closest to θ. Let Ω_j = {(x_[i], y_i); i = 1, …, j} denote the data accrued up to the first j patients (i.e. the doses administered and the observed binary toxicity outcomes), the likelihood function is given by

$$L(\beta ;{\mathrm{\Omega }}_j)=\prod _{i=1}^j{\{\phi (x_{[i]},\beta )\}}^{y_i}{\{1-\phi (x_{[i]},\beta )\}}^{1-y_i}.$$

Given the prior distribution and Ω_j, the posterior distribution for β is calculated using Bayes theorem and is given by

$$f(\beta |{\mathrm{\Omega }}_j)=\frac{L(\beta ;{\mathrm{\Omega }}_j)g(\beta )}{{\int }_0^{\infty }L(\beta ;{\mathrm{\Omega }}_j)g(\beta )d\beta }.$$

The model parameter β can then be estimated by the posterior mean as

$${\widehat{\beta }}_j=\frac{{\int }_0^{\infty }\beta L(\beta ;{\mathrm{\Omega }}_j)g(\beta )d\beta }{{\int }_0^{\infty }L(\beta ;{\mathrm{\Omega }}_j)g(\beta )d\beta }.$$

By substituting β̂_j into the dose-toxicity model, we obtain a new estimate of the dose-toxicity curve, φ(x_i, β̂_j). The (j + 1)th patient is then treated at the dose level whose estimated probability of toxicity is closest to θ, i.e., arg min_Xi |φ(X_i, β̂_j) − θ|. This process is repeated until a fixed number of patients have been treated or some pre-specified stopping criterion has been met. The final estimate of the MTD is the dose with a DLT rate closest to θ, based upon data from all treated patients.

As previously mentioned, a major drawback of the CRM is that the dose decision cannot be made for a new patient until all previously treated patients have been fully evaluated, i.e. either experiences a DLT or completes the follow-up without a DLT within the specified observation window. As such, accrual of new patients is suspended until all enrolled patients have completed the follow-up. Such a design constraint is particularly problematic for trials that involve radiation therapy since radiation is known to cause delayed toxicities and postponing enrollment of new patients as a result of incomplete observation of previous patients would result in a substantial increase in trial length. The introduction of the TITE-CRM [22] circumvents this challenge by allowing patients to be enrolled in a staggered fashion without the need to fully observe the toxicity outcomes in previous patients. Specifically, let T denote the toxicity observation window and suppose that an enrolled patient i has been followed for a duration of u_i, where 0 < u_i ≤ T, the TITE-CRM extends the CRM by using the weighted likelihood

$$\tilde{L}(\beta ;{\mathrm{\Omega }}_j)=\prod _{i=1}^j{\{w_i\phi (x_{[i]},\beta )\}}^{y_i}{\{1-w_i\phi (x_{[i]},\beta )\}}^{1-y_i},$$

where w_i is the weight assigned to patient i just prior to the entry of the (j + 1)th patient, such that

$$w_i=\{\begin{array}{cc}{u}_i/T;\hfill & \text{if patient}i\text{is still in follow-up without a DLT}\hfill \\ 1;\hfill & \text{if patient}i\text{has a DLT or has been followed for}T\text{without a DLT}.\hfill \end{array}$$ (2)

Essentially, patients who have not developed a DLT are weighted by the amount of time they have been followed as a proportion of the observation window, whereas patients who have experienced a DLT are assigned a full weight. Cheung and Chappell [22] demonstrated via simulation studies that the weight function in Equation (2) appears to be an adequate choice in many situations.

2.2. Five Competing Designs

In this section we examine an existing modification to the TITE-CRM and propose an alternative approach useful in the setting of phase I dose-finding trials with LO toxicities and fast patient accrual. A common goal of these modifications is to reduce the risk of exposing patients to dose levels that have excessive toxicity probability. Five competing designs are described below. The operating behavior of these designs is evaluated in a variety of settings using simulations; the results are presented in Section 4.

1. Design A. The standard 3 + 3 design

2. Design B. The unmodified TITE-CRM

3. Design C. A hybrid TITE-CRM with an initial rule-based transition stage as follows:

   1. Enroll a cohort of three patients at a time starting from the lowest dose.
   2. If no DLT is observed, escalate to the next higher dose. As soon as a DLT is observed, switch to the TITE-CRM.
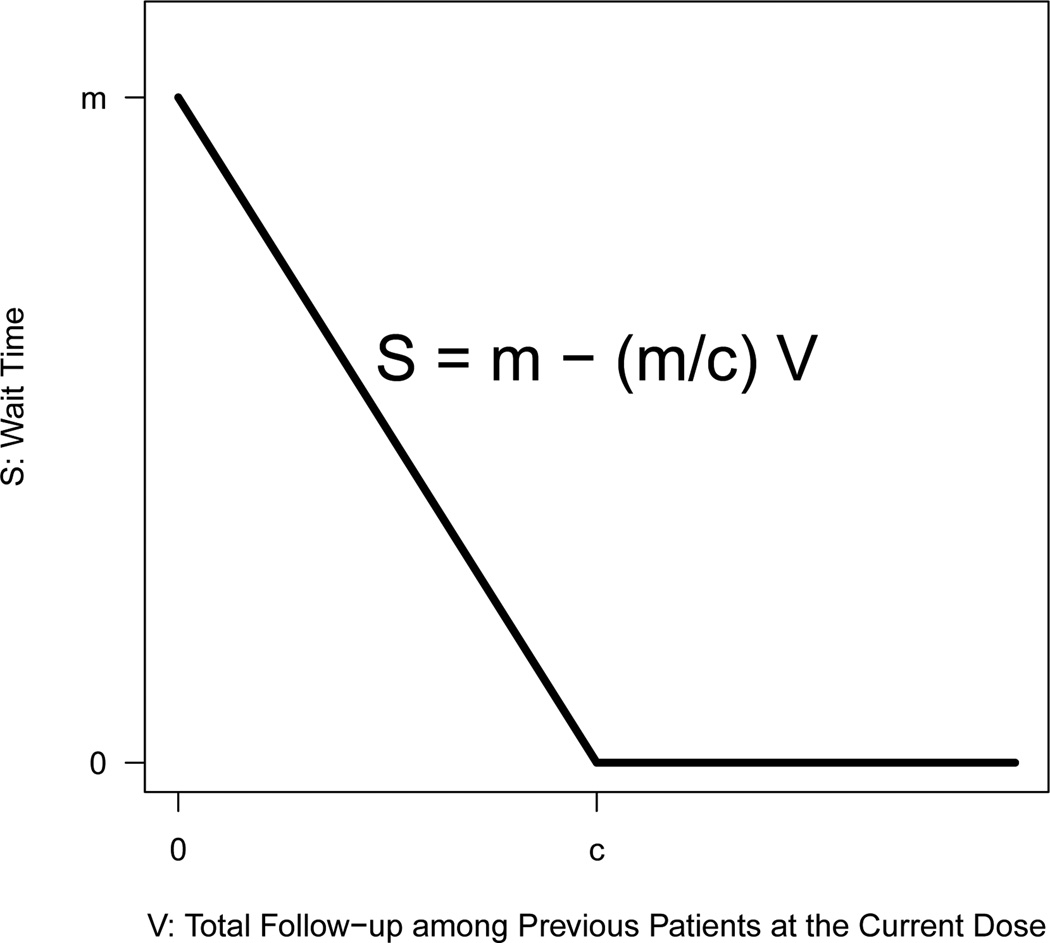
4. Design D. A TITE-CRM with adaptive wait time. Precisely, let S denote the wait time necessary before enrolling the next patient and V denote the sum of follow-up time among previous patients who have been treated at the dose that the current patient is given, then

   $$S=\{\begin{array}{cc}m-(m/c)V;\hfill & \text{if}V<c\hfill \\ 0;\hfill & \text{if}V\ge c,\hfill \end{array}$$ (3)

   where m(≤ T) represents, in the absence of any previous DLT follow-up information at the current dose, the maximum time the investigator is willing to wait before enrolling a new patient, and c specifies a threshold for V above which no accrual suspension is needed (i.e. enroll the next patient as soon as they become available), respectively.

5. Design E. The CRM design

Design C was previously described by Cheung and Chappell [22]. This design incorporates a conservative initial transition rule before switching to the more aggressive TITE-CRM. Design D is our modification to the TITE-CRM which essentially devises a rule for the wait time between two consecutive patients, expressed as a decreasing linear function of the amount of information available in previous patients who have been treated at the dose administered to the current patient. Figure 1 provides a graphical illustration of the adaptive wait time function in Design D. The wait time necessary before the study is open to accrual can be calculated based on Equation (3) as soon as a new patient is enrolled. To illustrate, suppose that in a hypothetical trial, the dose levels administered to the first three patients are (1, 2, 1), respectively. Suppose further that at the time the fourth patient enters the study, the first three patients have been followed for DLT at the respective given doses for 5, 3, and 2 months and it is determined by the algorithm to assign dose 1 to the fourth patient. It thus follows that the total follow-up time among the first three patients who have been treated at the dose the current patient is given (i.e. dose 1) is V = 5 + 2 = 7 months. Assuming m = 4 and c = 10 (unit in months), then the wait time necessary before the study is open to enroll the fifth patient, according to Equation (3), is S = 4 − (4/10) * 7 = 1.2 months. In general, Design D proceeds cautiously at the early stage of the trial, and as the trial progresses and more information becomes available, the wait time before the next enrollment decreases accordingly. In practice, the parameters m and c in Design D can be chosen by examining the design performance via simulations. In Section 4, we present simulation results based on m = 4 and c = 10 which are found to yield reasonable design properties as far as our motivating example is concerned. A detailed discussion on the calibration of these parameters is given in Section 5.

Figure 1.

Adaptive wait time function in Design D.

3. Simulation Set-up

The performance of the five competing designs described in Section 2.2 is examined in the context of a phase I trial in patients with recurrent malignant glioma. The purpose of the trial is to determine the MTD of the hypofractionated stereotactic radiotherapy when administered in combination with a fixed dose of bevacizumab. All patients will receive bevacizumab 10 mg/kg every two weeks of each 28-day cycle. After completion of the first cycle of bevacizumab, radiotherapy will start in cycle 2 and will be delivered in 3 fractions over one week. Following radiotherapy, patients will continue bevacizumab every two weeks until disease progression. DLT is defined as any grade ≥ 4 toxicity thought to be attributable to radiation or bevacizumab with respect to six months of follow-up (T = 6) after initiation of the study treatment. The MTD is defined as the dose associated with a target probability of DLT of 25%. The six doses of radiotherapy are 8, 9, 10, 11, 12, and 13 Gy/fraction. Based on past experience, the potential accrual rate is expected to be 3 patients per month.

All simulations were performed by adapting the titesim function in the R package dfcrm [31, 32]. Each scenario had 1,000 Monte Carlo simulation replicates. All simulated trials assumed a maximum sample size of 24, which is typical for phase I clinical trials. For CRM and TITE-CRM designs (Designs B-E), the prior estimates of the toxicity probabilities are p₁ = 5%, p₂ = 10%, p₃ = 25%, p₄ = 35%, p₅ = 50%, and p₆ = 70%, respectively. Thus, the prior guess of the MTD is the third dose. We assumed a logistic dose-toxicity model in Equation (1) with the intercept α = 3, and re-parameterized by substituting β with exp(β). O’Quigley and Shen [5] indicated that such a re-parameterization ensures a prior over the whole real line and provides some advantages in terms of coverage accuracy. A normal prior with mean 0 and variance 1.34 was assumed for the model parameter β, which is the default in the dfcrm package. For Design D, we chose m = 4 and c = 10. The calibration of these design parameters is provided in Section 5.

For each design, we investigated the six true toxicity probability configurations used in Chevret [16] (see Tables 1–6 in Section 4). In scenarios 1 and 2, the true DLT probabilities are either equal to or slightly higher than the prior probabilities assumed by the investigator, respectively; the MTD in these two scenarios is the third dose. In scenarios 3 and 4, the true toxicity probabilities are much higher than the prior estimates, and the lowest dose is the correct MTD. In scenarios 5 and 6, the doses are much less toxic than initially guessed, and the correct dose to be chosen are the fifth and sixth, respectively. Time to toxicity was simulated to mimic the motivating trial where DLT’s are more likely to occur late in the observation window. Specifically, we generated the patient’s failure time using a Weibull model, where the shape parameter was set to be 4 and the scale parameter was solved for such that the cumulative distribution function at T = 6 is equal to the true toxicity probability associated with each dose.

Table 1.

Comparison of four designs for scenario 1 (bold-faced numbers correspond to the true MTD)

Dose	True toxicity probability	Design
		A	B	C	D	E
Recommended dose level (%)
0	-	3	-	-	-	-
1	0.05	10	4	5	3	3
2	0.10	40	25	19	19	20
3	0.25	29	41	52	46	47
4	0.35	15	23	18	23	23
5	0.50	3	7	7	8	6
6	0.70	0	0	0	0	0
Dose level treated at (%)
1	0.05	26	8	31	18	13
2	0.10	30	8	27	17	22
3	0.25	27	12	15	25	32
4	0.35	13	15	19	20	21
5	0.50	4	18	18	14	10
6	0.70	1	40	0	7	2
Median DLT rate (min, max)		20 (5, 67)	46 (13, 88)	21 (5, 50)	27 (5, 59)	25 (8, 46)
Median trial length, months (min, max)		36 (6, 74)	13 (8, 20)	30 (13, 50)	38 (17, 50)	120 (62, 157)
Median number of patients (min, max)		15 (3, 30)	21 (14, 24)	19 (10, 24)	16 (10, 24)	19 (10, 24)

Table 6.

Comparison of four designs for scenario 6 (bold-faced numbers correspond to the true MTD)

Dose	True toxicity probability	Design
		A	B	C	D	E
Recommended dose level (%)
0	-	0	-	-	-	-
1	0.00	0	0	0	0	0
2	0.00	1	0	0	0	0
3	0.03	2	0	0	0	0
4	0.05	4	0	1	1	1
5	0.06	32	17	20	18	16
6	0.22	60	83	79	81	83
Dose level treated at (%)
1	0.00	15	6	14	6	6
2	0.00	15	6	14	7	6
3	0.03	16	7	15	8	7
4	0.05	17	11	18	9	8
5	0.06	19	15	21	17	20
6	0.22	19	56	18	53	52
Median DLT rate (min, max)		5 (0, 22)	13 (0, 50)	5 (0, 29)	13 (0, 53)	13 (0, 29)
Median trial length, months (min, max)		49 (26, 72)	12 (8, 18)	43 (28, 56)	38 (29, 53)	102 (92, 155)
Median number of patients (min, max)		21 (12, 30)	18 (14, 24)	22 (18, 24)	15 (13, 24)	16 (15, 24)

Motivated by both safety and efficiency considerations, many practical modifications to the CRM have been proposed by various authors [8, 17]. Among these, we adopted the following constraints into the CRM and TITE-CRM designs (Design B-E) in our simulation:

1. The first patient was always treated at the lowest dose, rather than the initial guess of the MTD.

2. Dose could not escalate more than one level at a time, although no restriction was placed on de-escalation.

3. In order to reduce the time it took to complete the trial, the trial would stop enrollment when 10 patients (not necessarily consecutive) had been treated at the same dose. For Design C, the patients treated at the initial transition stage would be counted towards these 10 patients.

4. Operating Characteristics

Tables 1–6 summarize the operating characteristics of the competing designs under the six true dose-toxicity scenarios described in the previous section. The true probability of DLT for each corresponding dose is specified in the second column of the tables. We define accuracy of a design as its ability to correctly identify the dose with the DLT probability closest to the target level of 0.25. The percentages of trials identifying each dose as the MTD are presented in the top halves of the tables. The bottom halves of the tables display the average percentage of patients allocated to each dose. The last three rows of the tables give the median percentage of observed DLT’s, the median trial duration, and the median number of patients used, together with the minimum and maximum of each distribution.

Tables 1 and 2 contain the simulation results for scenarios 1 and 2, where the true probabilities of toxicity are the same as or slightly higher than our prior guess, respectively. As far as the accuracy of the designs is concerned, the TITE-CRM and CRM designs (Designs B-E) clearly outperform Design A. In addition, Design A recommends an inactive dose much more frequently than its TITE-CRM and CRM counterparts, whereas no design selects a final dose more than two levels above the MTD in either scenario. Among Designs B-E, there does not appear to be an appreciable difference in accuracy, although Design C seems to offer a slight advantage in both scenarios.

Table 2.

Comparison of four designs for scenario 2 (bold-faced numbers correspond to the true MTD)

Dose	True toxicity probability	Design
		A	B	C	D	E
Recommended dose level (%)
0	-	8	-	-	-	-
1	0.09	22	11	17	12	11
2	0.16	35	34	27	28	29
3	0.27	25	37	43	42	40
4	0.38	10	16	12	14	18
5	0.57	1	3	2	4	2
6	0.75	0	0	0	0	0
Dose level treated at (%)
1	0.09	34	9	43	27	21
2	0.16	31	9	28	19	25
3	0.27	22	13	11	22	30
4	0.38	10	15	14	17	17
5	0.57	3	16	5	10	6
6	0.75	0	38	0	4	1
Median DLT rate (min, max)		20 (10, 67)	50 (13, 93)	20 (5, 50)	27 (6, 63)	26 (8, 44)
Median trial length, months (min, max)		35 (6, 73)	13 (9, 21)	23 (13, 49)	36 (16, 51)	119 (62, 159)
Median number of patients (min, max)		15 (3, 30)	23 (13, 24)	13 (10, 24)	16 (10, 24)	19 (10, 24)

With respect to patient allocation, the simulations indicate a clear contrast between Design A and Design B. Specifically, Design A tends to be overly conservative, allocating 56% and 65% of the patients to ineffective doses in two scenarios, respectively. In contrast, Design B is dangerously aggressive, exposing approximately 40% of th patients to the dose more than two levels higher than the MTD in both scenarios. An interesting observation to be made is perhaps in the hybrid nature of Design C manifested in the distribution of patient allocation. In particular, in contrast to Designs A and B, Design C appears to shift a significant proportion of patients towards the two ends of the dose range, resulting in a simultaneous increase in the percentage of under-treated and over-treated patients. Among the TITE-CRM competitors, Design D allocates patients to the optimal dose most frequently (25% and 22%, respectively). However, this advantage is somewhat compromised by a small increase in the percentage of patients treated at the dose more than two levels beyond the MTD. Overall, Design E assigns the highest percentage of patients to the optimal dose (32% and 30%, respectively), while maintaining a reasonable balance between under-treated and over-treated patients.

Design B tends to exhaust almost all planned sample size and requires substantially less time to complete the trial. This is not surprising since Design B requires no trial suspension during the DLT follow-up. This saving in trial duration, however, comes with a significant cost of high toxicity rates (46% and 50%). On the other hand, Design E in both scenarios requires about 120 months to complete the trial, which makes it an impractical design for the underlying setting. Among other designs, there does not appear to be pronounced differences in trial duration or required sample size, except for a notable advantage in trial length associated with Design C (median: 30 and 23 months, respectively).

Scenarios 3 and 4 represent phase I trials in which the lowest dose is the MTD. Tables 3 and 4 give the corresponding simulation results. Designs B-E again achieve markedly higher accuracy than the 3 + 3 design. The distribution of patient allocation once again elucidates the aggressive nature of Design B: 58% and 54% of the patients respectively are treated at doses more than two levels higher than the MTD, and the observed DLT rate exceeds 50% in both scenarios.

Table 3.

Comparison of four designs for scenario 3 (bold-faced numbers correspond to the true MTD)

Dose	True toxicity probability	Design
		A	B	C	D	E
Recommended dose level (%)
0	-	38	-	-	-	-
1	0.22	37	52	61	54	61
2	0.32	20	35	26	30	28
3	0.45	5	10	14	14	11
4	0.54	0	2	0	2	0
5	0.69	0	0	0	0	0
6	0.80	0	0	0	0	0
Dose level treated at (%)
1	0.22	63	17	68	51	55
2	0.32	27	13	23	23	26
3	0.45	9	13	5	15	14
4	0.54	2	13	3	7	4
5	0.69	0	14	1	3	1
6	0.80	0	31	0	1	0
Median DLT rate (min, max)		33 (13, 100)	54 (17, 95)	30 (8, 60)	33 (9, 90)	30 (13, 90)
Median trial length, months (min, max)		25 (5, 63)	13 (18, 20)	18 (13, 44)	29 (16, 52)	101 (61, 156)
Median number of patients (min, max)		12 (3, 27)	24 (11, 24)	10 (10, 24)	14 (10, 24)	16 (10, 24)

Table 4.

Comparison of four designs for scenario 4 (bold-faced numbers correspond to the true MTD)

Dose	True toxicity probability	Design
		A	B	C	D	E
Recommended dose level (%)
0	-	56	-	-	-	-
1	0.30	33	78	82	79	83
2	0.40	10	19	14	17	14
3	0.52	1	3	4	4	3
4	0.61	0	0	0	0	0
5	0.76	0	0	0	0	0
6	0.87	0	0	0	0	0
Dose level treated at (%)
1	0.30	75	22	79	63	71
2	0.40	20	13	17	19	18
3	0.52	4	12	3	12	8
4	0.61	1	12	1	4	2
5	0.76	0	13	0	1	1
6	0.87	0	29	0	0	0
Median DLT rate (min, max)		33 (13, 100)	58 (21, 95)	31 (8, 80)	38 (9, 83)	36 (15, 82)
Median trial length, months (min, max)		16 (5, 55)	13 (9, 20)	16 (13, 40)	26 (16, 52)	76 (61, 156)
Median number of patients (min, max)		6 (3, 24)	24 (10, 24)	10 (10, 24)	12 (10, 24)	12 (10, 24)

Among the CRM variants, Design C on average selects the correct dose most frequently, has the lowest percentage of over-treated patients and observed DLT rate, and completes the trial with fewer than half of the maximum sample size within a relatively short time-frame. Therefore, the fact that Design C gains significant improvement in accuracy over the 3+3 design, yet pays little penalty as far as conservative patient allocation is concerned, would argue strongly in favor of its use in these scenarios. Overall, Design D has comparable operating characteristics with Design C in these scenarios, but is slightly more aggressive with respect to patient allocation and requires longer trials in general. Design E again requires substantially lengthier trials (median: 101 and 76 months, respectively), which limits its practical use when late toxicities are expected.

Tables 5 and 6 summarize simulation results of scenarios 5 and 6, in which the lowest dose is far below the true MTD. In scenario 5, the dose-toxicity curve is steep around the MTD. In scenario 6, the toxicity probability is very low at the first five doses and the target is only reached at the highest dose level. The results again suggest that Design A is most conservative and recommends a suboptimal dose as the MTD far more often than Designs B-E. It also requires longer time to complete the trial than its TITE-CRM counterparts and utilizes most planned sample size. This is not surprising since many doses with low toxicity probabilities are tried before the target dose is reached. Designs B-D are comparable in design accuracy in both scenarios.

Table 5.

Comparison of four designs for scenario 5 (bold-faced numbers correspond to the true MTD)

Dose	True toxicity probability	Design
		A	B	C	D	E
Recommended dose level (%)
0	-	0	-	-	-	-
1	0.00	0	0	0	0	0
2	0.01	2	0	0	0	0
3	0.04	7	4	4	2	1
4	0.09	39	19	10	17	17
5	0.24	39	60	65	68	67
6	0.49	13	18	21	13	15
Dose level treated at (%)
1	0.00	14	6	14	6	6
2	0.01	15	6	15	7	6
3	0.04	17	8	14	10	9
4	0.09	22	12	19	17	21
5	0.24	22	17	31	29	40
6	0.49	10	52	8	32	19
Median DLT rate (min, max)		14 (0, 26)	30 (0, 65)	14 (0, 33)	25 (0, 63)	21 (0, 38)
Median trial length, months (min, max)		49 (20, 74)	12 (9, 20)	43 (21, 53)	39 (25, 51)	120 (88, 156)
Median number of patients (min, max)		21 (9, 30)	18 (15, 24)	22 (13, 24)	16 (12, 24)	19 (14, 24)

In scenario 5 where the highest dose is twice as toxic as the MTD, Design C and Design D again demonstrate significant advantage over Design B by markedly reducing the percentage of patients exposed to the toxic dose. Between these two designs, Design D is again more aggressive in terms of patient allocation, whereas Design C generally requires a longer trial and larger sample size. Finally, in scenario 6 we observe that Design A and Design C perform similarly with respect to patient allocation, trial duration, and required sample size. Both designs are overly conservative, allocating more than 80% of the patients to doses below the MTD. Of note, scenario 6 appears to be the only situation in which the unmodified TITE-CRM gives reasonable performance in the context of fast patient accrual and LO toxicities. In this setting, the operating characteristics of Design B and Design D are very similar except that the latter requires longer trials as a result of the built-in wait time between consecutive patients. The median trial length for Design E is 120 months and 102 months for these two scenarios, respectively.

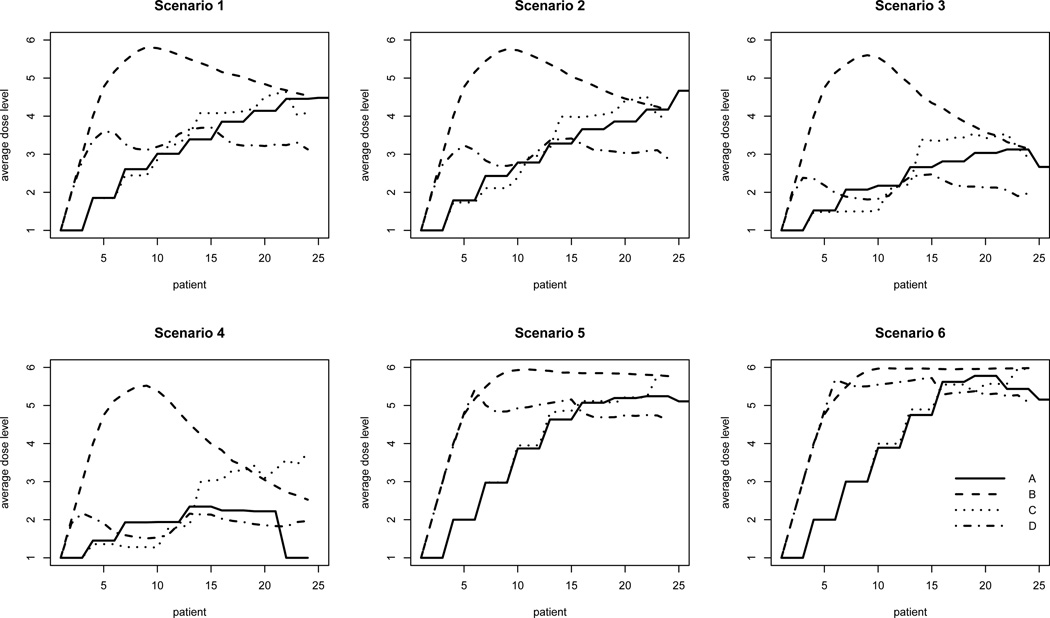
In Figure 2, the average dose level assigned to each patient over all simulation runs is plotted against the patient sequence. For ease of presentation, Design E is excluded from the plot due to its major disadvantage in terms of trial length as previously discussed. Note that since trials may stop before the planned maximum sample size is exhausted, the average dose level may be based on fewer than 1000 simulations since the number of simulations decreases as the trial progresses. Nevertheless, the purpose of this figure is to provide a visual impression of how each design assigns doses during the course of the entire trial. We observe that in all scenarios, Design B escalates rapidly during the initial stage of the trial and gradually converges to the correct dose. It is noteworthy that under scenarios 3 and 4 in which the lowest dose is the MTD, Design B quickly escalates beyond the MTD (i.e. the lowest dose) and remains above it throughout the entire course of the trial on average. This phenomenon explains the excessively high toxicity rates we observed in the simulation studies and further highlights the need for practical modifications to this approach in the underlying setting. In contrast, the 3+3 design proceeds most cautiously but at the expense of treating too many patients at ineffective doses (except for scenarios 3 and 4). Overall, Design C and Design D appear to represent reasonable compromises between the conservative 3 + 3 design and the overly aggressive unmodified TITE-CRM as far as in-trial allocation is concerned.

Figure 2.

Average dose level assigned over the course of the trial for each design. Dose indicated for each patient represents the mean dose based on available simulation runs. Since trials may stop before the planned maximum sample size (24) is exhausted, the mean dose may be based on fewer than 1000 simulations.

5. Calibration of Parameters in Design D

In this section, we focus on our proposed modification to the TITE-CRM (Design D). In particular, we discuss how the choice of the two design parameters, m and c, generally affect the operating characteristics of the design and provide practical guidelines as to how these parameters may be calibrated in practice. By examining Equation (3), we first note two special cases. When c = 0, the wait time necessary before enrolling the next patient is 0 for any value of m. This is essentially the unmodified TITE-CRM (Design B) in that no accrual suspension is required and the enrollment continues as soon as an eligible patient becomes available. When c → ∞ and m = T (the observation window for DLT), Design D corresponds to a CRM design since a maximum wait time T is required before the next patient may be enrolled, regardless of the amount of DLT follow-up information available in previously treated patients. Our modification slows down the patient accrual in a TITE-CRM design by incorporating an adaptive wait time between two consecutive patients. The wait time is expressed as a decreasing linear function of the total follow-up time available in previous patients who have been treated at the dose the current patient is given, and is bounded by an upper limit, m, selected by the investigator as a number between 0 and T. In this regard, our modification represents a compromise between the TITE-CRM and the CRM.

To examine the impact that the parameters m and c have on the operating characteristics of Design D, we performed simulation studies by varying the values of m and c. Specifically, we considered values of m in [2, 4, 6] and the values of c in [5, 10, 15, 20, 25]. For each pair-wise combination of m and c, design characteristics including trial length, percentage of patients experiencing a DLT, percentage of patients treated at doses above the MTD, percentage of trials correctly identifying the true MTD and patient number used in the trial were recorded. The simulation set-up follows that as described in Section 3. For the purpose of illustration, we present here only the simulation results based on scenario 1 described in Section 3. However, results for other plausible scenarios can be obtained similarly by changing the true toxicity probability configuration in the simulation.

Table 7 presents the simulation results based on scenario 1 and 10,000 simulation runs. As expected, for a fixed value of m, the trial length increases with increasing values of c. However, the mean percentage of patients experiencing a DLT and the mean percentage of patients treated above the MTD both decrease. The same trend can be observed for increasing values of m for any fixed value of c. For example, when m = 2, the average trial duration increases from 23 months (SD = 3.35) when c = 5 to 34 months (SD = 4.95) when c = 25. On the other hand, the mean percentage of patients who are treated at doses above the MTD decreases from 48% (SD = 33%) to 42% (SD = 30%), respectively. Similarly, when c = 10, the mean trial duration increases from 27 months (SD = 3.71) when m = 2 to 36 months (SD = 6.55) when m = 4, whereas the mean percentage of patients treated at doses above the MTD decreases from 45% (SD = 32%) to 41% (SD = 34%), respectively. In general, we observe that as the accrual suspension rule becomes more stringent (either increase m or c), the degree of toxicity is diminished but with a cost of a lengthier trial. Of note, neither the number of patients required for the trial nor the percentage of trials correctly selecting the true MTD alter drastically among the designs we considered, suggesting that the choice of m and c have relatively little impact as far as patient number and estimation precision are concerned.

Table 7.

Impact of design parameters (m, c) on Design D based on scenario 1, i.e. true toxicity probabilities (0.05, 0.1, 0.25, 0.35, 0.5, 0.7). The first number represents the mean and the second the standard deviation (in parenthesis).

	trial length	% with DLT	% treated above MTD	patient number	% select true MTD
Design D
m=2, c=5	23.2 (3.4)	30.9 (12.6)	47.6 (33.0)	18.7 (3.9)	43.9
m=2, c=10	26.5 (3.7)	30.0 (11.2)	45.3 (32.4)	18.6 (3.5)	44.2
m=2, c=15	29.3 (4.2)	29.4 (10.2)	43.7 (31.8)	18.6 (3.2)	43.7
m=2, c=20	31.8 (4.6)	29.2 (9.2)	43.1 (31.1)	18.8 (3.1)	43.6
m=2, c=25	34.1 (4.9)	28.8 (8.8)	42.1 (30.5)	19.2 (3.0)	44.2
m=4, c=5	31.0 (6.1)	28.4 (12.5)	42.5 (34.5)	17.9 (4.3)	45.8
m=4, c=10	36.3 (6.5)	27.9 (10.8)	40.5 (33.6)	17.4 (3.6)	44.8
m=4, c=15	40.7 (7.3)	27.4 (9.8)	38.3 (32.8)	17.3 (3.3)	43.4
m=4, c=20	44.9 (8.0)	27.1 (9.2)	38.1 (32.4)	17.6 (3.2)	43.9
m=4, c=25	49.2 (8.5)	27.1 (8.5)	38.0 (31.9)	17.9 (3.1)	44.8
m=6, c=5	37.2 (9.2)	26.6 (12.3)	38.5 (36.4)	16.1 (4.1)	46.4
m=6, c=10	44.8 (10.2)	26.3 (10.4)	36.9 (33.7)	16.9 (3.9)	47.0
m=6, c=15	50.9 (11.2)	26.1 (9.7)	35.9 (33.4)	16.8 (3.4)	46.6
m=6, c=20	56.6 (11.9)	25.8 (8.9)	35.2 (33.4)	16.9 (3.1)	44.7
m=6, c=25	62.0 (12.8)	25.5 (8.4)	34.0 (32.7)	17.1 (3.1)	45.3
Design A: 3+3	36.4 (10.3)	20.2 (6.6)	18.1 (20.2)	16.5 (4.4)	29.0
Design B: TITE-CRM	12.9 (2.0)	46.2 (11.0)	72.8 (16.1)	20.8 (3.2)	40.9
Design E: CRM	122.5 (18.8)	25.3 (6.2)	33.3 (30.3)	19.3 (2.9)	47.3

In general, it is not possible to find a unique combination of m and c that optimizes all design characteristics. As demonstrated previously, a short trial is typically accompanied by a high degree of toxicity, whereas a trial with a low degree of toxicity would require longer time to complete. As such, the parameters m and c in Design D should be chosen to reflect a practical balance between trial length and degree of toxicity. When designing a trial, such trade-offs should be carefully examined on the basis of feasibility and the particular clinical setting. In practice, it would be useful for the trial statistician to supply tables such as Table 7 to aid discussion with the clinical investigators. For example, one may first choose several reference designs such as the 3 + 3 design and the unmodified TITE-CRM (e.g. bottom 3 rows of Table 7) and calibrate the values of m and c according to the trial characteristics deemed important. To illustrate in the context of the motivating example, due to rapid change in the treatment of recurrent malignant glioma, the clinical investigator felt that a new trial is only of scientific relevance if it was to be completed within a 3-year time frame (the average trial duration based on a 3 + 3 design). If an unmodified TITE-CRM (Design B) was used, about 73% of patients on average would be treated above the MTD (see Table 7). Suppose it is desired to reduce this probability by half while allowing a 4% variation, then a design with a probability in the range of 32% ~ 40% would be considered acceptable. In this case, two designs, namely (m = 4, c = 10) and (m = 6, c = 5), are qualified designs as far as trial length and degree of toxicity are concerned. Note that both of these designs have about 45% probability of selecting the correct MTD, much higher than that of the 3 + 3 design (29%). If a CRM design was used, the trial would require on average 122 months to complete. Compared to the reference designs, the two qualified designs achieve the goals of keeping the trial length within a reasonable constraint and significantly reducing the percentage of patients allocated to toxic doses without compromising estimation accuracy.

6. Discussion

The results of our simulations indicate that in a phase I clinical trial where patient accrual is potentially rapid and toxicities are expected to occur near the end of the DLT follow-up window, the TITE-CRM is associated with a higher risk of treating patients at unsafe doses and selecting a final dose with excessive toxic probability. This is due to the fact that TITE-CRM allows patients to enroll in a continuous fashion without the need for complete DLT follow-up of previously treated patients. As a result, dose escalation occurs too rapidly at the beginning stage of the trial in the absence of toxic outcomes and patients may be exposed to doses that are assumed to be safe early but later found to be toxic. In this paper, we examine a modified TITE-CRM based on a two-stage approach proposed by the original TITE-CRM creator, and propose an alternative method by incorporating accrual suspension according to a simple waiting scheme. The design properties of these methods are evaluated against the CRM, the original TITE-CRM as well as the 3 + 3 design.

In all scenarios that we investigated, the operating behavior of the 3 + 3 design is generally poor. Although on average, the 3 + 3 design appears to be associated with the lowest toxicity rate, it does so at the cost of compromising on the design accuracy and efficiency by allocating a considerable proportion of patients to doses with no therapeutic effect. These observed deficiencies are in line with previously published criticisms of the 3 + 3 design for phase I trials. In fact, apart from its simplicity, we see no compelling reasons to advocate its continued use in phase I chemoradiation trials and call for a paradigm shift within the oncology research community to explore more efficient and accurate designs in this particular setting.

Compared with the TITE-CRM, both modified TITE-CRM designs markedly reduce the percentage of patients exposed to unsafe doses without shortchanging the design accuracy. When doses under consideration are generally toxic, Design C fares better in terms conservative patient allocation and final dose recommendation. Design D appears to be slightly more aggressive especially when the probability of toxicity increases sharply between dose levels. However, these situations do not typically reflect the practical reality since preclinical information about the study drug is often available and physician’s cautious inclination rarely leads to a dose range that is too toxic. On the other hand, when the doses chosen for testing are generally safe, Design C essentially converges to the 3 + 3 design and shares its design properties including longer trials, larger sample size, and allocating a substantial number of patients to presumably inactive doses. Despite these similarities, owing to its hybrid nature between a rule-based and an algorithm-based design, Design C still yields comparable estimation accuracy to CRM and other TITE-CRM competitors in all scenarios we considered.

From a practical perspective, both modified methods are straightforward and easy to implement in practice in that no special computer program is required other than a tool for carrying out a TITE-CRM trial. In particular, the simplicity of our proposed approach lies in the fact that the wait time before enrolling the next patient can be calculated immediately as soon as a new patient is enrolled. A R program for simulating the operating characteristics of our method is available upon request. Ultimately, the appropriate choice between these two designs lies in the balance between the risk and benefit in treating patients at ineffective or toxic doses. An understanding of the diseased patient population as well as the toxicity profile of the study drug would aid this decision. For example, for patients with terminal cancers in which long-term disease outlook is dismal and treatment options are limited, patient survival may outweigh the concerns of toxicity of the drug. Such circumstances would warrant choosing a more aggressive design such as Design D. On the other hand, if the toxicity profile of the drug is generally grievous, then the more conservative Design C may be an ethical choice.

The aggressive nature of the TITE-CRM when most toxicities occur near the end of the toxicity observation window was previously noted by Cheung and Chappell [22]. They cautioned that under these circumstances, some conservative modifications such as Design C would be necessary. Alternatively, they suggested using other weight functions. One specific proposal was an adaptive weighting scheme (see Cheung and Chappell [22] Equation (3)). In essence, if most toxic outcomes occur late within the DLT follow-up period, the adaptive weighting scheme assigns a much lesser weight to patients who have entered the trial for a relatively short period of time.We evaluated the effect of the adaptive weighting scheme in our simulations (results not shown). We found that the adaptive weighting scheme offers little improvement to the design characteristics in the underlying setting. In fact, in all scenarios we considered, the design properties of a TITE-CRM based on the adaptive weights were almost identical to Design B, which was based on the linear weights as indicated in Equation (2). A closer examination reveals that the adaptive weights reduce to the linear weights before any toxic outcome is observed. Therefore, if we assume that the accrual rate is 3 patients per month and most toxicities do not occur until the end of the 6-month follow-up period, about half of the patients would have been enrolled by the fourth month after study initiation. In the absence of any toxicities by this time, erroneous dose escalation would still occur even if the adaptive weights are used. In general, we found that the effect of adaptive weights on conservative dose assignment only sets in after toxic outcomes have been observed. Future work on alternative weighting schemes in this setting is needed.

In summary, the purpose of this work is to point out the difficulties and inadequacies of the TITE-CRM in the setting of fast patient accrual and late-onset toxicities and to offer an alternative modification to this approach. It is our hope to make efficient and accurate phase I designs such as the TITE-CRM more widely acceptable and accessible.