Validation of the Isotropic Fractionator: Comparison with Unbiased Stereology and DNA Extraction for Quantification of Glial Cells

Abstract

Background

The “isotropic fractionator” (IF) is a novel cell counting technique that homogenizes fixed tissue, recovers cell nuclei in solution, and samples and quantifies nuclei by extrapolation. Studies using this technique indicate that the ratio of glia to neurons in the human brain is approximately 1:1 rather than the 10:1 or 50:1 ratio previously assumed. Although some results obtained with the IF have been similar to those obtained by stereology, the IF has never been calibrated or validated. It is conceivable that only a fraction of glial cell nuclei are recovered intact or recognized after the homogenization step.

New Method

To rule out this simple explanation for the claim of a 1:1 glia-neuron ratio, we compared cell numbers obtained from adjacent, weight-normalized samples of human and macaque monkey white matter using three techniques: the IF, unbiased stereology of histological sections in exhaustively sectioned samples, and cell numbers calculated from DNA extraction.

Results and comparison of methods

In primate forebrains, the IF yielded 73,000–90,000 nuclei/mg white matter, unbiased stereology yielded 75,000–92,000 nuclei/mg, with coefficients of error ranging from 0.013–0.063, while DNA extraction yielded only 4,000–23,000 nuclei/mg in fixed white matter tissues.

Conclusions

Since the IF revealed about 100% of the numbers produced by unbiased stereology, there is no significant underestimate of glial cells. This confirms the notion that the human brain overall contains glial cells and neurons with a ratio of about 1:1 far from the originally assumed ratio of 10:1 in favor of glial cells.

1. Introduction

Numerical estimates of glial cells in the human brain vary by as much as 50-fold (Azevedo et al., 2009; Hilgetag and Barbas, 2009; Jacobson, 1991; Kandel et al., 2000). The glia-neuron ratio (GNR) has been reported with largely conflicting values (0.7:1, 1:1, 3:1, 10:1, 20:1, 50:1), based on different approaches (Azevedo et al., 2009; Brizzee et al., 1964; Haug, 1986; Hilgetag and Barbas, 2009; Jacobson, 1991; Kandel et al., 2000; Nurnberger and Gordon, 1957). The conflicting ratios are largely due to uncertainties in numbers of glial cells rather than neurons. The total number of neurons in the human brain has been estimated to be within a relatively narrow range, between 75 and 125 billion (Azevedo et al., 2009; Haug, 1986; Jacobson, 1991; Pelvig et al., 2008; Williams and Herrup, 1988). Unfortunately, this is not the case for their counterparts, the neuroglial cells. Although investigators have reported varying GNRs (Brizzee et al., 1964; Haug, 1986; Jacobson, 1991; Nurnberger and Gordon, 1957), most major textbooks and reviews agree upon a 10–50 fold numerical edge of glia over neurons. Some online encyclopedias (e.g., wikipedia) and popular and widely used web sites, however, state a much lower GNR. Therefore, resolution of the lingering dispute over widely diverging GNRs (and thus numbers of glial cells) has become pressing.

Technical limitations have prevented reliable estimates of total numbers of glial cells in the brain (Bass et al., 1971; Brizzee et al., 1964; Hilgetag and Barbas, 2009; Jacobson, 1991; Nurnberger and Gordon, 1957). Glial cells are small, much smaller than neurons, and it is therefore not surprising that their numbers are more difficult to establish, resulting in wide ranges based on different techniques, animal and human specimens of different ages and tissue quality, and possibly agendas of investigators. Analysis of histological sections is a powerful tool, especially when combined with stereological design-based methodology (Schmitz and Hof, 2005), but these methods cannot be applied globally (to the whole brain), only to well-defined, distinct brain regions, and they require that particles can be unambiguously recognized in tissue sections. Stereological design-based methods, although theoretically unbiased, also have their limitations (Baryshnikova et al., 2006; Guillery, 2002; Gardella et al., 2003; Schmitz and Hof, 2005; von Bartheld, 1999). An alternative approach is to extract and measure DNA content and to calculate cell numbers based on knowledge of DNA content per cell nucleus (Bass et al., 1971; Dobbing and Sands, 1973; Yuhas and Jabr, 2012; Jacobson, 1991; Margolis, 1969; Zamenhof et al., 1964). However, this technique also has its drawbacks (complete recovery of DNA is required; only total cell number, but not cell type is revealed). A third way is to homogenize brain tissue and determine densities of cell nuclei in re-suspended fluid samples (Nurnberger and Gordon, 1957). This approach was recently improved significantly and was termed the isotropic fractionator (“IF”) (Azevedo et al., 2009; Herculano-Houzel and Lent, 2005). Because of the limitations with the aforementioned two techniques (stereology and DNA extraction), there has been great interest in the new “IF” technique. But can the results of the novel technique be trusted? Is it possible that the required harsh homogenization and isolation steps destroy a major fraction of cell nuclei (Lovtrup-Rein and McEwen, 1966; Verkhratsky and Butt, 2013), and glial cell nuclei in particular (Hadjiolov et al., 1965; Kato and Kurokawa, 1967), and therefore are not recognized? Could the number of glial cells in white matter have been substantially underestimated?

Resolution of the current controversy and impasse requires rigorous validation and calibration of counting techniques (Coggeshall et al., 1990; Coggeshall, 1992; Yuhas and Jabr, 2012; von Bartheld, 2001, 2002). About 50% of the human brain consists of white matter (Baumann and Pham-Dinh, 2001; Fields, 2009, 2010), and white matter may contain more than 50% of all glial cells in the brain. However, white matter is often neglected in numerical estimates and calculations of cells in the brain, therefore it is particularly important to include white matter in the validation of the IF. There is considerable interest in changes of glia numbers and densities in the human brain, because such changes have been associated with a number of neurological and psychiatric diseases (Cotter et al., 2001; Hof et al., 2003; Morgan et al., 2010; Rajkowska, 2000; Vostrikov et al., 2007). Enhanced scrutiny and consideration of glial numbers in white matter is essential to establish an accurate GNR and to better understand glia-neuron interactions in physiology, pathophysiology, and in evolution. Preliminary data of our study have been reported in abstract form (Bahney et al., 2012).

2. Materials and methods

2.1. Human and Animal Materials

Two human brains and thirteen macaque monkey brains were used for this study. The human brains were from individuals who had donated their brains for teaching and research at the University of Nevada School of Medicine (Anatomical Donation Program). They were from adult donors and had been fixed either by conventional formaldehyde fixation (arterial perfusion with a 2:1 dilution of 37% formalin, followed by several months of fixation and storage in a 1% formalin solution), or by embalmic fluid, Maryland state concentrate (arterial perfusion with a 2:1 dilution of 6–9 gallons of 33.3% glycerin, 27.8% phenol, 33.3% methanol, 2.1% formaldehyde; fixation for several months in that dilution, followed by storage in 95% ethanol). The weight of the two human brains after fixation ranged from 845–1,174 g. Macaque monkey (cynomolgus) brains were obtained from Charles River Preclinical Services (Reno, NV). The protocol for euthanizing monkeys (for reasons not related to this study) was approved by their Institutional Animal Care and Use Committee (IACUC), assuring compliance with the United States Department of Agriculture, Public Health Service Office of Laboratory Animal Welfare Policy and the Animal Welfare act. Monkeys of either sex (13 monkeys, 2.5–7 yr of age) were sedated with ketamine (10 mg/kg), then administered 0.7 ml Beuthanasia-D solution (pentobarbital sodium and phenytoin sodium) followed by exsanguination. The brains were removed and placed in cold Krebs bicarbonate solution of the following composition (in mM): 118.5 NaCl, 4.7 KCl, 2.5 CaCl₂, 1.2 MgCl₂, 23.8 NaHCO₃, 1.2 KH₂PO₄, 11.0 dextrose during the transport on ice within 30 min to the University of Nevada, Reno. Brains were either processed unfixed (for DNA extraction) or were immersion-fixed in 4% paraformaldehyde, mostly for 3–4 weeks (range: 3–90 days), hemisectioned, and sampled as described below. The monkey brains weighed 70.9 ± 2.48 g (mean, ± SEM). For macaque monkeys, the brain atlas by Martin and Bowden (1996) was used for nomenclature.

2.2. Tissue processing

Using scalpel blades, tissue samples of about 10–100 μl volume were dissected from white and grey matter regions of human and cynomolgus brains. These were obtained from the corpus callosum, as indicated in Fig. 1A and B, as well as from white matter of the cingulate gyrus and the anterior cingulate gyrus, and the origins of the cerebellar peduncles in mid-sagittal sections of the cerebellum (indicated in Fig. 1A, B). Tissues were dissected and collected so that immediately adjacent samples could be processed for IF, stereology, and DNA extraction. In addition, four grey matter samples were obtained for IF analysis from the cynomolgus cingulate gyrus, adjacent to where white matter was obtained as described above. The weight of each sample was determined on a Sartorius BP 110 S balance prior to further tissue processing.

Fig. 1.

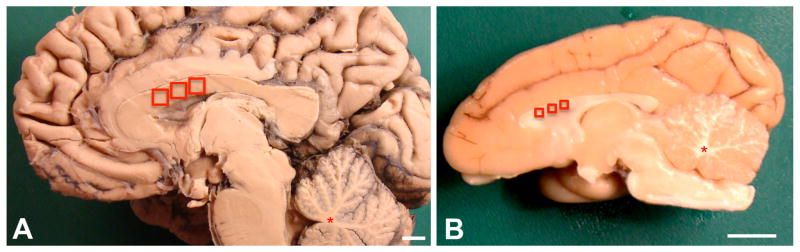
A–B. Examples of formaldehyde-fixed human and monkey hemi-brains showing the locations where adjacent samples were taken. Samples were obtained in the corpus callosum (red squares) and in the cerebellum (red asterisks) for subsequent processing by either the isotropic fractionator, by stereology, or (forebrain only) by DNA extraction. A. Human brain. B. Cynomolgus macaque brain. Scale bars = 1 cm.

2.2.1. Isotropic Fractionator (IF) processing

Processing of tissues for IF followed the protocol as described by Herculano-Houzel and Lent (2005). In brief, up to 100 mg tissue was homogenized in 1–2 ml standard solution (40 mM sodium citrate and 1% Triton X-100), using a Wheaton 15 ml glass tissue grinder until all visible fragments were dissolved. Homogenates were transferred to 15 ml conical tubes, along with the solution collected from several washes of the homogenizer. Tubes were centrifuged in an Eppendorf centrifuge (Model 5416) for 10 minutes at 4,000 g. Supernatants were collected and transferred to separate tubes and stained with 1% 4′6-diamidino-2-phenylindole (DAPI, Invitrogen) to verify that all nuclei were contained within the pellet. The nuclear pellets were resuspended in PBS with 1% DAPI. This mixture was agitated throughout the procedure to prevent sedimentation. Aliquots of 5 μl were removed and loaded onto a hemocytometer (Reichert Bright-Line). Counts of cell nuclei were performed per manufacturer’s instructions by using boundary lines to calculate the applicable volumes of each chamber. Counts were repeated 20 times, resulting in a coefficient of error (CE) of less than 0.1 (Table 1). Average nuclear density was multiplied by total suspension volume and divided by sample weight to obtain nuclei (and by extension, cells) per mg tissue. We estimated the contribution of presumptive endothelial cell nuclei by counting the number of nuclei with a flattened appearance in tissue samples and determining their percentage of total nuclei (Brasileiro-Filho et al., 1989; Davanlou and Smith, 2004; Ling et al., 1973).

TABLE 1.

Mean number of cells/mg tissue in white matter ± SEM obtained by three different methods.

Species	IF (cells/mg)	SEM	n	CE	Stereology (cells/mg)	SEM	n	CE	DNA (cells/mg)	SEM	n	CE
Human-embalmic
Forebrain	73,371	5,881	5	0.028					23,194	2,242	10	0.097
Callosum	70,744	5,391	3	0.019					20,744	2,680	5	0.129
Cortex	77,312	15,257	2	0.038					25,644	3,527	5	0.137
Cerebellum	14,851	1,879	3	0.061					-
Human-formalin
Forebrain	82,484	7,639	4	0.027	74,748	6,868	4	0.013	3,963	870	10	0.219
Callosum	72,276	3,967	2	0.031	69,624	11,770	2	0.016	4,938	1,649	5	0.333
Cortex	92,692	10,502	2	0.033	79,863	9,599	2	0.016	2,988	429	5	0.143
Cerebellum	32,520	2,179	2	0.063	39,497	5,403	2	0.031	-
Cynomolgus
Forebrain	90,118	6,809	7	0.043	92,212	11,197	7	0.025	22,390	3,054	4	0.136
Callosum	87,211	9,279	3	0.026	110,604	21,357	3	0.020	21,699	6,488	2	0.299
Cortex	92,300	10,750	4	0.018	84,344	11,281	4	0.013	23,081	3,591	2	0.155
Cerebellum	38,424	16,502	3	0.025	37,294	5,037	3	0.022	-

CE, coefficient of error; IF, isotropic fractionator; n, number of independent experiments (dissected samples per human brain or dissected samples from different cynomolgus brains); SEM, standard error of the mean; -, not determined due to small volume.

2.2.2. Paraffin embedding, sectioning and counting

Fixed tissue samples were dehydrated in an ascending alcohol series and embedded in Paraplast Plus Tissue Embedding Medium (McCormick Scientific). Samples were sectioned exhaustively into sections with either 15 or 25 μm thickness using a rotary microtome (AO Spencer 820). The microtome’s section advance was verified to be accurate within less than 6% of the nominal section thickness. Every 10th section was collected in a water bath at 45°C on Surgipath pre-cleaned Micro Slides Snow Coat X-tra glass slides or silane-coated glass slides (Fisherbrand, Fisher Scientific). The sections were dried for at least 24 hours at 45–48°C, were then deparaffinized and stained with 1% DAPI in PBS for 10–15 minutes. In addition, adjacent sections were stained with 0.03% thionin (Allied Chemical). All sections were dehydrated, cleared in xylene and mounted with Di-N-Butyl Phthalate in xylene (DPX, Electron Microscopy Sciences, refractive index = 1.52) under cover glasses (Corning, 11/2, 170 μm thick). Sections were examined using a Nikon Eclipse E600 microscope and analyzed using the Nikon NIS elements software version 4.0. The program’s graticule was used to perform systematic random sampling of 20–50 10,000 μm² areas (15–25% of the section) and to count DAPI-stained or thionin-stained nuclei, using an unbiased counting rule (Schmitz and Hof, 2005). Inclusion criteria for counting nuclei in white matter were a diameter of at least 3 μm (half maximal diameter of a typical glial nucleus, peak at 6 μm, data not shown), with unequivocal staining above background levels. Use of the unbiased counting rule and adherence to the inclusion criteria eliminated any nuclear fragments that could have been counted more than once, because of presence of fragments of the same nucleus in more than one sample area. The total area of each section was estimated by using either a point counting method, with points 100 μm apart (graticule), or the NIS software’s area function, by drawing a line around the section perimeter as seen with a 2x objective, and letting the program automatically calculate the area. The results were virtually identical, with the software’s program being less time-consuming. The average nuclear density was multiplied by the average section area and the number of sections cut. This was divided by the tissue sample weight to obtain the number of nuclei per mg sample tissue weight. The percentage of presumptive endothelial cell nuclei within samples was estimated by counting the number of nuclei with a flattened appearance that surrounded or were closely associated with blood vessels.

Final section thickness and position of cell nuclei in the z-axis of the tissue section were determined by focusing on the upper and then lower surface of the section with a 100x oil immersion objective (NA=1.25), using microscope immersion oil (Resolve, high viscosity, Stephens Scientific), and a z-axis encoder (MFC-1 focus controller and DRV-1 OPTI drive, Applied Scientific Instrumentation, Inc). In our hands, this optical system has a practical resolution of 0.4 μm and its accuracy was verified in an international calibration study (Kaplan et al., 2010). Distribution of thionin-stained glial cell nuclei in the z-axis was analyzed as described (Gardella et al., 2003) and plotted to estimate and evaluate the potential impact of lost caps (von Bartheld, 2012). We also prepared and analyzed cryosections, but found their morphological resolution to be suboptimal (Ward et al., 2008). Therefore, all data reported here was from the paraffin sections.

2.2.3. DNA extraction

Fixed and fresh tissue samples underwent a standard phenol chloroform extraction protocol. Samples were first placed in 300 μl digestion buffer (100 mM NaCl, 10 mM Tris, pH 8, 25 mM EDTA, pH 8, 0.5% SDS, and 0.2 mg/ml proteinase K, Promega) overnight at 56°C. An equal volume of phenol/chloroform/isoamyl alcohol (volume ratio of 25:24:1, pH 6.6) was added to the sample. Samples were vortexed and spun for 5 minutes in an Eppendorf centrifuge 5415C at a speed of 14,000 min⁻¹ (maximal speed). The upper aqueous layer was then transferred to tubes containing 1/10^th the volume of NaAc, pH 5.5. Then a 2.5x volume of 100% EtOH was added to the tube, mixed thoroughly, and spun for 10 minutes at maximal speed to pellet the DNA. The supernatant was removed, then an equal volume of 70% EtOH was added, and spun for 3 minutes, max speed. The pellet was dried and resuspended in 25–100 μl TE (10 mM Tris, 1 mM EDTA, pH 8). To obtain ng DNA/μl, these samples were examined on a nanodrop spectrophotometer, one of the most widely used methods for DNA quantification (Bhat et al., 2010; Sedlackova et al., 2013). In addition, we verified that our DNA concentrations were not abnormally low, by using the Picogreen fluorescent dye method (Genomics Center at the Univ. of Nevada, Reno). The observed values (ng/μl DNA) were multiplied by the entire sample volume and divided by the sample weight. Using this approach, the number of nuclei per mg tissue was determined by applying known pg DNA per nucleus of the relevant species: The result was multiplied by the reference value of 7.3 pg DNA content per human nucleus (Manfredi Romanini, 1985), 7.2 pg DNA content per macaque nucleus (Manfredi Romanini, 1985) and 2.5 pg DNA content per chicken nucleus (Jacobson, 1991). Using this approach, the number of nuclei per mg tissue was determined by applying known pg DNA per nucleus of the relevant species. We tested several modifications of the phenol-chloroform based DNA extraction protocol in an attempt to enhance DNA yield from fixed brain tissue, primarily white matter (e.g., Savioz et al., 1997). These modifications included: increasing the duration and concentration of proteinase K (from 0.2–2mg/ml), prior treatment overnight with “unfixing” buffer (200 mM NaCl, 10 mM Tris, pH 8, 25 mM EDTA, pH 8, 0.5% SDS, and 0.2 mg/ml proteinase K, Promega), manual homogenization of the tissue prior to treatment, placement of samples in a −20°C freezer overnight, and incubation of tissue for extended periods of time in lysis buffer. Fixed tissue was analyzed directly, or after it had undergone one or more of the above mentioned modifications. In addition, fresh, unfixed tissue was analyzed for DNA content. To verify that our DNA extraction protocol yielded similar amounts of DNA as those described in previous reports, we compared DNA yields for hatchling chicken optic lobes (tectum) with those reported by Margolis (1969). Optic tecta weighing between 60–70 mg each were flash frozen with liquid nitrogen, then crushed. The DNA was extracted as described above, and its quantity was determined by nanodrop spectrophotometry (ng DNA/μl).

2.3 Statistics

We used paired and unpaired Student’s t-tests and one-way analysis of variance (ANOVA) to compare cell numbers obtained by the three different methods. Statistical significance of differences between human and monkey tissues and between forebrain and cerebellum white matter was determined by unpaired Student’s t-test. A confidence level of p<0.05 was considered significant. Student’s t-test was used when two groups were compared, ANOVA when more than two groups were compared. The coefficient of error (CE) was calculated (Table 1) to verify that sufficient numbers of white matter samples were obtained from the regions indicated in this table. We furthermore calculated the magnitude of a glia recognition deficit that would have been needed with the IF, in order to tilt the GNR ratio from 1:1 to 2:1.

3. Results

3.1. Isotropic fractionator (IF)

3.1.1. Human brains

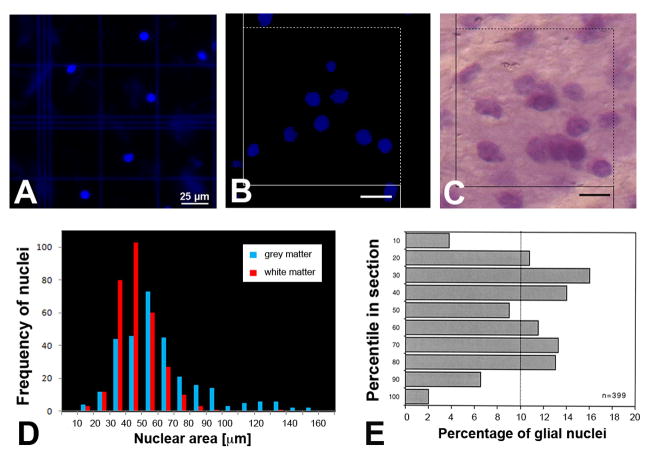
With both fixation procedures, embalmic fluid and formalin only, the IF yielded DAPI-stained nuclei in the hemocytometer chambers, as shown in Fig. 2A. Samples from white matter (corpus callosum and cingulate gyrus in the frontal lobe) revealed DAPI-stained nuclei with a mean diameter of 6.05 ± 0.09 μm (± SEM), and a mean area of 29.44 ± 0.89 μm² (Figs. 2A, D), consistent with a 4.3–7 μm diameter of an aldehyde-fixed macroglial cell nucleus (Ling et al., 1973). When plotted on a histogram, there was a normal distribution of nuclear sizes from forebrain white matter (Fig. 2D). When samples from forebrain grey matter (cingulate gyrus) were processed, the size of DAPI-stained nuclei was more heterogeneous and included larger sizes, with more than one peak in the histogram (Fig. 2D). This is consistent with the presence of several different types of cell nuclei, including glial cells (oligodendrocytes and astrocytes), and smaller and larger neurons. When the number of cell nuclei was quantified and calculated per mg of sample tissue, fixed with embalmic fluid, the forebrain contained 70,744–77,312 nuclei/mg, and cerebellar white matter yielded 14,851 ± 1,879 nuclei/mg with coefficients of error (CE) ranging from 0.019–0.061, as shown in Table 1. When fixed with formalin only, the number of nuclei per mg tissue was 72,276–92,692 in the forebrain and 32,520 ± 2,179 per mg cerebellar white matter, with a CE ranging from 0.027–0.063 (Table 1). This number includes between 8 and 13% of nuclei that were not circular and may have been endothelial cell nuclei. Our numbers of total cells per mg white matter forebrain tissue are largely within the range reported by Azevedo et al., 2009: mean = 71,953 ± 13.6%, range = 62,167–81,739 per mg cortical white matter.

Fig. 2.

A–E. Examples of stained cell nuclei measured with the isotropic fractionator (IF) in solution or in histological sections. A. Cell nuclei isolated from human white matter, stained with the fluorescent nuclear stain DAPI, and counted in a hemocytometer. B. Histological section of macaque white matter containing cell nuclei stained with DAPI. An unbiased counting box is shown, as used for counting of stained nuclei. Scale bar = 10 μm. C. Histological section of macaque white matter containing glial cell nuclei stained with thionin. An unbiased counting box is shown, as used for counting of stained nuclei. Scale bar = 10 μm. D. The sizes of cell nuclei from human white matter (red bars) show a normal distribution with a peak at 50 μm² when plotted for frequency in IF analysis. Cell nuclei from grey matter (blue bars) show multiple, broader peaks of maximal nuclear area, consistent with additional peaks of smaller and larger neuronal nuclei at 60 and 130 μm². E. The z-axis distribution of thionin-stained cell nuclei in white matter from macaque brain. The top of the tissue section (exposed to the cover slip) is shown as the 10 percentile, the bottom of the tissue section (against the glass slide) as the 100 percentile. Note the drop-off at the bin closest to the section surfaces, indicative of lost caps, and the two peaks at the 30^th and 70–80^th percentiles, indicative of section compression. The number (n) of sampled nuclei is indicated.

3.1.2. Nonhuman primate (cynomolgus) brains

The IF yielded intact DAPI-stained nuclei with similar shapes as those seen in human samples (Fig. 2B). The sizes of DAPI-stained nuclei from forebrain white matter samples were larger than those in humans (7.7 ± 0.07 μm in diameter), and 47.86 ± 1.09 μm² nuclear size area; such size differences are possibly due to differences in tissue fixation and processing. When the number of cell nuclei was quantified and calculated per mg of sample tissue, the cynomolgus forebrain contained 90,118 ± 6,809 nuclei/mg, and cerebellar white matter yielded 38,424 ± 16,502 nuclei/mg with a CE ranging from 0.018–0.043, as shown in Table 1. These numbers are very similar to those for the human samples (Table 1). To determine whether cell numbers obtained from forebrain grey matter were similar to those previously reported in primates, we also took samples from cortical grey matter in the cynomolgus cingulate gyrus. In these grey matter forebrain samples, the nuclei/mg yield was 103,585 ± 18,799 (n=4, data not shown), a number that is consistent with previous reports for the number of cells in cortex of non-human primates obtained by the IF method (86,000–122,000, Azevedo et al., 2009; Gabi et al., 2010).

3.2. Stereology of histological sections

3.2.1. Human brains

After fixation of cadavers in embalmic fluid, the morphology of brain samples was not adequate for quantitative histological analysis, presumably due to the extended period of time cadavers had been stored in 95% ethanol (Jordan et al., 2011). After fixation in formalin, tissue morphology was suitable for quantitative analysis using stereology of histological sections. In samples from white matter, the diameter of thionin-stained nuclei with the entire nucleus within the tissue section was 3.85 ± 0.03 μm, and covered an average area of 12.53 ± 0.22 μm². When the number of cell nuclei was quantified and calculated per mg of sample tissue, the corpus callosum contained 69,624 ± 11,770 nuclei/mg, the white matter cortex (cingulate gyrus) contained 79,863 ± 9,599 nuclei/mg, and cerebellar white matter yielded 39,497 ± 5,403 nuclei/mg with a CE ranging from 0.016–0.031, as shown in Table 1. The cortical numbers are within ranges previously reported for glial cells in the human cortex (66,000–85,000/mm³: Bass et al., 1971; Garcia-Amado and Prensa, 2012), and the cerebellar numbers are consistent with the relatively low numbers of glial cells in the cerebellum (Andersen et al., 1992; Azevedo et al., 2009; Gabi et al., 2010). Furthermore, these numbers are very similar to those obtained from adjacent samples in the same formaldehyde-fixed human brain but processed with the IF method (Table 1). We did not quantify samples from grey matter by stereology.

3.2.2. Nonhuman primate (cynomolgus) brains

The morphology of PFA-fixed brains was suitable to identify nuclei by using stereology of histological sections, as shown in Fig. 2C. In samples from forebrain white matter, the size of thionin-stained nuclei (in sections through the center of the nucleus) was 32.93 ± 0.53 μm² (Fig. 2B), with a mean diameter of glial cell nuclei of 6.48 μm after tissue processing (4.3–7 μm, Ling et al., 1973). In samples from forebrain grey matter, the size of DAPI-stained nuclei was more heterogeneous and included larger sizes, with several peaks in the histogram (similar to the graph shown in Fig. 2D). When the number of cell nuclei was quantified by stereology (using thionin-stained sections, since they were found to be equivalent to DAPI-stained tissue sections) and calculated per mg of sample tissue, the forebrain contained 92,212 ± 11,197 nuclei/mg, and cerebellar white matter yielded 37,294 ± 5,037 nuclei/mg with a CE ranging from 0.013–0.025, as shown in Table 1. These numbers are very similar to those obtained for the human samples (Table 1). The larger variability (SEM) compared with the human samples is likely explained by the inclusion of data from six different animals in the case of monkeys. Adjacent sections stained with thionin rather than DAPI showed similar numbers as with the DAPI stain, indicating that the two stains are equivalent for the purpose of identifying glial cell nuclei. This is important, because it means that the distribution of thionin-stained nuclei in tissue sections can be analyzed in lieu of DAPI-stained nuclei. It is difficult to quantitatively analyze the section thickness and distribution of fluorescent particles in the z-axis of tissue sections (Dorph-Petersen et al., 2001; Guillery, 2002; von Bartheld, 2012).

Z-axis distribution and estimation of bias due to lost caps

To determine whether our calculation of nuclei per mg tissue in histological sections may be biased due to lost caps (Baryshnikova et al., 2006; Hedreen, 1998; von Bartheld, 2012), we determined the z-axis distribution of nuclei, using thionin-stained material from cynomolgus forebrain white matter. As shown in Fig. 2E, a significant loss of nuclei occurred only in the outermost bins (2.1 μm) at the top and bottom surface of tissue sections, similar to a previous report (Andersen and Gundersen, 1999). In addition, there were significant peaks in densities in the bins adjacent to the outermost bins, consistent with section compression (Baryshnikova et al., 2006; Gardella et al., 2003). The loss in the outermost bins amounted to a total of 14% of measured nuclei. Therefore, we estimate that the true number of glial cells per mg may have been up to 14% larger than indicated in Table 1. This potential bias was taken into account in section 3.4 where the data from IF and from stereology are compared (Fig. 3C).

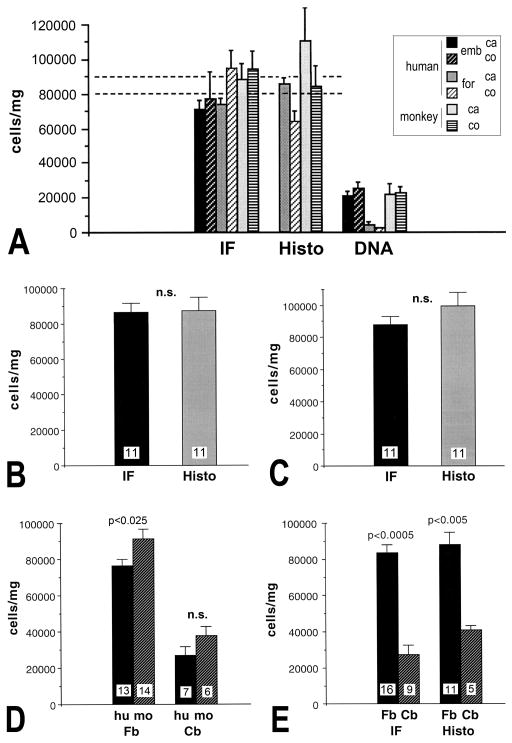
Fig. 3.

A–E. Comparison of cell numbers obtained by three different quantification techniques, the isotropic fractionator (IF), stereology of histological sections (Histo), and DNA extraction. All error bars=SEM. A. Comparison of IF, stereology and DNA-based quantification of cells in human and macaque monkey forebrain. emb, embalmic fixation; for, formalin fixation; ca, callosum; co, cortex. Note that IF and stereology yield about 80,000–90,000 cells/mg, while DNA extraction yields only a fraction (20,000 cells/mg). B. A paired Student’s t-test shows no statistically significant (n.s.) difference between the IF and stereology (p>0.4; the number on the bars indicates the number of independent experiments); data shown are for IF and stereology for formalin-fixed human forebrain samples and paraformaldehyde-fixed monkey forebrain samples. The number on each bar indicates the number of independent experiments. C. When stereology data (from panel B) are adjusted for maximal possible bias due to lost caps (+14%), the difference between the IF and stereology is still not significant (paired Student’s t-test). D. The glial density of human white matter differs from that of macaque white matter forebrain (Student’s t-test, using both IF and stereology data), but only when embalmic human samples are included; the difference in cerebellum was not significant; Cb, cerebellum; Fb, forebrain; hu, human; mo, monkey; n.s., not significant. E. The cerebellar white matter contains significantly lower glial cell densities than cortical white matter, in both human and macaque (based on both IF and stereology data).

Impact of the contribution of endothelial cells

Presumptive endothelial cell nuclei (nuclei with a flattened appearance) in histological sections from forebrain white matter ranged from 8–13% which is the same percentage as seen with the IF method. These numbers are similar to the ranges previously reported (Brasileiro-Filho et al., 1989; Davanlou and Smith, 2004: about 11–22%, although neurons were not measured and estimated by Brasileiro-Filho et al., 1989). Accordingly, the percentage of endothelial cells would not affect the total estimates of glial cells when compared between these two methods. Their numbers would minimally impact on GNRs, in that they would slightly reduce the fraction of glia among the non-neuronal pool.

3.3. DNA extraction

As a third method for estimation of cell content, we quantified DNA from white and grey matter. DNA was extracted from samples obtained from both human and cynomolgus forebrains, using a well-established value of 7.3 pg DNA per human nucleus and 7.2 pg DNA per macaque monkey nucleus to estimate cell number per mg tissue (Jacobson, 1991; Manfredi Romanini, 1985).

3.3.1. Human brains

We extracted DNA amounts that were equivalent to 20,744 cells per mg in the corpus callosum of the embalmic fluid-fixed human brain, and 25,644 cells per mg in the cingulate gyrus white matter (Table 1). The yield was much lower in the formalin-fixed brain, with DNA amounts equivalent to 3,963 cells per mg in corpus callosum, and 2,988 cells per mg cortical white matter. This difference in DNA retrieval is consistent with the known detrimental effect of long-term storage of brain tissues in formaldehyde (Niland et al., 2012; Srinivasan et al., 2002).

3.3.2. Nonhuman primate (cynomolgus) brains

In fixed tissue, the DNA yield from white matter forebrain was equivalent to only 22,390 ± 3,054 nuclei/mg (n=4). We explored several protocol modifications to optimize the DNA yield. There was an increase in yield for white matter, to 27,662 ± 2,486 nuclei/mg (n=3). Samples of fresh, unfixed cortical grey matter yielded 61,217 ± 4,718 nuclei/mg (n=3), which is a major improvement towards the presumed actual number (70,000–122,000) obtained by histology and the IF in our own and other’s previous studies (Table 2). The deficit in numbers, especially from white matter samples, is consistent with the known difficulties in retrieving DNA from lipid-rich tissue, such as white matter (Penn and Suwalski, 1969; Saldanha et al., 1984; Zamenhof et al., 1964). We did not attempt to isolate DNA from the white matter within the cerebellum, due to the small size of white matter tracts in these tissues (Fig. 1B).

TABLE 2.

Nuclei/mg or /mm³ of tissue from grey matter (GM) and white matter (WM) primate cortex.

Author/ Year	Heller & Elliott, 1954 (GM)	Robins et al., 1956 (GM)	Leuba & Garey, 1989 (GM)	Dombrowski et al., 2001 (GM)	Azevedo et al., 2009 (GM)	Gabi et al., 2010 (GM)	Azevedo et al., 2009 (WM)	Current study (WM)
IF					122,000	86,000 -113,000	72,000	70,000 - 92,000
Stereology			70,000	81,000 - 114,000				69,000 - 110,000
DNA	131,000 153,000	130,000 200,000						20,000 - 52,000*

^*range in samples including unfixed tissue

3.3.3. Chicken brains

To verify that our DNA extraction was comparable with previous studies (Margolis, 1969), we extracted DNA from hatchling chicken optic tecta (“optic lobes”). Optic lobes weighed 66.6 mg (mean, range of 63.5–70.8 mg, n=4) and yielded a mean of 757 ng DNA/μl (range between 693 and 818 ng/μl or mg, n=4). This is equivalent to 75.7 μg DNA per optic lobe, which is nearly identical to the ~160 μg DNA for two optic lobes combined, as reported previously (Margolis, 1969). Accordingly, our DNA extraction technique appears to be similarly efficient when compared to those of previous investigators reporting DNA yields in the literature.

3.4. Comparison of techniques and statistics

To determine how the three different techniques (IF, stereology and DNA extraction) compared with each other for yield of cellular numbers, we plotted the number of cells/mg in forebrain white matter. As can be seen in Fig. 3A, IF and histology yielded approximately equal numbers of about 80,000–90,000 cells/mg, while the DNA-based method yielded about 20,000 cells/mg–only a quarter of the expected values. This ratio was consistent among white matter samples from corpus callosum, cingulate cortex and cerebellum. Since our coefficient of error (CE) was less than the often considered “acceptable” threshold of 0.1 for both IF and stereology, we conclude that we analyzed a sufficient number of samples from each brain or region within each brain (Schmitz and Hof, 2005; Garcia-Amado and Prensa, 2012). To determine whether there was any statistically significant difference between IF and stereology, we performed a paired Student’s t-test, excluding the samples from embalmic human forebrain, because histology could not be obtained from those cases. The difference between estimates was not statistically significant (p>0.4), indicating that the two methods do not yield significantly different results (Fig. 3B). Since the z-axis analysis of the histological sections showed evidence of lost caps, we re-calculated the stereology values for the maximal possible bias (+14%) and compared the two techniques. As shown in Fig. 3C, with this adjustment, there still was no statistically significant difference between the numbers obtained by stereology and by the IF (p>0.05). To determine whether there was a difference in the glial cell numbers per mg tissue between humans and non-human primates, we compared the numbers between the two species. As shown in Fig. 3D, there was no significant difference in the cerebellar samples, but a small statistically significant difference in the forebrain samples. This difference may reflect differential shrinkage of the specimens of different ages and fixation parameters (Haug et al., 1984). To determine whether the numbers of glial cells per mg white matter differed significantly between samples from different white matter tracts, we compared the numbers with unpaired Student’s t-test. There was no significant difference between different forebrain areas (corpus callosum and cingulate cortex, data not shown), but there was a significantly lower number of glial cells in the cerebellar white matter when compared with forebrain white matter (Fig. 3E). This is consistent with the known low number of glial cells in the cerebellum (Andersen et al., 1992; Azevedo et al., 2009). Taken together, we conclude that the IF is a valid quantification method, including for determination of glial cell numbers in white matter, and yields numbers that are very close if not the same as obtained by stereology of histological sections.

Comparison of time requirements for the IF and stereology

We found that tissue processing per sample for IF was about 1–2 hours, compared with 10–15 hours for histological processing of each sample for stereology. The analysis of each IF sample required about 1–2 hours, versus about 2–3 hours for each stereology sample, for a skilled and experienced investigator. Thus, the IF is considerably faster, especially for tissue processing, than stereology of histological sections.

Discussion

The IF has several advantages over other cell counting techniques, including that total cell numbers of whole brains and large subdivisions within the brain can be relatively easily and rapidly estimated. The first version of the IF, then called “direct enumeration of nuclei” (Nurnberger and Gordon, 1957), had several major disadvantages: tissue and nuclei were not fixed, resulting in rapid destruction of nuclei during the dissociation period, and nuclei from small neurons could not be distinguished from those of glial cells. Not surprisingly, cerebellar estimates (and therefore whole brain estimates) were incorrect, despite validation attempts with histological sections from fixed tissue (Nurnberger and Gordon, 1957). In 2005, Herculano-Houzel and Lent introduced three major improvements of this–approach the fixation of tissue prior to homogenization, visualization of nuclei with DAPI, and the use of neuron-specific antibodies to distinguish neurons from glia (Herculano-Houzel and Lent, 2005). Based on a search of “isotropic fractionator” or “isotropic fractionation” in PubMed for the period of 2005–2013, the IF has been primarily used by current and former members and collaborators of the Herculano-Houzel, Lent and Kaas labs (17/21 papers =81%), with only 4/21 (=19%) by other investigators. The IF has never been calibrated or validated against traditional counting techniques, and this appears to be a major reason why the IF has not been adopted more generally in the field (Yuhas and Jabr, 2012; Verkhratsky and Butt, 2013). We validated the IF against two other types of cell counting methods, the so-called unbiased stereological method (optical disector, Schmitz and Hof, 2005), and calculation of cell numbers based on DNA extraction (Bass et al., 1971; Margolis, 1969; Robins et al., 1956; Zamenhof et al., 1964). We did not calibrate the IF directly against the absolute gold standard of 3-dimensional serial section reconstruction, but we have calibrated the so-called unbiased stereology technique with an exhaustive reconstruction in a previous study, albeit on neurons (Hatton and von Bartheld, 1999).

When comparing results from different counting approaches, it is best to compare fixed with fixed tissue or fresh with fresh, but not fresh with fixed tissue, due to differential shrinkage of different tissue components after fixation (Cragg, 1967; Haug et al., 1984; Haug, 1986; Nurnberger and Gordon, 1957). The cell numbers we obtained for white matter by histology/stereology (70,000–93,000/mg) were comparable with those previously reported for grey matter of primate – cortex about 70,000–114,000 nuclei/mg fresh weight of tissue (Table 2), when considering that total cell numbers tend to be similar in white matter and in grey matter of cortex (Bass et al., 1971; Fleischhauer and Vossel, 1979). The numbers we obtained by the IF method for grey matter primate cortex (70,000–93,000/mg) were also comparable with previous reports – about 86,000–122,000/mg fresh weight (Azevedo et al., 2009; Gabi et al., 2010). However, our DNA-based comparison yielded much lower values than expected (20,000–52,000/mg fresh weight) when compared with either the IF or histology-based methods (Table 2). The likely reasons for the deficiency of DNA-based methods are discussed below.

Since the main – but not the only – rationale for our study was to examine the claim of a much lower GNR (1:1) in the human brain than previously assumed, we focused our calibration study on glial cells, and specifically glial cells in white matter. Our data validate the method that was used to establish a GNR of about 1:1 in human and non-human primate brains (Azevedo et al., 2009; Gabi et al., 2010). A larger GNR (of 2:1) would require a much larger actual number of glial cells; but we find no evidence for a substantial deficit of glial cells with the IF when compared with the numbers revealed by stereology in weight-normalized samples of white matter. This argument is based on the following premises: (1) the GNR controversy is largely based on uncertainty about the number of glial cells rather than neurons; (2) if the IF significantly underestimates glial cells, then this will be apparent when adjacent samples of white matter are compared with histological methods (unbiased stereology); (3) one would need a substantial deficit of glial cells in the IF method to tilt the GNR ratio from the claimed 1:1 ratio to a ratio of 2:1 or even higher.

We argue that our three premises are well-supported: (1) The range of serious estimates of total numbers of neurons in the human brain by experts in the field is relatively narrow (Azevedo et al., 2009: 86 billion; Haug, 1986: 70–80 billion; Williams and Herrup, 1988: 84 billion). Accordingly, glia cell numbers are the ones in dispute (Herculano-Houzel, 2009). (2) Analysis and comparison of adjacent samples of white matter will reveal whether the IF underestimates the number of glia cells. White matter such as corpus callosum is composed, by definition, entirely or almost exclusively of glial cells (and a few endothelial cells) (Ling and Leblond, 1973). Thus, a glial deficit by the IF method will be readily apparent in white matter, while such a deficit could be obscured or reduced in grey matter due to contamination and the “dilution effect” of the numerous other cell types, including small neurons. The lack of a significant deficit of cells with the IF therefore shows that, for all practical purposes, the large majority of glial cell nuclei are not destroyed or damaged in a way that precludes their recognition after resuspension and loading in the hemocytometer. (3) Calculation of the magnitude of an IF-derived error that would tilt the GNR from 1:1 to 2:1. The specific hypothesis that we tested in this study was whether the GNR of 1:1 could be explained by loss of glia cell nuclei with the IF, and whether application of an empirically established correction factor may tilt the GNR from 1:1 closer to a traditionally accepted GNR of 2:1 or higher. Since we know the total numbers of neurons in the human brain with some certainty, we can calculate the number of glia cells that would be needed to significantly alter the GNR. Assuming that 50% of glia cells reside in white matter, that a typical human brain weighs 1,300 g (and thus white matter = 650 g, equivalent to 52 billion cells, with another 52 billion glia cells in grey matter), we can estimate that a human brain contains 104 billion non-neuronal cells, subtract 10.5% endothelial cells = 93.08 billion glia cell nuclei per human brain, resulting in a 1.08:1 GNR. If the GNR of the human brain actually were 2:1, the IF would need to destroy or otherwise make unrecognizable nearly 77 billion glia cell nuclei, yet there was no evidence for any deficit of such a dramatic magnitude. Even with a maximal bias of 14% between the stereological analysis of histological sections (due to lost caps) and the IF analysis, the GNR would still be 1.23:1 – much closer to a 1:1 GNR than a 2:1 GNR.

DNA extraction as a method to estimate cell numbers

DNA extraction has been used primarily in the 1950s and 1960s to estimate the number of cells, by applying the known amount of DNA per cell nucleus in a given species (Hess and Thalheimer, 1971; Jacobson, 1991; Margolis, 1969; Robins et al., 1956; Zamenhof et al., 1964). Some of these studies compared DNA content in primate cortex with glial and neuronal densities as obtained by histological techniques (Brizzee et al., 1964; Cragg, 1967; Bass et al., 1971; Ling and Leblond, 1973; Leuba and Garey, 1989). While theoretically an elegant solution (Jacobson, 1991), this approach has been criticized for a number of reasons: (1) many initial reports relied on DNA-P measurement, but P may not necessarily be representative of only DNA (Drasher, 1953); (2) it requires complete DNA extraction; (3) euploidy in brain cells is assumed, yet as many as 20% of adult human neurons are hyperploid (Mosch et al., 2007); (4) DNA extraction is problematic when lipids and lipoproteins are abundant in the tissue of interest, as is the case in white matter (Penn and Suwalski, 1969; Saldanha et al., 1984; Zamenhof et al., 1964); (5) aldehyde fixation causes DNA denaturation (Srinivasan et al., 2002) and possibly irreversible crosslinking of peptides to DNA, thereby decreasing the yield of DNA measurable by spectrophotometry (Savioz et al., 1997). Indeed, variability of DNA extraction is evident by divergent published reports of DNA yields, ranging from 33 μg/g to 970 μg/g (Niland et al., 2012; Saldanha et al. 1984; Winick, 1968). DNA extraction yields appeared more consistent in hatchling chick brain (Margolis, 1969), possibly because developing chick brains are not yet fully myelinated.

Conclusions

Based on our new calibration data, we confirm that the IF is valid. This validates recent studies claiming that the total number of glia cells in the human (and other brains) is indeed much lower than previously assumed, and that the GNR in the human brain is 1:1, or approximately 1:1. We furthermore provide compelling evidence that calls into question the DNA extraction approach as a valid and reliable method to estimate the number of cells in the brain, and especially the number of cells in white matter. The validation of the IF has far-reaching consequences, since this tool can now be used with confidence to address important questions about cell numbers and GNRs in brains, including human brains. Changes in glia numbers have been implicated in numerous neurological and psychiatric diseases such as mood disorder, depression, schizophrenia and Alzheimer’s disease (Andrade-Moraes et al., 2013; Cotter et al., 2001; Hof et al., 2003; Rajkowska, 2000; Vostrikov et al., 2007). The IF can be used in conjunction with stereological methods to address whether glial cells are displaced, reduced in total number, or altered in pathological conditions, and in addition the IF has already and will continue to help to gain new insights into brain evolution. Importantly, we show that the IF can be used for the study of human brains that are fixed by different conventional methods – in this respect the IF is a more versatile technique than histology/stereology. This should help to utilize the IF in a wide range of archived and fresh human pathology cases.

Highlights.

• Calibration shows that the isotropic fractionator is a valid counting technique

• The isotropic fractionator yields glia numbers comparable with unbiased stereology

• We validate the notion of a 1:1 ratio of glial cells to neurons in the human brain

• We support claims that a human brain contains less than 100 billion glial cells

• The isotropic fractionator can be used in human pathology when histology fails