Probing the role of interfacial waters in protein-DNA recognition using a hybrid implicit/explicit solvation model

Abstract

When proteins bind to their DNA target sites, ordered water molecules are often present at the protein-DNA interface bridging protein and DNA through hydrogen bonds. What is the role of these ordered interfacial waters? Are they important determinants of the specificity of DNA sequence recognition, or do they act in binding in a primarily non-specific manner, by improving packing of the interface, shielding unfavorable electrostatic interactions, and solvating unsatisfied polar groups that are inaccessible to bulk solvent? When modeling details of structure and binding preferences, can fully implicit solvent models be fruitfully applied to protein-DNA interfaces, or must the individualistic properties of these interfacial waters be accounted for? To address these questions, we have developed a hybrid implicit/explicit solvation model that specifically accounts for the locations and orientations of small numbers of DNA-bound water molecules while treating the majority of the solvent implicitly. Comparing the performance of this model to its fully implicit counterpart, we find that explicit treatment of interfacial waters results in a modest but significant improvement in protein sidechain placement and DNA sequence recovery. Base-by-base comparison of the performance of the two models highlights DNA sequence positions whose recognition may be dependent on interfacial water. Our study offers large-scale statistical evidence for the role of ordered water for protein DNA recognition, together with detailed examination of several well-characterized systems. In addition, our approach provides a template for modeling explicit water molecules at interfaces that should be extensible to other systems.

Introduction

Accurately modeling protein-DNA interactions is critical for attempts to decipher protein-DNA recognition by theoretical methods. Experiments have shown that proteins can contact DNA directly – forming hydrogen bonds and nonpolar contacts between protein sidechains and DNA bases – as well as indirectly, via ordered interfacial water molecules^1,2 (Fig. 1). In some cases, the number of indirect interactions is equal to or even greater than the number of direct interactions.³ Despite the widespread nature of these indirect interactions, current computational models used to study protein-DNA recognition rely mainly on the direct contacts between binding partners.⁴ The contribution from water-bridged interactions is usually ignored. Whether it is safe to do so depends on the role of these interfacial waters: are they just filling space, with little effect on the specificity of binding, or do they actively mediate the interactions between protein and DNA and contribute to interface stabilization either enthalpically or entropically? Ignoring functionally active water may lead to inaccuracies in theoretical predictions of interface configuration, DNA specificity, or the functional impact of interface mutations.

Figure 1.

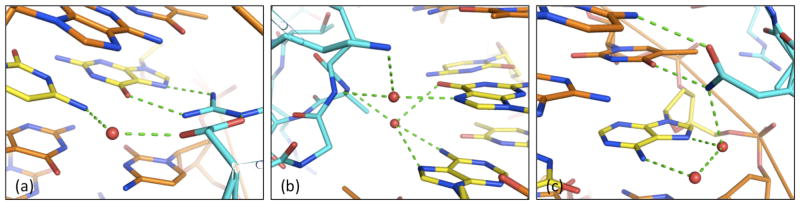
Bridging waters observed in high-resolution crystal structures: (a) a water contacts a base-pair already specified by direct sidechain hydrogen bonds; (b) ordered waters represent the only contacts to conserved bases; (c) a protein sidechain makes direct and water-mediated contacts; water-bridged DNA position shows weak preference for purines.

A range of experimental and theoretical studies have been carried out to explore the role of ordered water in protein-DNA binding.^5-7 High-resolution structural studies as well as biophysical techniques including double-mutant cycles, osmotic stress, and elevated hydrostatic pressure have been applied to several protein-DNA complexes – trp repressor/operator,^8,9 BamHI-DNA,^10,11 EcoRI-DNA,¹² and Hin-DNA,¹³ among others – to investigate the role of water in protein-DNA interactions. On the theoretical side, Jayaram and co-workers analyzed the location of interfacial water molecules and concluded that majority of water molecules serve to buffer electrostatic repulsions between electronegative atoms of the protein and DNA.¹⁴ Using molecular dynamics, Temiz and Camacho solvated protein-DNA complexes in a box of water molecules and found water-accessibility to be a critical determinant of hydrogen bond strength.¹⁵ Nevertheless, there remains considerable uncertainty as to the magnitude of water’s importance in determining the specificity of protein-DNA binding, and the strength of water-mediated interactions. Whereas Ferreiro et al. report that water-mediated interactions appear to be as important as direct hydrogen bonds in recognition,¹⁶ the double-mutant cycle experiments performed by Schreiber and coworkers suggest only a modest contribution of water bridges to residue-residue interaction energies.¹⁷

In this paper, we present a theoretical study aimed at probing the overall effect of interfacial water in protein-DNA recognition. To do so, water molecules at the protein-DNA interface need to be studied individually. Presently, a widely used and computationally efficient class of models for including the effect of aqueous solvation in biomolecular simulations are the implicit solvation models.¹⁸ Implicit solvation models avoid the computational cost of calculating thousands of solvent molecules explicitly, instead approximating a potential of mean force for the solvated biomolecular environment by averaging over the solvent degrees of freedom. Implicit solvation models often give reasonable agreement in terms of molecular structure, recognition, and functional properties. However, since the behavior of individual waters is ignored, such models are inadequate for investigating the properties of ordered water at protein-DNA interfaces.

To overcome the limitation of implicit solvation models, Jiang et al. adopted a “solvated rotamer” approach to model bridging waters at protein-protein interfaces.¹⁹ A simple energetic description of water-mediated hydrogen bonds was used to capture interactions between polar functional groups with one or more water molecules attached. Though effective, this method approximates the potential of solvated hydrogen bonds without including fully explicit water molecules in the calculation, which may lead to unphysical hydrogen bonding networks (waters donating or accepting more than 2 hydrogen bonds; waters in 3-way bridges for which no single orientation of the water hydrogen atoms satisfies all partners). A more precise way to study discrete waters is combining implicit solvation model with explicit water molecules.^20-22 The general idea of a hybrid implicit/explicit model is that a small number of solvent molecules in the vicinity of the solute are included explicitly, while the remaining bulk water is represented with an effective potential. Hybrid methods allow calculating critical water molecules in detail, but at the same time keep the calculation inexpensive.

Here, we apply a hybrid implicit/explicit solvation model to analyze the function of ordered, interfacial waters at protein-DNA interfaces. Water molecules are simulated as fully explicit, independent residues whose locations, orientations, and occupancies are optimized along with the protein and DNA by use of a Monte Carlo plus Minimization (MCM) algorithm²³ implemented in the Rosetta software package.²⁴ We focus on the waters that directly contact major and minor groove polar atoms of the DNA, ignoring phosphate and second-shell waters. We evaluate the prediction of water and protein sidechain conformations using a nonredundant benchmark of 116 high-resolution protein-DNA complexes, and assess DNA target site prediction on a subset of 62 complexes with sequence-specific interactions. In addition, four complexes are studied in detail to compare with available experiments. The effect of ordered water for the configuration of protein side-chain and DNA binding sequence is derived through comparison between simulations with and without explicit water molecules. The goal of this paper is to provide a statistical yet detailed study of the function of water in protein-DNA binding, while introducing and evaluating a simple and efficient approach for incorporating interfacial waters into protein-DNA interface prediction and design simulations.

Materials and Methods

A hybrid implicit/explicit solvation model

An overview of our hybrid implicit/explicit model is given in the results section. Here we provide implementation details on the representation and potential function. All modeling protocols were implemented within the Rosetta molecular modeling package,²⁴ adapted for modeling of DNA by Havranek et al.²⁵ To simulate a hydrated protein-DNA interface, we add 5 hydration-site residues to the molecular system for each interface basepair (Fig. 2). Three sites correspond to major groove waters and two to minor groove waters. Alternate conformers for explicit water molecules are built using a 3×3×3 grid with 0.5Å steps centered on equilibrium positions taken from the study of DNA hydration by Schneider and Berman;²⁶ 12 discrete rotations about the hydrogen-bond axis leading to the DNA anchor atom are applied in order to sample various water orientations (Fig. 2). During a simulation, these sites may be occupied either by explicit water molecules or by non-interacting ‘virtual’ residues (representing absence of water). Thus waters can appear, disappear, and change location and orientation throughout the optimization process.

Figure 2.

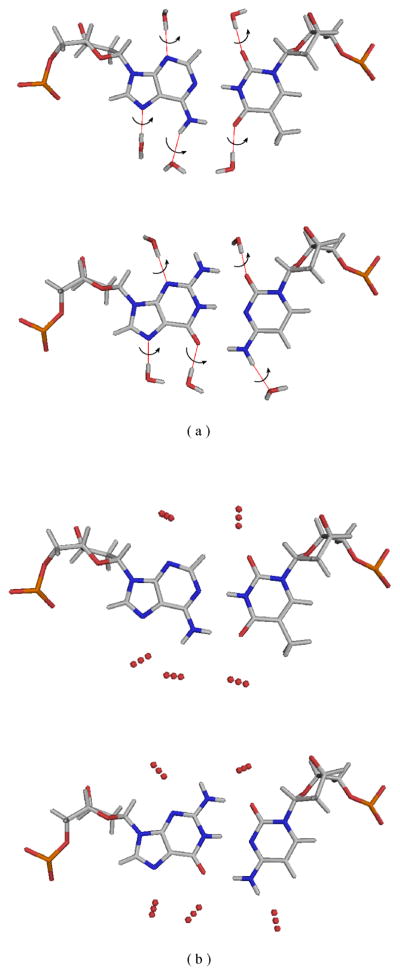
‘Rotamer’ building for explicit water residues: (a) rotations about the oxygen—anchor-atom axis sample water orientations; (b) a 1D slice through the 3D (3×3×3) grid of alternate oxygen positions.

When present, explicit waters are subject to Rosetta’s interatomic potentials (Lennard-Jones, orientation-dependent hydrogen bonding, EEF1 solvation,²⁷ short-ranged electrostatics), with atomic parameters that are loosely modeled on the CHARMM19 ²⁸ implementation of the TIP3P²⁹ water model (L-J well depth: 0.1591; L-J radius: 1.6Å; EEF1 DG-free: -6.7; atomic charges of -0.834 and 0.417). Except as described below, we use the all-atom potential function introduced previously for protein-DNA specificity prediction³⁰, which is a variant of Rosetta’s standard all-atom potential function that includes short-ranged electrostatics with a distance-dependent dielectric, and an orientation-dependent variant of the original EEF1 Gaussian solvent exclusion model. In this orientation-dependent solvation model, the desolvation penalty associated with bringing a neighboring atom nearby a polar atom depends not only on the distance between the two atoms but also the orientation of approach: the distance-dependent Gaussian contribution from the EEF1 model is multiplied by a scaling term that depends on the distance between the desolvating atom and the nearest optimal hydrogen bonding site for a water molecule (calculated on the basis of the hybridization and chemical neighborhood of the polar atom; additional details can be found in³⁰). To show the effect of this modification, we also include simulation results from the original isotropic EEF1 solvation model.

For comparison with the fully explicit 3-site water model, we developed a single-site water model in which only the location of the oxygen atom is explicitly represented during the molecular simulation. This oxygen atom is subject to the Lennard-Jones and implicit solvation potentials of the Rosetta force field just as in the 3-site model. In order to evaluate hydrogen bonding interactions, hydrogen positions are built on the fly during the calculation of residue-pair interaction energies with orientations that optimize Rosetta’s orientation-dependent potential. Thus the interaction energies are comparable in magnitude to those in the 3-site water model, and compatible with rotamer packing (which requires pairwise decomposable energies), however there is no guarantee that multiple interactions with the same water molecule will be mutually compatible (e.g., a single water may accept or donate more than 2 hydrogen bonds).

Simulation protocols

In our simulations, the protein backbone and DNA phosphorus atoms are held fixed; the protein sidechain conformations, water positions and occupancies, and DNA base and sugar conformations are optimized using a Monte Carlo protocol that incorporates gradient-based minimization prior to evaluation of the acceptance criterion. For DNA sequence calculations, base mutation moves are also included in the protocol, allowing energy-biased exploration of the space of possible target sites. To account for differing intra-DNA energies in the unbound state (e.g., G:C base pairs have an additional Watson-Crick hydrogen bond, and RpY base-steps have more favorable base stacking energies than YpR steps), we use the base-step reference energy model from Ref. ³⁰, with reference energies fit to give balanced sampling frequencies in unbound sequence-mutation simulations. We found that addition of explicit waters changed the energy balance between base steps, necessitating a refitting of the DNA reference energies for the explicit water simulations.

For DNA sequence calculations, if the movement of protein sidechains is to be constrained, as described below, a harmonic coordinate restraint was used to tether protein sidechain heavyatoms nearby their crystallographically determined locations; no penalty is applied until the coordinate deviation reaches 0.5Å, at which point the energetic cost increases quadratically, effectively tethering sidechains to their native rotamers but allowing relief of small clashes and optimization of hydrogen bonding geometry.

Benchmarking

For interface structure calculations, a benchmark set of 116 high-resolution protein-DNA complexes was constructed by taking all Protein Databank (http://www.rcsb.org/pdb/) entries with resolution better than 2.0 Angstroms (as of 11/18/2012) and removing redundancy using the PISCES³¹ webserver (http://dunbrack.fccc.edu/PISCES.php) with a sequence identity threshold of 40% (see Supplement for PDB identifiers). A subset of 62 complexes with DNA-sequence-specific interactions, primarily transcription factors and endonucleases, was selected manually (see Supplement) for DNA sequence calculations.

Protein sidechains were considered correctly modeled if all χ angles fell within 40 degrees of the native values. Explicit water correctness and recovery were assessed using a 1.4Å distance threshold. A heavyatom-heavyatom distance threshold of 6.0Å to any DNA base was used to select the flexible protein sidechains; DNA base pairs tested for sequence recovery were those within potential direct or water-mediated hydrogen bond distance of flexible protein sidechains, using a 3.4Å distance threshold for hydrogen bonding.

Results and Discussion

Overview

We developed and tested a simple, hybrid implicit/explicit water model for use at protein-DNA interfaces, implemented in the Rosetta software package.^24,25 In this model, five potential hydration sites are added to all DNA base pairs at the protein-DNA interface: three in the major groove and two in the minor groove (Fig. 2). These sites are treated as additional sequence positions that are appended to the molecular system. The equilibrium hydration positions are taken Schneider and Berman’s study of DNA hydration²⁶ with the addition of alternate position and orientation conformers (Fig. 2). To model the presence or absence of interfacial waters at these hydration sites, the chemical identity of the residues at these sites is allowed to flip between an explicit, interacting water residue type, and a non-interacting single-atom ‘virtual’ residue type (absence of water). Optimizing the number and position of interfacial waters can thus be viewed as a simple sequence design calculation in a restricted 2-residue alphabet, and can be easily integrated into simulations that simultaneously optimize the conformation and sequence of the protein and DNA molecules. During rotamer packing, the locations of these explicit waters are sampled via discrete alternate conformers (Fig. 2) analogous to protein sidechain rotamers; during gradient-based minimization, water positions and orientations are smoothly optimized simultaneously with protein and DNA degrees of freedom (for details, see Materials and Methods).

When a water residue occupies one of these potential hydration sites, its atoms are subject to Rosetta’s atomic interaction potentials (Lennard-Jones, orientation-dependent hydrogen bonding, EEF1 solvation,²⁷ short-ranged electrostatics) in a manner exactly analogous to the polar atoms of the protein or DNA. All that is needed to complete the model is an energy term that captures the entropic cost of introducing an ordered water molecule. We chose to model this entropic contribution as a combination of two terms: a fixed, orientation-independent cost for introducing the water (modeled using Rosetta’s sequence-dependent reference energy term and termed H2O_ref), and an additional orientation-dependent term that is proportional to the total hydrogen bonding energy of the ordered water³² (captured by downscaling the weight on hydrogen bonds involving explicit water residues and termed H2O_hbscale).

We performed two types of structure prediction simulation at protein-DNA interfaces: (1) water recovery simulations, in which the conformation of protein and DNA are constrained to remain nearby their observed conformations while the water positions and occupancies are optimized; (2) protein sidechain recovery simulations, in which the protein sidechains at the interface are randomized and re-optimized along with the waters in the presence of limited DNA flexibility. For both simulations, the original waters present in the crystal structure are used only for evaluation of the accuracy of the final predictions. Finally, we performed a set of DNA sequence recovery simulations, in which the DNA base-pairs at the interface were randomized and optimized throughout the simulation in the context of protein, DNA, and water flexibility. In the structure prediction simulations, we explored the effect of various water-entropy parameters, while in the more time-intensive DNA sequence recovery simulations we assessed the performance of a single entropy parameterization. The role of explicit interfacial waters is derived by comparing simulation results from the hybrid implicit/explicit model (‘3W’) and its fully implicit counterpart (‘NW’). For additional points of comparison, we assessed the performance of two alternate solvation models: an explicit water model with single-site waters (‘1W’), and a fully implicit solvation model without orientation dependence (‘NW LK-classic’) (for details, see Materials and Methods).

Water recovery

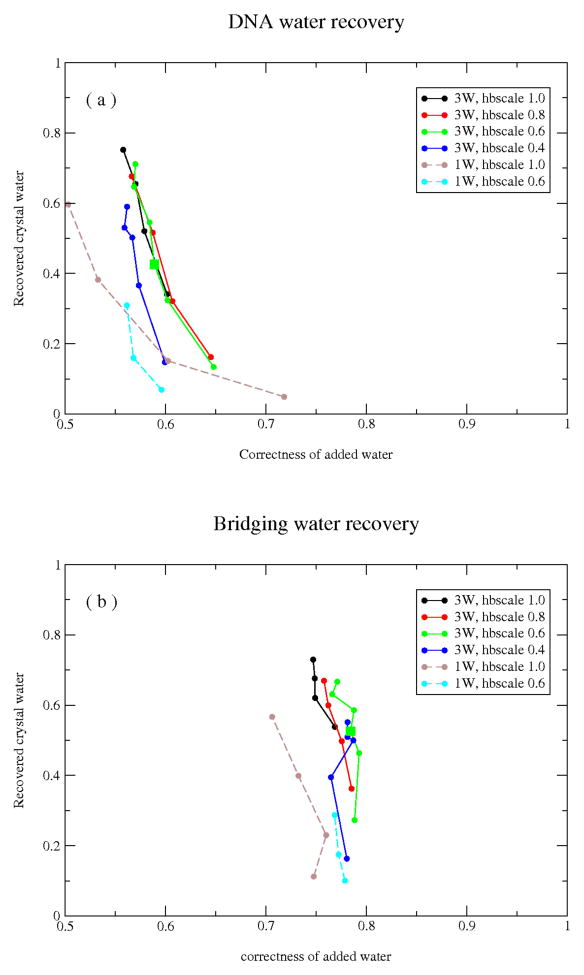
The results of the water-recovery simulations are given in Figure 3 and Supplementary Figure S1: (a), all DNA-bound waters; (b), ‘bridging’ waters that interact with both protein and DNA. Each point in these plots corresponds to a single choice of the water-entropy parameters, and represents the correctness (x-axis; fraction of simulated waters within 1.4Å of a crystal water) and recovery success (y-axis; fraction of crystal waters within 1.4Å of a simulated water) averaged over a set of 100 independent simulations for each of the members of our benchmark set of protein-DNA complexes. Each line in these plots connects simulations with the same H2O_hbscale value and a range of H2O_refwt’s. As the H2O_refwt parameter is decreased (i.e., the fixed cost for introducing a water is decreased), the number of occupied hydration sites increases, leading to an increase in the recovery of crystal waters and an overall decrease in the correctness of the simulated waters (see Supplementary Fig. S2 for examples of a hydrated interface at various H2O_refwt values). The H2O_refwt values were selected manually to explore a range of hydration-site occupancy rates that span that seen in the crystal structures (parameters tested are given in the Supplementary Data). For all DNA-bound waters, correctness of added waters is between 50% and 70%, while recovery of crystallographic waters is generally below 80%. Curves from the simulations with the fully explicit 3-site water model (‘3W’) are overall better than curves for the single-site water model (‘1W’). Considering just bridging waters (Fig. 3b), the correctness of added water is greater than for all waters, falling between 70% and 80%, and here again the 3-site waters give overall better performance than single-site waters.

Figure 3.

Prediction accuracy for DNA-bound water (a, water that directly contacts the DNA bases) and bridging water (b, water that interacts with both DNA and protein) from simulations with 3-site (‘3W’) and single-site (‘1W’) waters with a range of entropy parameters. The fraction of modeled waters that overlap with crystal waters (x-axis, 1.4Å distance threshold) is plotted against the fraction of crystal waters that overlap with modeled water (y-axis, same threshold). Recovery is averaged across all models for each member of the full benchmark set.

Protein sidechain recovery

These water-recovery results suggested to us that the hybrid model is able to realistically model a reasonable fraction of the ordered waters at protein-DNA interfaces (when the protein sidechains and DNA bases are constrained to remain nearby their crystal structure conformations). We next investigated whether addition of explicit waters could aid in predicting the conformations of interface sidechains. For each protein-DNA complex in the benchmark set, we performed 300 independent protein sidechain prediction simulations initiated from randomized starting conformations, with limited DNA backbone and base flexibility. The same range of water-entropy parameters were explored as in the water-recovery simulations.

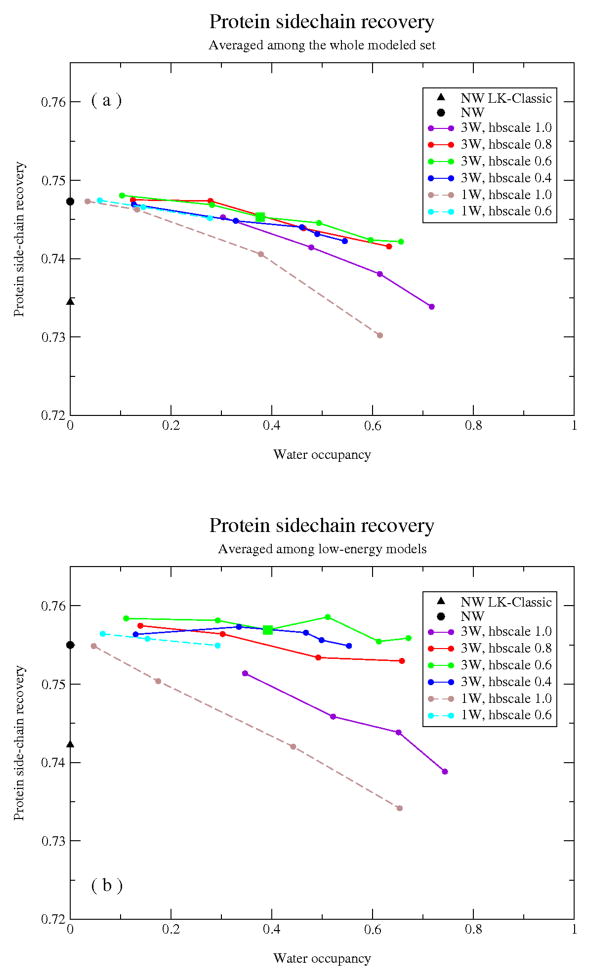
The results of these simulations are reported in Fig. 4, in which we have plotted the fraction of correctly predicted sidechains (y-axis) against the fraction of occupied hydration sites (x-axis; for comparison, roughly 45% of the sites are occupied by crystal-structure waters). We found that addition of the explicit interface waters did not noticeably improve overall sidechain recovery rates (Fig. 4a). At high rates of hydration site occupancy (low values for H2O_refwt/high values of H2O_hbscale) explicit waters begin to displace interface protein sidechains, substituting water-mediated contacts for direct protein-DNA contacts (Fig. 5a).

Figure 4.

Protein sidechain recovery from simulations with fully implicit (NW, NW LK-classic) and hybrid implicit/explicit (3W and 1W) solvation models (see text for model details). The fraction of correctly recovered protein sidechains (y-axis) is plotted against the fraction of potential hydration sites occupied by modeled water (x-axis). Sidechain recovery is averaged over the full set of models in (a), and the lowest-energy 20% of the models in (b).

Figure 5.

Examples of positive and negative effects of explicit waters on protein sidechain prediction. Crystal structure conformations are shown in grey with thin lines; modeled sidechains are shown in stick representation with carbons colored cyan (explicit water simulations) and magenta (implicit water simulations) and DNA in yellow. (a) A water inserts into the protein-DNA interface, displacing the protein sidechain (grey arrow) and replacing a direct with a water-mediated contact. (b) Hydrogen bonds to explicit waters (green dashed lines) help to correctly orient a protein sidechain.

Given that introduction of explicit water increases the number of degrees of freedom in our protein-DNA interface simulations, and hence might lead to less efficient energy optimization, we restricted our analysis to the lowest-energy models for each benchmark protein/entropy-parameter combination. Notably, when recovery rates were recalculated using just the lowest-energy 20% of the models, we found that overall performance was significantly improved, and moreover that the explicit water simulations were now competitive with and in many cases slightly superior to the fully implicit simulations (Fig. 4b). While the differences in recovery are small, visual examination of individual protein sidechains that are improved in the solvated simulations (Fig. 5b) suggests that the positive effect of the explicit waters is compatible with the observed location of crystal-structure waters.

Three further conclusions can be drawn from these simulations: that the anisotropic solvation model (‘NW’) out-performs the isotropic model (‘NW LK-classic’); that the single-site water simulations (‘1W’) are less accurate than the fully explicit 3-site water simulations (‘3W’); and that simulations relying exclusively on the orientation-independent, fixed-cost entropy model to modulate hydration rate (i.e., simulations with H2O_hbscale = 1) are less accurate than the simulations in which the full entropy model is used.

DNA sequence recovery

To investigate the role of interfacial waters in sequence-specific DNA recognition, we performed a set of DNA sequence recovery simulations comparing our hybrid solvation model to its fully implicit counterpart. In these simulations, both the DNA sequence and the protein sidechains at the interface are initially randomized and subsequently optimized by a Monte Carlo procedure that incorporates DNA base-pair mutation moves.³⁰ Energy-biased acceptance of these mutation moves allows for simultaneous optimization of the target-site DNA sequence and the protein and DNA conformations (as well as the water occupancies and positions, in the case of the explicit-water simulations). A subset of 62 protein-DNA complexes likely to display sequence-specific DNA binding was selected from the full benchmark set; 300 independent sequence recovery simulations were performed for each target; and the resulting models were sorted by energy from lowest to highest. We used two metrics to assess the DNA sequence recovery performance of these models: in the first metric (‘averaged recovery’), we calculate the overall fraction of the modeled DNA base pairs that match the crystal structure DNA sequence, averaging over all analyzed models for each target protein; in the second (‘consensus recovery’), we first calculated the most common base at each position in the analyzed models, and then computed the fraction of consensus sequence positions that match the crystal structure sequence. While less robust to stochastic fluctuations, the second metric directly tests our ability to infer the correct DNA target site from the final models. Due to the time consuming nature of the sequence-recovery simulations (and the need to refit the unbound DNA energy model for each water-entropy parameter set, see Materials and Methods), we selected for analysis a single water-entropy parameterization (H2O_hbscale=0.6, H2O_refwt=0.6) that gives a native-like degree of hydration site occupancy and acceptable performance in the water recovery and protein sidechain recovery simulations (indicated by the green square in Figs. 3 and 4).

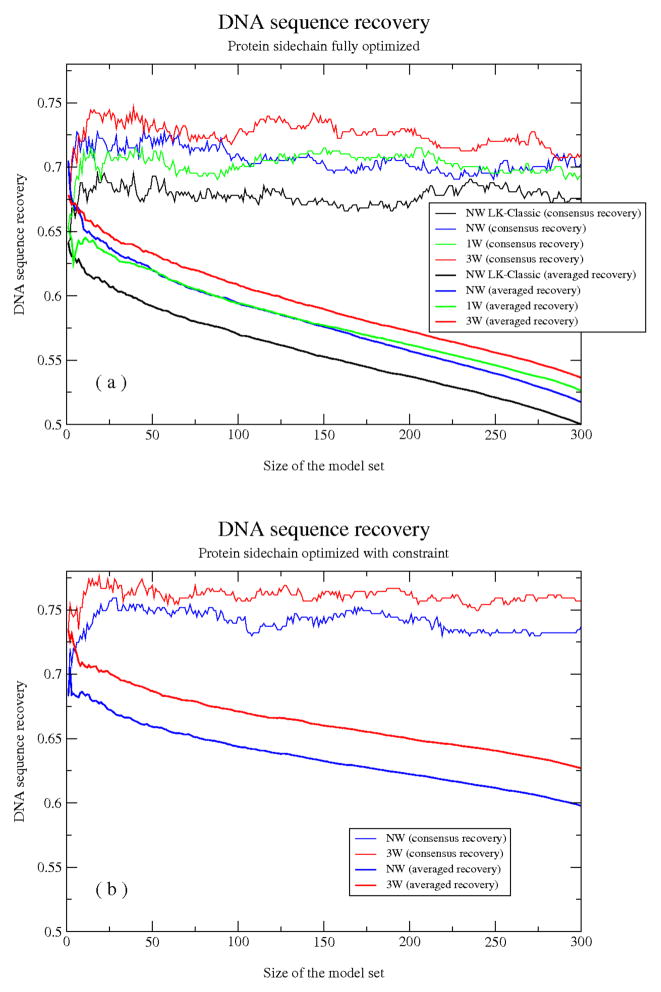
Sequence recovery results for four different solvation models are presented in Fig. 6a. To clearly illustrate the effect of filtering for low-energy models, we present results computed for all possible low-energy subsets, plotted as a function of the number of ‘low-energy’ models analyzed (x-axis, ranging from the single lowest-energy model at the left to the full set of 300 models on the right). We can see that lower energy models are on average better able to recover the target site from the crystal structure, and consensus recovery is greater than averaged recovery (since even a slight bias toward the correct base contributes 1 to this metric, versus 0.25 and above for averaged recovery). To fully capitalize on the strength of consensus averaging, a population size of ~20 models is required, with recovery results gradually declining for larger subsets as higher-energy models are included. The explicit water simulations with the 3-site model (‘3W’) yield the highest sequence recovery, superior to the single-site model (‘1W’) and the fully implicit models, while the anisotropic variant of the LK model (‘NW’) outperforms the original isotropic variant (‘NW LK-classic’).

Figure 6.

DNA sequence recovery from simulations with fully implicit (NW, NW LK-classic) and hybrid implicit/explicit (3W and 1W) solvation models (see text for model details). Fraction of correctly recovered DNA bases according to the consensus (thin lines) or averaged (thick lines) recovery schemes (y-axis) is plotted against the number of models over which recovery is calculated (x-axis; from the single lowest-energy model on the left to the full set on the right; models are sorted by energy). Results for unconstrained simulations initiated with randomized protein sidechain configurations are shown in (a); in (b), protein sidechains were constrained to remain nearby their crystal conformations with a flat-bottomed harmonic tether.

In this analysis we are tacitly assuming that the DNA sequence seen in the crystal structure is the preferred target site, which is not likely to be true at all interface sequence positions considered. For this reason, some mismatches between simulation and experiment may reflect recovery of true binding preferences, and indeed a specific example is given below. As an additional comparison, we performed DNA sequence recovery simulations in which the protein sidechains were constrained to remain nearby their crystal structure positions (for details see Materials and Methods), with the expectation that this should sharpen the implicit vs. explicit comparison by increasing the expected sequence recovery for an ‘optimal’ solvation model (by reducing affinity for alternate DNA sites whose binding requires a protein conformational change, for example, and minimizing noise introduced by sidechain prediction errors and conformational sampling difficulties). As expected, both the explicit and implicit solvation models give higher DNA sequence recovery in these simulations (Fig. 6b); notably, the explicit water simulations benefit more from tethering the protein sidechains (most visible in the averaged recovery plots).

We then analyzed the difference between the implicit (‘NW’) and explicit (‘3W’) water simulations on a per-position basis. Using the averaged recovery metric, we calculated the number of bases with improved, unchanged and worsened recovery due to the addition of explicit water (Fig. 7). In Fig. 7a, we can see that improved bases (red curve) outnumber worsened bases (black curve). For the full model set, about 60% of the bases are improved, 40% bases are worsened, and just a few bases remain same. The numbers of improved, worsened, and unchanged bases in simulations with constraints are shown in Fig. 7b. Compared with Fig. 7a, the number of improved bases (red curve) is similar, while the number of worsened bases (black curve) decreases and unchanged bases (green curve) increases. Visual examination of DNA sequence positions whose recovery is most improved in the simulations with explicit waters revealed that many are associated with bridging crystal structure waters whose presence is recapitulated by the explicit-water models, favoring recovery of the wild type base (models for the 6 positions with the largest improvement in DNA sequence recovery in the hybrid model are shown in Fig. S3). The specific bridging waters identified in this manner represent good candidates for interfacial waters with a role in sequence recognition. Thus, we propose that comparison of implicit and explicit water DNA sequence recovery simulations may represent a useful tool for investigating the role of individual waters in protein-DNA recognition.

Figure 7.

The effect on DNA sequence recovery of the addition of explicit interfacial water molecules analyzed on a per-position basis for unconstrained (a) and constrained (b) simulations.

Examples

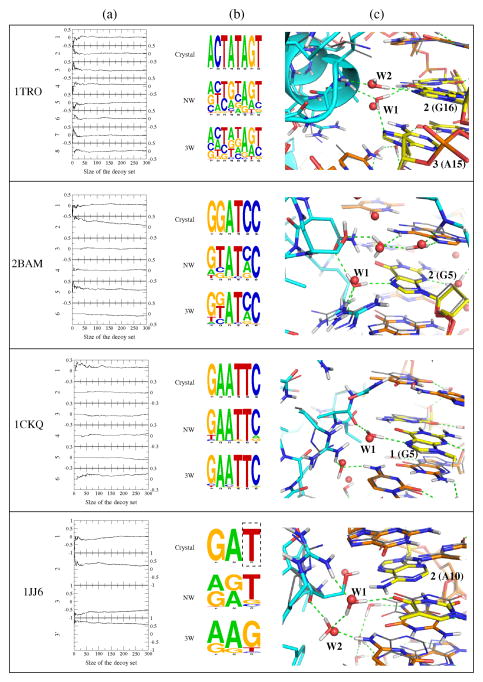
In the calculations above, we assessed the impact of water on DNA sequence recognition over a large benchmark set of high-resolution crystal structures. To gain additional insight into the details of water behavior in our simulations, we studied four specific cases for which experimental data are available on the role of water in binding. For each example, we performed unconstrained DNA sequence recovery simulations as described above, with and without explicit interfacial waters (‘NW’ and ‘3W’), and compared the results on a per-position basis across the DNA target site. Simulation results for these four examples are summarized in Fig 8 – which shows per-position differences in DNA sequence recovery between the implicit and explicit water simulations, DNA sequence logos derived from the simulations, and a representative low-energy model from the explicit water simulations superimposed on the template crystal structure. Details on the target site positions analyzed can be found in the Supplementary Data.

Figure 8.

Detailed results for four systems with experimental data on the role of water in binding. (a) Per-position differences in recovery across the DNA target site between ‘NW’ and ‘3W’ models (positive values reflect improvement in the explicit water simulations; results for 1JJ6 position 3′ are calculated with respect to the experimentally preferred G base). (b) Crystal structure sequence and DNA sequence logos derived from the 20% lowest-energy models. The boxed ‘T’ indicates a target site position at which experimental data indicates that a G is preferred. (c) Details of modeled waters at the protein-DNA interface, showing crystal-structure waters (red spheres), modeled waters (in sticks, with modeled hydrogen bonds shown as dashed lines), experimentally observed protein and DNA conformations (thin grey lines), and, in stick representation, the modeled protein (cyan carbons) and DNA (orange carbons, with yellow for emphasis) conformations.

(a). trp repressor (PDB ID 1TRO)

The high-resolution crystal structure of the trp repressor/operator complex is distinguished by a lack of direct hydrogen bond interactions between the protein and DNA bases.³ The core DNA target site sequence is seemingly recognized indirectly, both by the geometry of its phosphate backbone (which participates in 24 direct hydrogen bonds to the protein in the high-resolution crystal structure) as well as by several interfacial waters that bridge between the protein and the DNA bases. Evidence for the importance of one water in particular (labeled ‘W1’ in Fig. 8c) is provided by a double-mutation experiment in which a second mutation that is predicted to restore W1’s hydrogen bond network is able to partially revert the deleterious effect of a mutation at a neighboring site in the target.⁹

The core DNA sequence preferences are recovered almost equally well by the implicit and explicit water simulations, even though the three interfacial waters contacting the core half-site are well-recovered in the explicit water simulations (78% of low-energy models have W1 site occupied; W2 site: 83%; W3 site – which bridges to target site positions 1 or 8: 78%). There is some improvement visible in the sequence logo for the water simulations at position 4, while the per-position recovery plots indicate that the core motif positions 2 and 3 (and their palindromic counterparts 6 and 7) are better predicted in the very low energy water models. At the same time, the success of the implicit water simulations would seem to suggest that DNA backbone conformation plays a large role in DNA sequence recognition.

(b). Restriction endonuclease BamHI (PDB ID 2BAM)

The type II restriction endonuclease BamHI cleaves the palindromic target site GGATCC on both strands between successive guanine nucleotides. Off-target ‘star activity’ has been shown to increase with osmotic pressure, an effect that can be reversed by increased hydrostatic pressure, hinting at a role for interfacial water molecules in sequence specificity.¹⁰ Comparing the implicit and explicit water simulations (Fig. 8a), we see a substantial improvement in prediction accuracy at positions 2 and 5 for the explicit water simulations. Examination of low-energy models reveals that this improvement can be explained by successful recovery of a bridging water (‘W1’ in Fig 8c; 70% occupancy) that donates a hydrogen bond to the Guanine N7 atom. Together with a direct hydrogen bond to the partner base, this water-mediated contact effectively specifies G at this position.

(c). Restriction endonuclease EcoRI (PDB ID 1CKQ)

The role of water in the activity of the well-studied restriction endonuclease EcoRI has been investigated by a variety of experimental techniques, including binding and cleavage measurements at varying osmotic and hydrostatic pressures.¹² These studies suggest that as water activity decreases, off-target ‘star’ activity increases at sites such as TAATTC (the canonical site is GAATTC). A specific pair of interfacial waters that bridge to symmetrical target site positions 1 or 6 in the EcoRI-DNA complex structure has been postulated to play a role in discriminating against star sites with mismatches at these positions. Supporting this hypothesis, we see an increase in recovery of the canonical target site sequence in the explicit water simulations (Fig. 8b), exactly at positions 1 and 6, with the implicit simulations showing a greater preference for the star sites with T at position 1 (A at 6). Examination of the low-energy models (Fig. 8c) shows that the bridging water mentioned above (labeled W1) is well-recovered (72% occupancy). Thus, our simulations support the role of water in DNA sequence recognition by the endonuclease EcoRI and provide additional details regarding potential mechanisms.

(d). Hin recombinase (PDB ID 1JJ6)

Detailed structural analysis¹³ of Hin recombinase bound to wild type and mutant DNA sequences has suggested a role for a pair of bridging waters (W1 and W2 in Fig. 8c) in sequence recognition at positions 2 and 3 of the core GAT target site. Comparing our implicit and explicit water simulations, we do indeed see improved recovery of the wild type A at position 2. At position 3, experimental binding measurements suggest that Hin recombinase has a higher affinity for a target site with a G, rather than the T seen in the template crystal structure. Strikingly, the explicit water simulations are able to correctly recover this preference, even though the starting template structure has a T. Thus at both of the water-bridged target site positions, the explicit water simulations are more faithful to the experimental data, in agreement with the fact that the bridging water sites are highly occupied in low-energy models (100% for W1 and 93% for W2). There is a slight decrease in prediction accuracy at position 1, which does not have bridging water contacts either in the crystal structure or the models; this may be due to an explicit water in the models that forms a favorable interaction between a pair of bases on opposite strands at positions 1 and the preceding base pair.

Conclusion

Our results suggest that incorporating a limited number of explicit, interfacial water molecules into protein-DNA interface simulations can improve recapitulation of structures and binding preferences. Knowledge of the location of crystallographic waters is not required – the occupancy of the hydration sites is optimized by a Monte Carlo procedure – but could easily be incorporated to focus sampling, for example in interface design calculations in which a specific bridging water is known to be important for binding. In addition, we propose that comparison of simulation results with and without interfacial waters may represent a useful approach for identifying bridging waters with important roles in DNA sequence recognition. Here, the use of a hybrid model (as opposed to simulations with full explicit solvent) focuses the implicit/explicit comparison on the specific role played by individual interfacial waters, eliminating extraneous differences in simulation methodologies and treatment of bulk solvent.