Abstract
An innovative method is proposed for approximation of the set of radial diffusion equations governing mass exchange between aqueous bulk phase and intra-particle phase for a hetero-disperse mixture of particles such as occur in suspension in surface water, in riverine/estuarine sediment beds, in soils and in aquifer materials. For this purpose the temporal variation of concentration at several uniformly distributed points within a normalized representative particle with spherical, cylindrical or planar shape is fitted with a 2-domain linear reversible mass exchange model. The approximation method is then superposed in order to generalize the model to a hetero-disperse mixture of particles. The method can reduce the computational effort needed in solving the intra-particle mass exchange of a hetero-disperse mixture of particles significantly and also the error due to the approximation is shown to be relatively small. The method is applied to describe desorption batch experiment of 1,2-Dichlorobenzene from four different soils with known particle size distributions and it could produce good agreement with experimental data.
Keywords: Radial Diffusion model, Multiple-rate model, Sorption, Desorption, Modeling, hetero-disperse particles
Introduction
The quantification of mass transfer between porous particles and a surrounding bulk aqueous phase is needed in many hydrological applications, including cases involving particles suspended in surface water, in riverine/estuarine sediment beds, in soils and in aquifer materials One of the most common models to simulate rate-limited mass transfer between the intra-particle and surrounding aqueous phases is the radial diffusion model (e.g., Villermaux, 1974; Rao et al., 1980; Wu and Gschwend, 1986). Radial diffusion models may consider mass transfer resistances imposed by an aqueous boundary layer surrounding the particles, diffusion into intra-particle pore spaces, with the particle and pore geometry typically approximated by ideal forms such as spherical or cylindrical. These particle scale diffusive resistances are often combined with sorption to the intra-particle walls, and many sorption processes involving mono-disperse particles have been analyzed using radial diffusion models (Neretnieks, 1976a; Neretnieks, 1976b; Vrentas and Vrentas, 1998; Wiberg and Harris, 2002).
There have been some efforts to solve the radial diffusion equation for hetero-disperse systems. For example, Ruthven and Loughlin (1971) and Cooney and Adesanya. (1983) used the analytical solution for the uptake rate by a single sphere to obtain the uptake rate of a hetero-disperse particles mixture for a batch system in which the bulk concentration was held constant. Cooney and Adesanya. (1983) also used a finite difference method to solve the non-linear site saturation model by approximating the particle size distribution using 17 to 31 intervals. Rasmuson (1985), found an analytical solution for modeling the breakthrough curve for columns containing hetero-disperse particles with fixed boundary and initial conditions. Fong and Mulkey (1990) suggested a method for calculating a representative radius for a particle size distribution that can be used to approximate sorption rates for the hetero-disperse mixture using a mono-disperse radial diffusion model. Pedit and Miller (1995) solved the complete set of radial diffusion equations in a batch system containing a hetero-disperse particle mixture using a numerical approach. They used the method of lines to reduce the governing system of partial differential equations to a system of ordinary differential equations, and then used the Bubnor-Galerkin finite element method with a third order shape functions to solve the resulting set of equations. Karapanagioti et al. (2001) also used a finite difference method for modeling the mass exchange, biodegradation and sorption in a batch system with hetero-disperse particles. Basagaoglu et al. (2002) used a finite-difference method to solve the radial diffusion model for a hetero-disperse mixture of particles with non-linear site limited sorption reactions. They tested their model with a mixture of three spherical particle sizes in a batch system and also a mixture of three different shapes of particles (spherical, cylindrical and planar), each with a single size class.
Although the solution of the system of equations obtained from radial diffusion equation for a hetero-disperse mixture in a batch system is tractable, the computational effort needed for solving macroscopic transport problems in 1,2 or 3 dimensions, explicitly, is rather large (e.g. Dietrich et al., 2003). For a domain with homogenous media, using the method of temporal moments can reduce the computational effort significantly. Cunningham and Roberts (1998) and Neretnieks (1976a) used this method to investigate the impact of a distribution of time scales as an indicator of particle sizes and intra-particle effective diffusion on the transport of sorbing solute. They ignored the film resistance between aqueous phase and particles. This method can be used for determining the spatial moments of solute concentration in homogeneous columns. In practical applications other simplified models such as one-site models (Bahr and Rubin, 1987; Lapidus and Amundson, 1952; Oddson et al., 1970; Rao et al., 1980), two-site models (Cameron and Klute, 1977; Selim et al., 1976, and Nkedi-Kizza et al., 1984) or multiple-rate models (Haggerty and Gorelick, 1995) are used. Rao et al. (1980) also showed the failure of one-site models manifested as an apparent time dependence of the exchange rate coefficient. Log-normal or Gamma distributions are often assumed to govern the rate distribution for the multiple-rate models (Connaughton et al., 1993; Culver et al., 1997; Pedit and Miller, 1994). However because these simplified models are not directly based on the mechanisms involved in the sorption process, there is no way to relate the rates of sorption-desorption with the system’s physical characteristics such as particle size distribution of the media, diffusivity of the contaminants, pore size distribution in the particle and the tortuosity factor associated with the intra-particle pores. Thus the parameters involved in such models are usually treated as fitting parameters and therefore these models usually lack the capability of being generalized to other soil media and chemical properties than the one to which they have been fitted.
In order to take into account the physical characteristics of the media in multiple-rate serial models, there have been some efforts to find the link between multiple-rate models and radial diffusion models. Haggerty and Gorelick (1995) suggested a method for extracting the equivalent multiple-rate model from a normalized radial diffusion model by setting equal the bulk water concentrations obtained by a radial diffusion model and a multiple-rate model with an infinite number of sites. They used Laplace transformation of time dependent bulk dissolved concentrations and found the exchange rate distributions as infinite series so that the resulting multiple-rate model could predict exactly the bulk water concentrations associated with radial diffusion. However they used an assumption of no boundary layer between the grain and the bulk water (i.e. the concentration in the outermost part of the grain were assumed to be exactly equal to the bulk water concentration). Also in their approximation they matched the bulk concentrations obtained from the radial diffusion and its multiple-rate approximations, and therefore in their model although the bulk water concentration predicted by the radial diffusion model and its equivalent multiple-rate model are exactly equal, the rates they obtained as an infinite series do not represent any physical exchange rate between any part of the solid phase and bulk water. In addition in case of hetero-disperse mixtures of particle sizes, using an infinite series for the exchange rate and the mass associated with each exchange rate leads to having as many infinite series as the number of particle size classes, which will multiply the computational effort needed for solving the problem by the number of particle size classes selected.
The goal in the present study is to use a numerical method to obtain the multiple-rate model that can best approximate a radial diffusion model in terms of intra-particle concentration for hetero-disperse mixtures. In other words, we seek to approximate a serial mass transfer process with an effective set of parallel linear reversible reactions to incorporate the effect of distributed particle sizes on mass transfer controlled by radial diffusion (Figure 1). Our parallel reaction model uses a rate distribution associated with a multiple-rate model and requires significantly smaller computational effort compared to a comparable radial diffusion model for hetero-disperse particle mixtures. The advantage of this model with respect to previous multiple-rate models is that the exchange rate distribution here is obtained directly from the diffusive characteristics of the grains. Also because a numerical technique is used to solve the radial diffusion equation in this study, the model can be extended further for non-linear cases, various shape factors and different boundary conditions.
Figure 1.
Schematic of a) Radial diffusion model b) Multiple rate approximation
Our formulation follows Basagaoglu et al. (2002) and includes potentially important mass transfer limitation at the particle boundary represented through a film (boundary layer) transfer rate kb (below) that appears subsequently in dimensionless form as the Biot number Bi. Although in many subsurface porous media applications the film resistance may be unimportant (e.g., the Biot number may be relatively large) we include it for generality of application to surface and subsurface hydrological applications. Basagaoglu et al. (2003) found in an application to MTBE degradation in porous particles that the film diffusion was not limiting but pointed out that for less-sorptive solutes that it may become limiting; In general film transfer limitations may arise in a variety of configurations including desorption from initially-contaminated particles under low advective flows of the bulk solution such as contained sediments in river or lacustrine beds or quiescent pore water conditions and whenever particle boundaries are associated with morphological features such as armoring by precipitates or biofilms.
Each particle is conceptualized as a symmetric grain surrounded by a diffusive boundary layer. The exchange process is controlled by intra-particle diffusion and film resistance due to the boundary layer. The model produces a continuous distribution for the rate coefficient instead of a discontinuous series since the exchange rate obtained for a distance from the center of a grain is a continuous function of distance from the center of the grain.
For obtaining the exchange rate coefficient associated with any point (or distance from the center of the grain) inside a particle, the normalized radial diffusion method is solved numerically and then the optimal multiple exchange rate at each point is calculated by minimizing the sum of squared differences between the two over an appropriate time range.
Solution approach
Radial diffusion model
The equation for reactive (sorbing) diffusion of a dissolved compound within porous particles can be written as follows (Wu and Gschwend, 1986).
| (1) |
in which Sr is the total local contaminant mass concentration in the porous sorbent (M/M), Cr is the intraparticle contaminant concentration in the dissolved phase (M/L3), β is the porosity of the sorbent (−), Dm is the pore fluid diffusivity of the sorbate (L2/T), r is the radial distance from the center of a grain (L), and v is shape factor which is equal to 1 for planar, 2 for cylindrical, and 3 for spherical grains (−).
We assume that the sorption process inside the particle is fast, linear and reversible, in which case Sr = KpCr and Eq. 1 can be written as:
| (2) |
where
| (3) |
in which De is the sorption-retarded effective intra particle diffusivity (L2/T), Kp is the intra-particle equilibrium partition coefficient (L3/M), ρs is the bulk density (M/L3), and f (β,λ) is a correction factor in the diffusion coefficient (Wu and Gschwend, 1986) that includes the effect of tortuosity and intra-aggregate porosity.
For the purpose of finding the generic multiple-rate model, it is assumed that initially particles are clean, and that the bulk phase concentration is constant. Xxx more hereabout this b.c./i.c. configuration as a “characteristic case” and our speculation that it will give the right numbers for other cases. Xxx Therefore the initial and boundary conditions for the intraparticle contaminant concentration in a dissolved phase can be expressed as:
| (4) |
A symmetry boundary condition is used on the center of the grain.
| (5) |
and a film resistance boundary condition is imposed at the surface of the grain also assuming for the purpose of obtaining the generic multiple-rate distribution that the bulk concentration is maintained constant. This leads to the following boundary condition:
| (6) |
in which kb is the film resistance coefficient (L/T).
The normalized form of Eq. 2 can be written as follows:
| (7) |
where the dimensionless variables are defined as follows:
| (8) |
| (9) |
| (10) |
| (11) |
Where ξ is dimensionless distance from the center of the grain, τ is the dimensionless time, χ is the dimensionless concentration and Bi is the Biot number which indicates the level of importance of intra-particle diffusion with respect to film resistance coefficient. We adopt as a rule of thumb that Bi < 100 implies significant film resistance.
It is worth noting that the simplified boundary and initial conditions in Eqs. 4 and 5 and the assumption of fixed bulk concentration are imposed solely for obtaining the generic exchange-rate coefficient distribution. Having the generic exchange rate distribution, as is shown through several numerical tests in the next section, the multiple-rate model can be used for different boundary and initial conditions, including a variable bulk concentration. The normalized boundary conditions can be written as:
| (12) |
| (13) |
and the normalized initial condition is:
| (14) |
Now the solution to Eq. 7 can be expressed for any particle size, via the stretching normalizations in eqs. 8 through 11.
The solution to the PDE in Eq. 7 with boundary conditions 8 and 9 and initial condition 14 is obtained using an implicit finite difference method and can be expressed as a function of normalized time τ, normalized distance from the center ξ, and Bi. For sake of simplicity the numerical solution to the PDE is called χ, however it has some differences with the exact solution due to truncation errors and other types of possible errors in using a numerical technique. So from this point of the paper χ refers to the numerical solution to the normalized radial diffusion equation.
| (15) |
To obtain the generic rate coefficient distribution for a multiple-rate model that can represent the mass exchange to the normalized grain, the normalized radial diffusion model for the normalized grain is solved and then for each point among the set of points inside the grain within radius increments, the exchange rate coefficient that can best represent the concentration variation at that point is obtained by minimizing the difference between the solutions found from radial diffusion and the linear reversible sorption model.
The normalized radial diffusion PDE is solved for a large range of Bi with logarithmic increments (i.e. it is solved in range of 10−5 to 105 with increments of 1.2 as a multiplier). The time increments and radial grid sizes should be specified so that the computational intensity remains affordable while satisfying the stability conditions of the numerical method. In particular, insufficient resolution of the intra-granular dimension can lead to serious mass balance errors (Basagaoglu et al., 2002). So the radius is discretized into 100 grid points and the increment for τ is considered dependent on Bi. The simulation for each increment of Bi is continued until the average concentration inside the particle reaches 0.99 of the saturation concentration (i.e. the situation where the average normalized concentration (χ) inside the grain is greater than 0.99).
From the simulation results it was observed that from that for Bi values greater than about 100 the limiting process is not boundary layer exchange but intra-particle diffusion. On the other hand for small Bi values (i.e. below 0.1) the effect of intra particle diffusion becomes negligible and the controlling process becomes the film resistance.
Multiple-rate model
As outlined above, the goal is to fit the best possible single rate exchange model to each layer with identical distance from the center and to obtain a multiple-rate model by superposing all single rate models. In the multiple-rate approximation the intra-particle zones are treated as if they are directly exchanging mass with the bulk solvent (Figure 1b). Each intra-particle zone is associated explicitly with its own rate coefficient, the value of which drops with decreasing normalized radial coordinate value. The net diffusive reactive behavior is obtained by linear superposition (summation) of the individual mass transfers. The utility of this explicit linear approximation is suggested by the linearity of the governing differential eq 1. Thus the approximate parallel domain multiple-rate model can be written as follows:
| (16) |
C̑ is the intra-particle concentration found by the multiple-rate model approximation, M is the number of intra-particle zones in the multiple-rate model, and kf,i is the exchange rate (1/T) associated with the intraparticle zone i.
The normalized form of Eq. 16 for the fixed pore water concentration can be written as follows:
| (17) |
in which the normalized variables are defined as:
| (18) |
| (19) |
Now if we consider that each zone i in the multiple-rate model corresponds to a layer (or a range of distances from the center) in the discretized radial diffusion model, then for each layer i, κf,i is clearly a function of Bi and ξi as
| (20) |
Now for any specified Bi value and point inside the grain (i.e., ξ) κf,i is a constant and equation 17 can be solved analytically.
| (21) |
To determine the function κf(ξ, Bi) which makes the approximate solution χ̑ as close as possible to the numerical solution of the radial diffusion equation χ, it is necessary that for each particular value of Bi and ξi the value of κf be estimated such that it minimizes the difference between χ̑ and χ over the specified time span.
| (22) |
or
| (23) |
The optimization problem in Eq. 23 is solved using the steepest descent method for a range of Bi between 10−5 and 105 with logarithmic increments and ξ between 0 and 1 with increments of 0.01.
The result of the numerical solution of the optimization problem in Eq. 23 is presented in Figure 2. As can be noticed from the figures for Bi>10 the dependence on Bi is small indicating that the dominant factor in the sorption to the grain is intra-particle diffusion, on the other hand for Bi < 0.1 the κf variation with respect to ξ is small indicating that the dominant process in controlling the sorption is boundary layer diffusion. For most environmental systems the Biot number is greater than 100 (Ko et al., 2003) which indicates that usually film resistance does not control the mass exchange between water and particles.
Figure 2.
κf versus Bi and ξ for a) ν=3 and b) ν=2 obtained by minimizing the difference between the multiple rate and radial diffusion solutions
For the special case of no film resistance, Bi = ∞, the analytical solution of Eq. 7 can be used instead of the numerical solution. Adopting the method by Crank (1975) the analytical solution to Eq. 7 with boundary conditions (9) and χ(1) = 1 can be obtained from the following infinite series:
| (24) |
So in that case, substituting Eq. 24 into Eq. 23, the following expression should be minimized:
| (25) |
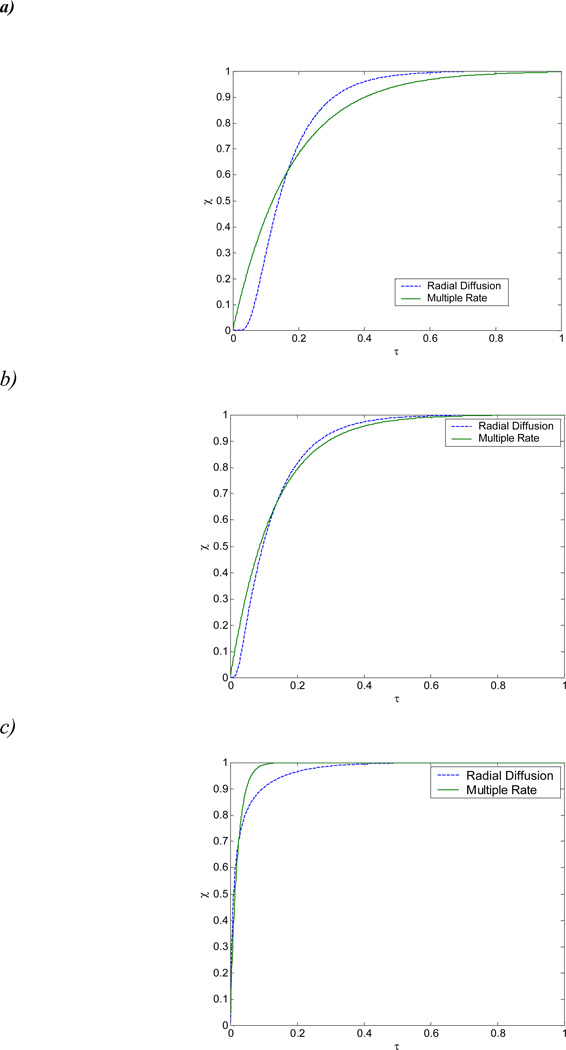
Eq. 25 was used to verify of the results obtained from the numerical solution of the normalized radial diffusion equation. The average concentration and flux versus time obtained from the radial diffusion solution is compared with those estimated with the multiple-rate model for Bi=100 in figure 3. It can be seen that there is a good agreement between two models for most values of τi. However, there are some degrees of discrepancies between the fluxes predicted by the multiple-rate and radial diffusion models for smaller flux estimates. Those discrepancies may arise either from the numerical errors involved in the method or the approximations introduced.
Figure 3.
Radial diffusion and estimated multiple rate model a) mass flux and b) average concentration versus time for a spherical particle with Bi = 100
The solutions to the normalized radial diffusion model and the multiple-rate model for the case of Bi = 100 at ξ=0.1, 0.5, 0.9 respectively, for a spherical particle (ν=3) versus time are shown in figure 4. Here the discrepancies are clear and their reason is the fundamental differences between the RD and MR models (i.e., in the serial models there will be a lag until the compounds reach the internal zones while in the parallel model no such lag exists.)
Figure 4.
Local intra-particle concentration versus time obtained by radial diffusion and its equivalent multiple-rate model for a spherical grain with Bi = 100 at ξ=0.1, ξ=0.5, and ξ=0.9.
Since the mass exchange rate coefficient distributions are derived based on a fixed bulk concentration using a numerical method, there is no guarantee that for a case with a variable boundary condition an identical rate-coefficient distribution would be obtained. To assess how well cases with variable bulk water concentration could be modeled using, the rate coefficient distributions obtained with a constant boundary concentration, analytical results for a normalized sphere under three different variable concentration cases with different initial fractions of chemical in the bulk water were compared with the results from our radial diffusion method. The variation in the bulk aqueous phase concentration with time for this case for bulk water fractions of 0.1, 0.5, and 0.9 are shown in figure 6. It can be noticed that the agreement is as good as for fixed pore water concentration cases (Figure 3) suggesting that the achieved mass exchange coefficient from the assumption of fixed aqueous concentration can be used to approximate variable aqueous concentration cases without a significant reduction in accuracy.
Figure 6.
Exchange rate distribution for a sphere with unit radius in comparison with the distribution suggested by Haggerty and Gorelick (1995)
Solution technique for media with hetero-disperse particles
If a media with particle size distribution ψ(R) is considered, (i.e., the fraction of mass with the particle size R is equal to ψ(R)) the objective will be to find the distribution of kf values, θ(kf) (i.e. the fraction of mass that has exchange rate of kf with the bulk solution) that provides the best agreement between the MR and RD models of the system.
To calculate the exchange rate distribution, the kf domain is first divided into different bins kf,1−kf,2, kf,2−kf,3, … kf,n−1−kf,n. The mass associated with each bin (i.e. kf,i−kf,i+1) can be calculated by summing the masses associated with the exchange rates between κfi and κfi+1 for each particle size where κf,i = kf,iR2/De. This is possible because from the solution of the minimization problem we obtained kf as a monotonically decreasing function of normalized distance from the center ξi. Therefore ξ can be expressed as a function of κf for a specified value of Biot number as follows:
| (26) |
where kb can be determined by the thickness of boundary layer and molecular diffusion coefficient of the contaminants.
The mass associated with the exchange rate bin kf,i−kf,i+1, Mi, can be calculated as:
| (27) |
Or if a measured (discrete) particle size distribution is available:.
| (28) |
in which Rj is the representative particle radius of the particle size bin and ΔRj is the increment of the bin.
The exchange rate distribution can therefore be obtained by computing the integral in Eq. 26 numerically and the multiple-rate batch sorption system can be written as follows:
| (29) |
| (30) |
where Ci is the intra-particle concentration associated with exchange rate kfi,, Cbulk is the concentration in bulk aqueous phase, KD is the equilibrium partitioning coefficient for entire intra-particle media (i.e. including intra-particle pores and solid phase) which is obtained from the following relationship.
| (31) |
In Figure 7 the exchange rate distribution obtained by the present method is compared with the one suggested by Haggerty and Gorelick (1995). It should be noted that the columns in the Haggerty and Gorelick distribution are representing dirac-delta functions multiplied by the values on the y axis because in their model exchange rates are expressed as infinite discrete series.
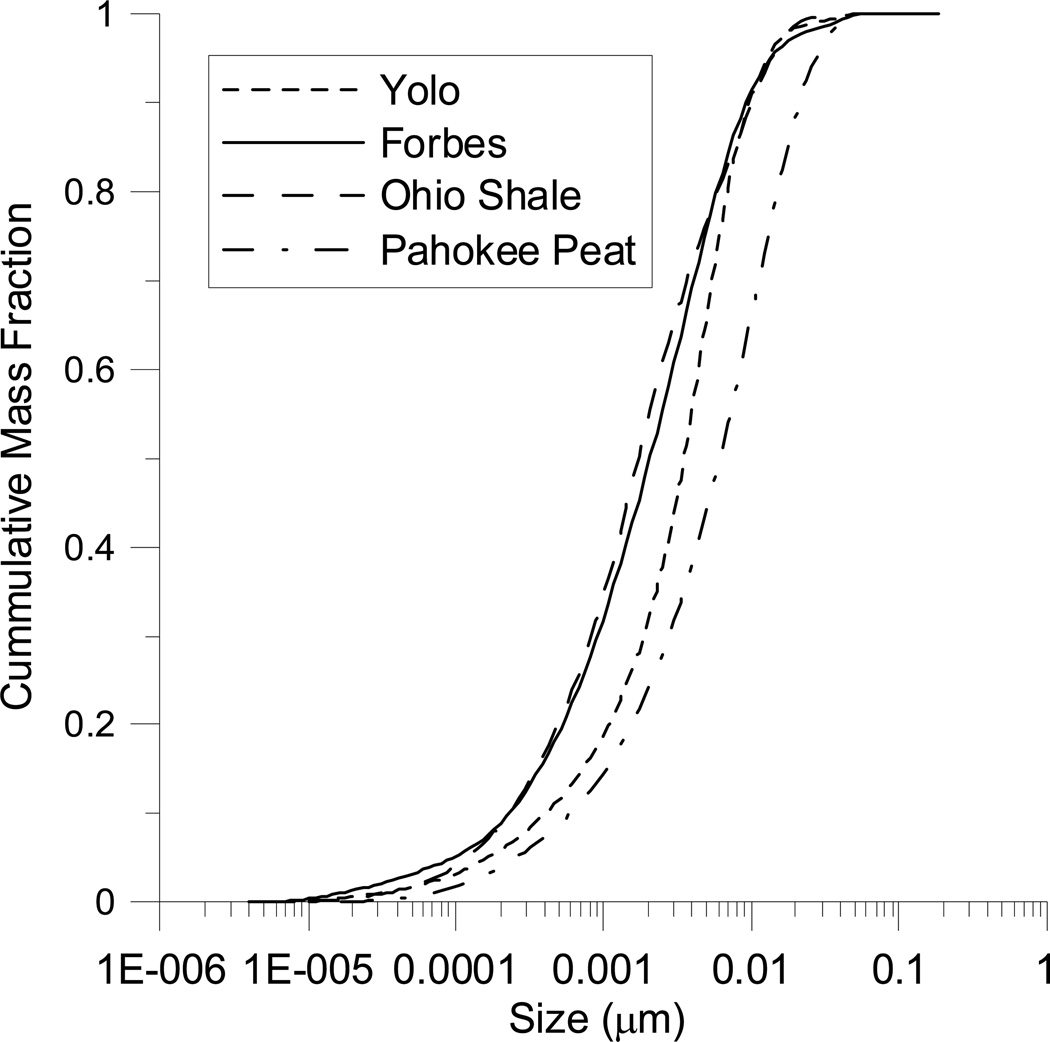
Figure 7.
Cumulative particle size mass distribution for four sorbents
Application
To illustrate the model’s application for describing sorption rates in hetero-disperse systems, it is used to describe batch sorption rate curves for 1,2 dichlorobenzene (1,2-DCB) on four natural sorbents: Yolo soil, Forbes soil, Ohio Shale and Pahokee Peat. Experimental procedures and results of 1,2-DCB sorption and desorption rates on these sorbents have been previously reported, including application of a multiple-rate model baesd on the γ-distribution (Ju and Young, 2005a). Table 1 summarizes the relevant properties of the sorbents and experimental conditions for each of them. The particle size distribution for each sorbent was determined by a laser-based particle counter (0.2–20µm: Particle Measurement Systems, Liquilaz) and a coulter counter (20–2000µm) and the cumulative particle size distributions are shown in Figure 8.
Table 1.
Summary of batch adsorption experimental conditions and fitted values of De, KD, and KD,∞.
| Sorbent | Average sorbent mass concentration (mg/cm3) |
Average Initial 1,2- DCB concentration (mg/L) |
Distribution Coefficient measured at 34 days (KD) (L/kg) |
Estimated Theoretical partitioning coefficient (KD,∞) (L/kg) |
Estimated intra- particle Diffusion Coefficient (De) (cm2/s) |
|---|---|---|---|---|---|
| Yolo | 0.1017 | 0.107 | 11.34 | 21.55 | 4.5×10−11 |
| Forbes | 0.0104 | 0.104 | 161.87 | 355.75 | 1.2×10−12 |
| Pahokee peat | 0.00195 | 0.103 | 665.54 | 1431.26 | 4.2×10−11 |
| Ohio Shale | 0.00098 | 0.104 | 1505.7 | 4069.45 | 5.7×10−13 |
Figure 8.
Computed and measured pore water concentration for a) Yolo, b) Forbes, c) Pahokee peat and d) Ohio shale
For purposes of present application (but not as part of the general formulation) the lower limit of the correlation suggested by Harriot, (1962) for the case of no externally supplied mixing was used to estimate film resistance coefficient, kb:
| (32) |
where Dl is the free liquid diffusivity (L2/T), Sc is the Schmidt number (−), and Re is the Reynolds number (−) associated with the particles, which are calculated using the following equations:
| (33) |
| (34) |
where ρl is liquid density, v is settling velocity of the particles that can be found by Stokes’ law ε is porosity of the media, μ is the viscosity and P is the power dissipation rate which is set equal to zero here since the only mixing process is falling of particles under their own weight during end-over-end tumbling of the batch reactors.
For each sorbent the intra-particle diffusivity (De) and theoretical ultimate distribution coefficient (KD,∞) are found so that the mean-squared difference between the measured and computed pore water distributions is minimized. KD is calculated from the experimental data using the following equation and is the ratio between the sorbed and bulk concentrations when all parts of solid phase reaches equilibrium.
The results are presented in Figure 9. λ shown on the figure legend is KD/KD,∞. In Figure 9 the time axis is shifted by 0.001 sec for plotting purposes. The effective intra-particle diffusion rates and theoretical partitioning coefficients for the four sorbents are summarized in Table 1.
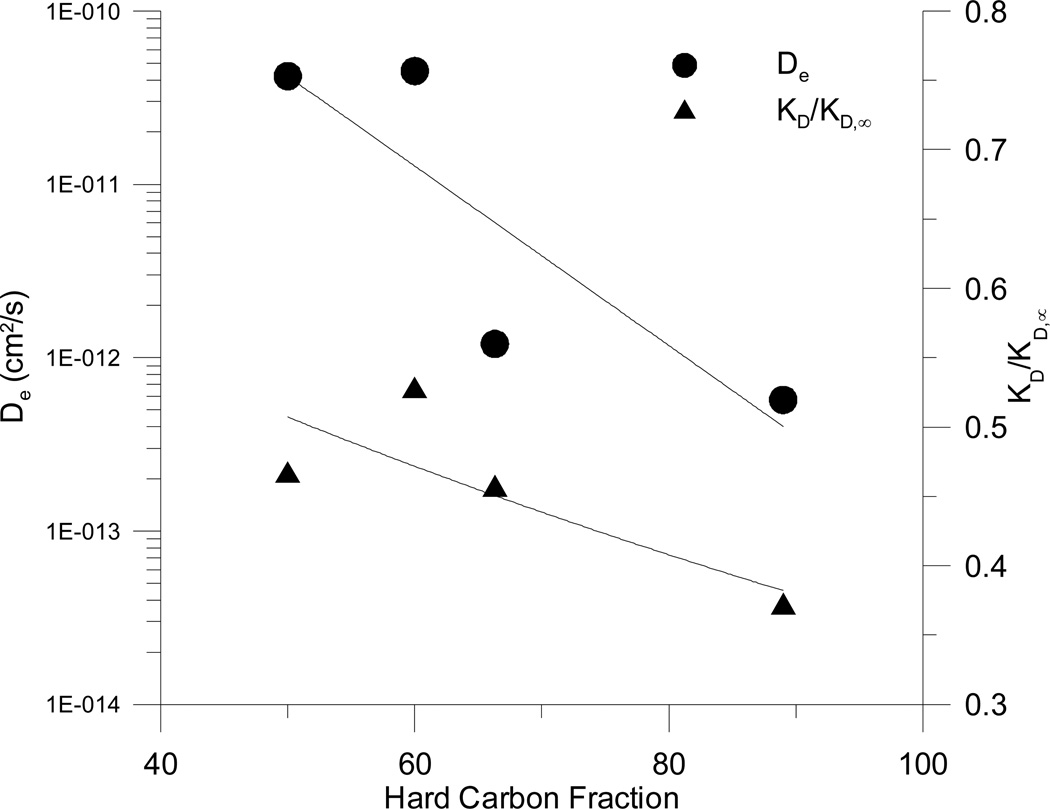
Figure 9.
Relationship between the hard carbon fraction of the sorbents and the fitted values of De and KD/KD,∞ for the four sorbents.
The fitted values of the effective diffusion coefficient for the four sorbents span a range of nearly two orders of magnitude (~6×10−13 to ~5×10−11 cm2/s). These fitted values are within the wide range observed previously for natural sorbents such as uptake of chlorinated benzenes by river sediments (8×10−12 to 1×10−9 cm2/s;Wu and Gschwend, 1986) and desorption of “aged” 1,2-dibromoethane by subsurface materials (2×10−17 to 8×10−17 cm2/s ; Steinberg et al., 1987). In particular, the values obtained for Yolo soil and Pahokee peat are within the range of values observed for chlorinated benzenes on Charles River sediment by Wu and Gschwend (1986). The smaller values of De observed for the other two sorbents are consistent with their much higher organic carbon normalized sorption capacities (Ju and Young, 2005b), which would contribute to increased intraparticle retardation. The unusual sorption characteristics of these materials were previously hypothesized to result from their higher hard carbon contents, where hard carbon is defined as organic carbon remaining after low temperature chemical oxidation (Ju and Young, 2005b). Figure 10 shows that both the effective diffusivity and the value of KD/KD,∞ tend to decrease with increasing hard carbon fraction of the sorbents. These findings are consistent with the hypothesis that the locus of high capacity and rate-limited sorption in natural sorbents is the hard carbon domain. According to this hypothesis, the larger the fraction of a sorbent’s organic carbon that is operationally defined as “hard” the slower will be the rate of approach to sorptive equilibrium and the larger the ultimate organic normalized distribution coefficient. Obviously, the exact configuration of the hard and soft carbon domains relative to one another and to the sorbent’s mineral phases will impact the effective diffusion coefficient, too; determination of this configuration is beyond current capabilities but its variability may account for some of the scatter in Figure 10.
Conclusions
A computationally efficient and reasonably accurate approximation of the radial diffusion model was presented for describing sorption reaction rates in hetero-disperse particle suspensions. Although there are some discrepancies at early times between the measured and computed solute concentrations during sorption (Figure 9) these arise from a combination of laboratory limitations (e.g., inaccuracies in measuring concentration at early times) and modeling approximations (e.g.,instant sorption to the outer surface of particles is ignored in the RD model). Further refinement of the model would require sorption rate data that was more nearly continuous at early times, such as from a differential batch adsorber, with such data in hand, the model could be modified to estimate the mass which sorbs to the surface of each particle.
The model fitting procedure employed here showed that a shape factor (ν) equal to 3 provided the best fit of the data. However, the physical characteristics of the particles suggest that the actual shape factor is smaller than 3. This discrepancy arises because, in reality, the internal porosity and thus the intra-particle diffusivities and sorptive surface areas are higher at outer layers of particles than in inner zones. Therefore another approach that could improve the results is to use an intra-particle diffusion rate that varies as a function of radial position.
Figure 5.
Bulk water concentration for a single size media obtained by radial diffusion and multiple rate models for porosity ε= 0.5, KD = 1 and grain radius R=1.
Acknowledgment
This research was partially funded by NSF project "Biogeochemical Cycling of Heavy Metals in Lake Coeur d'Alene Sediments" under Grant No. 0420374, and by NSF project"CMG: Toward Understanding the Transfer of Genetic Information in Subsurface Hydrology" under Grant No. 0416194. The sorption rate measurements in this study were conducted with the support of grant number 5 P42 ES04699 from the National Institute of Environmental Health Sciences, NIH. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIEHS, NIH.
Contributor Information
Arash Massoudieh, Civil and Environmental Engineering Dept, University of California, Davis, amassoudieh@ucdavis.edu.
Daeyoung Ju, Agricultural and Environmental Chemistry Graduate Group, University of California, Davis.
Thomas M. Young, Civil and Environmental Engineering Dept., University of California, Davis, tyoung@ucdavis.edu
Timothy R. Ginn, Civil and Environmental Engineering Dept., University of California, Davis, trginn@ucdavis.edu
References
- Bahr JM, Rubin J. Direct comparison of kinetic and local equilibrium formulations for solute transport affected by surface reactions. Water Resour. Res. 1987;23(3):438–452. [Google Scholar]
- Basagaoglu H, McCoy BJ, Ginn TR, Loge FJ, Dietrich PJ. A diffusion limited sorption kinetics model with polydispersed particles of distinct sizes and shapes. Adv. Water Resour. 2002;25:755–772. [Google Scholar]
- Basagaoglu H, Chung EE, Gandhi D, Scow KM, McCoy BJ, Ginn TR. Rate parameters for methyl tert-butyl ether biodegradation via a radial diffusion model. ASCE. J. Env. Eng. 2003;129(6):565–570. [Google Scholar]
- Cameron DR, Klute A. Convective-dispersive solute transport with a combined equilibrium and kinetic adsorption model. Water Resour. Res. 1977;13(1):183–188. [Google Scholar]
- Connaughton DF, Stedinger JR, Lion LW, Shuler ML. Description of time-varying desorption kinetics; release of naphthalene from contaminated sites. Environ. Sci. Technol. 1993;27(12):2397–2403. [Google Scholar]
- Cooney DO, Adesany BA. Effect of particle size distribution on adsorption kinetics in stirred batch systems. Chem. Eng. Sci. 1983;38(9):1535–1541. [Google Scholar]
- Culver TB, Hallisey SP, Sahoo D, Deitsch JJ, Smith JA. Modeling the desorption of organic contaminants from long-term contaminated soil using distributed mass transfer rates. Environ. Sci. Technol. 1997;31(6):1581–1588. [Google Scholar]
- Cunningham JA, Roberts PV. Use of temporal moments to investigate the effects of ninuniform grain-size distribution on the transport of sorbing solutes. Water Resour. Res. 1998;34(6):1415–1425. [Google Scholar]
- Dietrich JP, Basagaoglu H, Loge FJ, Ginn TR. Preliminary Assessment of Transport Processes Influencing the Penetration of Chlorine Into Wastewater Particles and the Subsequent Inactivation of Particle-Associated Organisms. Water Research. 2003;37:139–149. doi: 10.1016/s0043-1354(02)00239-7. [DOI] [PubMed] [Google Scholar]
- Dietrich JP, Loge FJ, Ginn TR, Basagaoglu H. Inactivation of particle-associated microorganisms in wastewater disinfection: Modeling of ozone and chlorine reactive diffusive transport in polydispersed suspensions. Wat. Res. 2007;41:2189–2201. doi: 10.1016/j.watres.2007.01.038. [DOI] [PubMed] [Google Scholar]
- Fong FK, Mulkey LA. Solute transport in aggregated media: Aggregate size distribution and mean radii. Wat. Resour. Res. 1990;26(6):1291–1303. [Google Scholar]
- Haggerty R, Gorelick MS. Multiple-rate mass transfer for modeling diffusion and surface reactions in media with pore-scale heterogeneity. Wat. Resour. Res. 1995;31(10):2383–2400. [Google Scholar]
- Ju D, Young TM. The Influence of Natural Organic Matter Rigidity on the Sorption, Desorption, and Competitive Displacement Rates of 1,2-Dichlorobenzene. Environmental Science & Technology. 2005a;39:7956–7963. doi: 10.1021/es050439x. [DOI] [PubMed] [Google Scholar]
- Ju D, Young TM. The Influence of the Rigidity of Geosorbent Organic Matter on Nonideal Sorption Behaviors of Chlorinated Benzenes. Water Research. 2005b;39:2599–2610. doi: 10.1016/j.watres.2005.04.058. [DOI] [PubMed] [Google Scholar]
- Karapanagioti HK, Gossard CM, Strevett KA, Kolar RL, Sabatini DA. Model coupling intraparticle diffusion/sorption, nonlinear sorption, and biodegradation processes. Journal of Contaminant Hydrology. 2001;48:1–21. doi: 10.1016/s0169-7722(00)00179-0. [DOI] [PubMed] [Google Scholar]
- Ko DCK, Porter JF, McKay G. Fixed bed studies for the sorption of metal ions onto peat. Trans Chem E. 2003;81(B):73–86. [Google Scholar]
- Lapidus L, Amundson NR. Mathematics of adsorption beds, 6. The effects of longitudinal diffusion in ion exchange and chromatographic columns. J. Phys. Chem. 1952;56:984–988. [Google Scholar]
- Neretnieks I. Adsorption in finite bath and countercurrent flow with systems having concentration dependent coefficient of diffusion. Chemical engineering and science. 1976a;31(11):465–471. [Google Scholar]
- Neretnieks I. Analysis of some adsorption experiments with activated carbon. Chemical engineering and science. 1976b;31(11):1029–1035. [Google Scholar]
- Nkedi-Kizza P, Biggar JW, Selim HM, Genuchten MT, Wierenga PJ, Davidson JM, Nielsen DR. On the equivalence of two conceptual models for describing ion exchange during transport through an aggregated oxisol. Water Resour. Res. 1984;20(8):1123–1130. [Google Scholar]
- Oddson JK, Letey J, Weeks LV. Predicted distribution of organic chemicals in solution and adsorbed as a function of position and time for various chemical and soil properties. Soil Sci. Soc. Am. Proc. 1970;34:412–417. [Google Scholar]
- Pedit JA, Miller CT. Heterogeneus sorption processes in subsurface systems, 1. Model formulations and applications. Environ. Sci. Technol. 1994;28(12):2094–2104. doi: 10.1021/es00061a018. [DOI] [PubMed] [Google Scholar]
- Pedit JA, Miller CT. Heterogeneous Sorption Process in Subsurface Systems. 2. Diffusion Modeling Approaches. Environ. Sci. Technol. 1995;29:1766–1722. doi: 10.1021/es00007a012. [DOI] [PubMed] [Google Scholar]
- Rao PSC, Jessup RE, Rolston DE, Davidson JM, Kilcrease DP. Experimental and mathematical description of non-adsorbed solute transfer by diffusion in spherical aggregates. Soil Sci. Soc. Am. J. 1980;44(4):684–688. [Google Scholar]
- Rasmuson A. The effect of particles of variable size, shape and properties on the dynamics of fixed beds. Chem. Eng. Sci. 1985;40(4):621–629. [Google Scholar]
- Ruthven DM, Loughlin KF. The effect of crystalline shape and size distribution on diffusion measurement in molecular sieves. Chem. Eng. Sci. 1971;26:577–584. [Google Scholar]
- Selim HM, Davidson JM, Mansell ES. Proceedings of the computer simulation conference, Am. Inst. of Chem. Eng. Washington D. C.: 1976. Evaluation of a two-site adsorption-desorption model for describing solute transport in soil; pp. 444–448. [Google Scholar]
- Villermaux J. Deformation of chromatographic peaks under the influence of mass transfer phenomena. J. Chromatogr. 1974;12:822. [Google Scholar]
- Vrentas JS, Vrentas CM. Integral Sorption in Rubbery Polymers. Journal of Polymer Science Part B: Polymer Physics. 1998;36(1):171–180. [Google Scholar]
- Wiberg PL, Harris CK. Desorption of p,p'-DDE from sediment during resuspension events on the Palos Verdes shelf, California: a modeling approach. Continental Shelf Research. 2002;22:1005–1023. [Google Scholar]
- Wu SC, Gschwend PM. Sorption kinetics of hydrophobic organic compounds to natural sediments and soils. Environ. Sci. Technol. 1986;20:717–725. doi: 10.1021/es00149a011. [DOI] [PubMed] [Google Scholar]