Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Nov 1.
Published in final edited form as: J Mol Model. 2013 Oct 2;19(11):5075–5087. doi: 10.1007/s00894-013-1990-x

Optimized CGenFF force-field parameters for acylphosphate and N-phosphonosulfonimidoyl functional groups

Lamees Hegazy §, Nigel G J Richards ‡,*
PMCID: PMC3904551  NIHMSID: NIHMS528961  PMID: 24085536

Abstract

We report an optimized set of CGenFF parameters that can be used to model small molecules containing acylphosphate and N-phosphonosulfonimidoyl functional groups in combination with the CHARMM force field. Standard CGenFF procedures were followed to obtain bonded interaction parameters, which were validated by geometry optimizations, comparison to the results of calculations at the MP2/6-31+G(d) level of theory, and molecular dynamics simulations. In addition, partial atomic charges were assigned so that the energy of hydrogen bonding of the model compounds with water was correctly reproduced. The availability of these parameters will facilitate computational studies of enzymes that generate acyladenylate intermediates during catalytic turnover. In addition, given that the N-phosphonosulfonimidoyl moiety is a stable transition state analog for the reaction of ammonia with an acyladenylate, the parameters developed in this study should find use in efforts to develop novel and potent inhibitors of various glutamine-dependent amidotransferases that have been validated as drug targets. Topology and parameter files for the model compounds used in this study, which can be combined with other CGenFF parameters in computational studies of more complicated acylphosphates and N-phosphonosulfonimidates are made available.

Keywords: CGenFF, Parameters, Acylphosphates, Sulfoximines, N-Phosphonosulfonimidates, Force Field, Drug Discovery

Introduction

A significant number of metabolic enzymes activate substrates for reaction by adenylation [1], including validated drug targets such as tRNA aminoacyl synthetases [2], glutamine-dependent NAD+ synthetase [3, 4] and aminoacyl-tRNA transamidating enzymes [5–7] (Fig. 1). In addition, recent studies have identified glutamine-dependent asparagine synthetase (ASNS) [8] (Fig. 1) as (i) a critical component in the development of prostate cancer [9], and (ii) a biomarker for ovarian cancer [10]. Although its precise physiological role remains hotly debated, ASNS has also been implicated in the molecular mechanisms underlying the onset of drug-resistant acute lymphoblastic leukemia [8, 11, 12]. ASNS inhibitors therefore have clinical potential for use in the treatment of leukemia and solid tumors, such as those of the prostate and ovary. Our group has reported that functionalized sulfoximines, such as 1 and 2 (Fig. 2), are the first small molecule inhibitors of human ASNS with nanomolar potency, and has established that these compounds can kill, or suppress, the proliferation of asparaginase-resistant MOLT-4 cells [13, 14]. Structure-based identification of sulfoximine derivatives that are more “druglike” [15, 16], and therefore possess improved cell permeability and bioactivity, using computational methods is precluded, however, by a lack of force field parameters that describe the N-phosphonosulfonimidoyl moiety. Similarly, efforts to obtain optimized structures of ASNS complexed to acyladenylates, such as 3, which are needed for virtual screening studies [17] are hampered by an absence of parameters for acylphosphates. We now report optimized parameters for both the acylphosphate and N-phosphonosulfonimidoyl functional groups, which have been obtained following the systematic procedures used to develop the CHARMM General Force Field (CGenFF) [18]. As a result, these parameters are compatible with the CHARMM all-atom additive force field used to simulate biological molecules [19, 20]. Our parameter values should also facilitate efforts to (i) obtain a detailed understanding of enzymes that catalyze acyladenylate formation and (ii) identify novel small molecules with potential clinical application as anti-cancer and antibacterial agents.

Fig. 1.

Fig. 1

Open in a new tab

Reactions catalyzed by enzymes that activate substrates by adenylylation and are validated drug targets.

Fig. 2.

Fig. 2

Open in a new tab

Structures of functionalized sulfoximines (1 and 2) that are nanomolar inhibitors of human asparagine synthetase (sulfoximine moiety is colored red). These compounds mimic the transition for the reaction of ammonia with the acyladenylate intermediate 3 (acylphosphate moiety highlighted in blue) that is formed during catalytic turnover. Compound 6 is an inhibitor of the enzyme γ-glutamylcysteine synthetase.

Computational Methods

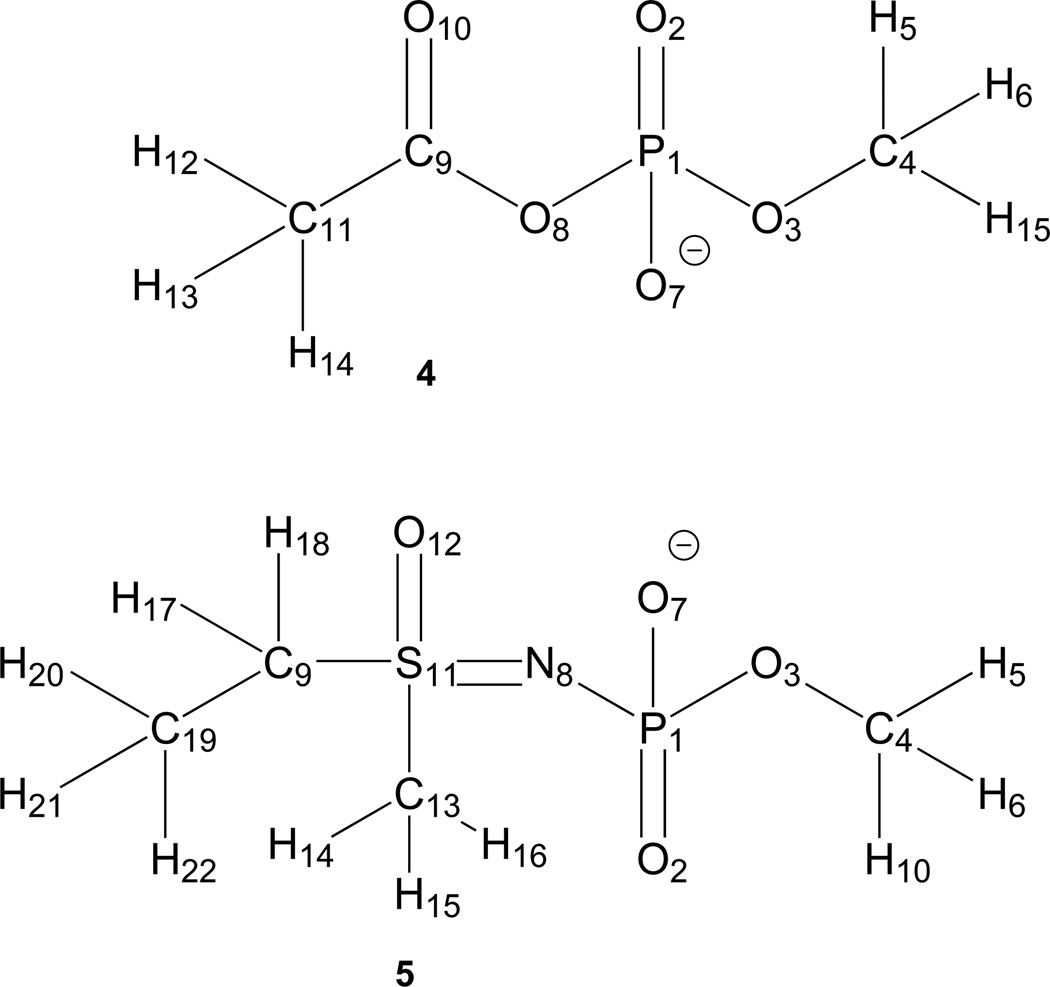
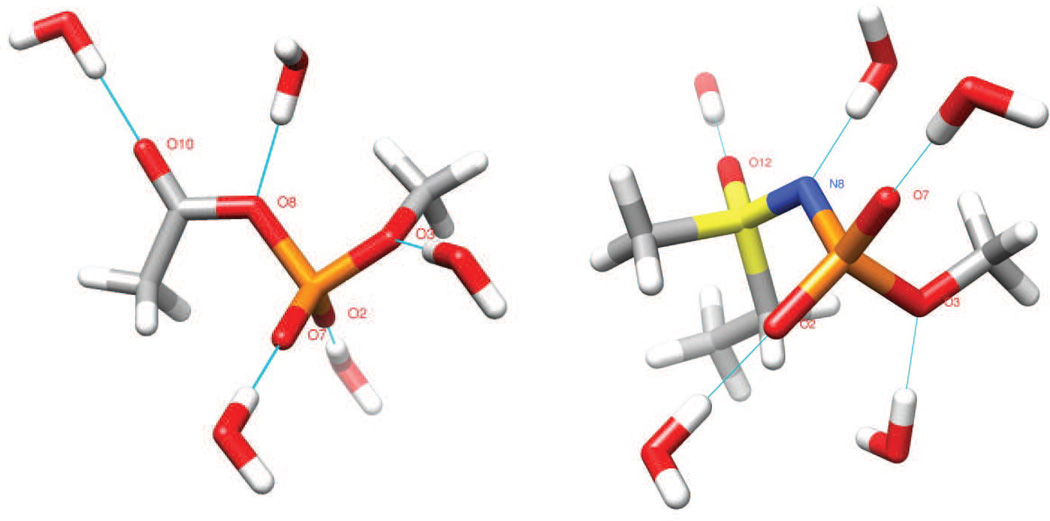
Calculations to obtain the missing parameters needed to describe the conformational and intermolecular energetics of functionalized acylphosphates and N-phosphorylated sulfoximines were performed on the model compounds 4 and 5 (Fig. 3). Initial guesses were obtained from the ParamChem web site (www.paramchem.org) using automated algorithms [21, 22]. The global energy minima for 4 and 5 were identified at the MP2/6-31+G(d) level of theory [23, 24], as implemented in Gaussian09 [25], by geometry optimization (default tolerances). Standard CGenFF Lennard-Jones parameters were used for all atoms, and an initial set of atomic partial charges was assigned by analogy to those of similar CGenFF atom types using ParamChem. Vibrational spectra were calculated for the optimized geometries of 4 and 5 to (i) ensure that these structures did represent energy minima, and (ii) obtain frequencies and their assignments to specific modes. The numerical values of all QM frequencies were scaled by 0.943 prior to comparison with those calculated using empirical potential energy functions [26]. As described elsewhere [18], water molecules in the TIP3P geometry [27] were placed around 4 and 5 so as to form hydrogen bonding interactions with all donor/acceptor groups (Fig. 4), and each model/water interaction distance was optimized at the HF/6-31G(d) level [28, 29] with the remaining degrees of freedom fixed. We note that both tetrahedral (“lone pair”) and trigonal hydrogen bonding interactions between water and oxygen atoms (R-O-R` and terminal oxygen atoms) were considered, and partial charges assigned in order to obtain the best agreement between the interaction energies for all orientations.

Fig. 3.

Fig. 3

Open in a new tab

Schematic representation of model compounds 4 and 5 showing atom numbering.

Fig. 4.

Fig. 4

Open in a new tab

Orientations of water molecules about the model compounds 4 (left) and 5 (right) used in atomic partial charge optimization. Note that only a single water molecule is hydrogen bonded to the model structure during each calculation; all waters are shown here merely for convenience. Atom coloring scheme: C, grey; H, white; N, blue; O, red; P, orange; S, yellow.

All empirical force field calculations were performed using the program CHARMM version 35 [30], which allowed us to define new atom types with names of up to six characters. An RMS gradient of 10−5 kcal/mol/Å was employed in energy minimizations and subsequent vibrational analyses were performed using the VIBRAN and MOLVIB modules in CHARMM. No non-bonded interaction distance cutoffs were used in these calculations.

A potential energy scan (PES) for each selected dihedral angle was calculated, in 15° increments, using the scan facility (keyword: “Opt = ModRedundant”) implemented within Gaussian09 [25], with structures being optimized at the MP2/6-31+G(d) level. Single point energies were subsequently determined for each structure at its optimized geometry using MP2/cc-pVTZ calculations. The corresponding PES calculated using the CHARMM empirical energy function employed the QM geometries as initial guesses, each structure being energy minimized with the dihedral angle of interest being restrained with a harmonic potential (force constant of 104 kcal/mol/rad). The harmonic restraints were not removed prior calculating conformational energies.

Each model compound 4 and 5 was solvated in octahedral box (28 Å × 28 Å × 28 Å) of TIP3P water molecules [27] and energy minimized by steepest descent (SD) and adopted basis Newton-Raphson (ABNR) algorithms [30]. Periodic boundaries were used in all MD simulations with the particle mesh Ewald method [31] being used to obtain electrostatic energies. Equations of motion were integrated over 1 fs time steps, with covalent bonds to hydrogen being constrained using the SHAKE algorithm [32]. After heating to 300 K (30 ps), each system was equilibrated for a further 40 ps in the NVT ensemble before the “production” MD simulation was performed in the NPT ensemble (2 ns). Constant temperature and pressure (1 atm) were achieved by coupling the systems to a Langevin thermostat and a Nosé–Hoover Langevin barostat, respectively [33, 34].

Missing loops in the X-ray crystal structure of γ-glutamylcysteine synthetase complexed with the N-phosphorylated sulfoximine 6 (Fig. 2) (1VA6) [35] were modeled using the CHIMERA interface to MODELLER [36, 37]. The resulting model complex was then solvated in octahedral box (87 Å × 87 Å × 87 Å) of TIP3P water molecules [27] and energy minimized by steepest descent (SD) and adopted basis Newton-Raphson (ABNR) algorithms so that the final structure possessed an RMS gradient of 10−5 kcal/mol/Å [30]. Periodic boundaries were used in this calculation with the particle mesh Ewald method [31] being used to obtain electrostatic energies.

Results and discussion

Parameterization

In order to ensure compatibility with the existing CHARMM force field for proteins and nucleic acids [19, 20], standard protocols [18] were used to generate missing parameters for bonds and bond angles in the model acylphosphate 4 and the N-phosphonosulfonimidoyl derivative 5 (Fig. 3). Thus, the lowest energy conformations for these two molecules were located by standard search procedures, and geometry optimization was carried out at the MP2/6-31+G(d) level given that both are mono-anions. Vibrational frequency analysis confirmed that these structures were true energy minima.

Water molecules were positioned about each of the lowest energy structures so as to make idealized hydrogen bonding interactions, and then atomic partial charges were optimized to give the best agreement between the non-covalent interaction energies and bond distances calculated using HF/6-31G(d) and CGenFF (Table 2). In this procedure, each molecule-water complex was built by optimizing the hydrogen bond distance between each model compound, at its MP2/6-31G(d) optimized geometry, and a TIP3P water while fixing all other degrees of freedom. Although a higher level of theory would have given more accurate results, QM calculations were performed with HF/6-31G(d) in order to be consistent with the methodology used to develop the CHARMM force field for biological molecules. The choice of optimized partial atomic charges was constrained by (i) requiring that the value on all hydrogen atoms was 0.09, (ii) maintaining the initial set of CGenFF charges on carbons C4 and in C11 in acylphosphate 4 and on carbons C4, C9 and C11 in N-phosphonosulfonimidoyl derivative 5, and (iii) the summation of all atomic charges to −1 (Table 1). After partial charge optimization, all CGenFF energies were within 0.2 kcal/mol of the corresponding HF/6-31G(d) value and the CGenFF distances were 0.2 Å shorter than those computed quantum mechanically (Table 2).

Table 2.

Interaction energies (kcal/mol) and distances (Å) of water complexed with acylphosphate 4 and N-phosphonosulfonimidoyl derivative 5 in different geometries (see Fig. 4)a

Interaction geometry ΔE (HF) ΔE (CGenFF) ΔΔE r (HF) r (CGenFF) ΔΔr
Acylphosphate 4
O2…HOH −11.4 −11.5 −0.1 1.89 1.70 −0.19
O7…HOH −11.8 −11.5 0.3 1.89 1.70 −0.19
O3…HOH −7.8 −7.8 0.0 2.03 1.77 −0.26
O8…HOH −7.7 −7.9 −0.2 2.18 1.91 −0.27
O10…HOH −8.3 −8.5 −0.2 1.96 1.76 −0.20
ADb −0.05 −0.22
RMSDb 0.21 0.05
AADb 0.18 0.22
Phosphonosulfonimidate 5
O2…HOH −13.0 −12.8 0.2 1.83 1.71 −0.12
O7…HOH −10.0 −11.3 −1.3 1.87 1.73 −0.14
O3…HOH(tet)c −10.0 −10.80 −0.8 1.95 1.76 −0.19
N8…HOH −10.0 −10.1 −0.1 2.07 1.99 −0.08
O12…HOH −7.8 −8.0 −0.2 1.98 1.77 −0.21
AD −0.44 −0.15
RMSD 0.53 0.04
AAD 0.52 0.15
Open in a new tab
a

Interaction energies were not scaled as both model compounds are anionic. All HF distances are also reported as their unscaled values; we note, however, that bulk hydrogen bonds are approximately 0.2 Å shorter than in vacuum.

b

AD, average deviation; RMSD, root mean square deviation; AAD, absolute average deviation.

c

The interaction between O3 and the water molecule was also modeled in a trigonel geometry (Figure 4): ΔE (HF) −9.9 kcal/mol, ΔE (CGenFF) −8.2 kcal/mol; r (HF) 2.02 Å, r (CGenFF) 1.81 Å. In general, the interaction energies and optimized distances between water molecules and oxygen atoms were modeled in a variety of geometries and all values used to develop the atomic partial charges. Only representative values are included here for clarity.

Table 1.

Optimized atomic partial charges for atoms in the model structures 4 and 5

Acylphosphate 4 N-Phosphonosulfonimidate 5
Atom Type Charge Atom Type Charge
P1 PG1 1.30 P1 PG1 0.20
O2 OG2P1 −0.71 O2 OG2P1 −0.46
O3 OG303 −0.46 O3 OG303 −0.28
C4 CG331 −0.17 C4 CG331 −0.17
H5 HGA3 0.09 H5 HGA3 0.09
H6 HGA3 0.09 H6 HGA3 0.09
O7 OG2P1 −0.71 O7 OG2P1 −0.46
O8 OG305 −0.38 N8 NG2D1 −0.38
C9 CG2O2 0.34 C9 CG321 0.02
O10 OG2D1 −0.48 H10 HGA3 0.09
C11 CG331 −0.27 S11 SG3O2 0.12
H12 HGA3 0.09 O12 OG2P1 −0.42
H13 HGA3 0.09 C13 CG331 0.11
H14 HGA3 0.09 H14 HGA3 0.09
H15 HGA3 0.09 H15 HGA3 0.09
H16 HGA3 0.09
H17 HGA2 0.09
H18 HGA2 0.09
C19 CG331 −0.27
H20 HGA3 0.09
H21 HGA3 0.09
H22 HGA3 0.09
Open in a new tab

Having established good parameters for calculating non-bonded interaction energies, we optimized the reference values for the bond lengths, bond and dihedral angles, and improper torsions. Force constants were adjusted so that the MOLVIB vibrational frequencies, together with contributions of different harmonic modes to each vibration, were in good agreement with MP2/6-31G(d) values that had been scaled by 0.943. Manual adjustment of the force constants then gave optimized CGenFF structures for 4 and 5 that were in excellent agreement with those calculated at the MP2/6-31+G(d) level of theory (Table 3), i.e. CGenFF-optimized structures had bond lengths and angles within 0.03 Å and 3° of the QM-derived values, respectively [18].

Table 3.

CGenFF- and MP2-Optimized Geometry of Model Compounds 4 and 5.

Coordinate MP2 CGenFF Difference Coordinate MP2 CGenFF Difference
Bond Lengths (Å) Angles (°)
Acylphosphate 4
P1-O8 1.75 1.75 0.00 O3-P1-O8 94 94 0
O8-O9 1.34 1.34 0.00 O2-P1-O8 106 108 2
O7-P1-O8 108 108 0
Dihedrals (°) O8-C9-O10 120 120 0
P1-O8-C9-C11 2 2 0
P1-O8-C9-O10 −178 −178 0
O2-P1-O8-C9 68 66 −2
O7-P1-O8-C9 −68 −68 0
O3-P1-O8-C9 179 177 −2
O8-P1-O3-C4 −69 −71 −2
Improper Torsions (°)
C9-C11-O10-O8 −0.1 0.0 0.1
Bond Lengths (Å) Angles (°)
Phosphonosulfonimidate 5
P1-N8 1.75 1.75 0.00 O3-P1-N8 100 100 0
N8-S11 1.53 1.53 0.00 O2-P1-N8 109 111 2
O7-P1-N8 108 107 −1
C9-S11-N8 112 112 0
P1-N8-S11 120 120 0
N8-S11-C13 111 111 0
N8-S11-O12 116 116 0
Dihedrals (°)
N8-S11-C9-C19 −176 −169 7
O2-P1-N8-S11 −24 −23 1
O7-P1-N8-S11 −161 −155 6
O3-P1-N8-S11 85 90 5
P1-N8-S11-C9 −49 −48 0
P1-N8-S11-O12 −171 −171 0
P1-N8-S11-C9 −49 −48 1
P1-N8-S11-C13 67 67 0
N8-P1-O3-C4 71 74 3
Open in a new tab

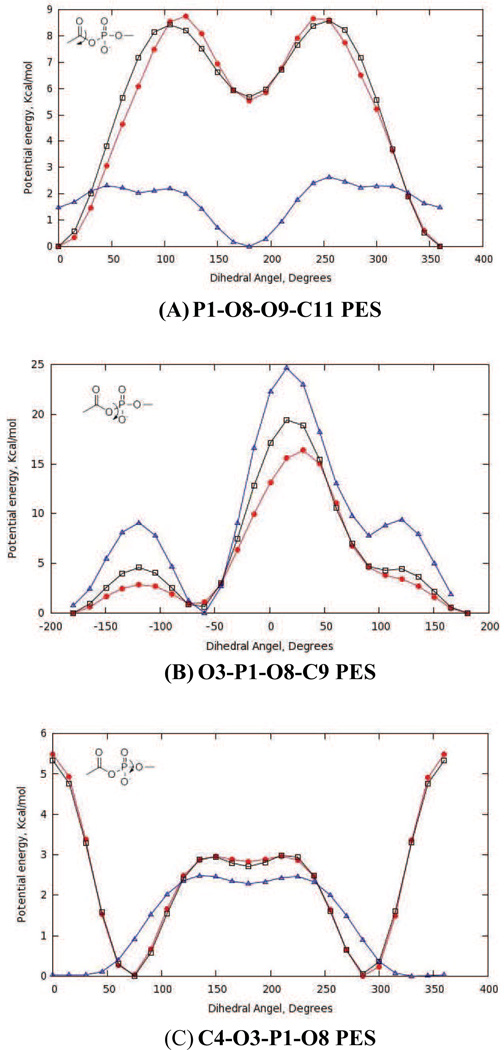
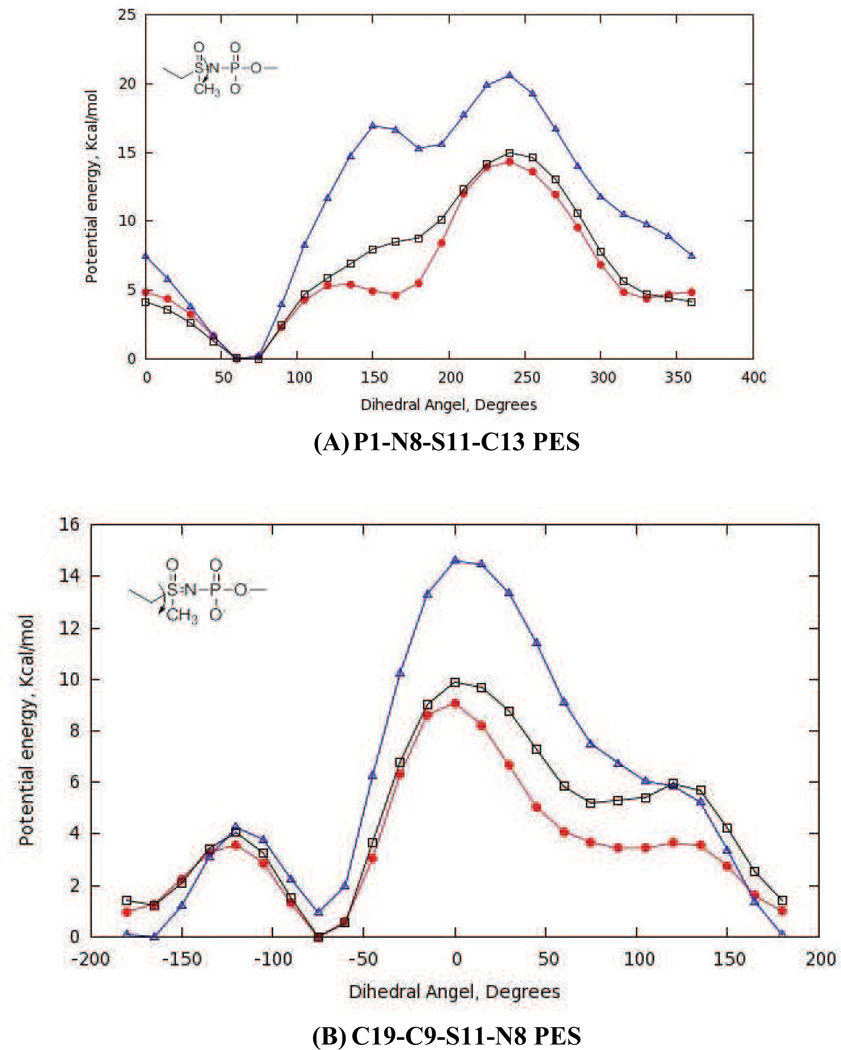
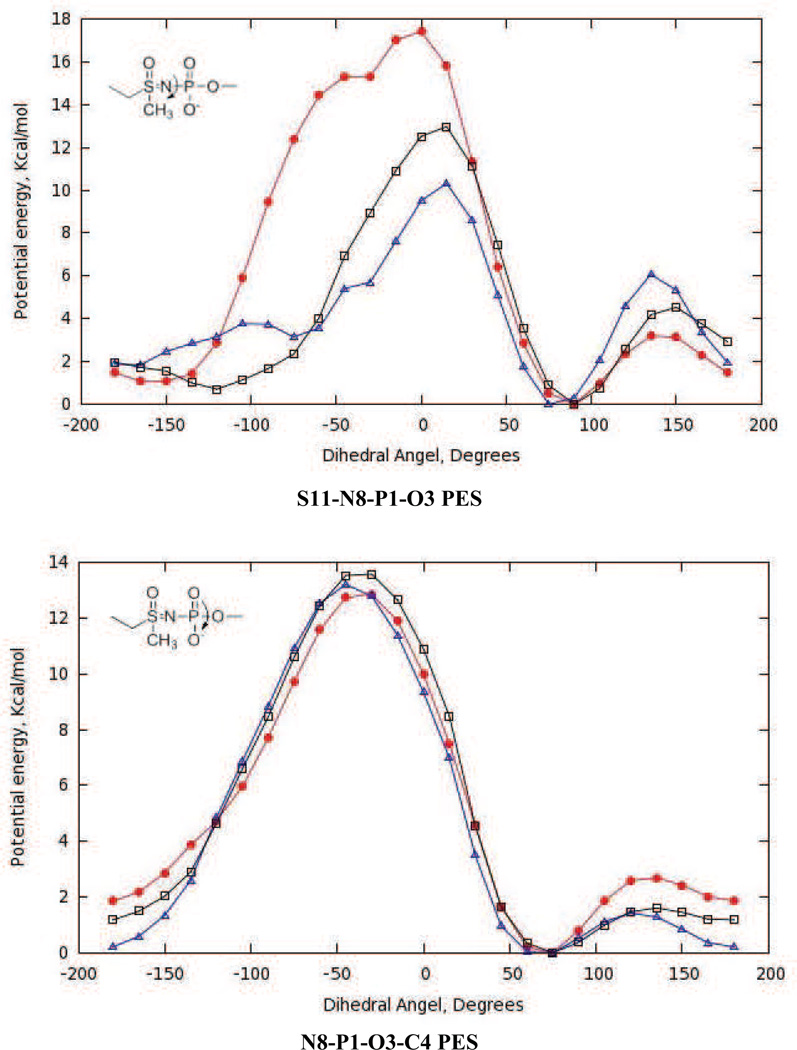
With optimized partial atomic charges and parameters for bonds and bond angles in hand, we adjusted the amplitudes, multiplicities and phases for the new dihedral angle interactions (Table 4 and Table S1 in supporting information). Thus, amplitudes for missing dihedrals composed only of non-hydrogen atoms were chosen so as to reproduce the adiabatic potential energy scans (PES) computed by ab initio methods (Fig. 5 and Fig. 6). Although the C4-O3-P1-O8 dihedral for the acylphosphate moiety was not a missing parameter in the CHARMM force-field, efforts to obtain good agreement between the QM and MM potential energy curves for our model compound 4 proved to be difficult. We therefore assigned a new atom type to O8 (Fig. 3), which enabled the development of optimized dihedral potentials for acylphosphate 4 while retaining the original parameterization of the C4-O3-P1-O8 dihedral interaction for modeling nucleic acids. The Lennard-Jones parameters for the OG305 atom type were identical to those of the OG303 atom type. On the other hand, for the O3-P1-O8-C9 dihedral angle (e.g. Fig. 5B) it proved impossible to identify parameters that completely reproduced the complete QM PES including minima and barriers heights. In this case, we therefore sought to maximize agreement between the QM and MM potential energy curves for the low energy regions rather than all the barrier heights.

Table 4.

Vibrational spectra computed for acylphosphate 4 at the scaled MP2 level and with CGenFFa

MP2/6-31G(d) scaled by a factor 0.943 CGenFF
Freqb Assign (%) Assign (%) Assign (%) Freqb Assign (%) Assign (%) Assign (%)
67.0 tdOPOC (98) 68.2 tdCCOP (65) tdOPOC(29)
81.8 tdCCOP (73) tdCOPO (23) 79.8 tdCOPO (47) tdOPOC (36) scPO4' (7)
100.5 tdCOPO (55) tdCCOP (33) scPO4' (9) 106.5 tdOPOC (33) tdCOPO (32) tdCCOP (23)
140.2 tdPOCH (69) dPOC9 (14) scPO4' (11) 141.2 tdPOCH (57) scPO4' (31) dPOC9 (8)
180.2 dPOC9 (53) tdPOCH (24) tdCOPO (12) 207.9 tdPOCH (29) dPOC9 (18) rPO4 (16)
194.3 tdPOCH (89) 239.4 dPOC4 (33) dPOC9 (19) rPO4 (14)
219.0 dPOC4 (41) twPO4 (18) scPO4' (8) 268.0 tdPOCH (90)
295.4 scPO4' (38) twPO4 (20) dCCO (12) 289.4 dPOC4 (31) scPO4' (19) twPO4 (9)
329.7 twPO4 (36) dPOC4 (19) saOP (12) 323.4 dCCO (28) twPO4 (24) dPOC9 (21)
343.8 dCCO (19) ssOP (17) saOP (16) 334.8 twPO4 (38) wPO4 (28) dCCO (9)
414.2 scPO4 (42) wPO4 (20) rPO4 (11) 417.2 ssOP (30) scPO4 (24) rPO4 (20)
460.0 wPO4 (32) dCCO (24) rC=O (15) 471.9 wPO4 (36) dPOC4 (19) twPO4 (14)
505.7 scPO4 (21) wPO4 (16) dPOC4 (15) 499.9 scPO4 (44) dCCO (27) dPOC9 (6)
515.2 rPO4 (54) scPO4 (13) ssOP (10) 537.0 rC=O (39) saOP (12) scPO4 (11)
564.4 tiOCOC (79) rCH3-C11 (14) 564.3 tiOCOC (90)
685.5 sCC (34) rC=O (25) saOP (16) 671.9 saOP (47) ssOP (11) rPO4 (9)
723.7 saOP (38) ssOP (32) sO3C (9) 679.6 ssCC (34) ssOP (18) rC=O (11)
906.9 sCC (33) sO8C (26) rC=O (11) 952.4 sO8C (34) ssPO (16) r'CH3C11 (11)
993.8 r'CH3C11 (38) ssPO (18) rCH3C11 (13) 996.4 r'CH3C11 (35) ssPO (34) rCH3C11 (10)
1035.2 sO3C (59) ssPO (25) r'CH3C11 (10) 1023.3 sO3C (23) ssPO (18) r'CH3C11 (13)
1043.3 rCH3C11 (53) r'CH3C11 (20) tiOCOC (20) 1040.1 sO3C (54) ssPO (16) ssOP (8)
1048.6 ssPO (46) sO3C (27) ssOP (9) 1046.7 rCH3C11 (64) r'CH3C11 (19) ad'CH3C11(10)
1135.9 rCH3C4 (72) r'CH3C4 (25) 1139.0 rCH3C4 (40) r'CH3C4 (37) ad'CH3C4 (19)
1157.5 r'CH3C4 (66) rCH3C4 (24) 1144.8 r'CH3C4 (39) rCH3C4 (34) adCH3C4 (24)
1243.9 saPO (93) 1187.6 saPO (92) wPO4 (6)
1258.8 sO8C(45) sCC (13) rC=O (12) 1232.3 sO8C (33) sCC (30) rC=O (23)
1373.0 sdCH3C11 (86) sCC (8) sO8C (5) 1387.2 sdCH3C11 (98)
1421.8 sdCH3C4 (99) 1429.7 ad'CH3C4 (58) adCH3C4 (23) r'CH3C4 (15)
1447.1 ad'CH3C4 (92) rCH3C11 (6) 1434.3 adCH3C11 (91)
1460.0 adCH3C11 (91) 1451.9 ad'CH3C11(88) rCH3C11 (8)
1465.0 ad'CH3C4 (92) ad'CH3C4 (34) 1469.4 adCH3C4 (52) ad'CH3C4 (21) rCH3C4 (21)
1488.9 adCH3C4 (59) adCH3C4 (36) 1615.8 sdCH3C4 (88) sO3C (11)
1673.5 sC=O (84) 1741.2 sC=O (88) sCC (5)
2914.5 ssCH3C4 (100) 2854.1 ssCH3C4 (100)
2936.5 ssCH3C11(100) 2913.1 saCH3'C4 (71) saCH3C4 (29)
3001.6 saCH3C4 (99) 2915.8 ssCH3C11(100)
3012.5 saCH3C4 (99) 2917.3 saCH3C4 (71) saCH3'C4 (29)
3023.1 saCH3C11 (76) ssCH3C11 (24) 2973.4 ssCH3'C11 (75) saCH3C11 (25)
3041.8 ssCH3C11 (76) saCH3C11 (24) 2975.9 saCH3C11 (75) ssCH3'C11 (25)
Open in a new tab
a

Optimized vibrational contributions from interactions for which parameters have been developed in this study are shown in bold font. s stands for bond stretching with the variations ss and sa for symmetric and asymmetric stretching, respectively. d means angle deformation with the variations sd and ad for symmetric and asymmetric deformation, respectively. td and ti stand for torsional and improper torsion deformation, respectively. sc stands for scissoring, r for rocking, w for wagging and tw for twisting.

b

Frequencies are expressed in units of cm−1.

Fig. 5.

Fig. 5

Open in a new tab

Potential energy scans (PES) for optimized dihedral angle parameters in model acylphosphate 4. QM PES (red), optimized (black) and initial (blue) MM PES. Interaction labels correspond to the atom numbers in Fig. 3.

Fig. 6.

Fig. 6

Fig. 6

Open in a new tab

Potential energy scans (PES) for optimized dihedral angle parameters in model sulfoximine 5. QM PES (red), optimized (black) and initial (blue) MM PES. Interaction labels correspond to the atom numbers in Fig. 3.

Parameter validation studies using energy minimization

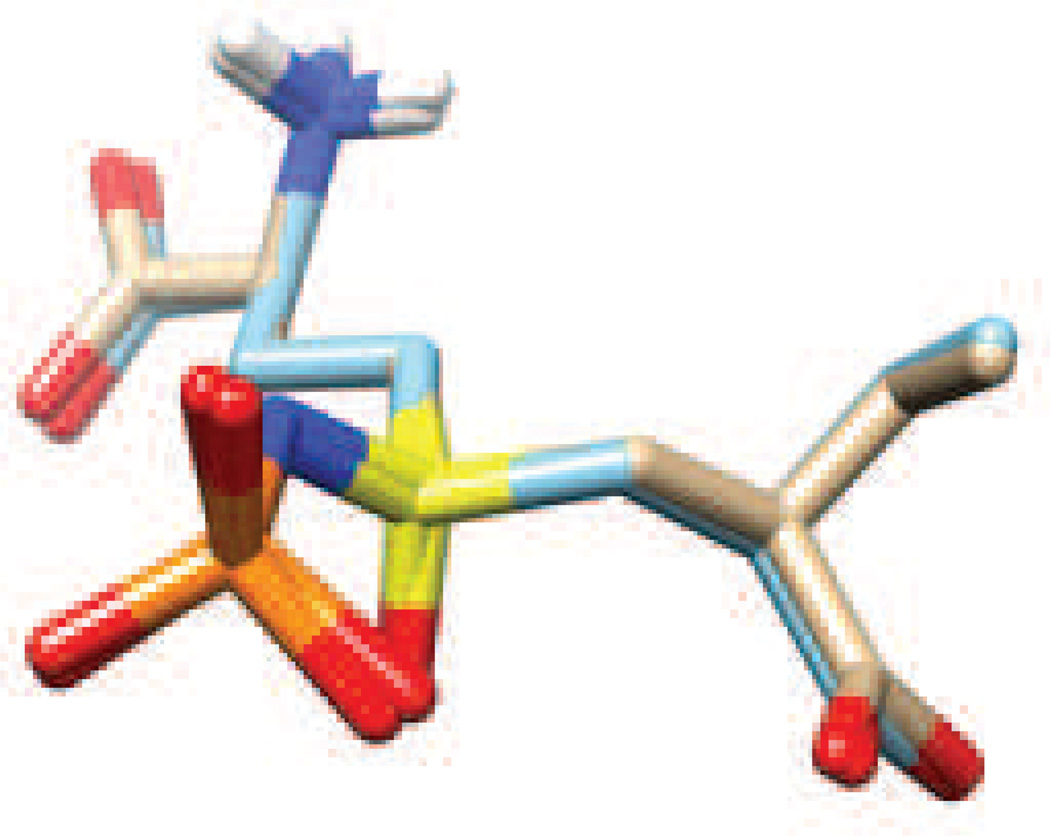
Our initial effort at parameter validation examined whether the extent to which those for the N-phosphonosulfonimidoyl functional group could reproduce data from X-ray crystal structures. Given the absence of small molecule structures for adenylylated sulfoximines in the Cambridge Structural Database [38] we chose to evaluate the performance of our parameters in modeling the sulfoximine phosphate 6 (Fig. 2) that is bound to the enzyme γ-glutamylcysteine synthetase [35]. After the insertion of missing loops in the X-ray crystal structure (1VA6) using the CHIMERA interface to MODELLER [36, 37], the resulting structure was energy minimized in an octahedral box of TIP3P water molecules [27]. Superimposition of the energy minimized structure of 6 with that in the original X-ray crystal structure showed good agreement between the optimized and experimental bond lengths and bond angles (Fig. 7).

Fig. 7.

Fig. 7

Open in a new tab

Superimposition (RMSD 0.2Å) of the N-phosphorylsulfoximine derivative 6 before (C, brown) and after (C, light blue) energy minimization of the complex of 6 bound to the enzyme γ-glutamylcysteine synthetase. Atom coloring scheme: H, white; N, blue; O, red; S, yellow; P, orange.

Parameter validation studies using molecular dynamics simulations

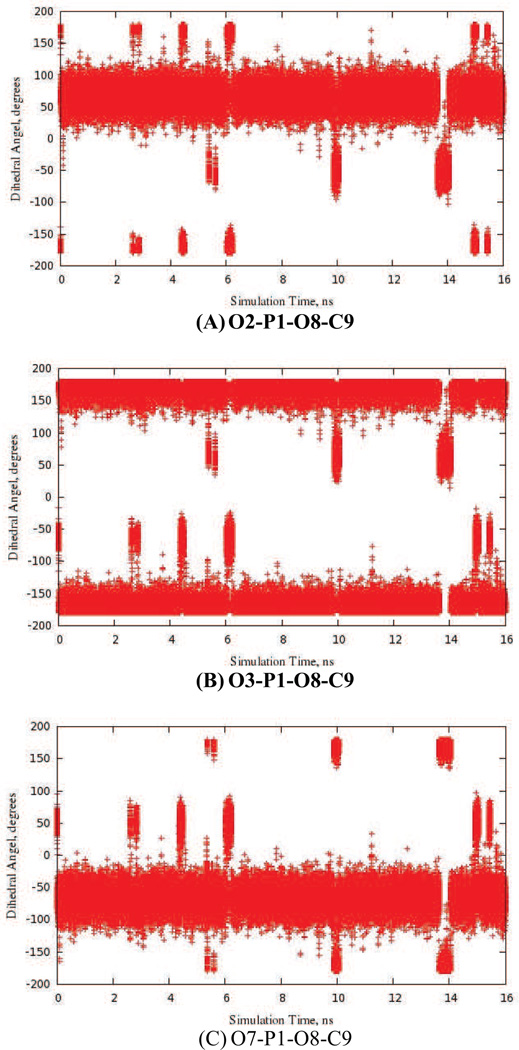
As a further validation of the new CGenFF parameters obtained using model compounds 4 and 5, we performed molecular dynamics (MD) simulations of these two small molecules in aqueous solution. Over a period of 16 ns, rotation of the phosphate group was observed (Fig 8 and Fig S1 in supporting information), and no major bond length or bond angle distortions occurred during the simulation. In addition, the torsion angles for which new parameters had been developed (Tables 5 and 6) fluctuated about values corresponding to minima on the potential energy surface (Figs 5 and 6). This data therefore suggests that these CGenFF parameters will be suitable for use in the simulated annealing [39], in silico docking [40] and free energy perturbation calculations [41] that will be undertaken as part of future drug discovery efforts.

Fig. 8.

Fig. 8

Open in a new tab

MD trajectory data (16 ns) showing that the phosphate moiety in the model acylphosphate 4 undergoes rotation during the simulation. Dihedral angles are labeled with the atom numbers shown in Fig. 3.

Table 5.

New bonded interaction parameters assigned for the acylphosphate moiety in 4

Bonds Atom Types Reqa KR
P1-O8 PG1-OG305 1.78 170
C9-O10 CG2O2-OG305 1.34 230
Bond Angles Atom Types Θeqb KΘ RUB KUB
P1-O8-C9 PG1-OG305- CG2O2 121.5 70
O2-P1-O8 OG2P1-PG1-OG305 103.0 60
O3-P1-O8 OG303-PG1-OG305 90.8 60
O7-P1-O8 OG2P1-PG1-OG305 103.0 60
O8-C9-O10 OG305- CG2O2- OG2D1 118.0 70 2.26 160
O10-C9-C11 OG305- CG2O2- CG331 104.0 30 2.33 5
Dihedral Angles Atom Types Kφc n δ
P1-O8-C9-O10 PG1-OG305-CG2O2-OG2D1 1.30 1 180
P1-O8-C9-O10 PG1-OG305-CG2O2-OG2D1 2.60 2 180
P1-O8-C9-C11 PG1-OG305-CG2O2-CG331 3.80 1 180
P1-O8-C9-C11 PG1-OG305-CG2O2-CG331 1.60 2 180
O2-P1-O8-C9 OG2P1-PG1-OG305-CG2O2 0.10 3 0
O3-P1-O8-C9 OG303-PG1-OG305-CG2O2 0.10 2 180
O3-P1-O8-C9 OG303-PG1-OG305-CG2O2 0.10 3 0
C4-O3-P1-O8 CG331-OG303-PG1-OG305 1.47 2 0
C4-O3-P1-O8 CG331-OG303-PG1-OG305 0.70 3 0
Improper Torsion Atom Types Kφd Φo
O8-O10-C11-C9 OG305-OG2D1-CG331-CG2O2 56 0
Open in a new tab
a

Req, reference bond distance (Å) and KR, force constant (kcal/mol/Å2).

b

Θeq, reference bond angle (°) and KΘ, force constant (kcal/mol/rad2).

c

Kφ, torsional potential (kcal/mol), n and δ, periodicity and phase offset (°) of the torsion, respectively.

d

Kφ, improper dihedral potential (kcal/mol/rad2) and Φo, reference improper dihedral angle (°).

Table 6.

New bonded interaction parameters assigned for the N-phosphonosulfonimidoyl functional group in 5

Bonds Atom Types Reqa KR
P1-N8 PG1-NG2D1 1.72 100
N8-S11 NG2D1-SG3O2 1.53 400
Bond Angles Atom Types Θeqb KΘ
P1-N8-S11 PG1-NG2D1-SG3O2 113.0 30
O2-P1-N8 OG2P1-PG1-NG2D1 106.0 50
O3-P1-N8 NG2D1-PG1-OG303 98.8 94
O7-P1-N8 OG2P1-PG1-NG2D1 106.0 50
N8-S11-C9 NG2D1-SG3O2- CG321 114.3 65
N8-S11-O12 NG2D1-SG3O2- OG2P1 119.0 65
N8-S11-C13 NG2D1-SG3O2- CG321 114.0 79
Dihedral Angles Atom Types Kφc n δ
P1-N8-S11-O2 PG1-NG2D1-SG3O2-OG2P1 2.50 1 180
P1-N8-S11-O2 PG1-NG2D1-SG3O2-OG2P1 1.00 2 0
P1-N8-S11-C9 PG1-NG2D1-SG3O2-CG321 1.00 2 0
P1-N8-S11-C13 PG1-NG2D1-SG3O2-CG331 1.00 1 0
P1-N8-S11-C13 PG1-NG2D1-SG3O2-CG331 0.60 2 0
O2-P1-N8-S11 OG2P1-PG1-NG2D1-SG3O2 0.50 4 0
O3-P1-N8-S11 OG303-PG1-NG2D1-SG3O2 1.80 1 0
O3-P1-N8-S11 OG303-PG1-NG2D1-SG3O2 3.00 2 0
N8-P1-O3-C4 NG2D1-PG1-OG303-CG331 0.40 1 0
N8-P1-O3-C4 NG2D1-PG1-OG303-CG331 0.80 2 0
N8-P1-O3-C4 NG2D1-PG1-OG303-CG331 0.35 3 0
N8-S11-C9-C19 NG2D1-SG3O2-CG321-CG331 1.40 1 180
N8-S11-C9-C19 NG2D1-SG3O2-CG321-CG331 0.001 3 0
N8-S11-C9-H17 NG2D1-SG3O2-CG321-HGA2 0.16 3 0
N8-S11-C13-H14 NG2D1- SG3O2-CG331-HGA3 0.18 3 0
Open in a new tab
a

Req, reference bond distance (Å) and KR, force constant (kcal/mol/Å2).

b

Θeq, reference bond angle (°) and KΘ, force constant (kcal/mol/rad2).

a

Kφ, torsional potential (kcal/mol/rad2), n and δ, periodicity and phase offset (°) of the torsion, respectively.

Summary

We have developed the first optimized set of CGenFF parameters for acylphosphates and N-phosphonosulfonimidates. Although we employed the recommended protocol for obtaining small molecule parameters that are consistent with the CHARMM force field, these values should also represent a useful starting point for the development of alternate sets of optimized parameters for acylphosphate and N-phosphonosulfonimidoyl functional groups for use with the AMBER [42] or GROMOS [43] force fields. More importantly, our results should be generally useful to medicinal chemists seeking to discover potent inhibitors of a variety of enzymes, including glutamine synthetase [44], HIV-1 protease [45], γ-glutamylcysteine synthetase [35,46], and Leishmania typanothione synthetase-amidase [47]. In the case of human ASNS, access to these parameters will also facilitate our efforts to use free energy perturbation methods to (i) delineate which diastereoisomer of 1 and 2 binds most tightly to the enzyme [13, 14], and (ii) examine the ability of novel sulfoximine derivatives to act as potent ASNS inhibitors. These calculations will be reported in due course.

Supplementary Material

894_2013_1990_MOESM1_ESM

Acknowledgements

The authors wish to thank Alex D. MacKerell, Jr., and Kenno Vanommeslaeghe (Maryland) for helpful discussions. Computational resources for this work were provided by the University of Florida High Performance Computing Center. Funding for this work was obtained from the National Institutes of Health (DK061666) and Indiana University Purdue University Indianapolis.

Footnotes

Supplementary material available

The calculated QM and MM vibrational spectra together with simulation trajectory data for the N-phosphonosulfonimidoyl derivative 5, and full topology and parameter information for the model compounds (4 and 5) employed in this study, is provided as Supplementary Material.

References

  • 1.Frey PA, Hegeman AD. Enzymatic reaction mechanisms. Oxford: Oxford University Press; 2007. [Google Scholar]
  • 2.Agarwal V, Nair SK. Aminoacyl tRNA synthetases as targets for antibacterial development. Med Chem Commun. 2012;3:887–898. [Google Scholar]
  • 3.LaRonde-LeBlanc N, Resto M, Gerratana B. Regulation of active site coupling in glutamine-dependent NAD+ synthetase. Nat Struct Mol Biol. 2009;16:421–429. doi: 10.1038/nsmb.1567. [DOI] [PubMed] [Google Scholar]
  • 4.Duckworth BP, Nelson KM, Aldrich CC. Curr Topics Med Chem. 2012;12:766–796. doi: 10.2174/156802612799984571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Curnow AW, Hong KW, Yuan R, Kim SI, Martins O, Winkler W, Henkin TM, Soll D. GlutRNA(Gln) amidotransferase: A novel heterotrimeric enzyme required for correct decoding of glutamine codons during translation. Proc Natl Acad Sci, USA. 1997;94:11819–11826. doi: 10.1073/pnas.94.22.11819. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Horiuchi KY, Harpel MR, Shen L, Luo Y, Rogers KC, Copeland RA. Mechanistic studies of reaction coupling in Glu-tRNA(Gln) amidotransferase. Biochemistry. 2001;40:6450–6457. doi: 10.1021/bi002599l. [DOI] [PubMed] [Google Scholar]
  • 7.Oshikane H, Sheppard K, Fukai S, Nakamura Y, Ishitani R, Numata T, Sherrer RI, Feng L, Schmitt E, Panvert M, Blanquet S, Mchulam Y, Soll D, Nureki O. Structural recruitment of glutamine to the genetic code. Science. 2006;312:1950–1954. doi: 10.1126/science.1128470. [DOI] [PubMed] [Google Scholar]
  • 8.Richards NGJ, Kilberg MS. Asparagine synthetase chemotherapy. Annu Rev Biochem. 2006;75:629–654. doi: 10.1146/annurev.biochem.75.103004.142520. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Sircar K, Huang H, Hu LM, Cogdell D, Dhillon J, Tzelepi V, Efstathiou E, Koumakpayi IH, Saad F, Luo DJ, Bismar TA, Aparicio A, Troncoso P, Navone N, Zhang W. Integrative molecular profiling reveals asparagine synthetase is a target in castration-resistant prostate cancer. Am J Pathol. 2012;180:893–903. doi: 10.1016/j.ajpath.2011.11.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Lorenzi PL, Llamas J, Gunsior M, Ozbun L, Reinhold WC, Varma S, Ji H, Kim H, Hutchinson AA, Kohn EC, Goldsmith PK, Birrer MJ, Weinstein JN. Asparagine synthetase is a predictive biomarker of L-asparaginase activity in ovarian cancer cell lines. Mol Cancer Therapeut. 2008;7:3123–3128. doi: 10.1158/1535-7163.MCT-08-0589. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Aslanian AM, Kilberg MS. Asparagine synthetase expression is sufficient to induce L-asparaginase resistance in MOLT-4 leukemia cells. Biochem J. 2001;357:321–328. doi: 10.1042/0264-6021:3570321. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Tong WH, Pieters R, Hop WCJ, Lanvers-Kaminsky C, Boos J, van der Sluis IM. No evidence of increased asparagine levels in the bone marrow of patients with acute lymphoblastic leukemia during asparaginase therapy. Ped Blood Canc. 2013;60:258–261. doi: 10.1002/pbc.24292. [DOI] [PubMed] [Google Scholar]
  • 13.Ikeuchi H, Ahn Y-M, Otokawa T, Watanabe B, Hegazy L, Hiratake J, Richards NGJ. A sulfoximine-based inhibitor of human asparagine synthetase kills L-asparaginase-resistant leukemia cells. Bioorg Med Chem. 2012;20:5915–5927. doi: 10.1016/j.bmc.2012.07.047. [DOI] [PubMed] [Google Scholar]
  • 14.Gutierrez JA, Pan Y-X, Koroniak L, Hiratake J, Kilberg MS, Richards NGJ. An inhibitor of human asparagine synthetase suppresses proliferation of an L-asparaginase-resistant leukemia cell line. Chem Biol. 2006;13:1339–1347. doi: 10.1016/j.chembiol.2006.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Hann MM, Keserü GM. Finding the sweet spot: the role of nature and nuture in medicinal chemistry. Nat Rev Drug Disc. 2012;11:355–365. doi: 10.1038/nrd3701. [DOI] [PubMed] [Google Scholar]
  • 16.Walters WP, Green J, Weiss JR, Murcko MA. What do medicinal chemists actually make? A 50-year retrospective. J Med Chem. 2011;54:6405–6416. doi: 10.1021/jm200504p. [DOI] [PubMed] [Google Scholar]
  • 17.Morris GM, Huey R, Lindstrom W, Sanner MF, Belew RK, Goodsell DS, Olson AJ. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J Comput Chem. 2009;30:2785–2791. doi: 10.1002/jcc.21256. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Vanommeslaeghe K, Hatcher E, Acharya C, Kundu S, Zhong S, Shim J, Darian E, Guvench O, Lopes P, Vorobyov I, MacKerell AD., Jr CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J Comput Chem. 2010;31:671–690. doi: 10.1002/jcc.21367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.MacKerell AD, Bashford D, Bellott M, et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
  • 20.Foloppe N, MacKerell AD. All-atom empirical force field for nucleic acids: I Parameter optimization based on small molecule and condensed phase macromolecular target data. J Comput Chem. 2000;21:86–104. [Google Scholar]
  • 21.Vanommeslaeghe K, MacKerell AD., Jr Automation of the CHARMM general force field (CGenFF) I: Bond perception and atom typing. J Chem Inf Mol Model. 2012;52:3144–3154. doi: 10.1021/ci300363c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Vanommeslaeghe K, MacKerell AD., Jr Assignment of bonded parameters and partial atomic charges. J Chem Inf Mol Model. 2012;52:3155–3168. doi: 10.1021/ci3003649. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Francl MM, Pietro WJ, Hehre WJ, Binkley JS, Gordon MS, DeFrees DJ, Pople JA. Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second row elements. J Chem Phys. 1982;77:3654–3665. [Google Scholar]
  • 24.Head-Gordon M, Pople JA, Frisch MJ. MP2 energy evaluation by direct methods. Chem Phys Lett. 1988;153:503–506. [Google Scholar]
  • 25.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA, Jr, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas Ö, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ. Gaussian 09. Wallingford: Gaussian Inc.; 2009. [Google Scholar]
  • 26.Scott AP, Radom L. Harmonic vibrational frequencies: An evaluation of Hartree-Fock, Möller-Plesset, quadratic configuration interaction, density functional theory, and semi-empirical scale factors. J Phys Chem. 1996;100:16502–16513. [Google Scholar]
  • 27.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79:926–935. [Google Scholar]
  • 28.Ditchfield R, Hehre WJ, Pople JA. Self-consistent molecular orbital methods. 9. Extended Gaussian-type basis for molecular orbital studies of organic molecules. J Chem Phys. 1971;54:724–728. [Google Scholar]
  • 29.Frisch MJ, Pople JA, Binkley JS. Self-consistent molecular orbital methods. 25. Supplementary functions for Gaussian basis sets. J Chem Phys. 1984;80:3265–3269. [Google Scholar]
  • 30.Brooks BR, Brooks CL, III, MacKerell AD, Jr, Nilsson L, Petella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, Caflisch A, Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kuczera K, Lazaridis T, Ma J, Ovchinnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu X, Yang W, York DM, Karplus J. CHARMM: The biomolecular simulation program. J Comput Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Darden T, York D, Pedersen L. Particle mesh Ewald: An Nlog(N) method for Ewald sums in large systems. J Chem Phys. 1993;98:10089–10092. [Google Scholar]
  • 32.Ryckaert JP, Ciccotti G, Berendsen HJC. Numerical integration of Cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J Comput Phys. 1977;23:327–341. [Google Scholar]
  • 33.Tobias DJ, Martyna GJ, Klein ML. Molecular dynamics simulations of a protein in the canonical ensemble. J Phys Chem. 1993;97:12959–12966. [Google Scholar]
  • 34.Feller SE, Zhang Y, Pastor RW, Brooks BR. Constant pressure molecular dynamics simulation. The Langevin piston method. J Chem Phys. 1995;103:4613–4621. [Google Scholar]
  • 35.Hibi T, Nii H, Nakatsu T, Kimura A, Kato H, Hiratake J, Oda J. Crystal structure of γ-glutamylcysteine synthetase: Insights into the mechanism of catalysis by a key enzyme for glutathione homeostasis. Proc Natl Acad Sci USA. 2004;101:15052–15057. doi: 10.1073/pnas.0403277101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera – a visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
  • 37.Marti-Renom MA, Stuart A, Fiser A, Sánchez R, Melo F, Sali A. Comparative protein structure modeling of genes and genomes. Annu Rev Biophys Biomol Struct. 2000;29:291–325. doi: 10.1146/annurev.biophys.29.1.291. [DOI] [PubMed] [Google Scholar]
  • 38.Allen FH. The Cambridge Structural Database: a quarter of a million structures and rising. Acta Crystallogr. B. 2002;58:380–388. doi: 10.1107/s0108768102003890. [DOI] [PubMed] [Google Scholar]
  • 39.Kirkpatrick S, Gelatt CD, Jr, Vecchi MP. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
  • 40.Schneider G. Virtual screening: an endless staircase? Nat Rev Drug Discov. 2010;9:273–276. doi: 10.1038/nrd3139. [DOI] [PubMed] [Google Scholar]
  • 41.Gallicchio E, Levy RM. Recent theoretical and computational advances for modeling protein-ligand binding affinities. Adv Prot Chem Struct Biol. 2011;85:27–80. doi: 10.1016/B978-0-12-386485-7.00002-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Wang JM, Wolf RM, Caldwell JW, Kollman PA, Case DA. Development and testing of a general amber force field. J Comput Chem. 2004;25:1157–1174. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
  • 43.Christen M, Hunenberger PH, Bakowies D, baron R, Burgi R, Geerke DP, Heinz TN, kastenholz MA, Krautler V, Oostenbrink C, Peter C, Trzesniak D, van Gunsteren WF. The GROMOS software for biomolecular simulation: GROMOS05. J Comput Chem. 2005;26:1719–1751. doi: 10.1002/jcc.20303. [DOI] [PubMed] [Google Scholar]
  • 44.Nilsson MT, Krajewski WW, Yellagunda S, Prabhumurthy S, Chamarahally GN, Siddamadappa C, Srinivasa BR, Yahiaoui S, Larhed M, Karleén A, Jones TA, Mowbray SL. Structural basis for the inhibition of Mycobacterium tuberculosis glutamine synthetase by novel ATP-competitive inhibitors. J Mol Biol. 2009;393:504–513. doi: 10.1016/j.jmb.2009.08.028. [DOI] [PubMed] [Google Scholar]
  • 45.Lu D, Vince R. Discovery of potent HIV-1 protease inhibitors incorporating sulfoximine functionality. Bioorg Med Chem Lett. 2007;17:5614–5619. doi: 10.1016/j.bmcl.2007.07.095. [DOI] [PubMed] [Google Scholar]
  • 46.Hiratake J, Irie T, Tokutake N, Oda J. Recognition of a cysteine substrate by E. coli γ-glutamylcysteine synthetase probed by sulfoximine-based transition-state analogue inhibitors. Biosci Biotechnol Biochem. 2002;66:1500–1514. doi: 10.1271/bbb.66.1500. [DOI] [PubMed] [Google Scholar]
  • 47.Fyfe PK, Oza SL, Fairlamb AH, Hunter WN. Leishmania trypanothione synthetase-amidase structure reveals a basis for regulation of conflicting synthetic and hydrolytic activities. J Biol Chem. 2008;283:17672–17680. doi: 10.1074/jbc.M801850200. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

894_2013_1990_MOESM1_ESM
NIHMS528961-supplement-894_2013_1990_MOESM1_ESM.pdf (413.2KB, pdf)

RESOURCES