Ligand and Structure-Based Classification Models for Prediction of P-Glycoprotein Inhibitors

Abstract

The ABC transporter P-glycoprotein (P-gp) actively transports a wide range of drugs and toxins out of cells, and is therefore related to multidrug resistance and the ADME profile of therapeutics. Thus, development of predictive in silico models for the identification of P-gp inhibitors is of great interest in the field of drug discovery and development. So far in silico P-gp inhibitor prediction was dominated by ligand-based approaches because of the lack of high-quality structural information about P-gp. The present study aims at comparing the P-gp inhibitor/noninhibitor classification performance obtained by docking into a homology model of P-gp, to supervised machine learning methods, such as Kappa nearest neighbor, support vector machine (SVM), random fores,t and binary QSAR, by using a large, structurally diverse data set. In addition, the applicability domain of the models was assessed using an algorithm based on Euclidean distance. Results show that random forest and SVM performed best for classification of P-gp inhibitors and noninhibitors, correctly predicting 73/75% of the external test set compounds. Classification based on the docking experiments using the scoring function ChemScore resulted in the correct prediction of 61% of the external test set. This demonstrates that ligand-based models currently remain the methods of choice for accurately predicting P-gp inhibitors. However, structure-based classification offers information about possible drug/protein interactions, which helps in understanding the molecular basis of ligand-transporter interaction and could therefore also support lead optimization.

Introduction

The ABC transporter (ATP binding cassette) family is one of the largest protein families comprising a group of functionally distinct proteins that are mainly involved in actively transporting chemicals across cellular membranes. Depending on the subtype, transported substrates range from endogenous amino acids and lipids, up to hydrophobic or charged small molecules.¹ In total, more than 80 genes for ABC transporters have been characterized across all animal families, among which fifty-seven genes were reported for vertebrates. Human ABC transporters comprise 48 different proteins that can be divided into seven different subfamilies: ABCA, ABCB, ABCC, ABCD, ABCE, ABCF, and ABCG.² The correct function of ABC transporters is of high importance, as mutations or deficiency of these membrane proteins lead to various diseases such as immune deficiency (ABCB2), cystic fibrosis (ABCC7), progressive familial intrahepatic cholestasis-2 (ABCB11), and Dubin–Johnson syndrome (ABCC2). Moreover, some highly polyspecific ABC transporters are known for their ability to export a wide variety of chemical compounds out of the cell. Overexpression of these so-called multidrug transporters, which include P-glycoprotein (P-gp, multidrug resistance protein 1, ABCB1), multidrug resistance related protein 1 (MRP1, ABCC1), and breast cancer resistance protein (BCRP, ABCG2), might lead to the acquisition of multidrug resistance (MDR), which is one major reason for the failure of anticancer and antibiotic treatment.³

Furthermore, P-gp plays an essential role in determining the ADMET (absorption, distribution, metabolism, excretion, and toxicity) properties of many compounds. Drugs that are substrates of P-gp are subject to low intestinal absorption, low blood-brain barrier permeability, and face the risk of increased metabolism in intestinal cells.⁴ Moreover, P-gp modulating compounds are capable of influencing the pharmacokinetic profiles of coadministered drugs that are either substrates or inhibitors of P-gp,^5,6 thus giving rise to drug–drug interactions. This urges on the development of suitable in silico models for the prediction of P-gp inhibitors in the early stage of the drug discovery process to identify potential safety concerns. So far the focus of prediction models was lying on ligand-based approaches such as QSAR,⁷ rule-based models⁸ and pharmacophore models.⁹⁻¹¹ Very recently, also machine-learning methods have been successfully used for the prediction of P-gp substrates and inhibitors.^12,13 In addition, grid-based methods, for example, FLAP (fingerprints for ligands and proteins) have been successfully applied to a set of 1200 P-gp inhibitors and noninhibitors with a success rate of 86% for an external test set.¹⁴ Subsequently, these models were used as virtual screening tool to identify new P-gp ligands. Also unsupervised machine learning methods (Kohonen self-organizing map) were used to predict substrates and nonsubstrates from a data set formed by 206 compounds. In this study the best model was able to correctly predict 83% of substrates and 81% of inhibitors.¹³ Recently, Chen et al. reported recursive partitioning and naïve Bayes based classification to a set of 1273 compounds. In this case, the best model predicted accurately 81% of the compounds of the test set.¹⁵ Because of the lack of structural information, developing prediction models using structure-based approaches has not been actively pursued. However, in the recent years the number of available 3D structures of ABC proteins^16,17 and the performance of experimental approaches¹⁸ has paved the way for the application of structure-based methods to predict drug/transporter interaction. In that sense, a small number of structure-based prediction models have been developed in the last two years. Bikadi et al. built a free web-server for online prediction of P-gp substrate binding modes based on a SVM classification model.^19,20 Molecular docking into the crystal structure and a homology model of mouse P-gp were used to additionally generate possible protein–ligand complexes, but was not used for classifying compounds. Dolghih et al. used induced fit docking into the crystal structure of mouse P-gp to separate P-gp binders from nonbinders on the basis of their docking score.²¹ Although the data sets were considerably small (126 and 64 compounds), an AUC of 0.93 and 0.90, respectively, could be observed. Very recently also Chen et al. used a set of 245 P-gp substrates and nonsubstrates to assess the prediction capability of docking.²² Nevertheless, based on the Glide docking scores SP and XP, no clear separation of the two classes could be observed.

However, the above-mentioned machine-learning and structure-based studies only used data sets of relatively small size, which might not be sufficient for the correct prediction of P-gp, which is known for its high polyspecificity. Thus, in the present study, we applied supervised machine-learning and structure-based techniques to predict P-gp inhibitors and noninhibitors, using a large and structurally diverse data set, comprising 1079 compounds. The methods applied comprised (1) ligand-based supervised machine learning (ML) methods, including random forest (RF), decision tree (DT), support vector machine (SVM), κ nearest neighbor (kNN) and binary QSAR (BQSAR), and (2) structure-based docking studies using five different scoring functions (ChemScore, GoldScore, ASP, ChemPLP, and XScore).

Computational Methods

P-gp Inhibitors Data Source

The publications from Broccatelli et al.¹⁴ and Chen et al.¹⁵ served as starting point for the present classification studies. A set of 2548 compounds reported as P-gp inhibitors and noninhibitors was compiled from both literature sources. In brief, Broccatelli et al. compiled a data set of 1275 compounds from more than 60 literature references. Threshold values for inhibitors and noninhibitors were assigned based on the IC₅₀ values and on the percentage of inhibition as suggested by Rautio et al.²³ Compounds with an IC₅₀ ≤15 μM, or >25–30% of inhibition were considered as inhibitors. Conversely, compounds possessing IC₅₀ and % of inhibition values of ≥100 μM or <10–12% were classified as noninhibitors. In addition, Tingjun Hou kindly provided us with the 3D structures of 797 inhibitors and 476 noninhibitors from their data set, as recently published by Chen et al.¹⁵ They used MDRR (multidrug-resistance ratio) values measured in adriamycin-resistant P388 murine leukemia cells for classification. The MDRR is calculated by dividing the compound’s ED50 in absence of adriamycin by the ED50 in presence of adriamycin, and thus represents the ability to revert MDR. Compounds with MDRR values greater than 0.5 were assigned inhibitors, whereas molecules with lower or equal to 0.4 MDRR values were considered as noninhibitors.

As for model development only 2D descriptors or fingerprints have been used, both data sets were analyzed in order to eliminate duplicated structures using 2D SMILES representations of each compound. Additionally, in case of stereoisomers, only one isomer was retained in the data set. While for the Chen database no duplicates have been found, from the Broccatelli data set 53 compounds have been removed due to identical 2D structures. Additionally 429 compounds were found to be present in both data sets. Among those, 33 compounds were differently annotated in the two data sets, and 17 possessed a permanent charge. Those molecules have been removed. The residual 346 compounds (132 inhibitors and 214 noninhibitors) were stored as external test set. Finally, the fused data set comprised 1699 unique compounds, from which 91 permanently charged molecules have been removed. This lead to a data set of 1608 compounds, comprising 1076 inhbitors and 532 noninhibitors.

Selection of Training and Test Set

The activity of the compounds was represented by the introduction of a binary variable (1 for inhibitor, 0 for noninhibitor). Subsequently, for assessing the internal predictivity of the models, the data set was divided into training and test set using D-optimal onion design (DOOD) as implemented in the MODDE software (version 7.0).²⁴ DOOD is a multivariate method, used for selecting training and test sets of reasonable size, which are representatives for the chemical property space defined by the molecular structures. The general principle of DOOD can be found elsewhere.^25,26 In the present study we used the scores from principal component analysis (R² = 0.99, 25 principal components) calculated by SIMCA-P.

Molecular Descriptors and Fingerprint Calculation

The 3D structures of the data set were imported into the modeling software MOE (Version 2010.10)²⁷ and subsequently energy minimized using the MMFF94x force field. The energy-minimized molecules were used to compute 62 2D descriptors implemented in MOE. The 2D molecular descriptors calculated comprised physicochemical properties, atom and bond counts, and pharmacophoric features. In addition, a set of 166 MACCS fingerprints and a set of 307 substructure fingerprints were calculated using the freely available software PaDEL (version 1.12).²⁸

Principle Component Analysis (PCA)

A PCA of the whole data set was conducted using the software SIMCA-p (version 10.5). The descriptors included for PCA have been selected based on the variable importance (VIP) calculated in SIMCA. A complete list of descriptors is provided in the Supporting Information, SI-Table 1.

Machine Learning Methods and Attribute Selection

For ligand-based classification, a set of representative machine learning methods such as SVM, kNN, DT, RF, and BQSAR was used. These classifiers are primarily used for ADMET property prediction, since they are efficient to handle large compound sets. The principles of these methods have been described in detail elsewhere.^29,30 SVM, RF, kNN, and DT classification experiments were performed using the WEKA data mining software (version 3.6.4),³¹ which provides a set of classifications, regressions, attribute (variable) selections and clustering methods. BQSAR was performed using the tool “QuaSAR-model” implemented in MOE. For descriptor selection, an automatic attribute selection procedure called BestFirst search algorithm, as implemented in WEKA was used.²⁹ The BestFirst attribute selection has been shown to be a better attribution selection method as compared to GeneticSearch or the use of all the descriptors.³²

Docking and Scoring

The atomic coordinates of human P-glycoprotein required for docking have been obtained by homology modeling. The model has been built on basis of the X-ray structure of murine P-gp (PDB ID 3G5U, 3.8 Å) as described in our previous work.³³ The template structure was chosen because of its high sequence identity and the fact that it represented the binding competent state of the transporter.

The protein was prepared using the Protein Preparation Wizard, implemented in the Schrödinger Suite (2011).³⁴ During the process, hydrogen atoms were added, optimal protonation states and ASN/GLN/HIS flips were determined. The 3D coordinates of the ligands were built with CORINA and energy minimized with MOE, using the MMFF94x force field.

According to our previous study,³⁵ the inhibitory activity of tertiary amines is due to the H-bond acceptor strength of the nitrogen rather than its positive charge, which suggested that the ligands might bind in an unprotonated way. On the other hand, recent experiments utilizing a charge-repulsion approach indicate that P-gp ligands probably possess a positive charge.³⁶ Thus, separate docking runs were performed considering neutral and charged molecules. The correct protonation state was calculated using the program LigPrep, implemented in the Schrödinger Suite. Two cyclopeptides could not be processed by LigPrep and thus have been excluded from the data set.

The remaining 1606 molecules, comprising 1073 inhibitors and 533 noninhibitors, were used for docking with the genetic algorithm-based GOLD suite (version 5.1.0).³⁷ The active site was specified as the entire transmembrane (TM) region of the protein, thus taking 20 Å around the coordinates of the center point (21.07, 57.95, −2.31) into consideration. All the docking runs were performed in high throughput mode as implemented in GOLD. Concerning the fitness function used during docking, either ChemScore (CS) or GoldScore (GS) has been chosen. Together with the different protonation settings of the ligand database (1606 compounds) this resulted in a total of four docking runs (Table 1). The resulting docking poses were subsequently rescored with five scoring functions implemented in GOLD, which comprised ChemScore, GoldScore, Astex Statistical Potential (ASP),³⁸ and Piecewise Linear Potential (ChemPLP),³⁹ as well as the external scoring function XScore.⁴⁰ Altogether there were four different docking runs, each of which was scored with five different fitness functions, resulting in 20 models for which the prediction capabilities have been investigated (Table 1).

Table 1. Summary of Docking Runs Performed and Scoring Functions Used in This Study.

docking run	ligand protonation state	main scoring function	rescoring functions
1	neutral	ChemScore	GoldScore, ASP, ChemPLP, XScore
2		GoldScore	ChemScore, ASP, ChemPLP, XScore
3	protonated	ChemScore	GoldScore, ASP, ChemPLP, XScore
4		GoldScore	ChemScore, ASP, ChemPLP, XScore

To get deeper insights into the binding modes of P-gp inhibitors and noninhibitors, the protein–ligand interaction fingerprints (PLIF) of the resultant complexes have been analyzed. As the standard PLIF tool in MOE does not support π–π-interactions, a customized svl script has been used that calculated fingerprints from interactions provided by the ligand interaction module in MOE. The types of intermolecular interaction provided comprised ionic, hydrogen bond, and π–π.

Model Evaluation

The quality of the classification models was evaluated in terms of standard parameters derived from the confusion matrix (true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN)). The predictive abilities of inhibitor and noninhibitor classification were calculated from sensitivity (eq 1) and specificity (eq 2) terms, respectively. The G-mean value (eq 3) was used to measure the balanced prediction of each of the two classes. Primarily, G-mean has been used for measuring the prediction performance on imbalanced data sets. As it takes into account both sensitivity and specificity, the measure is not biased toward the prediction of the majority class.

1

2

3

4

The quality of the overall binary classification model was estimated using Matthews’s correlation coefficient (MCC, eq 4). Similarly to G-mean, MCC evaluates the balanced prediction of the classification models, taking into account true and false positives and negatives.

N-Fold Cross Validation (N-FCV)

In addition to the internal and external test set prediction, the model quality was estimated via n-fold cross validation of the training set. In N-FCV, the original data set is divided into n subsets for n = 10 in the case of this study. Out of 10 subsets, 9 subsets (n – 1) were used as training set, and the remaining single subset was retained as validation data for testing the trained model. This process is repeated 10 times and each one of the 10 subsets was used exactly once for validation. In the present study all the N-FCV were carried out as implemented in WEKA.

Results and Discussion

Characterization of the Data Set

An initial set of 1608 P-gp ligands was divided into training and internal test set using D-optimal onion design (DOOD). Thus, the DOOD analysis resulted in 1201 training (841 inhibitors, 360 noninhibitors) and 407 test compounds (235 inhibitors, 172 noninhibitors) (internal test set). Principal component analysis (PCA) was performed as explained in the methods section, to inspect potential clusters and the coverage of the chemical space of the P-gp ligands. The first two principal components explained 71.7% of the variance in the data set. In Figure 1A, a scatter plot is shown, that represents the distribution of the compounds according the first two principal components. In this plot a distinct cluster of inhibitors at the right top corner could be observed, which mainly comprised cyclopeptolide derivatives (Figure 1A), which are chemically different from the other molecules. Moreover, there was quite a good separation between inhibitors and noninhibitors, which urged for the development of classification models. In order to understand the influence of the descriptors on the first two PCs, the loading plot was analyzed (Figure 1B). It can be seen from the loading plot that the majority of the inhibitors are highly influenced by the descriptors that provide hydrophobic information, e.g. the number of aromatic bonds (b_aro) or the partition coefficient (logP(o/w)). Furthermore, the high contribution of LogS to noninhibitors indicates that noninhibitors are considerably more hydrophilic than inhibitors. The hydrophobic requisite of P-gp inhibitors can be explained by the need of diffusing through the cell membrane in order to effectively bind to the hydrophobic active site of the protein.⁴¹

Figure 1.

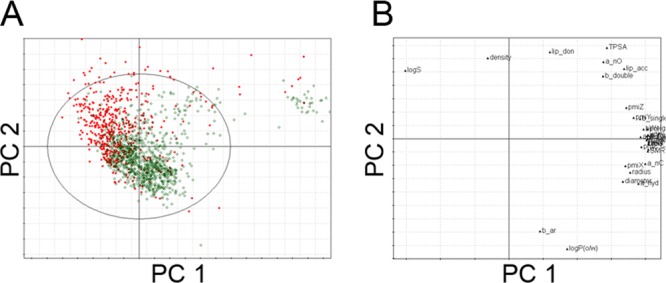
(A) Score plot from principal component analysis (first two principal components shown). Inhibitors are shown in green circles and noninhibitors are shown in red dots. (B) Loading plot of descriptors used for PCA analysis.

In addition, our previous docking study on propafenone-type ligands revealed that the active site of P-gp is primarily formed by the hydrophobic residues Tyr307, Tyr310, Phe343, Leu724, Phe336, Ile731, Ala761, and Val981 (Figure 2).³³

Figure 2.

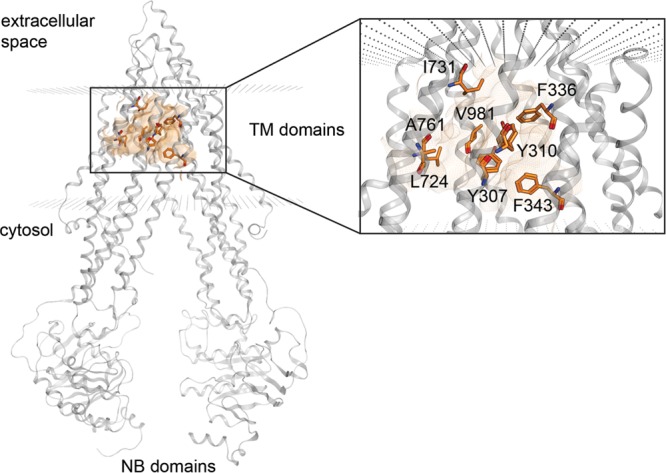
Hydrophobic binding site formed by nonpolar residues of both TM domains.

Furthermore, the distribution of inhibitors and noninhibitors (n = 1608) in the data set on the basis of some common molecular properties was studied. The analysis showed that inhibitors and noninhibitors could be reasonably well differentiated according to the logP, molecular weight, logS or molar refractivity (the distribution plots are provided in the Supporting Information, SI-Figure 1). From the intersection point of the inhibitor and noninhibitor distribution curve, the true classification (TP, TN) and misclassification (FP, FN) rates were calculated, which led to the statistical parameters, such as MCC, sensitivity, specificity and overall accuracy of the classification. The summary of the results is given in Table 2. The results show that molecular weight, logS, logP, and molar refractivity (MR) lead to a good discrimination between inhibitors and noninhibitors (MCC > 0.4, overall accuracy ≥ 69%). In particular, molecular weight and MR correctly discriminated 78% and 79% of the compounds at the intersection of 300 and 10, respectively. In that sense, compounds with a molecular weight of 300 and higher or a molar refractivity of 10 or higher were considered as inhibitors, and vice versa, lower molecular weight than 300 or lower molar refractivity than 10 indicated for noninhibitors. Comparably, in the The majority of P-gp inhibitors are of relatively bulky and hydrophobic nature compared to compounds that do not inhibit the protein. Imbalanced and hence poor separation was observed with the models derived from the number of hydrogen bond donors (sensitivity = 94%, specificity = 20%), hydrogen bond acceptors (sensitivity = 85% and specificity = 29%), and oxygen and nitrogen atoms (sensitivity = 83% and specificity = 31%).

Table 2. Models Obtained from Common Molecular Descriptors Distribution^a.

		confusion matrix
property	intersection point	TP	TN	FP	FN	sensitivity	specificity	MCC	accuracy
H-Acc	2.5b	902	156	385	165	0.85	0.29	0.16	0.66
H-Don	3.5c	1005	108	433	62	0.94	0.20	0.22	0.69
LogP	3	886	334	208	180	0.83	0.62	0.45	0.76
LogS	–4	896	355	186	171	0.84	0.66	0.50	0.78
MR	10	894	373	168	173	0.84	0.69	0.53	0.79
MolWt	300	1013	238	303	54	0.95	0.44	0.48	0.78
N+O	3.5d	883	168	373	184	0.83	0.31	0.16	0.65

^aNote: H-Acc, number of hydrogen bond acceptor; H-Don, number of hydrogen bond donors, LogP, logarithm of partition coefficient (octonal/water); LogS, logarithm of water solubility; MR, molar refractivity, MolWt, molecular weight, N + O, number of nitrogen and oxygen.

^bH-Acc ≤ 2, noninhibitors; H-Acc ≥ 3, inhibitors.

^cH-Don ≤ 3, inhibitors; H-Don ≥ 4, noninhibitors.

^dN+O ≤ 3, noninhibitors; N+O ≥ 4, inhibitors.

Development of Machine Learning Models

Different machine learning methods were used to build P-gp inhibitor and noninhibitor classification models using a set of 1201 training compounds encoded by physicochemical descriptors and fingerprints. Models have been either built from all descriptors or on the basis of descriptors selected by the BestFirst algorithm. These two scenarios were applied to three sets of X-variables such as 2D physicochemical properties (n = 62), MACCS fingerprints (n = 166) and substructure fingerprints (n = 307). In general, BestFirst algorithm descriptor based models performed better than the models obtained using all descriptors. According to the principle of parsimony, we discuss only models, which used the BestFirst algorithm for variable selection (Table 3 and 4); data describing the performance of the training set and 10-fold cross-validation of the training set are provided in the Supporting Information (SI-Table 2)). The BestFirst algorithm selected a set of descriptors for model generation as follows: 11 of 62 MOE 2D properties, 16 of 166 MACCS fingerprints, and 19 of 307 substructure fingerprints. With each descriptor set four different classification models were developed using the ML techniques RF, SVM, kNN, and BQSAR.

Table 3. Summary of Machine-Learning Models Based on BestFirst Feature Selection Method with the Internal Test Set^a.

		confusion matrix
descriptors	models	TP	TN	FP	FN	sensitivity	specificity	accuracy	G-mean
MOEb	RF	215	112	60	20	0.91	0.65	0.80	0.77
	SVM	219	109	63	16	0.93	0.63	0.81	0.77
	KNN	215	114	58	20	0.91	0.66	0.81	0.78
	BQSAR	196	120	52	39	0.83	0.70	0.78	0.76
MACCSc	RF	207	96	76	28	0.88	0.56	0.74	0.70
	SVM	199	75	97	36	0.85	0.44	0.67	0.61
	KNN	215	79	93	20	0.91	0.46	0.72	0.65
	BQSAR	158	117	55	77	0.67	0.68	0.68	0.68
SS-FPd	RF	215	73	99	20	0.91	0.42	0.71	0.62
	SVM	220	66	106	15	0.94	0.38	0.70	0.60
	KNN	220	67	105	15	0.94	0.39	0.71	0.60
	BQSAR	188	86	86	47	0.80	0.50	0.67	0.63
combinede	RF	215	118	54	20	0.91	0.69	0.82	0.79
	SVM	219	106	66	16	0.93	0.62	0.80	0.76
	KNN	207	124	48	28	0.88	0.72	0.81	0.80
	BQSAR	193	118	54	42	0.82	0.69	0.76	0.75

^aNote: RF, random forest; SVM, support vector machine, KNN, kappa nearest neighbor; BQSAR, binary QSAR.

^bBestFirst descriptors from 2D-MOE.

^cBestFirst descriptors from MACCS fingerprints.

^dSubstructure fingerprints.

^eBestFirst descriptors from all the calculated descriptors.

Table 4. Matthews Correlation Coefficient of the Models for the Internal Test Set Predictions (10-Fold Cross-Validations Are Provided in the Parentheses)^a.

	BestFirst descriptor models
classification methods	MOE	MACCS	SS-FP	combined
RF	0.60 (0.64)	0.47 (0.55)	0.40 (0.43)	0.63 (0.66)
SVM	0.61 (0.55)	0.31 (0.38)	0.40 (0.38)	0.59 (0.59)
KNN	0.61 (0.61)	0.43 (0.46)	0.40 (0.41)	0.61 (0.59)
BQSAR	0.54 (0.63)	0.35 (0.41)	0.32 (0.41)	0.51 (0.57)

^aNote: RF, random forest; SVM, support vector machine; kNN, kappa nearest neighbor; BQSAR, binary QSAR.

For the MOE 2D descriptors, all four models were able to correctly predict >75% of the compounds of the test set, whereupon the best model was obtained with kNN (MCC = 0.61, accuracy = 81%). Also regarding a balanced prediction, kNN performed best achieving a G-mean value of 0.78. However, highly similar performance was observed with the methods random forest (MCC = 0.60, accuracy = 0.80%, G-mean = 0.77) and SVM (MCC=0.61, Accuracy=0.81%, G-Mean=0.77). With 10-fold CV random forest outperformed kNN and SVM, showing an MCC value of 0.64 compared to 0.55 (SVM) and 0.61 (kNN) (Table 4).

The models created using MACCS fingerprints showed that random forest performed better than the other machine learning methods, correctly predicting 74% of the internal test set (MCC = 0.47). Also the kNN model correctly predicted more than 70% of the test compounds. However, the model suffers from a high false positive rate of more than 0.5. The MACCS fingerprints selected by the BestFirst algorithm are listed and explained in Supporting Information SI-Table 3. To get insights into the distribution of the structural keys, the frequency of the fingerprint bins selected by BestFirst for inhibitors and noninhibitors were compared. For instance, bins 50, 75, 86, 125, 129, 145, 155, and 162 are represented more often in the group of inhibitors, whereas bins 54, 84, and 139 are more prevalent in the set of noninhibitors (Supporting Information SI-Table 3). The bins more prevalent in inhibitors were mainly of hydrophobic nature, as for example, aromatic or ring substructures. On the other hand, bins more often hit by noninhibitors represent hydrophilic substructures, comprising the number of heteroatoms, hydroxylic groups, and primary amines. In Figure 3, an example of a phenylpyrazolon-type P-gp inhibitor with the matched MACCS fingerprints is depicted.

Figure 3.

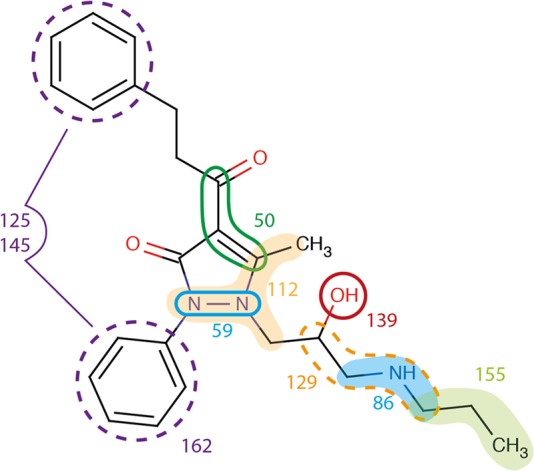
Schematic representation of occurrence of MACCS fingerprints in a phenylpyrazolon-type P-gp inhibitor.

Substructure/functional group fingerprints based models generally showed similar performance compared to the models developed from MACCS fingerprints. Analogous to the models generated on the basis of the MOE 2D descriptors, the methods RF, kNN, and SVM showed considerably similar statistics. All three were able to correctly predict more than 70% of the internal test set compounds, which resulted in an MCC of 0.4. However, the RF model showed a slightly better G-mean value because of a more balanced prediction. In a previous study, using a similar data set (the databases share over 80% similarity), the application of an FP growth algorithm revealed that alkyl–aryl ethers (59% of inhibitors in the data set), tertiary aliphatic amines (51%), and aromatic groups were significantly more present in inhibitors compared to noninhibitors. Moreover, phenols (18% of noninhibitors in the data set), carboxylic acids (11%), and primary amines (14%) were quite prevalent in noninhibitors.⁴²

The same groups have been selected by the BestFirst algorithm for model generation in this study, leading to a set of 16 fingerprints in total. Again inhibitors were mainly described by possessing alkylarylether and aromatic groups, as well as amines and secondary carbons. While also a high number of noninhibitors bear aromatic groups, they stand out for their relatively high occurrence of carboxylic acids and phenols (Supporting Information, SI-Table 2).

Although on basis of overall accuracy the models developed from three different descriptor sets (2D, MACCS and SSFP) performed relatively good, the majority suffered from a high number of false positives. Thus, additional models have been built by using a BestFirst selected set of descriptors derived from combining all descriptors. A set of 15 descriptors was selected, which comprised 4 MACCS keys, 2 substructure fingerprints, and 9 MOE 2D descriptors (Table 5).

Table 5. Descriptors Selected by the BestFirst Algorithm for the Combined Descriptor Set.

Descriptor set
MACCS	17 (CTC)
	50 (C=C(C))
	54 (QHAAQH)
	125 (aromatic ring > 1)
substructure fingerprint	84 (carboxylic acid)
	90 (carbothioic S ester)
MOE 2D	a_hyd
	a_nC
	b_single
	logP(o/w)
	b_rotR
	density
	logS
	vdw_area
	vsa_hyd

Considering the four subsequently generated models, the overall quality did not change significantly compared to the models developed using only BestFirst 2D descriptors, which showed the best statistics among the three descriptor sets. However, the combined descriptor models exhibited slight improvements in the prediction of noninhibitors, as can be noticed from increased G-mean values (all ≥ 75%). Additionally, the random forest model on the basis of the combined descriptor showed the best performance of all models developed in this study. Thus, it correctly predicted 215/235 inhibitors and 118/172 noninhibitors from the internal test set, resulting in an overall accuracy and MCC of 82% and 0.63, respectively.

Validation of External Compounds

As mentioned in the method section, considering the 2D constitution, 429 compounds were present in both the Chen et al. and the Broccatelli et al. data set, out of which 346 could be used as external test set. The models derived from the combined BestFirst descriptors were used to predict these 346 compounds. As can be seen from Table 6, SVM performed reasonably well, correctly predicting 97% of the inhibitors and 62% of the noninhibitors, resulting in an overall accuracy of 77%. Also with RF a similarly good accuracy of 75% could be observed. Interestingly, the BQSAR and the kNN model showed better prediction of noninhibitors, as can be seen from the comparably high specificity values of >70.

Table 6. External Test Set Predictions.

descriptors	models	sensitivity	specificity	accuracy	G-mean	MCC
MOE	RF	0.98	0.52	0.70	0.71	0.52
	SVM	0.99	0.51	0.69	0.71	0.52
	kNN	0.87	0.56	0.68	0.70	0.43
	B-QSAR	0.86	0.65	0.73	0.75	0.50
MACCS	RF	0.63	0.71	0.68	0.67	0.34
	SVM	0.27	0.93	0.68	0.50	0.28
	kNN	0.79	0.67	0.71	0.72	0.44
	B-QSAR	0.77	0.16	0.39	0.35	–0.09
SS-FP	RF	0.79	0.42	0.56	0.57	0.21
	SVM	0.94	0.24	0.51	0.48	0.23
	kNN	0.91	0.27	0.51	0.50	0.22
	B-QSAR	0.49	0.82	0.69	0.63	0.33
combined	RF	0.99	0.57	0.73	0.75	0.57
	SVM	0.97	0.62	0.75	0.77	0.59
	kNN	0.64	0.72	0.69	0.68	0.36
	B-QSAR	0.58	0.74	0.68	0.66	0.32

Although the models developed from different sets of descriptors and fingerprints performed quite good, there remained always the question whether the classification of P-gp inhibitors and noninhibitor can also be done using simple drug-likeness descriptors (molecular weight, hydrogen bond acceptor, hydrogen bond donor and LogP).⁴³ Thus, four models were developed using decision tree (DT), kNN, SVM and random forest as classifiers. All models were able to correctly identify >85% of inhibitors, but noninhibitors were predicted relatively poor (Table 7). The DT method provides easy interpretation of the model, however, previously it has been shown to lack predictability. Interestingly, in this case the DT approach showed good predictability, by exhibiting an overall accuracy of 75% with an MCC of 0.57 for the external test set. According to this model, noninhibitors possessed lower lipophilicity and lower molecular weight than inhibitors (see Supporting Information SI-Figure 2). This observation is in agreement with observations derived from the molecular property distribution plot and PCA analysis (Figure 1).

Table 7. Simplified Classification Models using Rule of Five Descriptors^a.

	confusion matrix
models	TP	TN	FP	FN	sensitivity	specificity	MCC	accuracy
RF	127	117	97	5	0.96	0.55	0.52	0.71
SVM	131	90	124	1	0.99	0.42	0.46	0.64
KNN	117	102	112	15	0.89	0.48	0.37	0.63
DT	126	132	82	6	0.95	0.62	0.57	0.75

^aStatistics describe the classification performance on the external test set. Note: RF, random forest; SVM, support vector machine; kNN, kappa nearest neighbor; DT, decision tree; MCC, Matthews’s correlation coefficient.

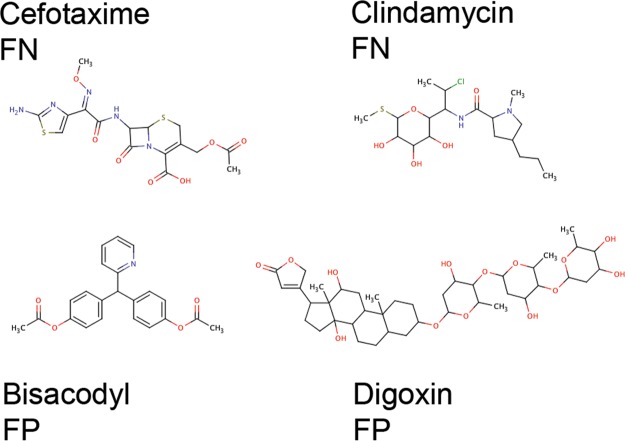
To understand the reason for a certain model output, selected compounds that were incorrectly classified by the combined descriptor-set models were analyzed. The results showed that 32 compounds (8% of the internal test set) were misclassified by all four methods (SVM, kNN, BQSAR, and RF), and more than 63% of the internal test set compounds were correctly classified by all methods. Among the 32 compounds, which were consistently false classified, 7 were misclassified as noninhibitors (FN), and 25 as inhibitors (FP). Representative examples are given in Figure 4. Cefotaxime was misclassified as noninhibitor by all for methods with a probability score of >0.9. Analyzing the molecular properties of Cefotaxime showed that the values for logP (−0.6), logS (−3.7), and MR (10.7) lie in the region for noninhibitors (Table 2). Interestingly, with this polar compound a strong inhibition of 82% (normalized to the inhibitory activity of cyclosporine A) in a calcein-AM efflux assay was observed.⁴⁴ This is quite surprising, as negatively charged compounds are not considered to interact with P-gp. Similarly, clindamycin, the physicochemical properties of which are rather located in the range of noninhibitors, showed an inhibition >80% in the same assay.⁴⁴ On the other hand the laxative Bisacodyl was misclassified as inhibitor by all methods. Regarding its physicochemical properties, the hydrophobic drug (logP = 4.2) exhibits values similar to P-gp inhibitors (low logS, high MR and molecular weight). As a matter of fact, taking a look at the assay data, Bisacodyl was not clearly identified as P-gp noninhibitor, but rather showed inconclusive data.⁴⁴ This might suggest a weak P-gp inhibitory activity under certain circumstances. Digoxin also exhibits inhibitor-like physicochemical properties, although it is not known for inhibiting the efflux pump. On the contrary, digoxin was identified as P-gp substrate and thus might still act as a competitive inhibitor in, for example, a rhodamine efflux assay. As has recently been demonstrated, the respective assay and assay conditions are of utmost importance for the assessment of P-gp inhibitory activity.⁴⁵ Thus, a more detailed analysis of the respective biological data might reveal other examples where the prediction might be in line with biological data.

Figure 4.

Examples of misclassified compounds in the test set.

Probability of Prediction of Inhibitors and Noninhibitors

Each classification model gives the probability of a compound for belonging to a certain class. In general, if the probability of a compound being an inhibitor is higher than 0.5, it is classified as inhibitor. However, the closer to 1, the higher is the confidence of this classification. In that sense, introducing probability cutoffs can lead to predictions with higher confidence. In Figure 5, the fraction of TP, FP, TN, and FN were plotted against their probabilities based on the combined RF model. As it can be already deduced from the figure, compounds with an inhibitor probability of >0.6 are more likely to be true positives. Similarly, it is highly probable to identify a true negative if its probability value for being an inhibitor is <0.4. Furthermore, Table 8 shows the detailed statistics for different probability cutoffs on the data set (training and internal test set) and the external test set. This analysis shows that especially the detection of TN benefits from introducing cutoffs, leading to a more balanced prediction. As expected, a threshold of <0.1/>0.9 resulted in the most accurate prediction, and should therefore be considered for virtual screening purposes. However, one has to bear in mind, that introduction of a cutoff comes at the expenses of the number of predicted compounds and the values have to be carefully selected according the given problem.

Figure 5.

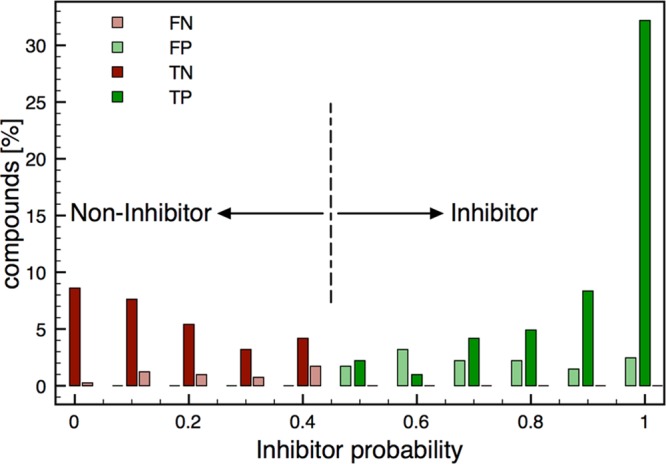
Probability Score of P-gp Inhibitors and Noninhibitors in the Test Set.

Table 8. Classification Statistics with Different Probability Cutoffs.

		sensitivity	specificity	accuracy	G-mean	MCC
training and internal test set	all	0.91	0.69	0.82	0.79	0.63
	<0.4/>0.6	0.94	0.68	0.84	0.80	0.66
	<0.3/>0.7	0.95	0.78	0.89	0.86	0.75
	<0.2/>0.8	0.97	0.73	0.89	0.84	0.74
	<0.1/>0.9	0.99	0.78	0.94	0.88	0.83
external test set	all	0.99	0.56	0.73	0.75	0.56
	<0.4/>0.6	1.00	0.56	0.74	0.75	0.59
	<0.3/>0.7	1.00	0.60	0.77	0.77	0.63
	<0.2/>0.8	1.00	0.50	0.75	0.71	0.58
	<0.1/>0.9	1.00	0.60	0.82	0.78	0.68

Applicability Domain

In addition to the classification models, an applicability domain (AD) experiment was performed to check the reliability of the developed compound prediction models. AD provides a first structural alert on the data set and is primarily used to check whether a new molecular entity (NME) is within the chemical space of the training set or not. There have been many AD approaches proposed and each had their own pros and cons. Some of the well-known AD approaches are descriptor “ranges”, “Euclidean distances (ED)”, and “probability density (PD)”.^46,47 In the present study, AD analysis was performed on the basis of the ED approach using the Ambit Discovery software (version 0.04).⁴⁸ Ambit Discovery preprocesses the given data set by principal component analysis in order to eliminate colinearities among the descriptors. Subsequently, the AD is estimated based on the ED approach for the internal and the external test set. The results showed all compounds from both data sets were found to be inside the chemical domain of the training compounds. An additional AD experiment was performed using a set of 986 FDA approved drugs from DrugBank. It had been observed that 973 compounds were predicted to be in the domain of the training set and only a small amount (13 compounds) of the FDA drugs were located outside. Some of these compounds were found to be peptides, for example, bacitracin, colistimethate, and degarelix, while others contained transition metals, as cisplatin or organoplatin. Thus, the models should be valid over a broad range of the druglike chemical space. The scoring plot of the first two principal components obtained by PCA of the FDA approved drugs, as well as the training and both test sets is provided in the Supporting Information (SI-Figure 3).

Bikadi et al. used SVM as the method of choice for developing machine learning models for the classification of substrates and nonsubstrates of P-gp. Although, they have used a much smaller data set, the prediction performance of the best model is similar to the SVM model presented here. Regarding the differences in data set size, it would have been extremely interesting to compare the applicability domain of both data sets, or how much of the FDA approved drugs are within the chemical space of the model compounds, respectively.

Structure-Based Classification

The publication of the mouse P-gp structure paved the way for structure-based studies. We recently showed that docking into a homology model of human P-gp based on this X-ray structure lead to poses consistent with QSAR data³³ and that these poses can successfully be exploited for identification of new P-gp inhibitors.⁴⁹ We thus used our homology model in a wider setting and docked a large set of P-gp inhibitors and noninhibitors into P-gp to investigate the possibility to use docking for classification purposes.

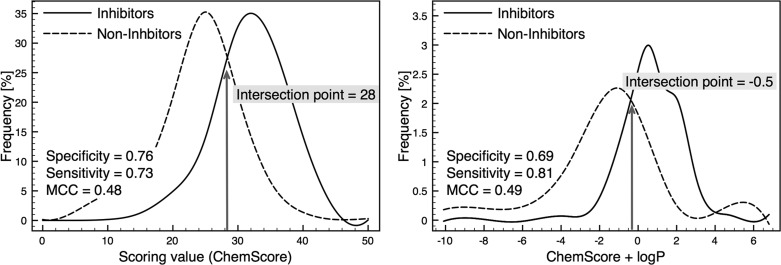
The scoring values of the different fitness functions were binned into ranges of 0.5 or 5, respectively, and plotted against the occurrence of inhibitors and noninhibitors. This resulted in two distinct curves for each scoring function (Figure 6a). The intersection point of those curves was used as classification criteria, and compounds scored higher than this point were considered as inhibitors. Vice versa, compounds showing lower scores were classified as noninhibitors. According to this criterion, the confusion matrix parameters, as well as other performance measures could be calculated and are summarized in Table 9. As can be seen from the results, the CS docking runs showed highest MCC values, especially when also using ChemScore as discrimination criteria. On the other hand, GS docking runs performed best when being rescored with the external fitness function Xscore. Rescoring CS docking results with GoldScore resulted in a dramatic decrease of performance. The different ligand protonation settings did not considerably affect the outcome. However ChemScore docking runs showed a slight preference for neutral ligands, while ChemPLP and ASP performed better with protonated ligands.

Figure 6.

Distribution of P-gp Inhibitors and Noninhibitors based on ChemScore scoring. Sensitivity, specificity and MCC were calculated from true and misclassification rate at intersection point of two curves. (A) Distribution based on ChemScore alone and (B) distribution based on a combined ChemScore-logP score.

Table 9. Summary of Models Obtained Using Different Scoring Functions.

	ligand protonation	scoring function	intersection point	sensitivity	specificity	accuracy	G-mean	MCC
CS docking run	neutral	Chemscore	28	0.76	0.73	0.75	0.75	0.48
		Goldscore	25	0.36	0.66	0.46	0.49	0.02
		ASP	25	0.76	0.62	0.71	0.68	0.36
		ChemPLP	50	0.66	0.69	0.67	0.68	0.34
		XScore	6	0.63	0.78	0.68	0.70	0.38
	charged	Chemscore	30	0.68	0.79	0.71	0.73	0.44
		Goldscore	18	0.50	0.42	0.47	0.46	–0.08
		ASP	29	0.60	0.79	0.67	0.69	0.38
		ChemPLP	50	0.70	0.68	0.70	0.69	0.37
		XScore	6	0.68	0.73	0.70	0.71	0.39
GS docking run	neutral	Chemscore	22	0.73	0.58	0.68	0.65	0.31
		Goldscore	45	0.61	0.75	0.66	0.67	0.34
		ASP	25	0.72	0.56	0.67	0.64	0.28
		ChemPLP	50	0.65	0.66	0.65	0.65	0.29
		XScore	6	0.65	0.73	0.68	0.69	0.36
	charged	Chemscore	25	0.59	0.75	0.64	0.66	0.32
		Goldscore	45	0.71	0.63	0.68	0.67	0.33
		ASP	25	0.74	0.57	0.68	0.65	0.31
		ChemPLP	50	0.70	0.65	0.68	0.67	0.33
		XScore	6	0.68	0.71	0.69	0.69	0.37
combined score (ChemScore + logP)			–0.5	0.81	0.69	0.77	0.75	0.49

With an MCC of 0.5 the CS docking run using neutral ligands performed best. Overall, this model accurately predicted 75% of the data set compounds. According to this model, all compounds that had a ChemScore value above 28 were predicted as inhibitors. The obtained ChemScore values for noninhibitors ranged from 0 to 40, whereas in the case of inhibitors the values varied from 10 to 50.

In terms of MCC and balanced prediction, the overall classification based on docking (ChemScore) was less accurate compared to models developed using SVM or random forest. Nevertheless, by correctly predicting 75% of the training and internal test set the docking model proved to be suited for classification studies. The study by Chen et al.²² used a similar approach for classifying a set of P-gp substrates and nonsubstrates. However, the results show no clear separation of the two classes based on the docking scores. On the one hand, this can be due to the focus on P-gp substrates instead of inhibitors. Given the fact, that most experimental methods cannot definitely distinguish substrates from inhibitors, this explanation might be doubtful. On the other hand, the size of the data set, which was considerably smaller than the one used in this study, seems to be the reason for the weak separation in terms of scoring values. This again points out the importance of a large data set, which provides a better coverage of the chemical space.

Dolghih et al.²¹ on the other hand could show that using induced fit docking a discrimination of substrates and nonsubstrates is feasible. With an AUC of 0.93, their protocol was able to identify P-gp substrates very well. However, in this case the selection of the data set was in favor for the structure-based classification. A detailed view on the compounds showed, that the metabolites selected as nonsubstrates were considerably smaller in terms of molecular weight. When applying the simple molecular weight classification model on the data set, an MCC of 0.59 could be achieved (Supporting Information SI-Table 5). As bigger molecules tend to be scored better by scoring functions, this introduces a strong bias.

However, it would not be surprising that induced fit docking would show a slightly better classification performance. The computational cost, however, renders this approach unsuitable for high-throughput virtual screening.

To improve the statistics of the structure-based classification without increasing computational cost, we tried to implement the fact that the compounds access the protein’s binding site via the lipid bilayer. In that sense, a score was calculated, combining ChemScore and the descriptor logP(o/w) (each normalized) (Figure 6b). This resulted in slightly improved statistics, as with this combined score 77% of the compounds could be predicted correctly, resulting in an MCC value of 0.49.

Subsequently, the ChemScore and the combined ChemScore-logP scoring models were applied on the external test set. As expected, the performance of the external validation was lower than for the data set consisting of training and internal test set. Both models showed high sensitivity values (<0.9), indicating that there were hardly any FN classified. However, high FP rates could be observed, which resulted in low specificity (<0.4) for both models. The model only relying on the ChemScore value was able to correctly classify 54% of the external test set compounds, while the model that was also taking the logP into account predicted 61% of the compounds correctly. This indicates that implementing information about the entry path of the molecules clearly increases a structure-based prediction model.

However, beside statistical performance measures like MCC, docking poses can also be evaluated by comparing them with experimental data. For the P-gp substrate verapamil, the following interacting residues on TM helices 1, 4, 5, 6, 7, 10, 11, and 12 are known: His61, Ala64, Leu65, Ser222, Ile306, Leu339, Ala342, Phe728, Ile868, Gly872, Phe942, Thr945, Leu975, Gly984, Val982.³³ Figure 7 shows the top view of the P-gp binding pocket with four different docking poses of verapamil, generated by the docking runs presented in Table 9. As can be noticed, all four poses are in vicinity of the experimentally derived interacting amino acid residues, which are rendered blue. Interestingly, the pose, which resulted from the GS docking run with neutral ligands (Figure 6-B), is located closest to most of the residues, while the corresponding CS docking run is placed only in vicinity to the residues on TM helices 4, 5, and 6. This suggests that the GS docking run could better reproduce the experimental data.

Figure 7.

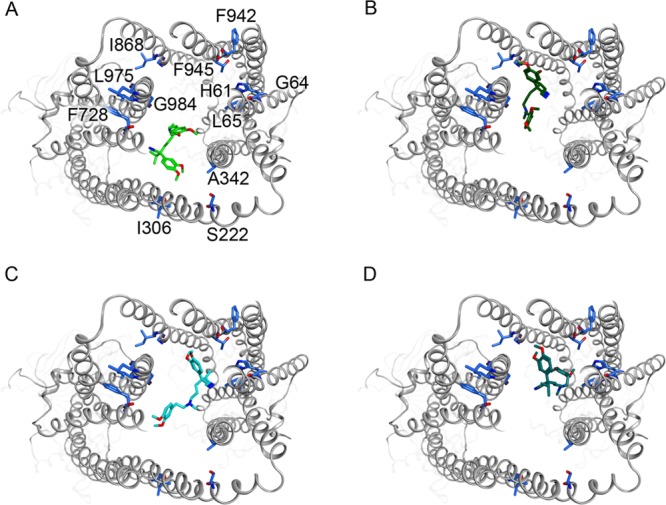
Verapamil docking poses generated by 4 different docking runs. (A) CS docking with neutral ligand, (B) CS docking run with positively charged ligand, (C) GS docking run with neutral ligand, and (D) GS docking run with positively charged ligand.

Protein–Ligand Interactions

Predicting protein–ligand interactions is a highly valuable analysis tool that helps to examine energetically favorable conformations or orientations of ligands in the protein active site. The protein ligand interaction fingerprints (PLIF) tool, implemented in MOE, computes different molecular interactions between residues of the binding site and the corresponding ligand conformation. In this study, PLIF analysis was performed on the basis of the docking poses generated by the CS docking run. As can be seen in Figure 8, there was no significant difference in interaction occurrences between inhibitors and noninhibitors. However, noninhibitors showed a higher number of H-bond interactions than inhibitors. This is in agreement with the results of the ML techniques, as they described noninhibitors being more hydrophilic than inhibitors. This also reflects the mode of action of P-gp, as its substrates have to cross the lipid bilayer in order to reach the protein’s active site. The main interacting amino acid residues for inhibitors are Phe303, Tyr307, Phe336, and Phe343, which are located on helices 5 and 6 of TM domain 1 (Figure 2). The low involvement of the corresponding helices in TM domain 2 might be traced back to a certain asymmetry of the crystal structure template, which was already pointed out in our previous study.³³

Figure 8.

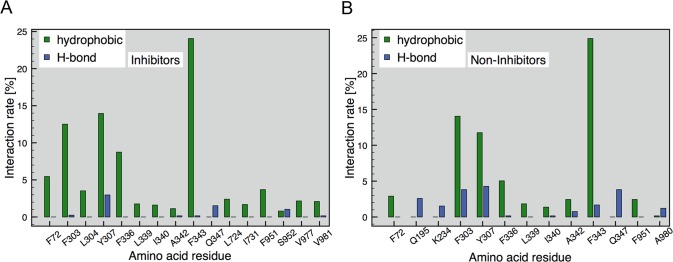
PLIF analysis. Important residues are shown with their hydrophobic and hydrogen bonding interactions: (A) inhibitors and (B) noninhibitors.

Conclusions

In the present study, we developed structure and ligand-based classification models from a set of 1608 P-gp inhibitors and noninhibitors. It could be observed that molecular properties, which could be linked to P-glycoprotein inhibition, are mainly hydrophobic parameters, such as logP and molar refractivity. Descriptor contributions, as well as the PLIF analysis, point toward distinct differences in the hydrophobic interaction pattern of inhibitors and noninhibitors, as the former are for instance considerably less water-soluble and bulkier. Models obtained by support vector machine and random forest in combination with BestFirst descriptors performed better than other ML models. Both models were performing good in discriminating inhibitors (>90% of the internal and external test sets) from noninhibitors, with overall accuracies of SVM and RF of 83/75 and 86/73%, respectively. Furthermore, an AD experiment using the BestFirst selection of the combined descriptor sets suggested that these models are applicable to predict drug-like compound libraries.

The structure-assisted docking model that used the GOLD implemented ChemScore scoring function predicted reasonably well P-gp inhibition (accuracy = 0.75, MCC = 0.48). The model was able to correctly predict 76% of P-gp inhibitors and 73% of noninhibitors. Adding the logP-value of the compounds to their docking score showed that implementing information about membrane diffusion of P-gp inhibitors could slightly improve the prediction (accuracy = 0.77, MCC = 0.49). However, structure-based classification on the external test set was less satisfying, showing an overall accuracy of only 0.61 (ChemScore + logP). Nevertheless, also in this case the method was highly predictive for inhibitors (97% correctly classified), but lacked specificity. As mentioned above, the models built in this study from ligand-based methods are efficient and precise and could be used for the identification of P-gp inhibitors or noninhibitors from virtual screenings of large compound libraries. Thus, they will be implemented in eTOXsys, a web-based, distributed system allowing prediction of potential toxicity risks, which is developed under the framework of the eTOX project.⁵⁰ As the analysis of simple properties demonstrated reasonable sensitivity values, these descriptors could be used as rapid and simple prefilter rules. Although structure-based classification models lacked overall accuracy for the external test set, they still might be useful in combination with ML techniques. Positively classified compounds of the latter could thus be processed by docking methods, which would further narrow the screening process for the identification of potent P-gp inhibitors. In addition, the PLIF analysis provided molecular protein–ligand interaction information, which may aid the optimization of ligands for P-gp inhibition. In conclusion, a workflow comprising prescreening with simple descriptors, classification by ML techniques and postprocessing by structure-based methods provides accurate prediction with information for further drug development.

Supporting Information Available

Additional materials as described in the text. All materials available free of charge via the Internet at http://pubs.acs.org

Author Present Address

F.K.: CeMM Research Center for Molecular Medicine of the Austrian Academy of Sciences, Lazarettgasse 14, 1090 Vienna, Austria

Author Contributions

F.K. and P.V. contributed equally to this manuscript.

The authors declare no competing financial interest.