Breast density quantification with cone-beam CT: A post-mortem study

Abstract

Forty post-mortem breasts were imaged with a flat-panel based cone-beam x-ray CT system at 50 kVp. The feasibility of breast density quantification has been investigated using standard histogram thresholding and an automatic segmentation method based on the fuzzy c-means algorithm (FCM). The breasts were chemically decomposed into water, lipid, and protein immediately after image acquisition was completed. The percent fibroglandular volume (%FGV) from chemical analysis was used as the gold standard for breast density comparison. Both image-based segmentation techniques showed good precision in breast density quantification with high linear coefficients between the right and left breast of each pair. When comparing with the gold standard using %FGV from chemical analysis, Pearson’s r-values were estimated to be 0.983 and 0.968 for the FCM clustering and the histogram thresholding techniques, respectively. The standard error of the estimate (SEE) was also reduced from 3.92% to 2.45% by applying the automatic clustering technique. The results of the postmortem study suggested that breast tissue can be characterized in terms of water, lipid and protein contents with high accuracy by using chemical analysis, which offers a gold standard for breast density studies comparing different techniques. In the investigated image segmentation techniques, the FCM algorithm had high precision and accuracy in breast density quantification. In comparison to conventional histogram thresholding, it was more efficient and reduced inter-observer variation.

I. Introduction

Breast density is a compositional measure of the relative amount of parenchymal tissue in the breast. In the basic model, the breast consists of two tissue compartments: glandular and adipose. Breast density is defined as the volumetric percentage of the glandular tissue. There is also a fibrous component in breast tissue that has a similar attenuation to glandular tissue and is therefore included in the glandular compartment of the model. Research has shown that breast density is a moderate to strong independent risk factor for the development of breast cancer. On average, women with high breast density have a four to six-fold increased risk for breast cancer, compared to women who have low breast density.(Boyd et al., 2002; Boyd et al., 2007; Harvey and Bovbjerg, 2004; McCormack and dos Santos Silva, 2006; Phipps et al., 2012; Wolfe, 1976; Yaghjyan et al., 2011) Despite the volume of evidence supporting the importance of breast density in risk analysis, breast density has only been included in a few emerging risk models, and improvements in risk discrimination are already being seen.(Vachon et al., 2007) Quantitative breast density measurements allow for stronger risk predictions on the individual level leading to personalized screening plans that will help to continue reducing breast cancer mortality rates. However, in a 2008 literature review by Jacobi et al.(Jacobi et al., 2008), none of the seven most prevalent risk models included breast density determinations of lifetime risk. This absence is caused by the lack of a generally accepted quantitative measure of breast density.

Mammography is the current standard for breast cancer screening; however, due to its projective nature, quantitative measures of breast density are difficult to implement. The most widely used measure of density is a lexical standard specified in the Breast Imaging Reporting and Data System (BI-RADS) published by the American College of Radiology. Each mammogram is given a rating from 1 to 4 depending on the amount of structural tissue. This category indicates how difficult it is to read the mammogram. Even so, the BI-RADS categories have been used to exhibit a correlation between mammographic density and relative cancer risk.(Vacek and Geller, 2004) Although the BI-RADS specification is useful for identifying patients who would benefit from further screening, its subjective, qualitative nature limits its use in quantitative predictive models. Planimetry, which requires an experienced radiographer to draw tissue boundaries by hand or with a computer, has a much stronger association with risk than categorical measures.(McCormack and dos Santos Silva, 2006) However, quantitative breast density measurements from mammography must overcome a fundamental difficulty. The aforementioned methods calculate a three-dimensional volumetric breast density from two-dimensional images. This requires an accurate model of compressed breast thickness and the knowledge of imaging parameters such as the compression ratio, paddle tilt, and beam energy to a high degree of precision that is difficult to achieve on clinical systems.(Kopans, 2008) The measurement is also dependent on the angle of the projection. Without a gold standard for comparison, it is challenging to prove the accuracy of these complex methods, though there is ongoing research in this area. (Alonzo-Proulx et al., 2003; Pawluczyk et al., 2003) It is more straightforward to use a three-dimensional imaging modality, such as magnetic resonance imaging (MRI) or computed tomography (CT), to quantify volumetric breast density.

Dedicated cone-beam breast CT is a developing modality that has a promising future in breast imaging.(Glick, 2007) Current breast CT systems generally employ a flat panel detector and image the breast in pendant geometry without the need for compression, offering a pain free experience for the patient. The radiation dose of breast CT is now within the FDA approved limits of conventional two-view mammography, and imaging times are on the order of 10–20 seconds.(Boone et al., 2001; Boone et al., 2004b) Phantom and simulation studies have compared the diagnostic capabilities of breast CT to conventional mammography with promising results.(Chen and Ning, 2002b; Gong et al., 2004; Lai et al., 2007; O'Connell et al., 2010; Yang et al., 2007) And an initial clinical study suggests that breast CT is significantly better than mammography for the visualization of soft tissue lesions.(Lindfors et al., 2008) The benefit of breast CT is that overlapping tissue structures do not obscure the image due to the three-dimensional nature of the modality. This allows for more accurate detection of tumors, improved characterization of lesions, and better segmentation of tissues.(Chen and Ning, 2003)

Anatomical noise induced by overlapping tissues can be removed in CT so that volumetric breast density can be quantified with standard segmentation using a single threshold that separates the glandular and adipose tissues. However, the presence of non-linear artifacts, such as beam hardening and scatter, may significantly decrease image quality. In many cases, the glandular and adipose peaks cannot be fully resolved in the histograms of CT images. This leads to uncertainties in threshold selection while using the standard segmentation method. In addition, such uncertainty results in variations between different observers and even the same observer at different times. The inter- and intra-observer differences associated with histogram thresholding reduce the precision of breast density measurements. Another practical aspect is the processing time for breast density quantification. Unlike planar mammography, breast CT generates many images to depict the 3D anatomy of the breast. The reader must view each layer to choose the best threshold values for image segmentation; this process can be time-consuming. It is desirable to have an automatic segmentation method so that breast density can be quantified objectively and efficiently.

In general, clustering algorithms are computerized methods that take a group of objects and assign them to a number of classes based on a specified similarity criterion. For the case of analyzing grayscale images, the algorithm classifies pixels with like gray values into distinct clusters allowing for the separation of different materials by their attenuation properties. The simplest segmentation algorithm is k-means clustering. Mathematically, for a given set of N pixels p = (p₁,p₂, …, p_N), k-means clustering separates the data into k sets S = {S₁,.S₂, …, S_k} with cluster centers c = (c₁,c₂,…,c_k) in a way that minimizes deviations from the cluster centers. An improved clustering algorithm, fuzzy c-means (FCM) clustering, allows each pixel to be assigned to each of the k classes to varying extents. Since image pixels have finite size, it is likely that multiple tissues are present within a voxel so that the gray value depends on the amount of each tissue; this is termed the partial volume effect. FCM clustering has been widely used in brain MRI image to segment gray matter from white matter.(Ramathilagam et al., 2011; Kannan et al., 2011; Ahmed et al., 2002; Phillips et a.l, 1995) More recently, it was introduced to assess areal breast density in full-field digital mammography.(Keller et al., 2012) It has been suggested that there is a strong association between FCM algorithm-estimated and radiologist-provided areal breast densities for both raw and processed digital mammograms.(Keller et al., 2012) However, the pixel values in a projection mammogram represent a line integral of the attenuation characteristics of the tissue. Thus, it is difficult to give a unique assignment of either glandular or adipose to each pixel. This problem is overcome when FCM clustering is used on breast CT images. Hence, it is interesting to investigate the precision and accuracy of this simple algorithm in breast density quantification.

One fundamental problem with breast density comparison studies is that there is no objective ground truth for comparison.(Kopans, 2008) Past studies have found good correlation coefficients with trained radiologists' visual assessments or with results from another modality, but these results merely show that current measures of breast density are consistent. As an example, consider comparisons between mammography and breast CT. The volumetric density measurements of breast CT are inherently different from areal measurements of mammography. Because of the superposition of tissue structures, areal density measures tend to be higher than volumetric measures on the BI-RADS scale, indicating that the two methods aren't necessarily measuring the same characteristic of the tissue.(Han et al., 2009) In order to evaluate the quantitative accuracy of any measurement of breast density, there needs to be an objective ground truth value that is independent of the imaging process.

In this study, we used the definitive chemical composition of the breasts, in terms of water, lipid and protein contents, as the objective ground truth. We define percent fibroglandular volume (%FGV) as the sum of the volumetric fractions of water and protein, and use it as the gold standard for breast density comparison.(Shepherd et al., 2011; Ducote et al., 2011b; Ding et al., 2012) The relation to breast density can be seen by noting that removing lipid from the %FGV calculation is similar to removing adipose tissue from the two component model. Hence, %FGV is related to the volumetric fraction of non-fatty tissue i.e., breast density. This study aims to evaluate the accuracy of quantitative measures of breast density using both histogram thresholding and FCM clustering applied to breast CT images of ex-vivo post-mortem breasts by comparing the results of image segmentation to the gold standard %FGV determined from chemical decomposition. The use of a definitive measure of breast tissue composition offers an objective comparison for the different segmentation methods.

II. Methods

II.A. Breast computed tomography

An experimental cone-beam CT system was used in this study. The system consisted of a tungsten target x-ray tube (Dynamax 78E) coupled to a Phillips Optimus M200 x-ray generator and a CsI flat-panel detector (PaxScan 4030CB, Varian Medical Inc., Palo Alto, CA) mounted on an optical bench. A high precision motor (Kollmorgen Goldline DDR D062M Danaher Motion, Wood Dale, IL) provided the rotational mechanism and served as the scanning stage. A TTL-logic signal from the flat panel controlled the timing of the x-ray pulse. The synchronizing of this signal with the x-ray pulse was implemented using a field programmable gate array. The detector had an intrinsic pixel size of 0.194 mm, but 2×2 hardware binning effectively increased the pixel size to 0.384 mm. The flat-panel detector dimensions were 40×30 cm², corresponding to an image size of 1024 by 768 pixels. The source-to-detector distance and the source-to-object distance were 1.5 m and 1 m, respectively. The flat-panel detector was operated at 7.5 frames per second while the motor was rotated at 1.0 rpm, acquiring 462 frames over 62 seconds for each scan in angular increments of 0.78°. Images were acquired at a beam energy of 50 kVp and a tube current of 2.5 mAs. A pre-filtration of 2 mm Al was used to shape the x-ray spectrum according to the published information from other pre-clinical dedicated breast CT systems.(Ning et al., 2010) The half-value layer of the beam after filtration was 2.2 mm of aluminum. The exposure at 50 kVp was measured with an ion chamber (Model 2026C, Radcal Corporation, Monrovia, CA)calibrated in the energy range between 50 and 140 kVp. The ion chamber was placed at the isocenter in the open beam. The exposure was measured as 4.4 mGy. Results from a previous Monte Carlo simulation were used to estimate the mean glandular dose (MGD) from the measured exposure.(Boone et al., 2004a). For a breast with 30% glandularity, the current imaging technique led to an estimated MGD of 3 mGy.

II.B. Postmortem breast preparation

The dataset for this study consisted of twenty pairs (left and right) of post-mortem breasts obtained from the Willed Body Program in the School of Medicine at the University of California, Irvine. The breasts were surgically removed from the cadavers to the pectoralis major muscle. The breasts ranged in mass from 136 to 2330 g and volume from 135 to 2466 cm³. The breast densities, as estimated by histogram thresholding of the CT images, ranged from 2% to 65%. This dataset was used for imaging studies over a period of three. The breasts were preserved by freezing, but were removed from the freezer and kept at approximately 4°C one day before the CT scan. The breasts were kept at room temperature for twenty minutes to allow for tissue relaxation before being weighed and packed for imaging. To prevent any water loss and to preserve the shape of the breast during the CT scan, all breasts were wrapped in a thin, very low attenuation, plastic film (GLAD cling wrap, The Glad Production Co., Oakland, CA) and placed in a cylindrical Styrofoam mold of approximately 10 cm in diameter. The skin of the breasts was included during imaging and chemical decomposition.

II.C. Image processing and reconstruction

Image acquisition was performed using proprietary software (Varian’s VIVA). The raw data underwent preprocessing: background normalization, veiling glare correction, and a correction for beam hardening.(Seibert and Nalcioglu, 1984, 1985; Ding et al., 2013) All preprocessing procedures were implemented in ImageJ, which is an open source image processing software package.(Abràmoff et al., 2004) X-ray scatter in the detector and its housing causes a glare artifact in the cone beam CT images. We performed glare corrections for the raw images in the projection domain following the methodology reported by Seibert et al.(Seibert and Nalcioglu, 1984, 1985) Two millimeter thick lead disks of various diameters were placed directly on the flat panel detector surface for imaging. The signals behind the lead disks were used to calculate the scatter radial extent and scatter fraction of the glare kernel that were then used to correct for glare. Beam hardening artifacts were corrected with a method based on the previously reported Signal-to-equivalent Thickness Calibration (STC),(Vavrik and Jakubek, 2009) using a set of BR12 slab phantoms (CIRS, Norfolk, VA, USA) which closely simulate the x-ray attenuation properties of breast tissue. A non-linear rational fitting function was applied directly to the projection images to correct the beam hardening artifact. Further details of the beam hardening and glare correction techniques have been reported in our previous study.(Ding et al., 2013)

After pre-processing the raw images, the data was reconstructed using a Feldkamp-based filtered back-projection algorithm from Exxim's COBRA suite (Exxim Computing Corporation, Pleasanton, CA USA). The CT images were reconstructed with a voxel size of 0.3 mm × 0.3mm × 0.3 mm. The voxels in the final CT images were presented as effective x-ray attenuation coefficients.

II.D. Image-based breast density quantification

The 50 kVp breast CT reconstructions were analyzed to quantify the volumetric breast density. Quantification was achieved by separating glandular and adipose tissues based on the gray values of the reconstructed image. The corrections described in section II.C benefitted this procedure by removing artifacts and increasing the contrast between the two tissues. Two algorithms were chosen for comparison: histogram thresholding and FCM clustering.

II.D.1. Histogram thresholding

Histogram thresholding is a standard technique used to segment medical images. By visual inspection of the reconstructed volume and the corresponding histogram, three thresholds were chosen: one to separate the breast from the background, one to separate adipose and glandular tissue, and one to separate glandular tissue from calcium deposits. The numbers of voxels of each tissue type were counted, and volumetric breast density was calculated as the quotient of glandular volume over the total volume of the breast. The forty images were arranged in a random order for a blind comparison study to prevent bias in the investigation of the right and left breast density correlation. Two medical physicists performed this measurement independently so that inter-observer variability could be assessed. The training session for the observers included five pairs of breast images, which had densities spanning a wide range from approximately 10% to 70%. The histogram thresholding process was also completed using ImageJ. (Abràmoff et al., 2004)

II.D.2. Fuzzy C-Means segmentation

The FCM algorithm is a generalization of the “hard” k-means algorithm to fuzzy logic. Instead of partitioning into distinct sets, each pixel is assigned a vector of membership values giving its level of belonging to each cluster. A membership matrix U is generated such that $\forall i{\sum }_{j=1}^k{u}_{\mathit{\text{ij}}}=1$, i.e. the sum of the cluster membership values for any pixel is one. Each value in the membership matrix can be interpreted as giving the amount of tissue from cluster j present in the ith voxel. The pixel was then assigned to the cluster to which it had the highest membership value. The objective function to be minimized in the fuzzy clustering case is(Pal and Bezdek, 1995)

$${𝒥}_q={\sum }_{i=1}^N{\sum }_{j=1}^{\mathrm{k}}{{\mathrm{u}}_{\text{ij}}}^{\mathrm{q}}{|\mathit{\text{pi}}-\mathit{\text{cj}}|}^2\text{where}1<q<\infty$$ Eq. 1

The parameter q determines the “fuzziness” of the segmentation. In the limit of q = 1, the memberships approach an all or nothing, “hard”, partitioning. Following common practice, this parameter was set to two for this experiment.(Pal and Bezdek, 1995) Eq. 1 was minimized through an iterative process where the best guess of the membership function and cluster centers at each step are given by the following:

$$u_{ij}=\frac{1}{{\sum }_{a=1}^k{(\frac{c_j-p_i}{c_a-p_i})}^{2/(q-1)}}$$ Eq. 2

$$C_j=\frac{{\sum }_{i=1}^N{u}_{\mathit{\text{ij}}}{p}_i}{{\sum }_{i=1}^N{u}_{\mathit{\text{ij}}}}$$ Eq. 3

Most of the images in this study were clustered into five classes although the two largest breasts, with the lowest breast density, required nine clusters. These values were chosen to be the minimum number of clusters needed for successful segmentation as determined by visual assessment. The clusters covered every voxel in the CT volume, including the background, skin, and glandular and adipose tissues. In general, skin was classified into the same cluster as glandular tissue, since the x-ray attenuation coefficients were very similar. After running the FCM algorithm, each cluster was assigned to glandular, adipose, or background to complete the segmentation. From an initial experimental observation, we always assigned only the cluster with highest gray values, i.e. x-ray attenuation coefficients, as glandular tissue for each image. Although the presence of calcifications in some voxels may result in higher gray values than normal glandular tissue, the number of these voxels was too few to form a distinct cluster in the current FCM clustering scheme. The segmentation of the entire breast from the background was accomplished by visually analyzing the separation between cluster centers, since the attenuation of the breast and the packing material were very different. The number of voxels of each tissue were recorded and used to calculate the volumetric breast density.

II.E. Chemical decomposition

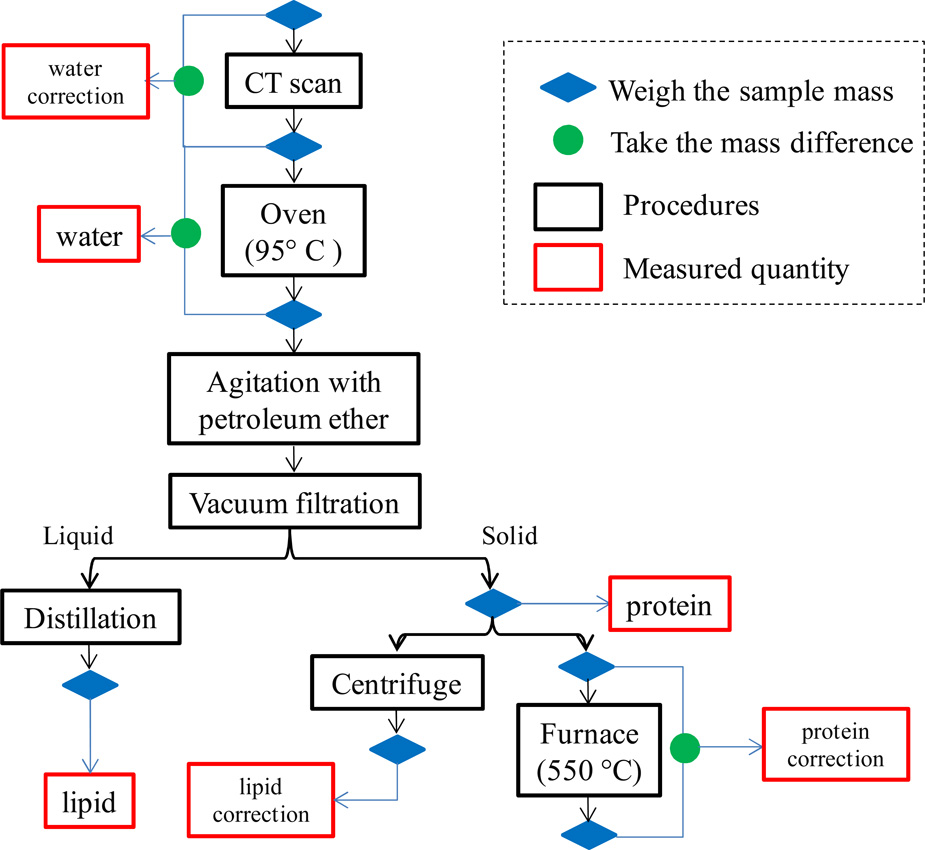
After imaging, each post-mortem breast was decomposed into water, lipid, and protein components using chemical procedures to measure the definitive composition of the breast. This data was the gold standard for the breast density comparison study. The skin was included in the chemical decomposition and the image analysis. The process of chemical decomposition was based on a USDA standardized procedure to determine the mass of water, lipid, and protein in organic tissue.(Agriculture, 2009) A flowchart of the decomposition procedure is given in Fig. 1. Each breast was weighed before and after CT imaging. The mass difference was assigned as water loss and was added to the final water mass after chemical decomposition (water correction in Fig. 1). For the decomposition, each postmortem breast was cut into 5 mm × 5 mm × 5 mm sized pieces and baked in a vacuum oven at approximately 95° C in order to evaporate the water. After at least 48 hours in the vacuum oven, the breasts were weighed at 1 hr intervals until the mass no longer changed. The total change in mass here was assumed to be water. The remaining dry material was mixed with pure petroleum ether and then agitated at 30° C for at least an hour to dissolve the lipid content into the ether solvent. After cooling at room temperature for at least 24 hours, the mixture was vacuum filtered through a Buchner funnel and washed with 1 L of additional ether to remove any remaining lipids. The lipid content was then measured by evaporating the petroleum ether under vacuum distillation and weighing the amount of material left behind.

Figure 1.

A flowchart for the chemical decomposition of the breast tissue. The percentages of the water, lipid, and protein contents were measured primarily from the baking, the distillation, and the filtration steps, respectively, with additional corrections from the other procedures.

The remaining solid in the filter contained mostly protein with small amounts of mineral and lipid. Further analysis was performed to measure the mass percentages of protein, mineral and lipid in the solid. The material was separated into two portions having approximately the same mass. One of them was analyzed, using procedures adapted from the Handbook of Food Analysis(Nollet, 2004), to determine its protein and mineral contents. The sample was placed in a crucible and baked in a furnace at 550 °C for 18 hours to oxidize all carbon-based compounds. The weight lost during this process was used to calculate the mass percentage of protein in the analyzed solid (protein correction in Fig. 1). The final protein mass of each breast was obtained by applying this percentage to the total mass of the remaining solid after vacuum filtration (protein in Fig. 1), assuming that the protein concentration is homogenous. The Ca content of the remaining solid was determined by removing water soluble minerals.

The other portion of the remaining solid was analyzed to determine the amount of residual fat and membrane bound lipids using a method reported by Bligh and Dyer.(Bligh and Dyer, 1959) The sample was mixed with chloroform, methanol, and water, and placed into a centrifuge for 10 min to separate the protein and lipid sediments. The mass percentage of lipid was calculated from the small amount of lipid remaining after removing the chloroform by heating (lipid correction in Fig. 1). The amount of lipid in the solid was calculated by applying this correction to the total mass remaining after filtration (protein in Fig. 1), and was added into the primary lipid mass from the distillation process. The volumetric fractions of water, lipid, and protein for each breast were then determined from the mass, using densities of 1, 0.924, and 1.35 g/cm³ respectively. The %FGV was calculated as the sum of the volumetric fractions of water and protein. Note that the mineral contents have been accurately determined during this analysis. Therefore, they can be safely excluded from the volumetric percentages of water, lipid, and protein.

II.F. Theoretical relation between percent fibroglandular volume and breast density

In this section, the theoretical relationship between percent fibroglandular volume (%FGV = (W + P) / (W + L + P)) and breast density (BD = G / (G + A)) is discussed. In the two-compartment model, the total breast volume is classified into glandular (G) and adipose (A) fractions, while in the three-compartment compositional model, it is categorized into water (W), lipid (L) and protein (P) fractions. Note that these values are fractions of the whole breast tissue, and their sums are normalized, i.e.

$$G+A=W+L+P=1$$ Eq. 4

Both glandular and adipose tissue contain water, lipid and protein, but in different relative amounts. Assuming that the volumetric fractions of water, lipid, and protein in pure glandular and pure adipose tissue are constants represented by W_G, L_G, P_G, W_A, L_A, and P_A, the two models can be related by the following three equations:

$$X=X_G*G+X_A*A\mathit{\text{for}}X\in \{W,L,P\}$$ Eq. 5

Due to the normalization conditions shown in Eq. 4, the volumetric breast density can be expressed as a function of %FGV as:

$$\mathit{\text{BD}}=\frac{\%\mathit{\text{FGV}}-(W_A+P_A)}{(W_G+P_G)-(W_A+P_A)}$$ Eq. 6

Defining %FGV_G = W_G + P_G and %FGV_A = W_A + P_A which correspond to the %FGV of glandular and adipose tissue respectively, the equation of interest becomes

$$BD=\frac{\%\mathit{\text{FGV}}-\%FG{V}_A}{\%{\mathit{\text{FGV}}}_G-\%{\mathit{\text{FGV}}}_A}$$ Eq. 7

The limits of this equation are as expected: breast density is equal to unity when the breast is completely glandular (%FGV = %FGV_G) and is zero when it is completely adipose (%FGV = %FGV_A). Hence, there is a direct linear relationship between the %FGV and breast density. Since all fraction values are positive and glandular tissue generally contains more water and protein than adipose tissue, it can be expected from Eq. 7 that the linear correlation between breast density and %FGV has a positive slope and a negative intercept. Such correlation has been validated in our previous study with ex-vivo bovine tissue samples.(Ducote et al., 2011a) The initial assumption that glandular and adipose tissues have the same composition in all breasts is not exact, as indicated by an early work from tissue chemical analysis.(Woodard, 1986) The uncertainty of the chemical compositions among either glandular or adipose tissue could result in variations in the slope and intercept values in Eq. 7. However, the linear association between the two quantities should remain the same.

II.G. Statistical analysis

To determine the precision of the image segmentation techniques, the volumetric breast density measured from the right breast was plotted with respect to the left breast for each of the techniques. Linear regression and SEE analysis were performed on the data. The accuracy of each algorithm was evaluated through the correlation between the measured volumetric breast density and the %FGV. Finally, the inter-observer variation for the histogram thresholding method has been investigated using two observers and a Bland-Altman plot.

III. Results

III.A Breast tissue chemical decomposition

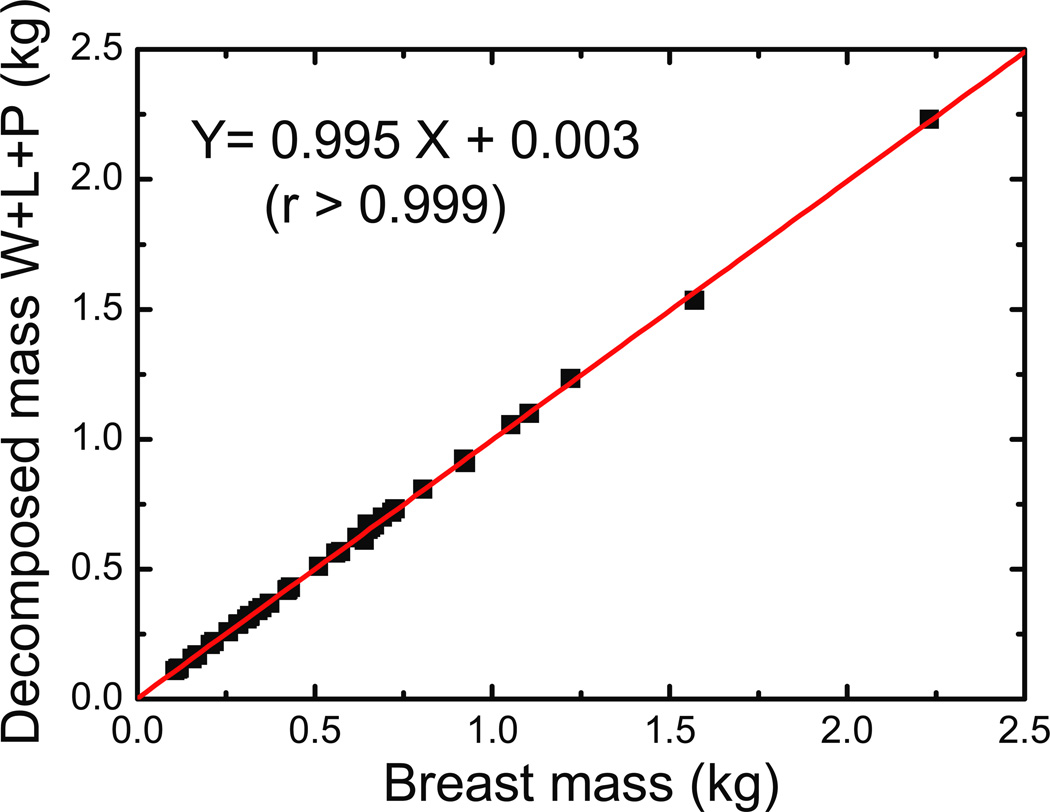
In this study, we used the composition of the post-mortem breasts obtained from chemical analysis as the gold standard for comparing quantitative breast density measurements. Hence, it is critical to evaluate the accuracy of the chemical decomposition. The experimental error was investigated by comparing the pre-imaging mass of each breast with the total mass of water, lipid, and protein after chemical decomposition. The association of the total mass before imaging and after chemical analysis is shown in figure 2. The best-fit line has a slope of 0.995 (±0.003), and an intercept of 0.003. The Pearson’s linear correlation coefficient, r, is larger than 0.999. A paired t-test was performed with the two sets of masses to confirm the null hypothesis. The p-value was calculated to be 0.988, indicating that there are no systematic differences between the two sets of masses. Furthermore, assuming the initial mass as the ground truth, the %RMS error was calculated for each breast. The averaged %RMS was determined to be 1.27%, which sets the limit for the error level of the chemical decomposition.

Figure 2.

Comparison of breast mass before imaging and after decomposition. The decomposed mass was calculated as the sum of the water, lipid and protein masses obtained after chemical analysis. A paired t-test revealed that the difference in breast mass is not significant with a p-value of 0.988.

In the current compositional model, breast tissue was assumed to have three components: water, lipid, and protein. However, human tissue also contains very small amounts of minerals, such as Ca, Na, and K. In Due to the presence of microcalcifications and arterial calcifications, there might be traceable amounts of calcium in breast tissue. In addition, some types of lipid have low solubility in organic solvents and were still present in the remaining solid material after the filtration procedure. For the above reasons, we analyzed the remaining solid further, as described in the methods section. The results suggested that, on average, the remaining solid contained 94.8% protein, 3.2% minerals, and 1.9% lipid by volume. The results of this analysis were used to adjust the final values for the volumetric fractions of water, lipid and protein and the %FGV. It should be noted that the volumetric fraction of protein in the breast is small. The minerals and lipids remaining in the solid material after the initial separation contributed little to the total volumetric fractions of water, lipid and protein.

The measured volumetric fractions of water, lipid and protein contents for all 40 postmortem breasts are summarized in Table 1. The averaged percentages for water, lipid, and protein components were 34.2%, 59.9%, and 5.8%, respectively. The average %FGV was approximately 40.0%, with a wide range from 14.3% to 73.9%. Statistically, due to the small amount of protein, the mean value of %FGV is close to that of the water fraction, and also coincides with the averaged breast density from recent clinical reports.(Boone et al., 2005; Yaffe et al., 2009)

Table 1.

Statistics for the chemical decomposition of the breasts and the breast density measured with histogram thresholding and FCM clustering techniques for all 40 port-mortem breasts.

Components	Median	Mean	Standard Deviation	Minimum	Maximum
Water	30.4%	34.2%	15.1%	12.3%	63.1%
Lipid	65.4%	59.9%	17.8%	26.0%	85.7%
Protein	4.7%	5.8%	2.7%	1.9%	11.4%
%FGV	34.5%	40.0%	17.8%	14.3%	73.9%
BD_Thresh	23.0%	26.9%	15.8%	1.9%	63.9%
BD_FCM	20.8%	24.6%	13.7%	4.4%	51.5%

The whole breast was decomposed into water, lipid, and protein, and, since the chemical compositions of glandular and adipose tissues are very different,(Hammerstein et al., 1979; Woodard and White, 1986) the composition of the whole breast varied largely due to the differences in breast densities. To compare our results with existing values from the literature, one can assume an average breast with a breast density of 25%, and calculate the percentages of the water, lipid, and protein contents from reported values of pure glandular and pure adipose tissues.(Hammerstein et al., 1979; Woodard and White, 1986) Using the data from Woodard and White,(Woodard and White, 1986) the an average breast composition calculated this way was 29% (26%~30%), 63% (60%~67%), and 7% (6~9%) for water, lipid, and protein volume fractions, respectively. The expected ranges for each component are shown in the corresponding parentheses. These results are in good agreement with previously reported results on breast composition.

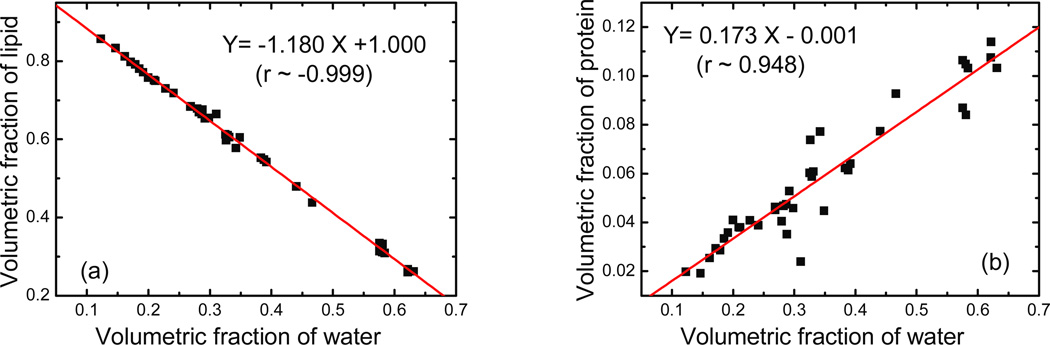
There is a strong correlation among the fractions of water, lipid and protein since breast tissue is composed of mainly these three materials. Examples of these correlations are presented in figure 3 (a) and (b) for the volumetric fractions of lipid and protein as a function of the water fraction. In both cases, the Pearson’s r is close to unity, indicating the strong linear correlation between the three components. As one would expect, the fraction of lipid decreases as the water fraction increases with a slope of −1.180 (±0.010). The protein fraction has a positive correlation with the water fraction with a slope of 0.173 (±0.009), since they both come primarily from glandular tissue.

Figure 3.

The correlation between volumetric fractions of (a) lipid and (b) protein compared to that of water measured during chemical decomposition. The best-fit line parameters are also given in the figures. A negative association was observed for lipid, while a positive slope was observed for protein. This is expected since adipose tissue contains mostly lipid whereas glandular tissue contains mostly water and protein.

III.B Image-based breast density quantification

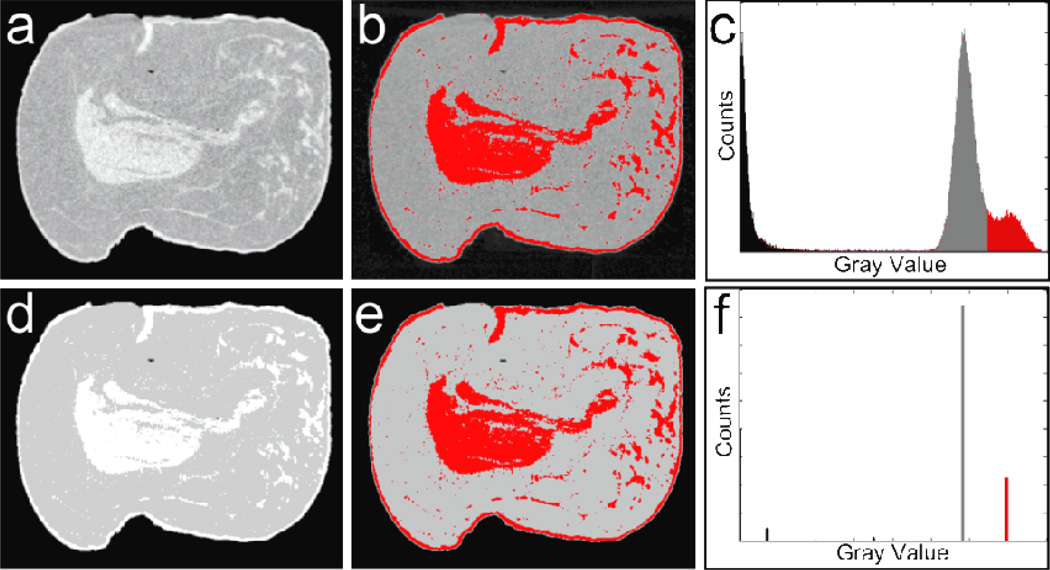
Examples of the image segmentations of a CT image for the histogram thresholding and the FCM clustering methods are depicted in figure 4. The gray values are correlated with the attenuation coefficient of the material; higher pixel values indicate greater attenuation. The gray values of the clustered images are given by the center of the cluster to which that pixel was assigned. The segmented images are visually similar for the two techniques; however, there is a significant difference between the histograms of the raw and clustered images. There are two main peaks in the raw histogram corresponding to the voxels that are predominantly glandular and adipose. Although the centers of the two peaks are well separated, their tails overlap, which leads to the uncertainty in threshold selection. Conversely, FCM was able to cluster the voxels into distinct classes. The two primary classes shown in the histogram represent glandular and adipose tissues. In this case, the segmentation becomes almost definite. The statistics of the image-based breast density quantifications are summarized in Table 1. The average breast density among all forty breasts measured with histogram thresholding and FCM clustering techniques were estimated to be 26.9% and 24.6%, respectively.

Figure 4.

Examples of segmentations for a CT image of a post-mortem breast: (a) the raw reconstructed image; (b) manual glandular selection from histogram thresholding; (c) the raw histogram showing the selected threshold; (d) the raw results of FCM segmentation, (e) the selected glandular clusters, (f) the FCM clustered histogram of the segmented image. Note the similarity in glandular selections and the striking difference in the histograms.

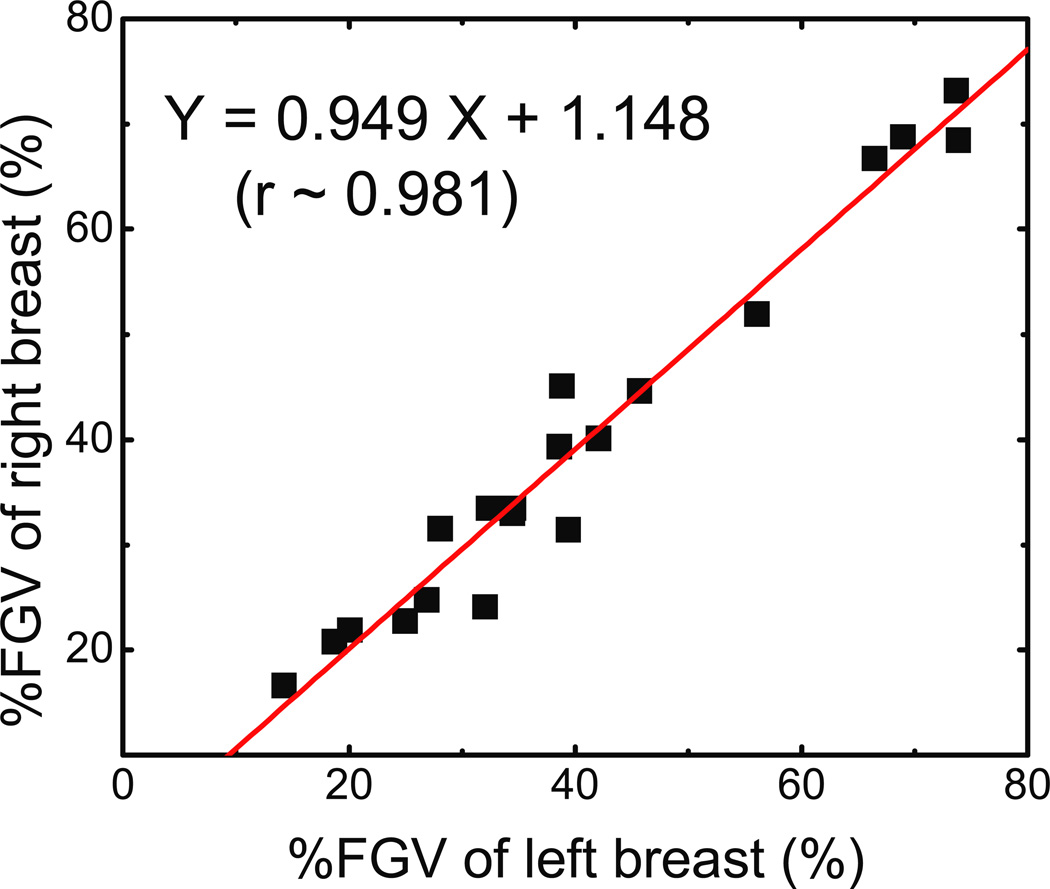
To evaluate precision, we calculated the breast density correlation between the right and left breasts under the assumption that the breast densities are equal for breasts from the same donor. This hypothesis was first tested with the compositional results from chemical analysis. The right and left correlation for the %FGV is plotted in figure 5 for the twenty post-mortem breast pairs. This analysis suggested that there is an excellent correlation between the compositions of the right and left breasts, evidenced by the linear fitting with a slope of 0.949 (±0.044), a Pearson’s r of 0.981, and a SEE of 3.53%.

Figure 5.

Left-right comparison for the percent fibroglandular volume (%FGV). It is expected that the left and right breasts from the same donor would have similar composition. The linear fit shown on the graph supports this expectation with a standard error of 3.53%.

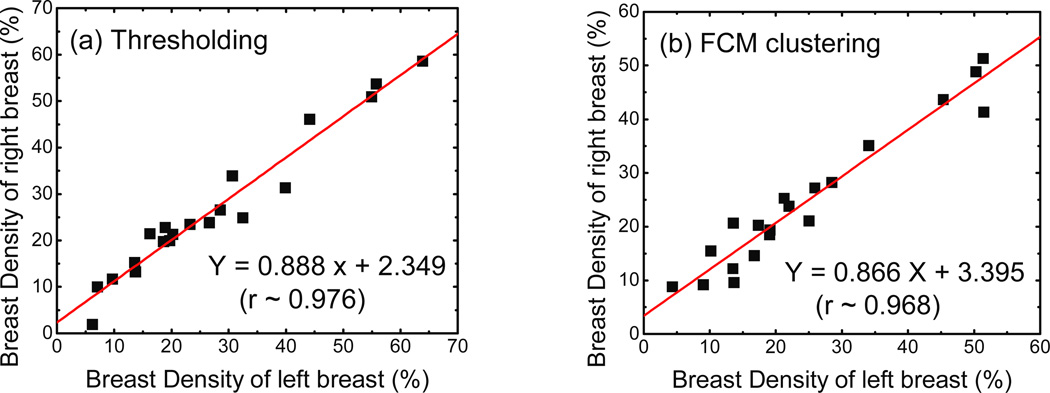
With that in consideration, we plotted the CT breast density results from the right and left breasts of each pair against each other. The results of these correlations obtained from histogram thresholding and FCM clustering techniques are shown in figure 6 (a) and (b), respectively. The slopes were 0.888 (±0.046) and 0.866 (±0.052) with Pearson’s A coefficients of 0.976 and 0.968 for the histogram thresholding and the FCM clustering techniques, respectively. The SEE were calculated to be 3.39% and 3.35%, respectively. These results indicate that the algorithms are reasonably precise in their measurements of breast density.

Figure 6.

Left-right comparisons for breast density measurements from (a) thresholding and (b) FCM segmentation. The linear fits for each method are also shown with standard errors of 3.39% and 3.35% respectively. Note that both methods have a Pearson’s r > 0.95. Hence both methods are precise in their measurements of breast density.

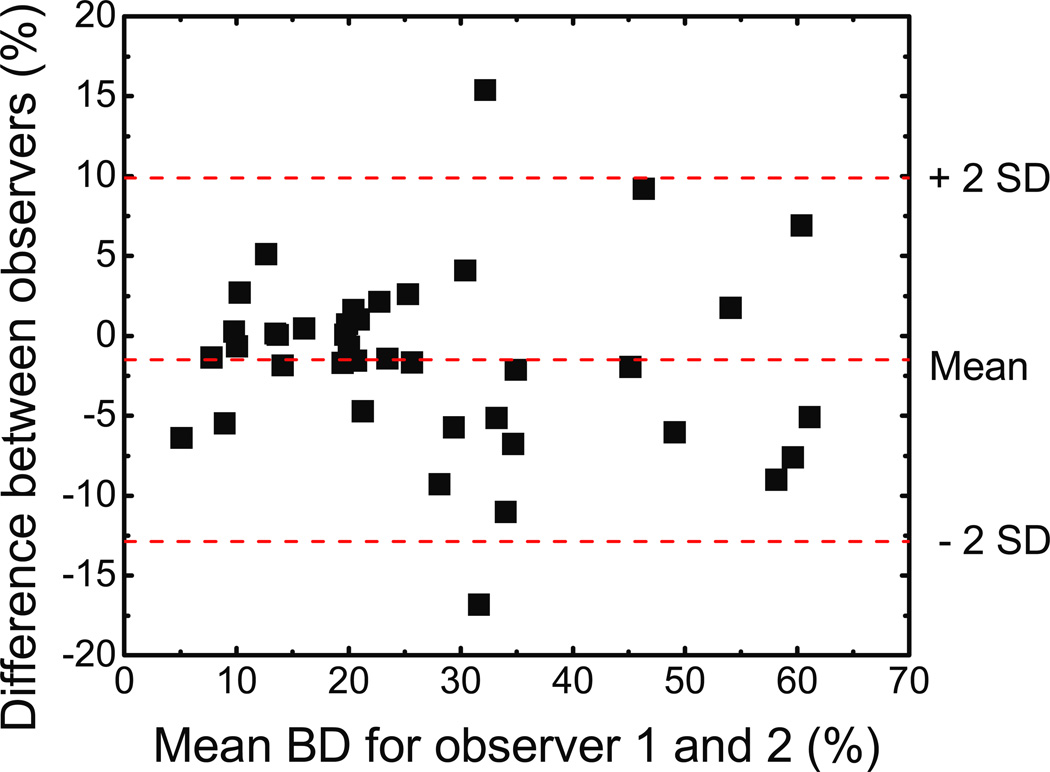
Two trained readers were asked to independently segment the images using the standard histogram thresholding technique. To examine the variability of the threshold selection procedure, a Bland-Altman plot was constructed using their breast density results and is presented in figure 7. For each point, the abscissa is the mean of the two readings and the ordinate gives the difference between them. The mean difference between the readings was 1.5% in breast density and the standard deviation about the mean was 5.7%. In general, the difference between the readings increases with breast density. As the fraction of glandular tissue increased, the peaks in the histogram became more convoluted, increasing the difficulty in choosing thresholds.

Figure 7.

Bland-Altman plot for the two observers for thresholding. The mean difference, depicted by the middle dashed line, was −1.5% in breast density, and the standard deviation (SD) of the differences was 5.7%. The limits of agreement are depicted as dashed lines above and below the middle line. The mean difference is small, but the variation between readers becomes significant as the breast density increases.

III.C Correlations between breast density and %FGV

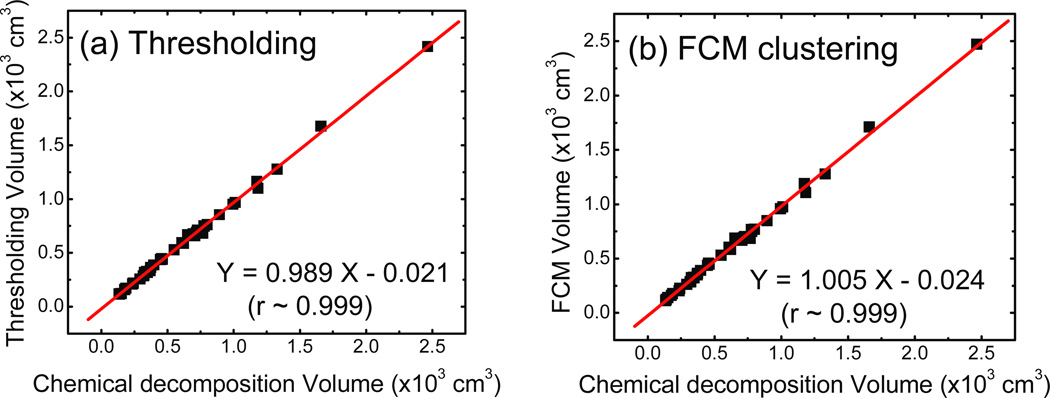
In order to evaluate the accuracy of the image based breast density measurements, we compared the total breast volumes measured in the image domain by each algorithm to those measured from chemical decomposition. The volume correlations are shown in figure 8 (a) and (b) yielding slopes of 0.989 (±0.007) and 1.005 (±0.008) for the histogram thresholding and the FCM clustering techniques, respectively. For both methods, the Pearson’s r was greater than 0.99. Therefore, breast volume measurements from both image-based methods are considered accurate.

Figure 8.

Total breast volume comparison for the (a) histogram thresholding and (b) FCM clustering techniques as a function of the value determined from chemical decomposition. The linear fits both have slopes that are very close to unity and correlation coefficients greater than 0.99. Hence, volume measurements in the image domain are considered accurate.

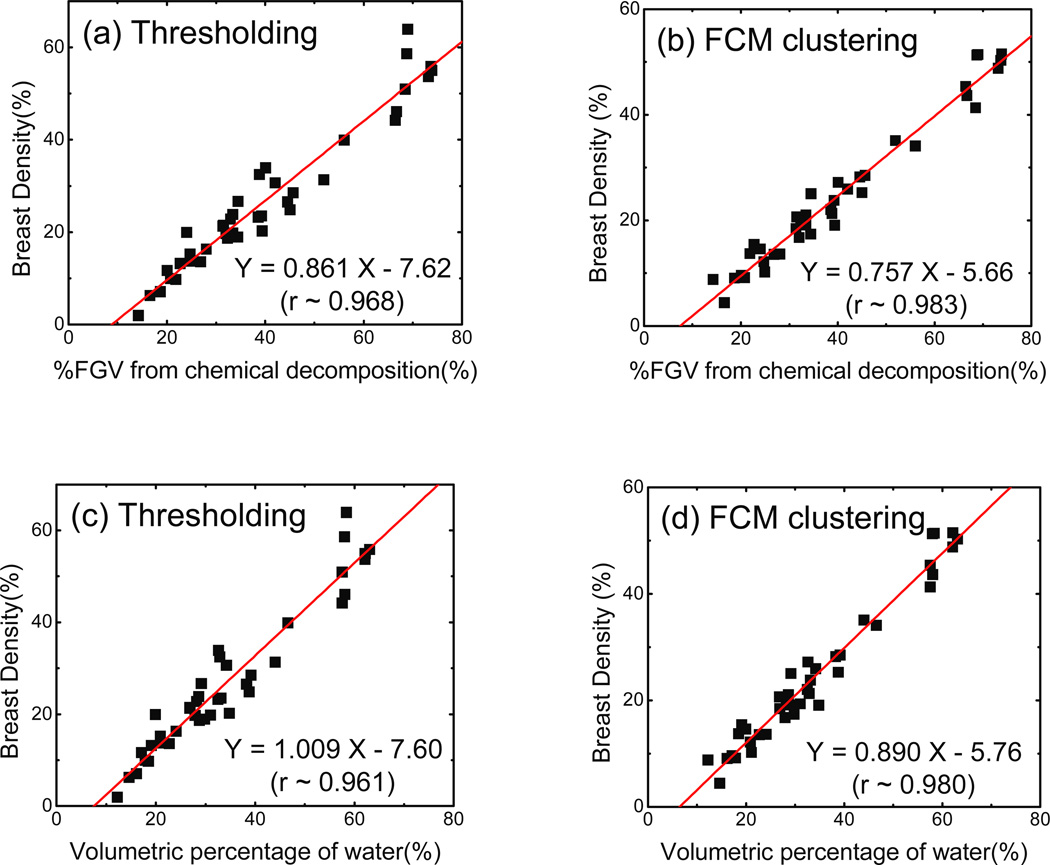
From the discussion presented in II.F, the relationship between volumetric breast density and %FGV is expected to be linear. The results of this study support this expectation and the linear regressions for each of the applied methods are depicted in figure 9 (a) and (b). The slopes of the linear fittings were 0.861 (±0.036) and 0.757 (±0.023) for the histogram thresholding and the FCM clustering techniques, respectively. Negative intercepts in the best-fit lines were observed in both cases in agreement with the model. FCM clustering had a stronger correlation with %FGV as evidenced by a Pearson’s A coefficient of 0.983 as opposed to 0.968 from the histogram thresholding method. The SEE for the thresholding and the FCM clustering techniques were calculated to be 3.92% and 2.45%, respectively. In figure 9(c) and (d) the breast densities from both segmentation methods are compared to the water percentage measured during the chemical decomposition. The correlation between breast density and water fraction in the breast was similar to the correlation between breast density and %FGV since glandular tissue is mostly water.

Figure 9.

Linear correlations between breast densities measured with both (a) the histogram thresholding and (b) the FCM clustering techniques and %FGV from chemical decomposition. The best-fit line and parameters are also given. Both methods correlate strongly with %FGV with Pearson’s A values of 0.968 and 0.983 respectively. The association between breast density and water fraction in the breast is also presented for (c) the histogram thresholding and (d) the FCM clustering techniques. The correlations are very similar to those for %FGV.

IV. Discussions

One of the main purposes of this study was to evaluate breast density measurements from image-based segmentation algorithms by comparing results to an objective ground-truth. Currently, there is no generally accepted procedure for measuring breast density. Most breast density studies employ a comparison across different imaging modalities, including mammography, breast CT, and breast MRI.(Wei et al., 2004) Image-based visual estimations of breast density from experienced radiologists have also been used in some clinical studies. However, none of these techniques can serve as the gold standard for breast density quantification.(Keller et al., 2012) In this paper, we performed a definitive chemical decomposition of post-mortem breasts, in terms of water, lipid, and protein contents, and used the quantitative %FGV as the gold standard for evaluating breast density. This compositional measurement is entirely independent of the imaging process; hence, it offers an objective standard for the comparison of image-based segmentation techniques. The decomposition can be performed with high accuracy and precision on post-mortem specimens using simple analytical chemistry procedures. Our chemical decomposition study on the 40 post-mortem breasts had an error level of approximately 1%, as discussed in section III.A.

Although chemical decomposition is not possible in clinical studies, this technique is a powerful tool for system calibration and breast density comparison studies, since it offers a gold standard. Current comparison studies across imaging modalities suffer from the bias introduced by the differences in the fundamental physical principles of each modality. In general, each imaging modality has its own scaling equation for breast density quantification. The absolute values of breast density recorded with different modalities may vary significantly and, sometimes, are not directly comparable. If a good calibration between image-based breast density and the tissue compositional analysis can be performed for each modality, it might be possible to convert breast densities measured with different imaging techniques into a standardized tissue composition metric (for example water fraction). This way, a unique parameter can be used in breast cancer risk models.

Alternatively, obtaining a gold standard for breast density quantification for a single modality could serve as the starting point for choosing robust algorithms for each modality. Assuming that an accurate algorithm can be found for breast CT, ongoing studies based on breast CT and mammography can then use this accepted method as a gold standard to evaluate mammographic methods. In this way, quantitative measures of breast density amongst different imaging modalities could be compared to evaluate their effectiveness.

In this study, two image-base segmentation techniques were investigated, histogram thresholding and FCM clustering. Thresholding has been an accepted technique for breast density measurement by manually segmenting the glandular and adipose tissues. Our result suggested that, in term of breast density quantification, the FCM–based clustering algorithm performed as well as, if not better than, the standard thresholding method in terms of accuracy and precision. An ideal segmentation algorithm would be precise, fast, and automatic. From this point of view, FCM clustering technique may offer great advantage for breast density quantification in future clinical applications.

The speed of the algorithm influences its applicability in both the clinic and research. In the clinic, it is necessary to receive results quickly in order to increase patient throughput. For research, future studies on breast density using three-dimensional imaging modalities may involve large numbers of patient in order to evaluate the relation between a quantitative measure of breast density and cancer risk. Such large cohort studies would benefit greatly from a fast, automatic algorithm. For the methods studied herein, analyses using histogram thresholding took much longer to complete, requiring training and visual inspection of the complete 3D image set of each breast. On the other hand, the FCM algorithm was implemented to run on the histogram of the 16-bit integer image volumes which considerably decreased the computation time. The clustering and was completed in a few seconds for each image. The speed of the FCM algorithm makes it a very good candidate for use in future studies.

Automation of the segmentation is another important consideration. For the algorithms evaluated in this experiment, FCM clustering was semi-automatic, but histogram thresholding was completely manual requiring selection of thresholds to separate the tissues for each image. Analysis of the variance between two readers for thresholding revealed that there is generally good agreement, but some cases had significant differences of over 10% in breast density. The FCM algorithm changed a continuous selection on the part of the reader into a discrete one. Comparing the histograms in figure 4, it is much simpler to select clusters for FCM than for thresholding. Therefore, the variation induced by observers can be eliminated with FCM. The human interaction in the FCM method also included determining the number of clusters to use for segmentation. The use of five clusters was chosen as being the minimum required for successful segmentation. However, in the case of the two largest breasts, with the lowest breast density, nine clusters were required to segment out the glandular tissue. With fewer clusters, the glandular tissue would not be assigned to its own cluster. Instead the “glandular” cluster became non-localized and included regions of glandular tissue throughout the adipose regions of the breast. The use of additional clusters would further segment the edge pixels of the breast since this is where the gray values varied the most. These additional clusters contained a small number of pixels and hence did not impact the overall breast density significantly with their inclusion or exclusion. Hence, inter-observer variation only has a minimal impact on the FCM segmentation.

The clustering algorithm used in this study may be further improved by making the selection of the number of clusters and image segmentation completely automatic. A fully automatic FCM-based image segmentation technique has been recently reported by Keller et. al. for mammography.(Keller et al., 2012) A fully automated algorithm is more ideal by removing human judgment from the calculations completely. This makes large cohort studies easier to analyze.

In the current study, the post-mortem breasts were imaged at 50 kVp. This tube voltage is much lower than what has been used in conventional clinical CT systems. However, due to the size and the tissue composition of a breast, low tube potential is generally preferable to maximize the contrast between glandular and adipose tissues. The tube voltage was thus selected based on previously reported spectral optimization studies for a dedicated breast CT system.(Chen and Ning, 2002a; Glick et al., 2007; McKinley et al., 2004; Kalender et al., 2012) One limitation is that x-ray scatter within the breast was not corrected in this study. Although there was a large air gap (~ 0.5 m) during imaging, the presence of x-ray scatter may reduce the contrast between the glandular and the adipose tissues, especially for larger breasts. This leads to greater uncertainty in breast density quantification, and contributes partially to the SEE for both segmentation techniques. An algorithm to correct for the body scatter is currently under investigation, so that the accuracy of the breast density quantification with cone-beam breast CT can be further improved.

V. Conclusions

Twenty pairs of post-mortem breasts were imaged with a bench-top cone beam CT flat panel based system at 50 kVp. Volumetric breast densities were quantified with two image-based segmentation methods based on the histogram thresholding and FCM clustering techniques. The breasts were chemically decomposed into water, lipid and protein components soon after imaging. The percent fibroglandular volume determined from the decomposition was used as the gold standard for breast density comparison. Both segmentation methods showed high precision in breast density quantification, evidenced by the good correlation between the right and left breast measurements. There is also a strong linear correlation for the volumetric breast densities obtained from both methods with respect to the tissue compositional metrics, %FGV and water fraction, determined from chemical analysis. The FCM-based image segmentation technique has shown equal or better precision and accuracy in breast density quantification as compared to the histogram thresholding method. The FCM algorithm was also much faster and eliminated the need for a trained reader. A fully automated FCM algorithm has great potential in large cohort breast density studies in breast CT, as it can offer a precise, time-efficient, and objective segmentation. Once an accepted quantitative measure has been found, breast density could be incorporated into assessments of cancer risk to improve their predictive power.